New field-induced single ion magnets based on prolate Er(III) and Yb(III) ions: tuning the energy barrier U_eff by the choice of counterions within an N₃-tridentate Schiff-base scaffold

Abstract

Lanthanides have relatively recently been recognized as ideal candidates for the construction of advanced magnetic materials that would allow for their future applications in spintronics and high-density data storage. Despite enormous progress that deals with the control of magnetic anisotropy and slow relaxation of magnetization in Single Molecule Magnets (SMMs), further improvements are still indispensable to go beyond the ultra-low temperature regime. We have thus prepared four lanthanide complexes ([ErL₂(OTf)(MeOH)₂](OTf)₂ (1), [YbL₂(OTf)₂](OTf) (2), [ErL(NO₃)₃(H₂O)](3) and [YbL(NO₃)₃(MeOH)]·MeCN (4)) with a tridentate Schiff-base ligand L, to unravel magneto-structural correlations in this new family of field-induced Single Ion Magnets (SIMs). Interestingly, as revealed by the single crystal X-ray diffraction, their structures are synthetically tuned by the choice of the applied counterion. The static and dynamic magnetic properties of 1–4 were investigated revealing that all compounds behave as field-induced Single Ion Magnets (SIMs). Their energy barriers U_eff decrease in the sequence: 4, 2, 3, 1, with an order of magnitude difference between the highest and the lowest value. To correlate the observed magnetic properties with spectroscopic data, low-temperature absorption spectroscopy was performed. This has allowed the determination of the energy levels of the Ln(III) ions and the exact composition of the state vectors for the Ln(III) ground multiplets via crystal-field analysis (CFA) and semiempirical superposition model (SPM) approach. Theoretical and magneto-structural correlation studies indicate that one can modulate the heterotopic coordination spheres around the prolate Er(III) and Yb(III) solely with the counterions. This leads to rarely observed high-coordinate SIM species with the LnN_xO_y first coordination sphere (where Ln – Er or Yb, x = 3 or 6, y = 2, 3 or 6). Their performance can be related to the intricate interactions between the electron density on the Ln ion and the crystal field created by the surroundings.

---

1. Introduction

Coordination compounds that exhibit slow relaxation of magnetization of purely molecular origin are named Single Molecule Magnets (SMMs).^1,2 Since the pioneering example of the Mn₁₂ complex³ demonstrated by Novak and co-workers,⁴ SMMs have been the subject of tremendous ongoing interest. Such systems have the potential to become the focal point of the next generation of advanced magnetic materials, thus giving access to high-density data storage devices and quantum computing.^5–10 The major challenge to render these species viable for such applications is to move from the ultra-low temperature regime at which they can currently operate thus constituting the main limitation. Almost a quarter of a century of extensive research has brought us certain guidelines that make the rational design of new SMMs possible.^10–16 Ishikawa and co-workers¹⁷ demonstrated in 2003 that phthalocyanine double-decker Ln complexes (where Ln is Tb(III) and Dy(III)) show the SMM behavior of a different relaxation mechanism than the one observed for d-block metal ions. This has gradually shifted the interest from polynuclear clusters¹⁸ towards mononuclear systems,^11,19,20 thus giving rise to the notion of Single Ion Magnets (SIMs).²¹ While lanthanides,^2,22–25 due to their large magnetic anisotropy,^26,27 have become the metals of choice, especially Kramer's Dy(III) and Er(III) ions, d-block metal ions such as Co(II)^19,28–31 or Fe(II)^19,29,32,33 have also shown to be worth attention.

It turns out that to enhance the effective barrier for magnetization reversal (U_eff) and the blocking temperature (T_B) of a molecular magnet, one needs to focus on suppression of the quantum tunneling of magnetization (QTM)^24,34 and fine-tuning of the relaxation processes.^13,35–37 A simple model was developed by Rinehart and Long, which correlates ligand architecture with Ln electron density, thus enabling the prediction of significant single-ion anisotropies.³⁸ At the same time, the aid of ab initio calculations^26,39–44 has become indispensable to further advance the field of molecular magnetism. It was shown that fine-tuning of the ligand environment^45–49 is indeed possible. However, the resulting SMM properties arise due to a subtle interplay between the ligands’ electrostatic potential^49–52 and the molecular symmetry^53–58 of the species under study. Tang and co-workers demonstrated for instance, that one may significantly modulate the relaxation behavior in Dy(III)-based SIMs via counterions and cis–trans isomerism in a pseudo D_4d coordination environment.⁵⁹ On the other hand, low-coordinate systems^{39,50,52,60–65} mostly based on radical and/or organometallic ligands^64,66–70 were well recognized as promising candidates for SMMs. Their drawback, e.g. chemical instability and cumbersome synthetic methodologies, may be overcome by the generation of molecules, where one or two metal–ligand bonds are significantly shorter than the others, effectively leading to a pseudo-coordination number 1 or 2.^71,72

Although the recently characterized top-notch SIM/SMM examples do show a very significant progress,^{58,59,64,66,72–77} the current leader being the SIM dysprosocenium [(Cp^ttt)₂Dy][B(C₆F₅)₄] congener with T_B reaching an unprecedented value of 60 K,^68,69 it is the poor understanding of relaxation mechanisms that hinders further progress.^13,35–37 Better understanding may be achieved due to close collaboration of theorists and experimentalists. Such an advancement will be contingent on the detailed magneto-structural correlations obtained for small libraries of isostructural compounds.^78–80 Thus such small steps may eventually lead to the application of SMMs in quantum devices.

Counterions are often used as a means to influence the characteristics of SMMs,^59,81–84 though cases when they actively participate in the first coordination sphere of SIMs, thus tuning the composition of the obtained framework, are rare. Based on our previous experience in the construction of lanthanide Schiff-base complexes with tridentate binding subunits^80,85–87 we have envisaged that the N₃-donor ligand L (Fig. 1)⁸⁸ should form monometallic lanthanide complexes of potentially different stoichiometry.

Fig. 1 Schematic representation of the Schiff base ligand L utilized in the present study. The ligand is shown in its cisoidal conformation, which is found in Ln-SIMs synthesized herein.

A Cambridge Structural Database (CSD) search revealed (cf. section 3.1 and Tables S4, S5, S8, S9‡) that the anticipated LnN_xO_y (where Ln – Er or Yb, x = 3 or 6, y = 2, 3 or 6) coordination sphere is rarely encountered, and there are hardly any examples of SIMs in such an environment. Our aim was to determine whether we can observe the SIM behavior in such a Ln high-coordination environment and if it is possible to fine-tune their properties via the choice of native counterions.

Herein, we present the synthesis as well as structural and magnetic characterization of four new lanthanide complexes, formed between the tridentate ligand L (2-(1-methyl-2-((1-methyl-1H-imidazol-2-yl)methylene)hydrazinyl)pyridine) and nitrate and triflate salts of the prolate Er(III) and Yb(III) metal centers. It was found that the ligand to metal stoichiometry of the obtained complexes depends directly on the counterion, thus giving rise to mononuclear compounds [ErL₂(OTf)(MeOH)₂](OTf)₂ (1), [YbL₂(OTf)₂](OTf) (2), [ErL(NO₃)₃(H₂O)](3) and [YbL(NO₃)₃(MeOH)]·MeCN (4) with ErN₆O₃ (1), YbN₆O₂ (2) and LnN₃O₆ (3 and 4) coordination spheres. This in turn affects their SMM properties, with U_eff and relaxation characteristics arising due to a subtle interplay of the Ln ground states and the spherical charge distribution of coordinated ligands. Low temperature optical absorption spectroscopy as well as theoretical calculations were performed, thus enabling a deeper explanation of the observed results.

2. Experimental

2.1 Reagents and physical measurements

All manipulations were performed under aerobic conditions unless otherwise stated. The metal salts, organic compounds and solvents were supplied by Aldrich and POCH. All chemicals mentioned above were of analytical grade quality and were used as obtained without further purification. Microanalyses were performed using a PerkinElmer 2400 CHN microanalyser. IR spectra were obtained with a PerkinElmer 580 spectrophotometer and peak positions are reported in cm⁻¹. ESI mass spectra were determined in methanolic solution with c = ∼10⁻⁴ M using a Waters Micromass ZQ spectrometer. Powder X-ray diffraction (PXRD) analyses were performed using a Bruker AXS D8 Advance diffractometer. Magnetic measurements were performed using a Quantum Design MPMS-XL magnetometer on ground crystalline samples sealed in gelatine capsules. The magnetic susceptibility data were corrected for the diamagnetic contribution of the sample holder and of the sample itself. In the latter case Pascal constants were used.⁸⁹ Optical electronic absorption spectra were recorded in the 3500–50 000 cm⁻¹ range at 4.2 K on a Cary-5000 UV-Vis-NIR spectrophotometer, equipped with an Oxford Instrument model CF1204 cryostat.

2.2 Synthesis and characterization of the lanthanide complexes

Ligand L was prepared as reported by us previously.⁸⁸ Varying the L : Ln(III) salt ratio has not led to compounds that differ in stoichiometry but only to a decrease in the overall yield. Hence, the procedure described below allows for the most efficient synthesis of compounds 1–4. For complexes 1 and 2 the molar ratio of the ligand to the corresponding metal salt was 2 : 1.

To a solution of L (101.0 mg, 0.46 mmol) in the mixture of MeOH/MeCN (1 : 1 v : v) the appropriate metal salt (0.23 mmol) was added (Er(CF₃SO₃)₃1 or Yb(CF₃SO₃)₃2). Yellow solutions formed instantly and the reaction mixtures were stirred for 24 hours at room temperature. After evaporation of solvents under reduced pressure, the residues were dissolved in a minimum volume of MeOH/MeCN (1 : 1 v : v) and precipitated by excess of Et₂O. Yellow solids were filtered via suction filtration and dried under vacuum.

[ErL₂(OTf)(MeOH)₂](OTf)₂ (1). Yield: 132.79 mg, 54.2%. Crystals suitable for X-ray analysis were obtained via slow diffusion methods in a MeOH/iPr₂O system. IR (KBr, cm⁻¹): ν_broad(O–H)_methanol 3438; ν(C–H)_arom 3025; ν_as(C–H)_aliph 2983; ν_s(C–H)_aliph 2947; ν(C=C) 1677, 1614, 1504; ν(C=N) 1443, 1328; δ(CH₃) 1383; ν_as(SO₃) 1293; ν_as(CF₃) 1256, 1245; ν_s(CF₃) 1172; ν_s(SO₃) 1030; γ(C–H)_arom 1023, 997, 889, 776. ESI-MS(+) m/z (%): 216 (100) [HL]⁺, 431 (15) [(HL)₂]⁺, 679 (10) [ErL(CF₃SO₃)₂]⁺.

Anal. calc. for [Er(C₁₁H₁₃N₅)₂(CF₃SO₃)(CH₃OH)₂] (810.92): C, 37.03; H, 4.23; N, 17.27; S, 3.95; found: C, 36.90; H, 4.18; N, 17.18; S, 3.89%.

[YbL₂(OTf)₂](OTf) (2). Yield: 138.04 mg, 56.0%. Crystals suitable for X-ray analysis were obtained via slow diffusion methods in a MeOH, MeCN/iPr₂O system. IR (KBr, cm⁻¹): ν_broad(O–H)_methanol 3467; ν(C–H)_arom 3147; ν_as(C–H)_aliph 2984; ν_s(C–H)_aliph 2936; ν(C=C) 1602, 1566; ν(C=N) 1466, 1318; δ(CH₃) 1363; ν_as(SO₃) 1289, ν_as(CF₃) 1247, 1221; ν_s(CF₃) 1161; ν_s(SO₃) 1027; γ(C–H)_arom 986, 869, 799, 749. ESI-MS(+) m/z (%): 216 (100) [HL]⁺, 687 (30) [YbL(CF₃SO₃)₂]⁺, 902 (40) [YbL₂(CF₃SO₃)₂]⁺. Anal. calc. for [Yb(C₁₁H₁₃N₅)₂(CF₃SO₃)₂] (901.70): C, 31.97; H, 2.91; N, 15.53; S, 7.11; found: C, 32.05; H, 2.90; N, 15.60; S, 7.02%.

For complexes 3 and 4 the molar ratio of the ligand to the corresponding salt was 1 : 1. To a solution of L (40.0 mg, 0.18 mmol) in the mixture of MeOH/MeCN (1 : 1 v : v) the appropriate metal salt (0.18 mmol) was added (Er(NO₃)₃·5H₂O – 3 and Yb(NO₃)₃·5H₂O – 4). Yellow solutions formed instantly and the reaction mixtures were stirred for 24 hours at room temperature. After evaporation of solvents under reduced pressure, the residues were dissolved in a minimum volume of MeOH/MeCN (1 : 1 v : v) and precipitated by excess of iPr₂O. Yellow solids were filtered via suction filtration and dried under vacuum.

[ErL(NO₃)₃(H₂O)] (3). Yield: 74.28 mg, 62.0%. Crystals suitable for X-ray analysis were obtained via slow diffusion methods in a MeOH/iPr₂O system. IR (KBr, cm⁻¹): ν_broad(O–H)_methanol 3426; ν(C–H)_arom 3147; ν_as(C–H)_aliph 2985; ν_s(C–H)_aliph 2972; ν(C=C) 1670, 1613, 1540; ν_as(NO₂) 1460, 1450; ν(C=N) 1439, 1325; δ(CH₃) 1384; ν_s,broad(NO₂) 1295, 1237; ν(NO) 1051; γ(C–H)_arom 1110, 1030, 1006, 997, 882, 773; δ(NO) 811. ESI-MS(+) m/z (%): 216 (100) [HL]⁺, 199 (10) [ErL(H₂O) − H⁺]²⁺, 230 (10) [ErL(NO₃)(H₂O)]²⁺, 253 (10) [ErL(NO₃)₂ + H⁺]²⁺. Anal. calc. for [Er(C₁₁H₁₃N₅)(NO₃)₃(H₂O)] (586.54): C, 22.52; H, 2.58; N, 19.10; found: C, 22.41; H, 2.67; N, 19.03%.

[YbL(NO₃)₃(MeOH)]·MeCN (4). Yield: 80.28 mg, 65.0%. Crystals suitable for X-ray analysis were obtained via slow diffusion methods in a MeOH, MeCN/iPr₂O system. IR (KBr, cm⁻¹): ν_broad(O–H)_methanol 3422; ν(C–H)_arom 3091; ν_as(C–H)_alif 2992; ν_s(C–H)_alif 2973; ν(C=C) 1668, 1614, 1503; ν_as(NO₂) 1461, 1450; ν(C=N) 1439, 1325; δ(CH₃) 1384; ν_s,broad(NO₂) 1297, 1238; ν(NO) 1051; γ(C–H)_arom1111, 1031, 1007, 995, 881, 773, 713; δ(NO) 811. ESI-MS(+) m/z (%): 216 (100) [HL]⁺, 242 (20) [YbL(NO₃)(MeOH)]²⁺, 273 (10) [YbL(NO₃)₂(MeOH) + H]²⁺. Anal. calc. for [Yb(C₁₁H₁₃N₅)(NO₃)₃ (CH₃OH)] (606.36): C, 23.77; H, 2.83; N, 18.48; found: C, 23.90; H, 2.94; N, 18.52%.

2.3 X-ray crystallography

Diffraction data were collected by the ω-scan technique on Agilent Technologies’ four-circle diffractometers on Xcalibur with an Eos CCD detector and graphite-monochromated MoKα radiation (λ = 0.71069 Å): 2 at room temperature, 3, 4 at 120(1) K and 1 at 100(1) K. The data were corrected for Lorentz-polarization as well as for absorption effects.⁹⁰ Precise unit-cell parameters were determined by a least-squares fit of reflections of the highest intensity, chosen from the whole experiment. The structures were solved with SIR92⁹¹ and refined with the full-matrix least-squares procedure on F² by SHELXL-2013.⁹² The scattering factors incorporated in SHELXL97 were used. All non-hydrogen atoms were refined anisotropically; hydrogen atoms in the complexes were placed in idealized positions and refined as a ‘riding model’ with isotropic displacement parameters set at the value 1.2 (1.5 for methyl or hydroxyl groups) times the factor U_eq of appropriate carrier atoms. In the structures of compounds 1 and 2 voids filled with diffused electron density were found; as the modelling of solvent molecules was in these cases unsuccessful, the SQUEEZE procedure⁹³ was applied. Crystals of compounds 3 and 4 were found to be two-component twins and this was taken into account both in data reduction and in structure refinement.

Crystallographic data (excluding structure factors) for structural analysis have been deposited with the Cambridge Crystallographic Data Centre, no. CCDC 1052304 (1), 1435579 (2), 1435585 (3), and 1435586 (4).‡

1: C₂₅H₃₄ErF₃N₁₀O₅S 2(CF₃O₃S), M_r = 1109.08, monoclinic, P2₁/n, a = 10.9049(4) Å, b = 15.0238(4) Å, c = 27.3563(9) Å, β = 100.350(4)°, V = 4408.9(3) ų, Z = 4, d_x = 1.67 g cm⁻³, F(000) = 2204, μ = 2.15 mm⁻¹, 18 023 reflections collected, of which 9184 were unique (R_int = 0.046), 8398 with I > 2σ(I), R(F)[I > 2σ(I)] = 0.070, wR(F²)(I > 4σ(I)) = 0.170, R(F)[all data] = 0.075, wR(F²)[all data] = 0.173, S = 1.12, max/min Δρ in the final ΔF map: 5.67/−3.19 e Å⁻³.

2: C₂₄H₂₆F₆N₁₀O₆S₂Yb CF₃O₃S, M_r = 1050.78, triclinic, P1̄, a = 11.3018(5) Å, b = 13.3845(6) Å, c = 14.5613(4) Å, α = 96.292(3)°, β = 99.214(3)°, γ = 107.796(4)°, V = 2040.55(15) ų, Z = 2, d_x = 1.71 g cm⁻³, F(000) = 1034, μ = 2.54 mm⁻¹, 21 875 reflections collected, of which 7183 were unique (R_int = 0.039), 6382 with I > 2σ(I), R(F)[I > 2σ(I)] = 0.056, wR(F²)(I > 4σ(I)) = 0.159, R(F)[all data] = 0.062, wR(F²)[all data] = 0.163, S = 1.31, max/min Δρ in the final ΔF map: 3.23/−1.11 e Å⁻³.

3: C₁₁H₁₅ErN₈O₁₀, M_r = 586.57, triclinic, P1̄, a = 8.3705(7) Å, b = 9.3039(7) Å, c = 12.7182(9) Å, α = 102.222(6)°, β = 103.692(7)°, γ = 102.763(6)°, V = 901.39(13) ų, Z = 2, d_x = 2.16 g cm⁻³, F(000) = 570, μ = 4.73 mm⁻¹, 5555 reflections collected, of which 3145 were unique (R_int = 0.068), 2826 with I > 2σ(I), R(F)[I > 2σ(I)] = 0.057, wR(F²)(I > 4σ(I)) = 0.149, R(F)[all data] = 0.065, wR(F²)[all data] = 0.154, S = 1.23, max/min Δρ in the final ΔF map: 4.16/−2.24 e Å⁻³.

4: C₁₂H₁₇N₈O₁₀Yb C₂H₃N, M_r = 647.43, triclinic, P1̄, a = 8.1752(5) Å, b = 11.5352(9) Å, c = 13.1045(10) Å, α = 66.989(7)°, β = 72.978(6)°, γ = 85.535(5)°, V = 1086.69(15) ų, Z = 2, d_x = 1.98 g cm⁻³, F(000) = 634, μ = 4.38 mm⁻¹, 4347 reflections collected, 3960 with I > 2σ(I), R(F)[I > 2σ(I)] = 0.049, wR(F²)(I > 4σ(I)) = 0.159, R(F)[all data] = 0.058, wR(F²)[all data] = 0.162, S = 1.39, max/min Δρ in the final ΔF map: 3.27/−5.07 e Å⁻³.

3. Results and discussion

3.1 Synthesis of lanthanide congeners and their single crystal X-ray characterization

The reaction of trivalent lanthanide salts Ln(OTf)₃ and Ln(NO₃)₃ where Ln – Er (1, 3) and Yb (2, 4) with an N₃-tridentate Schiff-base ligand L in methanol/acetonitrile 1 : 1 mixture leads to monometallic assemblies of the following formulae, [ErL₂(OTf)(MeOH)₂](OTf)₂ (1), [YbL₂(OTf)₂](OTf) (2), [ErL(NO₃)₃(H₂O)](3) and [YbL(NO₃)₃(MeOH)]·MeCN (4).

Crystal structures of 1 (a), 2 (b), 3 (c) and-4 (d) are shown in Fig. 2.

Fig. 2 The anisotropic-ellipsoid representation of the synthesized lanthanide complexes. Ellipsoids are drawn at the 50% probability level, hydrogen atoms are shown as spheres of arbitrary radii. For clarity only relevant atoms are labelled.

It is particularly interesting that utilization of the appropriate counterion allows tuning the stoichiometry of the formed assemblies: triflates always lead to the complexes with the final Ln : L ratio 1 : 2, whereas nitrates lead to the ratio 1 : 1, irrespective of the applied Ln : L ratio during the synthesis. For instance, when 1 mole of Er(OTf)₃ reacts with 3 moles of the Schiff base L, excess ligand stays unreacted even upon heating and application of solvothermal reaction conditions. Conversely, reaction in the equimolar ratio leads to small amounts of crystalline material which was established to be identical to 1, however with significant loss in the overall reaction yield.

In the triflate series, two molecules of ligand L coordinate to the Ln(III) centre by nitrogen atoms of pyridine, imine as well as imidazole moieties with distances in the range from 2.40 to 2.57 Å. The remaining coordination sites are filled by oxygen atoms that come from one monodentate OTf⁻ counterion and two molecules of methanol (1) or solely two triflates (2), thus giving rise to coordination numbers 9 and 8, respectively. Such a decrease in the coordination number for the Yb(III) analogue, together with the shortening of Ln–N and Ln–O bonds as well as distortions from planarity of the ligand L (Table S1‡), nicely demonstrate the lanthanide contraction phenomenon.⁹⁴

Calculations using SHAPE software,^95,96 which are based on the continuous shape measurements (SChM),⁹⁷ were conducted for the sake of symmetry comparisons as well as to gain deeper knowledge about structure/property relations with regard to the observed SIM behaviour. Note that when S = 0 it corresponds to a perfect polyhedron; the larger the value, the greater the deviation from the ideal geometry. The results (Tables S2 and S3‡) indicate that the Er(III) coordination polyhedron in 1 is best described as a tricapped trigonal prism (S = 0.971 – D_3h site symmetry); nonetheless, a similarly low value from SHAPE is obtained for capped square antiprism geometry (S = 1.129 – C_4v site symmetry). 2 shows more pronounced preference towards one shape and thus the coordination sphere around Yb(III) may be classified as a triangular dodecahedron (S = 1.845 – D_2d site symmetry).

It is also worth noting that search in CSD revealed that such erbium(III) and ytterbium(III) analogues are rarely observed. Apart from the herein presented compounds, there are only 10 reported unique structures that adopt the ErN₆O₃ coordination environment (eight of which are monometallic), whereas the YbN₆O₂ coordination sphere was observed in 26 compounds (fourteen of which are monometallic) (Tables S4 and S5‡). From the point of view of molecular similarity, there are only two compounds exhibiting significant structural resemblance to 1 (ITOCUR, ITODIG),⁹⁸ which belong to the family of N₃-tetrazolate/β-diketonate heteroleptic complexes. It is encouraging to see that such a ligand arrangement indeed is responsible for SIM behaviour, which was observed therein; hence additional comparison is possible (cf. section 3.2) Conversely, neither of the searched N₆O₂ eight-donor Yb(III) centres that are similar to 2 were found to display SIM behaviour, which means that 2 is a unique example of a Yb(III) compound that displays slow relaxation of magnetization (cf. section 3.3).

In the nitrate series, coordination of only one ligand L to each Ln(III) centre finds reflection in the lower degree of geometrical constriction. Hence 3 and 4 exhibit similar geometry that also involves three nitrates (one in mono-, two in bidentate modes) and one solvent molecule (H₂O or MeOH). The same coordination number 9, an almost fully planar N₃-tridentate Schiff base ligand L as well as similar bond lengths (Tables S6 and S7‡), show that lanthanide contraction does not apply for nitrate analogues. Moreover, noticeable similarities are found when SHAPE calculations are performed: the coordination polyhedron in both cases is most similar to the capped square antiprism, which indicates Ln site symmetry C_4v (S = 1.586 for 3 and S = 1.718 for 4). Pronounced differences are noticed, however, when we consider that ligand L, together with an equatorial nitrate as well as solvent molecule, constitutes a five-membered basal plane. One can thus discriminate between the binding modes of axial nitrates (compare schematic representations in Tables S6 and S7‡): two κ²-O₂NO for 3 represent a highly symmetric character and thus should contribute to the stabilization of the easy axis of magnetization along that direction. A similar situation happens for 4, i.e. the equatorial ligand field of nitrogen donor atoms (from L) interacts with the prolate electron density of Yb(III) and, together with axial counterions, favours the generation of the energy barrier for the reversal of the magnetization U_eff. The unsymmetrical character of the axial nitrates might contribute to the higher U_eff value of 4 than 3; nonetheless additional factors play the role here that are related to the relaxation processes. In fact, 4 was determined to exhibit the highest U_eff among compounds 1–4 (cf. section 3.3).

A CSD search (Tables S8 and S9‡) shows that such a nitrate mediated LnN₃O₆ coordination geometry (Er in 3 and Yb in 4) is more often encountered than the triflate mediated LnN₆O₃ (1)/LnN₆O₂ (2). There are 45 (18 monometallic) instances in the case of 3 (Er) and 54 (33 monometallic) for 4 (Yb). The most important result is that from all those compounds, there is only one instance of the field-induced SIM – [Yb(Murex)₃] (ZIXHUE – analogue of 4),⁹⁹ whereas it is highly plausible that some of the remaining ones (cf. Tables S8 and S9‡) could also exhibit SMM behaviour. With regard to the YbN₃O₆ family, Feng et al. found that from two isostructural Ln(N₃-mer)(hfac)₃ compounds (Ln – Dy and Yb, hfac – 1,1,1,5,5,5-hexafluoroacetylacetonate, N₃-mer – 4,5-bis[2,6-di(pyrazol-1-yl)-4pyridylmethylthio]-4′,5′ ethylenedithiotetrathiafulvene) only the dysprosium analogue exhibited slow relaxation of magnetization.¹⁰⁰ This stands in contrast with the herein synthesized 4, which exhibits field-induced SIM characteristics (cf. section 3.3). This clearly shows that one must also consider the electronic distribution of the negatively charged ligands for rational design of SMM behaviour.¹⁰¹

The results of the CSD survey as well as comparison of symmetry aspects therein enable us to postulate that in the case of the prolate lanthanide cations, a change of β-diketonates to nitrates could be beneficial for the construction of tunable magnetic materials with high-coordination numbers. What is more, it was noticed that equatorial positions in such nitrate complexes i.e. specifically the ones that are opposite to the N₃ tridentate ligand are particularly prone to eventual exchange with solvent molecules (e.g. H₂O, ROH, DMSO, DMF) leading to monodentate nitrates or their total extrusion from the coordination sphere.¹⁰² Bearing this in mind, an additional way of tuning the SMM properties and relaxation processes can be envisaged, namely by tuning the symmetry of the coordination sphere around the Ln(III) centre.

Concerning the crystal packing of the lanthanide complexes under study, 1 belongs to the monoclinic P2₁/n space group, whereas the remaining ones (2, 3 and 4) crystallize in the triclinic P1̄ space group. There are obviously differences in the crystal packing, but in general the electrostatic interactions and weak directional forces (e.g. H-bonding, π–π, CH⋯π interactions) are responsible for the crystals’ architecture. A somewhat globular shape of the complexes allows for many motifs. The structures with charged components (1, 2) can, in general, be described as the layers or bilayers of cations with anionic layers between them. When the neutral species are present (3, 4) there are voids in the crystal structures filled by solvent molecules, well-defined or diffused (cf. example in Fig. 3).

Fig. 3 van der Waals sphere representation of 4 as seen along the crystallographic a-axis. For clarity the acetonitrile molecules are not shown.

The type of counterions used is also responsible for the shortest intermetallic Ln–Ln interactions. Poorly coordinating triflates contribute to the isolation of metal ions (9.5–9.8 Å); hence magnetic properties in 1 and 2 are dominated by their SIM character. On the other hand, Er–Er and Yb–Yb distances in 3 and 4, respectively, are significantly shorter (5.9–6.0 Å), which is a consequence of equatorially coordinated nitrate and solvent molecules. Although in principle one could find the exchange interaction pathway between the Ln(III) centres in compounds 3 and 4, the magnetic data do not support that hypothesis.

3.2 DC magnetic properties

Erbium(III)^{52,61,62,101,103,104} and ytterbium(III)^35,105–107 based-SMMs are known in the literature; however, our CSD survey (cf. above) shows that examples of SIM properties in compounds with the LnN_xO_y subunit (where Ln – Er or Yb, x = 3 or 6, y = 2, 3 or 6) are hardly observed. Satisfactory elementary analysis as well as PXRD confirm the identity of the microcrystalline samples 1–4, including their phase purity (Fig. S1‡).

The static DC magnetic properties of complexes 1–4 were measured in the temperature range 1.8–300 K, under an applied magnetic field of 0.5 T. The dependence of the product function χ_mT versus T is shown in Fig. S2 and S3.‡ On cooling, χ_mT steadily decreases down to 1.8 K for each complex due to depopulation of the excited sublevels of Er(III) and Yb(III) ions. This effect arises from the splitting of the ground terms ⁴I_15/2 and ²F_7/2 of Er(III) and Yb(III) ions, respectively, due to the crystal field interactions. The dependence of the magnetization for each complex 1–4 was measured at 2 K in the magnetic field range 0–5 T (Fig. 4).

Fig. 4 Field dependence of the magnetization for compounds 1–4 at T = 2 K.

Comparison of the DC magnetic data for the complexes 1–4 with the theoretical values as well as the values reported in the literature (Table S10‡) shows good agreement.

3.3 AC magnetic properties

Dynamic AC magnetic susceptibility measurements were performed as a function of temperature and frequency for all complexes. In the absence of a DC field no SMM behaviour was observed for erbium (1, 3) or ytterbium (2, 4) complexes. These results indicate that the magnetization relaxation time (τ) is much shorter than the reciprocal of the angular frequency of the AC field (1/2πν). Magnetization follows the AC magnetic field due to QTM.^98,108 It is well-known that the QTM effect can be suppressed by the application of a small DC field.^99,109,110 Therefore, when the AC measurements were performed in the presence of an external DC field of 0.1 T, the observed dependence of the χ′′_M signals on frequency (Fig. 5) and temperature (Fig. 6) was characteristic of the thermally assisted relaxation processes and single-ion molecular magnet (SIM) behaviour.^61,98

Fig. 5 Frequency-dependence of the out-of-phase susceptibilities for complexes 1 (a), 2 (b), 3 (c), and 4 (d) in an applied DC field of 0.1 T (the solid lines are guides to the eye).

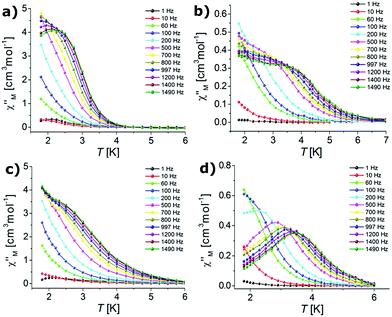Fig. 6 Temperature dependence of the out-of-phase susceptibilities for complexes 1 (a), 2 (b), 3 (c) and 4 (d) in an applied DC field of 0.1 T (the solid lines are guides for the eye).

The frequency dependent out-of-phase susceptibility signals show up at temperatures below 4 K for 1, whereas below 6 K for the other complexes. The maxima of the χ′′_M signals for Er(III) compounds 1 and 3 were in similar ranges: from 2.4 K (1400 Hz) to 1.8 K (600 Hz) and from 2.2 K (1400 Hz) to 1.8 K (600 Hz) for the triflate and nitrate analogues, respectively. For the Yb(III) complexes 2 and 4, the maxima of the χ′′_M signals were in the ranges from 3.7 K (1400 Hz) to 2 K (500 Hz) and from 3.7 K (1400 Hz) to 1.8 K (200 Hz) for the triflate and nitrate congeners, respectively. For 1 and 4, the out-of-phase susceptibility decreases after reaching the maximum with increasing frequency (tending to zero for 4), which indicates that the QTM has been effectively suppressed (Fig. 5). In the case of 2 and 3 the out-of-phase susceptibility increases slightly below 2.5 K, which may indicate that the QTM relaxation process has not been fully cancelled.^98,108

The values of the effective energy barriers U_eff and the relaxation times τ₀ were calculated by fitting the frequency dependence of χ′′_M at each temperature to the model:¹¹¹τ⁻¹ = BTⁿ + τ₀⁻¹ exp(U_eff/kT), where both Raman and Orbach relaxation processes are present (the BTⁿ term represents the Raman process, whereas the τ₀⁻¹ exp(U_eff/kT) term stands for the Orbach process).

Fig. 7 shows that linearity of experimental points is observed for Er(III) compounds (1 and 3) but deviation from linearity at low temperatures characterizes Yb(III) complexes (2 and 4). Please compare those results to the situation where no Raman relaxation component was present and only the Arrhenius model, τ = τ₀ exp (U_eff/k_BT), was applied (Fig. S4‡).

Fig. 7 Temperature dependence of the relaxation time for 1, 2, 3 and 4. The solid blue lines represent fitting of the Orbach/thermal regime, whereas the full temperature regime (red lines) represents the Raman relaxation regime. Quoted parameters were obtained from the linear high-temperature part of the curves.

These results corroborate that, in addition to the Orbach relaxation pathway, the Raman mechanism is operative in the relaxation of magnetization for 2 and 4. Raman relaxation processes were proposed as dominant for most of the Yb(III) complexes.^{108,112–116} The fitted parameters derived from the linear high-temperature part of the curves for all complexes are presented in Table 1.

Table 1 Best fit parameters to temperature dependence of the susceptibility and the relaxation time in the complexes studied obtained by fitting the data to the model where both Orbach and Raman processes are present

Complex	Ln(III)	Anion	U eff/kB [K]/Ueff [cm^−1]	τ 0 [s]	R [10^−5]
a R is the discrepancy factor between experimental and calculated values, defined as R = ∑(exp − calc)^2/∑(exp)^2.
1	Er(III)	OTf^−	6.1/4.2	8.9 × 10^−6	1.1
2	Yb(III)	OTf^−	11.7/8.1	4.6 × 10^−6	2.0
3	Er(III)	NO3^−	8.3/5.8	2.5 × 10^−6	1.3
4	Yb(III)	NO3^−	17.8/12.3	8.7 × 10^−7	4.1

---

The Cole–Cole plots² in the temperature ranges where the χ′′_M peaks show semicircular shapes are shown in Fig. 8.

Fig. 8 Cole–Cole plots for complexes 1 (a), 2 (b), 3 (c) and 4 (d). The solid line corresponds to the best fit obtained with a generalized Debye model.

The α parameters describing the distribution of the relaxation times in a magnetic system were extracted by fitting the Cole–Cole plots to the generalized Debye model^2,117 (cf., Tables S11–S14‡). The limiting value of α = 0 describes a single relaxation process, whereas α = 1 corresponds to an infinitely wide distribution of the relaxation times.² The wider the distribution of the relaxation times, the larger the value of α. A small value of the distribution coefficient α for complexes 1 (Er-OTf) (0.1285(1.8 K)–0.1430 (2.4 K)) and 4 (Yb-NO₃) (0.1256 (3.7 K)–0.1693 (2.0 K)) as well as moderate values of α for complexes 2 (Yb-OTf) (0.0820 (3.5 K)–0.2740 (2.3 K)) and 3 (Er-NO₃)(0.2893 (2.1 K)–0.3406 (1.8 K)) indicate that the relaxation process has a narrow distribution of relaxation time.^118,119

3.4 Optical absorption spectra

Absorption spectra at 4.2 K of compound 1 and 3 are shown in Fig. S6 and S5,‡ respectively. The well resolved lines observed in the region of 6500–21 200 cm⁻¹ for 1 and 6500–22 700 cm⁻¹ for 3 enable the assignment of crystal field (CF) components of seven and nine among nine possible lowest energy ^2S+1L_J multiplets for 1 and 3, respectively. Fig. S6a–i and S5a–i‡ present the high resolution spectra corresponding to the transitions from the ground ⁴I_15/2 multiplet to the energy levels of excited multiplets in 1 and 3, respectively. Please note that experimentally determined energy levels are also compared with the theoretical values. For 1 transitions to multiplets ⁴I_J (J = 13/2, 11/2, 9/2), ⁴S_3/2, ²H_11/2 and ⁴F_7/2 are observed, whereas for 3 also those to ⁴F_5/2 and ⁴F_3/2 are observed. In total, the energies of 34 and 37 experimental levels were determined from the analysis of the absorption spectra for 1 and 3, respectively. There is, however, an inherent limitation, which cannot be overcome, i.e. the higher lying levels (above about 24 000 cm⁻¹) are obscured by the absorption bands of the ligands. Thus, the number of the observed experimental energy levels, which could be used for CF fittings, was not too large. In spite of this limitation, the CF calculations yield reasonable results (see below). In this situation, the CF calculations for other Ln³⁺ ions in isostructural compounds would be desirable to increase the reliability of the present results.

Concerning the ytterbium compounds 2 and 4 the absorption spectra (Fig. S5 and S6‡) provide information only about the energy of three CF levels of the ²F_5/2 multiplet. For 2 three transitions to this multiplet are observed at 10 238, 10 328 and 10 614 cm⁻¹, whereas for 4 they are observed at 10 229, 10 305 and 10 408 cm⁻¹. Hence the absorption spectra for the Yb(III) compounds 2 and 4 do not provide sufficient data to perform full scale CF calculations, unlike in the case of the Er(III) compounds 1 and 3. Additional comments on the results for complexes 2 and 4 are provided in the ESI.‡

3.5 SPM and CF analysis

The methodology for the analysis of optical electronic absorption spectra follows that described in our earlier papers.^120,121 We employ a general approach based on the crystal-field analysis (CFA) and superposition model (SPM), which has been extensively utilized for Ln ions in low symmetry crystals.^122–128 The purpose of theoretical calculations was primarily to obtain the energy levels and exact composition of the state vectors for the ground multiplet, i.e.⁴I_15/2 of the Er(III) ion and ²F_7/2 of the Yb(III) ion, in the studied complexes. Such information, which was not available from other experiments, is indispensable for the interpretation of magnetic data. Moreover, these compounds do not exhibit luminescence; so such data cannot also be obtained from emission measurements. To this end, we recorded the absorption spectra described in section 3.4. These measurements do not directly provide information on the experimental splitting of the ground multiplet. Fortunately, based on the energies of the excited multiplets obtained from the absorption spectra, we are able to determine the CF parameters (CFPs), which subsequently may be utilized to calculate the energies and composition of the state vectors for the ground multiplet. The main difficulties encountered during the CF analysis concern the low local site symmetry and the existence of more than one type of ligands. To overcome these difficulties specific approximations have to be introduced.

The results of SPM and CF analysis are provided in details in the ESI.‡ The original crystallographic axis system (CAS) and the adopted modified CAS (CAS*) are depicted in Fig. S8 and S9‡ for compounds 1 and 3, respectively. The procedure used for the SPM calculations of CFPs and CF analysis of the absorption spectra is as follows. The SPM contributions to CFPs originating from nitrogen and oxygen atoms from coordinating ligands were separately taken into account. However, to reduce the number of adjustable parameters, as an approximation, we treat equally MeOH–oxygen and OTf–oxygen for compound 1, whereas we treat H₂O–oxygen and NO₃–oxygen for compound 3. This approximation may be considered well justified in the framework of SPM analysis.^122–128 Moreover, such an approximation should not seriously affect the major characteristics of the studied systems as the data presented below indicate. In principle it might, since OTf is negatively charged, whereas MeOH is not. Hence, instead of three sets of the intrinsic parameters, we utilize only two sets: B̄_kO (k = 4 and 6) describing the combined contributions to CF from ligands MeOH/OTf and ligands H₂O/NO₃ for compounds 1 and 3, respectively, and B̄_kN (k = 4 and 6) describing contributions to CF from nitrogen ligands for each compound. The intrinsic parameters with k = 4 and 6 were used to constrain the respective CFPs in fittings, whereas the five second-rank CFPs B₂₀, ReB_2q and ImB_2q (q = 1, 2) were varied independently in fittings. Fittings were carried out in two stages using 34 and 37 experimental levels determined from the analysis of absorption spectra for compounds 1 and 3, respectively (cf. section 3.4).

In the first stage fittings were carried out assuming the actual low site symmetry C₁. For compound 1 we obtained (in cm⁻¹) B_2q as: B₂₀ = −35, B₂₁ = −73 − i32 and B₂₂ = 44 + i93, whereas the k = 4 and 6 intrinsic parameters were obtained as: B̄_4N = 302, B̄_4O = 398, B̄_6N = 389, and B̄_6O = 170. This fitting yielded the rms value of 13.3 cm⁻¹. For compound 3 we obtained (in cm⁻¹) B_2q as: B₂₀ = −90, B₂₁ = −14 − i156 and B₂₂ = −59 − i52, whereas the k = 4 and 6 intrinsic parameters were obtained as: B̄_4N = 226, B̄_4O = 248, B̄_6N = 328, and B̄_6O = 479. This fitting yielded the rms value of 14.9 cm⁻¹. Using the so-fitted k = 4 and 6 intrinsic parameters and the geometric coefficients^122–128g_kq calculated for the geometry shown in Fig. S8 and S9‡ for compounds 1 and 3, respectively, the CFPs B_kq given in Table S15‡ are calculated (columns denoted SPM-C₁).

In the second stage fittings were carried out assuming the approximated site symmetry C₂. Importantly, the SPM calculations indicate that the CFPs with q odd reflecting the triclinic site symmetry, especially ReB₄₁ and ImB₄₁ as well as ReB₄₃ and ImB₄₃ (set SPM-C₁ in Table S15‡), are clearly smaller than the CFPs reflecting higher site symmetry. Hence, the SPM results fully justify the use of the C₂ symmetry approximation, i.e. neglecting the respective triclinic CFPs. The remaining major CFPs: B₂₀, ReB₂₂ and ImB₂₂ require suitable rotation to reduce ImB₂₂ to zero. The approximated CFP sets obtained in this way are denoted in Table S15‡ as C₂ = rotation Oz/−32.3° and C₂ = rotation Oz/−20.42° for compounds 1 and 3, respectively. Using these CFP sets as starting parameters in fittings we obtain the fitted CFPs denoted in Table S15‡ as the C₂ fit. It appears that the C₂ symmetry approximation is relatively better for compound 1 than for 3. This assertion agrees with the structural data obtained from the solid state, which show that, upon utilization of the MeOH/OTf⁻ uniformity approximation, the character of the axially coordinated nitrates is not fully symmetric. In fact, it was recently demonstrated that such a change in the position of coordinating nitrates notably alters the CF experienced by them as well as may affect the appearance of the QTM in SMMs.⁸³

To assess more quantitatively the quality of this approximation, one can compare the magnitudes of the CF field strength parameters,^122–128S_k, calculated for symmetries C₁ (all CFP parameters) and C₂ (triclinic CFPs omitted). For compound 1 we obtain (in cm⁻¹): S₂(C₁) = 83.8, S₂(C₂) = 66.9; S₄(C₁) = 204.8, S₄(C₂) = 200.4; S₆(C₁) = 300.8, S₆(C₂) = 296.0. Thus, in the case of B_4q and B_6q the C₂ symmetry is a very good approximation. For the second-rank CFPs this approximation is slightly worse, but also quite good since the contribution from the monoclinic CFPs amounts to about 80% of the total S_k value. The global S_k values are 215.6 cm⁻¹ for C₁ and 210 cm⁻¹ for C₂. Hence the contribution from monoclinic CFPs is about 97.4%, thus confirming that the C₂ symmetry approximation is quite reasonable for compound 1. For compound 3, we obtain (in cm⁻¹): S₂(C₁) = 117.7, S₂(C₂) = 63.7; S₄(C₁) = 194.9, S₄(C₂) = 193.6; S₆(C₁) = 316.4, S₆(C₂) = 284.6. Thus, in the case of B_4q the C₂ symmetry is a very good approximation. For B_6q this approximation is still acceptable since the contribution from the monoclinic CFPs amounts to almost 90% of the total S_k value. For the second-rank CFPs this approximation is somewhat worse, since the contribution from the monoclinic CFPs amounts to about 54% of the total S_k value. However, overall, taking into account the 2^nd-, 4^th-, and 6^th-rank CFPs, we can conclude that the C₂ symmetry is a good approximation also for compound 3. The global S_k values are 225 cm⁻¹ for C₁ and 202 cm⁻¹ for C₂. Hence the contribution from the monoclinic CFPs is about 90%. Additional comments on the computational procedure and the C₂ symmetry approximation are provided in the ESI.‡

The above results of SPM and CF analyses indicate that approximated monoclinic C₂ site symmetry can be used instead of the actual triclinic C₁ site symmetry. The goodness of this approximation appears to be higher in the case of compound 1, whereas it is slightly lower for compound 3. A good fit with small rms error was obtained; however, since the CFP values are only approximated the reliability of the fitted CF parameters needs to be verified by independent methods such as high-field/high-frequency electron paramagnetic resonance (HF²-EPR)¹²⁹ or luminescence studies (though Er(III) analogues did not exhibit such properties with ligand L). On the other hand, since these CFPs correctly describe the energy structure for the excited multiplets observed in the absorption spectrum, it can be assumed that the splitting of the ground multiplet ⁴I_15/2 of the Er(III) ion calculated using the approximated CFPs should be correct. This assumption is corroborated by the fact that the calculated variation of the magnetic susceptibility as a function of temperature reproduces the experimental data very well (cf. section 3.6).

It is also worth to correlate the semiempirical SPM calculations of CF parameters with the results obtained with SHAPE (Table S2‡) in order to avoid misinterpretation of either results. Neither of the compounds 1 or 3 perfectly match the idealized reference polyhedra, though the lowest obtained values (1 – S = 0.971 – D_3h site symmetry; 3 = 1.586 – C_4v site symmetry) are between the chemically significant distortions (CShM > 0.1) and the structurally severe distortions (CShM > 3).⁹⁵ This should be attributed to the fact, that there is no distinction between the types of atoms (herein nitrogen vs. oxygen), but they are treated as being equal to the ones in the corners of the corresponding model polyhedron. Compound 1 could be also potentially treated as the C_4v site symmetric species, since the value S = 1.129 does not significantly differ from that for the D_3h symmetry, the former being even lower than the value S = 3. On the one hand, both the C₂ and C₁ point symmetry groups are subgroups of the group C_4v. On the other hand, for the idealized polyhedral representation of the C_s symmetry we obtain the values S equal to 1.700 and 1.841 for 1 and 3, respectively. Comparison of the respective S values corroborates the presumed validity of C₂ monoclinic approximation.

Nonetheless, caution is necessary when comparing the local symmetry obtained using SHAPE with that indicated by SPM calculations. Note that the bond-length distances observed in the crystal structures of 1 (ca. 0.24 Å biggest difference) and 3 (ca. 0.20 Å biggest difference) are non-uniform. For example, for compound 1 the local symmetry cannot be D_3h because we have 3 oxygen atoms, and there is no three-fold axis that would transform the position of one atom into the other. There exists only one approximate two-fold axis passing through one of the oxygen atoms, which transforms the positions of the other two atoms into themselves. From the perspective of the local geometry such a descent in symmetry was observed before, for instance in the Dy-β-diketonate SMM systems.¹³⁰ It was also surmised that one should actually refer to the charge distribution of ligands around the metal ion. Therefore the molecular symmetry, which is related to the charge distribution of ligands around a metal ion,⁵¹ is decisive and not the apparent site symmetry obtained using SHAPE. Such an intricate situation of lowering real symmetry should be envisaged whenever the heterotopic complexes are constructed.¹³¹

The energy levels and components of the state vector for the ground multiplet ⁴I_15/2 of Er(III) obtained using the CFP set C₂-fit in Table S15‡ are listed in Tables S16 and S17‡ for compounds 1 and 3, respectively. The calculated composition of the state vectors reveals a very large degree of mixing of vectors |15/2, J_z〉 for the ground multiplet ⁴I_15/2 of Er(III) with different quantum numbers (abbreviated in Tables S16 and S17‡ as |J_z〉). This hinders the meaningful interpretation of magnetic data in terms of the energy levels that have a major effect on the variation of the magnetic susceptibility as a function of temperature. Consequently, it is very difficult to correlate the differences in the composition of the vectors within the ground multiplet ⁴I_15/2 for compounds 1 and 3 with the differences in their respective magnetic properties. The only conclusions that may be drawn on the basis of the present results are akin to those arrived at by Reid et al.¹³² The authors¹³² have considered the composition of the ground Kramers doublet of an erbium-based single-ion magnet ({C(NH₂)₃}₅[Er(CO₃)₄]·11H₂O) and concluded that significant mixing of |J_z〉 vectors leads to efficient relaxation of the magnetization. This may account for the relatively poor performance as an SMM in the case of compounds in which such mixing of |J_z〉 vectors occur. This would also explain why all Er(III) congeners (1, 3) exhibit field-induced SIM properties, and could possibly hint that a similar situation could occur in the case of the Yb(III) (2, 4) complexes.

The calculated splitting of the ground multiplet ⁴I_15/2 for the Er(III) ion in compound 1 (397 cm⁻¹) is slightly lower than that in compound 3 (441 cm⁻¹). On the other hand, the first excited level for the Er(III) ion in compound 1 lies at higher energy (47 cm⁻¹) than that in compound 3 (38 cm⁻¹). These preliminary spectroscopic results do not allow for their meaningful correlation with the respective magnetic results and can suggest that the Orbach processes are less possible. Nonetheless they do show that the determined U_eff values do not differ significantly, and this is what we observe experimentally.

3.6 Theoretical interpretation of magnetic susceptibility data

For the reasons given in section 3.5 (cf. also the ESI‡), variation of the magnetic susceptibility as a function of temperature is considered only for the Er(III) ion in compounds 1 and 3. Based on the energy levels and components of the state vector for the ground multiplet ⁴I_15/2 of Er(III) in Tables S16 and S17‡ the variation of magnetic susceptibility was calculated using the CONDON program^133,134 and compared with the experimental ones in Fig. 9 for compounds 1 (a) and 3 (b), respectively.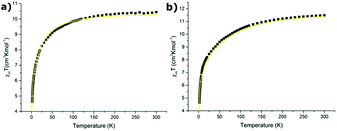

Fig. 9 The variation of magnetic susceptibility as a function of temperature: calculated one using data in Table S15‡ (yellow line) and experimental one (squares) for: (a) compound 1 and (b) compound 3.

It appears that the calculated variation of the magnetic susceptibility as a function of temperature reproduces very well the experimental data. This finding corroborates the assumption that the CFP sets obtained using SPM and CF analyses describe correctly the energy structure for the excited multiplets observed in the absorption spectrum. Consequently, we can expect that the splitting of the ground multiplet ⁴I_15/2 of the Er(III) ion calculated using the approximated CFPs should be physically reliable.

3.7 Magneto-structural correlation

Although it is difficult to provide a full correlation between the chemical composition of 1–4 and their SIM properties, certain dependencies were observed in the present study. All compounds exhibit slow relaxation of magnetization only in the presence of the external magnetic field, which indicates that QTM affects their U_eff values, even though Er(III) and Yb(III) are Kramers ions. One can thus envisage that isostructural complexes that bear prolate Ho(III) and Tm(III) ions should not exhibit a SIM characteristic at all.

The most obvious correlation is related to the choice of the anion, which determines whether only one or two molecules of the ligand L coordinates Ln(III) cations (Fig. S10‡). Please note that this results in coordination polyhedra being constituted by different coordinating atoms (nitrogen vs. oxygen). Their relative position allowed for anticipation that prolate Ln(III) ions are preferred to the oblate ones in terms of the SIM characteristic. For Er(III) and Yb(III) ions an equatorially coordinating geometry is preferable, since minimization of charge contact between the axially located f-element electron density and ligands is achieved. In addition, even though ligands are not completely on the equatorial plane or along the axial direction, observed magnetic data show that nitrate congeners exhibit higher U_eff values than their respective Ln(III) triflate analogues.

Such observations can be rationalized on the basis of the model proposed by Long and co-workers, which encompasses relationships between the shape of the electron density on the Ln ion and the crystal field in which it is placed.³⁸ Note that if exchange of the equatorial nitrate/solvent molecule to other N-donor ligands would happen, one could envisage even more efficient enhancement of Ln(III) anisotropy of its ground state. Importantly, it also explains why anisotropy of Ln(III) in 3 and 4 is enhanced in comparison to their triflate congeners 1 and 2. Such a nitrate induced stabilization of the easy axis of magnetization and thus SIM behaviour has recently been demonstrated for oblate Dy(III) ions.^83,131 In addition, we believe that the highest U_eff value of ca. 18 K (4) should be also related to the fact that only in compound 4 one can discriminate a single Ln–O bond that is ca. 0.8 Å shorter than the remaining ones. In the other compounds, there are always two Ln–O bond distances that are quite similar in length, possibly contributing to the significant mixing of Ln(III) |J_z〉 vectors.

From the Ln(III) point of view, Yb(III) complexes 2 and 4 outperform Er(III) compounds 1 and 3. Bearing in mind that for the former ones, apart from the thermal relaxation processes, optical–acoustic Raman relaxation occurs, this further shows the necessity of gaining more knowledge about the slow magnetic relaxation processes.

4. Conclusions

In this study, we have demonstrated a method for tuning the SIM properties in a new family of lanthanide complexes with LnN_xO_y subunits (where Ln – Er or Yb, x = 3 or 6, y = 2, 3 or 6) via the judicious choice of the nitrate or triflate counterions. Synthesized compounds ([ErL₂(OTf)(MeOH)₂] (OTf)₂ (1), [YbL₂(OTf)₂](OTf) (2), [ErL(NO₃)₃(H₂O)](3), and [YbL(NO₃)₃(MeOH)]·MeCN (4), L – tridentate Schiff-base ligand) were probed for their static and dynamic magnetic properties. Field-induced SIM characteristics has been observed in 1–4, though their U_eff energy barriers increase as follows: 1, 3, 2, 4, with an order of magnitude difference between 1 and 4. It is worth noting that slow relaxation of magnetization in Er(III) and Yb(III) mononuclear congeners with such a composition is very rarely observed, with 2 and 3 being the first SMM/SIM compounds containing the YbN₆O₂ and ErN₃O₆ subunits. To gain further insight into the observed magneto-structural correlations, low temperature absorption studies were done, followed by SHAPE, crystal-field analysis (CFA) and superposition model (SPM) calculations. It appears that the magnetic properties studied herein are a subtle interplay of the molecules’ symmetry and electrostatic interactions, which are fine-tuned by the counterions.

From the crystal engineering point of view,¹³⁵ we provide the design principles, which may serve for further modulation of the SMM properties. The most efficient SIM studied herein is compound 4, which exhibits the highest energy barrier U_eff, whereas such Yb(III) species may be valuable for quantum information processing (QIP).²¹ Hence, we plan to further explore the properties of such species upon their surface confinement^136,137 or as solvent-triggered magnetic switches.¹³⁸

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by the research grant #UMO-2016/21/B/ST4/02064 from the Polish National Science Center.

Notes and references

1. D. Gatteschi, R. Sessoli and J. Villain, - SINGLE-MOLECULE MAGNETS T2 - Molecular Nanomagnets, Oxford Scholarship Online, 2006.
2. J. Tang and P. Zhang, Lanthanide Single Molecular Magnets, Springer-Verlag, Berlin, Heidelberg, 2015.
3. T. Lis, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2042–2046.
4. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
5. L. Bogani and W. Wernsdorfer, Nature, 2008, 7, 179–186.
6. K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804.
7. F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Nature, 2017, 543, 226–228.
8. F. Donati, S. Rusponi, S. Stepanow, C. Wäckerlin, A. Singha, L. Persichetti, R. Baltic, K. Diller, F. Patthey, E. Fernandes, J. Dreiser, Ž. Šljivančanin, K. Kummer, C. Nistor, P. Gambardella and H. Brune, Science, 2016, 352, 318–321.
9. A. Gaita-Arino, H. Prima-Garcia, S. Cardona-Serra, L. Escalera-Moreno, L. E. Rosaleny and J. J. Baldovi, Inorg. Chem. Front., 2016, 3, 568–577.
10. J. Ferrando-Soria, J. Vallejo, M. Castellano, J. Martínez-Lillo, E. Pardo, J. Cano, I. Castro, F. Lloret, R. Ruiz-García and M. Julve, Coord. Chem. Rev., 2017, 339, 17–103.
11. T. Glaser, Chem. Commun., 2011, 47, 116–130.
12. P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923–3929.
13. J. Lu, M. Guo and J. Tang, Chem. – Asian J., 2017, 12, 2772–2779.
14. S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669.
15. L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043–10056.
16. M. Aldoshin Sergey, V. Korchagin Denis, V. Palii Andrew and S. Tsukerblat Boris, Pure Appl. Chem., 2017, 89, 1119–1144.
17. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
18. P. Abbasi, K. Quinn, D. I. Alexandropoulos, M. Damjanović, W. Wernsdorfer, A. Escuer, J. Mayans, M. Pilkington and T. C. Stamatatos, J. Am. Chem. Soc., 2017, 139, 15644–15647.
19. G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147.
20. S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392.
21. S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. S. Walsh and F. Tuna, Coord. Chem. Rev., 2017, 346, 216–239.
22. R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH, 2015.
23. R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341.
24. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
25. H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33.
26. L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090.
27. Y.-S. Meng, S.-D. Jiang, B.-W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381–2389.
28. S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018.
29. A. Eichhöfer, Y. Lan, V. Mereacre, T. Bodenstein and F. Weigend, Inorg. Chem., 2014, 53, 1962–1974.
30. V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M.-E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795.
31. D. Pinkowicz, F. J. Birk, M. Magott, K. Schulte and K. R. Dunbar, Chem. – Eur. J., 2017, 23, 3548–3552.
32. D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225.
33. P. P. Samuel, K. C. Mondal, N. Amin Sk, H. W. Roesky, E. Carl, R. Neufeld, D. Stalke, S. Demeshko, F. Meyer, L. Ungur, L. F. Chibotaru, J. Christian, V. Ramachandran, J. van Tol and N. S. Dalal, J. Am. Chem. Soc., 2014, 136, 11964–11971.
34. T. Glaser, V. Hoeke, K. Gieb, J. Schnack, C. Schröder and P. Müller, Coord. Chem. Rev., 2015, 289–290, 261–278.
35. K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606.
36. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nature, 2017, 8, 14620–14626.
37. A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059.
38. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
39. T. Gupta and G. Rajaraman, J. Chem. Sci., 2014, 126, 1569–1579.
40. S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Chem. Commun., 2014, 50, 15513–15516.
41. N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nature, 2013, 4, 2551–2557.
42. T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972–9008.
43. T. Gupta, G. Velmurugan, T. Rajeshkumar and G. Rajaraman, J. Chem. Sci., 2016, 128, 1615–1630.
44. G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610.
45. K. L. M. Harriman, I. Korobkov and M. Murugesu, Organometallics, 2017, 36(23), 4515–4518.
46. K. Zhang, C. Yuan, F.-S. Guo, Y.-Q. Zhang and Y.-Y. Wang, Dalton Trans., 2017, 46, 186–192.
47. L. Sun, S. Zhang, C. Qiao, S. Chen, B. Yin, W. Wang, Q. Wei, G. Xie and S. Gao, Inorg. Chem., 2016, 55, 10587–10596.
48. S. Zhang, H. Wu, L. Sun, H. Ke, S. Chen, B. Yin, Q. Wei, D. Yang and S. Gao, J. Mater. Chem. C, 2017, 5, 1369–1382.
49. L. Sun, S. Wei, J. Zhang, W. Wang, S. Chen, Y. Zhang, Q. Wei, G. Xie and S. Gao, J. Mater. Chem. C, 2017, 5, 9488–9495.
50. P. Zhang, J. Jung, L. Zhang, J. Tang and B. Le Guennic, Inorg. Chem., 2016, 55, 1905–1911.
51. J. Jung, X. Yi, G. Huang, G. Calvez, C. Daiguebonne, O. Guillou, O. Cador, A. Caneschi, T. Roisnel, B. Le Guennic and K. Bernot, Dalton Trans., 2015, 44, 18270–18275.
52. S. K. Singh, B. Pandey, G. Velmurugan and G. Rajaraman, Dalton Trans., 2017, 46, 11913–11924.
53. K. S. Lim, J. J. Baldoví, S. Jiang, B. H. Koo, D. W. Kang, W. R. Lee, E. K. Koh, A. Gaita-Ariño, E. Coronado, M. Slota, L. Bogani and C. S. Hong, Inorg. Chem., 2017, 56, 4911–4917.
54. J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310–3316.
55. H.-R. Tu, W.-B. Sun, H.-F. Li, P. Chen, Y.-M. Tian, W.-Y. Zhang, Y.-Q. Zhang and P.-F. Yan, Inorg. Chem. Front., 2017, 4, 499–508.
56. Y. Dong, P. Yan, X. Zou, T. Liu and G. Li, J. Mater. Chem. C, 2015, 3, 4407–4415.
57. S. Biswas, K. S. Bejoymohandas, S. Das, P. Kalita, M. L. P. Reddy, I. Oyarzabal, E. Colacio and V. Chandrasekhar, Inorg. Chem., 2017, 56, 7985–7997.
58. Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837.
59. J. Wu, J. Jung, P. Zhang, H. Zhang, J. Tang and B. Le Guennic, Chem. Sci., 2016, 7, 3632–3639.
60. N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103.
61. P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487.
62. A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, Angew. Chem., Int. Ed., 2015, 54, 5864–5868.
63. K.-X. Yu, Y.-S. Ding, T. Han, J.-D. Leng and Y.-Z. Zheng, Inorg. Chem. Front., 2016, 3, 1028–1034.
64. T. Pugh, N. F. Chilton and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 11082–11085.
65. F. Liu, S. Wang, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, F. Jin, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, Angew. Chem., Int. Ed., 2017, 56, 1830–1834.
66. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239.
67. T. P. Latendresse, N. S. Bhuvanesh and M. Nippe, J. Am. Chem. Soc., 2017, 139, 14877–14880.
68. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
69. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
70. K. L. M. Harriman, J. J. Le Roy, L. Ungur, R. J. Holmberg, I. Korobkov and M. Murugesu, Chem. Sci., 2017, 8, 231–240.
71. Y.-N. Guo, L. Ungur, G. E. Granroth, A. K. Powell, C. Wu, S. E. Nagler, J. Tang, L. F. Chibotaru and D. Cui, Nature, 2014, 4, 5471–5477.
72. P. E. Kazin, M. A. Zykin, V. V. Utochnikova, O. V. Magdysyuk, A. V. Vasiliev, Y. V. Zubavichus, W. Schnelle, C. Felser and M. Jansen, Angew. Chem., Int. Ed., 2017, 56, 13416–13420.
73. S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191.
74. C. R. Ganivet, B. Ballesteros, G. de la Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Chem. – Eur. J., 2013, 19, 1457–1465.
75. Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., 2016, 128, 16305–16308.
76. K. L. M. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, J. Am. Chem. Soc., 2017, 139, 1420–1423.
77. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450.
78. P. Hu, Y.-Y. Gao, F.-P. Xiao, L.-L. Zhu, L.-N. Wang, F. Su and M. Zhang, Polyhedron, 2017, 130, 40–46.
79. S. Chen, V. Mereacre, G. E. Kostakis, C. E. Anson and A. K. Powell, Inorg. Chem. Front., 2017, 4, 927–934.
80. A. Gorczynski, M. Kubicki, D. Pinkowicz, R. Pelka, V. Patroniak and R. Podgajny, Dalton Trans., 2015, 44, 16833–16839.
81. S. She, G. Su, B. Wang, Q. Lei, Y. Yang, L. Gong and B. Liu, Eur. J. Inorg. Chem., 2017, 2017, 2406–2412.
82. J. Wu, O. Cador, X.-L. Li, L. Zhao, B. Le Guennic and J. Tang, Inorg. Chem., 2017, 56, 11211–11219.
83. F. Ma, Q. Chen, J. Xiong, H.-L. Sun, Y.-Q. Zhang and S. Gao, Inorg. Chem., 2017, 56, 13430–13436.
84. B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2017, 56, 5076–5088.
85. V. Patroniak, A. R. Stefankiewicz, J.-M. Lehn, M. Kubicki and M. Hoffmann, Eur. J. Inorg. Chem., 2006, 2006, 144–149.
86. M. Wałęsa-Chorab, A. Gorczyński, M. Kubicki, Z. Hnatejko and V. Patroniak, Polyhedron, 2012, 31, 51–57.
87. D. Marcinkowski, M. Wałęsa-Chorab, A. Bocian, J. Mikołajczyk, M. Kubicki, Z. Hnatejko and V. Patroniak, Polyhedron, 2017, 123, 243–251.
88. A. Gorczyński, M. Zaranek, S. Witomska, A. Bocian, A. R. Stefankiewicz, M. Kubicki, V. Patroniak and P. Pawluć, Catal. Commun., 2016, 78, 71–74.
89. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536.
90. Agilent Technologies, CrysAlis PRO (Version 1.171.33.36d), Agilent Technologies Ltd, 2011.
91. A. Altomare, G. Cascarano, C. Giacovazzo and A. Guagliardi, J. Appl. Crystallogr., 1993, 26, 343–350.
92. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
93. A. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18.
94. C. E. Housecroft and A. G. Sharpe, Inorganic chemistry, 2007.
95. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708.
96. D. C. M. Llunell, J. Cirera, P. Alemany and S. Alvarez, Shape v. 2.0, Universitat de Barcelona, Barcelona, 2010.
97. M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575–5582.
98. J.-R. Jiménez, I. F. Díaz-Ortega, E. Ruiz, D. Aravena, S. J. A. Pope, E. Colacio and J. M. Herrera, Chem. – Eur. J., 2016, 22, 14548–14559.
99. X. Yi, K. Bernot, V. Le Corre, G. Calvez, F. Pointillart, O. Cador, B. Le Guennic, J. Jung, O. Maury, V. Placide, Y. Guyot, T. Roisnel, C. Daiguebonne and O. Guillou, Chem. – Eur. J., 2014, 20, 1569–1576.
100. M. Feng, S. Speed, F. Pointillart, B. Lefeuvre, B. Le Guennic, S. Golhen, O. Cador and L. Ouahab, Eur. J. Inorg. Chem., 2016, 2016, 2039–2050.
101. C. Das, A. Upadhyay, S. Vaidya, S. K. Singh, G. Rajaraman and M. Shanmugam, Chem. Commun., 2015, 51, 6137–6140.
102. B. Ahrens, S. A. Cotton, N. Feeder, O. E. Noy, P. R. Raithby and S. J. Teat, J. Chem. Soc., Dalton Trans., 2002, 2027–2030.
103. J. J. Le Roy, I. Korobkov and M. Murugesu, Chem. Commun., 2014, 50, 1602–1604.
104. J.-Y. Ge, L. Cui, J. Li, F. Yu, Y. Song, Y.-Q. Zhang, J.-L. Zuo and M. Kurmoo, Inorg. Chem., 2017, 56, 336–343.
105. F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175.
106. D.-Q. Wu, D. Shao, X.-Q. Wei, F.-X. Shen, L. Shi, Y.-Q. Zhang and X.-Y. Wang, Dalton Trans., 2017, 46, 12884–12892.
107. A. V. Gavrikov, N. N. Efimov, Z. V. Dobrokhotova, A. B. Ilyukhin, P. N. Vasilyev and V. M. Novotortsev, Dalton Trans., 2017, 46, 11806–11816.
108. J.-L. Liu, K. Yuan, J.-D. Leng, L. Ungur, W. Wernsdorfer, F.-S. Guo, L. F. Chibotaru and M.-L. Tong, Inorg. Chem., 2012, 51, 8538–8544.
109. Q.-W. Li, J.-L. Liu, J.-H. Jia, Y.-C. Chen, J. Liu, L.-F. Wang and M.-L. Tong, Chem. Commun., 2015, 51, 10291–10294.
110. H. L. C. Feltham, Y. Lan, F. Klöwer, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Chem. – Eur. J., 2011, 17, 4362–4365.
111. I. Oyarzabal, B. Artetxe, A. Rodriguez-Dieguez, J. A. Garcia, J. M. Seco and E. Colacio, Dalton Trans., 2016, 45, 9712–9726.
112. P.-H. Lin, W.-B. Sun, Y.-M. Tian, P.-F. Yan, L. Ungur, L. F. Chibotaru and M. Murugesu, Dalton Trans., 2012, 41, 12349–12352.
113. J.-D. Leng, J.-L. Liu, Y.-Z. Zheng, L. Ungur, L. F. Chibotaru, F.-S. Guo and M.-L. Tong, Chem. Commun., 2013, 49, 158–160.
114. Q.-W. Li, J.-L. Liu, J.-H. Jia, J.-D. Leng, W.-Q. Lin, Y.-C. Chen and M.-L. Tong, Dalton Trans., 2013, 42, 11262–11270.
115. F. Pointillart, B. L. Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. Commun., 2013, 49, 615–617.
116. J. Ruiz, G. Lorusso, M. Evangelisti, E. K. Brechin, S. J. A. Pope and E. Colacio, Inorg. Chem., 2014, 53, 3586–3594.
117. H. B. G. Casimir and F. K. du Pré, Physica, 1938, 5, 507–511.
118. S.-Y. Lin, C. Wang, L. Zhao, J. Wu and J. Tang, Dalton Trans., 2015, 44, 223–229.
119. T.-Q. Liu, P.-F. Yan, F. Luan, Y.-X. Li, J.-W. Sun, C. Chen, F. Yang, H. Chen, X.-Y. Zou and G.-M. Li, Inorg. Chem., 2015, 54, 221–228.
120. M. Karbowiak, C. Rudowicz and T. Ishida, Inorg. Chem., 2013, 52, 13199–13206.
121. M. Karbowiak, C. Rudowicz, T. Nakamura, R. Murakami and T. Ishida, Chem. Phys. Lett., 2016, 662, 163–168.
122. M. Karbowiak, P. Gnutek and C. Rudowicz, Phys. B, 2010, 405, 1927–1940.
123. M. Karbowiak, C. Rudowicz and P. Gnutek, Opt. Mater., 2011, 33, 1147–1161.
124. M. Karbowiak and C. Rudowicz, Chem. Phys., 2011, 383, 68–82.
125. M. Karbowiak, P. Gnutek, C. Rudowicz and W. Ryba-Romanowski, Chem. Phys., 2011, 387, 69–78.
126. M. Karbowiak, P. Gnutek and C. Rudowicz, Spectrochim. Acta, Part A, 2012, 87, 46–60.
127. M. Karbowiak, P. Gnutek and C. Rudowicz, Chem. Phys., 2012, 400, 29–38.
128. M. Karbowiak, J. Cichos and C. Rudowicz, J. Phys. Chem. A, 2012, 116, 10574–10588.
129. T. Ishida, T. Nakamura, T. Kihara and H. Nojiri, Polyhedron, 2017, 136, 149–154.
130. S.-D. Jiang, B.-W. Wang and S. Gao, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer, Berlin, Heidelberg, 2015, pp. 111–141.
131. K. S. Lim, J. J. Baldoví, W. R. Lee, J. H. Song, S. W. Yoon, B. J. Suh, E. Coronado, A. Gaita-Ariño and C. S. Hong, Inorg. Chem., 2016, 55, 5398–5404.
132. Y. Rechkemmer, J. E. Fischer, R. Marx, M. Dörfel, P. Neugebauer, S. Horvath, M. Gysler, T. Brock-Nannestad, W. Frey, M. F. Reid and J. van Slageren, J. Am. Chem. Soc., 2015, 137, 13114–13120.
133. H. Schilder and H. Lueken, J. Magn. Magn. Mater., 2004, 281, 17–26.
134. J. van Leusen, M. Speldrich, H. Schilder and P. Kögerler, Coord. Chem. Rev., 2015, 289–290, 137–148.
135. G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967.
136. E. Moreno Pineda, T. Komeda, K. Katoh, M. Yamashita and M. Ruben, Dalton Trans., 2016, 45, 18417–18433.
137. A. Caneschi, D. Gatteschi and F. Totti, Coord. Chem. Rev., 2015, 289–290, 357–378.
138. D.-Q. Wu, D. Shao, X.-Q. Wei, F.-X. Shen, L. Shi, D. Kempe, Y.-Z. Zhang, K. R. Dunbar and X.-Y. Wang, J. Am. Chem. Soc., 2017, 139, 11714–11717.

---

Footnotes

† Dedicated to Professor Jacek Gawroński on the occasion of 75th birthday.

‡ Electronic supplementary information (ESI) available: Selected X-ray crystallographic geometrical parameters, SHAPE calculations, Cambridge Structural Database (CSD) comparisons, optical absorption spectra, SPM and CF calculations. CCDC 1052304, 1435579, 1435585 and 1435586. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7qi00727b

§ Equal contribution of the two authors.

¶ Visiting Professor; On leave of absence from: Institute of Physics, West Pomeranian University of Technology Szczecin, Al. Piastów 17, 70–310 Szczecin, Poland.

---