Choosing the ideal photoinitiator for free radical photopolymerizations: predictions based on simulations using established data

Abstract

We present a tool for predicting the initiation efficiency of various type 1 (α-cleavage) photoinitiators for free radical photopolymerization. The amount of initiated polymer chains is crucial for the successful outcome of radical polymerizations. This is based on a subtle combination of intrinsic photoinitiator characteristics, i.e. quantum yields for dissociation, the absorption spectrum of the initiator in terms of its absorption bands and the corresponding absorption coefficients (ε), the rate constants of the primary radicals toward the monomer, and side reactions such as oxygen quenching. Equally important are the emission properties of the utilized light source (irradiation wavelengths, light intensity). We highlight that a balanced combination of all these factors is crucial for achieving optimal initiation performance.

---

Introduction

Excellent photoinitiator (PI) efficiency is an essential prerequisite for the preparation of high performance photopolymers.

The search for optimized photoinitiators^1–5 has been a major challenge and many attempts have been made to classify the performance of PIs. Many factors including UV-Vis absorption properties and their match with the desired irradiation wavelength(s), dissociation quantum yields and photobleaching behavior,^6–10 as well as the reactivity of primary radicals towards monomers,¹¹ and the tendency to undergo side reactions such as competing excited-state processes or oxygen quenching have been extensively discussed in the literature.^12,13

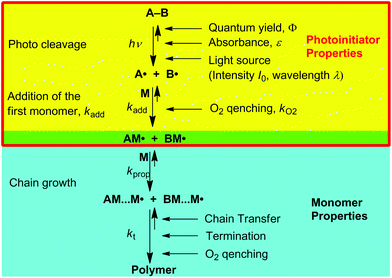
All these above aspects have a crucial influence on the outcome of a polymerization. The process of a radical polymerization represents schoolbook knowledge (Scheme 1). Detailed kinetic models for the overall radical photopolymerizations considering propagation and termination mechanisms,¹⁴ diffusion effects occurring at increased viscosity,¹⁵ as well as film thickness effects have been described by Bowman and coworkers.^16–20 Fundamental research on the addition kinetics of propagating C-centered radicals to monomer double bonds has been summarized by Fischer and Radom.²¹

Scheme 1 Principal steps of radical photopolymerizations (A–B: photoinitiator, A˙, B˙: primary radicals, M: monomer) and their characteristic parameters. The initiation is a two-step process consisting of radical generation followed by monomer addition (yellow background). Here, the ruling parameters are primarily based on the photoinitiator i.e. extinction coefficients (ε), quantum yields for photocleavage (Φ), the light source (intensity I₀ and wavelength λ), the radical to monomer addition rate constants k_add and side reactions such as oxygen (O₂) inhibition. Models for polymerizations considering propagation and termination rate constants (k_prop and k_t), side reactions and diffusion effects have been well established (blue background, see the main text).

The success of a photo-induced radical polymerization is substantially created within the initiation steps determined by the properties of the photoinitiator (Scheme 1, yellow area). It is, therefore, crucial having a quantitative estimate for the number (concentration) of starting radicals, an aspect, which hitherto has barely been elucidated. Here, the subtle interplay between intrinsic photoinitiator characteristics, i.e. quantum yields for dissociation, the absorption spectrum of the initiator in terms of its absorption bands and the corresponding absorption coefficients (ε), the rate constants of the primary radicals toward the monomer, and side reactions such as oxygen quenching together with technical factors like the character of the irradiation sources and irradiated cross sections, play a decisive role.

The aim of our work is showing how the individual features of a photoinitiator can be combined to fine tune the composition of formulations and to achieve an efficient polymerization. To this end, we have performed kinetic simulations including the effects of quantum yield, optical absorption, and penetration depth. The corresponding kinetic scheme is freely available on our website and can be adjusted by the users.‡

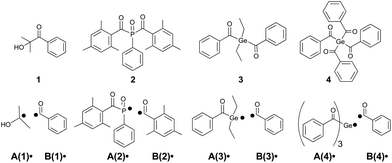
We have selected widely applied type I photoinitiators (α-hydroxy ketones, acylphosphane oxides and acylgermanes, see Scheme 2) as model compounds for our investigation. While α-hydroxy ketones and bisacylphosphane oxides such as 1 and 2, respectively, have been extensively used as industrial photoinitiators for many years,^4,22–26 bis- and especially tetraacylgermanes (3 and 4) represent an emerging class of visible light photoinitiators, featuring red-shifted absorption bands and improved biocompatibility.^27–31

Scheme 2 Structures of photoinitiators 1 (2-hydroxy-2-methylpropiophenone, Darocur® 1173), 2 (phenylbis(2,4,6-trimethylbenzoyl)phosphane oxide, Irgacure® 819), 3 (dibenzoyldiethylgermane) and 4 (tetrabenzoylgermane), together with their primary radicals A(1–4)˙ and B(1–4)˙.

All photoinitiators undergo triplet-state α-cleavage to produce two radicals (A(1–4)˙ and B(1–4)˙, Scheme 2). These add to the double bonds of suitable monomers starting the polymerization. However, even at this early stage of the polymerization undesired side reactions appear. Particularly oxygen may quench the triplet state and impede chain growth by forming peroxyl radicals.^12,32–34 Triplet state quenching by oxygen represents an excited state process competing with bond cleavage, reducing the quantum yield (Φ in eqn (1)) for radical generation. However, this process is known to be of low relevance for type I PIs due to their short-lived triplet states (lifetimes ∼10⁻⁹ s), but is far more pronounced in case of type II PIs (bimolecular PIs, e.g. benzophenone/amine systems), exhibiting long-lived triplet states.^12,34–36 In contrast, the reaction of primary radicals with oxygen is a highly relevant side reaction for type I PIs, since peroxyl radicals are unreactive toward monomer double bonds, thus inhibiting the initiation process.^12,33 Therefore we include oxygen quenching of primary radicals into our model.

In this contribution, we detail the factors influencing the start of the polymerization using kinetic simulations with emphasis on the real concentrations of the radicals formed from 1–4, providing a systematic in-depth analysis of the initiating procedure.

Experimental section and model development

The kinetic model has been developed using the public domain program COPASI,³⁷ utilizing the numeric LSODA solver (Livermore Solver for Ordinary Differential Equations) to perform the calculations. We have chosen realistic conditions matching photopolymerization applications (PI concentration: 2 mM, corresponding to 0.1 w% of compound 3 in the monomer butyl acrylate). The initiation reactions for bulk as well as solution polymerizations (7 M and 1 M butyl acrylate, respectively) have been simulated in absence and presence of air (oxygen concentration: 2 mM).^38,39 The total sample volume was set to 2 mL in a compartment with a cross section of 1 cm × 1 cm. For radical generation, different light sources with varying intensity (spectral photon flux) I₀ and wavelength λ have been considered (see the Results and discussion section).

The rate laws for the initiation reactions as outlined in Scheme 1 are summarized in eqn (1)–(3). The rate of radical generation R_i depends on the quantum yield of dissociation Φ, the spectral photon flux I₀ and the absorbance of the photoinitiator at the chosen irradiation wavelength:¹²

R_i = Φ·I₀·(1 − 10^{−ε·[PI]·d}), (1)

where ε is the wavelength-dependent molar extinction coefficient, [PI] the photoinitiator concentration and d the optical path length (d = 1 cm, in case the sample is irradiated from the side of the compartment).⁴⁰ Dissociation quantum yields of the photoinitiators 1–4 have been taken from published work (Φ(1) = 0.38,⁴¹Φ(2) = 0.6,⁴²Φ(3) = 0.85,²⁷Φ(4) = 0.38 (ref. 43)), while the extinction coefficients of the compounds have been determined by UV-Vis spectroscopy (for details see the ESI, section 1†). The quantum yields of 1–4 and their extinction coefficients at the main irradiation wavelength discussed throughout the text (385 nm) are summarized in Table 1.

Table 1 Dissociation quantum yields Φ and extinction coefficients at 385 nm ε₃₈₅ of photoinitiators 1–4

PI	Φ	ε 385 [L mol^−1 cm^−1]
a Data from ref. 41. b Ref. 42. c Ref. 27. d Ref. 43. e Determined using UV-Vis spectroscopy.
1	0.38^a	<1
2	0.60^b	740
3	0.85^c	255
4	0.38^d	1060

---

The rate laws for the addition of the primary radicals to the monomer are given in eqn (2):

R_{add, A˙} = k_{add, A˙}[A˙][M]; R_{add, B˙} = k_{add, B˙}[B˙][M], (2)

where R_{add, A˙} and R_{add, B˙} are the reaction rates for the addition of A˙ and B˙ radicals to the monomer M and [A˙], [B˙] and [M] are the corresponding concentrations. The rate constants k_add can be determined with laser-flash photolysis (LFP) or time-resolved IR experiments and have been taken from literature (see Table 2). As a typical monomer M for radical polymerization we have chosen butyl acrylate (BA).

Table 2 Rate constants k_add and k_ox for the reaction of photoinitiator radicals A(1–4)˙ and B(1–4)˙ with butyl acrylate (BA) and molecular oxygen (solvent: acetonitrile, measured at room temperature)

Radical	k add [L mol^−1 s^−1]	k ox [L mol^−1 s^−1]
a Data from ref. 46. b Ref. 47. c Ref. 11. d Ref. 43. e Own work, rate constants determined using LFP (for details see the ESI, section 1).
A(1)˙	1.3 × 10^7 ^a	6.6 × 10^9 ^a
B(1,3,4)˙	2.7 × 10^5 ^a	4.0 × 10^9 ^b
A(2)˙	1.1 × 10^7 ^c	2.7 × 10^9 ^c
B(2)˙	1.8 × 10^5 ^a	3.0 × 10^9 ^a
A(3)˙	2.6 × 10^8 ^d	2.9 × 10^9 ^e
A(4)˙	5.9 × 10^7 ^d	3.0 × 10^9 ^e

---

In air-saturated mixtures, the photoinitiator radicals form peroxyl radicals A-OO˙ and B-OO˙, competing with the first addition of monomers to A˙ and B˙. Like monomer addition, oxygen quenching follows second order kinetics (eqn (3)):

R_{ox, A˙} = k_{ox, A˙}[A˙][O₂] and R_{ox, B˙} = k_{ox, B˙}[B˙][O₂]. (3)

R _{ox, A˙} and R_{ox, B˙} are the reaction rates for the reaction of A˙ and B˙ with oxygen ([O₂]: oxygen concentration). The rate constants k_ox are listed in Table 2.

All rate constants given in Table 2 have been determined at room temperature. During the initiation reaction, the temperature in the sample is expected to increase slightly, since the addition of a PI-based radical to a monomer double bond is exothermic, creating a σ bond from a π bond.²¹ This may influence the addition rate constants, which are temperature dependent according to the Arrhenius equation.²¹ However, we anticipate that thermal effects play a minor role in our investigation of the initiation process, since the heat development in radical polymerizations is primarily attributed to the exothermic chain growth (propagation) reactions.⁸ This is also shown by thermal imaging experiments, demonstrating that heat development depends on the chosen monomer and the corresponding exothermicity of the propagation reactions.^44,45

Results and discussion

In this section, we will first discuss the radical generation efficiency of 1–4 depending on their dissociation quantum yields and extinction coefficients at a chosen irradiation wavelength. Then, the addition of the primary PI radicals to the monomer will be included into our model, describing the influence of the addition rate constants on the initiation efficiency (compare Table 2), also considering the photon flux of the irradiation source. As a final aspect, oxygen quenching is added to the model, highlighting the importance of high reactivity of the photoinitiator radicals towards monomers in order to overcome oxygen inhibition.

Radical generation

Fig. 1 presents the UV-Vis absorption spectra of 1–4 together with a simulation of the radical generation rates upon irradiation with a 385 nm low power LED. This wavelength was chosen since it matches the absorption bands of 1–4 and is commercially available at low cost (typical spectral photon flux: I₀ = 2 × 10⁻⁵ mol L⁻¹ s⁻¹, see the ESI section 1,† for an explanation of the units of I₀).^40,43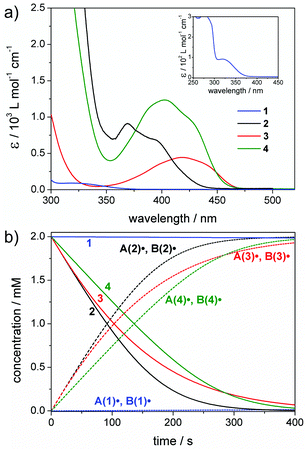

Fig. 1 (a) UV-Vis spectra of 1–4 recorded in acetonitrile. The inset shows the full spectrum of compound 1 (for experimental details see the ESI, section 1†). (b) Simulated concentration versus time plots for 1–4 and the primary radicals A(1–4)˙ and B(1–4)˙. Chosen conditions: irradiation at 385 nm (I₀ = 2 × 10⁻⁵ mol L⁻¹ s⁻¹), photoinitiator concentrations: 2 mM.

Bisacylphosphane oxide 2 shows the highest radical generation rate of all studied PIs at 385 nm (see the concentration vs. time plots in Fig. 1b). This can be traced back to a combination of a high dissociation quantum yield (Φ(2) = 0.6)⁴² and extinction coefficient (ε₃₈₅(2) = 740 L mol⁻¹ cm⁻¹). Bisacylgermane 3 displays a higher quantum yield than 2 (Φ(3) = 0.85),²⁷ yet exhibits rather low absorbance (ε₃₈₅(3) = 255 L mol⁻¹ cm⁻¹), making the overall rate of radical generation slower compared with 2. In contrast, tetraacylgermane 4 has a rather low quantum yield (Φ(4) = 0.38),⁴³ but high absorbance (ε₃₈₅(4) = 1060 L mol⁻¹ cm⁻¹), resulting in almost as efficient radical generation as observed for 3 (see Fig. 1b). The α-hydroxy ketone 1 (Φ(1) = 0.38)⁴¹ displays the lowest radical generation rate at 385 nm, due to the negligible absorbance at this wavelength (ε₃₈₅(1) < 1 L mol⁻¹ cm⁻¹).

In summary, Fig. 1b shows that efficient radical generation is achieved by a combination of a reasonably large quantum yield with a reasonably large extinction coefficient. Of course, low extinction coefficients (as is the case for 1 at 385 nm) can be compensated by increasing the PI concentrations – this, however, may be difficult in many practical applications due to limited solubility of many PIs and higher costs. Simulations of the radical generation efficiency at additional wavelengths (350 nm and at 450 nm) and at increased photon flux are provided in the ESI (section 2, Fig. S2–S4†).

At this point it has to be noted that high extinction coefficients do not per se improve the overall photoinitiator performance. Upon photoexcitation, several photochemical and photophysical processes may compete with bond cleavage (including luminescence or non-radiative energy loss etc.). Therefore, the nature of the electronically excited states generated upon irradiation of a PI is essential, with efficient bond cleavage only occurring from triplet states of n–π* character.^4,41 Detailed analysis of excited states for photoinitiator systems can be obtained from quantum-chemical calculations together with femtosecond spectroscopy, as was shown by Barner-Kowollik, Unterreiner and coworkers for α-hydroxy ketone based systems.^48–50 In our simplified model, we anticipate that high extinction coefficients are beneficial as long as an efficient excitation of n–π* bands is given.

Radical generation followed by monomer addition

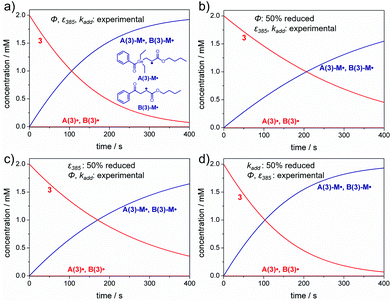
The generation of the primary radicals A˙ and B˙ is followed by their addition to the monomer (butyl acrylate, M), resulting in the addition radicals A-M˙ and B-M˙ (compare Scheme 3). We have chosen initiator 3 as a model compound for analyzing the effects of quantum yields, absorbance and rate constants on the rate of product radical formation. These simulations were performed for the photolysis of 3 in bulk butyl acrylate upon irradiation with the 385 nm low power LED (I₀ = 2 × 10⁻⁵ mol L⁻¹ s⁻¹). Fig. 2a displays the resulting simulations for the experimental values of Φ, ε₃₈₅ and k_add, whereas in Fig. 2b–d, one of these parameters has been successively reduced by 50% to show their impact on the product radical generation rate.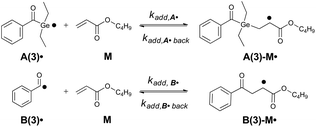

Scheme 3 Addition of primary radicals A(3)˙ and B(3)˙ towards the monomer M butyl acrylate. The rate constants of the forward reactions are k_add,A˙ and k_add,B˙, while k_{add,A˙ back} and k_{add,B˙ back} represent the rate constants of the reverse reactions. In our simulations, we set k_{add,A˙ back} and k_{add,B˙ back} to 20% of the corresponding forward rate constants k_add,A˙ and k_add,B˙, respectively (compare Fig. S11†).

Fig. 2 Simulation of the initiation reaction (radical generation followed by monomer addition) for compound 3 in bulk butyl acrylate at 385 nm (I₀ = 2 × 10⁻⁵ mol L⁻¹ s⁻¹, concentrations: 2 mM 3, 7 M butyl acrylate M, no side reactions) together with the chemical structures of A(3)-M˙ and B(3)-M˙. Concentration versus time plots for (a) Φ = 0.85, ε₃₈₅ = 255 L mol⁻¹ cm⁻¹, k_add,A(3)˙ = 2.6 × 10⁸ L mol⁻¹ s⁻¹, k_add,B(3)˙ = 2.7 × 10⁵ L mol⁻¹ s⁻¹; (b) Φ = 0.425, ε₃₈₅ = 255 L mol⁻¹ cm⁻¹, k_add,A(3)˙ = 2.6 × 10⁸ L mol⁻¹ s⁻¹, k_add,B(3)˙ = 2.7 × 10⁵ L mol⁻¹ s⁻¹; (c) Φ = 0.85, ε₃₈₅ = 127.5 L mol⁻¹ cm⁻¹, k_add,A(3)˙ = 2.6 × 10⁸ L mol⁻¹ s⁻¹, k_add,B(3)˙ = 2.7 × 10⁵ L mol⁻¹ s⁻¹; (d) Φ = 0.85, ε₃₈₅ = 255 L mol⁻¹ cm⁻¹, k_add,A(3)˙ = 1.3 × 10⁸ L mol⁻¹ s⁻¹, k_add,B(3)˙ = 1.35 × 10⁵ L mol⁻¹ s⁻¹.

Reduction of the dissociation quantum yield by a factor of 50% drastically lowers the product radical generation rate (compare Fig. 2a and b). In case of compound 3, 20% less product radicals are formed within the first 400 s under the chosen conditions. Similarly, reducing the extinction coefficient by 50% (and thus reducing the absorbance of the sample) reduces the initiation rate, yet to a slightly lower amount (15% less product radicals after 400 s, see Fig. 2c).

Concerning the addition rate constants, it is important to notice that in all cases both addition radicals A(3)-M˙ and B(3)-M˙ are formed at the same rate, although the germyl radical A(3)˙ displays a 1000 times higher addition rate constant towards butyl acrylate than the benzoyl radical B(3)˙ (k_add,A(3)˙ = 2.6 × 10⁸ L mol⁻¹s⁻¹, k_add,B(3)˙ = 2.7 × 10⁵ L mol⁻¹ s⁻¹, see Table 2). We attribute this result to a slow radical generation rate caused by irradiation with the low power LED. Only a small amount of primary radicals is formed simultaneously and these radicals may instantly react with the monomer, which is present in huge excess (bulk polymerization).

Fig. 2d thus shows that even a reduction of the addition rate constants by 50% does not markedly influence the product radical generation rate (compare Fig. 2a and d). Analogous results are obtained for initiators 1, 2 and 4 (see the ESI, section 3, Fig. S5–S7†).

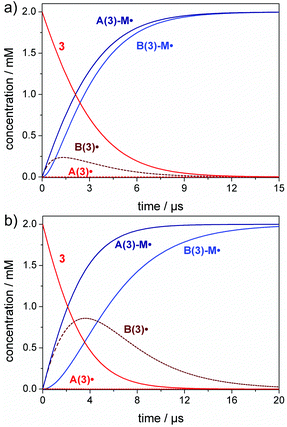
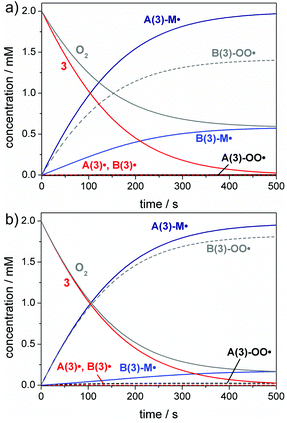
Only when radicals A˙/B˙ are generated rapidly through irradiation at very high light intensity (large spectral photon flux), the effect of the addition rate constants becomes visible. This is shown in Fig. 3, where we used a spectral photon flux of 1000 mol L⁻¹ s⁻¹, which is far beyond realistic conditions, but illustrates the effect of exceedingly rapid radical generation. Here, initiation occurs at a much faster time scale and the benzoyl radical B(3)˙ is observed as an intermediate, since the monomer is rather consumed by the more reactive germyl radical A(3)˙ (Fig. 3a).

Fig. 3 Simulation of the initiation reaction (radical generation followed by monomer addition) for compound 3 (2 mM) for irradiation with a hypothetical high power 385 nm lamp (I₀ = 1000 mol L⁻¹ s⁻¹): (a) bulk polymerization (7 M butyl acrylate, M), (b) solution polymerization (1 M butyl acrylate, M).

It is also relevant to consider the influence of the monomer concentration on the initiation rate (compare eqn (2)). The effects visible in Fig. 3a are more pronounced in solution polymerizations, where the monomer concentration is lower and the competition between the two radicals towards the monomer is higher (Fig. 3b). This results in a higher amount of the benzoyl radical B(3)˙ formed as an intermediate and a delayed formation of the B(3)-M˙ addition radical (compare Fig. 3a and b). The corresponding simulations for compounds 1, 2 and 4 are presented in the ESI (section 3, Fig. S8–S10†).

In a nutshell, our simulations demonstrate that the difference in the rate constants between the more reactive ketyl, phosphanoyl or germyl radicals A˙ compared with the less reactive benzoyl radicals B˙ are solely relevant upon irradiation with an extremely large photon flux (rapid radical generation). In contrast, equivalent initiation efficiencies are found for both types of radicals in case of polymerizations using conventional light sources such as LEDs.

It should be mentioned that our model so far encompasses ideal conditions for the initiation reactions. Particularly, it should be considered that the addition of photoinitiator radicals to the monomer is reversible, as has been shown by chemically induced dynamic nuclear polarization (CIDNP).⁵¹ To the best of our knowledge, rate constants for the reverse reaction (i.e. the dissociation of A-M˙ (or B-M˙) to the radicals A˙ (B˙) and the monomer M, see Scheme 3) are not available in literature.

To test the influence of reversibility, the upper limit for the rate constant for the reverse reaction k_add,back is set to 20% of the forward reaction k_add. The corresponding simulations are presented in the ESI (section 3, Fig. S11†) for low and high power irradiation at 385 nm. Compared to irreversible radical to monomer addition, the rate of adduct radical formation (A-M˙ and B-M˙) is only slightly lowered, and the primary radicals A˙ and B˙ are observed as photoproducts at higher concentrations in the reversible case (see Fig. S11†). However, these differences do not affect the results presented in Fig. 2 and 3. Therefore, for simplicity we concentrate only on irreversible addition reactions in our simulations.

In the next step, we consider alternative reaction pathways of the primary radicals, competing with the addition to the monomer. The most likely side reactions of the primary radicals are recombination to the parent photoinitiator (A–B), and escape from the primary radical pair cage to form recombination products containing two radicals of the same type (A–A or B–B).⁵² Yet, these reactions become insignificant when the monomer concentration is high.⁵¹ Assuming diffusion-controlled rates for these recombination reactions, the corresponding byproducts are formed in very low yields and thus, these reaction pathways are negligible for our model (see the ESI, section 3, Fig. S12†). Another possibility is recombination of a primary radical A˙ or B˙ with a growing polymer chain radical A-M or B-M˙, resulting in the termination products A-M-A, A-M-B, B-M-A and B-M-B. The corresponding simulation (see Fig. S13†) shows that these termination products are formed to a minor extent. Again, the reaction of the primary radicals with the monomer is favored over the reaction with a previously formed addition radical A-M˙ or B-M˙. This is due the significantly lower concentrations of the polymerizing radicals A-M˙ or B-M˙vs. the monomer concentration as well as the rather low termination rate constants k_t (k_t ∼ 10⁶–10⁸ L mol⁻¹ s⁻¹)^12,34,53 (see the ESI† for further details).

Moreover, the primary radicals may react with dissolved oxygen before adding to the monomer. As mentioned in the Introduction, oxygen inhibition is a major issue affecting photoinitiator performance. This is discussed in the next section.

Effects of oxygen inhibition on initiation efficiency

The reaction with oxygen primarily competes with the desired addition of A˙/B˙ to the monomer forming the peroxyl radicals A(3)-OO˙ and B(3)-OO˙. The corresponding rate constants, k_ox, are in the diffusion-controlled range, which is one to four orders of magnitude higher than the addition rate constants towards double bonds (e.g. butyl acrylate, Table 2). Therefore, even small oxygen concentrations as found in aerated polymerization mixtures ([O₂] ∼2 mM)^38,39 may result in high overall quenching rates (eqn (3)).

The competition between oxygen quenching and addition to the monomer is represented in Fig. 4. Bulk and solution polymerizations of photoinitiator 3 are simulated for irradiation with a low-power 385 nm LED. These simulations demonstrate that the benzoyl radical B(3)˙ rather reacts with oxygen than with the monomer, while the germyl radical A(3)˙ efficiently adds to the monomer, forming radical A(3)-M˙ even in presence of oxygen. This is rationalized by the higher monomer addition rate constant of radical A(3)˙ compared to B(3)˙. The combination of a high addition rate constant and high monomer concentration leads to a high monomer addition rate in case of radical A(3)˙, which clearly exceeds the rate of oxygen quenching. In contrast, the oxygen quenching rate of radical B(3)˙ is faster than the monomer addition rate. Monomer addition cannot efficiently compete with oxygen quenching in case of radical B(3)˙, since the monomer addition rate constant of B(3)˙ is over 10 000 times lower than the oxygen quenching rate constant (k_add,B(3)˙ = 2.7 × 10⁵ L mol⁻¹ s⁻¹, k_ox,B(3)˙ = 4 × 10⁹ L mol⁻¹ s⁻¹, see Table 2).

Fig. 4 Simulation of the initiation reaction for compound 3 in air-saturated butyl acrylate (385 nm low power LED, I₀ = 2 × 10⁻⁵ mol L⁻¹ s⁻¹, concentrations: 2 mM 3, 2 mM O₂): (a) concentration versus time plot for bulk polymerization (7 M butyl acrylate, M); (b) concentration versus time plot for solution polymerization (1 M butyl acrylate, M).

These effects are again more pronounced for solution polymerizations (compare Fig. 4a and b). Lower monomer concentrations lead to a reduced monomer addition rate, resulting in a stronger competition between initiation and oxygen quenching. Thus, barely any product radicals B(3)-M˙ are formed in solution, while oxygen quenching of the germyl radical A(3)˙ occurs to only a minor extent (Fig. 4b). Analogous simulations are obtained for compounds 1, 2 and 4 (see the ESI, section 4, Fig. S14–S16†).

Our results show that chain growth initiation is significantly suppressed unless the reactivity of at least one of the primary radicals towards the monomer is high enough to compete with oxygen quenching. Accordingly, monomer addition rate constants play an important role for initiation reactions in presence of even low amounts of oxygen.

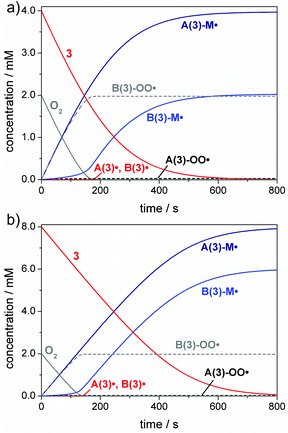
A common way circumventing this problem in the initiation step is increasing the PI concentration.^1,12,13,54Fig. 5 depicts simulations of the initiation reaction in air-saturated butyl acrylate solution for compound 3 at concentrations of 4 mM and 8 mM, corresponding to twice and four times the oxygen concentration (2 mM). As expected, the benzoyl radical B(3)˙ primarily undergoes oxygen quenching. However, after consumption of all oxygen, enough photoinitiator is still present to be cleaved and the benzoyl radical can initiate chain growth as well. This is evident from the increase of the B(3)-M˙ adduct radical concentration observed after an initial delay period (see Fig. 5a and b). These simulations suggest that benzoyl radicals act as efficient oxygen traps in polymerization mixtures, being in line with our previous study.⁵⁵ It has to be noted that Fig. 4 and 5 display simplified models as further diffusion of oxygen into the polymerization mixture in the course of the reaction has not been considered. The oxygen diffusion especially plays a role over the larger time-scales of the propagation reactions, and detailed kinetic models have been established previously by Bowman and coworkers considering these effects.^18,20,33

Fig. 5 Simulation of the initiation reaction in air-saturated butyl acrylate solution (385 nm low power LED, I₀ = 2 × 10⁻⁵ mol L⁻¹ s⁻¹, 2 mM O₂, 1 M butyl acrylate, M) containing (a) 4 mM and (b) 8 mM photoinitiator 3.

Scope of the model

A detailed description of our simulation program is provided in the ESI (section 5†). It can be easily adapted to any photoinitiator, light source and monomer, provided that the experimental values for quantum yields, extinction coefficients and rate constants are available. It has to be taken into account that these experimental data typically possess standard errors of up to 20%. Simulations showing the effect of such deviations are provided in the ESI (section 6, Fig. S21–S23†). They demonstrate that such deviations do not significantly affect the outcome of the predictions.

Importantly, the solubility of oxygen in the formulation depends on the type of monomer and the solvent.^38,56 Accordingly, appropriate oxygen concentrations have to be included in the modelling procedure (see eqn (3)).

Finally, photoinitiator performance strongly depends on the actual application, being influenced by the irradiation wavelength as well as the concentrations of photoinitiator, monomer and oxygen (see above). Additionally, the thickness of the formulation to be cured is crucial. Of course, high absorbance (corresponding to a high extinction coefficient) of the PI at the irradiation wavelength is desired (compare eqn (1)). However, very high absorbance will result in the light being mainly absorbed at the outer layers of the sample, thereby limiting the penetration depth and impeding efficient through-curing.^57,58 In this respect, efficient photobleaching (i.e. decomposition of the chromophoric system upon irradiation) of the initiator is highly desired.⁴³

We plan to further extend our model in the future, accounting for penetration depth and photobleaching effects.

Conclusions

To summarize, we have performed a systematic step-by-step analysis of photoinitiator performance. We have demonstrated the interplay of absorption properties, dissociation quantum yields, light intensities, irradiation wavelengths, and kinetics. Oxygen quenching as the major side reaction has been taken into account.

In principle, addition rate constants of the primary radicals towards the monomer play a negligible role in bulk polymerizations with conventional light sources when side reactions are excluded. Indeed, our simulations reveal that under ideal conditions, any photoinitiator will do its job in an almost perfect way. However, particularly oxygen quenching together with the subtleness of the photo-physical properties of the photoinitiator makes the distinction between a well-suited and hardly useful one. In these terms, a high amount of initiated polymer chains is achieved by a combination of high extinction coefficients at the irradiation wavelength (resulting in n–π* excitation), high dissociation quantum yields and excellent reactivity of the primary radicals towards the monomer, which is especially relevant to compete with oxygen inhibition or further side reactions of the primary radicals. This subtle combination of effects should be borne in mind when developing novel type I photoinitiating systems.

Our expandable modelling toolbox provides an access for predicting photoinitiator performance in photopolymer research and is also helpful for educational purposes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Jens T. Toerring for integrating the kinetic model into our website. G. G. and D. F. thank the FWF for funding (project I 1614). We additionally acknowledge financial support from Ivoclar Vivadent AG and NAWI Graz.

Notes and references

1. N. S. Allen, J. Photochem. Photobiol., A, 1996, 100, 101–107.
2. W. Rutsch, K. Dietliker, D. Leppard, M. Köhler, L. Misev, U. Kolczak and G. Rist, Prog. Org. Coat., 1996, 27, 227–239.
3. K. Dietliker, T. Jung, J. Benkhoff, H. Kura, A. Matsumoto, H. Oka, D. Hristova, G. Gescheidt and G. Rist, Macromol. Symp., 2004, 217, 77–98.
4. J. P. Fouassier and J. Lalevée, Photoinitiators for Polymer Synthesis: Scope, Reactivity and Efficiency, Wiley, Weinheim, 2012.
5. M. Haas, J. Radebner, A. Eibel, G. Gescheidt and H. Stueger, Chem. – Eur. J., 2018, 24, 8258–8267.
6. J. P. Fouassier, X. Allonas, J. Laleve and C. Dietlin, in Photochemistry and Photophysics of Polymer Materials, ed. N. S. Allen, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2010, pp. 351–419.
7. H. F. Gruber, Prog. Polym. Sci., 1992, 17, 953–1044.
8. G. Moad and D. H. Solomon, The Chemistry of Radical Polymerization, Elsevier, Amsterdam, Boston, 2nd edn, 2006.
9. Y. Yagci, S. Jockusch and N. J. Turro, Macromolecules, 2010, 43, 6245–6260.
10. Y. W. Marien, P. H. M. van Steenberge, K. B. Kockler, C. Barner-Kowollik, M.-F. Reyniers, G. B. Marin and D. R. D'hooge, Polym. Chem., 2017, 8, 3124–3128.
11. S. Jockusch and N. J. Turro, J. Am. Chem. Soc., 1998, 120, 11773–11777.
12. S. C. Ligon, B. Husár, H. Wutzel, R. Holman and R. Liska, Chem. Rev., 2014, 114, 557–589.
13. B. Husár, S. C. Ligon, H. Wutzel, H. Hoffmann and R. Liska, Prog. Org. Coat., 2014, 77, 1789–1798.
14. G. B. Desmet, Y. W. Marien, P. H. M. van Steenberge, D. R. D'hooge, M.-F. Reyniers and G. B. Marin, Polym. Chem., 2017, 8, 7143–7150.
15. J. M. Nölle, S. Primpke, K. Müllen, P. Vana and D. Wöll, Polym. Chem., 2016, 7, 4100–4105.
16. C. N. Bowman and C. J. Kloxin, AIChE J., 2008, 54, 2775–2795.
17. N. B. Cramer, T. Davies, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 4631–4636.
18. M. D. Goodner and C. N. Bowman, Chem. Eng. Sci., 2002, 57, 887–900.
19. P. M. Johnson, J. W. Stansbury and C. N. Bowman, Macromolecules, 2008, 41, 230–237.
20. A. K. O'Brien and C. N. Bowman, Macromol. Theory Simul., 2006, 15, 176–182.
21. H. Fischer and L. Radom, Angew. Chem., Int. Ed., 2001, 1340–1371.
22. H. Grützmacher, J. Geier, D. Stein, T. Ott, H. Schönberg, R. H. Sommerlade, S. Boulmaaz, J.-P. Wolf, P. Murer and T. Ulrich, CHIMIA, 2008, 62, 18–22.
23. A. Huber, A. Kuschel, T. Ott, G. Santiso-Quinones, D. Stein, J. Bräuer, R. Kissner, F. Krumeich, H. Schönberg, J. Levalois-Grützmacher and H. Grützmacher, Angew. Chem., Int. Ed., 2012, 51, 4648–4652.
24. J. Wang, G. Siqueira, G. Müller, D. Rentsch, A. Huch, P. Tingaut, J. Levalois-Grützmacher and H. Grützmacher, Chem. Commun., 2016, 52, 2823–2826.
25. S. Benedikt, J. Wang, M. Markovic, N. Moszner, K. Dietliker, A. Ovsianikov, H. Grützmacher and R. Liska, J. Polym. Sci., Part A: Polym. Chem., 2016, 54, 473–479.
26. D. Darvasiová, Z. Barberiková, A. Eibel, M. Schmallegger, G. Gescheidt, M. Zalibera and D. Neshchadin, Polym. Chem., 2017, 8, 1719.
27. B. Ganster, U. K. Fischer, N. Moszner and R. Liska, Macromolecules, 2008, 41, 2394–2400.
28. N. Moszner, U. K. Fischer, B. Ganster, R. Liska and V. Rheinberger, Dent. Mater., 2008, 24, 901–907.
29. J. Radebner, A. Eibel, M. Leypold, C. Gorsche, L. Schuh, R. Fischer, A. Torvisco, D. Neshchadin, R. Geier, N. Moszner, R. Liska, G. Gescheidt, M. Haas and H. Stueger, Angew. Chem., Int. Ed., 2017, 56, 3103–3107.
30. J. Radebner, M. Leypold, A. Eibel, J. Maier, L. Schuh, A. Torvisco, R. Fischer, N. Moszner, G. Gescheidt, H. Stueger and M. Haas, Organometallics, 2017, 36, 3624–3632.
31. N. Moszner, U. K. Fischer, I. Lamparth, P. Fässler, J. Radebner, A. Eibel, M. Haas, G. Gescheidt and H. Stueger, J. Appl. Polym. Sci., 2018, 135, 46115.
32. V. A. Bhanu and K. Kishore, Chem. Rev., 1991, 91, 99–117.
33. A. K. O'Brien and C. N. Bowman, Macromolecules, 2006, 39, 2501–2506.
34. C. Decker and A. D. Jenkins, Macromolecules, 1985, 18, 1241–1244.
35. R. Schwalm, UV coatings: Basics, Recent Developments and New Applications, Elsevier, Amsterdam, London, 2007.
36. Photopolymerisation and Photoimaging Science and Technology, ed. N. S. Allen, Springer, Netherlands, Dordrecht, 1989, Ch. 1, pp. 40–44.
37. S. Hoops, S. Sahle, R. Gauges, C. Lee, J. Pahle, N. Simus, M. Singhal, L. Xu, P. Mendes and U. Kummer, Bioinformatics, 2006, 22, 3067–3074.
38. L. Gou, C. N. Coretsopoulos and A. B. Scranton, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 1285–1292.
39. S. Horstmann, A. Grybat and R. Kato, J. Chem. Thermodyn., 2004, 36, 1015–1018.
40. E. Stadler, A. Eibel, D. Fast, H. Freißmuth, C. Holly, M. Wiech, N. Moszner and G. Gescheidt, Photochem. Photobiol. Sci., 2018, 17, 660–669.
41. S. Jockusch, M. S. Landis, B. Freiermuth and N. J. Turro, Macromolecules, 2001, 34, 1619–1626.
42. S. Jockusch, I. V. Koptyug, P. F. McGarry, G. W. Sluggett, N. J. Turro and D. M. Watkins, J. Am. Chem. Soc., 1997, 119, 11495–11501.
43. A. Eibel, J. Radebner, M. Haas, D. E. Fast, H. Freißmuth, E. Stadler, P. Faschauner, A. Torvisco, I. Lamparth, N. Moszner, H. Stueger and G. Gescheidt, Polym. Chem., 2018, 9, 38–47.
44. R. Geier, C. Wappl, H. Freiszmuth, C. Slugovc and G. Gescheidt, Polym. Chem., 2015, 6, 2488–2492.
45. A. Eibel, M. Schmallegger, M. Zalibera, A. Huber, Y. Bürkl, H. Grützmacher and G. Gescheidt, Eur. J. Inorg. Chem., 2017, 2017, 2469–2478.
46. C. S. Colley, D. C. Grills, N. A. Besley, S. Jockusch, P. Matousek, A. W. Parker, M. Towrie, N. J. Turro, P. M. W. Gill and M. W. George, J. Am. Chem. Soc., 2002, 124, 14952–14958.
47. M. Hoshino, R. Konishi, H. Seto, H. Seki, H. Sonoki, T. Yokoyama and H. Shimamori, Res. Chem. Intermed., 2001, 27, 189–204.
48. T. J. A. Wolf, D. Voll, C. Barner-Kowollik and A.-N. Unterreiner, Macromolecules, 2012, 45, 2257–2266.
49. E. Frick, C. Schweigert, B. B. Noble, H. A. Ernst, A. Lauer, Y. Liang, D. Voll, M. L. Coote, A.-N. Unterreiner and C. Barner-Kowollik, Macromolecules, 2016, 49, 80–89.
50. D. Voll, A. Hufendiek, T. Junkers and C. Barner-Kowollik, Macromol. Rapid Commun., 2012, 33, 47–53.
51. M. Griesser, D. Neshchadin, K. Dietliker, N. Moszner, R. Liska and G. Gescheidt, Angew. Chem., Int. Ed., 2009, 48, 9359–9361.
52. U. Kolczak, G. Rist, K. Dietliker and J. Wirz, J. Am. Chem. Soc., 1996, 118, 6477–6489.
53. M. D. Goodner and C. N. Bowman, Macromolecules, 1999, 32, 6552–6559.
54. H. J. Hageman, Prog. Org. Coat., 1985, 13, 123–150.
55. D. Hristova-Neeley, D. Neshchadin and G. Gescheidt, J. Phys. Chem. B, 2015, 119, 13883–13887.
56. S. L. Murov, I. Carmichael and G. L. Hug, Handbook of Photochemistry, Dekker, New York, 2nd edn, 1993.
57. D. E. Fast, A. Lauer, J. P. Menzel, A.-M. Kelterer, G. Gescheidt and C. Barner-Kowollik, Macromolecules, 2017, 50, 1815–1823.
58. A. Lauer, D. E. Fast, J. Steinkoenig, A.-M. Kelterer, G. Gescheidt and C. Barner-Kowollik, ACS Macro Lett., 2017, 6, 952–958.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional simulations and model description. See DOI: 10.1039/c8py01195h

‡ Link to the website: http://ptc-pc-139.tugraz.at/index.html.

---