Polyethenetetrathiolate or polytetrathiooxalate? Improved synthesis, a comparative analysis of a prominent thermoelectric polymer and implications to the charge transport mechanism

Abstract

1,1,2,2-Ethenetetrathiolate (ett⁴⁻) coordination polymers, such as poly[K_x(Ni-ett)], have been known for decades for their excellent thermoelectric properties. However in reality, ett⁴⁻ is neither a “true” comonomer which participates in the polymerization, nor represents a “true” repeat unit of the target polymer. Indeed, poly[K₂(Ni-ett)], which is formally the product of Ni-induced polymerization of ett⁴⁻, has a poor conductivity and needs to be oxidized to show attractive thermoelectric characteristics. The polymerization and oxidation processes are poorly controllable which causes irreproducibility of the polymer properties. To improve the synthesis reproducibility, we studied polymerization of potassium tetrathiooxalate (K₂tto), the convenient synthesis of which was developed in our recent work. Because K₂tto is the “true monomer”, and not its precursor, a high quality product is reproducibly formed simply by mixing K₂tto with NiCl₂ at room temperature. The procedure does not require additional components (bases), or special conditions (prolonged heating), which are usually needed for the preparation of this polymer from the monomer precursor 1,3,4,6-tetrathiapentalene-2,5-dione (TPD). Furthermore, as tto²⁻ is formally the product of two-electron oxidation of ett⁴⁻, the poorly controllable oxidation process is avoided and poly[Ni-tto] almost free from K is directly formed upon the complexation of Ni²⁺ and tto²⁻. Thus-obtained poly[Ni-tto] possesses conductivity in the range of 27–47 S cm⁻¹ and a Seebeck coefficient in the range of −38 to −55 μV K⁻¹, which are superior thermoelectric properties compared to poly[K_x(Ni-ett)] samples obtained by the previously reported methods. Redox and structural properties of poly[Ni-tto] were compared with those of poly[K_x(Ni-ett)] obtained by the reported methods. Furthermore, DFT calculations were performed to shed more light on generally promising properties of this class of materials. Particularly, possible packing models have been predicted for polymers, and the molecular dynamics simulations have been used to simulate the molecular arrangements under ambient conditions.

---

Introduction

Thermoelectrics^2,3 is one of the most rapidly developing applications of organic conductors in recent years. TE generators can be widely applied, for example, in different cooling systems, power generators on the basis of waste heat from the automobile exhaust systems, devices with an excess of solar thermal flux, wearable electronics and sensors, etc. Because of the absence of moving parts or hazardous working fluids, TE generators are technically simple, reliable and environmentally friendly. Therefore, TE materials have fundamental importance in terms of energy sources and environmental issues. The dimensionless figure of merit of such materials characterises the thermoelectric performance:

zT = α²σT/κ, (1)

which is a function of the Seebeck coefficient α, the electrical conductivity σ, the thermal conductivity κ and the ambient temperature T. Since the low thermal conductivity is the common feature of most organic compounds, the power factor (PF = α²σ) is a more widespread figure of merit for performance comparison. To build a complete thermoelectric unit with a maximum efficiency, both p-type and n-type organic semiconductors are required. While highly performing p-type materials are readily available, e.g. intrinsically conducting polymer PEDOT:PSS having a high Seebeck coefficient and impressive electrical conductivity, their n-type material counterparts are much less developed because of severe difficulties in their synthesis and poor air-stability. Few attempts were made to utilize solution-processable n-type polymers and small molecules in TE devices, e.g., n-doped naphthalenediimide-based polymer (P(NDIODT2))⁴ and self-doped perylene diimide (PDI) derivatives.⁵ However, these materials show rather poor TE performance mostly due to very low conductivity (<10⁻² S cm⁻¹). Recently, the BDPPV-based polymer doped with (4-(1,3-dimethyl-2,3-dihydro-1H-benzoimidazol-2-yl)phenyl)dimethylamine (N-DMBI) has been reported⁶ to show a high conductivity of 14 S cm⁻¹ and a promising thermoelectric (TE) power factor, PF, of 28 μW (m K²)⁻¹. However, this and other solution-processable donor–acceptor π-conjugated copolymers are much more expensive than their p-type counterparts, such as PEDOT:PSS, because of complicated, multistep synthesis and the involvement of expensive chemicals.

Coordination polymers in which bis-dithiolene units are bonded to transition metal ions are an interesting class of materials due to their high conductivity, promising Seebeck coefficient and good air-stability for both p- and n-type polymers.¹ Furthermore, they can be easily prepared from cheap precursors: 1,3,4,6-tetrathiapentalene-2,5-dione (TPD) and transition metal salts. Particularly attractive is poly[K_x(Ni-ett)] (poly(nickel-1,1,2,2-ethenetetrathiolate)), first obtained in 1983,⁷ as it shows the n-type of conductivity, the rare and most wanted conductivity type in organic materials.^8–11 The interest in this polymer was renewed after the studies by Sun et al. in 2012,¹ when its extraordinary thermoelectric properties (α = −120 to −140 μV K⁻¹, σ = 40–220 S cm⁻¹ and zT = 0.2–0.3) were reported. At the same time, an insolubility of poly[K_x(Ni-ett)] powder precludes its application in TE devices. Therefore, many researchers are focused on the development of solution-processable forms of poly[K_x(Ni-ett)]. Typically, the poly[K_x(Ni-ett)] powder synthesized according to the Sun et al.¹ protocol was used in these studies as the starting material to produce processable formulations, such as, by milling of poly[K_x(Ni-ett)] particles in the presence of solubilizing additives. Usually, the resulting processable composites possess much lower α and σ values than those claimed for the pristine poly[K_x(Ni-ett)] powder, which is not surprising because the active material in these composites is diluted by passive components. However, surprisingly, these studies either do not provide the α and σ values for the starting poly[K_x(Ni-ett)] powder, or give quite modest α and σ values. For example, in 2014 the group of Zhu⁹ reported σ = 8.31 S cm⁻¹, α = −67.4 μV K⁻¹ and PF = 3.71 μW mK⁻² for pure poly[K_x(Ni-ett)], which are more than 10 times smaller values (σ = 44 S cm⁻¹, α = −122 μV K⁻¹ and PF = 66 μW mK⁻²) than those reported for the same material two years earlier¹ by the same group. An even lower σ value of 1.14–1.51 S cm⁻¹ for the same polymer was reported in 2015 by Oshima et al.¹⁰ On the other hand, we were also not able to reproduce the outstanding characteristics of poly[K_x(Ni-ett)] reported by Sun et al., even after extensive optimization of the preparation conditions. We propose that the high sensitivity of the polymer identity (i.e., composition, crystallinity, and purity) to any variations of the preparation conditions might be responsible for the poor reproducibility of the thermoelectric properties of poly[K_x(Ni-ett)]. To circumvent this problem, a solid understanding of the polymerization mechanism and the structure–property relationship is needed.

For a long time, it was believed that poly[K_x(Ni-ett)] is formed by complexation of Ni²⁺ and ethenetetrathiolate anions (ett⁴⁻) generated in situ upon a MeOK-induced methanolysis of TPD (1). However, in reality, the stoichiometry of the resulting polymer deviates significantly from the theoretical poly[K₂(Ni-ett)] and the most useful thermoelectric properties were found for the formally oxidized form [K_x(Ni-ett)] with x ranging from 0.3 to 0.6.

Very recently, we proved that only one ring of TPD undergoes methanolysis under standard polymerization conditions and ett⁴⁻ is not formed even upon prolonged reaction of TPD and MeOK, presumably due to strong coulombic repulsions between the intermediate dithiolate anion, dmid²⁻, and methoxy anions.¹² It was proposed that opening of the second ring requires the charge neutralization of dmid²⁻ either upon interaction with oppositely charged Ni²⁺ (followed by the methanolysis of neutral Nidmid) or by oxidation of dmid²⁻ (i.e., via route C, Scheme 1). The importance of the oxidation process during the preparation of poly[K_x(Ni-ett)] was stated in many previous papers and the polymerization process was performed in air,¹³ iodine,¹⁴ or by electrochemical reaction.^11,15 Unfortunately, it turned out that the oxidation process is very difficult to control so that the resulting products possess unpredictably variable composition and irreproducible properties.

Scheme 1 Synthesis of polymers.

Despite the obvious importance of the oxidative process for polymerization, we found out that polymerization may also proceed under completely air-free conditions (and in the absence of other oxidants) upon extensive heating, which assumes an alternative, formally non-oxidative polymerization pathway. Particularly, we found that the intermediate dmid²⁻ formed upon the methanolysis of TPD undergoes a high-yield decarbonylation into tetrathiooxalate tto²⁻, which may be formally considered as the oxidation product of the tetraanion ett⁴⁻.¹² We postulated that tto²⁻ forms under the standard polymerization conditions and acts as the main comonomer which polymerizes with Ni²⁺ salts, contributing to the formation of electrostatically neutral polymer fragments.

We further proposed that dmid²⁻, after the complexation with Ni²⁺ to form charge-neutralized Ni₂dmid, undergoes further methanolysis and then acts as the second comonomer (synthetic equivalent of tetraanion ett⁴⁻) contributing to the formation of negatively charged units. As such, the stoichiometry of the resulting polymers (and their properties) is defined by the ratio of ett⁴⁻ to Ni-dmid which is difficult to control in reality because these are fluent, in situ forming, yet converted one into another intermediate. In addition, the resulting polymers may undergo oxidation by air during the polymerization, upon the purification process, storage or by utilization. All these factors may cause the irreproducibility of the polymer properties.

In this work, we benefit from the availability of the “true” monomer K₂tto convenient synthesis which was developed in our previous work.¹² We assume that involvement in the polymerization of the “true” monomer instead of its precursor (TPD) should eliminate uncertainness associated with the complex polymerization mechanism, as discussed above. Second, the polymerization of the monomer tto²⁻ should lead to the “fully oxidized” polymer poly[Ni-tto] so that the problematic oxidation step can be avoided. As follows from Scheme 1 (route D), the resulting polymer should be completely uncharged or contain negatively charged groups only at the chain ends. Because the presence of charged units may be essential to impart electrical conductivity, it was a priori unclear whether the polymer formed in such a way that has any benefit for TE application.

In this work, having the development of more reproducible synthesis of ethenetetrathiolate-based polymers for TE applications as the general goal, we investigate the Ni-induced complexation-polymerization of K₂tto, assess the properties of the resulting polymers and compare them with the properties of the poly[K_x(Ni-ett)] prepared according to the previously reported protocols.^1,9,10,13

Results and discussion

Polymerization I (prolonged heating, no prevention from oxygen)

Firstly, we attempted the preparation of poly[K_x(Ni-ett)], for which the outstanding thermoelectrical properties were previously reported.¹ The polymer designated as P1_methanol was obtained by prolonged heating of the solution of TPD and CH₃OK in methanol followed by the addition of NiCl₂ and further prolonged heating, as previously described. The last step assumes an exposure of the reaction mixture to air to ensure the oxidation and the final growth of the polymer chains. To this end, the reaction vessel was opened and the reaction mixture was stirred for different times and at variable temperature. Unfortunately, because particular details of the oxidation step were not properly disclosed in the original paper¹ (i.e., how exactly air was allowed to react with the reaction mixture and how long this process took place), we optimized the oxidation protocol aiming at the polymer with the highest σ and α values, and the optimal air-exposure time was found to be about 30 minutes.¹³

Prepared by us in such a way the polymer P1_methanol has the following characteristics: σ = 8.0 S cm⁻¹ and α = −29.9 μV K⁻¹, which are inferior characteristics than the ones reported by Sun et al.,¹ but closer to the results of Menon et al.¹³

We suggested that the properties of the polymer can be further improved by increasing its molecular weight, i.e., by suppressing too fast aggregation and precipitation of short oligomers during the chain growth. We assumed that solvents having a higher dielectric constant would be especially valuable for such purposes because they stabilize electrostatically charged intermediates. To verify this hypothesis, the same reaction was conducted in a methanol : N-methylformamide (MeOH : NMF) mixture (1 : 4). Isolation of the resulting polymer was performed by dilution of the dispersion in water under the ambient conditions leading to the formation of a precipitate which was filtered and rinsed with water. This leads to the material with apparently the same chemical structure like P1_methanol, designated as P1, but with an improved conductivity (σ = 24.3 S cm⁻¹) and Seebeck coefficient (α = −33.9 μV K⁻¹). As in the case of P1_methanol (ESI, Fig. SA1†), σ, α and PF values of P1 increase with the temperature increase (ESI, Fig. SA2†).

Elemental analysis performed by inductively coupled plasma optical emission spectrometry (ICP-OES) of P1 reveals the content of K = 5.14% and Ni = 25.66%, which corresponds to the formula of the polymer close to poly[K_0.3(Ni-ett)] (Table 1). As expected for the polymer obtained upon prolonged heating in air (routes D and C, Scheme 1), the observed K/Ni ratio in P1 is much less than 2 (Table 2). At the same time, the composition of P1 differs significantly from that of P_Sun (poly[K_x(Ni-ett)]) as it contained about a 10 times smaller amount of K which corresponds to a much stronger oxidized polymer. It should be noted that our optimization studies did not result in substantial reduction of K.

Table 1 Elemental composition of poly[K_x(Ni-ett)] and poly[Ni-tto] polymers (weight %). The presence of hydrogen may be attributed to water molecules, which are strongly coordinated with the polymer and cannot be completely removed

	K	Ni	S	C	H
poly[Kx(Ni-ett)] (P1)	5.14	25.66	46.80	12.80	0.99
Data of Sun et al.^1	0.57	25.85	—	12.99	1.12
Data of Menon et al.^13 (for 30 min polymer)	8.71	22.06	47.31	9.08	0.78
Theoretical (if x = 0.3)	5.27	26.35	57.59	10.79	0
Theoretical (if x = 0.6)	10.01	25.04	54.71	10.25	0
poly[Ni-tto] (P3)	1.78	25.08	58.80	13.67	0.82
Theoretical	—	27.82	60.79	11.39	0

---

Table 2 Atomic ratios of poly[K_x(Ni-ett)] and poly[Ni-tto] polymers

	Ni : K	K : Ni	S : C	Ni : C	Ni : S
poly[Kx(Ni-ett)] (P1)	3.39	0.295	1.37	0.41	0.30
Theoretical (if x = 0.3)	3.33	0.3	2	0.5	0.25
Theoretical (if x = 0.6)	1.67	0.6	2	0.5	0.25
poly[Ni-tto] (P3)	9.39	0.106	1.61	0.38	0.23
Theoretical	—	—	2	0.5	0.25

---

Polymerization II (oxygen-free conditions, low temperature)

By comparing the TE performance of P1 and P_Sun,¹ one can correlate the outstanding σ and α values of P_Sun with the low content of K, which in turn reflects the low concentration of charges. To verify this hypothesis, we prepared a negative reference P2 having a strongly charged backbone expecting that it should have much worse σ and α values compared to P1 and P_Sun. Formally, the polymer poly[K₂(Ni-ett)] could be obtained upon Ni-induced polymerization of synthon K₄ett (route A, Scheme 1), however according to the modern vision of the polymerization mechanism,¹² the intermediate K₄ett is not formed under real reaction conditions because of coulombic repulsions between dmid²⁻ and methoxy anions. If the polymerization proceeds at elevated temperature, it involves oxidative decarbonylation (route D) leading to the oxidation of the polymer backbone. To avoid oxidations, we performed polymerization at room temperature and under oxygen-free conditions. To compensate the negative charge of dmid²⁻ and trigger the polymerization, we added Ni salt soon after the addition of MeOK to TPD and the reaction mixture was stirred for 4 days at 18 °C. Black precipitate was filtered in a glovebox and washed with deionized degassed water and dry methanol. The as synthesized polymer P2 has a low electrical conductivity of 0.2 S cm⁻¹ and a small, yet positive Seebeck coefficient of α = +2.8 μV K⁻¹. Interestingly, washing of this polymer with water in an open atmosphere not only slightly increases the conductivity of such a product forming designated as P2-ox up to 0.4 S cm⁻¹, but more importantly, it reverses the sign of the Seebeck coefficient leading to α = −23.3 μV K⁻¹. The improvement of the conductivity and Seebeck coefficient by the “post-polymerization” oxidation can be attributed to adjustment of the backbone oxidation state being more appropriate for charge transportation (Scheme SE1†), but also to the oxidation-induced formation of longer polymer chains, as shown in Scheme SE2.† Elemental analysis of P2 reveals the high content of K (corresponding to the formula poly[K_0.82(Ni-ett)]); the air-oxidation followed by rinsing with water significantly reduced the K content (Table SD1†).

Polymerization III (two-step procedure)

Previous experiments demonstrated that more oxidized polymers with a reduced content of K have better TE properties. In principle, polymerization of the “oxidized” monomer K₂tto and NiCl₂ should lead to the either completely uncharged polymer or to the polymer having charges only at the chain ends (Scheme 1, route D).¹⁶

P3 (poly[Ni-tto]) was prepared simply by mixing NiCl₂ solution and the solution of the monomer K₂tto, synthesized and purified as reported in our previous work.¹² Elemental analysis (Table 1) reveals for P3 the lowest content of K among the polymers prepared in our work (1.78). Theoretically, infinite P3 chains should not contain potassium and its presence may indicate the charged end groups. This can be used for the calculation of the polymerisation degree; the atomic Ni/K ratio of 9.39 found for P3 (Table 2), corresponds to an average polymerisation degree of 19.

This simple and fast reaction of K₂tto and NiCl₂ conducted at room temperature and under ambient conditions results in the polymer P3 having a conductivity in the range of σ = 27.2–47.3 S cm⁻¹ and Seebeck coefficient in the range of α = −38.5 to −55.1 μV K⁻¹ (Table 3), which is the highest TE performance for polymers obtained by us and others, except for the studies of Sun.^1,11

Table 3 Thermoelectric properties of the obtained polymers

Polymer	σ [S cm^−1]	α [μV K^−1]	max. PF [μW mK^−2]
poly[Kx(Ni-ett)] (P1methanol)	1.4–8.0	“−21.4”–“−29.9”	0.72
poly[Kx(Ni-ett)] (P1)	24.3	−33.9	2.79
P2	0.2	+2.8	0.0002
P2-ox	0.4	−23.3	0.02
poly[Ni-tto] (P3)	27.2–47.3	“−38.5” to “−55.1”	14.40

---

The electrical conductivity increases with the temperature rise, which suggests a semiconducting behaviour (Fig. 1). The simultaneously measured negative value of the Seebeck coefficient and the power factor are also increased. The temperature dependences of σ and α values show hysteresis and the σ and α values measured after cooling are ∼10% higher than those obtained at the same temperature before heating. The same measurements of the annealed sample (1 hour at 110 °C) showed no change in properties after measurements (ESI, Fig. SA4†), so the observed hysteresis may be attributed to an annealing-effect.

Fig. 1 The electrical conductivity, the Seebeck coefficient and the power factor of poly[Ni-tto](P3), measured on compressed pellets at 300–380 K (the arrows show the direction of the measurement sequence).

Besides the relatively high conductivities and Seebeck coefficient, an important advantage of our method is its batch-to-batch reproducibility. Although some variations in the key TE characteristics are observed (more than 30 batches studied herein displayed quite a narrow range of σ of 27.2–47.3 S cm⁻¹), they are much smaller than those for polymers produced by other methods. For example, the σ value of poly[K_x(Ni-ett)] varies in a range of several orders of magnitude, according to the data of different authors.^7–11 Most importantly, our reaction is almost insensitive to the particular details of the reaction conditions, such as time, temperature, and air exposure, whereas alternative methods crucially depend on the reaction parameters. Furthermore, the polymer P3 possesses an outstanding environmental stability: while the conductivity of P1 drops 2 times over a few days, the conductivity of P3 remains at almost the same level over one month (Fig. SA3†).

Comparison of P3 and P1

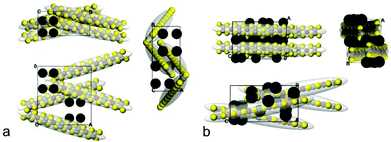
Hence, we demonstrated that the polymer P3 obtained from the monomer K₂tto clearly outperforms, in terms of its thermoelectric properties, long-term environmental stability and reproducibility of the synthesis, polymers formed from the monomer precursor TPD by the method described previously. To shed more light on the origin of this difference, we compared the structure, chemical composition and redox properties of the two polymers in more detail.

To shed light on the structure of both polymers, the computer modelling at the atomistic level has been applied as a combination of DFT calculations, classical MD simulations and crystal packing prediction. The first 3D-model for P1 was proposed in 1988 by Vogt et al.¹⁷ from the results of Extended X-Ray Absorption Fine Structure (EXAFS) measurements. In this model, the polymeric chains were arranged in parallel layers with an interlayer distance of 4.55 Å (Ni⋯Ni distance) and an intermolecular distance within the layer of 4.3 Å (S⋯S length). Assuming that the chains of P1 and P3 are oligomers, as follows from the estimations based on data from Table 1, here we resort to a simplification that the chains for the packing predictions consist of four units (see the Experimental part). Although the packing prediction approach admittedly ignores the disorder/amorphousness of the samples, it takes into account the packing effects, i.e. the conformational changes of the polymers, and considers explicitly the location of K⁺ counterions. Therefore, this approach can provide insight into the specific molecular interactions of the polymers.

To better model the structural arrangement observed in the polymers, we used the experimentally found density of pressed pellets. From the packing prediction, 26 unit cells with the experimentally found density of ρ = 2.047 g cm⁻³ have been observed for P1 and 5 unit cells with the experimental density of ρ = 2.1062 g cm⁻³ have been found for P3. As follows from Fig. 2, both polymers have two structural elements: the π-stacked columns and the herringbone packed arrangements. For P1, the counterions are located in-between the π-stacked columns on both sides from the backbone, i.e. they are intercalating between the polymer stacks.¹⁷

Fig. 2 (a) Three projections of the predicted unit cell of P3. The parameters of the unit cell are: orthorhombic Pna2₁ symmetry, a = 8.79 Å, b = 20.57 Å, c = 18.74 Å, α = β = γ = 90°, and density ρ = 2.1062 g cm⁻³. (b) Three projections of the predicted unit cell of P1. The parameters of the unit cell are: orthorhombic Pna2₁ symmetry, a = 14.84 Å, b = 11.61 Å, c = 21.70 Å, α = β = γ = 90°, and density ρ = 2.047 g cm⁻³. The carbon, sulphur, nickel and potassium are shown as CPK spheres in grey, yellow, red and black, respectively. The light-grey ellipsoids show the motion groups used in the packing predictions.

For the investigation of the structural properties of both polymers, the unit cells depicted in Fig. 2 were replicated thrice in each direction, and MD simulations were conducted. The initial (the simulation time τ = 0) and the last (τ = 3 ns) snap-shots for three projections of the supercells are given in ESI in Fig. SB4 and SB5.† The thermal disorder, simulated in the MD runs at T = 289 K, makes the packings less ordered, and therefore more realistic. The overall packing mode is nevertheless preserved. For example, the average π-distances 3.85 Å and 3.62 Å for P3 and P1, respectively, are lower than the values measured for the polymers in ideal unit cells (4.27 Å for P1) which can be attributed to the more disordered state of the real solids. The greatest differences from the above mentioned model we see at the positions of mobile counterions, as follows from the visual inspection of the snapshots from Fig. SB4 and SB5.† For both polymers, the backbones retain the planarity (see Table SB1†), which indicates the conformational rigidity of the polymers (φ angles do not exceed 12 degrees).

The close contacts S⋯Ni and S⋯S and the contacts of K⁺ cations with the backbones are illustrated in Fig. SB6† as distribution functions. The distribution of distances for P3 is bimodal with two maxima located at 2.95 and 3.45 Å, the monomodal function for P1 shows the average distances K⁺⋯S/Ni/C, S⋯Ni, and S⋯S at 3.18 Å. These distances of close contacts coincide well with the experimentally obtained data for [Ni(dmid)₂]ⁿ species.¹⁸ Despite the fact that the network of the contacts seems to be denser for P1, as follows from the inserts of Fig. SB6,† it is more structured for P3. Remarkably, the polymer chains in P3 are held together via shorter stabilising contacts. The intermolecular distances Ni–Ni on average are much shorter for P3 (3.79 Å) and are in the range of 4.38 Å for P1 and the latter value is in accordance with the data reported by Vogt et al. The shorter Ni–Ni distances in P3 may account for the improved transportation of charge carriers in this polymer as compared to P1, assuming that the hopping of charges occurs predominantly via the Ni posts.

From the radial distribution functions g(r) (Fig. SB7†) of K⁺ and S, Ni and C atoms of the polymers it follows that K⁺ ions are preferably coordinated with sulphur: the first sharp peak is at 3.05 Å and 3.03 Å for P3 and P1, respectively, and the second one is located at 5.53 Å for both polymers. However, what is most important for us is to estimate the difference in distances from Ni to K, because positively charged K⁺ may potentially prohibit the transportation of electrons (due to their opposite charge). The g_K–Ni(r) functions show the first two peaks at 4.73 and 5.73 Å (P3) and 4.11 and 4.71 Å (P1).

The last aspect we touch on here is the analysis of the smoothed averaged concentration profiles along the axes of the supercells for the different parts of the MD trajectory as summarized in Fig. SB8.† The π-stacks are less prone to thermal disorder (panel A in Fig. SB8a and SB8b†), and the corresponding profiles are almost unaffected during the MD runs for both polymers. In contrast, the herringbone motifs for P1 are more affected by thermal motion (panels B and C in Fig. SB8a and SB8b†). The P3 polymer structure remains unchanged which provides information about the possible origin of a high conductivity in polymers of such a type.

Thus, our structural and theoretical investigations shed light on generally valuable electronic properties of this polymer type. It was particularly found that for both polymers, the backbones retain their planarity even at the elevated temperatures used for simulations; the packed chains preserve close S⋯Ni, S⋯S and Ni–Ni contacts and have small π–π distances, which are important prerequisites for efficient electrical conductivity.

The major difference between the two polymers is in the number of K cations per polymer unit. The larger content of K cations in poly[K_x(Ni-ett)] may explain its lower conductivity, since positively charged species should act as traps for electrons. Our calculations show that poly[K_x(Ni-ett)] has a significant fraction of states with a relatively small distance between Ni and K, further confirming this assumption.

XPS was used to investigate the composition and chemical structure of the polymers. As expected for the related compounds, many peaks on the XPS survey spectra of P1 and P3 have identical positions and similar shapes (Fig. SC2†). Herein, we discuss mostly the peaks which might account for the difference in the properties of the polymers. The peaks corresponding to K have the same shape for the two polymers but the intensity of the peaks for P1 is much higher, in full accordance with the elemental analysis. The most interesting information comes from the analysis of C and S high-resolution spectra.

To facilitate analyses, the C 1s spectra (Fig. 3) were deconvoluted into five component peaks: S, B, C, D, and E (BE corresponding to ≈285.94; 286.62; 287.86; and 289.17 eV). The spectrum of P1 is mostly represented by the component peak S which can be assigned to the thioenol type of carbon (C=^SC̲–S).¹⁹ The peaks B, C, D, and E which were previously assigned for a similar polymer to carbon atoms bonded to sulphur in different oxidation states are small in P1.

Fig. 3 High-resolution C 1s and K 2p XPS spectra and their deconvolution for poly[K_x(Ni-ett)] (a) and poly[Ni-tto] (b) samples.

Compared to P1, the P3 spectrum in the C 1s area has a more complex shape. Besides the component S, it is represented by higher energy peaks, among which the peak at 287.86 eV has the highest intensity. This peak can be assigned to the C–^SC̲=S group, in which carbon forms the double bond with sulphur. The presence of these peaks and their high intensity are two of the most important differences between P3 and P1 or similar polymers prepared previously.

Valuable information comes from the comparison of the S 2p spectra. The S 2p spectra were deconvoluted into the four component peaks O, P, Q, and R.²⁰Fig. 4 shows the S 2p spectra recorded from the poly[K_x(Ni-ett)] and poly[Ni-tto] samples. Due to the spin–orbit coupling all S 2p spectra are composed of S 2p_3/2 and S 2p_1/2 peaks. The experimentally determined coupling constant (ΔBE = |BE[S 2p_3/2] − BE[S 2p_1/2]| = 1.18 eV with BE = binding energy) was in excellent agreement with the literature.²¹

Fig. 4 High-resolution S 2p spectra and their deconvolution for poly[K_x(Ni-ett)] (a) and poly[Ni-tto] (b) samples (thin black lines show the component peaks of the S 2p_3/2 spectra, the component peaks of the S 2p_1/2 were drawn in grey, and the component peaks of the S 2p_1/2 were assigned with letters in grey and apostrophes).

Component peaks appearing in the region of 162–164 eV (component peaks O and P) resulted from photoelectrons escaping from sulphide-like bonded sulphur.^11,13 The binding energy values found for the component peaks O (BE[S 2p_3/2] = 162.2 eV) were characteristic of sulphides whereas the component peaks P (BE[S 2p_3/2] = 163.1 eV) arose from disulphides.

Oxidized sulphur species were detected as the component peaks Q (BE[S 2p_3/2] = 164.05 eV) and R (BE[S 2p_3/2] = 168.87 eV). The component peaks Q were assigned to sulphur in formally lower oxidation states, such as sulfenic and/or sulfinic acids, whereas the peaks R were typical for higher oxidized sulphur species, such as in organic sulphates (S̲O₄²⁻), sulfuric (half) esters (C–O–S̲O₄⁻) and sulfonic acids (C–S̲O₃⁻).²⁰ It was previously reported that component peaks in this region dominate the spectrum of S 2p after intensive oxidation of the polymer for 24 hours.¹³ These component peaks are especially intense in P1 which reflects that very severe oxidations occurred in this polymer.

Thus the XPS results clearly indicate that oxidation of P1 which is an important step for the successful polymerization process is accompanied by severe oxidations of sulphur which likely results in the degradation of the regular structure of the polymer and reduces electrical conductivity.

In contrast, the polymerization of the monomer K₂tto which does not require the oxidation step leads to the polymer P3 with much less oxidized sulphur which most likely accounts for its better conductive properties.

Cyclic voltammetry (CV) measurements were performed to compare the redox properties of the polymers and estimate the energy levels of their frontier orbitals. As seen from Fig. 5, the two polymers differ strongly in the position of the first oxidation potential: poly[Ni-tto] has a quasi-reversible redox wave centred at −0.59 V (−4.5 eV against a vacuum, assuming a redox potential of ferrocene of −5.09 eV). This process, assignable to a redox of nickel atoms, could be responsible for the transportation of the electrons in the n-type polymer poly[Ni-tto]. The irreversible cathodic process of a major intensity centred at 0.9 V can be assigned to the oxidation of sulphur atoms in poly[Ni-tto].

Fig. 5 Cyclic voltammograms of poly[Ni-tto]- and poly[K_x(Ni-ett)]-films measured in CH₃CN solution.

The redox behaviour of poly[K_x(Ni-ett)] differs significantly. The reduction of Ni ions occurs at a much more electropositive potential (∼−3.5 eV, −1.59 V) and it is irreversible. This is consistent with a more reduced environment for Ni atoms in P1. A partial reduction of Ni ions occurs in the range of −4.7 to −5.0 eV (−0.39 to −0.09 V). In accordance with this, the transportation of electrons is less efficient in P3 as it involves higher energy states.

UV-vis-near IR spectroscopy and implications to the charge transportation mechanism

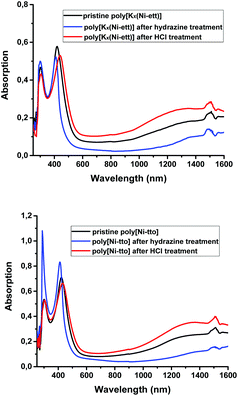
UV-vis-near IR spectroscopy measurements were performed to better understand the electronic properties of the two polymers. As seen from Fig. 6, pristine poly[K_x(Ni-ett)] and poly[Ni-tto] have very similar spectra: two peaks in the UV-vis region with λ_max = 303 and 429 nm and a broad IR signal with λ_max ∼ 1500 nm.

Fig. 6 UV-Vis absorption spectra of poly[K_x(Ni-ett)] and poly[Ni-tto] solutions.

In general, absorption spectroscopy is a powerful tool to monitor the doping process of organic π-conjugated semiconductors. As a rule, π-conjugated molecules (small molecules, oligomers or polymers) are not conductive in their pristine, neutral state and their doping (partial oxidation or reduction) is needed for the generation of charge carriers (holes or electrons). Normally, doping-generated charge carriers can be seen in absorption spectra by the appearance of broad bands assignable to charge-transfer complexes and polarons. From these, one could tentatively attribute bands in the IR region in Fig. 6 to doping-generated negatively charged polarons. The presence of these peaks in the as-synthesized polymer (i.e., which was not intentionally doped) may corroborate with the intrinsically conductive state of this n-type polymer.

To verify this idea, we attempted to change the doping level of the polymers while monitoring their absorption spectra. To this end, the as-prepared polymers were dissolved in a polar solvent (NMF) and a portion of hydrazine was added. We assumed that since hydrazine is a strongly reducing agent, it may act as the n-type dopant generating new charge carriers – electrons (or at least, their concentration should stay constant if the as-prepared polymer is fully doped). However, in contrast to this expectation, addition of hydrazine clearly reduces the IR absorptions and induced a blue shift of the absorptions in the UV-vis region for both polymers (Fig. 6). Furthermore, the addition of hydrochloric acid (which acts as a typical p-dopant for many electron-rich polymers like polyaniline, polypyrrole, and polythiophenes) slightly increased the absorption in the IR region.

To understand whether the observed changes in the absorption spectra are connected with the change in the (mobile) charge carrier concentrations, conductivity measurements for pressed pellets of pristine polymers and those exposed to different vapours were undertaken. It should be noted that this procedure always allows the same results to be obtained (within the measurement device error range) regardless of the concentration of the reactant vapors and time of exposure. On the one hand, this indicates good reproducibility of the results; on the other hand, it limits us in the ability to create a larger set of data to construct more precise dependencies (for example, to increase the number of points for Fig. 7). Quite surprisingly, these measurements revealed relatively small changes of the conductivity upon exposure to HCl and hydrazine vapours (Table 4). This is in a sharp contrast with the behaviour of doped organic semiconductors based on π-conjugated molecules, which change their conductivity by orders of magnitude upon such treatments.

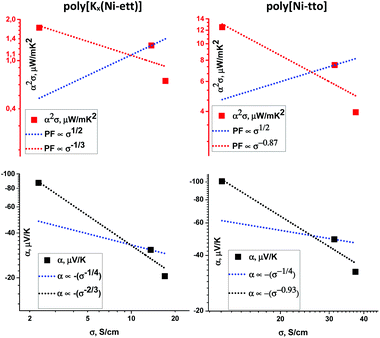Fig. 7 Seebeck coefficient (bottom) and power factor (top) as a function of electrical conductivity for poly[K_x(Ni-ett)] (left) and poly[Ni-tto] (right). Samples are obtained by exposure to hydrazine or HCl vapors, under oxygen-free conditions. The blue dashed lines indicate an empirical fit of α proportional to σ^−1/4 as well as PF proportional to σ^1/2, found for p-type π-conjugated polymers.²³ The black and red dashed lines indicate the dependency obtained from the fit of the measured data (see legend).

Table 4 Thermoelectric properties of polymers after exposure to hydrazine and HCl vapours

Probe	σ [S cm^−1]	α [μV K^−1]	PF [μW mK^−2]
Pristine poly[Kx(Ni-ett)]	13.6	−30.8	1.29
poly[Kx(Ni-ett)] upon exposure to hydrazine vapours	17.0	−20.5	0.71
poly[Kx(Ni-ett)] upon exposure to HCl vapours	2.3	−87.0	1.74
Pristine poly[Ni-tto]	31.3	−48.9	7.49
poly[Ni-tto] upon exposure to hydrazine vapours	37.3	−32.6	3.96
poly[Ni-tto] upon exposure to HCl vapours	12.3	−100.8	12.50

---

This fact suggests a different charge transportation mechanism in poly[Ni-tto] compared to conventional organic semiconductors. We postulate that transition metal ions, but not the π-conjugated system, play the key role in the electrical transportation in poly[Ni-tto]. The fact that the change of the kind of the metal from a relatively electropositive Ni to more electronegative Cu (here we mean redox characteristics of metals – standard reduction potentials) changes the conduction type from electrons (n-type) to holes (p-type),¹ supports this hypothesis. On the other hand, the fact that the deprotonation of the polymer, which certainly takes place upon addition of hydrazine (as seen from absorption spectroscopy data), has a modest effect on the conductivity, excludes the active participation of the π-conjugated system in the charge transportation. Indeed, the added protons should react with electron-rich parts of the backbone (sulphur atoms having lone electron pairs and C=C double bonds), but not with Ni cations. If the π-conjugated part of the polymer would participate in the charge transportation, its alteration should inevitably change the conductivity, which is not the case.

As such, we propose that the charge transportation in poly[Ni-tto] occurs via the hopping of electrons between Ni centres which reversibly cycle their oxidation state. The fact that the polymer formed by the conventional method from TPD needs to be oxidized to show any attractive electrical properties, suggests that the most efficient electron transportation occurs when Ni is surrounded by more oxidized thiooxalate-type sulphur atoms, as they are in tto²⁻, but not as they are in ett⁴⁻ ligands. The redox process, presumably responsible for the electron transportation, takes place in poly[Ni-tto] in the potential range of −4.1 to −4.7 eV, an optimal for electron conduction in an organics energy window.

On the other hand, a not too low energy level accounts for the good stability of poly[Ni-tto] against oxidation (oxidation potential of oxygen is −5.1 eV), compared to other organic n-type materials such as NDI-based polymers with their LUMO in the −4.0 eV range.²²

Although the proposed charge-transportation mechanism plausibly explains the experimental observations, clearly more investigations are needed to shed a light on the conductivity mechanism, which are currently undergoing.

As such, the experiments with acid/hydrazine treatments are important for understanding the charge transport mechanism. On the other hand, they discover the way for the further enhancement of the Seebeck coefficient and power factor of the polymers. Fig. 7 shows the interdependence of σ, α and PF for poly[Ni-tto] and poly[K_x(Ni-ett)] pressed pellets treated differently with hydrochloric acid and hydrazine. As usual, a decrease in the conductivity is accompanied by the increase of the Seebeck coefficient, which is a qualitatively well-established trend. What is however peculiar for the polymers studied herein is the slope of α versus σ dependence. While a relatively shallow dependence (α ∝ σ^−1/4) was empirically found for several “typical” π-conjugated polymers in the p-doped state, such as P3HT,²³ here we observed a steeper dependency on the conductivity for the poly[K_x(Ni-ett)] and poly[Ni-tto] of α ∝ σ^−2/3 and α ∝ σ^−0.93, respectively. Accordingly, the power factor follows a σ^−1/3 and σ^−0.87 dependency for poly[K_x(Ni-ett)] and poly[Ni-tto], respectively, instead of the previous published α ∝ σ^1/2 proportionality (Fig. 7).²³ Interestingly, this quantitative difference leads to important qualitative consequences for the dependence of the power factor on σ: if the power factor increases with the conductivity increase for π-conjugated polymers, the power factor increases with the conductivity decrease for both poly[Ni-tto] and poly[K_x(Ni-ett)].

This difference in the dependencies further highlights the different transport mechanism in π-conjugated versus coordination polymers investigated herein.

Conclusions

In conclusion, having the development of a more reproducible procedure for the preparation of ethenetetrathiolate-based polymers for TE applications, as the general goal, we investigated the Ni-induced complexation-polymerization of K₂tto. While the most widely used literature method involves the monomer-precursor TPD in the polymerization, we used the “true” monomer K₂tto for these purposes. This simplification of the chemical process (elimination of two problematic steps – double ring disclosure and oxidation of ett⁴⁻) favourably influenced both the reproducibility of the synthesis and the TE properties of the resulting polymer. Thus-obtained poly[Ni-tto] possesses a conductivity in the range of σ = 27–47 S cm⁻¹ and a Seebeck coefficient in the range of α = −38 to −55 μV K⁻¹, which are superior thermoelectric properties compared to poly[K_x(Ni-ett)] samples obtained by the previously reported methods. The data obtained in this work suggest that the charge transportation in poly[Ni-tto] occurs via the hopping of electrons between Ni centres which reversibly cycle their oxidation state whereas the C=C double bonds play a relatively minor role in the charge transportation, in a sharp contrast with the transport mechanism in conventional π-conjugated polymers. Cyclic voltammetry measurements reveal that the redox of Ni atoms at −4.1 to −4.7 eV is most likely responsible for the electron transportation in poly[Ni-tto] and this is a quite optimal energy window for the conduction of electrons in organics. This relatively high energy level accounts for a good stability of poly[Ni-tto] against oxidation. An interesting finding of this work is that the power factor of the polymer can be further enhanced by the treatment of the polymer with hydrazine vapours associated with a moderate decrease of the conductivity and a relatively strong increase of the Seebeck coefficient. Although the exact origin of this phenomenon is not clear, the observed trend is just opposite to the behaviour of the typical π-conjugated polymers such as p-doped P3HT. This fact further highlights the different charge-transport mechanism in poly[K_x(Ni-ett)]versus π-conjugated polymers. DFT calculations shed light on the generally valuable electronic properties of this polymer. The polymer retains its planarity even at the elevated temperatures used for simulations; the packed chains preserve small π–π distances and Ni–Ni distances which are important prerequisites for efficient electrical conductivity. The larger content of K cations in poly[K_x(Ni-ett)] may explain its lower conductivity, since positively charged species should act as traps for electrons. Our calculations show that poly[K_x(Ni-ett)] has a significant fraction of states with a relatively small distance between Ni and K, further confirming this assumption.

Experimental

Materials

Chemicals and solvents were purchased from Aldrich or TCI Europe and used as received unless otherwise stated. The monomer K₂tto was synthesized and purified as reported in our previous work.¹²

Synthesis of polymers

All reactions were carried out under an inert atmosphere using a MBraun glovebox with a purifier unit, unless otherwise indicated.

Preparation of P1. 1.557 g (22.2 mmol; 4,6 equivalents) of potassium methoxide was dissolved in 20 ml methanol. To this solution, 1.0 g 1,3,4,6-tetrathiapentalene-2,5-dione (4.8 mmol) was added. This solution was heated at 80 °C with reflux for 20 h. The obtained solution was then added to the solution of 1.141 g nickel(II) chloride hexahydrate (4.8 mmol) in 80 ml MeOH (P1_methanol) or N-methylformamide (NMF) (P1). This mixture was heated and stirred for an additional 20 h. Then the vessel was opened in air and the reaction mixture was stirred for 30 minutes at room temperature. 100 ml water was added and very intensively shaken; black precipitates were separated by suction filtration, washed with water and MeOH and then dried under vacuum at r.t. overnight.

Preparation of P2. 1.557 g (22.2 mmol; 4,6 equivalents) of potassium methoxide was dissolved in 20 ml methanol. To this solution, 1.0 g 1,3,4,6-tetrathiapentalene-2,5-dione (4.8 mmol) was added. After complete dissolution (about 5 minutes) this solution was immediately added to the solution of 1.141 g nickel(II) chloride hexahydrate (4.8 mmol) in 25 ml MeOH. The reaction mixture was stirred for 4 days at 18 °C. Black precipitate was filtered in a glovebox and washed with deionized degassed water and dry methanol. The washing of this polymer with water under an open atmosphere leads to P2-ox. Then polymers were dried under vacuum at r.t. overnight.

Preparation of P3. 1.557 g (22.2 mmol; 4,6 equivalents) of potassium tetrathiooxalate was dissolved in 20 ml NMF. The obtained solution was then added dropwise to the solution of 1.141 g nickel(II) chloride hexahydrate (4.8 mmol) in 25 ml NMF. This mixture was stirred for 10 minutes. Then 100 ml water was added under an ambient atmosphere, and very intensively shaken; black precipitates were separated by suction filtration, washed with water and MeOH and then dried under vacuum at r.t. overnight. The treatment with hydrazine or HCl vapours was carried out in a desiccator.

Characterization techniques

Because electrical conductivity, measured in pellets, depends on the pellet density (see the ESI†), all pellets were pressed with the same pressure – 10 Ton/1327 cm². The sheet resistance was measured by a 4-point probe (Euris GmbH and Keithley 2400 sourcemeter) at room temperature. The measurement of the Seebeck coefficient was performed with a SRX (Fraunhofer IPM). To ensure better electrical and thermal contact of the prepared thin films carbon foil was applied. No further (sputtered) gold contacts were used whatsoever. The thermocouple distance for measuring the temperature and voltage was set to 2.5 mm. During Seebeck measurement a temperature gradient of approximately 3 K was applied. Each sample was measured 4–6 times; the percentage of error inherent with Seebeck coefficient measurements is not more than 10%. Measurements of the electrical conductivity and Seebeck coefficient were performed under ambient conditions, with the exception of temperature-dependent measurements, which were performed under vacuum. The contents of carbon, hydrogen, sulphur and chlorine were obtained by CHNS analysis (Elementar, Vario MICRO cube, burning at 1150 °C). The analysis of potassium and nickel was carried out using an inductively coupled plasma optical emission spectrometer, ICP-OES (OPTIMA 7000 DV, PerkinElmer). Each sample was dissolved in 65% nitric acid and diluted with deionized water prior to analysis. After separation of all polymers it is possible to prepare only very dilute solutions in NMF. For this reason, only a limited number of the characterization techniques can be used. The optical absorption spectra from 200 nm to 2400 nm were measured for very dilute solutions in NMF in disposable cuvettes (12.5 mm thickness) with a Varian Cary 5000. All XPS studies were carried out by means of an Axis Ultra photoelectron spectrometer (Kratos Analytical, Manchester, UK). The spectrometer was equipped with a monochromatic Al Kα (hν = 1486.6 eV) X-ray source of 300 W at 15 kV. The kinetic energy of photoelectrons was determined with a hemispheric analyser set to pass energy of 160 eV for wide-scan spectra and 20 eV for high-resolution spectra. During all measurements, electrostatic charging of the sample was avoided by means of a low-energy electron source working in combination with a magnetic immersion lens. Later, all recorded peaks were shifted by the same value as was necessary to set the C 1s peak to 285.00 eV, which was assumed as a reference value for the carbon–sulphur bonds (Oeter, Ziegler, and Göpel 1993). Quantitative elemental compositions were determined from peak areas using experimentally determined sensitivity factors and the spectrometer transmission function. The powdery samples were mounted as pellets on double-sided adhesive tapes. The spectrum background was subtracted according to Shirley. The high-resolution spectra were deconvoluted by means of the Kratos spectra deconvolution software. Free parameters of component peaks were their binding energy (BE), height, full width at half maximum and the Gaussian–Lorentzian ratio. Cyclic voltammetry (CV) measurements were performed under a nitrogen atmosphere in a freshly prepared anhydrous and deoxygenated solution of tetra-n-butylammonium hexafluorophosphate in acetonitrile (0.1 M). The three-electrode setup consisted of a platinum disc working electrode and platinum wires as the counter electrode and pseudo-reference electrode. The thin film of the analysed material was deposited at the working electrode by drop-casting followed by solvent evaporation. The voltammograms were recorded at a scan rate of 50 mV s⁻¹ and referenced to the half-wave potential of the added internal standard ferrocene, adjusted here to 0.00 V.

Simulation techniques

For the isolated symmetrical models of poly[Ni-tto] and poly[K_x(Ni-ett)] illustrated in Fig. 8, the density functional theory (DFT) calculations are performed using Gaussian 09.²⁴ Equilibrium geometries of neutral “units” (Ni-tto)_n, where n = 1–4 for P3, their dianions and ion-pairs with two potassium cations, and (K_xNi-ett)₃ chains for P1 as electrically neutral complexes with two K⁺ cations (Fig. 8b), respectively are determined by employing the hybrid B3LYP^25,26 functional with the Stuttgart-Dresden (SDD) effective core potential and the accompanying basis set for the Ni atom²⁷ and 6-31G* basis set for the remaining atoms. This combination of the functional and the basis set has been recently used in theoretical studies of square-planar nickel complexes with diverse ligands.^28–31 The potassium cations are placed next to the most negatively charged atoms of dianions (see Fig. SB2 in the ESI†) with an initial interatomic distance “CCNi centroid-K⁺” and “SS-K⁺” exceeding 3.12 Å.³²

Fig. 8 (a) The structural models of P3: from one unit (top) to four units (bottom). The “unit” refers to the number of Ni(II) coordinated with four S atoms. Two potassium cations are shown schematically at the ends of the chain. (b) The structural model of P1: the model containing three units is presented with two possible positions of the potassium cations shown here as black spheres: on both sides (top) and on one side (bottom) from the molecular plane. The precise positions of K⁺ ions are discussed in the main text. The carbon, sulphur, nickel and potassium are shown as CPK spheres in grey, yellow, red and black, respectively.

At the next stage, the ground state geometries of all systems are further optimized applying the integral equation formalism of the polarizable continuum model (IEFPCM)³³ to simulate the solvent environment, as the experiments are conducted in NMF. In the IEFPCM model, the molecular cavity is constructed applying the Universal Force Field (UFF); the shape of the cavity is defined by interlocking spheres centred on each solute atom having van der Waals radii scaled by a factor of 1.1. Harmonic vibrational frequency calculations are used to confirm that the structure of each state in a vacuum or in the solvent is a true minimum. For the geometry optimization stage, the convergence criteria are chosen according to ‘very tight’ settings with an accurate numerical integration grid (‘ultrafine’ settings).

The vertical transition energies to the first fifty excited states are calculated for each system having optimized geometries in NMF using the time-dependent DFT (TD-DFT), the CAM-B3LYP functional, that relies on the Coulomb attenuating method.³⁴ The selected range-separate hybrid functional with the coefficients α = 0.19 and β = 0.46 and the range-separate parameter ω = 0.33 bohr⁻¹ gives the adequate predictions of the UV-Vis absorption spectra of Ni complexes, as follows from recent publications.^35,36 The electronic spectra are simulated employing Gaussian functions with the half-width at half height of 0.333 eV to build a continuous spectrum from a collection of transition peaks corresponding to the time-dependent DFT transition energies and oscillator strengths. For the analysis of UV-Vis-NIR, IR or Raman spectra and frontier orbitals, GaussView 5.0 is used.³⁷ The visualization of the molecular structures is performed in QuteMol.³⁸

To predict possible packing arrangements of oligomers, the crystal structure classical calculations are performed using a Polymorph module implemented in BIOVIA Material Studio 9.0.³⁹ The equilibrium geometries of (Ni-tto)₄ and (K_xNi-ett)₄ obtained in DFT calculations are further used in Polymorph modelling. For these simulations, the UFF parameters are employed.⁴⁰ The UFF simulations have been utilized by Vaid et al. in computational studies of one-dimensional Ni-containing polymers.⁴¹ The calculation is performed using the Ewald summation method for electrostatic (Ewald accuracy: 10⁻⁵ kcal mol⁻¹, buffer width: 0.5 Å) and van-der-Waals (Ewald accuracy: 10⁻⁵ kcal mol⁻¹, buffer width: 0.5 Å, repulsive cut-off: 6 Å) interactions. The following ten space groups are considered for the packing prediction: P2₁/c, P1̄, P2₁2₁2₁, C2/c, P2₁, Pbca, Pna2₁, Cc, Pbcn, and C2. For all stages of the packing prediction (Monte Carlo packing, pre-clustering, unit cell optimisation and ranking), the convergence criteria are chosen according to ‘ultrafine’ settings which correspond to the energy convergence of 2 × 10⁻⁵ kcal mol⁻¹. For each oligomer, the Polymorph prediction is repeated several times, and the possible crystal structures are selected. The selection criteria are the densities ρ = 2.1062 and 2.047 g cm⁻³, which correspond to the density of the pellet of poly[Ni-tto] and poly[K_x(Ni-ett)], and the lowest lattice energy E_L of the unit cell.

Finally, an NVT molecular dynamics simulation in the Forcite module of BIOVIA Material Studio 9.0 is employed on the supercells with spatial dimensions of 3a, 3b and 3c, where a, b and c are the unit cell parameters predicted in Polymorph. The settings of the simulations are: UFF, at T = 298 K, Nose thermostat, the Ewald summation method for electrostatic (Ewald accuracy: 10⁻⁵ kcal mol⁻¹, buffer width: 0.5 Å) and van der Waals (Ewald accuracy: 10⁻⁵ kcal mol⁻¹, buffer width: 0.5 Å, repulsive cut-off: 6 Å) interactions, 3 ns MD trajectory with the time step Δτ = 1 fs.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We gratefully acknowledge support from the AiF Research Association, IGF-Project No 18165 BR/1, the European Regional Development Fund (ERDF) and Free State of Saxony.

References

1. Y. Sun, P. Sheng, C. Di, F. Jiao, W. Xu, D. Qiu and D. Zhu, Adv. Mater., 2012, 24, 932.
2. J.-H. Bahk, H. Fang, K. Yazawa and A. Shakouri, J. Mater. Chem. C, 2015, 3, 10362.
3. Y. Chen, Y. Zhao and Z. Liang, Energy Environ. Sci., 2015, 8, 401.
4. R. A. Schlitz, F. G. Brunetti, A. M. Glaudell, P. L. Miller, M. A. Brady, C. J. Takacs, C. J. Hawker and M. L. Chabinyc, Adv. Mater., 2014, 26, 2825.
5. B. Russ, M. J. Robb, F. G. Brunetti, P. L. Miller, E. E. Perry, S. N. Patel, V. Ho, W. B. Chang, J. J. Urban, M. L. Chabinyc, C. J. Hawker and R. A. Segalman, Adv. Mater., 2014, 26, 3473.
6. K. Shi, F. Zhang, C.-A. Di, T.-W. Yan, Y. Zou, X. Zhou, D. Zhu, J.-Y. Wang and J. Pei, J. Am. Chem. Soc., 2015, 137, 6979.
7. H. Poleschner, W. John, F. Hoppe, E. Fanghänel and S. Roth, J. Prakt. Chem., 1983, 325, 957.
8. C. Faulmann, J. Chahine, K. Jacob, Y. Coppel, L. Valade and D. de Caro, J. Nanopart. Res., 2013, 15, 1953.
9. F. Jiao, C.-A. Di, Y. Sun, P. Sheng, W. Xu and D. Zhu, Philos. Trans. R. Soc., A, 2014, 372, 20130008.
10. K. Oshima, Y. Shiraishi and N. Toshima, Chem. Lett., 2015, 44, 1185.
11. Y. Sun, L. Qiu, L. Tang, H. Geng, H. Wang, F. Zhang, D. Huang, W. Xu, P. Yue, Y.-S. Guan, F. Jiao, Y. Sun, D. Tang, C.-A. Di, Y. Yi and D. Zhu, Adv. Mater., 2016, 28, 3351.
12. R. Tkachov, L. Stepien, A. Roch, H. Komber, F. Hennersdorf, J. J. Weigand, I. Bauer, A. Kiriy and C. Leyens, Tetrahedron, 2017, 73, 2250.
13. A. K. Menon, E. Uzunlar, R. M. W. Wolfe, J. R. Reynolds, S. R. Marder and S. K. Yee, J. Appl. Polym. Sci., 2017, 134, 6829.
14. R. Vicente, J. Ribas, P. Cassoux and L. Valade, Synth. Met., 1986, 13, 265.
15. Y. Sun, J. Zhang, L. Liu, Y. Qin, Y. Sun, W. Xu and D. Zhu, Sci. China: Chem., 2016, 59, 1323.
16. J. R. Reynolds, F. E. Karasz, C. P. Lillya and J. C. W. Chien, J. Chem. Soc., Chem. Commun., 1985 . Previously, the tetrathiooxalate-anion was polymerized in the presence of a Ni-salt; however, this work did not attract much attention because of moderate thermoelectric characteristics (conductivities in the range from 0.001 to 20 S cm⁻¹ and the Seebeck coefficient of −20 μV K⁻¹) reported for the products.
17. T. Vogt, C. Faulmann, R. Soules, P. Lecante, A. Mosset, P. Castan, P. Cassoux and J. Galy, J. Am. Chem. Soc., 1988, 110, 1833.
18. H. Yang, J.-L. Liu, L.-C. Zhou and X.-M. Ren, Inorg. Chem. Front., 2014, 1, 426.
19. G. Beamson and D. Briggs, High resolution XPS of organic polymers: The Scienta ESCA300 database, Wiley, Chichester op., 1992.
20. https://srdata.nist.gov/xps/EngElmSrchQuery.aspx?EType=PE&CSOpt=Retri_ex_dat&Elm=S , and references therein.
21. J. F. Moulder and J. Chastain, Handbook of x-ray photoelectron spectroscopy: A reference book of standard spectra for identification and interpretation of XPS data, Perkin-Elmer Corporation Physical Electronics Division, Eden Prairie op., 1992.
22. Y. Shin, A. Welford, H. Komber, R. Matsidik, T. Thurn-Albrecht, C. R. McNeill and M. Sommer, Macromolecules, 2018, 51(3), 984.
23. A. M. Glaudell, J. E. Cochran, S. N. Patel and M. L. Chabinyc, Adv. Energy Mater., 2015, 5, 1401072.
24. M. J. Frisch, et al., Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016.
25. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
26. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
27. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866.
28. H. Fukui, R. Kishi, T. Minami, H. Nagai, H. Takahashi, T. Kubo, K. Kamada, K. Ohta, B. Champagne, E. Botek and M. Nakano, J. Phys. Chem. A, 2008, 112, 8423.
29. C. M. Amb, C. L. Heth, S. J. Evenson, K. I. Pokhodnya and S. C. Rasmussen, Inorg. Chem., 2016, 55, 10978.
30. C. A. Mitsopoulou, Coord. Chem. Rev., 2010, 254, 1448.
31. C. Makedonas and C. A. Mitsopoulou, Inorg. Chim. Acta, 2007, 360, 3997.
32. C. C. Kirkpatrick, J. N. Truong and B. A. Kowert, J. Comput. Chem., 2017, 38, 93.
33. B. Mennucci, E. Cancès and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506.
34. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51.
35. L. Pilia, M. Pizzotti, F. Tessore and N. Robertson, Inorg. Chem., 2014, 53, 4517.
36. L. W. C. Paes, J. A. Suárez, A. M. Márquez and J. F. Sanz, Theor. Chem. Acc., 2017, 136, 1172.
37. R. Dennington, GaussView, Version 5, Semichem Inc, Shawnee Mission KS, 2009.
38. M. Tarini, P. Cignoni and C. Montani, IEEE Trans. Vis. Comput. Graph., 2006, 12, 1237.
39. Dassault Systèmes BIOVIA, Discovery studio modeling environment, release 9.0, San Diego: Dassault Systèmes, Discovery studio modeling environment, release 9.0, Dassault Systèmes, San Diego, 2015.
40. A. K. Rappe, K. S. Colwell and C. J. Casewit, Inorg. Chem., 1993, 32, 3438.
41. D. Tiana, C. H. Hendon, A. Walsh and T. P. Vaid, Phys. Chem. Chem. Phys., 2014, 16, 14463.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8py00931g

---