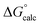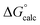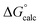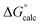Computer simulations of the catalytic mechanism of wild-type and mutant β-phosphoglucomutase

Abstract

β-Phosphoglucomutase (β-PGM) has served as an important model system for understanding biological phosphoryl transfer. This enzyme catalyzes the isomerization of β-glucose-1-phosphate to β-glucose-6-phosphate in a two-step process proceeding via a bisphosphate intermediate. The conventionally accepted mechanism is that both steps are concerted processes involving acid–base catalysis from a nearby aspartate (D10) side chain. This argument is supported by the observation that mutation of D10 leaves the enzyme with no detectable activity. However, computational studies have suggested that a substrate-assisted mechanism is viable for many phosphotransferases. Therefore, we carried out empirical valence bond (EVB) simulations to address the plausibility of this mechanistic alternative, including its role in the abolished catalytic activity of the D10S, D10C and D10N point mutants of β-PGM. In addition, we considered both of these mechanisms when performing EVB calculations of the catalysis of the wild type (WT), H20A, H20Q, T16P, K76A, D170A and E169A/D170A protein variants. Our calculated activation free energies confirm that D10 is likely to serve as the general base/acid for the reaction catalyzed by the WT enzyme and all its variants, in which D10 is not chemically altered. Our calculations also suggest that D10 plays a dual role in structural organization and maintaining electrostatic balance in the active site. The correct positioning of this residue in a catalytically competent conformation is provided by a functionally important conformational change in this enzyme and by the extensive network of H-bonding interactions that appear to be exquisitely preorganized for the transition state stabilization.

---

Introduction

β-Phosphoglucomutase (β-PGM) provides an important model system for probing the mechanisms of enzyme-catalyzed phosphoryl transfer.^1–13 This enzyme catalyzes the interconversion between β-glucose-1-phosphate (β-G1P) and β-glucose-6-phosphate (β-G6P), providing a rate-acceleration of 10²¹-fold relative to the corresponding uncatalyzed reaction in aqueous solution.^14,15 This large rate acceleration makes this enzyme particularly attractive as a model system for understanding biological phosphoryl transfer, as well as enzyme catalysis in general.

Structurally, β-PGM is a member of the haloacid dehalogenase superfamily, belonging to subclass I (c1).¹⁶ Members of this superfamily are characterized by possessing a Rossmanoid fold in their core, and a more flexible domain that can assume open or closed conformations, working as a cap (Fig. 1). The cap contains a four-helical bundle, while the core is composed of a six parallel β-sheet hairpin motif surrounded by the α-helices. This cap closure is crucial for the catalytic activity of the enzyme, as it creates a tight hydrogen bonding network that keeps the substrate and catalytic residues in the correct position for efficient catalysis.⁸

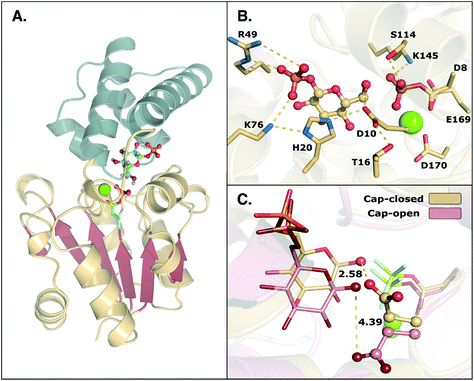Fig. 1 (A) Structure of the phosphorylated L. lactis β-PGM (PDB ID: 2WF8). The cap, represented in grey to the left, is composed of a four helical bundle. The core, in yellow and red, is composed of six β-sheets located between four α-helices. (B) A representation of the active site from the same crystal structure, with bound β-G1P, an Mg²⁺ ion, a phosphorylated aspartate (D8), and relevant residues forming a tight H-bonding network. (C) Comparison of the cap-closed and cap-open conformations of the side chain of residue D10, as found in different crystal structures¹⁰ of L. lactis β-PGM in complex with BeF₃⁻. The structure with the D10 side chain in a cap-closed conformation (PDB ID: 2WF8) forms a hydrogen bond between the aspartate and the nucleophilic oxygen of the substrate (O–O distance of 2.58 Å), whereas in the structure with the D10 side chain in a cap-open conformation (PDB ID: 2WF9), the side chain is twisted away from the reacting atoms (O–O distance of 4.39 Å) and points out of the active site.

A comparison of kinetic data between the wild-type (WT) and several mutant forms of the enzyme, as well as pH-rate profiles and structural information, have led to the suggestion of the catalytic mechanism shown in Fig. 2.^6,8 This is a two-step “ping-pong” mechanism, involving nucleophilic attack of β-G1P on phosphorylated D8 to yield glucose-1,6-bisphosphate (β-G1,6BP), followed by substrate release and rebinding in the opposite orientation to facilitate the conversion of β-G1,6BP to β-G6P. Mutational analysis has highlighted the importance of both D8 (the initially phosphorylated aspartate) and a second nearby aspartate, D10, in the catalytic cycle.^6,8 In particular, mutation of D10 to a range of residues appears to abolish the catalytic activity of the enzyme, highlighting that this residue is essential for the catalytic activity of the enzyme.⁸ This has led to the suggestion that a deprotonated D10 initially acts as a general base, activating the nucleophile to attack the phosphorylated D8 to yield β-G1,6BP, followed by a second phosphoryl transfer reaction from the 1-position of β-G1,6BP back to D8, where D10 protonates the leaving group.^6,8 However, based on structural considerations, it has also been suggested that D10 contributes to keeping β-PGM in its active, closed conformation.^1,6

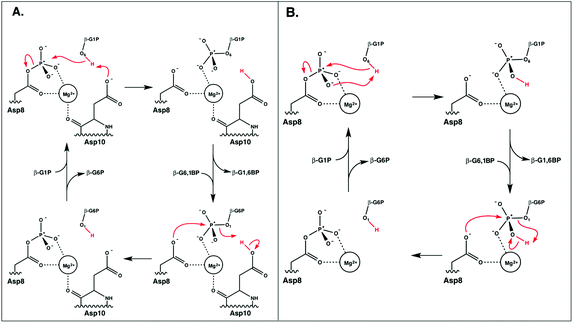Fig. 2 The two mechanisms studied in this work. (A) The D10-assisted mechanism, originally postulated in ref. 8, proposes that D10 acts as a general acid/base and the proton, highlighted in red, is transferred to and from the nucleophilic hydroxyl of the glucose. (B) The substrate-assisted mechanism has the phosphoryl group acting as the acid–base catalyst.

In the present work, we complement these kinetic studies by a systematic computational analysis of the catalysis of WT β-PGM and its D10C, D10N, D10S, T16P, H20A, H20Q, K76A, D170A point mutants, as well as the E169A/D170A double-mutant,^6,8 to unravel the structural and/or electrostatic role of these residues in catalysis by this enzyme. To explore the energetics of the two phosphoryl transfer steps in the conversion of β-G1P into β-G6P for both wild-type β-PGM and a range of mutant forms of the enzyme we have performed empirical valence bond (EVB) calculations.^17,18 This method allows us to extensively sample the dynamics of each of these proteins in aqueous solution, and consistently compare the corresponding activation free energies with a single set of EVB parameters. We demonstrate that, in line with the corresponding reaction in aqueous solution,¹⁹ there is a strong energetic preference for the D10-assisted pathway in the β-PGM active site. This mechanism is also the only mechanism that quantitatively reproduces changes in activity upon mutation of key active site residues. Finally, examining the alternate structural and energetic roles for D10 in greater depth in both wild-type and mutant enzymes shows that in addition to its potential role in acid–base catalysis, in both mechanisms, D10 is important for correct positioning of the reacting fragments as well for creating an optimal electrostatic environment for the reaction to take place.

Methodology

Choice of methodology

In line with our recent work,^20,21 our methodology of choice for this study was the empirical valence bond (EVB) approach.^17,18 This approach combines standard molecular dynamics (MD) simulations with free energy perturbation/umbrella sampling (FEP/US) calculations to allow for the accurate description of chemical reactivity within the framework of valence bond theory (for a recent review, see ref. 22). This approach is extremely fast, allowing us to perform the extensive sampling required to obtain convergent free energy profiles and observe local structural rearrangements as the system responds to the charge changes on the reacting atoms along the reaction coordinate, while still providing a physically meaningful description of the bond-making and bond-breaking processes involved. Here, we have performed extensive EVB calculations of the chemical steps (Fig. 2) for the reaction catalyzed by wild-type β-PGM and a range of experimentally characterized mutant forms of the enzyme,^6,8 considering different mechanisms for each reaction step, as well as the structural and energetic consequences of each mutation.

Initial system setup for the simulations of the enzymatic reaction

As shown in Fig. 2, the reaction catalyzed by β-PGM is a two-step process, comprising first the conversion of β-G1P → β-G1,6BP, followed by the independent conversion of β-G1,6P → β-G6P (after releasing β-G1,6BP so that it can re-bind in the opposite orientation). We have considered two possible mechanisms for these processes in our EVB calculations: a general-base catalyzed mechanism in which the nucleophilic hydroxyl group (position 6 of β-G1P) attacks the phosphorylated D8, with its proton transferred to the D10, as seen in Fig. 2A (“D10-assisted mechanism”), and a substrate-assisted mechanism, where the same nucleophilic attack takes place, but the hydroxyl group is deprotonated by one of the non-bridging oxygens of the phosphate group, as seen in Fig. 2B (“substrate-assisted mechanism”). To maintain microscopic reversibility, this is followed by release and rebinding of either β-G1,6BP with a dianionic phosphate group opposite a protonated D10, or β-G1,6BP with a protonated monoanionic phosphate group opposite an anionic D10. For both mechanisms, in the second step, the group transfer is coupled to proton transfer to the leaving group to yield β-G6P, and for both reaction steps, the reaction was modeled as a two-state process, with phosphoryl transfer and proton transfer being coupled in the same reaction step.

For the first step of the reaction shown in Fig. 2 (the conversion of β-G1P → β-G1,6BP), the initial structure used in the simulations was taken from the Protein Data Bank (PDB ID 2WF8^10,23). This structure is of β-PGM in its closed conformation, inhibited by β-G6P and BeF₃⁻ as an analogue for the phosphate group on D8. The metal fluoride was manually converted back to a phosphate, and the β-G6P in this structure was replaced with β-G1P, which was adjusted in the active site so as to allow for optimal hydrogen bonding interactions and with the OH group of the sugar oriented to be in line for nucleophilic attack on the phosphorylated Asp. Note that, as shown in Fig. 1, there are numerous hydrogen bonding interactions keeping the substrate in place (in particular interactions between R49, K76 and the phosphate group in the 1-position), and therefore, even when altering the starting position of the substrate, it moved back to the same position after equilibration. In order to verify that the substrate positioning after equilibration is not an artifact of having manually placed the substrate in the active site, we also performed molecular dynamics simulations of β-PGM in complex with a phosphonate analogue of β-G1P (PDB ID 4C4R, converting the phosphonate back to the phosphate by atom replacement)¹³ to verify that the substrates equilibrate to similar positions in both cases.

To reduce computational cost, we divided the system into three regions as is commonly performed in similar work:^24,25 a reactive region, containing all the reacting atoms taking part in the EVB calculation, an active region, where all the atoms within 24 Å of the transferring phosphorus atom were allowed to move freely, and an external region, where all the remaining atoms were constrained to their initial positions. The protonation states for all histidines were inspected using MolProbity,²⁶ as well as visual inspection, and protonation patterns (at the δ- vs. the ε-positions) were assigned accordingly (for a full list of ionized residues in our simulations, see Table S1†). All other ionizable residues within 18 Å of the transferring phosphorus were ionized, whereas residues outside this region were kept neutral for system stability. Additionally, depending on the mechanism being modeled, the proton in the attacking hydroxyl group of β-G1P was placed in one of two positions: pointing either towards a non-bridging oxygen of the phosphate or towards the D10 side chain. The resulting hydrogen bonding interaction kept the proton in place during all subsequent equilibration runs.

A similar procedure was performed for the second step of the reaction (the conversion of β-G1,6P → β-G6P), using the structure of Allen and co-workers (PDB ID: 1O03¹). In this case, the substrate was kept in the position presented in the crystal structure and the MgF₃⁻ was converted to a phosphoryl group and allowed to relax to a tetrahedral phosphate bound to the substrate. In the case of the mutant forms of β-PGM, all mutants were generated using the mutagenesis tool implemented in PyMol.²⁷ The rotamers yielding the smallest strain force and largest number of hydrogen bonds were chosen for the subsequent simulations. In the case of the H20Q rotamer, the side chain conformation of Q20 that kept the same hydrogen bonding pattern as the original histidine was chosen for subsequent simulations.

As with previous work,^20,21 we modeled the catalytic Mg²⁺ using an octahedral cationic dummy model,^28–30 which describes the metal center using a set of dummy atoms as shown in Fig. S1.† These dummy particles are tightly bonded to each other and to the central atom, but not to the surrounding ligands. Therefore, the entire dummy model is allowed to freely rotate around its frame, allowing for flexibility in ligand binding while simultaneously maintaining a stable coordination geometry and providing a reliable description of the electrostatics involved (see ref. 28 and 29 for further details). The parameters used to describe the dummy model were presented in ref. 29.

Finally, the full system was solvated in a spherical droplet of TIP3P water molecules³¹ of 24 Å radius, centered on the phosphorus atom of the transferred phosphoryl group. This droplet was subjected to a 10 kcal mol⁻¹ Å⁻² surface restraint on its outer layer (the outer 15% or 3.6 Å of the sphere) to keep it stable, in line with the surface constrained all atom solvent model³² to describe the boundary conditions. This droplet was large enough to encompass nearly all the enzyme, and all atoms that fell outside the sphere were subjected to a 200 kcal mol⁻¹ Å⁻² positional restraint to keep them at their crystallographic positions, in line with our previous work²¹ and similar QM/MM studies of enzymatic reactions.²⁴ As outlined above, only residues within the inner layer (i.e. the active region) of the droplet were ionized, in order to maintain system stability.

Initial molecular dynamics equilibration of the system

To equilibrate the wild-type and mutant enzymes in preparation for EVB simulations, each system was gradually heated from 1 K to 300 K over 80 ps of simulation time, while applying a 200 kcal mol⁻¹ Å⁻² harmonic force constant on the solute atoms to restrain them to their crystallographic positions. This allowed the solvent molecules to equilibrate around the protein and the removal of any initial bad contacts. The system was then cooled down to 5 K for another 10 ps, and then gradually heated to 300 K for 90 ps of simulation time, while the force constants of the harmonic restraint were gradually decreased from 200 to 0.5 kcal mol⁻¹ Å⁻². Finally, a 10 ns equilibration was performed at 300 K for all enzyme simulations using a 0.5 kcal mol⁻¹ Å⁻² position restraint on the substrate atoms, the carboxylic group of the nucleophile, and the side chain of the D10, to keep the reacting atoms in place. The RMSD of the mobile region of the system to equilibrate, as shown in Fig. S2 and S3.† The use of a shorter equilibration time allows us to run a larger number of independent EVB trajectories, as outlined below.

An angle restraint of 10 kcal mol⁻¹ rad⁻² with an equilibrium angle 180° was introduced between the center of the Mg²⁺ dummy model and the side chain of D8 (Mg²⁺–O_metal–O_free, where O_metal corresponds to the oxygen atom closest to the Mg²⁺, and O_free the oxygen not coordinated to it). We have discussed the challenges with classical simulations of metal ions at length in ref. 29, and refer interested readers to that work for further information. Finally, following the initial equilibration step, we performed an additional 500 ps of molecular dynamics simulations on each structure, during which time ten snapshots of the system were taken (one every 50 ps) to be used as starting points for ten subsequent EVB simulations of each system.

Empirical valence bond calculations

All EVB calculations were performed using the standard free energy perturbation/umbrella sampling (EVB-FEP/US) procedure outlined in ref. 18. The key feature of the EVB approach is that the reacting atoms use Morse instead of harmonic potentials to describe bonds that are changing during the reaction, allowing bond forming and breaking processes to be described by classical simulations. All standard MD and EVB simulations were performed using the OPLS-AA/M force field^33–35 as implemented in the Q simulation package (Version 5.0.6³⁶). OPLS-AA/M parameters for atoms included in the EVB region (Fig. S4 and S5†) were generated with Macromodel 9.1³⁷ (version 2001, Schrödinger LLC), and partial charges for the phosphorylated aspartate and the substrates were calculated at the HF/6-31G* level of theory, using Gaussian 09 rev. D01³⁸ and the standard RESP procedure.³⁹ All EVB parameters used in this work are described in the ESI.† For each simulation, all atoms in the system were subjected to a 30 Å cutoff for their non-bonded interactions, except for the EVB atoms, which were subjected to a 99 Å cutoff (i.e. essentially no cutoff). Long-range interactions were treated using the local reaction field (LRF) approach.⁴⁰ All standard MD and EVB simulations used 1 fs time steps, and the temperature of the system was regulated using the Berendsen thermostat,⁴¹ with a 100 fs bath relaxation time. Finally, all EVB-FEP/US simulations of the enzymatic reaction were performed at 300 K, using 51 EVB-FEP/US windows of 200 ps length per window for the enzymatic runs, running ten replicates from different starting structures for each system. Therefore, each individual EVB trajectory was 10.2 ns in length, leading to 102 ns sampling for each system, and ∼5 μs sampling in total for all enzymatic reactions considered in this work, considering all mutants, different proton donors/acceptors, and different reaction steps.

Calibration of the EVB parameters

The EVB approach relies on the calibration of a set of empirical parameters to describe the energetics of a reaction of interest^17,18 by specifically describing the coupling between different valence bond (VB) states, as well as the position of the corresponding VB parabolas relative to each other. These parameters are obtained by parameter fitting to a well-defined reference state based on either experimental data or high-level quantum chemical calculations. Once the reference state has been calibrated, all parameters are kept unchanged when moving to subsequent systems. A suitable reference state could be, for example, either the corresponding uncatalyzed reaction in aqueous solution or the wild-type enzyme when comparing a series of mutants. Note here that rigorous theoretical considerations have shown the coupling parameter between the different VB states to be phase-independent,⁴² which greatly reduces computational complexity and allows for direct comparison of the same reaction with the same parameters in different reaction environments.

In the case of the present study, the background uncatalyzed reaction, i.e. acetyl phosphate hydrolysis, is a well-studied reaction, for which there exist extensive kinetic measurements,^43,44 making it straightforward to perform our EVB fitting. For both substrate- and solvent-assisted pathways, the uncatalyzed reaction was modeled using a truncated system by capping the EVB atoms shown in Fig. 3 with methyl groups, so that the same reacting atoms are involved in our modeling of both the enzymatic reaction and the corresponding background reaction in aqueous solution. Note that for simplicity of the calibration, the Mg²⁺ ion was not included in the corresponding uncatalyzed reaction.

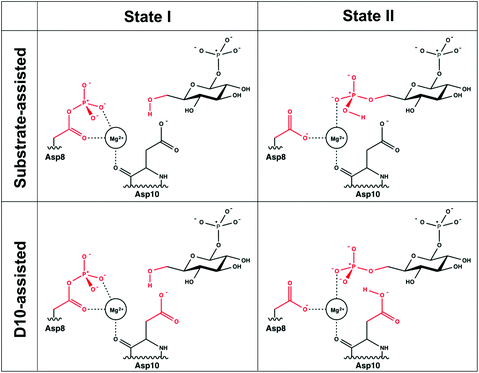Fig. 3 The two valence bond states corresponding to the first step for the two mechanisms studied in this work. For the second step, the valence bond states are inverted, with the reacting atoms from the substrate being connected to the position 1 instead of position 6 (see Fig. 2). The reacting atoms used for the EVB calculations are represented in red. The atoms shown in black were not included as explicit reacting atoms when setting up our EVB system.

The observed first order rate constant for acetyl phosphate hydrolysis in aqueous solution at 25 °C is 1 × 10⁻⁵ s⁻¹ (ref. 45), corresponding to an activation free energy (ΔG^‡) of 23.9 kcal mol⁻¹ and the reaction rate appears to be insensitive to either nucleophilic or general base catalysis.⁴⁴ The reaction free energy of acetyl phosphate hydrolysis in aqueous solution has been measured to be −10.3 kcal mol⁻¹ (ref. 46). Detailed quantum chemical calculations of the hydrolysis of a range of phosphate esters, including acetyl phosphate, strongly suggest that this corresponds to a more dissociative solvent-assisted pathway rather than a more associative substrate-assisted pathway.^19,47,48 In particular, in the case of acetyl phosphate hydrolysis, two different functionals both suggested that the substrate- assisted pathway is between 7–9 kcal mol⁻¹ higher in energy than the solvent-assisted pathway,¹⁹ a trend we also observed in quantum chemical calculations of the hydrolysis of both methyl triphosphate¹⁹ and also phosphate monoester dianions with good leaving groups.⁴⁸ Therefore, for the first step of the reaction, we fit our background reaction in aqueous solution to activation and reaction free energies of 23.9 and −10.3 kcal mol⁻¹ respectively for the D10-assisted pathway, and in the case of the substrate-assisted pathway, we fit the activation free energy to an 8 kcal mol⁻¹ higher value, in line with the quantum chemical calculations of ref. 19.

Metadynamics simulations of the conformational change of the D10 side chain

Metadynamics⁴⁹ is a method in which sampling is enhanced by introducing an additional bias potential acting on a selected number of degrees of freedom, often called as collective variables (CVs). Metadynamics is currently becoming a powerful enhanced sampling algorithm for the efficient and rapid computation of multidimensional free energy surfaces.^50–52 In order to confirm which of the D10-conformations shown in Fig. 1C is energetically preferred, well-tempered metadynamics (WT-MetaD⁵³) simulations were performed to determine the relative free energies of the two D10 conformations, and the associated barrier to the side chain rotation. The simulations were performed with GROMACS v.5.1.4^54–56 interfaced with the PLUMED plugin (v2.3.0⁵⁷), in combination with the OPLS-AA force field^33,35 for compatibility with our EVB simulations. The starting structure was taken from β-PGM in complex with β-G1,6P and Mg²⁺ at the ground state (PDB ID: 1O03¹), in which D10 is present in the “cap-closed” conformation. The same β-G1,6P and Mg²⁺ force field parameters as in the EVB calculation were used in the WT-MetaD simulations (see the ESI† for parameters). The protonation states of His were treated the same as in the EVB simulations, as listed in Table S1,† and all other ionized residues (Asp, Glu, Arg and Lys) were modeled with standard states at physiological conditions, i.e. Asp and Glu are negatively charged while Arg and Lys are positively charged (as the full system is now being considered in these simulations unlike the truncated system in the EVB simulations). The resulting complex was put in the center of an octahedral box filled with TIP3P water molecules,³¹ with at least 10 Å distance between the surface of the complex and the edge of the box. 10 Na⁺ ions were added to neutralize the system. After the system setup was complete, a 5000-step minimization was performed using the steepest descent and conjugate gradient methods, followed by the heating up of the solvated system from 0 to 300 K over a 500 ps MD simulation in an NVT ensemble, using the velocity rescaling thermostat⁵⁸ with a time constant of 1.0 ps for the bath coupling. This was again followed by a further 500 ps of simulation in an NPT ensemble at 300 K and 1 atm, controlled by the same thermostat and a Parrinello–Rahman barostat⁵⁹ with a time constant of 2.0 ps. Positional restraints of 1000 kJ mol⁻¹ nm⁻² were applied on every heavy atom in each of the xyz directions for the first two steps of equilibration. Afterwards, the positional restraints were gradually reduced to 100 kJ mol⁻¹ nm⁻² over five 500 ps steps of the NPT equilibration. The last configuration was then used as the starting conformation of the WT-MetaD simulations. For the WT-MetaD sampling, the Gaussian-shape biasing potentials were added on the dihedral of the D10 side chain (C-CA-CB-CG). The biasing potentials were added every 1 ps with an initial height of 0.3 kcal mol⁻¹, decreased gradually on the basis of adaptive biasing with a bias factor of 16. The width of the Gaussians was set at 0.3 radians. Three independent 1200 ns WT-MetaD simulations were performed in an NPT ensemble at 300 K and 1 atm, using a velocity rescaling thermostat with a time constant of 1.0 ps and a Parrinello–Rahman barostat⁵⁹ with a time constant of 2.0 ps. For all the simulations, the LINCS algorithm^60,61 was applied to constrain all the bonds, using a 2 fs time step. The results obtained from the three independent runs were averaged to determine the relative free energies of the two different states.

Results and discussion

Comparing the alternative catalytic mechanisms

The mechanisms considered in this work (Fig. 2) are both concerted A_ND_N reactions, differing only in the identity of the proton donor/acceptor (D10 vs. the substrate itself). For the first step of the reaction (conversion of β-G1P → β-G1,6BP), we equilibrated the system with the proton on the nucleophile OH group pointing towards D10. To model the second reaction step, two initial protonation patterns were considered in order to maintain microscopic reversibility: (1) the binding of a dianion opposite a protonated D10 and (2) the binding of a phosphate monoanion opposite a deprotonated D10. The resulting energetics are shown in Table 1.

Table 1 Calculated and observed^a activation (ΔG^‡) and reaction free energies (ΔG°) for the two reaction steps involved in the isomerization of β-G1P into β-G6P for the wild-type and mutant variants of L. lactis β-PGM. All energies are given in kcal·mol⁻¹

System	D10-assisted mechanism				Substrate-assisted mechanism				Rate-limiting step
	Step I (β-G1P → β-G1,6P)		Step II (β-G1,6P → β-G6P)		Step I (β-G1P → β-G1,6P)		Step II (β-G1,6P → β-G6P)
	ΔG^‡calc		ΔG^‡calc		ΔG^‡calc		ΔG^‡calc		ΔG^‡exp^a
a Experimental values obtained from ref. 6 and 8. Experimental measurements were made at pH 7.0 and 25 °C. Note that the calculated ΔG° values denote the free energy difference between bound reactant and product states, rather than the free substrate/free product, which is why this value changes depending on the specific variant. b Not determined.
WT	11.8 ± 1.7	−5.6 ± 2.1	14.4 ± 0.6	−1.3 ± 0.7	16.9 ± 2.9	−18.0 ± 4.0	21.2 ± 0.9	−20.3 ± 1.5	14.8
D10C	n.d.^b	n.d.^b	n.d.^b	n.d.^b	17.1 ± 1.0	−12.9 ± 2.4	32.9 ± 3.6	−9.5 ± 2.5	>21.7
D10N	n.d.^b	n.d.^b	n.d.^b	n.d.^b	19.0 ± 1.8	−16.1 ± 3.0	31.8 ± 3.2	−11.0 ± 3.1	>21.7
D10S	n.d.^b	n.d.^b	n.d.^b	n.d.^b	18.7 ± 1.6	−10.1 ± 2.3	33.1 ± 3.4	−11.8 ± 3.5	>21.7
T16P	12.9 ± 2.3	−6.3 ± 3.9	16.3 ± 1.1	1.3 ± 2.6	15.6 ± 3.1	−19.0 ± 3.4	21.3 ± 3.6	−17.5 ± 3.9	19.6
H20A	14.1 ± 2.1	−3.6 ± 1.3	16.1 ± 1.0	2.1 ± 1.5	16.2 ± 1.4	−16.4 ± 2.3	21.4 ± 3.2	−17.5 ± 3.6	19.6
H20Q	14.9 ± 2.9	−4.0 ± 2.2	15.7 ± 1.1	−0.6 ± 1.5	14.1 ± 1.9	−19.5 ± 2.9	20.4 ± 1.4	−17.6 ± 2.4	15.6
K76A	11.9 ± 1.1	−6.7 ± 1.9	17.4 ± 1.5	3.3 ± 1.9	18.7 ± 2.5	−17.9 ± 3.1	22.8 ± 0.7	−18.0 ± 1.7	17.2
D170A	11.1 ± 0.4	−8.8 ± 1.2	18.8 ± 1.2	4.6 ± 1.3	17.7 ± 3.2	−22.5 ± 3.1	24.8 ± 1.1	−11.9 ± 2.6	20.8
E169A/D170A	8.0 ± 0.9	−13.8 ± 1.9	25.3 ± 1.3	14.3 ± 1.3	19.5 ± 2.8	−19.5 ± 4.6	26.6 ± 3.3	−14.4 ± 3.3	21.5

---

In our previous quantum chemical studies of the uncatalyzed hydrolysis of acetyl phosphate in aqueous solution,¹⁹ we predicted that a solvent-assisted pathway would be preferred over a substrate-assisted pathway by ∼7–9 kcal mol⁻¹, depending on the functional used to model the reaction. In the case of the enzyme catalyzed reaction (Table 1), we obtain a discrimination of 5.1 kcal mol⁻¹ in the first reaction step (β-G1P → β-G1,6BP), and 4.3 kcal mol⁻¹ in the second reaction step, in favor of the D10-assisted pathway (β-G1,6BP → β-G6P). In the case of the D10-assisted pathway, the second reaction step is rate-limiting, with a calculated activation free energy of 14.4 kcal mol⁻¹, which is in good agreement with the experimental value of 14.8 kcal mol⁻¹ (ref. 6 and 8, although this value provides only a maximum limit for the activation free energy if bond-breaking is not rate-limiting, and the real experimental value could be lower than this). In contrast, the substrate-assisted pathway is substantially higher in energy, with an activation free energy of 21.2 kcal mol⁻¹.

Interestingly, a distance comparison of the relevant P–O and O–H distances during the second step of the reaction (Fig. 4) shows that while the proton and phosphoryl transfer processes are fairly synchronous in the D10-assisted pathway, they are decoupled in the substrate-assisted pathway. In the latter case, deprotonation of the nucleophile precedes nucleophilic attack in the first reaction step, and protonation of the leaving group happens after the phosphoryl group has begun to transfer. Therefore, in the substrate-assisted pathway this protonation is not a driving force for formation of the transition state for the energetically expensive conversion of β-G1,6BP → β-G6P (in contrast to the first step where it precedes phosphoryl group transfer). Rather, the presence of the proton on the monoanionic phosphate assists in reducing the electrostatic repulsion between the nucleophile and the phosphoryl group during the reaction. Protonation of the leaving group is ultimately required in the second reaction step as it affects the stability of the product state, where a less stable deprotonated product state would increase the barrier to the corresponding transition state by shifting the VB parabola. Therefore, even in the substrate-assisted pathway, the D10 side chain contributes to the reduction of the activation barrier by helping position the reacting fragments for more facile proton transfer to the leaving group at some point along the reaction coordinate, although this contribution is not large enough to overcome how energetically unfavorable this pathway is in the corresponding uncatalyzed reaction.¹⁹

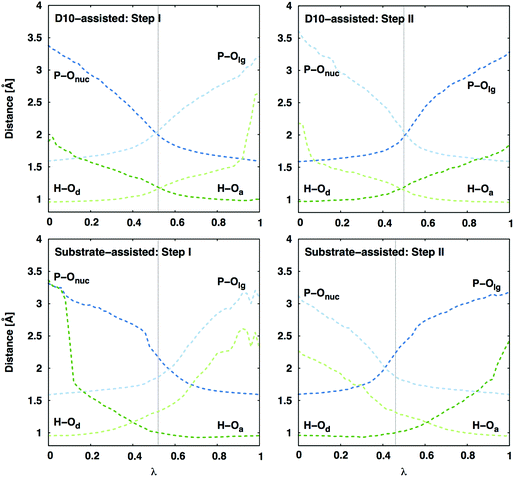Fig. 4 Average P–O and H–O distances (in Å) along the reaction coordinate λ (0 corresponds to the reactant state, and 1 is product state) for both mechanisms in the active site of wild-type β-PGM. Standard deviations of the measured distances are between 0.01 and 0.15 Å (decreasing as the bond is formed and thus the reacting fragments are better kept in place). Here, ‘O_nuc’ represents the nucleophilic oxygen, ‘O_lg’ the oxygen where the leaving group is formed, and ‘O_d/a’ represents the proton donor/acceptor for the different steps (see Fig. 2). The vertical dashed line indicates the transition state. The D10-assisted mechanism is a synchronous process for both the phosphoryl group and proton transfers, whereas in the substrate-assisted mechanism the proton is transferred to the phosphate before the phosphoryl transfer in the Step I, and after the transfer of the phosphoryl group in the Step II.

Probing the structural and catalytic role of the D10 side chain

An examination of all available crystal structures of β-PGM in the Protein Data Bank²³ shows that in the cap-closed conformation of the enzyme, the D10 side chain points into the active site and forms hydrogen bonding interactions with T16 and H20. On the other hand, in the cap-open conformation the D10 side chain has lost its interactions with T16 and H20 and points out of the active site. The only exception to this is a 1.4 Å crystal structure of β-PGM in complex with G6P and BeF₃⁻ (PDB ID: 2WF9¹⁰), where the D10 side chain can be found in the same position as it typically occupies in the cap-open conformation of the enzyme (referred to henceforth as “cap-closed” and “cap-open” conformations of D10 respectively). However, even in this complex, as D10 has moved into its “cap-open” position, the cap has started to open compared to a fully cap-closed position, reinforcing the additional structural role of D10.

Thus, having characterized the fundamental structural and energetic changes involved in the substrate- vs. D10-assisted pathways in the reaction catalyzed by wild-type β-PGM, an interesting follow-up question is the potential role of D10 in keeping the β-PGM cap closed, as was suggested by ref. 8, versus any role it may play in acid–base catalysis. An overlay of the structures of β-PGM in its fully-closed and fully-open conformations can be seen in Fig. 5, which illustrates that the cap of the enzyme undergoes a substantial displacement (RMSD of 5.14 Å) upon ligand binding (Fig. 5A). A comparison of the key residues lining the binding pocket in the open and closed conformations (Fig. 5B) shows that there is a substantial displacement in three key residues, specifically the side chains of D10, T16 and H20. These three residues are very far apart in the open conformation (D10 and H20 are more than 7 Å apart), but move within hydrogen bonding distances of each other upon cap closure. To better illustrate this, we have created simple animations of the cap-closure using the “Morph” module implemented in Chimera,⁶² which are provided as ESI† to the manuscript. These animations were created from a simple linear interpolation between the two structures, and therefore have limited physical meaning (for example, in the case of the close-up of the active site, it can be seen that at one point the D10 and T16 side chains come extremely close to each other, beyond what would be physically reasonable). However, the animations can still provide an easier overview of how the protein has to change shape to facilitate the cap closure than can be obtained from just comparing the two static structures to each other. From the close-up animation of the active site residues, it can be seen that the side chains of both D10 and H20 flip during the cap closure to come into hydrogen bonding distance with each other, and that the shifted D10 is further stabilized by a hydrogen bonding interaction with the hydroxyl group of the T16 side chain. These interactions presumably help keep the cap in a closed conformation, although it is of course equally possible that the cap closure and associated movement of T16 and H20 play a role in positioning D10.

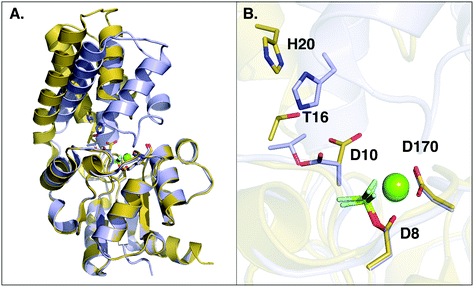Fig. 5 Overlay of open (in yellow, PDB ID: 2WFA) and closed (in grey, PDB ID 2WF8) conformations of wild-type L. lactis β-PGM. (A) The overall conformational change between the open and closed forms, where the core domain of both conformers was aligned. (B) A close-up of the active site, showing the repositioning of key active site residues upon the conformational change. A movie showing the movement of the whole system between the open and closed conformations as well as the changes in key interaction distances upon the conformational change can be found as ESI.†

The overall importance of cap closure and positioning of D10 to the β-PGM catalyzed reaction can also be deduced from the approximate rate for the competing hydrolysis of the phosphorylated D8 side chain from a cap-open conformation of the enzyme (2.6 × 10⁻² s⁻¹ at 25 °C (ref. 63)), corresponding to an activation free energy of 19.7 kcal mol⁻¹. This is ∼1000-fold faster than the rate of the corresponding uncatalyzed hydrolysis of acetyl phosphate (2.3 × 10⁻⁵ s⁻¹, ref. 45), but still significantly slower than the rate of the enzyme-catalyzed reaction.^6,8 This is most likely due to a loss of key interactions involved in transition state stabilization, the suboptimal positioning of the D10 side chain in the cap-open conformation (Fig. 1) as well as increased solvent-accessibility to the active site with D10 in the cap-open conformation (PDB ID: 2WF9).

There is a possibility that the “cap-open” conformation of the D10 side chain is actually the preferred ground state for β-PGM, and that there is a free energy penalty associated with bringing it into the catalytically active “cap-closed” conformation where the D10 side chain points into the active site (assuming that D10-movement is decoupled from the overall conformational change of the enzyme). Therefore, we have performed metadynamics simulations of the rotation of the D10 side chain from its cap-closed to the cap-open conformation (see the Methodology section) in the closed form of the enzyme. These calculations indicated that there is a free energy difference of 0.8 ± 0.9 kcal mol⁻¹ between the two states (in favor of the “cap-open” conformation), and an activation barrier of 3.1 ± 0.6 kcal mol⁻¹ for the conformational transition between the two states (Fig. 6). However, the free-energy difference between the two states is within the error of the calculations, and thus both states are effectively equally viable, with at most a negligible energetic penalty involved in placing the D10 side chain in a catalytically favorable “cap-closed” conformation. Once positioned in this conformation, this side chain, in turn, contributes to maintaining the solvent-excluded cap-closed conformation of the enzyme through an intricate network of hydrogen bonds that keep the catalytic residues in place during the reaction.

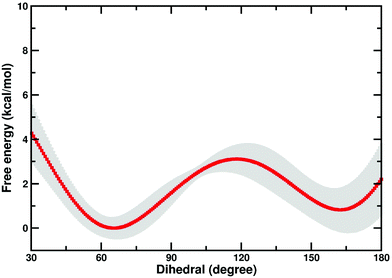Fig. 6 Free energy profile (kcal mol⁻¹) for the transition between the “cap-open” and “cap-closed” conformations of the D10 side chain, obtained as described in the Methodology section. For a schematic of the two side chain conformations, see Fig. 1. Shown here is an average over the three independent metadynamics simulations (with the shaded area showing the standard deviation at each point), and the corresponding calculated energies relative to the respective free energy minima.

Finally, we note that a detailed examination of all β-PGM structures available in the Protein Data Bank shows a strong correlation between the position of the β-PGM cap and whether D10 is pointing into or out of the active site, and, most importantly, even in the closed structures with metal-fluoride phosphate analogues (e.g. PDB IDs: 2WFA, 2WF8 and 2WF9 with BeF₃⁻, in their active sites^1,10,13), D10 is able to adopt its “cap-closed” conformation suggesting that charge repulsion alone will not push it out of the active site. These experimental structural data corroborate our computational structural and energetic analysis in that the D10 side chain contributes to a stabilization of a cap-closed desolvated active site and positioning the reacting fragments in the correct position for efficient nucleophilic attack.

Probing key active site mutations

By performing linear response approximation (LRA) analysis on the ensemble of Michaelis complex and transition states structures obtained from our EVB simulations, it is possible to compare the electrostatic contributions of different amino acid side chains to the calculated activation barriers (see e.g.ref. 64 and 65). As the two reaction steps are mirror images of each other, these contributions are also qualitatively mirror images of each other (Fig. 7).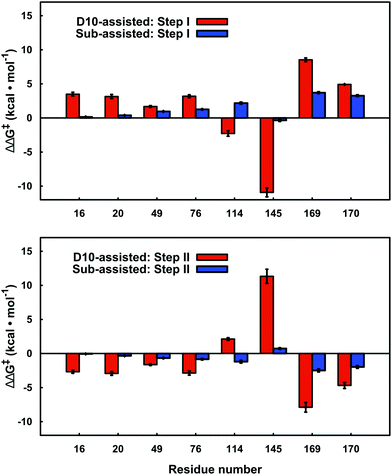

Fig. 7 Electrostatic contributions of individual amino acid side chains to the calculated activation barrier for both steps of the D10- and substrate-assisted mechanisms. The residue contributions were calculated using the linear response approximation, as described in ref. 64 and 65. The error bars indicate standard deviations over ten independent trajectories. Positive and negative values indicate destabilizing and stabilizing contributions, respectively. Only residues that give significant contributions of >1.0 kcal mol⁻¹ for at least one of the mechanisms are highlighted here.

Our LRA results allow for the prediction of the residues that make the largest contributions to the calculated activation barriers, and the results independently highlight as being important several key point mutations that have already been studied experimentally.^6,8 The more rigorous EVB activation free energies of these mutants, which consider both the D10- and substrate-assisted mechanisms, are compared to experimental values obtained from first-order rate constants^6,8 in Fig. 8 and Table 1. In the case of the D10-assisted pathway, we obtain reasonable activation free energies for all β-PGM variants with the exception of the E169A/D170A variant, where we significantly overestimate the activation free energies (taking into account the caveat that the experimental values are maximum activation free energies only, should bond-breaking not be rate limiting). This is most likely due to the fact that the simultaneous mutation of two metal binding residues significantly disrupts the structure compared to the wild-type enzyme, making it challenging to make meaningful computational predictions in the absence of a crystal structure of this protein variant.

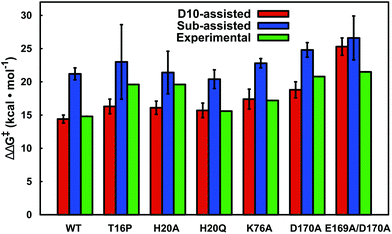Fig. 8 A comparison between calculated and experimental activation free energies for wild-type β-PGM and a series of active site mutants. The calculated values correspond to the activation barrier obtained for the second step, which is the rate-limiting step. The individual energetics for both reaction steps are shown in Table 1. All values are averages over ten independent simulations from different starting structures, and the error bars represent the standard deviations over the ten simulations. Note that the D10-variants have not been included in this figure as this form of the enzyme is inactive (see Table 1).

In the case of the substrate-assisted pathway, the first reaction step appears to be fairly insensitive to truncation of D10. Interestingly, the second reaction step appears to be highly sensitive to truncation of D10, thus causing significant increases in the (already high) activation free energies for this step. We note that for these variants, the reactions were so slow that experimentally it was only possible to estimate an upper limit for the rate of this reaction (k_cat < 10⁻³ s⁻¹ (ref. 8)). This would in turn provide a lower limit of ca. 21.7 kcal mol⁻¹ for the corresponding activation barrier, highlighting the importance of D10 to the observed catalytic activity of this enzyme. In all variants, the substrate-assisted pathway is energetically unfavorable and unlikely to appear as a competitor to the D10-assisted pathway.

All β-PGM variants presented in Table 1 and Fig. 8 involve the substitution of a residue that interacts with D10 either directly or via an intervening residue. The effect of each mutation considered is described in detail below.

D10S, D10C and D10N. As soon as D10 is replaced by either serine, cysteine or asparagine, the proton to be transferred always forms a hydrogen bond to either one of the non-bridging phosphate oxygens of the phosphorylated D8 (Step I) or to the carboxylate group of the D8 side chain (Step II). Thus, for the reaction to occur in Step II, the hydrogen atom needs to rotate back to the leaving group oxygen rather than interacting with the D8 side chain. Among the three D10 mutants being considered in this work, S10 changed the original interaction network within the active site the least. In particular, this variant retained the WT H-bonding interactions to the side chain of T16 for both steps of the reaction (see Fig. 1 for an overview of the relative positions of these side chains). In contrast, the simulations of the D10N mutant showed the largest structural perturbations compared to the WT and other D10 mutants.

Interestingly, the reactions involving the D10 mutants are much more endergonic in the second reaction step than for the wild-type reactions (Table 1). These differences are quite large and can be explained in terms of changes in charge–charge interactions in the active site. That is, as soon as D10 is mutated to a non-charged residue, the electrostatic repulsion between the phosphate group and the carboxylic side chain of D10 in the Michaelis complex of the wild-type enzyme is removed. This leads to a significant reduction in energy of the Michaelis complex compared to the product complex, where either D10 would be protonated (and thus non-charged) in the wild-type or there would be a non-charged residue to start with at this position in the mutants.

T16P. T16 was shown to be an essential component of the hinge that opens and closes the cap and core domains in L. lactis β-PGM.⁸ Its mutation to proline would reduce the ability of the cap to open and close, as proline has a limited range of possible dihedral angles that its backbone can assume. Moreover, in the wild-type enzyme, the T16 side chain forms a hydrogen bond with the carboxylic group of D10 and is thus important for positioning the D10 side chain. To test this hypothesis, we performed a 10 ns molecular dynamics simulation on the closed conformation of this mutant and saw no significant conformational changes in the backbone (RMSD below 1.0 Å, as shown in Fig. S2 and S3†) on the timescale of our simulations. Despite removal of an important interaction that would hold D10 in place, the H-bonds between D10 and both H20 and Y80 were maintained, holding the D10 side chain close to the cap-closed conformation found in the wild-type enzyme. As can be seen in Table 1, this variant does not alter the enzyme's catalytic efficiency. Thus, it is possible that the loss in efficiency for this mutant is associated with the reduced ability of the enzyme to undergo conformational change upon substrate binding.⁶⁶ This is also the case for the H20A variant, which we shall discuss next.

H20A and H20Q. H20 is a residue in the cap domain that stays parallel to the sugar ring once the substrate is bound. It is part of a hydrogen bonding network involving also D10 and K76, which presumably helps maintain D10 in its cap-closed conformation during the chemical reaction, as well as working cooperatively with the side chains of R49 and K76 to position the substrate through interactions with the non-reactive phosphate group of the substrate. Of all the mutants studied in this work, H20Q was the one that least affected the catalytic proficiency of β-PGM. That is, the Q20 side chain also fulfills the positioning role of H20, and this mutation does not cause any abrupt changes to the H-bonding network that links D10 to K76 in the wild-type, nor on the stability of the D10 position. In the case of the H20A, this mutation breaks the H-bond network between D10 and K76, and has been proposed to affect the ability of the enzyme to reach a closed conformation.⁶⁶ Additionally, although the interaction between D10 and H20 present in the wild-type is lost during the second step of the reaction, the remaining H-bond interactions (from the substrate, T16 and Y80) still keep D10 in its cap-closed conformation. Finally, β-G1,6BP and D8 remain in a very similar position when compared to the wild-type enzyme, with the distances between the phosphorus atom of the transferred phosphoryl group and the nucleophilic oxygen of D8 remaining nearly the same for both enzyme variants. As with T16P, our calculations suggest that this mutation does not affect catalysis once the enzyme is in its cap-closed conformation. This suggests that the loss of catalytic efficiency could be associated with the cap closure, as it has been previously speculated,⁶⁶ and the 19.6 kcal mol⁻¹ barrier observed experimentally for T16P and H20A could be associated with the conformational change of the enzyme in the rate-limiting step once the substrate is bound.

K76A. K76 is a cap domain residue taking part in an essential H-bonding network that extends all the way to the hinge residue T16, passing through H20 and D10. Although too far from the non-reacting phosphoryl group to create a direct H-bonding interaction with the substrate (3.85 Å between the N of the amino group of K76 and the closest non-bridging oxygen of the phosphoryl group of the substrate after MD equilibration), the positive charge of its side chain still makes a significant electrostatic contribution to the binding of the non-reactive phosphoryl group and also the overall reactivity. In fact, Fig. 7 shows that K76 has a contribution of ∼1 kcal mol⁻¹ to reducing the activation barrier of the second step of the reaction, and its removal could therefore affect the catalytic proficiency of the enzyme. As would be expected, the K76A mutation affects the H-bonding network formed by D10 and H20 already after only 10 ns of equilibration. Particularly, loss of the interaction with the K76 side chain made the H20 side chain become more flexible, oscillating more around its initial position (RMSF of 0.48 Å, compared to 0.34 Å for the wild-type). This in turn affects the H-bonding interaction with D10, although D10 itself is not significantly displaced from the cap-closed conformation for the second step. Neither is the reactive phosphate or the sugar ring (compared to the wild-type), and only the non-reactive phosphate group is slightly displaced (note that this phosphate group is primarily kept in place by interaction with R49).

D170A and E169A/D170A. Of all mutants considered in this work, D170A and the E169A/D170A double mutant were the most challenging to model, as D170 is a metal coordinating residue. Therefore, unsurprisingly, its truncation to alanine makes the Mg²⁺ ion less stable in the active site when compared to the wild-type enzyme. Surprisingly, however, both variants conserve most of the H-bond network present in the wild-type after 10 ns of equilibration for each step. In terms of energetics, Fig. 7 shows that both E169 and D170 contribute stabilizing interactions to the calculated activation barrier for the second step of the reaction of the wild-type enzyme for both mechanisms (∼2 kcal mol⁻¹ for both residues for the substrate-assisted pathways, while ∼8 kcal mol⁻¹ for E169A and 5 kcal mol⁻¹ for D170A for the D10-assisted pathway). Thus, unsurprisingly, removing these residues increases the activation barrier for this step. Interestingly, the truncation of both residues to alanine affects the second step of the D10-assisted pathway much more than it does the substrate-assisted pathway, with a difference of 15.2 kcal mol⁻¹ between the two pathways, which is in a similar range as the sum of the electrostatic contributions attributed to these residues when comparing the different mechanisms (Fig. 7). Therefore, the E169A/D170A double mutant could be an experimental indicator of discrimination between the two pathways, which in this case would indicate a preference for a substrate- rather than a D10-assisted pathway.

Finally despite the changes in activity across this series of β-PGM variants, as can be seen from Table S2† these changes do not have a significant effect on the transition state geometries for the different reaction steps. This is in good agreement with our recent comparative studies of different members of the alkaline phosphatase superfamily,^21,67 which showed that electrostatic flexibility and cooperativity of the different active site residues was more important than the precise details of the transition state geometry. Such considerations are important to take into account when attempting to design suitable metal fluoride transition state analogues as structural and electrostatic probes of the binding of the actual transition state.^11,12 Interestingly, with the exception of the D10 mutants, all other mutants studied in this work show significant barrier reductions compared to the uncatalyzed reaction, and this even holds in the case of the E169A/D170A double mutant, which involves the removal of two metal-coordinating charged residues directly next to the reacting center. Moreover, although some residues like T16 and H20 do not contribute directly to transition state stabilization, as they do not have any direct interactions with the reacting atoms, their removal significantly affects the activity of the enzyme. This is due to the disruption of the tight H-bonding network shown in Fig. 1B, and the presence of D10 as a central residue, which is fundamental to keeping all the reacting fragments in their optimal position for the reaction to occur. Therefore, even when the effect of the mutations on the activity is only indirect, e.g. by disruption of the position of D10, this residue remains an electrostatically fundamental piece of the active site.

Following from this, there has been considerable interest in the role of active site plasticity in enzyme promiscuity and evolution.^68–70 In particular, we have demonstrated the importance of electrostatically flexible active sites in facilitating evolution in the highly promiscuous members of the alkaline phosphatase superfamily.^21,71,72 There have also been recent studies of the evolution of β-lactamases, which argued that these enzymes became increasingly rigid along their evolutionary trajectory from generalists to specialists.⁶⁸ Our present observations further corroborate the trend from flexibility to rigidity with enzyme specialization, as in the current case, we are studying instead a highly specific enzyme (from a superfamily with many promiscuous members⁷³) that appears to need to maintain a very tight and finely tuned network of active site interactions to facilitate efficient catalysis.

Conclusions

In the present work, we have performed a detailed EVB study of WT β-PGM and its mutants to probe the role of D10 and other active site residues in the enormous catalytic activity of this enzyme. Previous computational and experimental studies have assumed that the D10 side chain acts as an acid–base catalyst in this reaction.^4,7,9 However, as it has been suggested that substrate-assisted pathways may occur in enzyme-catalyzed phosphoryl transfer reactions,^67,74–76 we have considered whether such a mechanism is also viable in the present case, which would assign a more indirect catalytic role to D10. We have previously suggested that the large energy difference between the two pathways makes it less likely that such a mechanism will operate in biological phosphoryl transfer reactions (at least for the hydrolysis of phosphate esters with good leaving groups¹⁹), and our present calculations demonstrate that, at least in the case of β-PGM, the enzyme strongly discriminates between the two pathways. Interestingly, our analysis shows that every amino acid that makes a significant electrostatic contribution (>1.0 kcal mol⁻¹) to the calculated activation free energies appears to interact differently with the transition states for each of the two different pathways (Fig. 7). Most strikingly, there is a large contribution from the K145 side chain to the activation free energy for group transfer via a D10-assisted mechanism, which vanishes almost in the substrate-assisted mechanism. Therefore, we suggest that truncation of this residue would provide a direct experimental test of the discrimination between the two pathways.

Our results also point to significant structural importance of D10 in addition to its obvious role in acid base catalysis. The most obvious structural role for this residue is assisting in keeping the cap closed, as also pointed out by Dai and co-workers.⁸ This is facilitated by the extended H-bonding network to H20, K76 and finally the hinge residue T16, substrate positioning through H-bonding interactions with the nucleophilic OH group of β-G1P and the reactive phosphate of the bisphosphate, and an extended H-bonding network involving T16 and D10. In addition to this, the negative charge of D10, which is in close proximity to both nucleophile and substrate, creates charge–charge repulsion between this side chain and the reactive phosphate group of the bisphosphate, which both destabilizes the bisphosphate formed in the first step, thus assisting release of the bisphosphate in the active site, and also destabilizes the ground state in the energetically costly second step of the reaction, assisting in reduction of the activation barrier. This is evidenced by the fact that removal of this charge–charge repulsion in the D10 mutants counter intuitively increases the activation barrier, and variants of such ground state destabilization have recently been suggested to be important for phosphoryl transfer enzymes.⁷⁷ However, we note that while there does appear to be a contribution from ground-state destabilization, the PGM active site is particularly well preorganized for transition state stabilization, with an extensive network of H-bonding interactions keeping the transition state in place (Fig. 1B), and this will still be the dominant factor for the observed barrier reduction compared to aqueous solution. Therefore, the role of D10 is multi-faceted and shows the importance of structural organization for efficient transition state stabilization in biological phosphoryl transfer reactions, as manifested through the positioning of a single residue in the active site.

Finally, there has been considerable interest in the role of active site plasticity in enzyme promiscuity and evolution.^68–70 In particular, we have demonstrated the importance of electrostatically flexible active sites in facilitating evolution in the highly promiscuous members of the alkaline phosphatase superfamily.^21,71,72 There have also been recent studies of the evolution of β-lactamases, which argued that these enzymes became increasingly rigid along their evolutionary trajectory from generalists to specialists.⁶⁸ Our present observations further corroborate the trend from flexibility to rigidity with enzyme specialization, as in the current case, we are studying instead a highly specific enzyme (from a superfamily with many promiscuous members⁷³), that appears to need to maintain a very tight and finely tuned network of active site interactions to facilitate efficient catalysis.

Conflicts of interest

There are no conflicts to declare.

Funding sources

The Carl Tryggers Foundation for Scientific Research (CTS 11:226) has provided postdoctoral fellowships to Gaël Marloie and Mauricio Esguerra. Lynn Kamerlin acknowledges funding from the Swedish Research Council (VR Grant 2015-04928) and the Knut and Alice Wallenberg Foundation (Wallenberg Academy Fellowship). All calculations were performed on the High-Performance Computing Center North (HPC2N) and Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX) through generous allocations of supercomputing time by the Swedish National Infrastructure for Computing (SNIC), as well as the Da Vinci GPU cluster at Uppsala University.

Acknowledgements

We would like to thank Dr Fernanda Duarte for valuable discussion.

References

1. S. D. Lahiri, G. F. Zhang, D. Dunaway-Mariano and K. N. Allen, Science, 2003, 299, 2067–2071.
2. G. M. Blackburn, N. H. Williams, S. J. Gamblin and S. J. Smerdon, Science, 2003, 301, 1184.
3. K. N. Allen and D. Dunaway-Mariano, Science, 2003, 301, 1184.
4. C. E. Webster, J. Am. Chem. Soc., 2004, 126, 6840–6841.
5. L. W. Tremblay, G. F. Zhang, J. Y. Dai, D. Dunaway-Mariano and K. N. Allen, J. Am. Chem. Soc., 2005, 127, 5298–5299.
6. G. F. Zhang, J. Dai, L. B. Wang, D. Dunaway-Mariano, L. W. Tremblay and K. N. Allen, Biochemistry, 2005, 44, 9404–9416.
7. I. Berente, T. Beke and G. Náray-Szabó, Theor. Chem. Acc., 2007, 118, 129–134.
8. J. Y. Dai, L. Finci, C. C. Zhang, S. Lahiri, G. F. Zhang, E. Peisach, K. N. Allen and D. Dunaway-Mariano, Biochemistry, 2009, 48, 1984–1995.
9. E. Marcos, M. J. Field and R. Crehuet, Proteins: Struct., Funct., Bioinf., 2010, 78, 2405–2411.
10. J. L. Griffin, M. W. Bowler, N. J. Baxter, K. N. Leigh, H. R. W. Dannatt, A. M. Hounslow, G. M. Blackburn, C. E. Webster, M. J. Cliff and J. P. Waltho, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6910–6915.
11. N. J. Baxter, L. F. Olguin, M. Golicnik, G. Feng, A. M. Hounslow, W. Bermel, G. M. Blackburn, F. Hollfelder, J. P. Waltho and N. H. Williams, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14732–14737.
12. N. J. Baxter, M. W. Bowler, T. Alizadeh, M. J. Cliff, A. M. Hounslow, B. Wu, D. B. Berkowitz, N. H. Williams, G. M. Blackburn and J. P. Waltho, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4555–4560.
13. Y. Jin, D. Bhattasali, E. Pellegrini, S. M. Forget, N. J. Baxter, M. J. Cliff, M. W. Bowler, D. L. Jakeman, G. M. Blackburn and J. P. Waltho, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12384–12389.
14. C. Lad, N. H. Williams and R. Wolfenden, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5607–5610.
15. R. Wolfenden, Chem. Rev., 2006, 106, 3379–3396.
16. A. M. Burroughs, K. N. Allen, D. Dunaway-Mariano and L. Aravind, J. Mol. Biol., 2006, 361, 1003–1034.
17. A. Warshel and R. M. Weiss, J. Am. Chem. Soc., 1980, 102, 6218–6226.
18. A. Warshel, Computer Modeling of Chemical Reactions in Enzymes and Solutions, Wiley, New York, 1991.
19. A. Barrozo, D. Blaha-Nelson, N. H. Williams and S. C. L. Kamerlin, Pure Appl. Chem., 2017, 89, 715–727.
20. M. Ben-David, J. L. Sussman, C. L. Maxwell, K. Szeler, S. C. L. Kamerlin and D. S. Tawfik, J. Mol. Biol., 2015, 427, 1359–1374.
21. A. Barrozo, F. Duarte, P. Bauer, A. T. P. Carvalho and S. C. L. Kamerlin, J. Am. Chem. Soc., 2015, 137, 9061–9076.
22. A. Shurki, E. Derat, A. Barrozo and S. C. L. Kamerlin, Chem. Soc. Rev., 2015, 44, 1037–1052.
23. H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242.
24. V. Lopéz-Canut, M. Roca, J. Bertrán, V. Moliner and I. Tuñón, J. Am. Chem. Soc., 2011, 133, 12050–12062.
25. M. Sánchez-Tarín, K. Świderek, M. Roca and I. Tuñón, J. Phys. Chem. B, 2015, 119, 1899–1911.
26. V. B. Chen, W. B. Arendall, J. J. Headd, D. A. Keedy, R. M. Immormino, G. J. Kapral, L. W. Murray, J. S. Richardson and D. C. Richardson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 12–21.
27. The PyMol Molecular Graphics System, Schrödinger, LLC, New York, NY, 2013.
28. J. Åqvist and A. Warshel, J. Am. Chem. Soc., 1990, 112, 2860–2868.
29. F. Duarte, P. Bauer, A. Barrozo, B. A. Amrein, M. Purg, J. Åqvist and S. C. L. Kamerlin, J. Phys. Chem. B, 2014, 118, 4351–4362.
30. Q. Liao, S. C. L. Kamerlin and B. Strodel, J. Phys. Chem. Lett., 2015, 6, 2657–2662.
31. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
32. G. King and A. Warshel, J. Chem. Phys., 1989, 91, 3647–3661.
33. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
34. M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509.
35. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
36. J. Marelius, K. Kolmodin, I. Feierberg and J. Åqvist, J. Mol. Graphics Modell., 1998, 16, 213–225.
37. Schrödinger Release 2013-3: MacroModel version 10.2, Schrödinger LLC, New York, 2013.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Rev. D.01, Gaussian Inc., Wallingford CT, 2009.
39. P. Cieplak, W. D. Cornell, C. Bayly and P. A. Kollman, J. Comput. Chem., 1995, 16, 1357–1377.
40. F. S. Lee and A. Warshel, J. Chem. Phys., 1992, 97, 3100–3107.
41. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
42. G. Y. Hong, E. Rosta and A. Warshel, J. Phys. Chem. B, 2006, 110, 19570–19574.
43. D. E. Koshland Jr., J. Am. Chem. Soc., 1952, 74, 2286–2292.
44. G. Di Sabato and W. P. Jencks, J. Am. Chem. Soc., 1961, 83, 4393–4400.
45. P. J. Briggs, D. P. Satchell and G. F. White, J. Chem. Soc. B, 1970, 1008–1012.
46. J. Gerstein and W. P. Jencks, J. Am. Chem. Soc., 1964, 86, 4655–4663.
47. F. Duarte, J. Åqvist, N. H. Williams and S. C. L. Kamerlin, J. Am. Chem. Soc., 2015, 137, 1081–1093.
48. F. Duarte, A. Barrozo, J. Åqvist, N. H. Williams and S. C. L. Kamerlin, J. Am. Chem. Soc., 2016, 138, 10664–10673.
49. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
50. A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843.
51. G. Bussi and D. Branduardi, in Reviews in Computational Chemistry, 2015, vol. 28, pp. 1–49.
52. L. Alessandro and L. G. Francesco, Rep. Prog. Phys., 2008, 71, 126601.
53. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
54. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
55. D. van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
56. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
57. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
58. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
59. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
60. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
61. B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122.
62. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
63. M. Goličnik, L. F. Olguin, G. Q. Feng, N. J. Baxter, J. P. Waltho, N. H. Williams and F. Hollfelder, J. Am. Chem. Soc., 2009, 131, 1575–1588.
64. A. J. Adamczyk and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9827–9832.
65. I. Muegge, H. Tao and A. Warshel, Protein Eng., 1997, 10, 1363–1372.
66. J. Dai, L. Finci, C. Zhang, S. Lahiri, G. Zhang, E. Peisach, K. N. Allen and D. Dunaway-Mariano, Biochemistry, 2009, 48, 1984–1995.
67. J. Luo, B. van Loo and S. C. L. Kamerlin, FEBS Lett., 2012, 586, 1622–1630.
68. T. S. Zou, V. A. Risso, J. A. Gavira, J. M. Sanchez-Ruiz and S. B. Ozkan, Mol. Biol. Evol., 2015, 32, 132–143.
69. N. Tokuriki and D. S. Tawfik, Science, 2009, 324, 203–207.
70. E. Dellus-Gur, A. Toth-Petroczy, M. Elias and D. S. Tawfik, J. Mol. Biol., 2013, 425, 2609–2621.
71. G. H. Hou and Q. Cui, J. Am. Chem. Soc., 2013, 135, 10457–10469.
72. F. Sunden, A. Peck, J. Salzman, S. Ressl and D. Herschlag, eLife, 2015, 4, e06181.
73. E. Kuznetsova, M. Proudfoot, C. F. Gonzales, G. Brown, M. V. Omelchenko, I. Borozan, L. Carmel, Y. I. Wolf, H. Mori, A. V. Savchenko, C. H. Arrowsmith, E. V. Koonin, A. M. Edwards and A. F. Yakunin, J. Biol. Chem., 2006, 281, 36149–36161.
74. A. Jeltsch, J. Alves, H. Wolfes, G. Maass and A. Pingoud, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 8499–8503.
75. T. Schweins, M. Geyer, K. Scheffzek, A. Warshel, H. R. Kalbitzer and A. Wittinghofer, Nat. Struct. Biol., 1995, 2, 36–44.
76. M. Klähn, E. Rosta and A. Warshel, J. Am. Chem. Soc., 2006, 128, 15310–15323.
77. L. D. Andrews, T. D. Fenn and D. Herschlag, PLoS Biol., 2013, 11, e1001599.

---

Footnote

† Electronic supplementary information (ESI) available: Further simulation details and all parameters necessary to reproduce our empirical valence bond calculations. See DOI: 10.1039/c8ob00312b

---