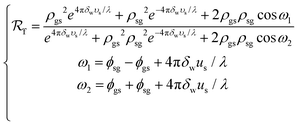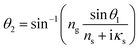Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correction: Modelling of thermal transport through a nanocellular polymer foam: toward the generation of a new superinsulating material
Guilong
Wang
 *ab,
Chongda
Wang
b,
Jinchuan
Zhao
bc,
Guizhen
Wang
d,
Chul B.
Park
*b,
Guoqun
Zhao
*a,
Wouter
Van De Walle
e and
Hans
Janssen
e
*ab,
Chongda
Wang
b,
Jinchuan
Zhao
bc,
Guizhen
Wang
d,
Chul B.
Park
*b,
Guoqun
Zhao
*a,
Wouter
Van De Walle
e and
Hans
Janssen
e
aKey Laboratory for Liquid-Solid Structural Evolution and Processing of Materials, School of Materials Science and Engineering, Shandong University, Jinan, Shandong 250061, China
bMicrocellular Plastics Manufacturing Laboratory, Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, Ontario M5T3G8, Canada
cCentre for Precision Engineering, School of Mechatronics Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
dKey Laboratory of Chinese Education Ministry for Tropical Biological Resources, Hainan University, Haikou, Hainan 570228, China
eKU Leuven, Department of Civil Engineering, Building Physics Section, Kasteelpark Arenberg 40 – Box 2447, BE-3001 Heverlee, Belgium
First published on 13th September 2018
Abstract
Correction for ‘Modelling of thermal transport through a nanocellular polymer foam: toward the generation of a new superinsulating material’ by Guilong Wang et al., Nanoscale, 2017, 9, 5996–6009.
The authors have noticed that the finite discretization for dθ1 used in calculating the integrals of eqn (34) and (35) in the published paper had significant effects on the calculation accuracy. In the published paper, the range of θ1 was divided into 1000 equidistant Δθ1 pieces. It was found that the finite discretization was not fine enough, and this led to calculation errors in the cases where the cell wall became extremely thin (<4 nm) either at small cell sizes or at high void fractions. It was found that θ1 should be divided into several thousands of intervals in discretization to ensure a high calculation accuracy, as shown in Fig. C1.
The authors have recalculated the data presented in the published paper by using a much finer discretization with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 intervals. With a much finer discretization,
000 intervals. With a much finer discretization, 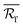 increased significantly at high void fractions compared to the original case. Subsequently, both λrad and λeff decreased obviously at high void fractions. Thus, the originally published Fig. 8 should be replaced by the updated version of Fig. 8 provided below. It should be noted that λcon was not affected by discretization. Thus, the data in Fig. 8b was not changed.
increased significantly at high void fractions compared to the original case. Subsequently, both λrad and λeff decreased obviously at high void fractions. Thus, the originally published Fig. 8 should be replaced by the updated version of Fig. 8 provided below. It should be noted that λcon was not affected by discretization. Thus, the data in Fig. 8b was not changed.
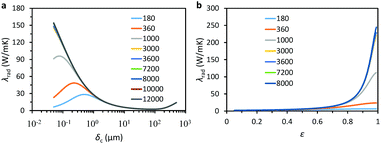
Regarding the data presented in the originally published Fig. 9, λeff, λrad, and 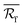 changed obviously at small cell sizes when using a much finer discretization in the calculations. Thus, this figure should be replaced by the updated version of Fig. 9 provided below. In the updated version of Fig. 9c, it should be noted that the behaviour of the radiative thermal conductivity as a function of the cell size changes significantly in comparison with the data presented in Fig. 9c of the published paper. In the updated version of Fig. 9c, the radiative thermal conductivity reduced first to a certain minimum level, and then increased gradually to a certain maximum value with decreasing cell size. This in turn led to the increase in the total thermal conductivity upon decreasing the cell size, as shown in the updated version of Fig. 9a, instead of it reaching a certain maximum value and subsequently decreasing with reducing cell size as shown in the original version of Fig. 9a. This phenomenon was due to the sharp decrease in the reflectance of the single cell wall with decreasing cell size (Fig. 9d), and increasing the number of cell walls could not offset the adverse impact on the total reflectance of IR waves.
changed obviously at small cell sizes when using a much finer discretization in the calculations. Thus, this figure should be replaced by the updated version of Fig. 9 provided below. In the updated version of Fig. 9c, it should be noted that the behaviour of the radiative thermal conductivity as a function of the cell size changes significantly in comparison with the data presented in Fig. 9c of the published paper. In the updated version of Fig. 9c, the radiative thermal conductivity reduced first to a certain minimum level, and then increased gradually to a certain maximum value with decreasing cell size. This in turn led to the increase in the total thermal conductivity upon decreasing the cell size, as shown in the updated version of Fig. 9a, instead of it reaching a certain maximum value and subsequently decreasing with reducing cell size as shown in the original version of Fig. 9a. This phenomenon was due to the sharp decrease in the reflectance of the single cell wall with decreasing cell size (Fig. 9d), and increasing the number of cell walls could not offset the adverse impact on the total reflectance of IR waves.
As shown in the original versions of Fig. 9a and c, both λeff and λrad first decreased, then increased, and finally decreased again, upon reducing the cell size. Thus, both λeff and λrad showed maximum peak values. In order to explain the final downward trend of the two variables, it was stated in the published paper that the increase in the rate of the cell wall number (n) was much faster than the declining rate of the wavelength-averaged reflectance of the single cell wall 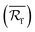 . However, this was not true because n and
. However, this was not true because n and 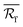 were not compared over an equivalent numerical range. In fact, if an equivalent numerical range were to be employed, it would be found that the decrease in
were not compared over an equivalent numerical range. In fact, if an equivalent numerical range were to be employed, it would be found that the decrease in 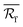 would be so fast that the increase in n could not offset its adverse impact on the total reflectance of IR waves. Subsequently, the maximum peak values that appeared in the original versions of Fig. 9a and c should not have existed, as shown in the updated versions of Fig. 9a and c. It was inferred that, as the cell size reduced indefinitely,
would be so fast that the increase in n could not offset its adverse impact on the total reflectance of IR waves. Subsequently, the maximum peak values that appeared in the original versions of Fig. 9a and c should not have existed, as shown in the updated versions of Fig. 9a and c. It was inferred that, as the cell size reduced indefinitely, 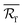 would gradually approach zero and
would gradually approach zero and 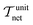 would approach one. According to eqn (41) shown in the published paper, the radiative thermal conductivity would finally approach its maximum value of
would approach one. According to eqn (41) shown in the published paper, the radiative thermal conductivity would finally approach its maximum value of 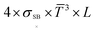 , which is 257.5 mW m−1 K−1.
, which is 257.5 mW m−1 K−1.
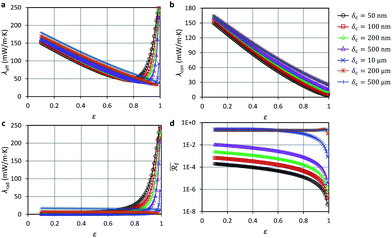
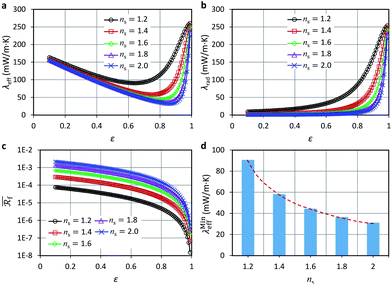
When calculating with a much finer discretization, 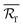 decreased significantly at high void fractions compared with the originally published data. Subsequently, both λrad and λeff increased significantly at high void fractions in comparison with the original data. Thus, Fig. 10 in the published paper should be replaced by the updated version of Fig. 10 provided below. Notably, it can be seen in the updated version of Fig. 10b that the maximum value of λrad could be up to 250 mW m−1 K−1, which is much larger than the maximum value reported in the original version of Fig. 10b. Consequently, the maximum value of λeff reported in the updated version of Fig. 10a was also much larger than the maximum value reported in the original version of Fig. 10a.
decreased significantly at high void fractions compared with the originally published data. Subsequently, both λrad and λeff increased significantly at high void fractions in comparison with the original data. Thus, Fig. 10 in the published paper should be replaced by the updated version of Fig. 10 provided below. Notably, it can be seen in the updated version of Fig. 10b that the maximum value of λrad could be up to 250 mW m−1 K−1, which is much larger than the maximum value reported in the original version of Fig. 10b. Consequently, the maximum value of λeff reported in the updated version of Fig. 10a was also much larger than the maximum value reported in the original version of Fig. 10a.
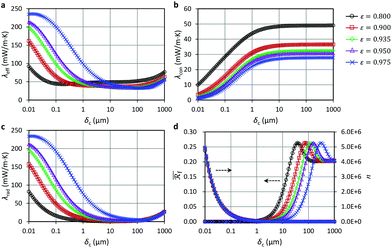
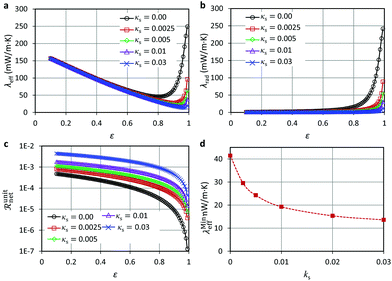
For the same reason, Fig. 11 in the published paper should also be replaced by the updated version of Fig. 11 provided below. Notably, both λrad and λeff increased significantly at high void fractions in comparison with the original data. However, the change in discretization here did not change the variation trend of the variables. Moreover, the minimum effective thermal conductivity (λMineff) calculated for the different cases only changed slightly.
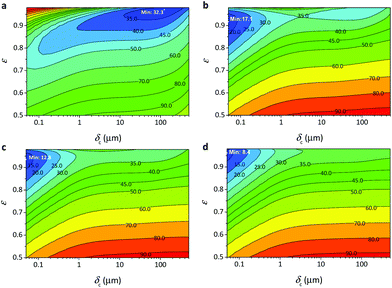
Fig. 12 in the published paper should also be replaced by the updated version of Fig. 12 provided below. Overall, the contour isotherms of the thermal conductivity did not exhibit any obvious changes in comparison with the original version of Fig. 12, except for the data at small cell sizes and high void fractions.
Also, the formulas (23)–(33) in the paper need to be corrected because the refraction angle, θ2, which should be a complex number, was mistakenly processed as a real number when preparing the original article. However, these errors did not affect the calculation results, because θ2 had been correctly taken as a complex number in all previous modelling and calculation works.
The formula (23) in the article should be changed to the following:
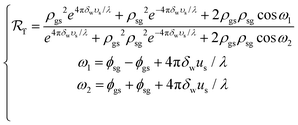 | (23) |
In the updated formula (23), us and υs are employed to simplify the notation, and their values are determined by us + iυs = (ns + iκs)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2. To calculate the complex refraction angle, θ2, the formula (24) should be changed to:
θ2. To calculate the complex refraction angle, θ2, the formula (24) should be changed to:
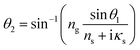 | (24) |
Accordingly, for the incident radiation wave with the electric vector perpendicular to the plane of incidence, formulas (25) and (26) which were used to determine ρgs, ρsg, ϕgs, and ϕsg should be respectively replaced with the following formulas:
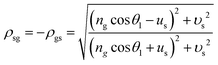 | (25) |
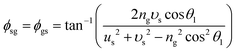 | (26) |
Meanwhile, for the incident radiation wave with the electric vector parallel to the plane of incidence, formulas (27) and (28) should be respectively changed to the following:
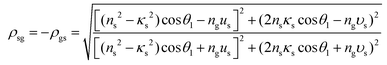 | (27) |
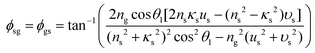 | (28) |
The formula (29) used to calculate the transmittance of polymer film in the article should be changed to the following:
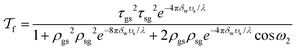 | (29) |
For the incident radiation wave with the electric vector perpendicular to the plane of incidence, formulas (30) and (31) used to determine τgs and τsg should be respectively replaced with the following formulas:
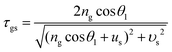 | (30) |
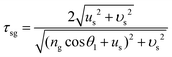 | (31) |
Meanwhile, for the incident radiation wave with the electric vector parallel to the plane of incidence, formulas (32) and (33) should be respectively changed to the following:
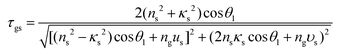 | (32) |
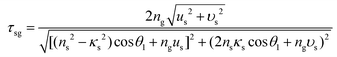 | (33) |
In addition to the above corrections, eqn (36) in the published paper should be changed to the following:
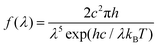 | (36) |
These errors do not affect the main conclusions of the paper. The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.
| This journal is © The Royal Society of Chemistry 2018 |