Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Adhesion strategies of Dictyostelium discoideum – a force spectroscopy study†
Nadine
Kamprad
ab,
Hannes
Witt
 a,
Marcel
Schröder
ab,
Christian Titus
Kreis
a,
Oliver
Bäumchen
a,
Marcel
Schröder
ab,
Christian Titus
Kreis
a,
Oliver
Bäumchen
 a,
Andreas
Janshoff
*c and
Marco
Tarantola
a,
Andreas
Janshoff
*c and
Marco
Tarantola
 *ab
*ab
aMax Planck Institute for Dynamics and Self-Organization, Am Faßberg 17, 37077 Göttingen, Germany. E-mail: marco.tarantola@ds.mpg.de
bUniversity of Goettingen, Institute for Non-linear Dynamics, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
cUniversity of Goettingen, Institute for Physical Chemistry, Tammannstr. 6, 37077 Göttingen, Germany. E-mail: andreas.janshoff@chemie.uni-goettingen.de
First published on 2nd November 2018
Abstract
Biological adhesion is essential for all motile cells and generally limits locomotion to suitably functionalized substrates displaying a compatible surface chemistry. However, organisms that face vastly varying environmental challenges require a different strategy. The model organism Dictyostelium discoideum (D.d.), a slime mould dwelling in the soil, faces the challenge of overcoming variable chemistry by employing the fundamental forces of colloid science. To understand the origin of D.d. adhesion, we realized and modified a variety of conditions for the amoeba comprising the absence and presence of the specific adhesion protein Substrate Adhesion A (sadA), glycolytic degradation, ionic strength, surface hydrophobicity and strength of van der Waals interactions by generating tailored model substrates. By employing AFM-based single cell force spectroscopy we could show that experimental force curves upon retraction exhibit two regimes. The first part up to the critical adhesion force can be described in terms of a continuum model, while the second regime of the curve beyond the critical adhesion force is governed by stochastic unbinding of individual binding partners and bond clusters. We found that D.d. relies on adhesive interactions based on EDL-DLVO (Electrical Double Layer-Derjaguin–Landau–Verwey–Overbeek) forces and contributions from the glycocalix and specialized adhesion molecules like sadA. This versatile mechanism allows the cells to adhere to a large variety of natural surfaces under various conditions.
In its natural habitat the soil-dwelling amoeba Dictyostelium discoideum (D.d.) faces a multitude of surface geometries and chemical substrate compositions or wetting states while hunting for its bacterial prey or undergoing essential life cycle states.1 Particularly, the inevitable variations in surface chemistry force D.d. to adapt its adhesive competence in order to survive in different environments. On a mesoscopic level, surface adhesion is relevant for migration and aggregation of individual cells, while a plethora of biochemical processes depend on signal cascades associated with substrate adhesion mediated by specific molecules.2,3 The main participants of the interaction with the substrate are usually the cell-enveloping glycocalyx, peripheral or transmembrane proteins and the lipid plasma membrane.
General unspecific adhesion mechanisms have been studied for bacterial biofilms to whole gecko components with methods bridging pN to μN force sensitivity.4–6 Often, the opposing surface is lined with fibrillar extracellular matrix biopolymers expelled by cells,7 which are, however, absent in the adhesion process of vegetative D.d.8–11 This raises the question of how D.d. manages to adhere and migrate in the absence of specific ligands on variable surfaces formed by a heterogeneous environment. In general, apart from specific lock-and-key recognition, adhesion mainly originates from EDL-DLVO (Electrical Double Layer-Derjaguin–Landau–Verwey–Overbeek) forces12,13 comprising intermolecular, long-ranged attractive van der Waals (v.d.W.) interactions based on polarizability and either attractive or repulsive electrostatics due to the presence of permanent charges and ions in solution.14 Short-ranged attractive forces arise from salt bridges, hydrogen bonds and hydrophobic interactions.15 Repulsive forces originate from the steric hindrance of repeller molecules and the thermal excitation of undulations (ranging from pm to nm distance at room temperature),16 the latter ones being directly linked to the dynamic states of the membrane and its mechanical properties.17 Finally, more long range water-based interactions may involve capillary forces depending on humidity and wettability.
Apart from these general contributions to cellular adhesion, cells also employ specific adhesion molecules – such as in the case of D.d. sadA (Substrate Adhesion A) – to bind to surfaces. SadA is a transmembrane protein that is found to be responsible for cell–substrate adhesion and also relevant for phagocytosis, suggesting an important role in force transmission and the association of so-called actin foci.18–20 Integrin-similar cascades have been described for sadA,21,22 involving further transmembrane proteins like phg1A and sibA, actin linkers like talin A and cross-linkers like cortexilin as well as contractile contributions especially via myosin II and VII.11,19,23–31 Different signaling cascades and adhesion forces become relevant upon starvation induced development and multicellular aggregation involving the cell–cell adhesion molecule csaA, which has been nicely shown previously.32 However, while integrins frequently bind to cellular self-expelled fibrillar structures with specific domains containing RGD-amino acid motifs in the extracellular matrix, in the case of D.d. substrate interactions, the cell does not produce ligands for sadA, neither is the environment presenting them, thereby raising the question about the nature and strength of the interaction.
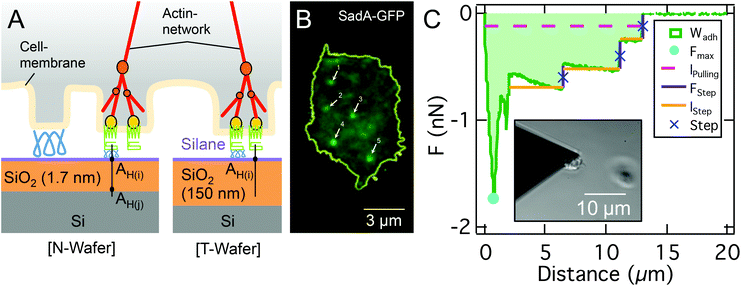
In this study, we examined the cell–substrate adhesion of vegetative D.d. on tailored model surfaces with Atomic Force Microscopy based Single Cell Force Spectroscopy (AFM-based SCFS) to identify the relevant forces involved in adhesion. Furthermore, we analysed the role of sadA in the adhesion strategies of D.d. Therefore we could describe the first part of the force retraction curve up to the critical adhesion force using a continuum wetting model and attribute the second regime to stochastic unbinding events of individual binding partners and bond clusters (Fig. 1). To obtain a more precise insight into the magnitude of the involved forces, we (i) combine protein knockout and glycolytic digestion to identify the molecular components relevant for D.d. adhesion, (ii) modify electrostatic forces within the osmoregulatory regime of D.d.33–35 (iii) provide model silicon substrates with different oxide layer thicknesses leading to different v.d.W. interactions36,37 and (iv) quantify the contribution of hydrophobicity by using silane-based surface modification. To aid the analysis of these experiments we develop a theoretical description based on a continuum model that treats the cell as a liquid droplet wetting a surface, starting from minimization of the free energy including the work of adhesion and cortical tension under constant volume constraint. This approach permits us to discriminate adhesion based on wetting of the surface and adhesion relying on stochastic formation and dissolution of adhesion clusters. Using model surfaces we could show that EDL-DLVO forces play a pivotal role in the adhesion of D.d. together with short-ranged interactions. We found that sadA organizes in nanoscopic clusters that withstand external loading even after passing the critical adhesion force determined from the wetting model. This provides D.d. with a considerably enlarged adhesion energy and an enhanced lifetime under the applied load through a balanced bio-nano interface.
1. Experimental
1.1 Cell culture and preparation
For optical experiments, D.d. wildtypes AX2-214 and AX3, the mutant sadA0 in an AX3 background19 and AX2 lines labeled with HG1694-GFP and ddLimE-GFP, kindly provided by the Gerisch lab, were used. Cells were cultured (ForMedium™, UK) at 22 °C. Before the experiments cells were washed and resuspended at 2.5 × 105 cells in 1 ml phosphate buffer (PB, 2 mM KH2PO4 + 14.7 mM Na2HPO4·H2O at pH 6 (both Merck, Germany)). Cells were used for three hours after the transfer to phosphate buffer.α-Mannosidase (αM, Sigma-Aldrich, Germany) cleaves the glycan moiety of glycoproteins bearing a characteristically terminal α-D-mannosyl residue and influences adhesion significantly.38 For the experiments here, 2.5 × 105 cells in 1 ml PB were incubated with 5 μl αM for 30 min, before the cells were transferred to PB. Experiments were performed under identical conditions as those with untreated cells.
1.2 Model substrates, hydrophobic treatment and preparation
We used two kinds of model substrates based on silicon wafers (Si-Mat Silicon Materials, Germany) with different v.d.W. characteristics: ‘N-Wafers’ exhibit a native 1.7 nm SiO2-layer and ‘T-Wafers’ possess a 150 nm thick thermally grown SiO2-layer. These substrates are well characterized, including the isoelectric point, the total surface energy, Lifshitz-van der Waals interaction energy, Lewis acid–base components, and RMS roughness36,37 and summarized in Table S1.† Notably, at the pH used here (pH = 6) these substrates are negatively charged36 and the roughness ranges between 0.15 nm and 0.23 nm, well below scales relevant for contact guidance of D.d.39,40For experiments carried out on hydrophobic surfaces, substrates were functionalized with octadecyltrichlorosilane (OTS) to make the otherwise hydrophilic SiO2-surface hydrophobic. Silanization of the Si-wafers followed an established protocol.41 The success of functionalizations was controlled by measuring the advancing and receding contact angles (Dataphysics OCA 50, Germany) of ultra pure water (18.2 MΩ cm, 0.055 μS cm−1, NANOpure Diamond, Barnstead), as shown in Fig. S1 and Table S1.†
For SCFS and flatness experiments wafers were cut into small squares (5 mm × 5 mm), cleaned with ethanol (ethanol absolute, p.A, ACS, Ph.Eur, USP, Chemsolute, Germany) in an ultra sound bath for 5 min, dried with N2 and attached with two-component glue (JPK biocompatible glue, Germany) to a glass surface (AFM: ∅ 35 mm × 1 mm, Asylum Research, UK; Optical experiments: μ-Dish, 35 mm high glass bottom, Ibidi, Germany).
1.3 Single cell force spectroscopy
Substrate adhesion strength was analyzed with an AFM-based SCFS setup (Asylum MPF-3D Bio, UK). We used tipless cantilevers (Arrow TL2-50, Nano World, Switzerland) with a resonance frequency of f0 = 6 kHz in liquid and a mean spring constant of k = 0.03 N m−1. The spring constant was calibrated with the thermal noise method before attaching a cell.42 As the lateral spring constant is substantially larger than the normal spring constant (the ratio of normal spring constant to lateral one is roughly proportional to L2/h2 with the length of the cantilever L and the torsional moment arm h, which is here approximately the height of the cell),43,44 we neglected the influence of torque, that might arise from a non-central cell attachment, on the detected forces.To foster adhesion of a cell on the cantilever, cantilevers were functionalized with a polyphenolic adhesive protein mixture (Corning® Cell-Tak™, BD Bioscience, USA; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 diluted with 1 mM NaCO3 and rinsed with ultra pure H2O). Single cells were attached to the front of the cantilever by picking them from the substrate utilizing optical feedback (insert in Fig. 1C). After an incubation time of 2 min to allow the cell to establish stable adhesion to the cantilever, the cantilever was moved towards the substrate with a velocity of 2.5 μm s−1 until a constant force of 0.5 nN was reached. This force was kept constant for 30 s, before the cell was retracted with a velocity of 2.5 μm s−1 resulting in a characteristic force–distance (FD) curve, as shown in Fig. 1C. This cycle was repeated up to 5 times per cell with 30 s relaxation time between cycles. Measurements include at least 11 cells and a minimum of 50 FD-curves. The choice of these parameters relies on earlier work by us.45 We have shown that the Cell-Tak™ functionalisation is not affecting cellular development and yields reasonably stronger adhesion forces than the forces of cell–substrate interaction. The contact times were chosen to allow for new actin foci formation (half-lifetime of 15 s). Stable approach settings were achieved above 250 pN contact forces (while forces above 5 nN sometimes provoked irreversible cell deformations). Retraction velocities yielded non-linearities above 4 μm s−1 pulling speed. Nevertheless, in rare cases multiple adhesion force maxima due to strong cell shape changes or cell-cantilever detachments occur, which can easily be identified optically.
30 diluted with 1 mM NaCO3 and rinsed with ultra pure H2O). Single cells were attached to the front of the cantilever by picking them from the substrate utilizing optical feedback (insert in Fig. 1C). After an incubation time of 2 min to allow the cell to establish stable adhesion to the cantilever, the cantilever was moved towards the substrate with a velocity of 2.5 μm s−1 until a constant force of 0.5 nN was reached. This force was kept constant for 30 s, before the cell was retracted with a velocity of 2.5 μm s−1 resulting in a characteristic force–distance (FD) curve, as shown in Fig. 1C. This cycle was repeated up to 5 times per cell with 30 s relaxation time between cycles. Measurements include at least 11 cells and a minimum of 50 FD-curves. The choice of these parameters relies on earlier work by us.45 We have shown that the Cell-Tak™ functionalisation is not affecting cellular development and yields reasonably stronger adhesion forces than the forces of cell–substrate interaction. The contact times were chosen to allow for new actin foci formation (half-lifetime of 15 s). Stable approach settings were achieved above 250 pN contact forces (while forces above 5 nN sometimes provoked irreversible cell deformations). Retraction velocities yielded non-linearities above 4 μm s−1 pulling speed. Nevertheless, in rare cases multiple adhesion force maxima due to strong cell shape changes or cell-cantilever detachments occur, which can easily be identified optically.
The data were analyzed using a custom Matlab script, which returns the maximal adhesion force (Fmax, minimum of the FD-curve), the adhesion work (Wadh, integral between the baseline and FD-curve) and step features (instantaneous rupture events as shown in Fig. 1C). In order to identify steps, the curves were filtered by removing well defined high frequency signals by taking the spectrum, identifying peaks and then applying notch filtering, followed by a median filter to smooth the data while retaining the steps. The derivative of the force is used to locate the steps. Finally a threshold is applied on the identified steps based on the step amplitude being at least 2 standard deviations above the background. The step parameters analyzed consist of the number of steps per curve, the step force FStep, the length between two consecutive steps lStep, and the combined length until the last step, i.e. total detachment of the cell lpulling, is reached.
To control the effect of D.d. development, we performed SCFS (in PB on glass) for up to 6 hours of starvation. This set of experiments revealed a strong reduction in the number of steps and a switch of the step forces every 3 hours of development (as shown in Fig. S2†). Therefore, we have chosen the 0–3 h interval for our experiments.
To experimentally test the relationship between the maximal adhesion force and the cell radius, we performed SCFS (parameters as described above) with integrated optical microscopy (AFM: CellHesion 200, JPK Instruments, Germany; Microscope: IX81, Olympus, Japan; objective: 10× UPlanFL N/0.30/Ph1, ∞/-/FN26.5 with additional 1.6× magnification, Olympus, Japan; Camera: Orca Flash 2.8 C11440, Hamamatsu, Japan). During the experiments, a bright field image was acquired for each measurement series. To determine the radius of the cells, the contour of the cell was tracked in Fiji.46 Assuming a perfect circle, a mean radius was calculated.
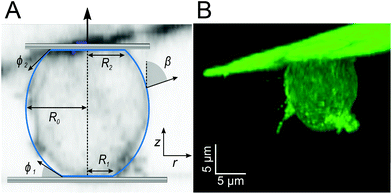
To assess the three dimensional structure of the cells under an applied load we used a combination of Confocal Laser Scanning Microscopy (CLSM: IX83 with FV1200, Olympus, Japan; Camera: XM10, Olympus, Japan; objective: 60×/1.35O ∞/0.17/FM26.5, Olympus, Japan) and SCFS. In contrast to the brightfield experiments we used AX2 carA-1-GFP labelled cells (WT cells expressing an GFP-tagged version of one of the major cAMP receptors), which are used here for membrane visualization. SCFS experiments were performed in force clamp mode, by retracting the cantilever to a pulling force of 0.2 nN with a velocity of 2.5 μm s−1 and keeping it at a constant force for 50 s to image the cell, as shown in Fig. 2. Three dimensional reconstructions were created with Imaris (Bitplane, Switzerland). General image analysis was performed with Fiji.46
1.4 Cell shape: flatness
We used AX2+HG1694-GFP and AX3+ddLimE-GFP to visualize the cytoplasm or the cell cortex, respectively, as a measure for the whole cell body volume. During initial starvation, cells were seeded in a concentration of 3 × 103 cells per cm2 on the model substrates and allowed to settle down for at least 30 min. We used a Spinning Disc Microscope (Microscope: IX83, Olympus, Japan; SD-Unit: CSU-X1, Yokogawa, Japan; Camera: iXon Ultra EMCCD dual cam setup, Andor, UK; objective: 100× LUMPlanFI/1.00w, ∞/0, Olympus, Japan) to record z-stacks (0.5 μm step size) of single cells. The contour of the cell was detected by a custom Matlab script. The flatness factor was defined as the square root of the contact area to the cube root of the voxel volume of the whole object.471.5 Variation of the ionic strength
In order to dissect the contribution of electrostatic interactions to cell adhesion, the concentration of mono- and divalent ions in the PB (ionic strength (IS): 16 mM) was increased in two steps. As an example of a monovalent ion, we used potassium (potassium chloride KCl, Sigma Aldrich, Germany).35 We increased the concentration to 5 mM KCl (IS: 21 mM) without removing the head of the AFM. After 5 min the measurement was repeated 3 times. Afterwards KCl (solved in PB) was again added to increase the concentration to 20 mM (IS: 26 mM). As an example of divalent ions, we used magnesium (magnesium chloride MgCl2, Sigma-Aldrich, Germany).35 Like described for KCl, we increased the concentration from 0 to 5 mM (IS: 31 mM) to 20 mM (IS: 76 mM). These measurements were repeated for 10 cells per ionic strength.1.6 Statistical analysis
Statistical analysis is performed using the two-sample test implemented in IgorPro. [*] refers to a P-value of the Wilcoxon Rank <0.1, [**] for P < 0.05, and [***] for P < 0.01.2 Theoretical analysis
2.1 Geometry
The typical morphology of a D.d. cell attached to the cantilever is shown in Fig. 2. It is convenient to parametrize the geometry of the cell by the function U(r) = sin(β) with the distance to the axis of symmetry r and the angle β between the normal on the cell membrane and the cell axis z (see Fig. 2A).48–51z = 0 lies in the equatorial plane. From the image, we infer that adhesion is strong enough to neglect bending contributions to the free energy. Therefore, the shape of the cell is obtained from variation of the free energy functional assuming constant volume V: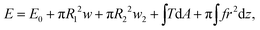 | (1) |
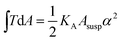 , with KA being the area compressibility modulus and Asusp being the surface area of the suspended cell.52–56 This is essentially due to the fact that minimization of eqn (1) is identical to minimizing the area of the membrane and a consequence of the natural boundary conditions.
, with KA being the area compressibility modulus and Asusp being the surface area of the suspended cell.52–56 This is essentially due to the fact that minimization of eqn (1) is identical to minimizing the area of the membrane and a consequence of the natural boundary conditions.
The shape of the adherent cell is defined by the contact radius between the cell and substrate R1 and between the cell and cantilever R2, the equatorial cell radius R0, the contact angles ϕ1 towards the substrate and ϕ2 towards the cantilever. When we assume that in-plane tension T in the cell cortex and the pressure difference ΔP across the membrane are uniform and continuous, the contour of the cell can be derived from the Young–Laplace law
| ΔP = T(C1 + C2), | (2) |
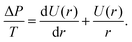 | (3) |
Since ΔP/T is a constant for a given force F, U(r) can be obtained from integration as
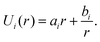 | (4) |
In order to determine ai and bi, we use the angle at the cell equator and the contact angles as boundary conditions. The differences in adhesion to the cantilever and the substrate lead to different contact angles, giving rise to different boundary conditions for the upper and the lower hemisphere of the cell (indicated by i = 1, 2). At the equator the normal of the cell contour is orthogonal to the cell axis, therefore β = π/2 at r = R0. Geometry dictates β = ϕi at r = Ri. This leads to
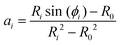 | (5) |
bi = Ri![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕi) − aiRi2. sin(ϕi) − aiRi2. | (6) |
Inserting eqn (4) into eqn (3) gives ΔP = 2Tai. Since ΔP and T are constant over the cell surface, it follows that a1 = a2. Therefore, if the three radii and one contact angle are known, the second contact angle can be directly calculated. The shape of the cell needs to obey three boundary conditions: cell volume conservation, the force balance across the membrane, and the Young–Dupré equation at the interface, as we will introduce in the following.
2.2 Volume conservation
Assuming a spherical shape of the suspended cell with initial radius Rsusp, the initial volume V of the cell is V = 4/3πRsusp3. The volume of the adhered cell can be obtained as the volume of a solid of revolution by integration. Again, we need to treat both hemispheres separately. The volumes are given by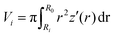 | (7) |
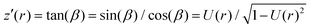 , using the identities
, using the identities 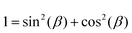 and U(r) = sin(β). Therefore, the volume of the adherent cell can be obtained by numerically integrating
and U(r) = sin(β). Therefore, the volume of the adherent cell can be obtained by numerically integrating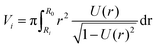 | (8) |
Since the total volume of the cell is conserved on the experimental timescales, we can use
| V = V1 + V2. | (9) |
2.3 Force balance
To solve the force balance at the contact with the substrate we consider the pressure acting on the contact area πR12ΔP and the vertical force arising from the membrane tension at the perimeter of the contact area 2πR1T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ) to get the force:
sin(ϕ) to get the force:F = 2πR1T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ1) − πR12ΔP. sin(ϕ1) − πR12ΔP. | (10) |
Eqn (3) and (4) give us ΔP = 2Ta to get:
F = 2πR1T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ1) − πR12Ta. sin(ϕ1) − πR12Ta. | (11) |
The membrane tension T arises from pre-stress T0 and the elastic response of the cell against area dilation
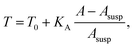 | (12) |
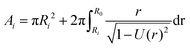 | (13) |
The total cell surface area is then A = A1 + A2.
2.4 Young–Dupré equation
As a third condition, a result from the natural boundary condition of the first variation of eqn (1), the contact angle ϕ1 and the surface tension need to satisfy the Young–Dupré equation at the contact to the substratew = T(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1), ϕ1), | (14) |
2.5 Computational force–distance curves
In order to calculate the cell shape, we solve the set of equations given by volume conservation (eqn (9)), the force balance (eqn (11)), and the contact angle (eqn (14)) numerically using the nonlinear least-squares solver lsqnonlin provided by MATLAB (Mathworks, USA). These three equations give access to three of the five parameters describing the system R0, R1, R2, F and ϕ1. In single cell force spectroscopy experiments, the cantilever is commonly coated with polyphenolic adhesive proteins or poly-D-lysine giving rise to strong adhesion of the cell to the cantilever. Therefore, we assume that the contact radius R2 between the cell and cantilever remains constant during the experiment. This set of equations can now be solved for a fixed force F with the parameters R0, R1, and ϕ1 or with a fixed contact radius R1 and the parameters F, R0, and ϕ1. Finally the free contour z(r) of the cell can be calculated by integrating z′(r) for both hemispheres: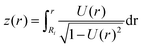 | (15) |
The total height of the cell zmax is obtained by integrating both hemispheres to R0. The resulting computational curve is shown in Fig. 3. Remarkably, the shape of the curve is similar to the curve predicted by the Johnson–Kendall–Roberts (JKR) model describing the adhesive contact of two elastic bodies.57 When the critical adhesion force Fcrit (the first local maximum of the pulling force) is reached from the left, the solution of the model represents unstable equilibrium conditions and detachment proceeds spontaneously and abruptly. The same behavior has been described by Lin and Freund.51 Compared to the experimental data, we find that in the experiment attachment persists beyond this point of stability due to the presence of binding clusters. Now single unbinding events are dominating the shape of the curve beyond Fcrit as will be discussed below.
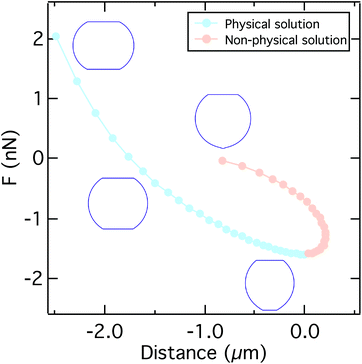 | ||
| Fig. 3 A typical force distance curve calculated using the solution of eqn (9), (11), and (14) by varying the contact radius R1. Up to the critical adhesion force we get a physical solution (light blue). The right branch of the curve presents a non-physical solution (light orange). Insets show the typical shape of the cell under compression, at zero force, at the critical adhesion force, and for a small contact radius. Parameters used to calculate the curve can be found in Table S2.† | ||
2.6 Deriving the critical adhesion force
An approximate analytical expression for the critical adhesion force of the sessile droplet cell model was first obtained by Brochard-Wyart and de Gennes.48 We start with the force balances at the equator| F = 2πR0T − πR02ΔP, | (16) |
F = 2πR1T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ1) − πR12ΔP. sin(ϕ1) − πR12ΔP. | (17) |
Substituting ΔP with eqn (2) and solving eqn (16) for the total curvature gives us:
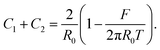 | (18) |
Substitution of eqn (18) into eqn (17) and solving for the force lead to
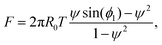 | (19) |
| F = 2πR0T(ψ·ϕ1 − ψ2). | (20) |
The maximum of the force with respect to ψ can be obtained by differentiation yielding ψ = ϕ1/2. Substitution into eqn (20) gives the critical adhesion force
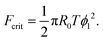 | (21) |
Finally, the Young–Dupré eqn (14) can be simplified by using a Taylor series expansion of the cosine and truncation after the leading term to give
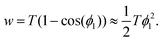 | (22) |
Eqn (21) and (22) and approximating the equatorial radius of the cell by the radius of the cell in suspension R0 ≈ Rsusp provide the final expression for the critical adhesion force
| Fcrit = πwRsusp. | (23) |
To test the validity of the assumptions, we compare the maximum adhesion force according to eqn (23) with the maximum adhesion force according to the numerical solution (Fig. 5A) showing excellent agreement. Interestingly eqn (23) only differs by a factor of 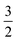 from the solution of the JKR model of elastic contacts.57 Notably, we only used the force balance at the equator and at the contact together with the Young–Dupré equation to derive eqn (23). This means that eqn (23) is independent of the pulling geometry, which does typically not consist of parallel plates as assumed in the model but shows a slight angle (see Fig. 2) that could be corrected using the wedging technique.58,59 The independence from the pulling geometry shows that eqn (23) can also be applied to data obtained by other methods, such as micropipette aspiration.
from the solution of the JKR model of elastic contacts.57 Notably, we only used the force balance at the equator and at the contact together with the Young–Dupré equation to derive eqn (23). This means that eqn (23) is independent of the pulling geometry, which does typically not consist of parallel plates as assumed in the model but shows a slight angle (see Fig. 2) that could be corrected using the wedging technique.58,59 The independence from the pulling geometry shows that eqn (23) can also be applied to data obtained by other methods, such as micropipette aspiration.
3 Results & discussion
3.1 Two stages of cell unbinding
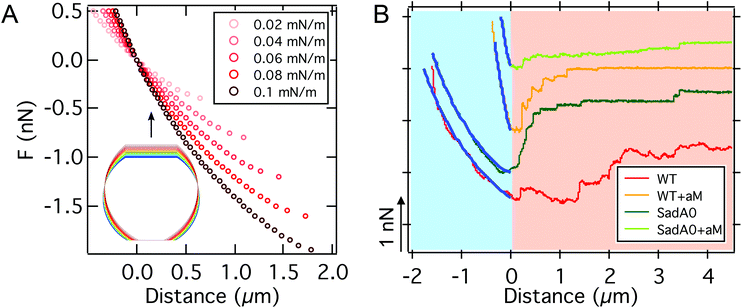 | ||
| Fig. 4 A: Computational FD curves up to the critical adhesion force for different adhesion energies per unit area w. The inset shows the shape evolution during pulling (increasing pulling forces from blue to red). B: Comparison between computational (blue) and experimental FD curves for different cell modifications on T-OTS. We find excellent agreement up to the critical adhesion force where a continuum (light blue background) treatment is valid. In the second part of the FD curve the force progression is dominated by stochastic (light orange background) bond rupture. Parameters used to calculate the curves can be found in Table S2.† | ||
The shape of the force distance curve obtained by this approach for the unbinding of a cell from the substrate quantitatively reproduces the experimentally obtained force distance curves up to the critical adhesion force, the first local pulling force maximum, that usually also coincides with the absolute maximum of the pulling force (see Fig. 4). At this point, however, the model diverges from the experimentally observed force progression. We attribute the existence of this regime beyond the critical force to effects on the molecular level not captured by our mean field description. In these later stages of unbinding, single unbinding events, cluster dissolution and protein unfolding dominate, as will be discussed below. The computational curve up to the critical adhesion force is determined by the membrane tension, the area compressibility modulus, the size of the cell, and the adhesion strength. The curves shown in Fig. 4A were calculated for a typical radius of D.d. of Rsusp = 6.5 μm, a cortical tension T0 between 0.1 mN m−1 and 3 mN m−1, an adhesion energy per unit area w between 0.02 mN m−1 and 0.11 mN m−1 and an area compressibility modulus KA between 50 mN m−1 and 100 mN m−1 (see Table S2†). The agreement between experiment and theory is valid for both cells with and without the main adhesion molecule sadA. This indicates that, in this part of the curve, the description of the adhesion by the adhesion energy density w is valid even in the presence of specialized binding molecules without explicitly considering their binding and unbinding kinetics.
Notably, the model contains no bulk elasticity and considers no impact from the cytoplasm besides volume conservation. Instead, the elasticity observed in the experiment originates completely from the mechanical response of the cell cortex and the contact to the substrate (see Fig. S3†).
Although the shape of the curve depends on the elastic parameters of the cell cortex, the model leads to a simple approximate equation for the critical adhesion force Fcrit ≈ πwRsusp with the adhesion energy per unit area w and the radius of the cell in suspension Rsusp.
Comparing the approximate analytical solution (line) with the rigorous numerical treatment (dots) (see Fig. 5A), we find excellent agreement. To test this prediction experimentally, we obtained force distance curves for 27 individual cells on glass substrates and estimated the cell radius from bright field micrographs (see Fig. 5B). Despite the large variance of critical adhesion forces typical of SCFS the results follow generally the prediction as demonstrated by a linear regression which gives w = 0.165 mN m−1 with R2 = 0.18. Eqn (23) indicates that the critical adhesion force is independent of cell mechanics, making it the most suitable observable for the adhesion strength w, instead of the commonly used adhesion energy Wadh obtained from integration of the whole force distance curve, which also captures the viscoelastic properties of the cell and the second unbinding regime due to the presence of adhesion clusters as discussed below.62,63 Consequently, variations in the elastic parameters KA and T0 only have a minor impact on the maximum adhesion force, but dramatically alter the shape of the curve (see Fig. S3†), thereby impacting the adhesion lifetime of the cell when it is subjected to a force ramp. A softer cell therefore displays a larger integral adhesion energy Wadh and stays longer in contact with the substrate but the critical adhesion force remains unaffected.
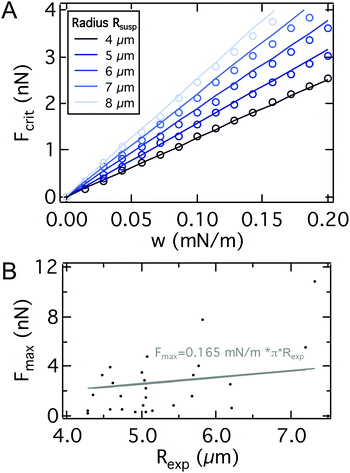 | ||
| Fig. 5 A: Comparison between the critical adhesion force as a function of the adhesion energy per unit area from eqn (23) (line) and from a numerical solution of the model for different cell radii Rsusp (dots). We find excellent agreement. Parameters used to calculate the curves can be found in Table S2.† B: SCFS-BF microscopy combination for single cell radius Rexpversus Fmax detection. Linear regression (gray) yields an adhesion energy per unit area of AX2 of 0.165 mN m−1. | ||
Only in rare cases, the critical adhesion force Fcrit can be different from the maximum adhesion force Fmax (compare the bright green, the ocher and the dark green curves in Fig. 4B with the red curve). Therefore, we will use the maximal adhesion force Fmax as an approximation for the critical adhesion force Fcrit, since its automatic determination is more robust.
3.2 Manipulation of the sadA adhesome and the glycocalyx
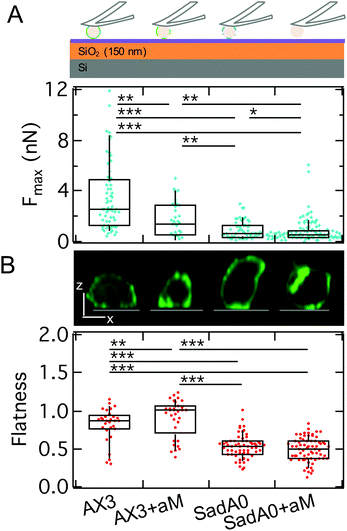
To identify the molecular basis for adhesion we first manipulated the adhesome by a knockout of one of the main adhesive transmembrane proteins, sadA (sadA0 mutant in AX3 background). SadA is an important adhesive protein, often co-localized with adhesion proteins of the TM9 family like phg1A or sibA.19,31 In addition to the knockout of sadA, glycolysis with α-mannosidase (αM) was used to enzymatically degrade 1′–5′-linked mannose, which is a common structure of the glycocalyx of D.d. It was shown that this glycolytic treatment leads to a reduction of D.d. adhesion.38,45 SCFS measurements were performed on model substrates displaying different v.d.W. characteristics (vide infra). Here, we show results for the least adhesive substrate, the T-OTS wafers for four different categories: wildtype cells (AX3), αM treated wildtype cells (AX3+αM), sadA knockout cells (sadA0) and sadA0 with αM treatment (sadA0+αM) (Fig. 6A, integrated adhesion energy in Fig. S4†). Measurements include more than 11 cells and 57 force curves per category.As discussed above we will use the maximal adhesion force Fmax as the main readout for the adhesion energy density w. We found a significant decrease of the median of Fmax from 2.5 nN for the untreated wildtype to 1.4 nN after glycolysis and to 0.7 nN for the sadA0 mutant. Simultaneous glycolysis and sadA knockout even leads to a further decrease of the median of Fmax to 0.5 nN. By contrast, the spreading behavior of the cells assessed by the cell flatness factor (square root of the contact area over the cube root of the volume) is only slightly changed to a more adherent state for the αM treatment, while sadA knockout leads to a clearly less adherent shape (Fig. 6B). A more detailed look at the flatness data showed that glycolysis mainly leads to a volume reduction at constant contact area, while the sadA knockout instead evokes a volume increase and a contact area decrease.
From the cell volume obtained for the flatness assessment we can estimate the radius of the cells in suspension assuming a spherical shape of the suspended cell with V = 4/3πRsusp3. We found median cell radii of 5.9 μm and 5.0 μm for wildtype cells without and with glycolytic treatment, respectively. The sadA0 mutant showed significantly increased radii of 7.3 μm and 7.0 μm without and with glycolytic treatment. This increase in size is still below the size described for multinucleated cells, where cell surface areas of about 175 μm2 where reported correlating with radii of up to 9 μm (for fixated and flattened cells).19 From the radius and the critical adhesion force we can calculate the adhesion energy density using eqn (23). We find 0.13 mN m−1 for the untreated wildtype, which is dramatically decreased to 0.03 mN m−1 for the sadA knockout. Glycolysis also leads to a decrease in adhesion energy density to 0.09 mN m−1, while the combination of knockout and glycolysis leads to a further decrease to 0.02 mN m−1.
The adhesion energy found here agrees well with the data collected by different methods: HeLa cells, for example, were shown to have an adhesion energy per unit area of 0.09 mN m−1 to 1.5 mN m−1 as detected via pipette aspiration,65 while D.d. WT AX2 showed an adhesion energy per unit area of 0.22 mN m−1, with talin and cortexillin null mutants going down to 0.06 or 0.15 mN m−1 based on interference contrast imaging.66 This agrees with the reduction of w we describe here for the sadA knockout as both talin and cortexillin were shown to be direct binding partners of sadA.
Beyond the critical rupture force Fcrit governed by continuum mechanics the cells often remain attached to the substrate at a few small spots that are also visible in the fluorescence images of sadA stained cells (Fig. 1B). Eventually, also the last attachment points are released stochastically and the cell separates entirely from the substrate. In the following, we scrutinize these steps.
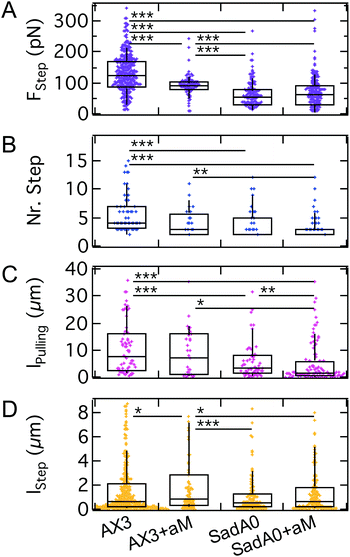
We monitored the step force, the number of steps, the step length and the total pulling length indicative of the overall lifetime of the attachment (Fig. 7). The median step force is reduced by a factor of 2 between wildtype (120 pN) and sadA0 cells (50 pN), while αM treatment is less effective (90 pN). The number of steps decreases from a median of 4 for the wildtype to 2 for sadA0 with αM treatment. Likewise, the amount of force curves without any steps increases from 4% for wildtype cells to 23% after αM treatment. SadA knockout even leads to 33% of curves without steps, which increases to 46% for αM treated sadA0 cells. This trend is similar for the pulling length, ranging from medians of 7.6 μm to 6.8 μm to 3.09 μm to 1.63 μm. Only the step length shows no clear trend, ranging between 520 nm and 860 nm.
In combination, we find that the effect of sadA knockout on step properties dominates over glycocalyx degradation. This agrees with earlier experiments, where it was shown that AX3 cells exposed to 5 μM Latrunculin A cytoskeleton–a substrate of sadA–yield a median Fmax of 0.2 nN (ref. 45) and show comparable results for the step detection: 62% of curves showed no steps, with a maximum of 4 steps per curve and elevated step forces of 290 pN.
The strong dependency on sadA indicates that the steps are mainly mediated by sadA. This means that sadA affects D.d. adhesion in two ways: by increasing the adhesion energy per unit area w and by acting as pinning points for the occurrence of structures inducing steps. Interestingly, these two effects are related to two different binding lifetimes of sadA since the steps occur after the critical adhesion force is reached. A possible explanation for this observation might be the formation of nanoscale clusters that display a larger dynamic strength compared to single dispersed bonds. This is in agreement with sadA-GFP labelling, showing bright spots in the TIRF images (Fig. 1B), which might identify these clusters. Additionally, from a mechanical point of view, cortical cellular organization might be influenced and thus the tension. Also – from a biochemical point of view – the knock out might have side effects which could be ameliorated by a knock down in the future.
As we have shown here, the rupture events are sensitive to sugar digestion, especially when the sadA adhesome is still present, which might indicate surface glycosylation of sadA. Other modifications have been proposed previously, like posttranslational modification due to phosphorylations of the sadA cytoplasmic domain, and even the occurrence of different isoforms when undergoing different adhesional states is conceivable.18 Since cluster stability might be compromised, also co-clustering might be disturbed, i.e. anchoring of the cluster partners like sibA (mediating adhesion) or phg1A (mediating phagocytosis) to the cytoskeleton might be affected.30
We however found that glycolysis is less efficient in effecting the occurrence of steps when applied to sadA0 cells, where all step parameters (step force, number of steps and step length) remain constant besides the pulling length. As the glycocalyx constitutes the first interface relevant to general adhesion, interfering with the composition might also induce general effects as found upon amoeboid-like cancer cell migration.67
In general, cells with sadA knockout and glycocalyx degradation showed only a minimal amount of adhesion, implying that we were able to identify two major molecular components mediating substrate adhesion of D.d. Interestingly even the cells missing both components adhered to surfaces and were viable demonstrating the robustness of D.d.
3.3 Variation of electrostatic interactions
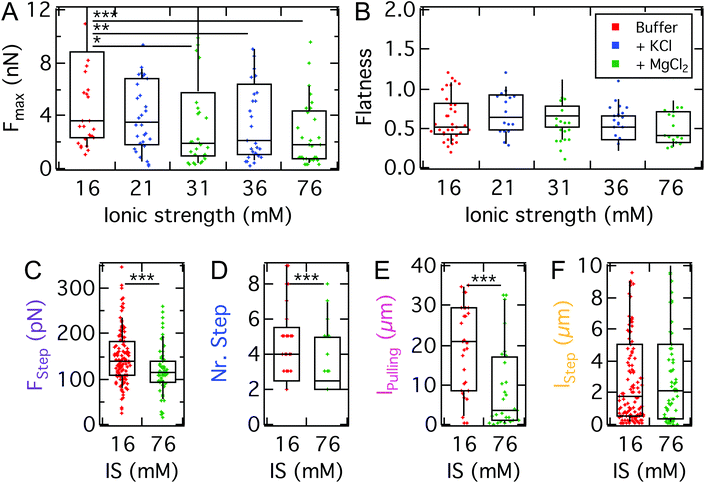
After identifying the impact of cell mechanics and the molecular basis for D.d. adhesion, we aim to dissect the physical interactions guiding D.d. adhesion. In the soil, D.d. cells usually face a heterogeneous, three-dimensional environment. This creates a situation where ordered extension of pseudopodia under topographic control can be beneficial for the cellular adhesion and migration.68,69 This requires on the one hand collective actin fiber dynamics,70,71 on the other hand also a selection of the surfaces to adhere to.72,73 The fluid-filled porous environment however can also have significant ionic strengths. To assess to which extent electrostatic interactions contribute to D.d. adhesion we modulated the ion content of the buffer. For this purpose, we used the non-silanized T-wafer (T-SiO2). To modulate the ionic strength we employed potassium and magnesium ions, which were shown to have negligible impact on the migratory behavior of D.d.35 We also restricted the range of ion concentrations to the osmoregulatory regime of D.d.Our measurements show that the maximal adhesion force Fmax of D.d. cells decreases with increasing ionic strength of the buffer (Fig. 8A). Although for monovalent K+ ions we observed no significant decrease of median Fmax from K+-free buffer (PB, IS: 16 mM, 3.7 nN, w = 0.24 mN m−1) to a K+-rich buffer (5 mM KCl, IS: 21 mM, 3.5 nN, w = 0.22 mN m−1), increasing the ionic strength further to 36 mM reduced the median Fmax significantly to 2.1 nN (w = 0.13 mN m−1). For the divalent ion Mg2+, the median of Fmax decreases significantly to 1.9 nN upon addition of 5 mM MgCl2 (IS: 31 mM, w = 0.12 mN m−1) but no further decrease is observed upon administration of 20 mM MgCl2 (IS: 76 mM). For comparison, the adhesion work Wadh is shown in Fig. S5 and listed in Table S3.† The flatness parameter did not change over the observed concentrations, so we can exclude osmotic swelling and changes of the spreading morphology of the examined D.d. cells.
Similar to the impact on continuum adhesion, step analysis unveils a strong effect of the ionic strength especially on the pulling length, where the median is reduced by a factor of 7 (21 μm to 3 μm), while the step force and step number are only slightly affected. In contrast, the step length remains unaffected.
It has been shown that in the buffer used here both the model substrates used here36,37 and the cell surface of D.d. are negatively charged in this developmental stage.74–76 The trend of decreasing attractive Fmax with increasing ionic strength is in agreement with earlier findings by Socol et al.75 A possible explanation might be the fact that the disjoining pressure is proportional to the ion concentration of the bulk solution. As a consequence, repulsive electrostatic forces that arise from osmotic pressure in the cleft between the cell and substrate contribute more strongly if the ion concentration increases reducing the overall adhesion force. Interestingly, Maeda reported a reduction of the negative surface charge upon development of D.d.,76 which according to our finding might impact the adhesive and migratory behavior of the cells. Furthermore, Hellio et al. could show that negatively charged particles, which mimic the surface of the bacteria D.d. preys on, were ingested more efficiently by D.d. compared to positively charged ones, despite the negative surface charge of D.d. A molecular explanation for the observed adhesion reduction might be a possible impact of the ionic strength on the structure of sadA. The three dimensional structure proposed by Fey et al.19 suggests a comparably bulky, folded extracellular domain containing three EGF domains. Some EGF-like domains have been shown to bind divalent ions, especially calcium.77 This binding process might lead to a less adhesive conformational state which could possibly explain the strong effect of magnesium ions, which also agrees with the strong effect on the pulling length observed in the step analysis.
It needs to be considered that the mM regime of ionic strengths employed here might be too low to induce effects comparable to the realistic soil groundwater case, where sudden changes can be of several decades reaching the molar ionic strength regime.78 However, for these drastic changes osmotic effects are expected to play a predominant role.
In conclusion, we found that electrostatic interactions play an important attractive role in D.d. adhesion, similarly in magnitude to the findings for the contribution of the glycocalyx. Interestingly, also the pulling length decreases, which we attribute to a reduced lifetime or dynamic strength of the point-like adhesion spots formed by sadA. This might point at electrostatic interactions as the physical basis for the strong adhesion of sadA to varying surfaces, but could also originate from an impact of the ionic strength on the organization of sadA in small clusters.
3.4 Role of van der Waals forces and substrate hydrophobicity
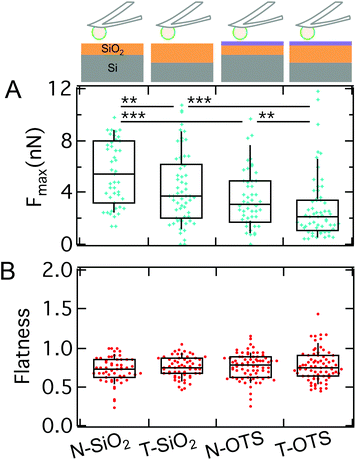
So far, we could show that electrostatics and the presence of sadA and the glycocalyx are decisive factors for D.d. adhesion. Since a specific receptor for sadA is missing, adhesion needs to rely on a more generic interaction potential based on DLVO forces. While electrostatic contributions to D.d. adhesion have been studied previously,75 only recent advances allow to systematically scrutinize the influence of long-ranged v.d.W. forces.36,37 In the following we will quantitatively describe the contribution and relevance of long-ranged attractive v.d.W. interactions and short ranged repulsive hydrophobic forces by using two different model substrates: (i) N-wafers with a thin, native SiO2-layer showing enhanced v.d.W. interactions due to the larger contributions from the underlying silicon (larger refractive index) and (ii) T-wafers with a thicker SiO2-layer and therefore reduced v.d.W. interactions. In addition, we looked at the impact of short-ranged repulsive interactions by applying a hydrophobic OTS-coating (termed N-OTS and T-OTS, respectively) in comparison to untreated and thus hydrophilic wafers (in the following N-SiO2 and T-SiO2, respectively). Cell adhesion to the substrates was measured using AX2 cells of D.d., a wildtype strain, which shows similar adhesion forces to AX3 on glass (median maximum adhesion forces of ∼7.7 nN on glass,79 see also Table S3†). Subsequent cycles of attachment and retraction, sometimes while switching back and forth between different model substrates, were recorded, without any significant changes of the general trend shown in Fig. 9 and Fig. S6.† The measurements include more than 14 cells and 50 force curves per category.Comparing the median Fmax on different model substrates with the same surface treatment, we find a strongly increased adhesion on N-wafers with enhanced v.d.W. interactions (3.1 nN on N-OTS (w = 0.2 mN m−1) and 5.4 nN on N-SiO2 (w = 0.34 mN m−1)) compared to T-wafers (2.1 nN on T-OTS (w = 0.13 mN m−1) and 3.7 nN on T-SiO2 (w = 0.26 mN m−1)). This result clearly shows that long-ranged v.d.W. interactions considerably contribute to the adhesion force of D.d. This finding is in line with the previous work on the adhesion of the bacterium Staphylococcus carnosus on the same set of model substrates.36,80 For D.d. Loomis et al. predicted v.d.W. forces in the pN to nN range in agreement with our results.38
The magnitude of v.d.W. interactions acting uniformly on the whole cell area is presumably a major barrier towards directed cell migration. While D.d. in the vegetative state is moving in a random fashion hunting for bacteria, it needs to switch to directed migration during the developmental state. Therefore D.d. needs a major reorganization of the cytoskeleton and the adhesom during its life cycle to overcome the uniform v.d.W. forces. However, in the vegetative state explored here, local fluctuations of the ventral-membrane substrate distance or the position of sadA clusters are conceivable triggers for random adhesion and migration dynamics. The symmetry breaking during the D.d. life cycle has been described to be fostered by cell–cell contacts.81
In addition to v.d.W. forces, we see that maximal adhesion forces on hydrophilic surfaces are strongly enhanced compared to the hydrophobic OTS surfaces. This is expected from Lifshitz's theory, which predicts that the van der Waals attraction through an aqueous solution increases if the dielectric constants of the cells and the surface match.12
On the same model surfaces, we determined the flatness of more than 50 single D.d. cells to assess the spreading morphology. Interestingly, besides the vast differences in adhesion force, we find no differences in spreading behavior showing that mechanical homeostasis prevails (Fig. 9B). As a control, the flatness was calculated for conventional glass surfaces (μ-Dish) and yielded comparable outcomes to our previous results,82i.e. increased spreading morphology as compared to the model substrates. While hydrophilic treatment would usually increase wetting, we detect no changes of flatness here. This indicates that forces arising from actomyosin cortical activity maintain a homeostatis of the spreading behaviour. Previous work has described similar results for D.d. based on fluorescence and RICM studies.81,83 They could show that the equilibrium of protrusive forces and adhesion forces allows D.d. to adhere and maintain shape on a multitude of substrates, while multicellular development and the occurrence of cell–cell contacts significantly interfere with this equilibrium.
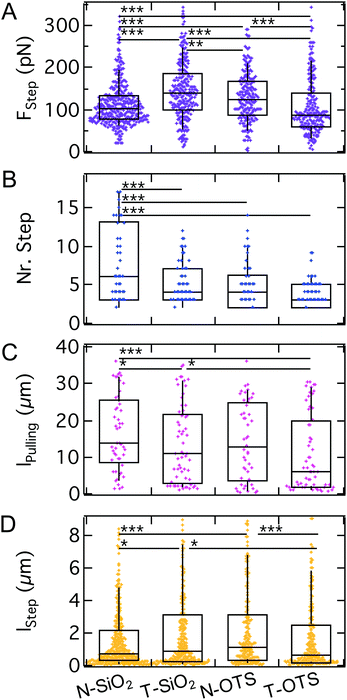
While it is an intuitive result that v.d.W. interactions contribute to the adhesion energy density w and, therefore, to the critical adhesion force, the question remains how they impact the stochastic unbinding events present in the second part of the force curve. Therefore, we analyzed step mechanics by extracting the same parameters as before: step force, step length, pulling length and the number of steps per curve (see Fig. 1C).
As shown in Fig. 10, the step force median increases from N-SiO2 to T-SiO2 (100 pN to 140 pN), but decreases from N-OTS to T-OTS (120 pN to 90 pN). The median number of steps per curve decreases when going from the N-wafer with increased v.d.W. interactions to the T-wafer from 6 to 4 and from 4 to 3 for hydrophilic and hydrophobic surfaces, respectively. The amount of FD curves showing no steps was smaller than 5% for all substrates. The pulling length shows each a decrease from N-wafers to T-wafers (from 14 μm to 11 μm and from 13 μm to 6 μm for hydrophilic and hydrophobic surfaces, respectively). The step length follows the trend of the step force, an increase for hydrophilic surfaces from N-wafers to T-wafers (0.7 μm to 0.9 μm) and a decrease for hydrophobic surfaces from N-wafers to T-wafers (1.1 μm to 0.7 μm). In summary, we find that step characteristics show no clear trend, neither for the model substrates, nor for the switch between hydrophilic and hydrophobic surfaces, while the number of steps correlates weakly with the surface properties. The sadA clusters anchoring the steps do not respond to changes of the bulk surface properties as strongly as the maximum adhesion force. This suggests that sadA binding relies on local interactions like hydrogen-bonding instead of hydrophobic interactions and long-ranged v.d.W. forces. Since sadA is coupled to the actin cytoskeleton it is conceivable that the cell is capable of adjusting or maintaining the step forces and also the lifetime of the bonds similarly to integrins that display an intricate energy potential.
4 Conclusion
Motile cells require reversible adhesion to solid surfaces to accomplish force transmission upon locomotion. In contrast to mammalian cells, D.d. cells do not express integrins forming focal adhesions but are believed to rely on more generic interaction forces that guarantee a larger flexibility; even the ability to swim has been described for D.d.84–86Indeed, amoeba of D.d. are found to adhere non-specifically on a wide range of substrates displaying both hydrophilic and hydrophobic surfaces without forming focal adhesions. Instead they employ a dual strategy of dense molecular contacts acting as a continuum of stickers and stochastic opening of a small number of adhesion clusters formed by sadA, thus an initial continuum regime and a secondary regime governed by stochastic bond dynamics. Knockout of sadA results in both a considerable decrease of adhesion forces and diminishing the number and dynamic strength of steps due to the disappearance of adhesion clusters in the contact zone. This indicates that sadA is not only dispersed in the contact zone but also forms small clusters that allow the cells to stick to the substrate even after passing the critical rupture force obtained from stability analysis. The extended lifetime (almost an order of magnitude) of these adhesion spots ensures that the cell remains partly in contact although the majority of the adhesion zone has vanished. This is pivotal for propulsion of cells hunting for bacteria even on heterogeneous substrates that would otherwise not permit to exert sufficient traction force for locomotion.
Electrostatic and van der Waals interactions turned out to be key forces of D.d. to form stable molecular bridges to arbitrary substrates, with a strong preference for hydrophilic surfaces. This indicates that short-range attractive forces also participate in the adhesion process. Uniformly distributed non-specific forces are presumably a major challenge for cells showing directed migration. However, it was found that traction forces are in the same regime (200 pN), which suggests that internal forces are sufficient to overcome the barrier if the cells start to migrate.38
We also found that the lifetime of the adhered state is dependent on cellular mechanics, i.e., softer cells remain attached substantially longer than stiffer cells although the critical force is identical.
In summary, we were able to distinguish two different mechanisms of D.d. adhesion based on continuum wetting and nanocluster unbinding. We found that these two fundamentally different regimes rely on the adhesion protein sadA and electrostatic interactions, while v.d.W. interactions and the glycolytic degradation mostly impact adhesion at the continuum level.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Max Planck Society and the MPG fellow program, the SFB 937 ‘Collective behaviour of soft and biological matter’ (Project A8) and the Volkswagen Foundation Initiative LIFE (Project Living Foam) for funding. We thank Katharina Gunkel and Maren-Stella Müller for their essential help in the cell culture as well as the following labs for additional ideas and help with cell lines and vectors: Günther Gerisch, Wiliam F. Loomis and dictybase.org. We are also very much indebted to Eberhard Bodenschatz for fruitful and lively discussions. Open Access funding provided by the Max Planck Society.References
- R. H. Kessin, Dictyostelium: evolution, cell biology, and the development of multicellularity, Cambridge University Press, 2001, vol. 38 Search PubMed.
- P. N. Devreotes, S. Bhattacharya, M. Edwards, P. A. Iglesias, T. Lampert and Y. C. Miao, Annu. Rev. Cell Dev. Biol., 2017, 33, 103–125 CrossRef CAS PubMed.
- C. H. Stuelten, C. A. Parent and D. J. Montell, Nat. Rev. Cancer, 2018, 296–312 CrossRef CAS PubMed.
- O. Bäumchen, H. Hähl, P. Loskill and K. Jacobs, Phys. J., 2015, 14, 37–43 Search PubMed.
- C. T. Kreis, M. Le Blay, C. Linne, M. M. Makowski and O. Bäumchen, Nat. Phys., 2018, 14, 45–49 Search PubMed.
- Y. F. Dufrêne, Trends Microbiol., 2015, 23, 376–382 CrossRef PubMed.
- T. Pollard, W. Earnshaw and J. Lippincott-Schwartz, Cell biology, Springer Spektrum, Heidelberg, 2007 Search PubMed.
- A. Sebe-Pedros, A. J. Roger, F. B. Lang, N. King and I. Ruiz-Trillo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10142–10147 CrossRef CAS PubMed.
- B. Varnum, K. B. Edwards and D. R. Soll, Dev. Biol., 1986, 113, 218–227 CrossRef CAS PubMed.
- G. Gerisch, J. E. Segall and E. Wallraff, Cell Motil. Cytoskeleton, 1989, 14, 75–79 CrossRef CAS PubMed.
- I. Weber, E. Wallraff, R. Albrecht and G. Gerisch, J. Cell Sci., 1995, 108, 1519–1530 CAS.
- J. Israelachvili, Intermolecular and surface forces, Academic Press, 1992, p. 437 Search PubMed.
- V. Parsegian, Van der Waals Forces, Cambridge University Press, 2006, p. 398 Search PubMed.
- D. Leckband and J. Israelachvili, Q. Rev. Biophys., 2001, 34, 105–267 CrossRef CAS PubMed.
- G. Bell, Science, 1978, 618–627 CrossRef CAS.
- E. Sackmann and A. S. Smith, Soft Matter, 2014, 10, 1644–1659 RSC.
- D. Boal, Mechanics of the cell, Cambridge University Press, Cambridge, 2012 Search PubMed.
- A. S. Kowal and R. L. Chisholm, Eukaryotic Cell, 2011, 10, 662–671 CrossRef CAS PubMed.
- P. Fey, S. Stephens, M. A. Titus and R. L. Chisholm, J. Cell Biol., 2002, 159, 1109–1119 CrossRef CAS PubMed.
- A. F. Vinet, T. Fiedler, V. Studer, R. Froquet, A. Dardel, P. Cosson and J. Pieters, Mol. Biol. Cell, 2014, 25, 688–701 CrossRef PubMed.
- R. Zaidel-Bar, S. Itzkovitz, A. Ma'ayan, R. Iyengar and B. Geiger, Nat. Cell Biol., 2007, 9, 858–868 CrossRef CAS PubMed.
- A. Harwood and J. C. Coates, Curr. Opin. Cell Biol., 2004, 16, 470–476 CrossRef CAS PubMed.
- K. Swaminathan, M. Stumpf, R. Müller, A. C. Horn, J. Schmidbauer, L. Eichinger, A. Müller-Taubenberger, J. Faix and A. A. Noegel, Sci. Rep., 2015, 5, 14437 CrossRef CAS PubMed.
- T. Bukahrova, G. Weijer, L. Bosgraaf, D. Dormann, P. J. van Haastert and C. J. Weijer, J. Cell Sci., 2005, 118, 4295–4310 CrossRef CAS PubMed.
- M. Tsujioka, S. Yumura, K. Inouye, H. Patel, M. Ueda and S. Yonemura, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12992–12997 CrossRef CAS PubMed.
- J. Niewohner, I. Weber, M. Maniak, A. Müller-Taubenberger and G. Gerisch, J. Cell Biol., 1997, 138, 349–361 CrossRef CAS PubMed.
- S. Cornillon, R. Froquet and P. Cosson, Eukaryotic Cell, 2008, 7, 1600–1605 CrossRef CAS PubMed.
- S. Cornillon, L. Gebbie, M. Benghezal, P. Nair, S. Keller, B. Wehrle-Haller, S. J. Charette, F. Brückert, F. Letourneur and P. Cosson, EMBO Rep., 2006, 7, 617–621 CAS.
- S. Cornillon, E. Pech, M. Benghezal, K. Ravanel, E. Gaynor, F. Letourneur, F. Brückert and P. Cosson, J. Biol. Chem., 2000, 275, 34287–34292 CrossRef CAS PubMed.
- R. Froquet, M. Le Coadic, J. Perrin, N. Cherix, S. Cornillon and P. Cosson, Mol. Biol. Cell, 2012, 23, 679–686 CrossRef CAS PubMed.
- J. Perrin, M. Le Coadic, A. Vernay, M. Dias, N. Gopaldass, H. Ouertatani-Sakouhi and P. Cosson, J. Cell Sci., 2015, 128, 2269–2277 CrossRef CAS PubMed.
- M. Benoit, D. Gabriel, G. Gerisch and H. E. Gaub, Nat. Cell Biol., 2000, 2, 313–317 CrossRef CAS PubMed.
- Y. C. Miao, S. Bhattacharya, M. Edwards, H. Q. Cai, T. Inoue, P. A. Iglesias and P. N. Devreotes, Nat. Cell Biol., 2017, 19, 329–340 CrossRef CAS PubMed.
- A. Pietuch, B. R. Brückner and A. Janshoff, Biochim. Biophys. Acta, Mol. Cell Res., 2013, 1833, 712–722 CrossRef CAS PubMed.
- D. F. Lusche, D. Wessels and D. R. Soll, Cell Motil. Cytoskeleton, 2009, 66, 567–587 CrossRef CAS PubMed.
- P. Loskill, H. Hahl, N. Thewes, C. T. Kreis, M. Bischoff, M. Herrmann and K. Jacobs, Langmuir, 2012, 28, 7242–7248 CrossRef CAS PubMed.
- C. T. Kreis, PhD thesis, Universität Göttingen, 2017 Search PubMed.
- W. F. Loomis, D. Fuller, E. Gutierrez, A. Groisman and W. J. Rappel, PLoS One, 2012, 7, e42033 CrossRef CAS PubMed.
- X. Y. Sun, M. K. Driscoll, C. Guven, S. Das, C. A. Parent, J. T. Fourkas and W. Losert, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12557–12562 CrossRef CAS PubMed.
- M. K. Driscoll, X. Y. Sun, C. Guven, J. T. Fourkas and W. Losert, ACS Nano, 2014, 8, 3546–3555 CrossRef CAS PubMed.
- M. Lessel, O. Bäumchen, M. Klos, H. Hahl, R. Fetzer, M. Paulus, R. Seemann and K. Jacobs, Surf. Interface Anal., 2015, 47, 557–564 CrossRef CAS.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- C. Brunner, PhD thesis, Universität Leipzig, 2010 Search PubMed.
- R. J. Cannara, M. Eglin and R. W. Carpick, Rev. Sci. Instrum., 2006, 77, 053701 CrossRef.
- M. Tarantola, A. Bae, D. Fuller, E. Bodenschatz, W. J. Rappel and W. F. Loomis, PLoS One, 2014, 9, e106574 CrossRef PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld and B. Schmid, et al. , Nat. Methods, 2012, 9, 676 CrossRef CAS PubMed.
- S. Vogel, Comparative biomechanics: life's physical world, Princeton University Press, 2013 Search PubMed.
- F. Brochard-Wyart and P.-G. de Gennes, C. R. Phys., 2003, 4, 281–287 CrossRef CAS.
- E. Schäfer, M. Vache, T.-T. Kliesch and A. Janshoff, Soft Matter, 2015, 11, 4487–4495 RSC.
- E. A. Evans and R. Skalak, Mechanics and Thermodynamics of Biomembranes, CRC Press, 1980, p. 254 Search PubMed.
- Y. Lin and L. Freund, Int. J. Solids Struct., 2007, 44, 1927–1938 CrossRef.
- G. E. Wang and J. J. Lannutti, J. Mater. Sci., 1995, 30, 3171–3176 CrossRef CAS.
- B. Daily, E. Elson and G. Zahalak, Biophys. J., 1984, 45, 671–682 CrossRef CAS PubMed.
- R. Lipowsky and U. Seifert, Mol. Cryst. Liq. Cryst., 1991, 202, 17–25 CrossRef CAS.
- E. Bormashenko, Colloids Surf., A, 2009, 345, 163–165 CrossRef CAS.
- V. A. Lubarda, Soft Matter, 2012, 8, 10288 RSC.
- E. Barthel, J. Phys. D: Appl. Phys., 2008, 41, 163001 CrossRef.
- M. P. Stewart, A. W. Hodel, A. Spielhofer, C. J. Cattin, D. J. Müller and J. Helenius, Methods, 2013, 60, 186–194 CrossRef CAS PubMed.
- E. Sariisik, C. Popov, J. P. Müller, D. Docheva, H. Clausen-Schaumann and M. Benoit, Biophys. J., 2015, 109, 1330–1333 CrossRef CAS PubMed.
- E. Sackmann and R. F. Bruinsma, ChemPhysChem, 2002, 3, 262 CrossRef CAS PubMed.
- S. Sen, S. Subramanian and D. E. Discher, Biophys. J., 2005, 89, 3203–3213 CrossRef CAS PubMed.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- A. Diz-Muñoz, O. D. Weiner and D. A. Fletcher, Nat. Phys., 2018, 14, 648–652 Search PubMed.
- M. Krieg, J. Helenius, C.-P. Heisenberg and D. Muller, Angew. Chem., Int. Ed., 2008, 47, 9775–9777 CrossRef CAS PubMed.
- M.-J. Colbert, F. Brochard-Wyart, C. Fradin and K. Dalnoki-Veress, Biophys. J., 2010, 99, 3555–3562 CrossRef CAS PubMed.
- R. Simson, E. Wallraff, J. Faix, J. Niewöhner, G. Gerisch and E. Sackmann, Biophys. J., 1998, 74, 514–522 CrossRef CAS PubMed.
- J. C.-H. Kuo, J. G. Gandhi, R. N. Zia and M. J. Paszek, Nat. Phys., 2018, 14, 658–669 Search PubMed.
- M. K. Driscoll, X. Sun, C. Guven, J. T. Fourkas and W. Losert, ACS Nano, 2014, 8, 3546–3555 CrossRef CAS PubMed.
- O. Nagel, C. Guven, M. Theves, M. Driscoll, W. Losert and C. Beta, PLoS One, 2014, 9, e113382 CrossRef PubMed.
- M. Jasnin, M. Ecke, W. Baumeister and G. Gerisch, Structure, 2016, 24, 1031–1043 CrossRef CAS PubMed.
- M. Priebe, M. Bernhardt, C. Blum, M. Tarantola, E. Bodenschatz and T. Salditt, Biophys. J., 2014, 107, 2662–2673 CrossRef CAS PubMed.
- J. Helenius, M. Ecke, D. J. Müller and G. Gerisch, Biophys. J., 2018, 115, 150–162 CrossRef CAS PubMed.
- F. Knoch, M. Tarantola, E. Bodenschatz and W. J. Rappel, Phys. Biol., 2014, 11, 046002 CrossRef PubMed.
- R. Hellio and A. Ryter, J. Cell Sci., 1985, 79, 327–342 CAS.
- M. Socol, C. Lefrou, F. Bruckert, D. Delabouglise and M. Weidenhaupt, Bioelectrochemistry, 2010, 79, 198–210 CrossRef CAS PubMed.
- Y. Maeda, Dev., Growth Differ., 1980, 22, 679–685 CrossRef.
- Z. Rao, P. Handford, M. Mayhew, V. Knott, G. G. Brownlee and D. Stuart, Cell, 1995, 82, 131–141 CrossRef CAS PubMed.
- S. Ramezanian, H. X. Ta, B. Muhunthan and N. Abu-Lail, Biointerphases, 2018, 13, 041005 CrossRef PubMed.
- H. Leonhardt, M. Gerhardt, N. Höppner, K. Krüger, M. Tarantola and C. Beta, Phys. Rev. E, 2016, 93, 012414 CrossRef PubMed.
- N. Thewes, P. Loskill, P. Jung, H. Peisker, M. Bischoff, M. Herrmann and K. Jacobs, Beilstein J. Nanotechnol., 2014, 5, 1501–1512 CrossRef PubMed.
- C. L. Wang, S. Chowdhury, M. Driscoll, C. A. Parent, S. K. Gupta and W. Losert, J. R. Soc., Interface, 2014, 11, 20140684 CrossRef PubMed.
- T. J. Lampert, N. Kamprad, M. Edwards, J. Borleis, A. J. Watson, M. Tarantola and P. N. Devreotes, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E7727–E7736 CrossRef CAS PubMed.
- C. P. McCann, E. C. Rericha, C. L. Wang, W. Losert and C. A. Parent, PLoS One, 2014, 9, e87981 CrossRef PubMed.
- M. K. Driscoll, C. McCann, R. Kopace, T. Homan, J. T. Fourkas, C. Parent and W. Losert, PLoS Comput. Biol., 2012, 8, e1002392 CrossRef CAS PubMed.
- A. J. Bae and E. Bodenschatz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, E165–E166 CrossRef CAS PubMed.
- N. P. Barry and M. S. Bretscher, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11376–11380 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C8NR07107A |
| This journal is © The Royal Society of Chemistry 2018 |