Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Angle-resolved photoelectron spectroscopy and scanning tunnelling spectroscopy studies of the endohedral fullerene Li@C60†
M.
Stefanou
 a,
H. J.
Chandler
a,
H. J.
Chandler
 b,
B.
Mignolet
b,
B.
Mignolet
 c,
E.
Williams
a,
S. A.
Nanoh
b,
J. O. F.
Thompson
a,
F.
Remacle
c,
E.
Williams
a,
S. A.
Nanoh
b,
J. O. F.
Thompson
a,
F.
Remacle
 c,
R.
Schaub
c,
R.
Schaub
 b and
E. E. B.
Campbell
b and
E. E. B.
Campbell
 *ad
*ad
aEaStCHEM and School of Chemistry, University of Edinburgh, David Brewster Road, Edinburgh, EH9 3FJ, UK. E-mail: eleanor.campbell@ed.ac.uk
bEaStCHEM and School of Chemistry, University of St Andrews, KY16 9ST, UK
cTheoretical Physical Chemistry, Research Unit MOLSYS, University of Liège, B4000 Liège, Belgium
dDivision of Quantum Phases and Devices, School of Physics, Konkuk University, Seoul 143-701, South Korea
First published on 18th October 2018
Abstract
Gas phase photoelectron spectroscopy (Rydberg Fingerprint Spectroscopy), TDDFT calculations and low temperature STM studies are combined to provide detailed information on the properties of the diffuse, low-lying Rydberg-like SAMO states of isolated Li@C60 endohedral fullerenes. The presence of the encapsulated Li is shown by the calculations to produce a significant distortion of the lowest-lying S- and P-SAMOs that is dependent on the position of the Li inside the fullerene cage. Under the high temperature conditions of the gas phase experiments, the Li is mobile and able to access different positions within the cage. This is accounted for in the comparison with theory that shows a very good agreement of the photoelectron angular distributions, allowing the symmetry of the observed SAMO states to be identified. When adsorbed on a metal substrate at low temperature, a strong interaction between the low-lying SAMOs and the metal substrate moves these states to energies much closer to the Fermi energy compared to the situation for empty C60 while the Li remains frozen in an off-centre position.
1. Introduction
Shortly after the ground-breaking publication on the discovery of C60,1 evidence was obtained for the possibility of capturing metal atoms inside the fullerene carbon cages.2 Since then endohedral fullerenes have been the subject of many studies probing their formation, properties and potential applications.3,4 The most commonly studied endohedral fullerenes, M@C2n, are formed by the carbon cage growing around the metal atom(s) and in most cases the energetically favourable fullerene cage does not have the same structure as the equivalent empty cage. It is e.g. challenging using this technique to extract and purify macroscopic amounts of M@C60 with the highly symmetrical Ih C60 fullerene cage structure. One alternative way to produce such species is to implant metal ions inside the C60 cage. This method was used to produce Li@C60.5,6 Early experiments on the isolated material showed the considerably higher reactivity compared to C60 with a tendency for the purified material to oligomerise.7 Thin films were shown to exhibit metallic conductivity if kept under high vacuum conditions.8 More recently, the production of Li@C60 has been upscaled and commercialised by using a related plasma implantation technique.9 The purified material is stabilised by forming a hexafluorophosphate salt.10 The availability of macroscopic amounts of the purified material in the form of the salt allowed the predicted off-centre geometry of the Li11,12 to be experimentally confirmed by X-ray diffraction9 and charge transfer between the encapsulated Li and the carbon cage was confirmed by UPS and XPS measurements.13 Many characterisation studies have now been reported with the strong electron-accepting nature of the Li+@C60 cation compared to C60 being particularly interesting for potential photovoltaic devices.14 The state-of-the-art with respect to current studies of [Li+@C60]PF6− and the reduced “superatom” Li@C60 have been recently summarised in a book.15In this paper we combine, for the first time, gas phase Rydberg Photoelectron Spectroscopy, TDDFT calculations and low temperature Scanning Tunnelling Spectroscopy (STS) studies on isolated Li@C60 to obtain information about the diffuse low-lying Rydberg-like “Super-Atom Molecular Orbitals” (SAMO) that have been studied in detail for empty C60.16–21 This provides a direct probe of the influence of the encapsulated Li on the electronic structure of the fullerene and, in particular, of these fascinating high symmetry “superatom” excited states that have been speculated to play an important role in the electronic properties of the solid phase.21,22 We show that the presence of the off-centre Li strongly distorts the lowest-lying S- and P-SAMO states of the endohedral fullerene. TDDFT calculations show the sensitivity of the electronic binding energies on the position of the Li that is expected to be highly mobile under the conditions of the gas phase experiments.23 The low temperature STM/STS studies, for which the Li is static, show a strong interaction between the SAMO states and the metal substrate, moving the binding energies for the S- and Pz-SAMO significantly closer to the Fermi energy.
2. Methods
2.1. Photoelectron spectroscopy
The photoelectron spectra and time-of-flight mass spectra are obtained using a combined velocity map imaging (VMI) photoelectron spectrometer and a Wiley–McLaren type time-of-flight ion mass spectrometer. The setup has been described in detail previously.24,25An effusive molecular beam of Li@C60 was produced by heating [Li+@C60]PF6− salt (Idea International Inc., >80% purity) to a temperature of 620 K. The oven consisted of a small quartz capillary placed inside a heated molybdenum cylinder. Neutral Li@C60 molecules were evaporated from the oven along with some neutral C60 that would appear to be produced via destructive reactions that occur within the oven (see section 3.1 and ESI† for more details). The material was first degassed at a temperature of ca. 590 K for at least 20 hours until traces of solvent and other impurities from the oven were no longer visible in the mass spectrum (ESI, Fig. S1†). The neutral molecular target was ionised with ∼100 fs laser pulses at a number of different wavelengths (800 nm, 600 nm, 540 nm, 400 nm, 267 nm). The 800 nm light was produced by the fundamental output of a regenerative amplified Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sapphire laser system (800 nm, 120 fs pulse duration). The 400 nm and 267 nm pulses were produced by frequency doubling or tripling the output of the laser. All other wavelengths were produced using a non-collinear optical parametric amplifier (NOPA). In all cases the laser, linearly polarised in the vertical direction, was focused into the interaction region using a 30 cm focal length fused silica lens and the overall intensity of light was controlled using a neutral density filter. The laser intensity was adjusted to ensure that predominantly singly-charged parent ions were observed in the mass spectra with no significant contributions from fragment ions.
sapphire laser system (800 nm, 120 fs pulse duration). The 400 nm and 267 nm pulses were produced by frequency doubling or tripling the output of the laser. All other wavelengths were produced using a non-collinear optical parametric amplifier (NOPA). In all cases the laser, linearly polarised in the vertical direction, was focused into the interaction region using a 30 cm focal length fused silica lens and the overall intensity of light was controlled using a neutral density filter. The laser intensity was adjusted to ensure that predominantly singly-charged parent ions were observed in the mass spectra with no significant contributions from fragment ions.
The produced photoelectrons were extracted at right angles to the laser and molecular beam onto an integrated 40 mm dual MCP/phosphor detector using a set of velocity map imaging electrostatic lenses. The image was recorded using a CCD camera controlled via a LabVIEW program. The VMI images were recorded for 107–108 laser shots (depending on signal intensity). The obtained images were inverted using a POP inversion algorithm that was modified to include Legendre polynomials up to the 10th order.26 The energy scale was calibrated using the well-known peaks from multiphoton ionisation via Freeman-type resonances in Xe.27 Post-inversion, any thermal (or non-resolved) electron background was removed by fitting and subtracting a single exponential function. The C60 component (see section 3.1) was subtracted from the signal by determining the ratio of C60+ to Li@C60+ from the mass spectrum, obtained under similar laser and oven conditions, and subtracting the appropriate intensity of a pure C60 photoelectron spectrum obtained under identical conditions. The SAMO peak structure in the resulting pure Li@C60 photoelectron spectrum was then fitted by multiple Lorentzian functions (see Fig. 4). The fit procedure was developed and described in detail previously for the analysis of C60 photoelectron spectra.20
The photo-ions were extracted using a Wiley–McLaren set of electrostatic lenses onto an MCP detector situated 42 cm from the interaction region. The time-of-flight signal was recorded using a 500 MHz oscilloscope. Each mass spectrum was recorded for 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots and calibrated using the Xe mass peaks or fragment ions from C60. The photoelectron spectra reported here were all obtained for relatively low values of the laser intensity where the mass spectra showed very little if any contribution from multiple ionisation or fullerene fragmentation.
000 laser shots and calibrated using the Xe mass peaks or fragment ions from C60. The photoelectron spectra reported here were all obtained for relatively low values of the laser intensity where the mass spectra showed very little if any contribution from multiple ionisation or fullerene fragmentation.
2.2. Scanning tunnelling microscopy (STM)
Experiments were performed in an ultrahigh vacuum (UHV) surface analysis system, with a base pressure below 1 × 10−10 mbar, consisting of a preparation chamber allowing for standard sample preparation and molecular deposition, and a microscope chamber housing a CreaTec low-temperature STM. STM acquisition was performed at liquid helium temperature (LHe, ∼5 K) with electrochemically etched W tips and applying the bias to the sample (tip remains grounded). Imaging was achieved using the constant-current mode, and spectroscopy was achieved by recording constant-current dI/dV data (measured by a lock-in technique with a superimposed modulation amplitude of 25 mV and frequency of 1470 Hz). The Au(111) and Cu(110) crystals were cleaned by repeated cycles of Ar+ sputtering at 300 K, and annealing in vacuum at 820 K and 770 K respectively. To produce the Cu(110)–(2 × 1)O reconstruction, molecular oxygen was deposited onto a sample held at 623 K at a partial pressure of 5 × 10−8 mbar for 45 s. A mixture of Li@C60 and C60 molecules was deposited using a molecular evaporator, consisting of a small quartz-glass capillary tube containing the molecular sample ([Li+@C60]PF6− salt, >80% purity, as above), surrounded by a heating element. The evaporator was degassed at approximately 570 K for several hours, similar to the treatment used for the gas phase measurements. The molecules were then dosed for 4 minutes at approximately 665 K at a partial pressure of 5 × 10−8 mbar. After deposition, the Au(111) sample was either annealed to 570 K for 30 s in order to form large hexagonally close-packed islands by mass diffusion, or annealed only to 320 K for 1 h in order to reduce mass transport and ensure some fullerenes are found to be isolated. The Cu(110)–(2 × 1)O sample was also maintained at 320 K for ∼1 h after deposition, to avoid mass transport as the fullerenes were to be studied when isolated. In all preparation cases, the anneal procedure is needed to desorb unwanted pollution from the material in the evaporator. Both substrates were then quenched down to LHe temperature for STM data acquisition. The sublimation temperature used here (ca. 665 K) is compatible with what is reported for the sublimation of unfilled C60 molecules in previous STM studies28 and slightly higher than that used for the gas phase experiments.2.3. Theoretical treatment
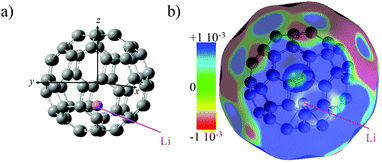
The electronic structure of neutral Li@C60 (open shell) was computed for different isomers at the unrestricted DFT level to determine the most stable one. We used the B3LYP functional29 with the 6-31+G(d) basis set for the carbon atoms and the 6-311+g(2df) basis set for the Li atom. The conformer with the Li atom lying at the centre of the cage is higher in energy than off-centre isomers (up to 19 kcal mol−1).30 The Li is situated 1.58 Å away from the centre of the cage towards the centre of a cage hexagon in the most stable conformer. Several off-centre isomers with the Li atom at slightly different positions were found to be within 1 kcal mol−1, comparable to the numerical accuracy. In agreement with previous theoretical studies12,31–33 and X-ray diffraction measurements on the (Li@C60+[PF6]−) salt,9 charge transfer in the neutral Li@C60 fullerene occurs between the encapsulated Li and the C60 cage. The computed NBO natural charge of the lithium atom is +0.7.The computed electrostatic potential of the most stable off-centre isomer exhibits an electro-attractor character on the side of the cage where the Li is located and an electro-donor character on the side of the cage opposite the position of the Li, Fig. 1. The anisotropy in the charge distribution is reflected by the sign of the permanent dipole moment along z (the axis passing through the centre of the cage and the Li atom) that is negative (−0.7 a.u.), meaning the vector is going from the side of the cage where the electrostatic potential surface is electro-donor to the side where the Li is located.
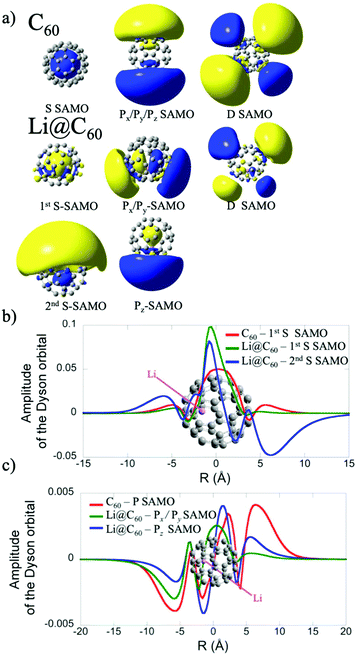
The electronic structure of the most stable isomer's excited states was computed at the TDDFT level with the long-range corrected CAM-B3LYP functional34 to account for the charge transfer character of the SAMO state. For the TDDFT computations, we used the same basis as for the ground state but augmented by five sets of s, p and d basis functions (with exponent of 0.2095, 0.0810, 0.0110, 0.0027 and 0.001) centered at the centre of the C60 cage. The effect of the basis set and functional on the excitation energies of the SAMO states has been discussed in an earlier work.35 The photoelectron angular distributions of the SAMO electronic states (accounting for the random orientation of the fullerene) were computed from the Dyson orbitals, as described earlier.17 The Dyson orbitals for the S- and P-SAMOs are shown in Fig. 2a along with those for C60 for comparison. The presence of Li inside the cage clearly breaks the symmetry and significantly distorts the orbitals. Note that the higher electron density lobe in the distorted 2nd S-SAMO for Li@C60 is at the opposite side of the cage to the Li+. This is in contrast to the distorted Pz-SAMO where the higher electron density lies close to the Li+. These two SAMOs may look similar but there is a maximum of amplitude at the position of the Li atom for the S-SAMO while for the Pz-SAMO there is a nodal surface (Fig. 2c).
3. Results and discussion
3.1. Li@C60 sample characterisation
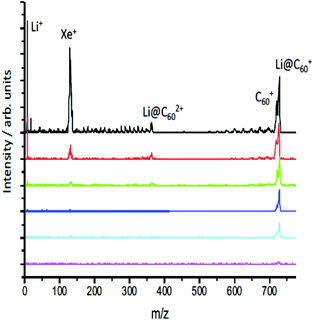
When initially heated to a temperature of ca. 600 K, the [Li+@C60]PF6− sample emits neutral species that produce peaks in the positive ion mass spectrum on laser ionisation, particularly around 300–400 u that can be attributed to tetrabutylammonium hexafluorophosphate and other impurities (ESI.1 Fig. S1†). After heating for some hours, these signals disappear leaving only the singly-charged Li@C60+ and C60+ species when ionisation takes place with low intensity pulses, as can be seen in Fig. 3. As the laser intensity is increased, it becomes possible to observe doubly-charged parent species and a small amount of fullerene fragment ions. The appearance of a significant Li+ peak is correlated with the onset of fragmentation, indicating a decay channel corresponding to the loss of Li+ from the ionised fullerene cage as it fragments. Note that the photoelectrons, discussed in section 3.2, are emitted before the cage fragmentation can take place. For low laser intensities, the relative intensity of the parent C60+ and Li@C60+ mass peaks typically does not change during the course of a measurement, but is slightly dependent on laser intensity due predominantly to the difference in ionisation energies of the two species (ESI.1, Fig. S2†).The evaporation of neutral Li@C60 is in agreement with UPS and XPS studies of evaporated films produced from the same starting material.13 These studies showed the Li@C60 material was present in the neutral state when sublimed to form a thin film at a temperature of 623 K, and that PF6 was absent from the film.13 Furthermore, the authors could not rule out the presence of neutral C60 in the film. As the sublimation temperature was increased to 823 K and beyond, the UPS signal from the film attributed to the presence of endohedral Li@C60 decreased strongly and the UPS spectra near the Fermi level for sublimation temperatures >820 K took on the form obtained earlier in studies of films of exohedrally-doped LiC60.36 Photoionisation experiments at 540 nm as a function of oven temperature showed evidence of the onset of thermal decay for temperatures >600 K (ESI.1, Fig. S3†). At our standard sublimation temperature of 620 K, there was a noticeable decrease in the measured intensity ratio with age of the material, and it was important to measure the mass spectra to monitor the ratio throughout the photoelectron measurements. The results are also consistent with early photoionisation37 and thermal desorption spectroscopy studies38 of Li@C60 produced by Li+ implantation. MALDI analysis of a dichlorobenzene solution of the starting material used in the current study showed only trace amounts of C60 in both positive and negative mode mass spectra, indicating that the C60 was formed via decomposition reactions within the oven at the elevated temperatures used for sublimation.
The relative intensities of the Li@C60+ and C60+ mass peaks are wavelength dependent, reflecting the different excitation/ionisation probabilities. The measured Li@C60+/C60+ ratio ranges from 2.8 at 540 nm to 0.6 at 267 nm. In all cases studied here, at least two photons are needed to ionise both C60 (IE 7.6 eV (ref. 39)) and Li@C60 (IE 6.5 eV (ref. 13)). Due to the reduced symmetry of the Li@C60, there are many more transitions with significant oscillator strengths that will provide a higher probability for laser excitation, particularly for the first photon absorption. We thus expect the Li@C60+/C60+ ratio measured by the mass spectrometer to overestimate the relative amount of neutral endohedral Li@C60 in the molecular target.
The STM studies provide a more quantitative measure of the relative amounts of C60 and Li@C60 that are sublimed from the oven. Fig. 4 shows an image of a large hexagonally close packed fullerene island on a Au(111) single crystal formed by deposition from the evaporator at a temperature of 665 K for 4 minutes followed by a post-adsorption anneal to 573 K for 30 s. Fig. 4(a) was obtained for a bias voltage of −2.5 V, thus imaging occupied states, while Fig. 4(b) shows unoccupied states with a bias voltage of +2.5 V. Each distinct feature is a fullerene. C60 has been extensively studied by low temperature STM to provide information on the local electronic structure. Of particular relevance here are the studies by Schull et al.40 and Gardener et al.28 of C60 adsorbed on Au(111). These authors clearly showed the dependence of topographical appearance and dI/dV spectra on the orientation of C60 on the Au surface. By comparing our results with these studies, we can identify the majority of the fullerenes in Fig. 4 to be empty C60 oriented either with the cage sitting on a hexagon (type 1, darker trefoil appearance in Fig. 4(b)); sitting on a single bond between a hexagon and a pentagon (type 2, asymmetric dumbbell appearance in Fig. 4(b)); or sitting on a double bond between two adjacent hexagons (type 3, symmetric dumbbell appearance). A fourth type of fullerene becomes apparent at the bias voltage of +2.5 V. Some of the fullerenes appear to light up at this voltage, showing a diffuse circular image with no apparent structure. As will be discussed in section 3.3, these fullerenes can be identified as Li@C60. A statistical analysis of images of large islands such as the one shown in Fig. 4 revealed that ca. 13% of the deposited fullerenes can be attributed to Li@C60 and 87% to empty C60. A more detailed analysis of the cage orientations is given in ESI.2.† The results in Fig. 4 were obtained following the de-gassing procedure for ca. 100 hours, similar to the treatment in the gas phase experiments to ensure “clean” mass spectra. A significantly higher proportion (>90%) of Li@C60 could be observed in the STM experiments when the degassing procedure was reduced to <10 hours.
Although we observe the three well-known orientations of C60 on Au(111), it was striking that the endohedral Li@C60 was always found to be oriented with the cage sitting on a hexagon, indicating a significantly stronger interaction with the substrate for this orientation compared to C60. These results are consistent with the recent room temperature STM measurements on films containing Li@C60, reported by Yamada et al. where they also observed that a few percent of the deposited fullerenes showed a similar anomalous bias dependence for +2 V to +3 V that was interpreted to be due to the endohedral Li@C60.41 DFT calculations, reported in the same paper, gave a stronger binding energy for the Li@C60 compared to C60 for the hexagon-down orientation (2.91 eV compared to 2.24 eV). It was also shown that the most energetically favourable configuration had the Li displaced vertically upwards from the centre by 1.54 Å, similar to the displacement of 1.58 Å obtained in our calculations for the gas phase isolated Li@C60.
3.2 Gas phase rydberg fingerprint photoelectron spectroscopy
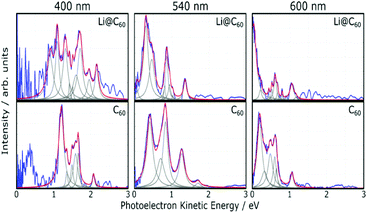
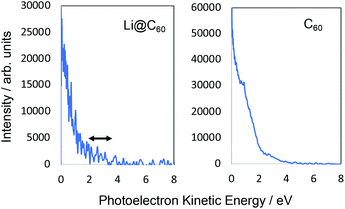
Fig. 5 shows angle-integrated Rydberg Fingerprint spectra for 3 representative laser wavelengths. In all cases, the laser intensity was adjusted to ensure that there was no contribution from multiply-ionised species in the mass spectra. The Rydberg Fingerprint technique, as applied to the spectroscopy of fullerene SAMOs and Rydberg states, has been described previously.19 The advantage of the method is that the excited states are rapidly populated via internal conversion processes following multi-photon excitation and can be observed as peaks in the photoelectron spectra independent of the laser wavelength and the extent of vibrational excitation. Once populated, the SAMO states are efficiently ionised via absorption of one additional photon from the same (35–120 fs) laser pulse. The measured photoelectron kinetic energy (KE) is simply related to the binding energy (EBind) of the SAMO electron via EBind = hν − KE, where hν is the photon energy. The predominance of the SAMO peak structure is related to the very short photoionisation lifetime of the SAMOs for ionisation with photons in the visible range of the spectrum compared to the much longer lifetime, and hence lower ionisation efficiency, of excited valence states.17Fig. 5 compares the photoelectron spectra obtained from the Li@C60 sample with the known photoelectron spectra from a pure C60 sample. The C60 component in the raw Li@C60 photoelectron spectra (cf. mass spectra in Fig. 3) has been subtracted according to the relative intensities of the corresponding mass peaks under very similar ionisation conditions.The photoelectron spectra for Li@C60 (after subtraction of the C60 component) show similarities with the corresponding C60 spectra but with clear differences in the relative intensities of peaks and also some small shifts in the position of the peaks. The SAMO peak structure is clearly visible. It is particularly prominent for an excitation wavelength of 540 nm, similar to the situation for C60 where the peak appearing at the lowest photoelectron kinetic energy is attributed to the S-SAMO, followed by the P-SAMO and D-SAMO. More Lorentzian functions are needed to fit the Li@C60 spectra indicating a splitting and broadening of the SAMO peaks compared to C60. The Li@C60 spectrum obtained for a wavelength of 400 nm is more difficult to fit and shows more structure that is likely to be due to ionisation of excited valence states. The lowering of the symmetry of Li@C60 broadens the band structure and leads to a breakdown of the optical selection rules.42 Hence there are more optically active excited states in Li@C60 than in C60.
Fig. 6 shows the photoelectron spectra obtained for Li@C60 and C60 using 267 nm. As reported previously,43 the SAMO peaks are not visible in the C60 spectrum. For this wavelength, just two photons are needed to ionise the molecules. The photon energy is not high enough to access the SAMO states after absorption of one photon (the excitation energy for the lowest-lying S-SAMO in C60 is 5.7 eV) whereas absorption of a second photon will lead directly to ionisation. The low intensity tail in the spectrum extending to ca. 4.5 eV indicates some energy relaxation and ionisation from unresolved Rydberg and high-lying excited valence states in a 3-photon process. Li@C60 has a much lower ionisation energy (6.5 eV (ref. 13)) and the excitation energy of the lowest SAMO state (EBind ∼ 2 eV, see below) is ca. 4.5 eV (just below the photon energy of 4.55 eV. Unlike the C60 situation where direct optical excitation of the S-SAMO is forbidden, according to the TDDFT calculations there is a small oscillator strength for direct optical excitation of the SAMOs for Li@C60 (see Table 2). Although the data is noisy, there is some very small intensity structure in the photoelectron spectrum in the 2–3.5 eV range that looks similar to the SAMO peaks measured for longer wavelengths, but the signal to noise ratio is not sufficiently good to make a definite assignment. The cut-off in both spectra lies at ca. 4.5 eV (i.e. close to the photon energy), as is typically the case for Rydberg Fingerprint photoelectron spectra.
We primarily base our assignment of the SAMO peaks on the photoelectron angular distributions as they provide a fingerprint of the ionised states and strongly depend on the azimuthal quantum number l.16 As discussed previously for C60,19 since the excited states are incoherently populated, the final step in the photoionisation process can be considered to be a single-photon ionisation from the excited states with energies within one photon below the IP. In this case, the photoelectron angular distribution for a random orientation of the molecule can be described as44,45
I(θ) ∝ (1 + βP2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)) θ)) | (1) |
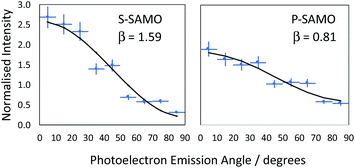
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is the second order Legendre polynomial. The anisotropy parameter varies between +2 and −1, which corresponds to ionisation parallel and perpendicular to the laser orientation. For the single-photon ionisation from an atomic s-state (l = 0) in the absence of electron correlations, β = 2.0, independent of photoelectron energy. The situation is more complex for ionisation from higher angular momentum states since exit channels (Δl = ± 1) can interfere and the value of β varies with the kinetic energy of the photoionised electron. The VMI data is divided into 9 angular segments, each with a width of 10° and within each segment the photoelectron intensity is integrated as a function of kinetic energy. Fig. 7 shows two representative examples of angular distributions for data obtained at 540 nm. The data is fitted using eqn (1) to extract the value of β.
θ) is the second order Legendre polynomial. The anisotropy parameter varies between +2 and −1, which corresponds to ionisation parallel and perpendicular to the laser orientation. For the single-photon ionisation from an atomic s-state (l = 0) in the absence of electron correlations, β = 2.0, independent of photoelectron energy. The situation is more complex for ionisation from higher angular momentum states since exit channels (Δl = ± 1) can interfere and the value of β varies with the kinetic energy of the photoionised electron. The VMI data is divided into 9 angular segments, each with a width of 10° and within each segment the photoelectron intensity is integrated as a function of kinetic energy. Fig. 7 shows two representative examples of angular distributions for data obtained at 540 nm. The data is fitted using eqn (1) to extract the value of β.
We provide an assignment of the SAMO peaks in Table 1 based on the variation of the anisotropy parameter with the kinetic energy of the photoelectron. The extracted values of β for all data are summarised in Fig. 8 where they are plotted as a function of photoelectron kinetic energy and compared with the theoretical calculations. The experimental values determined for empty C60 are shown as empty black symbols for comparison.17
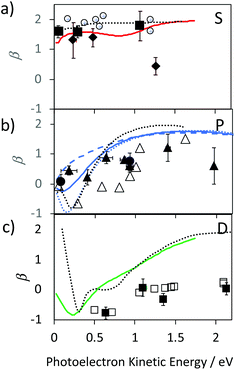 | ||
| Fig. 8 Experimental values for the Li@C60 SAMO β-parameters, full symbols, compared with TDDFT calculations for the ground state Li position within the cage (1.58 Å from centre), coloured lines. Earlier reported values for C60 are shown for comparison (empty black symbols and dotted black line).17 (a) S-SAMO. Full diamonds: Peak 2, full squares Peak 3 (Table 1). Full red line: theoretical S2 state (Table 1). (b) P-SAMO. Full circles: Peak 1, full triangles Peak 4–8 (Table 1). Full blue line: averaged over the entire P-band, blue dashed line: Pz, blue dotted line: Px,y. (c) D-SAMO. Full squares: Peak 9 (Table 1). | ||
| Peak Nr | SAMO | 400 nm | 540 nm | 600 nm | 800 nm | C60/eV |
|---|---|---|---|---|---|---|
| 1 | P | 2.17 ± 0.04 | 2.22 ± 0.01 | — | — | — |
| 2 | S | 2.03 ± 0.02 | 2.00 ± 0.02 | 2.02 ± 0.03 | — | 1.9 ± 0.1 |
| 3 | S | 1.84 ± 0.03 | 1.82 ± 0.02 | 1.83 ± 0.03 | — | |
| 4–7 | P | 1.40 ± 0.15 | 1.43 ± 0.06 | 1.42 ± 0.08 | 1.37 ± 0.09 | 1.47 ± 0.02 |
| 8 | P | 1.13 ± 0.02 | — | 1.14 ± 0.04 | 1.14 ± 0.02 | |
| 9 | D | 0.97 ± 0.03 | 0.95 ± 0.02 | 0.98 ± 0.05 | 0.91 ± 0.03 | 1.02 ± 0.01 |
The electronic states with experimental binding energies, EBind, of 2.0 and 1.8 eV have anisotropy parameters that do not vary significantly with the electron kinetic energy, suggesting S-like characters. However, the mean value of β is around 1.4, lower than for C60, indicating a breaking of spherical symmetry of the excited state's wavefunction. The Dyson orbitals of the S-SAMO, which represent the wavefunction of the ionised electron, are centred on the off-centred Li, which breaks the spherical symmetry. Furthermore, for the second band of S-SAMO for which most of the electronic density is localized outside of the cage, the Dyson orbital exhibits a strong asymmetry (see Fig. 2a and b) with a mushroom shape. The anisotropy parameter is lower than 2 and oscillates around 1.5, in good agreement with the experimental values. Therefore, these bands are labelled as S-SAMO electronic states.
The two bands between 1.13 and 1.40 eV have an anisotropy parameter that increases almost linearly as the photoelectron kinetic energy increases from 0 to 1.5 eV. This behaviour is similar to the P-SAMO of C60,16 except for low kinetic energies (<0.5 eV) where the dip is missing due to the symmetry breaking. The effect of the Li atom on the P-SAMO Dyson orbitals is the strongest for the Pz component that goes through the centre of the cage and the Li atom. For the perpendicular Px and Py components, the Dyson orbital is shifted toward the Li atom and slightly distorted compared to the P-SAMO of C60 (Fig. 2a and c). As a consequence, the variation of the anisotropy parameter with the kinetic energy for Px,y is close to the one in C60. For the Pz-SAMO, there is a stronger effect of the Li atom on the Dyson orbitals (Fig. 2a and c), which completely breaks the two-lobe structure of the P-SAMO. The Pz-Dyson orbital has mainly one lobe outside the cage (Fig. 2a), which results in an anisotropy parameter significantly different to the ones of the Px- and Py-SAMO (Fig. 8) without a dip at low kinetic energies. As the calculated Px, Py- and Pz-SAMO states are close in energy (within 0.05 eV), we computed the anisotropy parameter from the photoelectron angular distributions of these three SAMO states. Since there is a good agreement with the anisotropy parameter of the bands at 1.13 and 1.40 eV, we assigned these bands to P-SAMO states. For the D-SAMO states, the Li atom does not have a significant effect on the symmetry of the SAMO (Fig. 2a) and the anisotropy parameter is very similar to the one of C60 (Fig. 8c). We assigned the band at 0.95 eV to the D-SAMO as the anisotropy parameter is close to the one of the D-SAMO of C60. This confirms the very small influence of the Li on these orbitals where there is little electron density inside the cage.
We now turn to the binding energies of the SAMO states for which the computed energies, Table 2, are off by several tenths of eV compared to the experimental values. Several factors can explain these discrepancies. Firstly, there is a large number of isomers that could be accessed in the experiment (620 K). At this high temperature the lithium atom can access different positions within the cage46 which can affect the excited state's excitation energy. Earlier calculations indicated that for electronically excited states, including the S-SAMO, the potential minimum can even be located at the centre of the cage.11,32 In order to estimate the influence of the Li position within the cage, calculations were carried out for 3 different positions of the Li along an axis connecting the centre of the cage with the centre of a hexagon. The results are summarised in Table 2. Secondly, the Li atom's partial charge could also affect the binding energies of the SAMO. For these reasons we will mainly compare the experimental binding energies of Li@C60 to the experimental ones of C60.
| Peak Nr | Transition dipole moment/a.u. | Binding energies/eV | |||
|---|---|---|---|---|---|
| 1.58 Å | 1.58 Å | 0.8 Å | 0 Å | ||
| S1 | 2 | 0.06 | 3.71 | 4.30 | 4.63 |
| S2 | 3 | 0.63 | 1.43 | 1.48 | 1.53 |
| P1 | 1 | 0.04 | 1.70 | 2.00, 2.23 | 2.63 |
| P2 | 4–8 | — | — | 1.87 | 1.30 |
| D | 9 | 0.09 | 1.15 | 1.16 | 1.18 |
In Li@C60, the experimental peak positions are close to those of C60 but slightly shifted with a broader distribution and a higher number of peaks for the bands that we associate with the S- and P-SAMO states. A similar broadening and multiple-peak structure associated with the P-SAMO is observed in the scanning tunnelling spectroscopy data, discussed in section 3.3. The largest shift in binding energies is seen for a peak that we have assigned as a P-SAMO on the basis of the photoelectron angular distributions. This appears at a higher binding energy (smaller photoelectron kinetic energy) than the S-SAMO and has no equivalent peak in the C60 spectra. It is in reasonable agreement with the theoretical binding energy for the P1-SAMO (Table 2), calculated for a more central position of the Li (0.8 Å from the cage centre). The S-SAMO seems to be split with one component slightly but significantly shifted to a higher binding energy by only about 0.1 eV and a second component shifted to lower binding energies by approximately the same amount. The calculated Dyson orbital (Fig. 2a, second S-band) shows that in this case the orbital is distorted by having slightly increased electron density at the opposite side of the cage from the Li position, thus leading to a reduction of symmetry. The calculations indicate that the split in energy levels observed in the experiment is due predominantly to different positions of the Li being probed in the hot, gas phase molecule. The electron density for the D-SAMOs (Fig. 2a) lies predominantly outside the fullerene cage and is only slightly distorted by the presence of the Li. The observed binding energy and peak width is very close to that of C60.16
3.3 STM
Scanning tunnelling spectroscopy (STS) provides an additional means of obtaining information about the SAMOs and other empty states of the neutral molecule coupled to a metal substrate. The name SAMO, for the low-lying diffuse Rydberg states with electron density centred on the hollow fullerene cage centre, was first coined in a paper that reported low temperature (77.3 K) STS and imaging experiments for C60 deposited on Cu(111) and partially-oxidised Cu(110)–(2 × 1)O surfaces where some peaks in the constant-current dI/dV plot were associated with the S, Pz and Px,y SAMOs.21 A later, higher resolution study of C60 on Cu(111) used iso-dI/dV mapping to image the S- and P-SAMO states. They showed sharp resonances in the constant-current dI/dV plot for the S (l = 0) and P (l = 1) C60 SAMOs at bias voltages of 4 V and 5.2 V, respectively. They also showed that the l = 1, m = 0 state (Pz) is shifted by 0.2 V to lower bias voltage compared to the l = 1, m = ±1 peak, showing that the interaction with the metal surface lifts the degeneracy among the m states.47In order to compare the STS of deposited Li@C60 with the gas phase studies, it was necessary to prepare isolated molecules. Fig. 9 shows images of two isolated fullerenes on Cu(110)–(2 × 1)O obtained for a sample bias of +2.5 V with Fig. 10 showing similar data but for molecules deposited on Au(111) (see ESI.3, Fig. S5† for additional large scale STM images). The contrast in the images of the isolated molecules is not as good as for the island imaging (Fig. 4), but it is possible to identify the fullerene on the left in Fig. 9 as being Li@C60 (diffuse structureless image) and on the right as being C60 (trefoil structure is just visible). Similarly, in Fig. 10, the left-hand side fullerene is identified as Li@C60 and the right-hand side one as C60. The corresponding constant-current dI/dV spectra are shown below the images (see also ESI.3†). The spectra on the bottom-right of both Fig. 9 and 10 confirm that these are isolated C60 molecules. The peak positions determined for C60 are close to those reported by Reecht et al.47 and Schull et al.40 The interaction with the metal substrate lifts the degeneracy of the P-SAMO with the Pz-SAMO (m = 0) being shifted down in energy by a few 100 mV compared to the Px–y-SAMOs.47 This can be seen as a small peak or shoulder to the left of the main C60 P-SAMO peak in Fig. 9 and 10.
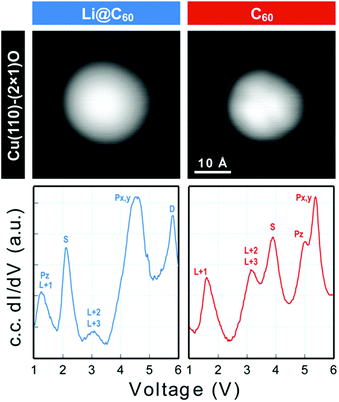 | ||
| Fig. 9 (a) Image of isolated fullerene molecules deposited on Cu(110)–(2 × 1)O obtained for a bias voltage of +2.5 V and the corresponding constant-current dI/dV spectra. Left: Li@C60. Right: C60. The assignment marked on the C60 spectrum is identical to that of Reecht et al.47 | ||
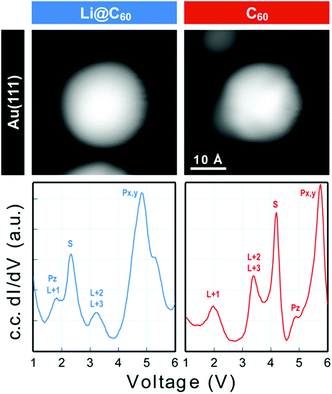 | ||
| Fig. 10 Image of two isolated fullerene molecules deposited on Au(111) obtained for a bias voltage of +2.5 V and the corresponding constant-current dI/dV spectra. Left: Li@C60; Right: C60. The assignment marked on the C60 spectrum is identical to that of Reecht et al.47 | ||
The spectra obtained for the molecules identified as Li@C60 on both substrates are very similar to each other and clearly different from C60 (see ESI.3† for a direct comparison). The measured peak positions for C60 and Li@C60 are listed in Table 3, along with the C60 peak positions that are reported in the literature.
| C60/V | Li@C60/V | |||||||
|---|---|---|---|---|---|---|---|---|
| Au(111)48 | Au(111) this work | Cu(111)47 | O/Cu(110)21 | O/Cu(110) this work | Au(111) this work | O/Cu(110) this work | ||
| HOMO | −1.7 ± 0.2 | SOMO | 0 | 0 | ||||
| LUMO | 1.0 ± 0.2 | 0.8 | 0.8 | Pz-SAMO/LUMO+1 | 1.5 | 1.2 | ||
| LUMO+1 | 2.2 ± 0.2 | 2.1 | 1.8, 2.2 | 1.4 | 1.8–2.1 | S-SAMO | 2.2 | 2.1 |
| LUMO+2,3 | 3.5, 3.8 | 3.2 | 3.2 | 3.2 | LUMO+2,3 | 3.2 | 3.0 | |
| S-SAMO | 4.2 | 4.0 | 3.8 | 4.0 | P1 | 4.5 | 4.0 | |
| P-SAMO | 5.4, 6.0 | 5.4, 5.6 | 5.2 | 5.0, 5.4 | P2 | 5.3 | 4.7 | |
As has been observed previously for C60,40 the orbital energies for Li@C60 are shifted slightly upwards on Au(111) compared to the Cu surface but the main features are very similar. The sharp peak in the Li@C60 spectra that appears for a voltage just above 2 V can be assigned to the S-SAMO. This is the structure responsible for the bright, homogeneous image of the Li@C60 that allows it to be clearly identified in Fig. 4 for a bias voltage of +2.5 V. The broad peak structure in the range 4.5–5.5 V can be assigned to P-SAMOs possibly with some underlying contribution from unoccupied valence states (LUMO+x). The S-SAMO is clearly shifted much further down in energy compared to the gas phase spectra (ΔES–P ∼ 0.6–0.8 eV for the gas phase compared to ΔES–P ∼ 3 V on Au or O/Cu) and also compared to the situation for empty C60 (ΔES–P ∼ 0.6 V for the gas phase compared to ΔES–P ∼ 1.5 V on Au or O/Cu). This can be related to the higher reactivity of the neutral radical Li@C60 species with the metal surface, due to a combination of the different charge distribution on the fullerene cage and the asymmetry of the orbitals. The most energetically favourable position for the Li inside the fullerene cage when the molecule is sitting on a Au substrate is close to the centre of the top hexagon, Fig. 11.41 In contrast to the gas phase experiments, where the Li is expected to be mobile inside the cage, the Li is expected to be frozen in position for the low temperature STM experiments. The distorted S-SAMO (Fig. 2) will therefore be oriented such that the electron density will be maximised in the vicinity of the substrate, potentially leading to a strong hybridisation of orbitals and correspondingly high energetic stabilisation such as is observed in the STS. The S-SAMO peak that we observe at ≿ 2 V is in very good agreement with the DFT calculations reported by Yamada et al. for Li@C60 on Cu(111).41 They reported a sharp peak and greatly enhanced LDOS for E − EF ≿ 2 V which they interpreted as being due to an alteration of the LUMO+2 state. We believe, based on our STS data, the comparison with gas phase results and STM images that the S-SAMO interpretation is more reasonable. The calculations of Yamada et al. also showed the close similarity in the LDOS of the occupied states for Li@C60 and C60 in good agreement with the STM images for negative bias potentials (Fig. 4 and ESI†).
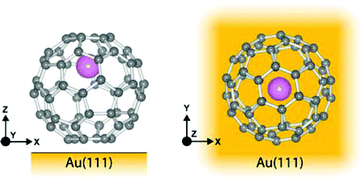 | ||
| Fig. 11 Illustration of Li@C60 on Au(111) showing the most energetically favourable orientation. (a) Side view (b) top view. | ||
Based on the comparison with gas phase data and TDDFT calculations where a P-like orbital is observed to be shifted to binding energies lying below that of the S-SAMO, we tentatively assign the peak at ca. 1.5 V to the Pz-SAMO, possibly with some underlying LUMO+1 valence state contribution. As for the S-SAMO argument, we can consider that the interaction with the metal substrate will be stronger for the Li@C60 Pz-SAMO compared to that of the C60, combining with the asymmetric electron density distribution to produce the large shift to lower voltage observed in Fig. 9 and 10. The DFT calculations from Yamada et al. also show some structure at around 1 eV that looks significantly different from the C60 LDOS and may be partially attributable to the Pz-SAMO although this was not discussed in that paper.41
In order to compare the SAMO orbital energies determined from STS experiments with the gas phase SAMO electron binding energies, we consider the LUMO-SAMO energy differences. Note that the orbital energies in Table 3 for Li@C60 are measured with respect to the LUMO since Li@C60 is a radical species with an unpaired electron. The HOMO–LUMO gap for gas phase C60 was taken to be 1.6 eV (ref. 49) and the ionisation energy of Li@C60 was taken to be 6.5 eV.13 The energy differences are summarised in Table 4 for both C60 and Li@C60. For C60, the strongest shift down in energy when the molecule is adsorbed on the Cu substrate is observed for the S-SAMO (0.9 eV). The next largest shift is for the Pz-SAMO (0.5 eV) with the Px,y-SAMOs shifting only slightly due to the weaker interaction with the substrate (ca. 0.1 eV). Li@C60 shows a similar but stronger trend. The S-SAMO shifts down in energy by 2.4 eV, the peak we are tentatively attributing to the Pz-SAMO by 3.1 eV and the Px,y by ca. 1 eV. The much larger shift in energy for Li@C60 can be attributed to two main factors: the higher reactivity of the radical Li@C60 with the metal substrate and the asymmetry in the electron density distributions of the S- and Pz-SAMOs.
| ΔE(LUMO-SAMO)/eV | ||||
|---|---|---|---|---|
| C60/O/Cu(110) | C60 PES | Li@C60/O/Cu(110) | Li@C60 PES | |
| S-SAMO | 3.2 | 4.1 | 2.1 | 4.5 |
| Pz-SAMO | 4.0 | 4.53 | 1.2 | 4.3 |
| Px,y-SAMO | 4.4 | 4.53 | 4.0–4.7 | 5.0–5.4 |
Conclusions
We have combined Rydberg Fingerprint Spectroscopy on gas phase Li@C60 with TDDFT calculations and STS results for Li@C60 on metal substrates under low temperature (5 K), UHV conditions. The two complimentary experimental techniques provide information on the properties of the diffuse Rydberg-like SAMO states that have previously been reported for C60. The asymmetric position of the Li inside the fullerene cage strongly distorts the symmetry of the lowest lying S- and P-SAMOs with calculations of the binding energies of these states in the isolated molecule shown to be strongly dependent on the position of the Li. When adsorbed on a metal substrate, the S- and Pz-SAMOs shift much more strongly down in energy compared to the situation for C60. The STS results presented for Li@C60 are in good agreement with recent DFT calculations although the interpretation given here is new.The stable asymmetric position of Li in the low temperature STM experiments combined with the strong interaction of the asymmetric SAMO states with the metal surface provides encouragement for the possibility of an experimental demonstration of the theoretically discussed31,32 molecular switch involving the motion of Li inside the cage. This will be the subject of a future publication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. S., E. B., J. O. F. T. and E. E. B. C. gratefully acknowledge financial support from the Leverhulme Foundation (RPF-298 “PES of hollow nanomaterials”) and helpful contributions and advice from Dr J. Olof Johansson and Dr Tanja van Mourik. E. E. B. C. gratefully acknowledges Idea International Inc. (Sendai) for providing a sample of Li@C60+[PF6]−. M. S. and H. J. C. acknowledge the financial support of EPSRC DTP studentships (EP/M508214/1 and EP/N509644/1). R. S. acknowledges financial support from the Scottish Funding Council through SRD-Grant (HRO7003). The work of FR and BM is supported by the Fonds de la Recherche Fondamentale Collective (#T.0132.16 and J.0012.18) and by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES) under Award # DE-SC0012628. BM and FR thank the Fonds National de la Recherche (FRS.FNRS, Belgium) for its support. Computational resources were provided by Consortium des équipements de calcul intensif (CECI, FNRS 2.5020.11).Notes and references
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Naure, 1985, 318, 162 CAS.
- J. R. Heath, S. C. O'Brien, Q. Zhang, Y. Liu, R. F. Curl, F. K. Tittel and R. E. Smalley, J. Am. Chem. Soc., 1985, 107, 7779–7780 CrossRef CAS.
- H. Shinohara, Rep. Prog. Phys., 2000, 63, 843 CrossRef CAS.
- Endohedral Fullerenes: Electron Transfer and Spin, ed. A. A. Popov, Springer, 2017 Search PubMed.
- R. Tellgmann, N. Krawez, S. H. Lin, I. V. Hertel and E. E. B. Campbell, Nature, 1996, 382, 407 CrossRef CAS.
- E. E. B. Campbell, R. Tellgmann, N. Krawez and I. V. Hertel, J. Phys. Chem. Solids, 1997, 58, 1763–1769 CrossRef CAS.
- A. Gromov, D. Ostrovskii, A. Lassesson, M. Jönsson and E. E. B. Campbell, J. Phys. Chem. B, 2003, 107, 11290–11301 CrossRef CAS.
- V. N. Popok, I. I. Azarko, A. V. Gromov, M. Jönsson, A. Lassesson and E. E. B. Campbell, Solid State Commun., 2005, 133, 499–503 CrossRef CAS.
- S. Aoyagi, E. Nishibori, H. Sawa, K. Sugimoto, M. Takata, Y. Miyata, R. Kitaura, H. Shinohara, H. Okada, T. Sakai, Y. Ono, K. Kawachi, K. Yokoo, S. Ono, K. Omote, Y. Kasama, S. Ishikawa, T. Komuro and H. Tobita, Nat. Chem., 2010, 2, 678 CrossRef CAS.
- H. Okada, T. Komuro, T. Sakai, Y. Matsuo, Y. Ono, K. Omote, K. Yokoo, K. Kawachi, Y. Kasama, S. Ono, R. Hatakeyama, T. Kaneko and H. Tobita, RSC Adv., 2012, 2, 10624–10631 RSC.
- B. I. Dunlap, J. L. Ballester and P. P. Schmidt, J. Phys. Chem., 1992, 96, 9781–9787 CrossRef CAS.
- Y. S. Li and D. Tománek, Chem. Phys. Lett., 1994, 221, 453–458 CrossRef CAS.
- H. Yagi, N. Ogasawara, M. Zenki, T. Miyazaki and S. Hino, Chem. Phys. Lett., 2016, 651, 124–126 CrossRef CAS.
- Y. Kawashima, K. Ohkubo and S. Fukuzumi, J. Phys. Chem. A, 2012, 116, 8942–8948 CrossRef CAS PubMed.
- Y. Matsuo, H. Okada and H. Ueno, Endohedral Lithium-Containing Fullerenes, Springer, 2017 Search PubMed.
- J. O. Johansson, G. G. Henderson, F. Remacle and E. E. B. Campbell, Phys. Rev. Lett., 2012, 108, 173401 CrossRef PubMed.
- B. Mignolet, J. O. Johansson, E. E. B. Campbell and F. Remacle, Chemphyschem, 2013, 14, 3332–3340 CrossRef CAS PubMed.
- J. O. Johansson, E. Bohl, G. G. Henderson, B. Mignolet, T. J. S. Dennis, F. Remacle and E. E. B. Campbell, J. Chem. Phys., 2013, 139, 084309 CrossRef.
- J. O. Johansson, E. Bohl and E. E. B. Campbell, Philos. Trans. R. Soc., A, 2016, 374, 20150322 CrossRef PubMed.
- E. Bohl, K. P. Sokół, B. Mignolet, J. O. F. Thompson, J. O. Johansson, F. Remacle and E. E. B. Campbell, J. Phys. Chem. A, 2015, 119, 11504–11508 CrossRef CAS PubMed.
- M. Feng, J. Zhao and H. Petek, Science, 2008, 320, 359–362 CrossRef CAS.
- J. Zhao, M. Feng, J. Yang and H. Petek, ACS Nano, 2009, 3, 853–864 CrossRef CAS.
- S. Aoyagi, A. Tokumitu, K. Sugimoto, H. Okada, N. Hoshino and T. Akutagawa, J. Phys. Soc. Jpn., 2016, 85, 094605 CrossRef.
- J. O. Johansson and E. E. B. Campbell, Chem. Soc. Rev., 2013, 42, 5661–5671 RSC.
- J. O. Johansson, G. G. Henderson and E. E. B. Campbell, J. Phys. Chem. A, 2014, 118, 8067–8073 CrossRef CAS PubMed.
- G. G. Henderson, PhD, University of Edinburgh, 2013.
- V. Schyja, T. Lang and H. Helm, Phys. Rev. A, 1998, 57, 3692–3697 CrossRef CAS.
- J. A. Gardener, G. A. D. Briggs and M. R. Castell, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235434 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- Z. Slanina, F. Uhlík, S.-L. Lee, L. Adamowicz and S. Nagase, Int. J. Mol. Sci., 2008, 9, 1841–1850 CrossRef CAS.
- P. Delaney and J. C. Greer, Appl. Phys. Lett., 2004, 84, 431–433 CrossRef CAS.
- R. Jorn, J. Zhao, H. Petek and T. Seideman, ACS Nano, 2011, 5, 7858–7865 CrossRef CAS.
- E. B. Campbell Eleanor, S. Couris, M. Fanti, E. Koudoumas, N. Krawez and F. Zerbetto, Adv. Mater., 1999, 11, 405–408 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- B. Mignolet and F. Remacle, AIP Conf. Proc., 2016, 1790, 020015 CrossRef.
- J. Schnadt, P. A. Brühwiler, N. Mårtensson, A. Lassesson, F. Rohmund and E. E. B. Campbell, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4253–4256 CrossRef CAS.
- F. Rohmund, A. V. Bulgakov, M. Hedén, A. Lassesson and E. E. B. Campbell, Chem. Phys. Lett., 2000, 323, 173–179 CrossRef CAS.
- C. Kusch, N. Krawez, R. Tellgmann, B. Winter and E. E. B. Campbell, Appl. Phys. A, 1998, 66, 293–298 CrossRef CAS.
- J. de Vries, H. Steger, B. Kamke, C. Menzel, B. Weisser, W. Kamke and I. V. Hertel, Chem. Phys. Lett., 1992, 188, 159–162 CrossRef CAS.
- G. Schull, N. Néel, M. Becker, J. Kröger and R. Berndt, New J. Phys., 2008, 10, 065012 CrossRef.
- Y. Yamada, A. V. Kuklin, S. Sato, F. Esaka, N. Sumi, C. Zhang, M. Sasaki, E. Kwon, Y. Kasama, P. V. Avramov and S. Sakai, Carbon, 2018, 133, 23–30 CrossRef CAS.
- B. Mignolet, E. E. B. Campbell and F. Remacle, AIP Conf. Proc., 2017, 1906, 030027 CrossRef.
- J. O. Johansson, G. G. Henderson and E. E. B. Campbell, EPJ Web Conf., 2013, 41, 02015 CrossRef CAS.
- J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 48, 942–943 CrossRef CAS.
- J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 49, 4252–4252 CrossRef.
- J. Hernández-Rojas, J. Bretón and J. M. Gomez Llorente, J. Phys. Chem. Solids, 1997, 58, 1689–1696 CrossRef.
- G. Reecht, H. Bulou, F. Scheurer, L. Limot and G. Schull, New J. Phys., 2017, 19, 113033 CrossRef.
- X. Lu, M. Grobis, K. H. Khoo, S. G. Louie and M. F. Crommie, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 115418 CrossRef.
- S. Leach, M. Vervloet, A. Desprès, E. Bréheret, J. P. Hare, T. John Dennis, H. W. Kroto, R. Taylor and D. R. M. Walton, Chem. Phys., 1992, 160, 451–466 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Temperature-dependent mass spectrometry, laser power ionisation dependence and STM imaging details. DOI: 10.1039/c8nr0788a. Raw experimental data files are available at DOI: 10.7488/ds/2394 |
| This journal is © The Royal Society of Chemistry 2019 |