Probing Lewis acid–base interactions in single-molecule junctions

Abstract

A novel strategy to regulate the tunneling mechanism for charge transport through an organoborane wire via Lewis acid–base interactions has been developed. A change from LUMO- to HOMO-dominated charge transport upon the addition of the fluoride is verified both experimentally and theoretically.

---

The investigation of the electronic transport properties of circuits comprising individual molecules as basic building blocks is an area of increased focus for the field of molecular electronics, a subfield of nanoscience or nanotechnology.^1–3 Regulating charge transport at the single-molecule level is a key step in the development of molecular circuits. In the last decade, several methods were applied for this purpose, including electrochemical gating,^4–6 pH variation,^7–9 light irradiation,¹⁰ chemical tuning of two distinct charge transport pathways,¹¹ and mechanical control of the molecular conformation or metal-molecule contact geometry^12,13 as well as the insertion of a heteroatom in the aromatic core.^14,15 Although these results provide important insights into the electronic properties of single-molecule junctions, it is highly desirable to realize molecular devices exhibiting a controllable current flow. Deliberate manipulation and control of charge transport through intermolecular interactions is an essential prerequisite for processing and storing information in molecular electronic devices. Among the reported systems, intermolecular interactions investigated in molecular junctions include metal coordination bonds,¹⁶ hydrogen bonds,^17–19 charge-transfer effects,²⁰ host–guest interactions²¹ and π–π stacking.^22,23

In the investigation below, our interest in Lewis acid–base interactions stems from the fact that they are quite strong and prevalent in supramolecular coordination chemistry,²⁴ as well as in organic synthetic methodologies, such as controlling regioselectivity in silylation²⁵ and catalytic processes.^26–28 As a consequence, we set our course towards exploiting strong Lewis acid–base interactions to regulate the tunneling mechanism, and hence to affect the electron transport through molecular wires. A specific system consisting of a linear phenylene ethynylene wire, whereby the central phenyl moiety is 2,5-disubstituted by dimesitylboryl groups (BMes₂), was chosen, because organoborane is primarily of great importance in the development of fluoride probes with high sensitivity and selectivity.²⁹ Fluoride anions show a high binding affinity to the B atom by virtue of strong Lewis acid–base interactions, leading to the formation of a covalent B–F bond which interrupts the π-conjugation extended through the B atom. The resulting organofluoroborate displays an intrinsic electronic structure significantly different from the corresponding organoborane.^30,31 Recently, Wenger et al. demonstrated that fluoride binding to an organoboron wire led to the decrease of electron transfer rates by more than two orders of magnitude.³² It is therefore of interest to determine if this change in electron transfer rate is reflected in a change in molecular conductance, despite the fact that these processes take place at different energies and under different environmental conditions.

To address this issue and also to explore the Lewis acid–base interactions in molecular electronics, experimental and theoretical studies on the electrical conductances of the organoborane 1 (Chart 1) in the presence and absence of tetra-n-butylammonium fluoride (TBAF) were carried out (see Fig. S3† for the relaxed structure of the molecules). The target compound 1 was prepared in 43% yield via Sonogashira cross-coupling reaction of S-4-iodophenyl ethanethioate with 1,4-bis(diethynyl)-2,5-bis(dimesitylboryl)benzene, and characterized by NMR and high-resolution mass spectrometry after purification by column chromatography (ESI†). Charge transport measurements of single-molecule junctions were performed using a mechanically-controllable break junction (MCBJ) technique under ambient conditions. The contacted point between two gold electrodes was repeatedly formed and broken in a solution of 1 (0.01 mM) in a mixture of THF : mesitylene (v/v 1 : 4) under the control of a piezostack and stepper motor.^33,34 A solution of TBAF (4 equivalents) in the same mixture solvent was then added leading to in situ formation of the corresponding organofluoroborate (1·2F) due to the strong Lewis acid–base interactions, as evidenced by absorption spectral titrations (Fig. S1†). The lack of formation of 1·F is in line with the reported organoboranes containing two dimesitylboryl groups spatially distant from each other.^35,36Chart 1 shows the schematics of molecular junctions through 1 and 1·2F via S–Au bonds between the two gold electrodes.

Chart 1 A schematic diagram of the single-molecule conductance measurements through 1 and 1·2F.

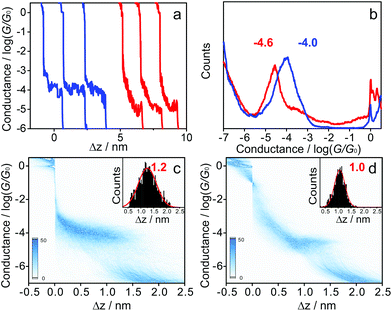
Fig. 1a shows typical individual stretching traces from the MCBJ measurements of 1 and 1·2F molecules, plotted in the logarithmic scale. Following an initial plateau at 1 G₀, corresponding to only gold-atom contacts (conductance quantum G₀, G₀ = 2e²/h), a sharp conductance decrease occurs after the rupture of gold–gold atomic contacts, followed by clear molecular plateaus of the molecular junction in the range of 10^−3.0G₀ to 10^−5.5G₀. Different with the relatively flat conductance plateaus of 1, the conductance of 1·2F decreases sharply with junction elongation. The different conductance tendency can be generally ascribed to the inherent variation of molecule-electrode interfaces of molecular junctions.^33,37 To carry out a meaningful statistical analysis, thousands of individual traces were used to construct the one-dimensional (1D) conductance histograms, displayed in Fig. 1b. The most probable conductance of 1 is located at 10^−4.0±0.1G₀, which is comparable to the value of the corresponding oligo(phenylene-ethynylene) (OPE) wire.³⁸ Upon addition of TBAF (4 equivalents), the resulting organofluoroborate (1·2F) has a conductance at 10^−4.6±0.1G₀, which is ca. 4 times lower than that of 1. The decreased conductance is ascribed to the interruption of the π-conjugation by the population of the boron p_π orbital due to fluoride binding, as evidenced by drastic changes in the photophysical properties upon the addition of the fluoride (Fig. S1†). The lowest absorption bands are ascribed to an intramolecular charge-transfer transition from the HOMO delocalized over the OPE moiety to the LUMO localized on the diborylphenylene moiety.³⁹ Consequently, the extent of the π-conjugation in the LUMO through the vacant p-orbital on the boron atom is relevant to the charge-transfer transition energy.^39–41 In other words, the extended π-conjugation accounts for the low-lying LUMO of the borane. The electron-deficient borane as a Lewis acid interacts readily with a fluoride as a Lewis base to afford the corresponding electron-rich borate, which substantially shifts the LUMO to a high energy level, leading to a larger HOMO–LUMO gap.^31,42,43 To confirm our interpretation, control experiments on bis[(4-acetylthiophenyl)acetylene (Fig. S2†) and 1,10-decanedithiol (Fig. S3†) have been carried out, indicating that the conductance value in both cases remains unchanged in the presence of TBAF. All experimental results are rationalized by DFT calculations (Fig. 2).

Fig. 1 Single-molecule conductance measurements of 1 and 1·2F. (a) Typical individual conductance – relative distance traces for 1 and 1·2F recorded from conductance measurements at V_bias = 100 mV, blue for 1 and red for 1·2F. (b) One-dimensional (1D) conductance histograms of 1 (blue) and 1·2F (red). (c, d) Two-dimensional (2D) conductance histograms and stretching distance Δz distributions (inset) of 1 (c) and 1·2F (d).

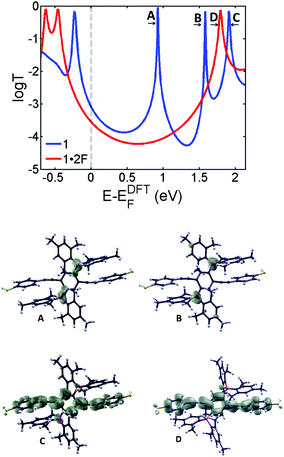Fig. 2 DFT transmission coefficients of molecules 1 (blue curve) and 1·2F (red curve). The lower graphics show the local density of states (LDOS) of the LUMO (A), LUMO+1 (B) and LUMO+2 (C) of 1 and the LUMO (D) of 1·2F. The transport resonances of 1 at E_F = 0.93 eV (A) and 1.6 eV (B) correspond to localized states on the boryl groups as shown by LDOS, and at E_F = 1.9 eV (C) correspond to localized state in the backbone and the LUMO (D) of 1·2F at E = 1.8 eV. Wave functions of (D) and (C) are very similar, because (C) evolves into the LUMO of 1·2F. The boron resonances are removed in 1·2F (D). The relative positions of the transmission curves are beyond DFT. To yield agreement with experiment (at E = 0 eV), the red curve has been shifted by approximately 0.4 eV relative to the bare DFT curve as discussed above as well as in the ESI (Fig. S4†).

The two-dimensional (2D) histograms are displayed in Fig. 1c and d. Two clear intensity clouds are observed for 1 (Fig. 1c) and 1·2F (Fig. 1d). It is noted that the shapes of the conductance clouds are quite different, which can be attributed to the change of the microscopic structure of molecular junctions during the stretching process. We note that the conductance clouds vary in different ways with mechanical stretching. The variation can be attributed to microscopic structure changes of the molecular junctions. The stretching distance distributions of the borane and borate (insets of Fig. 1c and d) suggest a slight difference due to the geometry change around the boron center after fluoride binding.³¹ The broader stretching distance distribution of 1 indicates that the rupture of molecular junctions varies significantly from junction to junction. After the treatment with TBAF, the stretching fluctuation was suppressed, leading to a narrower peak at a shorter Δz value.

To demonstrate that the decrease in conductance is due to the addition of fluoride atoms, we also present an analysis of the transport^44,45 properties of 1 and 1·2F by calculating the transmission probability T(E) of electrons with energy E passing from one electrode to another through molecules 1 and 1·2F using the Gollum transport code.⁴⁶Fig. 2 shows the transmission coefficients of the borane 1 (blue) and the borate 1·2F (red) calculated using material-specific mean field Hamiltonian obtained from the SIESTA⁴⁷ implementation of density functional theory (DFT). As shown by the blue curve of Fig. 2, the transmission coefficient of 1 possesses two resonances (at 0.93 eV and 1.6 eV respectively) associated with the LUMO and LUMO+1 of 1. As illustrated by the local density of states (LDOS) calculations in Fig. 2, these arise from the two degenerate states associated with the empty p-orbitals of the boron atoms, which are split due to their indirect coupling via the para-connected central phenyl ring. Their presence causes the mid-gap conductance of 1 to be higher than that of 1·2F, due to the resonance A in the blue curve of Fig. 2. The addition of two fluorides (red curve) removes these resonances from the vicinity of the HOMO–LUMO gap. Consequently, the conductance of 1·2F is reduced compared to that of 1. The experimental conductance ratio of 10^−4.0±0.1/10^−4.6±0.1 is approximately 4, which is consistent with the Fermi energy of 1·2F in the presence of counterions being increased by 0.4 eV compared with the DFT-predicted value.

Conclusions

The regulation of the dominant molecular orbital of the molecular wire via Lewis acid–base interactions is for the first time verified experimentally and theoretically. The effect of a declining electrical conductance is correlated with a decrease of charge transfer rates in such molecules³² and is distinct from the gating of single molecule junction conductance by charge transfer complex formation,⁴⁸ which was found to have the opposite effect of increasing the electrical conduction by introducing resonances in the HOMO–LUMO gap. The ability to control transport resonances at a molecular scale has potential applications in the design of new thermoelectric materials^49,50 and chemical sensors.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the European Commission (EC) FP7 ITN “MOLESCO” (project no. 606728), UK EPSRC (grant no. EP/M014452/1 and EP/N017188/1), National Key R&D Program of China (2017YFA0204902), the National Natural Science Foundation of China (No. 21673195, 21722305) and Thousand Youth Talents Plan of China. H.S. and S.S. acknowledge the Leverhulme Trust for Leverhulme Early Career Fellowship no. ECF-2017-186 and ECF-2018-375.

References

1. A. Coskun, J. M. Spruell, G. Barin, W. R. Dichtel, A. H. Flood, Y. Y. Botros and J. F. Stoddart, Chem. Soc. Rev., 2012, 41, 4827–4859.
2. J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific, Singapore, 2010.
3. R. Frisenda, D. Stefani and H. S. J. van der Zant, Acc. Chem. Res., 2018, 51, 1359–1367.
4. R. J. Nichols and S. J. Higgins, Acc. Chem. Res., 2016, 49, 2640–2648.
5. Z. H. Li, H. Li, S. J. Chen, T. Froehlich, C. Y. Yi, C. Schönenberger, M. Calame, S. Decurtins, S. X. Liu and E. Borguet, J. Am. Chem. Soc., 2014, 136, 8867–8870.
6. M. Baghernejad, D. Z. Manrique, C. Li, T. Pope, U. Zhumaev, I. Pobelov, P. Moreno-Garcia, V. Kaliginedi, C. Huang, W. J. Hong, C. Lambert and T. Wandlowski, Chem. Commun., 2014, 50, 15975–15978.
7. Z. H. Li, M. Smeu, S. Afsari, Y. J. Xing, M. A. Ratner and E. Borguet, Angew. Chem., Int. Ed., 2014, 53, 1098–1102.
8. Y.-P. Zhang, L.-C. Chen, Z.-Q. Zhang, J.-J. Cao, C. Tang, J. Liu, L.-L. Duan, Y. Huo, X. Shao, W. Hong and H.-L. Zhang, J. Am. Chem. Soc., 2018, 140, 6531–6535.
9. G. Yang, S. Sangtarash, Z. Liu, X. Li, H. Sadeghi, Z. Tan, R. Li, J. Zheng, X. Dong, J. Liu, Y. Yang, J. Shi, Z. Xiao, G. Zhang, C. Lambert, W. Hong and D. Zhang, Chem. Sci., 2017, 8, 7505–7509.
10. E. S. Tam, J. J. Parks, W. W. Shum, Y. W. Zhong, M. B. Santiago-Berrios, X. Zheng, W. T. Yang, G. K. L. Chan, H. D. Abruna and D. C. Ralph, ACS Nano, 2011, 5, 5115–5123.
11. C. C. Huang, S. J. Chen, K. B. Ornso, D. Reber, M. Baghernejad, Y. C. Fu, T. Wandlowski, S. Decurtins, W. J. Hong, K. S. Thygesen and S. X. Liu, Angew. Chem., Int. Ed., 2015, 54, 14304–14307.
12. S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230–234.
13. H. Bi, C.-A. Palma, Y. Gong, P. Hasch, J. Reichert, J. V. Barth, C.-A. Palma, M. Elbing, M. Mayor and M. Mayor, J. Am. Chem. Soc., 2018, 140, 4835–4840.
14. S. Sangtarash, H. Sadeghi and C. J. Lambert, Nanoscale, 2016, 8, 13199–13205.
15. X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z.-Y. Xiao, W. Hong, C. J. Lambert and S.-X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176.
16. P. T. Bui and T. Nishino, Phys. Chem. Chem. Phys., 2014, 16, 5490–5494.
17. L. Wang, Z.-L. Gong, S.-Y. Li, W. Hong, Y.-W. Zhong, D. Wang and L.-J. Wan, Angew. Chem., Int. Ed., 2016, 55, 12393–12397.
18. T. Nishino, N. Hayashi and P. T. Bui, J. Am. Chem. Soc., 2013, 135, 4592–4595.
19. C. Zhou, C. Jia, Y. Lin, C. Gu, G. He, X. Guo, X. Li, J. Yang, Z. Gong, Y. Zhong and X. Guo, Nat. Commun., 2018, 9, 807.
20. A. Vezzoli, I. Grace, C. Brooke, K. Wang, C. J. Lambert, B. Q. Xu, R. J. Nichols and S. J. Higgins, Nanoscale, 2015, 7, 18949–18955.
21. W. Zhang, S. Y. Gan, A. Vezzoli, R. J. Davidson, D. C. Milan, K. V. Luzyanin, S. J. Higgins, R. J. Nichols, A. Beeby, P. J. Low, B. Y. Li and L. Niu, ACS Nano, 2016, 10, 5212–5220.
22. S. Martin, I. Grace, M. R. Bryce, C. S. Wang, R. Jitchati, A. S. Batsanov, S. J. Higgins, C. J. Lambert and R. J. Nichols, J. Am. Chem. Soc., 2010, 132, 9157–9164.
23. S. Fujii, T. Tada, Y. Komoto, T. Osuga, T. Murase, M. Fujita and M. Kiguchi, J. Am. Chem. Soc., 2015, 137, 5939–5947.
24. R. D. Adams, B. Captain, W. Fu and M. D. Smith, J. Am. Chem. Soc., 2002, 124, 5628–5629.
25. T. Wakaki, M. Kanai and Y. Kuninobu, Org. Lett., 2015, 17, 1758–1761.
26. A. Gallo, A. Fong, K. C. Szeto, J. Rieb, L. Delevoye, R. M. Gauvin, M. Taoufik, B. Peters and S. L. Scott, J. Am. Chem. Soc., 2016, 138, 12935–12947.
27. W. Zheng, S. Nayak, W. Yuan, Z. Zeng, X. Hong, K. A. Vincent and E. Tsang, Chem. Commun., 2016, 52, 13901–13904.
28. S. E. Denmark and G. L. Beutner, Angew. Chem., Int. Ed., 2008, 47, 1560–1638.
29. T. W. Hudnall, C. W. Chiu and F. P. Gabbai, Acc. Chem. Res., 2009, 42, 388–397.
30. C.-H. Zhao, A. Wakamiya, Y. Inukai and S. Yamaguchi, J. Am. Chem. Soc., 2006, 128, 15934–15935.
31. S. Yamaguchi, S. Akiyama and K. Tamao, J. Am. Chem. Soc., 2001, 123, 11372–11375.
32. J. Chen and O. S. Wenger, Chem. Sci., 2015, 6, 3582–3592.
33. W. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304.
34. W. Hong, H. Valkenier, G. Meszaros, D. Z. Manrique, A. Mishchenko, A. Putz, P. M. Garcia, C. J. Lambert, J. C. Hummelen and T. Wandlowski, Beilstein J. Nanotechnol., 2011, 2, 699–713.
35. Y. Sun, Z. M. Hudson, Y. Rao and S. Wang, Inorg. Chem., 2011, 50, 3373–3378.
36. Y. You and S. Y. Park, Adv. Mater., 2008, 20, 3820–3826.
37. Y.-H. Kim, H. S. Kim, J. Lee, M. Tsutsui and T. Kawai, J. Am. Chem. Soc., 2017, 139, 8286–8294.
38. V. Kaliginedi, P. Moreno-Garcia, H. Valkenier, W. J. Hong, V. M. Garcia-Suarez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262–5275.
39. C. H. Zhao, A. Wakamiya, Y. Inukai and S. Yamaguchi, J. Am. Chem. Soc., 2006, 128, 15934–15935.
40. D. S. Miller and J. E. Leffler, J. Phys. Chem., 1970, 74, 2571–2574.
41. B. G. Ramsey, J. Phys. Chem., 1966, 70, 611–618.
42. S. Yamaguchi, S. Akiyama and K. Tamao, J. Organomet. Chem., 2002, 652, 3–9.
43. S. Yamaguchi, T. Shirasaka and K. Tamao, Org. Lett., 2000, 2, 4129–4132.
44. S. Sangtarash, C. Huang, H. Sadeghi, G. Sorohhov, J. Hauser, T. Wandlowski, W. Hong, S. Decurtins, S.-X. Liu and C. J. Lambert, J. Am. Chem. Soc., 2015, 137, 11425–11431.
45. Y. Geng, S. Sangtarash, C. Huang, H. Sadeghi, Y. Fu, W. Hong, T. Wandlowski, S. Decurtins, C. J. Lambert and S.-X. Liu, J. Am. Chem. Soc., 2015, 137, 4469–4476.
46. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, S. Hatef and L. A. Algharagholy, New J. Phys., 2014, 16, 093029.
47. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
48. A. Vezzoli, I. Grace, C. Brooke, K. Wang, C. J. Lambert, B. Xu, R. J. Nichols and S. J. Higgins, Nanoscale, 2015, 7, 18949–18955.
49. M. G.-S. Víctor, J. L. Colin, M. David Zs and W. Thomas, Nanotechnology, 2014, 25, 205402.
50. H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2015, 15, 7467–7472.

---

Footnotes

† Electronic supplementary information (ESI) available: Full experimental information and characterization data as well as computational methods and additional results. See DOI: 10.1039/c8nr06562d

‡ These authors have contributed equally.

---