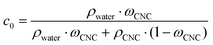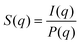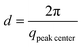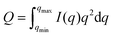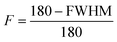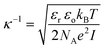Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assembly of cellulose nanocrystals in a levitating drop probed by time-resolved small angle X-ray scattering†
Yingxin
Liu
 ab,
Michael
Agthe‡
a,
Michaela
Salajková
c,
Korneliya
Gordeyeva
a,
Valentina
Guccini
ab,
Andreas
Fall§
a,
Germán
Salazar-Alvarez
ab,
Christina
Schütz¶
ab,
Michael
Agthe‡
a,
Michaela
Salajková
c,
Korneliya
Gordeyeva
a,
Valentina
Guccini
ab,
Andreas
Fall§
a,
Germán
Salazar-Alvarez
ab,
Christina
Schütz¶
 *ab and
Lennart
Bergström
*ab and
Lennart
Bergström
 *a
*a
aDepartment of Materials and Environmental Chemistry, Stockholm University, 106 91 Stockholm, Sweden. E-mail: christina.schuetz@gmail.com; lennart.bergstrom@mmk.su.se
bWallenberg Wood Science Center, KTH, 100 44 Stockholm, Sweden
cDepartment of Biosciences, University of Oslo, 0371 Oslo, Norway
First published on 18th September 2018
Abstract
Assembly of bio-based nano-sized particles into complex architectures and morphologies is an area of fundamental interest and technical importance. We have investigated the assembly of sulfonated cellulose nanocrystals (CNC) dispersed in a shrinking levitating aqueous drop using time-resolved small angle X-ray scattering (SAXS). Analysis of the scaling of the particle separation distance (d) with particle concentration (c) was used to follow the transition of CNC dispersions from an isotropic state at 1–2 vol% to a compressed nematic state at particle concentrations above 30 vol%. Comparison with SAXS measurements on CNC dispersions at near equilibrium conditions shows that evaporation-induced assembly of CNC in large levitating drops is comparable to bulk systems. Colloidal states with d vs. c scalings intermediate between isotropic dispersions and unidirectional compression of the nematic structure could be related to the biphasic region and gelation of CNC. Nanoscale structural information of CNC assembly up to very high particle concentrations can help to fabricate nanocellulose-based materials by evaporative methods.
Introduction
Assembly of nano-sized building blocks into complex architectures is both a promising route for the fabrication of functional materials and also a design principle in nature.1–4 With the significant advances during the last decades in tailoring assembled structures and functionalities of synthetic nanoparticles,5,6 there is a rapidly growing interest to utilise nanoparticles from renewable sources in sustainable materials. However, producing sustainable nanomaterials with tailored and hierarchical structures is challenging and requires better understanding on how to exercise the structural control of assemblies of bio-based nanoparticles.7,8Nanocellulose is a fibrous nanoparticle that can be readily extracted from wood and other sources (e.g. cotton, ramie and bacteria).9 The helical orientation of nanocellulose in plant cell walls has been shown to contribute to both the mechanical strength of wood,10–12 as well as the brilliant colour of different organisms.13–15 Rod-like cellulose nanocrystals (CNC) with a high aspect ratio produced by e.g., sulphuric acid hydrolysis are colloidally stable in aqueous dispersions and form a chiral nematic (cholesteric) liquid crystalline phase at relatively low concentrations.10,16 Drying of CNC dispersions results in films with a helically arranged structure and iridescent optical appearance with potential applications as sensors and coatings.3,17–19 Studies of the assembly and compression of the chiral nematic structure during film formation are sparse and restricted to relatively low particle concentrations.20
The helical assembly (e.g., the chiral nematic pitch) of CNC as a function of the particle concentration has been studied in both bulk phase and in constrained spherical geometries.16,21–26 However, recent studies on emulsion drops and micro-drops generated by microfluidics were restricted to a relatively narrow concentration range of CNC and were invariably performed on aqueous drops dispersed in organic solvents containing surfactants or surface active copolymers,21–23 which may have a significant influence on the nucleation of the cholesteric phase.27
Acoustic levitation of aqueous drops is a convenient approach which has been used to study the crystallization and agglomeration of proteins as well as the assembly of nanoparticles.28–30 Levitating drops that slowly shrink as the water evaporates constitute a system that does not require the addition of surfactants and allows assembly to be studied without the presence of a solid substrate. Here, we have quantified the nanoscale assembly of cellulose nanocrystals in an acoustically levitating drop by time-resolved small angle X-ray scattering (SAXS). The volume change of the surfactant-free drop was continuously monitored as the water evaporated, and we probed the structural features of CNC dispersions from 1 vol% to ∼38 vol%, which is significantly higher than previous studies have investigated. The changes in scaling of the separation distance as a function of particle concentration were related to the transition of CNC dispersions from an isotropic phase to a compressed nematic state and the effect of gelation.
Results and discussion
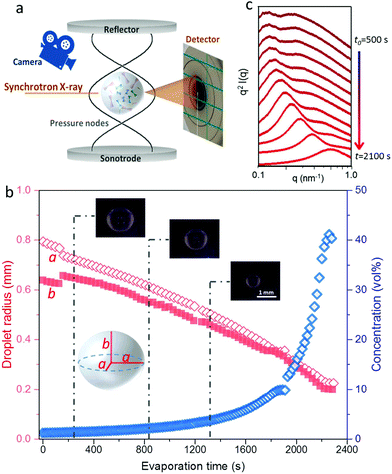
We have followed the evaporation-induced assembly of CNC in aqueous levitating drops using in situ SAXS. Fig. 1a shows a schematic illustration of the experimental set-up, where the levitating drop was confined between two pressure nodes of an ultrasonic wave. The shrinkage of the drop was recorded using a USB camera (Fig. 1a), and the drop volume and particle concentration were estimated from the measured equatorial and polar radius (Fig. 1b). The CNC drop displayed a constant water evaporation rate of ∼10 × 10−4 mm3 s−1 until ∼1000 s (Fig. S1†), where the evaporation rate decreased. Hindered water evaporation of CNC dispersions was recently studied and related to the formation of a particle network.31–33Fig. 1c shows representative SAXS curves of the shrinking CNC drop, which covered a particle concentration range from 1.5 vol% to 25 vol% (referring to the top and bottom curves, respectively). The growth of the primary peak in the SAXS curves is directly related to the time-dependent shrinkage of the drop and thus the increase of CNC concentrations. The primary scattering peak is related to the center-to-center separation distance (d = 2π/qpeak center, q is the scattering vector) between neighbouring particles.16 The shift of the scattering peak towards higher q with increasing particle concentrations in Fig. 1c indicates a decreasing proximity between CNC particles, which is also observed in the development of the structure factors with increasing particle concentrations (Fig. S2†). The scattering curves also displayed a secondary peak, which previously has been related to the formation of anisotropic 2-dimensional CNC aggregates.34The structural features of the CNC dispersion in a levitating drop with an initial diameter of ∼1.5 mm was analyzed by power law scaling of the separation distance with CNC concentration. Fig. 2 shows that the separation distance continuously decreased from 50 nm to 5 nm as the CNC concentration increased from 1 vol% to more than 35 vol%. The reproducibility of the retrieved concentration-dependent separation distances from the SAXS measurements was confirmed by a repeated measurement on the other levitating drops with the same initial CNC concentration, as shown in Fig. S3.†
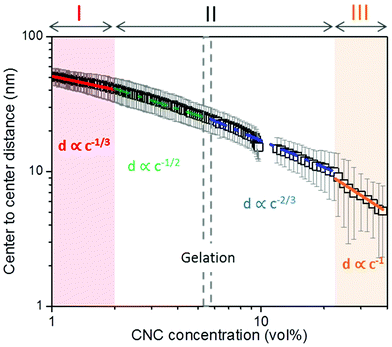 | ||
| Fig. 2 Center-to-center separation distance (d) between CNC particles as a function of the particle concentration (c). The error bar results from the standard deviation of the fitted Gaussian peaks. The solid curves describe a power law relation (d ∝ c−x) with exponents of; 1/3 (red); 1/2 (green); 2/3 (blue) and 1 (orange), respectively, dividing the CNC assembly process into 3 sequential stages. All the fitting show an adjusted R-square value above 0.98 (see fitting details in Fig. S4†). The gelation threshold around 6 vol% of the CNC dispersions was determined from the gravity-driven flowing ability in tilted vials. | ||
The scaling of the CNC dispersion at low concentrations (between 1 vol% and 2 vol%) followed d ∝ c−1/3 (Fig. 2, Stage I), which is characteristic for isotropic contraction of randomly aligned particles. Indeed, this concentration range coincided with the isotropic state of the CNC dispersion, as shown in the phase diagram of Fig. S5a.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 The isotropic state is also confirmed by the absence of any birefringent regions when the dispersion was placed between crossed polarizers (Fig. S6†). The scaling for unidimensional compression of the nematic phase (d ∝ c−1) was obtained only at very high concentrations (above 23 vol%, Stage III). Hence, there is a significant concentration range (between 2 and 23 vol%) where the structural change of CNC drop displayed transitional scaling exponents from −1/3 to −1. At particle concentrations above 2 vol% up to ∼6 vol%, the CNC dispersion followed a scaling of d ∝ c−1/2. The concentration dependence of the separation distance in the levitating CNC drops within this concentration range was in good agreement with the previous study of Schütz et al. (Fig. S5b†),16 where biphasic CNC dispersions with concentrations between 1.9 vol% and 5.2 vol% were measured in sealed capillaries (near equilibrium conditions) by SAXS. The close correspondence in scaling behavior of these two data sets suggests that the geometrical constraints of the relatively large levitating drop (with a diameter between 1.2 mm to 0.8 mm) have an insignificant influence on the structural evolution of CNC assembly,21,22 and thus implies that the power law scaling of d ∝ c−1/2 is characteristic for the biphasic state of bulk CNC dispersions. In addition, no characteristic peaks of a hexagonal packing structure (expected peak position ratio of 1
16 The isotropic state is also confirmed by the absence of any birefringent regions when the dispersion was placed between crossed polarizers (Fig. S6†). The scaling for unidimensional compression of the nematic phase (d ∝ c−1) was obtained only at very high concentrations (above 23 vol%, Stage III). Hence, there is a significant concentration range (between 2 and 23 vol%) where the structural change of CNC drop displayed transitional scaling exponents from −1/3 to −1. At particle concentrations above 2 vol% up to ∼6 vol%, the CNC dispersion followed a scaling of d ∝ c−1/2. The concentration dependence of the separation distance in the levitating CNC drops within this concentration range was in good agreement with the previous study of Schütz et al. (Fig. S5b†),16 where biphasic CNC dispersions with concentrations between 1.9 vol% and 5.2 vol% were measured in sealed capillaries (near equilibrium conditions) by SAXS. The close correspondence in scaling behavior of these two data sets suggests that the geometrical constraints of the relatively large levitating drop (with a diameter between 1.2 mm to 0.8 mm) have an insignificant influence on the structural evolution of CNC assembly,21,22 and thus implies that the power law scaling of d ∝ c−1/2 is characteristic for the biphasic state of bulk CNC dispersions. In addition, no characteristic peaks of a hexagonal packing structure (expected peak position ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) √3
√3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) were observed in Fig. 1c,35–37 which indicates that the scaling power of −1/2 excludes the packing of the CNC particles into a hexagonal lattice.
2) were observed in Fig. 1c,35–37 which indicates that the scaling power of −1/2 excludes the packing of the CNC particles into a hexagonal lattice.
Chiral nematic assembly of CNC is always accompanied and competing with gelation at high concentrations (above 6–9 vol%).3,19,38 The competition between gelation and self-assembly is still poorly understood, but of significance for producing CNC-based materials with controllable helical orientation and chiral nematic pitch.3,19 Investigation of the gravity-driven flowing ability of CNC dispersions in tilted vials at different concentrations suggests that the gelation threshold of CNC used in this study was around 6 vol% (Fig. S7†). It is interesting to note that a change of the scaling relation from d ∝ c−1/2 to d ∝ c−2/3 occurred at a CNC concentration of 6 vol%, which indicates that the scaling of d ∝ c−2/3 may reflect the competition between gelation and unidirectional compression of the fully nematic phase. Fig. S8† shows that the Porod invariant Q ∝ ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ·c·(1 − c), where ρ and c are the average electron density difference between CNC and the solvent and CNC concentration, respectively,39 increased until a maximum value is obtained around an evaporation time of ∼2000 s, which corresponds to a CNC concentration of ∼20 vol%. This particle concentration corresponds to the onset of the unidimensional compression, and the increase of the scattering power (i.e. the magnitude of Q) may thus reflect the fusion and rearrangement of the cholesteric tactoids in the viscoelastic dispersion, similar to a recent study using electron microscopy.26 Fig. S9† shows that the order parameter (F) increases with increasing CNC concentrations and reaches a maximum value at a CNC concentration of ∼20 vol%. The decrease of Q and F at higher particle concentrations (i.e., longer evaporation time) is likely related to the formation of defects, cracks and possibly also voids, similar to previous findings in studies on assembly of iron oxide nanoparticles in levitating drops.39 In addition, we have evaluated the ionic strength effect on the assembly of CNC. The separation distance was always larger than the corresponding Debye length (Fig. S10†), which suggests that agglomeration of CNC is of minor importance in this study.
·c·(1 − c), where ρ and c are the average electron density difference between CNC and the solvent and CNC concentration, respectively,39 increased until a maximum value is obtained around an evaporation time of ∼2000 s, which corresponds to a CNC concentration of ∼20 vol%. This particle concentration corresponds to the onset of the unidimensional compression, and the increase of the scattering power (i.e. the magnitude of Q) may thus reflect the fusion and rearrangement of the cholesteric tactoids in the viscoelastic dispersion, similar to a recent study using electron microscopy.26 Fig. S9† shows that the order parameter (F) increases with increasing CNC concentrations and reaches a maximum value at a CNC concentration of ∼20 vol%. The decrease of Q and F at higher particle concentrations (i.e., longer evaporation time) is likely related to the formation of defects, cracks and possibly also voids, similar to previous findings in studies on assembly of iron oxide nanoparticles in levitating drops.39 In addition, we have evaluated the ionic strength effect on the assembly of CNC. The separation distance was always larger than the corresponding Debye length (Fig. S10†), which suggests that agglomeration of CNC is of minor importance in this study.
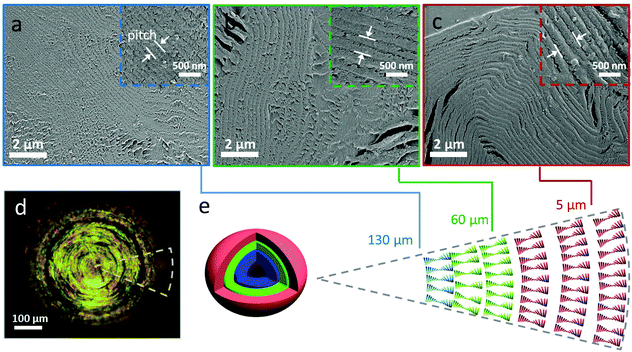
The SEM images of the internal structure in Fig. 3a–c shows that the dry CNC bead displayed a layered microstructure, which is characteristic for the chiral nematic structure.3,11,17 The chiral nematic structure of the CNC bead was further evidenced by the birefringent appearance under crossed polarizers. In contrast to previous studies on CNC assembled in small drops in surfactant-containing systems,22,23 we did not observe any significant structural differences between the core (Fig. 3a) and outer shell (Fig. 3c) of the assembled bead beyond the pitch value. The helical pitch, measured on SEM micrographs (Fig. 3a–c) within the bead ranged from 410 ± 60 nm to 220 ± 30 nm from the outer layer to the core of the bead, which is significantly smaller than the pitch of CNC assembled in small, confined droplets (pitch of ∼1.3 μm),22 but similar to the pitch (∼200 nm) observed in CNC films prepared by drop casting a dispersion on the substrate in Fig. S11.†
Conclusions
The structural evolution of CNC dispersions during evaporation have been quantified using a substrate-free levitating setup combined with SAXS, covering a very wide concentration range; from 1 vol% up to 38 vol%. The nanoscale assembly was evaluated by analyzing the scaling of the separation distance as a function of the particle concentration, and the scaling relations was related to the transition from an isotropic state to a compressed chiral nematic structure. Complemented by the phase diagram, a scaling relation of d ∝ c−1/2 from 2 vol% to 6 vol% was characteristic for the structural features of biphasic dispersions, while the change of scaling into d ∝ c−2/3 around 6 vol% correlated well with the gelation threshold of CNC. The dry CNC beads displayed chiral nematic structures of e.g., similar pitch values compared to the casted planar CNC films. This study provides a quantitative tool to study assembly at very high particle concentrations in drops that are sufficiently large to resemble bulk systems, of relevance for fabricating CNC-based photonics.Experimental section
Preparation and characterization of cellulose nanocrystals
CNC with an average length of 178 ± 76 nm and an average diameter of ∼4 nm were fabricated using a sulfuric acid hydrolysis protocol.16 The sulfate half-ester groups on the CNC surface provided a charge of 0.23 mmol g−1, as determined by polyelectrolyte titration. The initial volume fraction of CNC, c0, was calculated in the following equation:where ρ is the density (1.6 g cm−3 and 1 g cm−3 for CNC and water, respectively),9ωCNC the CNC mass fraction (1 wt%).
Drop levitation
Generally, a 1.5–3 μL drop of aqueous CNC dispersions (1 vol%) was placed into the acoustic field of the levitator (TEC5, model 13K11, f0 = 100 kHz) where the drop was stabilized by adjusting the distance between the reflector and transducer, as well as the acoustic power. The acoustic levitator was encapsulated in a glass chamber with four opening sides, for the X-ray beam going through and a USB camera (1.3 M pixels, magnification up to 200×) recording, respectively. Image J and Origin 2015 were used to analyze the shrinkage of drop volume, and the average particle concentration as a function of the evaporation time was calculated using following equations:| Vdrop(t) = 4/3πa2b |
| VCNC = c0V0,drop |
| c(t) = VCNC/Vdrop(t) |
Small angle X-ray scattering
SAXS experiments were performed on the beamline I911-4 at MAX-lab, Sweden. The beamline applies a multipole wiggler where the Si (111) monochromator provides X-ray with a wavelength of 0.91 Å. The beam size was 0.2 × 0.3 mm2. A hybrid pixel CCD detector Pilatus 1 M (pixel size 172.0 μm) was used to obtain the 2-dimensional SAXS patterns and the distance from the sample to the detector was set to 1921.8 mm after calibration with silver behenate. The exposure time for each measurement was 10 s. The background scattering of deionized water was subtracted prior to the radial integration using bli9114.40 The scattering intensity I(q) of CNC dispersions reflects a combination of form factor P(q) and structure factor S(q).
P(q) solely depends on the shape and dimension of CNC particles, while S(q) reflects how the nanoparticles are arranged with respect to each other. The structural peaks in the SAXS curves were Gaussian fitted and used to determine an average center-to-center particle separation distance by the equation:
Porod invariant calculation
The Porod invariant, Q, of CNC drops during evaporation was calculated by the equation:where I (q) is the scattering intensity and q the scattering vector.
Order parameter calculation
The scattering intensity was plotted as a function of azimuthal angles along the crystalline cellulose (200), and the full width at half (FWHM) was obtained by Gaussian peak fitting. The order parameter, F, is calculated by the equation:Scanning electron microscopy
CNC bead was mounted on a silver pin using epoxy resin (Epoxy embedding medium, Fluka) and sectioned using ultramicrotome Leica EMFC7 equipped with a diamond knife (Diatome). The sample was sputter coated with a thin layer of platinum (Cressington 308R). The cross-sectional surface of CNC beads was characterized by scanning electron microscope (Hitachi S-4800).Polarized optical microscopy
The polarized optical image of the CNC bead was taken in the reflection mode of a Nikon Eclipse FNI light microscope and then recorded by an inline camera with a CCD sensor (2 M pixels).Calculation of Debye length
The Debye length, κ−1, was calculated using the following formula:where εr is the dielectric constant, εo the permittivity of free space, kB the Boltzmann constant, T the temperature in Kelvin, NA the Avogadro number, e the elementary charge and I the ionic strength.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Wallenberg Wood Science Center and the Swedish Research Council (VR) for funding. Thanks are given to MAX IV for the synchrotron beam time under the proposal (20130343 and 20140492) and the levitator. Ana Labrador and Tomás S. Plivelic are acknowledged for the technical assistance. We thank Bruno Frka-Petesic, Oliver Willekens, Daniela Stoeckel and Wim Thielemans for useful discussions. CS thanks the Alexander von Humboldt Foundation for funding under the Feodor Lynen scholarship.Notes and references
- L. Bergström, E. V. Sturm née Rosseeva, G. Salazar-Alvarez and H. Cölfen, Acc. Chem. Res., 2015, 48, 1391–1402 CrossRef PubMed.
- P. Fratzl, J. R. Soc., Interface, 2007, 4, 637–642 CrossRef PubMed.
- J. P. F. Lagerwall, C. Schütz, M. Salajkova, J. Noh, J. Hyun Park, G. Scalia and L. Bergström, NPG Asia Mater., 2014, 6, e80 CrossRef.
- J. C. Weaver, G. W. Milliron, A. Miserez, K. Evans-Lutterodt, S. Herrera, I. Gallana, W. J. Mershon, B. Swanson, P. Zavattieri, E. DiMasi and D. Kisailus, Science, 2012, 336, 1275–1280 CrossRef PubMed.
- T. Wang, D. LaMontagne, J. Lynch, J. Zhuang and Y. C. Cao, Chem. Soc. Rev., 2013, 42, 2804–2823 RSC.
- B. Wicklein, A. Kocjan, G. Salazar-Alvarez, F. Carosio, G. Camino, M. Antonietti and L. Bergström, Nat. Nanotechnol., 2015, 10, 277–283 CrossRef PubMed.
- F. G. Omenetto and D. L. Kaplan, Science, 2010, 329, 528–531 CrossRef PubMed.
- A. R. Studart, Adv. Mater., 2012, 24, 5024–5044 CrossRef PubMed.
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994 RSC.
- J. F. Revol, H. Bradford, J. Giasson, R. H. Marchessault and D. G. Gray, Int. J. Biol. Macromol., 1992, 14, 170–172 CrossRef PubMed.
- J. F. Revol and R. H. Marchessault, Int. J. Biol. Macromol., 1993, 15, 329–335 CrossRef PubMed.
- M. Eder, K. Jungnikl and I. Burgert, Trees, 2009, 23, 79–84 CrossRef.
- S. Vignolini, P. J. Rudall, A. V. Rowland, A. Reed, E. Moyroud, R. B. Faden, J. J. Baumberg, B. J. Glover and U. Steiner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15712–15715 CrossRef PubMed.
- R. M. Graham, D. W. Lee and K. Norstog, Am. J. Bot., 1993, 80, 198–203 CrossRef.
- O. D. Onelli, T. van de Kamp, J. N. Skepper, J. Powell, T. S. dos Rolo, T. Baumbach and S. Vignolini, Sci. Rep., 2017, 7, 1373 CrossRef PubMed.
- C. Schütz, M. Agthe, A. B. Fall, K. Gordeyeva, V. Guccini, M. Salajková, T. S. Plivelic, J. P. F. Lagerwall, G. Salazar-Alvarez and L. Bergström, Langmuir, 2015, 31, 6507–6513 CrossRef PubMed.
- J. H. Park, J. Noh, C. Schütz, G. Salazar-Alvarez, G. Scalia, L. Bergström and J. P. F. Lagerwall, ChemPhysChem, 2014, 15, 1477–1484 CrossRef PubMed.
- M. Giese, L. K. Blusch, M. K. Khan and M. J. MacLachlan, Angew. Chem., Int. Ed., 2015, 54, 2888–2910 CrossRef PubMed.
- R. M. Parker, G. Guidetti, C. A. Williams, T. Zhao, A. Narkevicius, S. Vignolini and B. Frka-Petesic, Adv. Mater., 2017, 1704477 Search PubMed.
- Y. Liu, D. Stoeckel, K. Gordeyeva, M. Agthe, C. Schütz, A. B. Fall and L. Bergström, ACS Macro Lett., 2018, 7, 172–177 CrossRef.
- Y. Li, J. Jun-Yan Suen, E. Prince, E. M. Larin, A. Klinkova, H. Thérien-Aubin, S. Zhu, B. Yang, A. S. Helmy, O. D. Lavrentovich and E. Kumacheva, Nat. Commun., 2016, 7, 12520 CrossRef PubMed.
- R. M. Parker, B. Frka-Petesic, G. Guidetti, G. Kamita, G. Consani, C. Abell and S. Vignolini, ACS Nano, 2016, 10, 8443–8449 CrossRef PubMed.
- P. X. Wang, W. Y. Hamad and M. J. MacLachlan, Angew. Chem., Int. Ed., 2016, 55, 12460–12464 CrossRef PubMed.
- X. M. Dong, J. F. Revol and D. G. Gray, Cellulose, 1998, 5, 19–32 CrossRef.
- X. M. Dong, T. Kimura, J. F. Revol and D. G. Gray, Langmuir, 1996, 12, 2076–2082 CrossRef.
- P. X. Wang, W. Y. Hamad and M. J. MacLachlan, Nat. Commun., 2016, 7, 11515 CrossRef PubMed.
- P. X. Wang and M. J. MacLachlan, Philos. Trans. R. Soc., A, 2018, 376, 20170042 CrossRef PubMed.
- A. M. Seddon, S. J. Richardson, K. Rastogi, T. S. Plivelic, A. M. Squires and C. Pfrang, J. Phys. Chem. Lett., 2016, 7, 1341–1345 CrossRef PubMed.
- A. Omrane, S. Santesson, M. Alden and S. Nilsson, Lab Chip, 2004, 4, 287–291 RSC.
- J. Polte, F. Emmerling, M. Radtke, U. Reinholz, H. Riesemeier and A. F. Thünemann, Langmuir, 2010, 26, 5889–5894 CrossRef PubMed.
- F. Jativa, C. Schütz, L. Bergström, X. Zhang and B. Wicklein, Soft Matter, 2015, 11, 5374–5380 RSC.
- L. Pauchard and C. Allain, C. R. Phys., 2003, 4, 231–239 CrossRef.
- R. Duggal, F. Hussain and M. Pasquali, Adv. Mater., 2006, 18, 29–34 CrossRef.
- M. Uhlig, A. Fall, S. Wellert, M. Lehmann, S. Prévost, L. Wågberg, R. von Klitzing and G. Nyström, Langmuir, 2016, 32, 442–450 CrossRef PubMed.
- E. E. Maier, R. Krause, M. Deggelmann, M. Hagenbüchle, R. Weber and S. Fraden, Macromolecules, 1992, 25, 1125–1133 CrossRef.
- S. T. Hyde, Langmuir, 1997, 13, 842–851 CrossRef.
- E. Grelet and R. Rana, Soft Matter, 2016, 12, 4621–4627 RSC.
- D. G. Gray, Philos. Trans. R. Soc., A, 2018, 376, 20170038 CrossRef PubMed.
- M. Agthe, T. S. Plivelic, A. Labrador, L. Bergström and G. Salazar-Alvarez, Nano Lett., 2016, 16, 6838–6843 CrossRef PubMed.
- A. Labrador, Y. Cerenius, C. Svensson, K. Theodor and T. Plivelic, J. Phys.: Conf. Ser., 2013, 425, 072019 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr05598j |
| ‡ Current address: Center for Free-Electron Laser Science, University of Hamburg, 22761 Hamburg, Germany. |
| § Current address: RISE Bioeconomy, Box 5604, 114 86 Stockholm, Sweden. |
| ¶ Current address: Physics and Materials Science Research Unit, University of Luxembourg, 1511 Luxembourg, Luxembourg. |
| This journal is © The Royal Society of Chemistry 2018 |