Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stable-radicals increase the conductance and Seebeck coefficient of graphene nanoconstrictions†
Mohammed
Noori
ab,
Hatef
Sadeghi
 *a and
Colin J.
Lambert
*a and
Colin J.
Lambert
 a
a
aThe Theory of Molecular-scale Transport, Department of Physics, Lancaster University, Lancaster, UK. E-mail: h.sadeghi@lancaster.ac.uk; c.lambert@lancaster.ac.uk
bDepartment of Physics, College of Science, University of Thi-Qar, Iraq
First published on 3rd October 2018
Abstract
Nanoscale thermoelectricity is an attractive target technology, because it can convert ambient heat into electricity for powering embedded devices in the internet of things. We demonstrate that the thermoelectric performance of graphene nanoconstrictions can be significantly enhanced by the presence of stable radical adsorbates, because radical molecules adsorbed on the graphene nanoconstrictions create singly-occupied orbitals in the vicinity of Fermi energy. This in turn leads to sharp features in their transmission functions close to Fermi energy, which increases the electrical conductance and Seebeck coefficient of the nanoconstrictions. This is a generic feature of radical adsorbates and can be employed in the design of new thermoelectric devices and materials.
Introduction
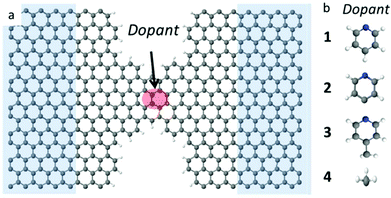
Graphene has attracted huge interest for its extraordinary thermal, mechanical, electrical and spintronic properties.1,2 It was recently demonstrated that stable electrode gaps below 5 nm can be formed using electroburning of graphene junctions.3–6 Motivated by recent experimental progress in using such electrodes to probe transport through single molecules,3,4,7–14 theoretical studies have also focused on the electrical properties of graphene nanoconstrictions formed by incomplete electroburning of narrow graphene junctions.3,14–18Graphene nanoribbons with zigzag edges have been predicted to show half metallic and spin filtering properties,19,20 with high densities of states near the graphene Fermi energy, which are attractive for thermoelectricity. However, these effects are not easy to isolate and control experimentally. In this paper, we demonstrate that states close to the graphene Fermi energy could be created by doping graphene constrictions with radical adsorbates, leading to a significant improvement in their electrical and thermoelectric properties. As prototypes for different non-radical and radical molecules, we dope the nanoconstriction with four different molecules (see Fig. 1) namely a non-radical pyridine (C5H5N) 1, a pyridine radical (C5H4N) 2, a 4-picoline radical (C6H6N) 3, and a methyl radical (CH3) 4.
Results and discussion
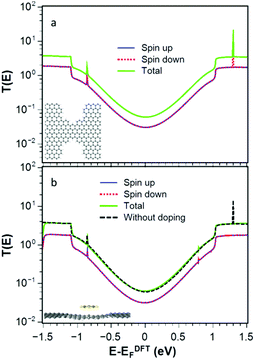
We investigate quantum transport through such constriction when each dopant 1–4 is attached to the narrow region of the constriction (shaded red dot Fig. 1a). In what follows, our aim is to investigate how the electrical and thermoelectric properties of graphene nanoconstrictions change when doping with one of these molecules. We calculate the transmission coefficient T(E) which describes the probability that electrons with energy E can pass from the left to the right graphene electrode through the nanoconstriction (Fig. 1a). We first obtain the material-specific mean-field Hamiltonian of each structure from optimized geometry of each junction using the SIESTA implementation of density functional theory (see Method for detail). We then combine the DFT Hamiltonian with our quantum transport code Gollum to obtain T(E) and use the Landauer formula to obtain electrical conductance G (see Methods for more detail). Since the radicals normally have unfilled orbitals, they are spin polarized. We therefore calculate the transmission function T↑ for majority and T↓ for minority spins. The total transmission function is defined to be T(E) = (T↑ + T↓). With this notation, in the low temperature limit, the Landauer formula simplifies to G = (e2/h)T(EF).We have designed the graphene nanoconstriction of Fig. 1a to ensure that the graphene constriction is not spin polarized. To explore the electrical properties of the bare junction shown in Fig. 1a, we computed the transmission coefficient without doping. Fig. 2a shows the spin up (blue line), the spin down (red dashed line), and total transmission coefficient (green line). The transmission functions are independent of spin, which confirms that the bare junction is not spin polarized. Fig. 2b shows the spin dependent and total transmission coefficient for graphene nanoconstriction junction in the presence of non-radical pyridine 1. The solid lines in the graph show the transmission coefficient for the spin up, down and total transmission coefficient. For comparison, the transmission coefficient for bare structure is also shown in the graph by black dashed line. The transmission through this nanoconstriction is also non-spin polarized and it is apparent that introducing a non-radical dopant does not have a significant effect on the transmission coefficients.
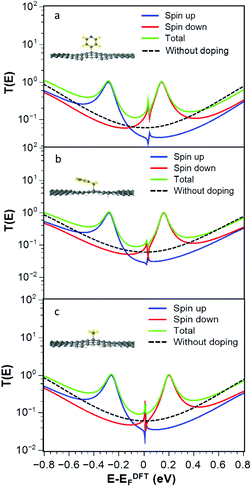
For the radicals 2, 3 and 4, Fig. 3a–c show that the transmission functions become spin dependent. After geometry relaxation, we find that all three radicals are covalently bound to the graphene nanoconstrictions. As shown in Fig. 3, extra resonances close to the Fermi energy appear in the spin-dependent transmission coefficient. The total transmission coefficient (green curve) is much higher than the bare junction transmission (dashed black line) over a wide energy range near the Fermi energy. Regardless of the Fermi energy of leads, the conductance in the presence of the radicals is therefore predicted to increase. This is a general feature of these junctions and does not depend on the type of radical. This increase is due to the singly occupied orbital in the outer shell of the radical molecule.
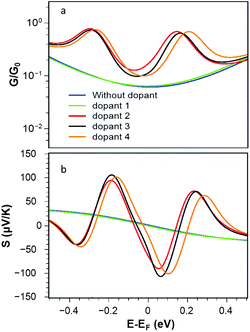
Fig. 4a shows that the corresponding room-temperature electrical conductances with radicals (pyridine 2, 4-picoline 3 and methyl 4) are also much higher than those of the bare and non-radical cases. Fig. 4b shows that the presence of radical dopants not only enhances the electrical conductance of the graphene nanoconstrictions, but also it enhances the Seebeck coefficient of these junctions. Fig. 4b shows the Seebeck coefficients S of these junctions over a range of Fermi energies at room temperature. It is clear that large positive and negative values of S are achievable compared to bare and non-radical cases.
It is worth mentioning (see Fig. S1 and S2 of the ESI†) that doping of graphene nanoconstrictions with n-type and p-type dopants such as TTF and TCNE21 has a much less pronounced effect on the conductance and Seebeck coefficient of graphene nanoconstriction compared with stable radical adsorbates. TTF and TCNE create localised bound states, which are weakly coupled to the continuum of states in the graphene nanoconstriction, resulting in Fano-resonances. This leads to some enhancement, but not as strong as stable radical adsorbates.20
Conclusion
We demonstrated a simultaneous increase in the electrical conductance and Seebeck coefficient of graphene nanoconstrictions using stable radical adsorbates, which create transmission resonances close to the Fermi energy. This increases electrical conductance up to an order of magnitude and enhances the Seebeck coefficient for a wide range of Fermi energies. The Seebeck coefficient of bare graphene nanoconstrictions is low, because the transmission function is symmetric with respect to the Fermi energy and therefore, its slope near the Fermi energy is low. In contrast, adsorbed radical create new spin states near the Fermi energy, which increases the slope of the transmission function and enhances the Seebeck coefficient. We demonstrated that this behaviour is a generic feature of graphene nanoconstrictions in the presence of adsorbed radicals.Methods
The molecular device we study in this work is illustrated schematically in Fig. 1. The geometry of each graphene nanoconstriction junctions was relaxed to a force tolerance of 20 meV Å−1 using the SIESTA22 implementation of density functional theory (DFT), with a double-ζ polarized basis set (DZP) and generalized gradient functional approximation (GGA-PBE) for the exchange and correlation functionals, which is applicable to arbitrary geometries. A real-space grid was defined with an equivalent energy cutoff of 150 Ry.To calculate thermoelectronic properties of the molecules in the junction, from the converged DFT calculation, the underlying mean-field Hamiltonian H was combined with our quantum transport code, Gollum23,24 to calculate the transmission coefficient T(E) for electrons of energy E passing from the source to the drain. The electrical conductance G(T) = e2/h(L↑0 + L↓0), and the Seebeck coefficient25S(T) = −(L↑1 + L↓1)/|e|T(L↑0 + L↓0), of the junction are calculated from the electron transmission coefficient T(E) where 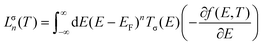 and σ is spin-up or down, f(E,T) is the Fermi–Dirac probability distribution function f(E,T) = (e(E−EF)/kBT + 1)−1, T is the temperature, EF is the Fermi energy, e is electron charge, and h is the Planck's constant.
and σ is spin-up or down, f(E,T) is the Fermi–Dirac probability distribution function f(E,T) = (e(E−EF)/kBT + 1)−1, T is the temperature, EF is the Fermi energy, e is electron charge, and h is the Planck's constant.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
H.S. acknowledges the Leverhulme Trust for Leverhulme Early Career Fellowship no. ECF-2017-186. This work is supported by UK EPSRC grants EP N017188/1, EP/M014452/1 and the Ministry of Higher Education and Scientific Research, University of Thi-Qar, Iraq.Notes and references
- A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2007, 81, 109–162 CrossRef.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- H. Sadeghi, J. A. Mol, C. Siong, G. A. D. Briggs, J. Warner, C. J. Lambert, C. Lau, A. Briggs, J. Warner and C. J. Lambert, Proc. Natl. Acad. Sci. U. S. A., 2016, 112, 2658–2663 CrossRef PubMed.
- F. Prins, A. Barreiro, J. W. Ruitenberg, J. S. Seldenthuis, N. Aliaga-Alcalde, L. M. K. Vandersypen and H. S. J. J. Van Der Zant, Nano Lett., 2011, 11, 4607–4611 CrossRef CAS PubMed.
- S. Leitherer, P. B. Coto, K. Ullmann, H. B. Weber and M. Thoss, Nanoscale, 2017, 9, 7217–7226 RSC.
- C. Nef, L. Pósa, P. Makk, W. Fu, A. Halbritter, C. Schönenberger and M. Calame, Nanoscale, 2014, 6, 7249–7254 RSC.
- C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D. H. Qu, H. Tian, M. A. Ratner, H. Q. Xu, A. Nitzan and X. Guo, Science, 2016, 352, 1443–1445 CrossRef CAS PubMed.
- P. Gehring, H. Sadeghi, S. Sangtarash, C. S. Lau, J. Liu, A. Ardavan, J. H. Warner, C. J. Lambert, G. A. D. Briggs and J. A. Mol, Nano Lett., 2016, 16, 4210–4216 CrossRef CAS PubMed.
- H. Sadeghi, S. Sangtarash and C. J. Lambert, Beilstein J. Nanotechnol., 2015, 6, 1413–1420 CrossRef CAS PubMed.
- J. A. Mol, C. S. Lau, W. J. M. Lewis, H. Sadeghi, C. Roche, A. Cnossen, J. H. Warner, C. J. Lambert, H. L. Anderson and G. A. D. Briggs, Nanoscale, 2015, 7, 13181–13185 RSC.
- C. S. Lau, J. A. Mol, H. Sadeghi, J. A. Mol, S. Sangtarash and C. J. Lambert, Nano Lett., 2015, 1, 1–7 Search PubMed.
- E. Burzurí, J. O. Island, R. Díaz-Torres, A. Fursina, A. González-Campo, O. Roubeau, S. J. Teat, N. Aliaga-Alcalde, E. Ruiz and H. S. J. Van Der Zant, ACS Nano, 2016, 10, 2521–2527 CrossRef PubMed.
- S. Lumetti, A. Candini, C. Godfrin, F. Balestro, W. Wernsdorfer, S. Klyatskaya, M. Ruben and M. Affronte, Dalton Trans., 2016, 45, 16570–16574 RSC.
- H. Sadeghi, S. Sangtarash and C. Lambert, Nano Lett., 2017, 17, 4611–4618 CrossRef CAS PubMed.
- C. M. Tan, Y. H. Zhou, C. Y. Chen, J. F. Yu and K. Q. Chen, Org. Electron., 2016, 28, 244–251 CrossRef CAS.
- C. Jia, B. Ma, N. Xin and X. Guo, Acc. Chem. Res., 2015, 48, 2565–2575 CrossRef CAS PubMed.
- H. Sadeghi, S. Sangtarash and C. Lambert, Phys. E, 2016, 82, 12–15 CrossRef CAS.
- N. Algethami, H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2018, 18, 4482–4486 CrossRef CAS PubMed.
- Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954–17961 CrossRef CAS.
- A. Vezzoli, I. Grace, C. Brooke, K. Wang, C. J. Lambert, B. Xu, R. J. Nichols and S. J. Higgins, Nanoscale, 2015, 7, 18949–18955 RSC.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 093029 CrossRef.
- H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2015, 15, 7467–7472 CrossRef CAS PubMed.
- H. Sadeghi, Nanotechnology, 2018, 29, 373001 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr04869j |
| This journal is © The Royal Society of Chemistry 2018 |