Split resonances for simultaneous detection and control measurements in a single bulk acoustic wave (BAW) sensor

Abstract

A self-referenced resonator consisting of two distinct areas of the top electrode made from Mo and a thin (5–30 nm) functional Au layer is shown. The fundamental frequencies for both the shear (∼1 GHz) and longitudinal (∼2 GHz) modes are split in two, such that mass attachment on the functional layer region causes frequency shifts in only one of the resonances, allowing a new approach of using the difference between the two frequencies to be used to measure mass attachment; this reduces the importance of device-to-device variability in absolute resonant frequency as a result of device fabrication.

---

Gravimetric biosensors based on thin film bulk acoustic wave (BAW) resonators have attracted significant interest in recent years mainly due to their high sensitivities, small size and low power, which makes them well-suited to mobile sensing applications, such as point-of-care medical diagnostics.¹ These devices can operate in the GHz frequency range; their sensing principle is based on the resonant frequency shift, Δf_r, due to mass attachment and this mass sensitivity is proportional to f_r ² according to Sauerbrey.² However, these sensors cannot distinguish among different binding molecules, therefore they need a functionalized layer on the resonator surface. Indeed, such functionalization layers have been reported in DNA sequencing,³ detection of human fibrinogen,⁴ pesticides,^5,6 potassium ions⁷ and cancer biomarkers.^8,9 Typical functional layers with biological affinity such as gold, carbon nanotubes, graphene oxide, ZnO nanowires, supramolecular monolayers or titanium dioxide are needed to achieve this selectivity with acoustic wave devices.^7,10–14 Despite this, shifts in frequency are still observed due to changes in the surroundings (i.e. temperature, pressure, humidity) of these devices and cannot be differentiated from “real” mass attachment.^15–17 Such effects pose a major challenge for the reliable detection of low quantities of biological compounds. Several methods have been proposed to compensate or measure the surrounding conditions of gravimetric BAW resonators. Active compensation techniques using external circuits or a reference device close to the resonator are complex and are costly.^18,19 A passive compensation technique reported by García-Gancedo et al. was based on using a thicker silicon dioxide as the first acoustic reflector layer, which produced two resonances that can be tracked simultaneously to monitor temperature variations and mass attachment.²⁰ Nonetheless the SiO₂ layer, which is part of the reflector does not add selectivity to the device and its thermal properties are strongly influenced by the deposition conditions.

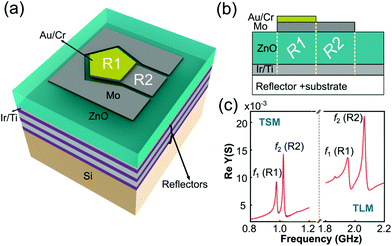
In this work a simpler mechanism to split the fundamental resonance mode of the gravimetric sensor into two closely separated, distinct frequencies using an additional functional layer thickness is proposed as shown in Fig. 1.

Fig. 1 (a) Device architecture of the ZnO based SMR with the functional Au layer only on a pentagonal section of the Mo top electrode, illustrating the regions corresponding to the first (R1) and second (R2) resonances. (b) Cross-section of the device to show the layers present in each resonator. (c) A typical frequency split (f₁ and f₂) due to the two resonance regions (R1 and R2) observed in both the thickness shear mode (TSM) and thickness longitudinal mode (TLM) of the same device.

The resonator (R1) that has the Au layer can also be easily functionalized to become sensitive and selective to biological species, whereas the second resonator (R2) without the Au functional layer has negligible frequency shifts since it is not selective to the biological species. The bottom ground electrode which is common to both regions of the BAW resonator is purposefully not patterned; this simplifies the device fabrication. A high density material such as Au is necessary such that a thin layer causes significant frequency splitting while at the same time maintaining mass sensitivity. Resonator R2 can be used to detect other surface effects. Crucially, both resonators have a common top electrode and so a self-referenced device is achieved, which obviates the need for prior knowledge of the initial resonant frequency as the separation of the resonances alone can be used as the sensing mechanism for mass attachment. The effect of Au thickness on the resonance spectral separation is modelled and characterized herein by fabricating ZnO-based solidly mounted resonators (SMRs).

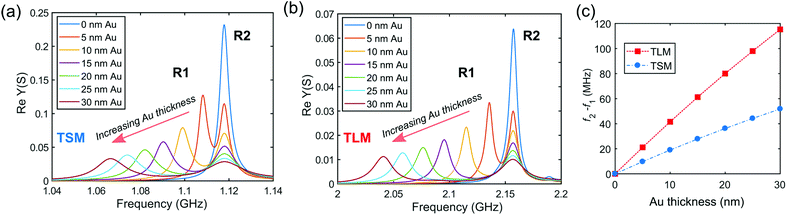
Finite element method (FEM) simulations illustrated in Fig. 2 demonstrate the resonator region that is activated at different frequencies. FEM simulations were carried out using COMSOL® Multiphysics 5.3 (solid mechanics and electrostatics modules) in 3D with the dimensions of the SMR fabricated. Due to the symmetry of the device, only half of the structure was simulated to reduce computation time. For each resonance region, 500 frequency points were simulated using a free triangular mesh with a 2 μm minimum element size to generate 106 074 degrees of freedom to solve. Material properties from the default COMSOL® Multiphysics library were used with a rotated (∼30° to the z-axis) piezoelectric crystal for the ZnO layer. A low reflecting boundary condition and mass damping model was used to simulate the effect of the ZnO surface roughness and increased Au thickness respectively.

Fig. 2 Displacement maps from FEM simulations in the x direction in (a) and (b) for the shear mode at ∼1.1 GHz and the z direction in (c) and (d) for the longitudinal mode at ∼2.1 GHz demonstrating the resonator region (R1 or R2) that vibrates at the different resonant frequencies.

From the FEM simulations in Fig. 3 the lower frequency (f₁) corresponds to the Au/Cr/Mo region (R1) whereas the higher frequency (f₂) corresponds to the Mo region (R2) only for both the thickness shear mode (TSM) and the thickness longitudinal mode (TLM). The separation of the split resonances, f₂ − f₁, depends on the Au thickness, and increases with a thicker Au layer. Without Au/Cr, the SMR exhibits a single resonance as shown in Fig. 3(a) and (b) and the admittance amplitude is higher than when a layer of Au/Cr is attached because of the reduced size of the uncoated region. The FEM simulations in Fig. 3(a)–(c) illustrate the frequency separation, which is approximately linear within the Au thickness range investigated. The separation of the two frequencies of the two regions increases by ∼50 MHz and ∼120 MHz for the shear and longitudinal modes respectively as the Au thickness increases from 0 to 30 nm.

Fig. 3 (a) Frequency spectra for the TSM with increasing Au thickness from FEM simulations showing the frequency shifts and damping with additional Au on R1; (b) corresponding spectra for the TLM with increasing Au thickness and; (c) frequency separation between the split resonances for both the TLM and TSM.

The fabrication process of the shear and longitudinal mode ZnO (with inclined c-axis ∼30°) based SMRs is described in our previous works (see ESI†).^17,21 After the SMR fabrication, the pentagonal region for the functional layer is defined by standard ultra-violet photolithography using AZ2020 nLoF photoresist. By means of thermal evaporation (E306A, Edwards, West Sussex, UK), 5 nm of Cr is deposited as an adhesion layer for the subsequent Au layer, the thickness of which is varied from 5 to 30 nm in 5 nm steps. Lift-off is carried out in n-methyl-2-pyrrolidone, acetone, iso-propanol and de-ionized water to leave a pentagonal shape region (area of 1.42 × 10⁻⁴ cm²) on the resonator with the added Au/Cr layer.

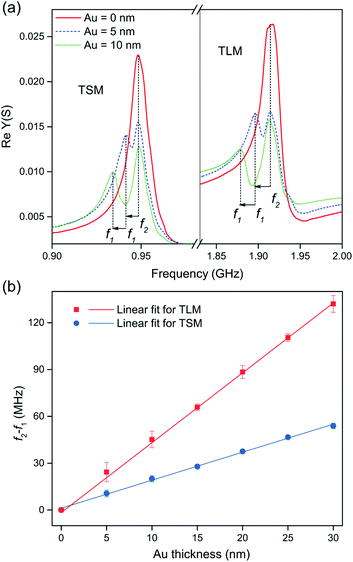
The fabricated SMRs are then characterized on a coplanar probe station by measuring the electrical admittance (Y) in the frequency range from 0.5 GHz to 3.0 GHz using 150 μm pitch ground-signal-ground radio-frequency (RF) probes (Picoprobes, GGB industries Inc., Naples, FL, USA), connected to a vector network analyzer (Model E5062A, Keysight Technologies, Santa Rosa, CA, USA). For each Au layer thickness, 25 devices were tested and average results are calculated. The measured electro-acoustic responses of the fabricated split mode resonators are shown in Fig. 4. Without any Au, the devices had quality factors, Q, of approximately 60 and electromechanical coupling coefficients of 4.3% and 2.9% for the TSM and TLM respectively.

Fig. 4 The increase in the difference between the resonances f₂ − f₁ observed in a representative SMR device due to gradual Au deposition on a pentagonal section of the Mo top electrode: (a) TSM and TLM showing a single mode for 0 nm of Au and split modes at different frequencies for 5 and 10 nm of Au. (b) Difference between the resonant frequencies f₂ − f₁ for the TSM and TLM depending on the Au thickness.

After the deposition of the Au/Cr layer on the pentagonal section of the Mo top electrode of the SMR device, a clear split of the TSM and TLM into two distinct frequencies is observed in Fig. 4(a). Similar to the FEM simulations in Fig. 3, the new resonance at f₁ that appears after Au deposition, shifts towards lower frequencies, whilst the original resonance at f₂ stays at the same frequency at all times. This is because the added Au/Cr layer acts as a mass load only on region R1 of the resonator. Additional experiments showing the increase in the difference between the two resonances f₂ − f₁ in TLM of the SMR device due to the mass attachment of thiol on Au are described in detail in the ESI (section 5).† The experimental measurement of f₂ − f₁ shown in Fig. 4(b) is slightly different to the simulation of f₂ − f₁ (Fig. 3(c)) probably due to uncertainty in the experimental thickness or the assumption of ideal material properties in the simulation. The thin films in the fabricated SMRs used physical vapor deposition techniques such as sputtering and evaporation; therefore, the properties of the materials are slightly different from the bulk material, which together with the surface morphology at each interface influence the nucleation of atoms and hence morphology of the next layer. These were not accounted for in the FEM simulations. With 5 nm Au, the electromechanical coupling of f₂ is reduced by ∼30% for both modes whereas the Q-factor showed variable changes (see ESI†). The electromechanical coupling coefficients for f₁ were ∼(0.8–1.5)% with Q-factors ranging from 15 to 70, which were not significantly different from the simulated Q-factors (see ESI†). The extracted gradients of the experimental data are 1.62 MHz nm⁻¹ and 4.53 MHz nm⁻¹ for the TSM and TLM respectively. Corresponding values from the FEM simulations were 1.61 MHz nm⁻¹ and 3.90 MHz nm⁻¹. From the Sauerbrey's equation for quartz crystal microbalance (QCM), the frequency gap can be approximated using (1):

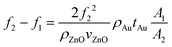where ρ_ZnO is the ZnO material density, v_ZnO is the corresponding acoustic velocity for ZnO (v_l for the TLM and v_s for the TSM), t_Au is the thickness of the Au layer, A₁ is the area of the Au layer of 1.42 × 10⁻⁴ m² and A₂ is the total device area of 2.74 × 10⁻⁴ m². Using literature values (ρ_ZnO = 5680 kg m⁻³, ρ_Au = 19 320 kg m⁻³, v_l = 6330 m s⁻¹, v_s = 2730 m s⁻¹),^22,23 and measured values (f₂ for TSM = 0.95 GHz and f₂ for TLM = 1.92 GHz) the calculated gradients are obtained as 1.16 MHz nm⁻¹ and 2.05 MHz nm⁻¹ for the TSM and TLM respectively. Using the values from the FEM simulation for f₂ (TSM = 1.12 GHz and TLM = 2.16 GHz), the estimated gradients are 1.62 MHz nm⁻¹ and 2.60 MHz nm⁻¹. The discrepancy between the calculated shift and the experimental shift for the longitudinal mode can be attributed to the fact that the Sauerbrey's equation underestimates the sensitivity of thin film BAW resonators because the electrode thicknesses are no longer negligible like in QCMs.²⁴ A more complex analysis is necessary to obtain the relation between the gap and the Au thickness, and incorporating the Cr adhesion layer.

It is worthwhile noting that the devices presented here are based on both TSM and TLM, rendering these devices suitable for sensing in both liquid and gas environments.²¹ The undeniable advantage of having mass sensitive and mass insensitive modes in a single device can potentially result in simpler, more controllable and more reliable tracking tool for selective mass sensing, whilst eliminating other surface effects (e.g. temperature, humidity, pressure). This can perhaps avoid undesirable false responses without the need for additional ‘control’ devices or complicated electronics. Another potential benefit of having the split resonances is the fact that significant deviations of the resonant frequencies across devices exist due to thickness variation and orientation of the piezoelectric layer in BAW resonators. In particular, this affect devices operation in the shear resonance that need off-axis piezoelectric layers, which cannot be grown uniformly over large substrates.²⁵ Having two frequencies – one that is mass sensitive and one that is mass insensitive – in this case provides each sensor with its own reference resonant frequency to extract the frequency shift, and eventually the amount of target molecules detected. To demonstrate the viability of the split resonances for FBAR sensors, the real-time sensing in liquid environments using microfluidics²⁶ and biological sensing experiments²⁷ should be considered for future works.

Conclusions

In this work, solidly mounted resonators with a functional high density Au layer to split the fundamental resonance modes are shown. Devices are modelled and fabricated exhibiting shear mode resonances at ∼1 GHz and longitudinal modes at ∼2 GHz. The addition of thin Au layers on part of the top electrode splits the resonances and offers the advantage of having a mode that is sensitive to binding on the Au layer and one that remains insensitive to mass binding. The frequency gap is dependent on the Au thickness and is ∼120 MHz for 30 nm Au. A significant achievement of this technique is the ability of each device to have its own reference frequency which enhances reliability and circumvents non-uniformity effects.

Conflicts of interest

AJF is Director of Sorex Sensors Ltd, which is commercialising FBAR sensors.

Acknowledgements

This work was supported by Cancer Research UK through a Cambridge Institute Early Detection Programme Pump-Priming 2016 award. Financial support from the Cambridge Commonwealth, European and International trust is also acknowledged. We are grateful for the help of Prof. Enrique Iborra (Universidad Politécnica de Madrid) in the fabrication of some of the reflectors used in this work under the IC1208 Cost action programme.

Notes and references

1. A. J. Flewitt, J. K. Luo, Y. Q. Fu, L. Garcia-Gancedo, X. Y. Du, J. R. Lu, X. B. Zhao, E. Iborra, M. Ramos and W. I. Milne, J. Nonnewton. Fluid Mech., 2015, 222, 209–216.
2. G. Sauerbrey, Z. Phys., 1959, 155, 206–222.
3. M. Nirschl, A. Blüher, C. Erler, B. Katzschner, I. Vikholm-Lundin, S. Auer, J. Vörös, W. Pompe, M. Schreiter and M. Mertig, Sens. Actuators, A, 2009, 156, 180–184.
4. L. García-Gancedo, J. Pedrós, E. Iborra, M. Clement, X. B. Zhao, J. Olivares, J. Capilla, J. K. Luo, J. R. Lu, W. I. Milne and A. J. Flewitt, Sens. Actuators, B, 2013, 183, 136–143.
5. W. H. Liu, D. Chen, Y. Xu, P. Wang and J. J. Wang, Electron. Lett., 2013, 49, 924–925.
6. D. Chen, J. Wang, Y. Xu and D. Li, Sens. Actuators, B, 2012, 171–172, 1081–1086.
7. H. Zhang, W. Pang, M. S. Marma, C.-Y. Lee, S. Kamal-Bahl, E. S. Kim and C. E. McKenna, Appl. Phys. Lett., 2010, 96, 123702.
8. T. Y. Lee and J. T. Song, Thin Solid Films, 2010, 518, 6630–6633.
9. D. Chen, J. J. Wang, D. H. Li and Z. X. Li, Electron. Lett., 2011, 47, 1169.
10. L. García-Gancedo, Z. Zhu, E. Iborra, M. Clement, J. Olivares, A. J. Flewitt, W. I. Milne, G. M. Ashley, J. K. Luo, X. B. Zhao and J. R. Lu, Sens. Actuators, B, 2011, 160, 1386–1393.
11. X. Zhao, F. Pan, G. M. Ashley, L. Garcia-Gancedo, J. Luo, A. J. Flewitt, W. I. Milne and J. R. Lu, Sens. Actuators, B, 2014, 190, 946–953.
12. Y. Lu, Y. Chang, N. Tang, H. Qu, J. Liu, W. Pang, H. Zhang, D. Zhang and X. Duan, ACS Appl. Mater. Interfaces, 2015, 7, 17893–17903.
13. D. Singh, A. A. Narasimulu, L. Garcia-Gancedo, Y. Q. Fu, T. Hasan, S. S. Lin, J. Geng, G. Shao and J. K. Luo, J. Mater. Chem. C, 2013, 1, 2525.
14. X. Le, X. Wang, J. Pang, Y. Liu, B. Fang, Z. Xu, C. Gao, Y. Xu and J. Xie, Sens. Actuators, B, 2017, 255, 2454–2461.
15. I. Katardjiev and V. Yantchev, Vacuum, 2012, 86, 520–531.
16. X. L. He, L. Garcia-Gancedo, P. C. Jin, J. Zhou, W. B. Wang, S. R. Dong, J. K. Luo, A. J. Flewitt and W. I. Milne, J. Micromech. Microeng., 2012, 22, 125005.
17. G. Rughoobur, M. DeMiguel-Ramos, J.-M. Escolano, E. Iborra and A. J. Flewitt, Sci. Rep., 2017, 7, 1367.
18. S. Razafimandimby, C. Tilhac, A. Cathelin, A. Kaiser and D. Belot, Analog Integr. Circuits Signal Process., 2006, 49, 237–247.
19. S. Rai, Y. Su, W. Pang, R. Ruby and B. Otis, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2010, 57, 552–561.
20. L. García-Gancedo, J. Pedrós, X. B. Zhao, G. M. Ashley, A. J. Flewitt, W. I. Milne, C. J. B. Ford, J. R. Lu and J. K. Luo, Biosens. Bioelectron., 2012, 38, 369–374.
21. G. Rughoobur, M. DeMiguel-Ramos, T. Mirea, M. Clement, J. Olivares, B. Díaz-Durán, J. Sangrador, I. Miele, W. I. Milne, E. Iborra and A. J. Flewitt, Appl. Phys. Lett., 2016, 108, 34103.
22. T. B. Bateman, J. Appl. Phys., 1962, 33, 3309–3312.
23. F. H. Villa-López, G. Rughoobur, S. Thomas, A. J. Flewitt, M. Cole and J. W. Gardner, Meas. Sci. Technol., 2016, 27, 25101.
24. G. Wingqvist, J. Bjurström, A. C. Hellgren and I. Katardjiev, Sens. Actuators, B, 2007, 127, 248–252.
25. G. Rughoobur, H. Sugime, M. DeMiguel-Ramos, T. Mirea, S. Zheng, J. Robertson, E. Iborra and A. J. Flewitt, Sens. Actuators, B, 2018, 261, 398–407.
26. M. Zhang, W. Cui, X. Chen, C. Wang, W. Pang, X. Duan, D. Zhang and H. Zhang, J. Micromech. Microeng., 2015, 25, 025002.
27. M. Zhang, J. Huang, W. Cui, W. Pang, H. Zhang, D. Zhang and X. Duan, Biosens. Bioelectron., 2015, 74, 8–15.

---

Footnote

† Electronic supplementary information (ESI) available: FEM simulation, device fabrication and electro-acoustic characterization. See DOI: 10.1039/c8nr04665d

---