Giant resistive switching in mixed phase BiFeO₃via phase population control

Abstract

Highly-strained coherent interfaces, between rhombohedral-like (R) and tetragonal-like (T) phases in BiFeO₃ thin films, often show enhanced electrical conductivity in comparison to non-interfacial regions. In principle, changing the population and distribution of these interfaces should therefore allow different resistance states to be created. However, doing this controllably has been challenging to date. Here, we show that local thin film phase microstructures (and hence R–T interface densities) can be changed in a thermodynamically predictable way (predictions made using atomistic simulations) by applying different combinations of mechanical stress and electric field. We use both pressure and electric field to reversibly generate metastable changes in microstructure that result in very large changes of resistance of up to 10⁸%, comparable to those seen in Tunnelling Electro-Resistance (TER) devices.

---

The renaissance of interest in multiferroic research, evident over the last decade or so, has been almost exclusively centred around the perovskite oxide bismuth ferrite (BiFeO₃ or BFO). Initially, the room temperature magnetoelectric multiferroic properties seen in thin films were the dominant focus;¹ subsequently, however, it became apparent that BFO had many additional striking properties, such as an extremely high spontaneous polarisation (of order 100 μC cm⁻²),² above band-gap photovoltaic behaviour³ and domain walls that, at least in some cases, behave as pseudo-2D sheet conductors.⁴ More recently, researchers have been interested in the drastic effect that epitaxial constraint can have on the symmetry and crystal structure seen in BFO thin films.⁵ Almost uniquely, under some epitaxial conditions and at specific film thicknesses, BFO films grow as mixtures of two rather different monoclinic symmetry states: one approximately tetragonal (T) and the other approximately rhombohedral (R). Interfaces between R and T regions are highly elastically strained, as the shapes, dimensions and orientations of the unit cells associated with the two phases are very different. Moreover, on transitioning from R to T, the orientation of polarisation with respect to the thin film surface changes distinctly. Strong strain and polarisation differences, combined with the fact that the films are in a mixed R–T phase space, should result in profound property malleability or plasticity. Changes in the surrounding thermodynamic environment are therefore expected to alter the relative proportion of R and T states resulting in large effects on both film surface topography and out-of-plane polarisation. Indeed, the presence of what appears to be a strain-driven morphotropic-phase boundary in BFO is directly responsible for numerous novel functional properties such as enhanced spontaneous magnetization⁶ (confined to the R phase) and piezoelectricity,^7–9 a shape-memory effect, and electrical conduction along mixed-phase interfaces.^10–12

A key requirement for exploiting the functional properties of mixed phase systems in BFO is precise deterministic control of the relative population and distribution of the R–T phases and the boundaries that separate them. In this work, we experimentally demonstrate how localized stress and electric fields can be used to inject and erase conductive boundaries in an epitaxially strained thin film of BFO through alteration of the mixed-phase population in a reversible and complementary manner. The observed phase competition and its control using applied external fields are both found to be consistent with energy-based effective Hamiltonian simulations. Indeed, our modelling predicts phase ratios for the entire range of experimental parameters including epitaxial strain, uniaxial stress and electrical fields. A direct comparison between theoretical predictions and experimental results illustrates the potential of the developed understanding in allowing complete deterministic control of the mixed phase microstructure and, by extension, the overall functional response of the BFO. By controlling mixed phase populations using electrical bias and nanoscale stress, we have demonstrated a resistive switch device which exhibits a maximum “ON–OFF” resistance ratio of up to six orders of magnitude (10⁸%). This is comparable to the remarkable resistance changes seen in Tunneling Electroresistance (TER) devices,^13,14 but at much greater ferroic film thicknesses.

Stress-induced injection of conductive boundaries in strained BiFeO₃

We have examined stress-induced injection of conductive R–T boundaries in a 50 nm thick epitaxially strained BiFeO₃ film grown on a single crystal LaAlO₃ (LAO) substrate with a 5 nm buffer layer of (La,Sr)CoO₃ (LSCO) to act as the bottom electrode. A region of the film with native mixed phase microstructure was switched to the T-state, through application of −4 V. Subsequently, stress was applied to a part of this area, through the AFM probe, resulting in the creation of R-phase needles as seen in topographic images in Fig. 1a–c. Conducting atomic force microscopy (c-AFM) measurements were performed on the native state as well as after both electrical switching and local pressure application using a DC voltage below the ferroelectric coercive field. Comparison of the conductive response (Fig. 1d–f) following the application of each respective stimulus shows evidence of negligible current registered within the native state or the electrical field-written T-phase dominated microstructure. Substantially increased current is observed, however, in the regions of newly formed R-phase needle structures nucleated through localised stress application. Systematic stress-induced writing of four conductive regions in a previously bias-written state (Fig. 1g and h) illustrates the reliability of the approach towards writing conductive areas in the film. Higher resolution c-AFM mapping reveals that the highest currents are observed at the R/T boundaries in agreement with earlier reports in similar systems.^10,11 The stress-induced conduction observed at the R/T boundaries is found to be stable over time and does not decay over a period of several days. Focused-ion-beam cut cross-sections, taken from both as-grown and stress-written regions (see ESI†), were analysed using scanning transmission electron microscopy (STEM) and nanobeam electron diffraction (NBED) to investigate the in-plane crystallographic deformation of the BFO film across the interfaces between the R- and T-phases. The data confirms the epitaxial nature of the BFO film where the as-grown T-phase shows an in-plane lattice parameter of 0.371 nm in comparison to the in-plane pseudo-cubic lattice constant of 0.379 nm for the substrate LAO, values which are consistent with existing literature.^5,15 The interfaces in the stress-induced regions are found to be significantly more abrupt with rapid changes in the in-plane crystallography between the two phases and a notable enhancement in the associated strain gradients. It has previously been rationalized that the bandgap in BFO is controlled by the degree of O 2p and Fe 3d orbital overlap and hence by the Fe–O–Fe bond angle.^11,16 Therefore, rapid changes in the unit cell dimensions – as observed from the increased strain changes at the R/T interfaces here – are likely to lead to increased orbital overlap by a straightening of the aforementioned bond angle and thus a reduction of the bandgap. Another possible origin of the enhanced conductivity at interfaces is migration of O vacancies to the newly created strained interfaces, introducing defect energy levels into the bandgap.¹⁷ Since the conduction is confined to the stress-written R/T boundaries, their injection and removal using different stimuli in a precise manner provides a novel reversible approach to controlling the resistive state of the film. Such control using electric field and nanoscale stress is demonstrated below.

Fig. 1 Stress injection of conductive boundaries in mixed phase strained BiFeO₃ thin films. (a) AFM topography images collected from a single area showing the mixed phase as grown film, an electrically-written T-phase region (b) and a subsequently stress-written mixed phase region (c), respectively. In the top and bottom panels, R-phase needles can be seen as the dark striations. Corresponding c-AFM measurements of the initial mixed-phase state (d), electrically-written T-phase (e) and stress-written mixed phase regions (f), respectively show that the initial and the purely T-phase written region is non-conducting whereas significantly increased currents on the order of tens of pA are observed in the regions populated by the stress-written R-phase needles. (g, h) Systematic stress-induced writing of four conductive regions in a previously bias-written state illustrates the reliability of the approach towards writing of conductive states in the film.

Dual control of R/T phases via selective application of stress or electric fields

The strained BFO film can be reversibly driven between T-phase and R-phase rich microstructures through the application of either electric field or stress,¹⁸ respectively. To illustrate the change in phase behaviour, Fig. 2 shows the topography in a 2 × 2 μm region under the application of local bias and stress. It should be noted that the initial microstructure is comprised of both the R phase and T phase, where topography mapping reveals banded needle-like R phase structures within a T phase matrix. Application of −3 V dc bias through a conducting AFM probe triggers reorganization of the ferroelectric domain structure into a locally T phase-dominated region. Subsequent application of a force of 750 nN (corresponding to an estimated 1.8 GPa of stress) to the same area, causes the affected region to again become populated with needle-like structures associated with the R phase. It was shown in Fig. 1 that the interfaces of such stress-induced phases are conducting and that, in effect, the stress results in the injection of conducting boundaries in the scanned region. Crucially, the observed transformation behavior is seen to be reversible and the chosen region can be switched between T- and R-dominated microstructures by the application of electric field or pressure application, as required. The repeatability of changes in microstructure is highlighted in the ESI† along with Piezoresponse Force Microscopy (PFM) imaging to confirm the ferroelectric nature of the electrically/mechanically-written regions. These results illustrate the viability of changing the mixed phase microstructure as a means to systematically tune the local functional response (electrical conduction in particular). However, to establish full deterministic control of the resulting phase populations, greater fundamental insight was needed.

Fig. 2 Reversible dual control of R/T phases in epitaxially strained BFO via selective application of stress or electric fields. (a) Topography and accompanying schematic cross-section of the initial state of the film, where regions of R phase are observable as banded needle-like structures (dark) within a flat T phase matrix (bright), (b) after application of −3 V dc through the tip to the region marked by the dashed white lines and (c) after subsequent tip-application of a 750 nN loading force to the same region. The bias application drives the films into a T-dominated state while stress increases the R-phase population in the subjected region. The competition between the phases can be reversibly controlled by the selective application of the two stimuli.

Effective Hamiltonian calculations evaluating the phase competition under applied stimuli as a function of misfit strain

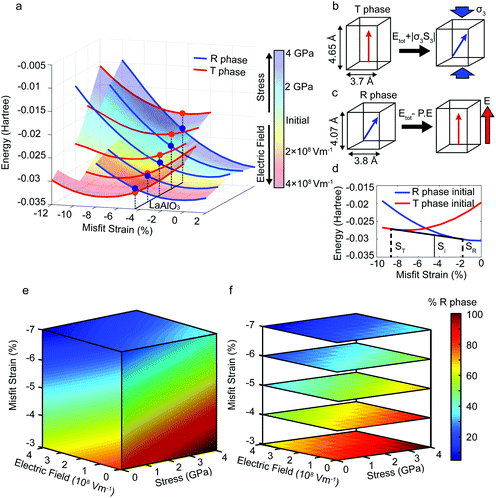
Theoretical calculations were expected to provide insight into the interplay of phase co-existence in mixed phase systems with applied stimuli. In this context, density functional calculations and phase field simulations have previously been used to suggest that a critical misfit strain separates the stability of T and R phases in epitaxially strained BiFeO₃ thin films.^19–21 These calculations have been used to evaluate the dependence of heterophase polydomains²² as well as the competition between the phases with increasing misfit strains.²³ While such calculations can predict the equilibrium mixed phase states that develop as a function of misfit strain, the extent to which application of external fields can further alter the phase distribution has not been analysed. We have hence used a first-principles-based effective Hamiltonian technique, developed by Prosandeev et al.,²⁴ to consider the energy of separate cells of the T phase and R phase under different thermodynamic conditions of applied electric field, applied uniaxial stress and biaxial epitaxial constraint. To begin with, the simulations calculate the energy of each phase as a function of epitaxial misfit strain, as shown in Fig. 3a, demonstrating a competition between the two phases in a BFO film. At the highest misfit strains, the calculations confirm that the highly-strained T phase has lower energy (as expected) and is thus stabilized, while at intermediate strains the energy of the two phases becomes comparable, leading to a coexistence of the two phases. The energy curves were then calculated under varying combinations of applied stress and electric field to estimate the phase competition under the different external stimuli. For the studied film grown on (001) LaAlO₃, the energy of the T and R phases are comparable, with the R phase slightly lower, when no external fields are applied. Under applied fields, the calculations suggest that the T phase should be stabilised by electrical bias application while the R phase should be stabilised by mechanical stress, as depicted in the cartoon in Fig. 3b and c. This is in good agreement with the experimental observations shown in Fig. 2. In the calculations, application of an electric field, E, results in reduction of total energy (E_tot) by a term of the form P·E, where P is the polarisation. On the other hand, application of uniaxial stress (σ₃) along the [001] pseudo-cubic direction on the film results in an increase of the total energy by a term of the form |σ₃S₃|, where S₃ corresponds to the strain component along the [001] direction of the simulated cell. As the T phase possesses higher spontaneous polarization, the increase in P as a result of the switch from the R phase to the T phase results in a net reduction in total energy and therefore stabilizes T phase under applied electric field. In an analogous manner, application of uniaxial stress makes the R phase the energetically favoured state due to its smaller axial ratio in comparison to the T phase.

Fig. 3 Effective Hamiltonian calculations evaluating the phase competition in strained BFO under applied stimuli at any chosen misfit strain. (a) Energy curves as a function of misfit strain under varying electric field and uniaxial stress applied along the [001] axis. The dark line corresponds to a constant misfit strain of −4.4%, equivalent to that of BFO on LAO, with the red and blue dots highlighting the energy of the T- and R phases, respectively, at that strain. The overlaid color bar corresponds to the stresses or electric fields under which the energy curves were calculated. Schematic illustration of the transformations from (b) T- to R-phase under stress and (c) R- to T-phase under electric field along with the accompanying unit cell lattice parameters. (d) Schematic of a common tangent which can be drawn between the R-and T-phase energy curves, along which it is energetically favorable for the two phases to co-exist. (e) Graphical representation showing the continuous variation in the proportion of R-phase with misfit strain, electric field and uniaxial stress. (f) Discrete slices at any selected values of constant misfit strain can predict the R–T phase competition as a function of applied stimuli.

An appealing feature of the calculated energy curves under applied stimuli is that they enable prediction of the relative mixed phase populations using the common tangent method which is regularly employed in the analysis of mixed phase regions in conventional phase diagrams.²³ The “lever rule” can then be applied to estimate the relative fractions of each phase; usually this is done at a fixed global composition,^25,26 but here it is done at a fixed value in misfit strain: the relative proportion of R and T phases are calculated by drawing a common tangent for each pair of energy curves (Fig. 3d) and then applying the lever rule, in the form

S_i = x_TS_t + x_RS_r, (1)

where S_i is a strain value chosen between limiting values of S_t and S_r (the strains where the tangent intersects the energy curves) and x_T and x_R are the fractional phase populations. The calculations are then expanded to a broader range of applied stresses, electric fields and misfit strains, where each set of energy curves allows prediction of the mixed phase population under the chosen set of thermodynamic variables. Fig. 3e depicts these results in the form of a 3-dimensional diagram with the three axes defined by misfit strain, uniaxial stress and electric field, respectively (for details, see ESI†). It should be noted that the stress and electric field are external variables that can be manipulated freely while the misfit strain is dictated by the choice of substrate. Every point in this diagram represents the relative ratio of the two phases for the selected set of thermodynamic variables. The limiting cases are seen at the two extremes of the diagram, which predict mostly R phase at low values of misfit strain, high applied uniaxial stress and zero applied field, while mostly T phase is expected to dominate at large misfit strains, large applied electric fields and zero applied uniaxial stress.

Discrete 2D sections of the diagram taken perpendicular to the vertical axis, shown in Fig. 3f, map the relative phase populations for constant values of misfit strain and represent the behaviour predicted for the mixed phase microstructures when grown on different substrates. For the specific case of the studied 50 nm thick BFO film grown on LAO, a mixed phase microstructure with 52% R and 48% T phases is expected in the absence of other applied fields. However, the proportion of R phase can be reduced to a predicted 33%, through application of an electric field of 4 × 10⁸ V m⁻¹, or conversely increased to 70% under 4 GPa of uniaxial stress. The diagram thus clearly illustrates the pliable nature of the BFO microstructure under equilibrium: application of uniaxial stress is seen to cause a monotonic increase in the proportion of R phase, while conversely, increasing electric field causes a monotonic increase in the proportion of T phase. Any functionality (e.g. conduction) associated with the generated mixed phase microstructure can thus also be directly controlled via external fields.

Direct comparison of experimental dual-control mixed-phase microstructure with corresponding theoretical predictions

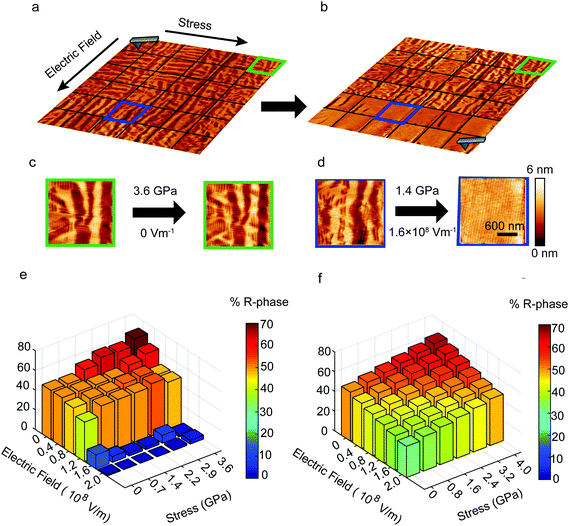
The theoretical predictions for the effects of applied field variables on the mixed phase populations for a given misfit strain were tested on the BiFeO₃/LSCO/LAO heterostructures discussed above. For each set of values of uniaxial stress and electric field, the ratio of the R/T phase in the resulting microstructure has been experimentally determined and compared with the predicted values (Fig. 4). A large representative area of the film (18 × 18 μm²) was chosen and subdivided into a grid (3 × 3 μm²) such that the initial phase proportion within each square sub-region was similar. Starting from one end, the electric field and uniaxial stress were increased in discrete steps from one sub-region to the next and the resulting topography of each square sub-region was recorded. The topography for each sub-region was numerically analyzed and the resulting R phase content was estimated. The results were plotted on a 3 dimensional grid plot (Fig. 4e) where the stress is stepwise varied between 0 and 3.6 GPa and the electric field is increased simultaneously in steps between 0 to 2 × 10⁸ V m⁻¹. This plot is then compared to the theoretical estimates calculated from effective Hamiltonian calculations for a similar range of variables (Fig. 4f). Under initial examination, higher levels of experimentally applied stress coupled with minimal electric fields are seen to induce a number of new R phase needles to appear as well as enlargement of pre-existing needles, as particularly evident in the enlarged topographic region shown in Fig. 4c. For intermediate values of stress and electric fields, monotonic competition between the two phases is experimentally observed and is consistent with the theoretical predictions. Under further increased electric field, the effect of applied stress appears to diminish until the resulting topography becomes mostly T phase dominated (Fig. 4d). A good overall match in trends of behaviour between the experiments and energy based analysis is observed in the two grid-plots, compared directly in Fig. 4e–f; as can be seen, the theoretical calculations have been especially effective in evaluating the monotonic increase in the proportion of R phase in the intermediate regions of bias and stress. The correlation between theory and experiment, under combined application of stress and electric field is promising for the general validity of this approach in evaluating deterministic dual control in such mixed-phase microstructures. It is worth mentioning that the calculations consider equilibrium when the uniaxial stress and electric fields are applied, but the experiments measure resultant microstructures after the fields have been applied and removed. The correlation between prediction and observation hence strongly suggests that the microstructure developed under the applied fields is largely maintained (in a metastable configuration) once the fields have been removed.

Fig. 4 Direct comparison of experimental writing of mixed-phase R/T microstructure employing ‘dual control’ with the corresponding theoretical predictions. Topography of 50 nm thick BFO thin film grown on LAO (a) before and (b) after carrying out the dual control experiment where varying levels of stress and bias are applied simultaneously. Highlighted panels are enlarged in (c) and (d). Numerical estimations of the R- and T-phase populations under applied fields are also shown in (e) resulting in an experimental map with estimated stress and electric field as the two axes, which can then be compared with (f) corresponding theoretical predictions. For intermediate values of stress and electric fields, monotonic competition between the two phases is experimentally observed consistent with the theoretical predictions.

Some deviations are observed in the limiting cases of highest stress and large electric fields (Fig. 4e–f). These deviations could arise from several factors ranging from an underestimate of the applied stress, surface area based analysis of phase populations (instead of volume-based estimates⁵), limiting kinetics in microstructural development (such that equilibrium is not achieved) and the fact that experiments observe microstructures after the removal of the applied fields. Nevertheless, the overall agreement in the trends in microstructural development found in experiment and predicted through theoretical calculations demonstrates the obvious potential for deterministic control of structural reorganisation of mixed phase microstructures by changing the applied fields.

Demonstration of a proof-of-concept resistive switch based on reversible control of conductive boundaries

The conductive interfaces between the injected mixed phase boundaries can be reversibly switched on and off by manipulation of the associated microstructure: the introduction of significant amounts of R-phase is associated with high R–T boundary densities and hence high electrical conduction, while T-phase dominated microstructures lack R–T boundaries. While small currents of the order of few pA are typically observed at individual R–T boundaries, a microscopic probe should create a large number of such interfaces acting in parallel, resulting in large currents upon the application of stress. Conversely, the removal of the R-phase through application of bias is expected to remove these large currents thereby giving rise to large on–off ratios between the two states. A proof-of-concept microscopic resistive switching device based on reversible control of the conductive boundaries in mixed phase BiFeO₃ was therefore investigated, using the geometry illustrated in Fig. 5a. Pt top electrodes approximately 100 nm thick and 25 μm in diameter were deposited on the BiFeO₃ film. Using the LSCO bottom electrode, I–V characteristics of the capacitor were measured between the electrodes in a two-probe setup using a conductive tungsten microprobe with a diameter comparable to the Pt electrode.

Fig. 5 Demonstration of a proof-of-concept resistive switch based on reversible control of R–T conductive boundaries with large on–off conductance ratio. (a) Schematic illustration of the Pt-BiFeO₃-LSCO-LaAlO₃ setup used to measure I–V characteristics between top (Pt) and bottom (LSCO) electrodes after application of bias and stress to the film. (b) The as grown sample prior to stress application shows pA levels of current whereas in (c), after application of stress, there is an increase in the current by six orders of magnitude which can be reset through the subsequent application of bias. Therefore the observed current within epitaxially strained BiFeO₃ can be controlled repeatedly through a combination of bias and stress application via nucleation and erasing of the R- and T-phases and associated boundaries to achieve up to 10⁸% increase in conductance of the studied film. The inset in (c) shows the same current–voltage response on the logarithmic scale after application of stress and bias respectively.

The top–bottom electrode geometry provides an out-of-plane analogue to the in-plane conductive domain wall-based memristor⁴ where the number of conductive channels defines the resistive state of the capacitor. Stress was applied to the film through the top electrode via the microprobe (estimated to be around 1 GPa for ∼1 s) to drive the microstructure into an R-rich state and the bias was applied to the bottom electrode for a few seconds to switch the microstructure to a T-rich state. Following each stress and biasing cycle, the I–V response of the film was recorded between 0 and 2 V, with the maximum value of probe voltage being chosen to avoid any switching of states. Before the application of stress and bias cycles, the as-grown film shows low leakage current of the order of <1–2 pA which is removed through application of switching voltage as shown in Fig. 5b. Upon the application of stress (Fig. 5c), a remarkable increase in the current up to several μA is observed. This represents a six orders of magnitude increase (10⁸% over the insulating T-phase rich state) and a giant resistive switching response. The large current is then turned off through application of a switching voltage for a few seconds which drives the film into a T-rich state. In this state, the film shows no observable current. The stress and bias cycles were repeated several times to demonstrate that the resistive state of the film switches repeatedly and the large current response returns upon the application of microscopic stress. The presence and retention of this large resistive switching response within the material is thus reversible and non-volatile (see ESI† for retention and cyclability of the stress induced conducting state and bias induced resistive state), with switching between the two states obtained through a repeated cycle of electric field and stress application. Further precise control of the microscopic applied stress facilitated by full automation (future work) is envisioned to achieve a wide range of conductive states. Our simple proof-of-concept device demonstrates a promising opportunity for microscopic control of the mixed phase microstructure via applied external stimuli and thus facilitates control of the resistive state of the film. This could be further exploited towards more complex resistance-change based devices and/or sensors.

In summary, we have demonstrated deterministic and reversible control of mixed ferroelectric phases and subsequent tuning of the conductive properties of the interfaces between these structures by selective application of stress and electrical fields. Theoretical free-energy based calculations provide excellent insight into the experimentally observed behavior and also yield a quantitative framework to predict modifications of mixed phase populations where electric field, stress and misfit strain can be used as independent handles to control the final microstructure. Reasonable correlation between experiments and theoretical predictions shows the clear potential for fully deterministic control of the mixed phase microstructure. By employing electrical bias and nanoscale stress, reversible control has been achieved creating a microscopic resistive switching device exhibiting a maximum current modulation ratio (I_on/I_off) of 10⁸%. Beyond mixed phase ferroelectrics, we envisage that such combinatorial manipulations of mixed phase systems via external fields could have broader implications for tuning their functional behaviour in general.

Experimental methods

Thin film processing

Epitaxial BFO thin films of thickness ∼50 nm were grown using the pulsed laser deposition technique on (001)-oriented LAO substrates with bottom LSCO electrodes of 5 nm thicknesses. Details of the sample preparation technique have been reported elsewhere.²⁷

Mechanical and electrical writing

The mechanical and electrical writing as well as imaging of the resulting topography and domain structure was carried out using a Veeco Dimension 3100 AFM system with a Nanoscope IIIa controller. The mechanical writing was performed by increasing the deflection set-point (i.e. the cantilever deflection voltage maintained by the atomic force microscope feedback loop proportional to the applied force or stress) to a Pt-coated Si tip (Nanosensors PPP-EFM) while scanning. From a combination of force–distance measurements and subsequent tuning methods, the spring constant was found to be 2.8 N m⁻¹. Each 1 V of deflection setpoint from the tip corresponds to a loading force of about 150 nN.

Conducting atomic force microscopy measurements

Conductivity measurements were undertaken with a c-AFM application module (TUNA, Veeco Instruments), with current-amplification settings set to 10 pA V⁻¹. All data was acquired by applying 2.4 V DC sample bias under ambient conditions at room-temperature, with all c-AFM measurements made immediately after electrical and mechanical switching.

Current–voltage (I–V) measurements

Microscopic I–V measurements were undertaken through use of the c-AFM application module (TUNA, Veeco Instruments), applying a 0–2 V ramp. Macroscopic resistive switching I–V measurements were obtained through a conventional two-probe set up in contact with 100 nm thick Pt surface electrodes and utilising a Keithley voltage source applying a 0–2 V ramp.

Electron microscopy

Cross sections were prepared by standard protocols using an FEI Helios Nanolab 460f1. STEM was performed on a C_S corrected FEI Titan operated at 300 kV. NBED was performed with a convergence semiangle α = 0.5 mrad. Strain was quantified from NBED patterns using a dedicated script developed by CEA, Grenoble.

Author contributions

D.E., N.B, J.M.G., R.G.P.M. and A.K. conceived of and designed the experiments. D.M. and A.G. grew the studied films. K.M.H, A.B.N., M.A. and M.D. undertook the structural studies of the film. S.O.S, D.W, B.X. and L.B. undertook the theoretical calculations presented in the study. S.V.K. supervised the part of research undertaken at ORNL. A.K. supervised the research and helped in data analysis and interpretation. D.E., N.B., L.B., J.M.G and A.K. primarily wrote the manuscript with input from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AK gratefully acknowledges funding from the Engineering and Physical Sciences Council through grant # EP/N018389/1. A. B. N. and A. K. gratefully acknowledge support by Department of Education and Learning, Northern Ireland through the US-Ireland R&D partnership grant no. USI-082. A portion of this research was conducted at the Center for Nanophase Materials Sciences, which is sponsored at Oak Ridge National Laboratory by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy under user proposal CNMS2013-298. MA and KH are grateful to Dr N. Bernier (CEA, Grenoble) for providing a dedicated script for processing the NBED patterns and useful discussions on the strain gradient quantification. S. O. S. and L. B. thank the DARPA grant HR0011-15-2-0038 under the MATRIX program. B. X. acknowledges funding from Air Force Office of Scientific Research under Grant No. FA9550-16-1-0065. S. P. thanks ONR Grant No. N00014-17-1-2818. D. W. thanks the Natural Science Foundation of China under Grant No. 11574246. The authors acknowledge financial support from the European Union under the Seventh Framework Programme under a contract for an Integrated Infrastructure Initiative (ESTEEM2) for instrument time. The work was also supported by a Department of Employment and Learning Northern Ireland (DELNI) studentship.

References

1. J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, Science, 2003, 299, 1719–1722.
2. J. F. Li, J. L. Wang, M. Wuttig, R. Ramesh, N. Wang, B. Ruette, A. P. Pyatakov, A. K. Zvezdin and D. Viehland, Appl. Phys. Lett., 2004, 84, 5261–5263.
3. S. Y. Yang, J. Seidel, S. J. Byrnes, P. Shafer, C. H. Yang, M. D. Rossell, P. Yu, Y. H. Chu, J. F. Scott, J. W. Ager, L. W. Martin and R. Ramesh, Nat. Nanotechnol., 2010, 5, 143–147.
4. J. Seidel, L. W. Martin, Q. He, Q. Zhan, Y. H. Chu, A. Rother, M. E. Hawkridge, P. Maksymovych, P. Yu, M. Gajek, N. Balke, S. V. Kalinin, S. Gemming, F. Wang, G. Catalan, J. F. Scott, N. A. Spaldin, J. Orenstein and R. Ramesh, Nat. Mater., 2009, 8, 229–234.
5. R. J. Zeches, M. D. Rossell, J. X. Zhang, A. J. Hatt, Q. He, C. H. Yang, A. Kumar, C. H. Wang, A. Melville, C. Adamo, G. Sheng, Y. H. Chu, J. F. Ihlefeld, R. Erni, C. Ederer, V. Gopalan, L. Q. Chen, D. G. Schlom, N. A. Spaldin, L. W. Martin and R. Ramesh, Science, 2009, 326, 977–980.
6. Q. He, Y. H. Chu, J. T. Heron, S. Y. Yang, W. I. Liang, C. Y. Kuo, H. J. Lin, P. Yu, C. W. Liang, R. J. Zeches, W. C. Kuo, J. Y. Juang, C. T. Chen, E. Arenholz, A. Scholl and R. Ramesh, Nat. Commun., 2011, 2, 225.
7. A. R. Damodaran, C. W. Liang, Q. He, C. Y. Peng, L. Chang, Y. H. Chu and L. W. Martin, Adv. Mater., 2011, 23, 3170–3175.
8. J. X. Zhang, B. Xiang, Q. He, J. Seidel, R. J. Zeches, P. Yu, S. Y. Yang, C. H. Wang, Y. H. Chu, L. W. Martin, A. M. Minor and R. Ramesh, Nat. Nanotechnol., 2011, 6, 97–101.
9. R. K. Vasudevan, M. B. Okatan, Y. Y. Liu, S. Jesse, J. C. Yang, W. I. Liang, Y. H. Chu, J. Y. Li, S. V. Kalinin and V. Nagarajan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 020402.
10. K. E. Kim, B. K. Jang, Y. Heo, J. H. Lee, M. Jeong, J. Y. Lee, J. Seidel and C. H. Yang, NPG Asia Mater., 2014, 6, e81.
11. J. Seidel, M. Trassin, Y. Zhang, P. Maksymovych, T. Uhlig, P. Milde, D. Kohler, A. P. Baddorf, S. V. Kalinin, L. M. Eng, X. Q. Pan and R. Ramesh, Adv. Mater., 2014, 26, 4376–4380.
12. Y. Heo, B. K. Jang, S. J. Kim, C. H. Yang and J. Seidel, Adv. Mater., 2014, 26, 7568–7572.
13. H. Yamada, V. Garcia, S. Fusil, S. Boyn, M. Marinova, A. Gloter, S. Xavier, J. Grollier, E. Jacquet, C. Carretero, C. Deranlot, M. Bibes and A. Barthelemy, ACS Nano, 2013, 7, 5385–5390.
14. Z. Wen, C. Li, D. Wu, A. D. Li and N. B. Ming, Nat. Mater., 2013, 12, 617–621.
15. D. Mazumdar, V. Shelke, M. Iliev, S. Jesse, A. Kumar, S. V. Kalinin, A. P. Baddorf and A. Gupta, Nano Lett., 2010, 10, 2555–2561.
16. G. Catalan and J. F. Scott, Adv. Mater., 2009, 21, 2463–2485.
17. M. Brazier, S. Mansour and M. McElfresh, Appl. Phys. Lett., 1999, 74, 4032–4033.
18. Y. J. Li, J. J. Wang, J. C. Ye, X. X. Ke, G. Y. Gou, Y. Wei, F. Xue, J. Wang, C. S. Wang, R. C. Peng, X. L. Deng, Y. Yang, X. B. Ren, L. Q. Chen, C. W. Nan and J. X. Zhang, Adv. Funct. Mater., 2015, 25, 3405–3413.
19. A. J. Hatt, N. A. Spaldin and C. Ederer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054109.
20. B. Dupe, I. C. Infante, G. Geneste, P. E. Janolin, M. Bibes, A. Barthelemy, S. Lisenkov, L. Bellaiche, S. Ravy and B. Dkhil, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 144128.
21. J. C. Wojdel and J. Iniguez, Phys. Rev. Lett., 2010, 105, 037208.
22. W. Zhang, J. Ouyang and A. L. Roytburd, Scr. Mater., 2012, 66, 499–502.
23. Z. H. Chen, S. Prosandeev, Z. L. Luo, W. Ren, Y. J. Qi, C. W. Huang, L. You, C. Gao, I. A. Kornev, T. Wu, J. L. Wang, P. Yang, T. Sritharan, L. Bellaiche and L. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 094116.
24. S. Prosandeev, D. W. Wang, W. Ren, J. Iniguez and L. Bellaiche, Adv. Funct. Mater., 2013, 23, 234–240.
25. W. W. Cao and L. E. Cross, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4825–4830.
26. P. Arigur and L. Benguigui, J. Phys. D: Appl. Phys., 1975, 8, 1856–1862.
27. V. Shelke, V. N. Harshan, S. Kotru and A. Gupta, J. Appl. Phys., 2009, 106, 104114.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr03653e

‡ These authors contributed equally to the work.

---