Regioselectivity of the Pauson–Khand reaction in single-walled carbon nanotubes

Abstract

Chemical functionalization of nanotubes, in which their properties can be combined with those of other classes of materials, is fundamental to improve the physicochemical properties of nanotubes for potential technological applications. In this work, we theoretically and experimentally examine the Pauson–Khand reaction (PKR) on zig-zag, armchair, and chiral single-walled carbon nanotubes (SWCNTs). Our benchmarked density functional theory (DFT) calculations show that an alternative pathway to the widely accepted Magnus reaction pathway has significantly lower energy barriers, thus suggesting the use of this alternative pathway to predict whether a PKR on SWCNTs is favored or hampered. Accessible energy barriers of up to 16 kcal mol⁻¹ are estimated and our results suggest that semiconducting SWCNTs react faster than metallic ones, although both types can be functionalized. Guided by our theoretical predictions, cyclopentenones are successfully attached to SWCNTs by heating and are, subsequently, characterized in the laboratory.

---

Introduction

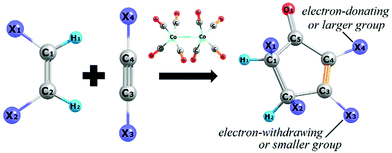
First reported in the early 1970s by Pauson and Khand et al., the [2 + 2 + 1] cycloaddition between an alkene, an alkyne, and a carbon monoxide unit (CO) leads to the formation of cyclopentenones mediated or catalyzed by a transition metal; originally a complex of cobalt(0) (see Scheme 1).^1–3 This chemical transformation, usually termed as the Pauson–Khand reaction (PKR), has gained attention within the field of organic chemistry since many natural products can be synthesized from it.^4–18 Besides cobalt, also other transition metals perform well in the PKR such as rhodium,^19–21 ruthenium,^22,23 palladium,²⁴ iridium,^25,26 iron,^27,28 tungsten,²⁹ molybdenum,^30,31 and chromium.^32,33

Scheme 1 The Pauson–Khand reaction and its regiochemistry.

The PKR depends upon steric and electronic factors. From Scheme 1, one would expect up to sixteen different isomers; two regioisomers due to the groups X₁ and X₂ in the alkene, two regioisomers because of the groups X₃ and X₄ in the alkyne, and four enantiomers originating from each one of the four mentioned regioisomers. However, the alkene stereochemistry remains intact according to the reaction mechanism and only two stereoisomers are possible. That is, in the case of cis-alkenes the groups in stereocenters X₁ and X₂ always end up on the same side of the ring. In this regard, the theoretical products of a PKR may be predicted based on steric arguments, but selectivity also depends on electronic factors. That is, the carbon atom of the alkyne substituted by an electron-donating or a larger group usually ends up at the α-position in the resulting cyclopentenone, leaving the β-position to the alkyne carbon atom substituted by an electron-withdrawing or a smaller group as depicted in Scheme 1. These observations were confirmed by analyzing a series of alkynes with substituents electronically and/or sterically differentiated.^34,35 In fact, based on a study regarding diarylalkynes, it can be demonstrated that the alkyne polarization via inductive effect has a significant impact on the regioselectivity of the PKR.^36,37

The scope of the PKR and variations thereof encompasses several functional groups.³⁸ Two approaches can be distinguished: intramolecular and intermolecular PKR. In the case of the intramolecular version, some of us previously demonstrated that fulleropyrrolidines endowed with one or two propargyl groups at the C-2 position of the pyrrolidine ring (1,6-enynes) undergo the PKR leading to cyclopentenones fused to the fullerene moiety.^39,40 On the other hand, there are studies in which cyclopentenones are successfully synthesized via intermolecular PKR;^41–44 although this approach is more limited since olefins without strain are poorly reactive with the exception of ethylene.^45,46 Studies on the chemical functionalization of carbon nanostructures via the PKR are rather scarce and, to our knowledge, this cycloaddition has not been studied in single-walled carbon nanotubes (SWCNTs) yet. These materials have attracted interest due to their remarkable physical properties.^47–53 Besides, functionalized SWCNTs have become useful assemblies in the fields of materials, medical, and biological sciences.^54–56 Nonetheless, the actual application of these materials may be hindered because their selective purification is hard to achieve due to their poor solubility in conventional solvents or the formation of agglomerates because of strong π-stacking tendencies.^57,58 These problems can be partially or totally solved with proper chemical modifications.^59–62 In view of that, in this contribution the PKR in SWCNTs is first quantum-chemically explored with the aim of analyzing whether the PKR can be a suitable synthetic strategy for the chemical functionalization of SWCNTs. Then, the PKR is experimentally proved and added to the toolbox of chemical reactions useful to functionalize SWCNTs.

The generally accepted reaction mechanism was initially proposed by Magnus et al.;^63,64 subsequently, theoretical studies by Nakamura⁶⁵ and Pericàs⁶⁶et al. based on density functional theory (DFT) corroborated the main steps of the reaction. Within the purposes of the current manuscript, a graphical representation of the overall PKR mechanism in SWCNTs with 2-heptyne as the alkyne and catalyzed by dicobalt octacarbonyl [Co₂(CO)₈] is provided in Scheme 2.

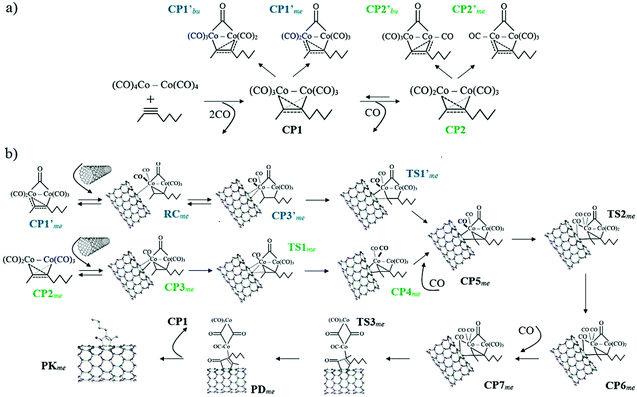Scheme 2 Mechanism of the Pauson–Khand reaction in single-walled carbon nanotubes with 2-heptyne as the alkyne and dicobalt octacarbonyl [Co₂(CO)₈] as the catalyst. (a) Complexation between Co₂(CO)₈ and 2-heptyne. (b) Progress of the reaction from the nanotube insertion. Blue and green labels respectively correspond to the alternative and generally-accepted pathways. The alternative pathway converges to the generally-accepted mechanism from CP5 (black labels). Labels given as in a previous work⁶⁵ along with subscripts indicating what carbon atom of the alkyne react first: the one linked to methyl “me” or butyl “bu”.

Results and discussion

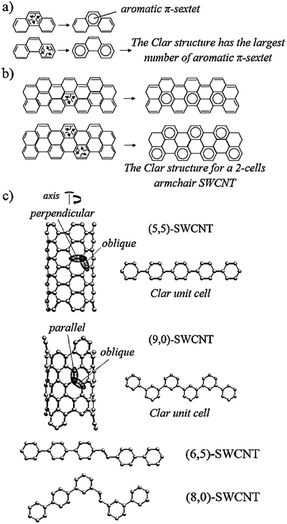
This section is outlined as follows. Computational investigations are firstly introduced starting with the description of the models used in the quantum-chemical modeling of reactions in SWCNTs. The main goal in this subsection is to validate the approach implemented in the current study. After that, the complexation step is discussed in detail to introduce an alternative pathway to the generally-accepted mechanism. The PKR in armchair, zig-zag, and chiral SWCNTs with 2-heptyne is described in the following subsections (the PKR with acetylene is illustrated in Fig. S1,† see also related discussion). Then, the main factors inducing the regioselectivity of the PKR are analyzed in terms of structural conformations and electronic interactions. Finally, experimental investigations demonstrating the successful synthesis of cyclopentenones attached to SWCNTs provide evidences that strengthen the conclusions achieved from the quantum-chemical study.

All mechanisms are formulated under the following description (see Scheme 2). In the initial step, that is complexation, Co₂(CO)₈ releases two CO and coordinates with the alkyne substrate. The resulting complex of cobalt, CP1, reversibly releases a third CO thus forming CP2. Then the wall of a SWCNT reaches the coordination sphere of a cobalt atom with a vacant site in CP2 and forms CP3. Upon the reversible SWCNT coordination, the SWCNT insertion takes place resulting in the formation of a cobaltacycle, CP4. Then, this intermediate recovers one CO giving rise to CP5. The resulting cobaltacycle in CP5 can be formed via an alternative pathway, in which both first coordination spheres of the two cobalt atoms keep six CO units instead of five through every step (see pathway starting from CP1′ in Scheme 2b). This step is important because the course of the PKR is usually determined by the nanotube insertion since the regiochemistry and stereochemistry of the final adduct can be controlled from this step. The CO insertion generates the next intermediate, CP6, and a subsequent coordination of another CO to cobalt gives rise to CP7. A reductive elimination leads to the pre-product, PD, and the decomplexation step produces the final adduct, PK. The theoretical work is therefore based on this description for the PKR in SWCNTs with acetylene or 2-heptyne as the alkyne. 2-Heptyne is included in this study because it reduces experimental difficulties associated to the manipulation of acetylene; besides, results based on an asymmetric alkyne strengthen the conclusions derived in this work.

Computational investigations

Modeling chemical reactions in SWCNTs. Before formulating the reaction mechanisms of interest, it is convenient to describe the models used to reach the purposes of this work. Quantum-chemical modeling of chemical reactions in SWCNTs can be appropriately done with chemical structures regarding the Clar theory (see Scheme 3a and b).^67–72 Clar networks are more stable than their counterpart Kekulé structures as aromaticity provides some extra stability to conjugated systems.^73–77 Following this order of ideas, the PKR is studied by taking into consideration an armchair SWCNT with chiral indices (5,5) (6.78 Å of diameter) and a zig-zag SWCNT with chiral indices (9,0) (7.05 Å of diameter). The length of both structures is 3-Clar unit cells [ca. 12.20 Å for (5,5)-SWCNT and 11.20 Å for (9,0)-SWCNT]. Some advantages can be achieved by using Clar networks since these are fully benzenoid structures, have a closed-shell singlet ground state with frontier molecular orbitals entirely delocalized, and faster convergence can be reached in their electronic properties with respect to the number of unit cells. All these features are not true for conventional models of SWCNTs. For instance, the ground state of a non-Clar (9,0)-SWCNT is a quintet spin state with the four frontier electrons completely localized at the edges of the nanotube.^67,78 The Clar structures considered in this manuscript and the available reaction sites for the PKR are depicted in Scheme 3c, as well as the Clar unit cells for (6,5)- and (8,0)-SWCNT. Additionally, metallic SWCNTs are defined with the (n,n) chiral indices, semimetallic with (n,0) (n a multiple of 3), and otherwise they are semiconductors.

Scheme 3 Graphical representation of Clar's aromatic π-sextet rule in (a) phenanthrene, and (b) a 2-cell SWCNT. The rule states that a Clar structure is the one with the largest number of aromatic π-sextets, and it better agrees with experimental evidence. (c) The SWCNT structures studied in this work. The picture also illustrates the cycloadditions to the parallel, oblique, and perpendicular positions relative to the nanotube axis.

The complexation step. Among all the chemical species shown in Scheme 2a, only CP1 has been completely isolated and characterized.⁷⁹ Some photochemical studies reveal the successful trapping of intermediates like CP2, in which cobalt is not only coordinated to an alkyne but also to other species.^80–83 We are not aware of any study regarding the trapping of an isolated CP2. Moreover, McGlinchey et al. demonstrated that elimination of CO to form CP2 can be difficult for some ethynyl complexes; in addition, they concluded that some pentacarbonyl complexes, CP2, do not continue along the Magnus pathway because of the unfavorable relative orientation of the cobalt-coordinated alkyne and alkene.⁸⁴

Some bond distances for the CP1 (CP1′) and CP2 (CP2′) structures formed with acetylene are shown in Fig. 1. In all the cases, the C–C bond shows a double-bond character (typical ethylene C–C bond distance, ca. 1.33 Å). The Co–Co distance enlarges when the number of coordinated CO ligands increases going from 2.36 Å in CP2 to 2.47 Å in CP1 and from 2.43 Å in CP2′ to 2.50 Å in CP1′. The four C(alkyne)–Co bond distances remain more or less constant in CP1 and CP2, 1.96 and 2.01 Å, respectively.

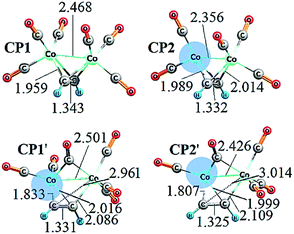Fig. 1 Main bond distances (in Å) for the structures involved in the complexation step. A shaded region represents a vacant site on a cobalt atom.

The CP1′ and CP2′ structures differ from CP1 and CP2 in the coordination of one CO unit as it is μ₂-coordinated to both Co atoms. As a matter of fact, CO-bridging ligand complexes have been previously reported.⁸⁵ Moreover, the distances of 1.83 and 2.96 Å in CP1′ between C–Co suggest that only one Co atom is η²-coordinated to the alkyne, and the other is η¹-coordinated. A similar observation is done for CP2′. As a concluding remark, a vacant site in cobalt, wherein the coordination with an olefin can occur, like the one in CP2 can be also formed without releasing another CO from CP1 due to a simple geometrical rearrangement leading to CP1′ (see Fig. 1).

The analysis outlined in this subsection has direct consequences in the energetics and, in turn, the formulation of the reaction mechanism for the PKR. The relative thermodynamic stability of the CP1 (CP1′) and CP2 (CP2′) structures is reported in Table 1. The CP1′ structure seems to describe better the complexation step based on thermodynamic arguments, which is attributed to the fact that the decoordination of another CO from CP1 to form CP2 (CP2′) leads to a Co atom that disobeys the 18-electron rule, which is not common for the first-row transition metals like cobalt, thus causing a strong thermodynamic destabilization of the species.

Table 1 Comparison of relative electronic and Gibbs energies (in kcal mol⁻¹) for structures formed in the complexation step

Acetylene			2-Heptyne
Species	ΔErel	ΔGrel	Species	ΔErel	ΔGrel
CP1	0.0	0.0	CP1	0.0	0.0
CP1′	16.5	16.7	CP1′me	17.5	15.8
CP2	56.9	43.9	CP1′bu	18.7	16.0
CP2′	70.7	58.2	CP2	56.3	40.6
			CP2′me	72.6	58.4
			CP2′bu	73.8	59.4

---

In the case of the structures formed with 2-heptyne, there are two regioisomers of CP1′ and CP2′ which depend on the group that is linked to the cobalt atom with the vacant site. For instance, CP1′_me means that the alkyne carbon atom with the methyl group is linked to the metal with the vacant site, then this carbon atom undergoes first the alkene or SWCNT insertion. As illustrated in Table 1, the thermodynamic stability follows the sequence CP2′_bu < CP2′_me < CP2 < CP1′_bu < CP1′_me < CP1, and once again the CP1′_me and CP1′_bu structures are more suitable to describe the complexation step.

Nakamura's DFT-results in the case of the electronic energy of CP2 with acetylene strongly differ from ours. They calculated an electronic energy of CP2 relative to CP1 of 26.4 and 21.2 kcal mol⁻¹ at the B3LYP^86,87/631LAN and B3LYP/6311SDD//B3LYP/631LAN levels of theory, respectively.⁶⁵ In this regard, Table 1 shows that CP2 is highly destabilized since its electronic energy is 57 kcal mol⁻¹ higher than that of CP1. It is not easy to identify the reason of such a large difference. It could be related to the use of a different hybrid functional along with gaussian basis sets in Nakamura's calculations. Nevertheless, it is likely that the main difference comes from the methodology used by Nakamura and coworkers that does not include relativistic corrections via the zeroth-order regular approximation, the frozen-core approximation, solvent effects associated to a large dielectric constant (33.0), and dispersion corrections (see below Computational details). However, as far as we know, there are no studies regarding structures like CP1′, which certainly is more stable than CP2. Even if we are overestimating the energy of both complexes, CP1′ in fact keeps six CO units so that the 18-electron rule is fulfilled in the cobalt atom with the vacant site thus gaining stability, unlike the cobalt atom in CP2 with the vacant site generated by the removal of CO from CP1.

The PKR in metallic SWCNTs. A detailed discussion concerning the complexation step was given in the previous subsection with the aim of introducing an alternative reaction pathway to the generally-accepted Magnus mechanism.^63,64 In this subsection, both mechanisms are compared for the PKR in metallic (5,5)-SWCNTs. Changes in Gibbs energy are given with respect to the energy of CP1 since the formation of this complex is common for any PKR, although it is formed in a preactivation step from Co₂(CO)₈ and acetylene or 2-heptyne with an energy cost of ΔG ∼18 kcal mol⁻¹.

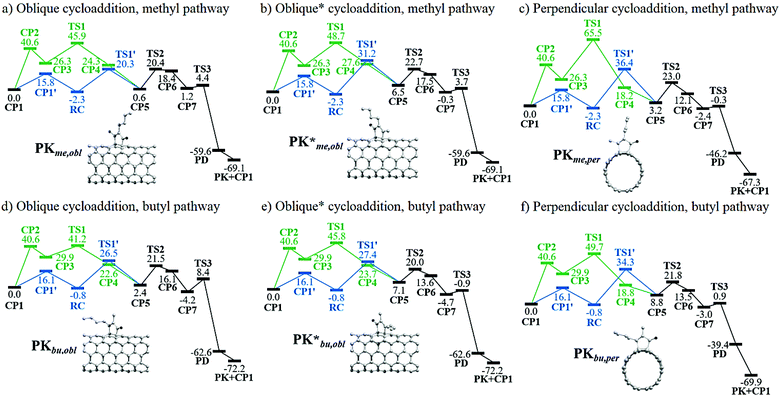
The nomenclature defined in Schemes 2 and 3c is jointly adopted in this subsection; that is, if the alkyne carbon atom with the methyl group is initially linked to the oblique position of the nanotube, then a PK adduct can be generated in what we called the “methyl” pathway, PK_me,obl (Fig. 2a). The distinction in the reaction pathways is given by the nanotube insertion. Because of symmetry arguments, only one PK adduct at the perpendicular position is possible, PK_me,per. Nonetheless, it can be observed in Scheme 3c that the formation of PK at the oblique position can be done via two pathways. Given the insertion of one carbon of the alkyne to one carbon localized at the perpendicular position of the nanotube, the cycloaddition leading to PK can evolve to either the perpendicular or oblique position; labeled the latter as PK_me,obl. Otherwise, the produced adduct is PK*_me,obl. Therefore, six PK adducts can be differentiated: PK_me,obl, PK*_me,obl, PK_me,per, PK_bu,obl, PK*_bu,obl, and PK_bu,per; wherein the three later adducts are originated when the alkyne carbon atom with the butyl group is linked to the nanotube, i.e. via the “butyl” pathway.

Fig. 2 Gibbs energy profiles in kcal mol⁻¹ for the Pauson–Khand reaction with 2-heptyne in (5,5)-SWCNT. Blue and green lines respectively correspond to the alternative and generally-accepted pathways. The alternative pathway converges to the generally-accepted mechanism (black lines).

A graphical representation of the different pathways related to the PKR in (5,5)-SWCNT with 2-heptyne is given in Fig. 2. The nanotube coordination in the Magnus mechanism is an endergonic process forming CP3 from CP1 by more than 26 kcal mol⁻¹ with an energy barrier of 40.6 kcal mol⁻¹. On the other hand, this step is slightly exergonic with an energy barrier of ca. 16 kcal mol⁻¹ in the alternative pathway that leads to a reactant complex RC. Then, within the Magnus mechanism, the nanotube insertion is an exergonic process to form CP4 from CP3 which releases from 2 to 11 kcal mol⁻¹, except for the slightly endergonic process via a methyl oblique cycloaddition (forming CP4*_me,obl). The energy barriers in these cases range from 11 to 39 kcal mol⁻¹, being the lowest and highest ones viaTS1_bu,obl and TS1_me,per, respectively. These results suggest that the nanotube insertion through the Magnus mechanism should occur at the oblique position and via the butyl pathway. In contrast, the nanotube insertion via the alternative pathway is an endergonic process requiring an energy from 3 to 10 kcal mol⁻¹ to form CP5 from RC. This step has an energy barrier from 23 to 39 kcal mol⁻¹, being the lowest and highest ones through TS1′_me,obl and TS1′_me,per, respectively. As a result, the oblique methyl pathway is kinetically favored in the alternative pathway. Even though the nanotube insertion via the Magnus mechanism is thermodynamically and kinetically favored as compared to the alternative one, the nanotube coordination is certainly hampered. However, although structures like CP3^88,89 and CP4⁸⁵ had been previously discussed, thus supporting the original idea of Magnus, some CP3-like structures were found to hamper the course of the PKR due to an unfavorable relative orientation of the cobalt-coordinated alkyne and alkene.⁸⁴ Consequently, we conclude that the Magnus mechanism is only favored in those cases in which CP3 is more stable than CP1′; electronic factors like the double-bond delocalization in SWCNTs and the steric hindrance bring about a destabilization of CP3 resulting in a non-operative Magnus pathway in PKRs involving SWCNTs. Therefore, a favored or hindered PKR may be predicted by TS1′ rather than TS1 in terms of kinetic arguments. Consequently, the PKR at this stage of the reaction should preferably proceed viaTS1′_me,obl because of the lowest energy barrier of 22.6 kcal mol⁻¹.

Henceforth, the alternative pathway converges to the Magnus mechanism such that the following steps are identical for both pathways. The CO insertion is an endergonic process which requires an energy from 5 to 18 kcal mol⁻¹ to form CP6 from CP5. The energy barriers in these cases range from 13 to 20 kcal mol⁻¹, being the lowest and highest ones viaTS2*_bu,obl (TS2*_bu,per) and TS2_me,obl (TS2_me,per, TS2_bu,obl), respectively. Based on these results, it can be concluded that the oblique butyl pathway is kinetically favored at this stage of the reaction. TS2*_bu,obl is 6.9 kcal mol⁻¹ lower than TS2_me,obl. Nevertheless, it should be taken into consideration that in the previous step TS1′*_bu,obl is 5.6 kcal mol⁻¹ higher than TS1′_me,obl. Subsequently, the PKR should rather proceed via the oblique position, although both methyl and butyl pathways are feasible so far.

The formation of CP7 from CP6 is an exergonic process releasing an energy from 15 to 20 kcal mol⁻¹; then the formation of PD is strongly thermodynamically favored because more than 36 kcal mol⁻¹ are released through the reductive elimination step. The energy barriers for such a step range from 2 to 13 kcal mol⁻¹, being the lowest and highest ones through TS3_me,per and TS3_bu,obl, respectively. With the exception of TS3_bu,obl, the energy barriers through the distinct pathways are nearly identical since the energy differences among them is less than 2 kcal mol⁻¹; therefore, the PKR proceeds indistinctly at this stage of the reaction. The formation of the PK adduct occurs releasing ca. 70 kcal mol⁻¹ in all the cases. Overall, based on Fig. 2, it is concluded that the turnover-frequency determining intermediate (TDI) and transition state (TDTS)^90–93 are respectively RC and TS1′ (TS2_me,obl has almost the same energy as TS1′_me,obl and both could be considered TDTSs in this case). On the other hand, CP1 is the TDI and TS1 is the TDTS for all the Magnus pathways with energy barriers ranging from 41 to 66 kcal mol⁻¹. These results suggest that the alternative pathway is certainly more efficient for the PKR, being the oblique methyl pathway the kinetically most favored with an effective energy barrier (the so-called energetic span) of 22.6 kcal mol⁻¹viaTS1′_me,obl. As a result, this functionalization is indeed viable under laboratory conditions.

The previous analysis is exactly done in the case of the PKR regarding acetylene resulting in no mechanistic differences (see Fig. S1†); therefore, here we only report the most relevant results. That is, the determinant states are CP1, CP2 and TS1′; wherein CP1 is the TDI in any case, yet the TDTS is CP2 in the Magnus mechanism leading to an energy barrier of 43.9 kcal mol⁻¹. On the other hand, TS1′ is the TDTS for the alternative pathway with a more effective energy barrier of 29.4 kcal mol⁻¹viaTS1′_obl. As a matter of fact, our results suggest that the PKR in (5,5)-SWCNT with acetylene could be difficult to proceed in the laboratory in view of that an energy barrier of at least 29.4 kcal mol⁻¹, viaTS1′_obl, must be overcome.

The PKR in semimetallic SWCNTs. In the case of the PKR in (9,0)-SWCNT with 2-heptyne, the cycloaddition can occur at the parallel and oblique positions with respect to the nanotube axis; then six PK adducts can be differentiated analogous to the previous subsection. The nanotube coordination in the Magnus pathway must overcome an energy barrier of 40.6 kcal mol⁻¹ in an endergonic process by 24.4 kcal mol⁻¹ to form CP3_me (or 26.4 kcal mol⁻¹ to form CP3_bu). The nanotube insertion leading to CP4_me,par from CP3_me involves an energy barrier of 23.6 kcal mol⁻¹ in an endergonic process by 17.4 kcal mol⁻¹. However, given that CP1 is the TDI and TS1_me,par is the TDTS in the Magnus mechanism, the overall energy barrier reaches 48.0 kcal mol⁻¹ (see Fig. 3). Even though we did not perform calculations for the other five pathways (i.e. viaTS1_me,obl, TS1*_me,obl, TS1_bu,par, TS1_bu,obl, and TS1*_bu,obl), the current outcomes and the results obtained in the former subsection suggest that the Magnus mechanism is kinetically less favored. In view of that, now we focus on the cycloaddition via the alternative pathway to (9,0)-SWCNT with 2-heptyne; indeed, unlike the Magnus mechanism, this pathway is an exergonic process releasing from 5 to 7 kcal mol⁻¹ to form RC with a lower energy barrier of ca. 16 kcal mol⁻¹viaCP1′.

Fig. 3 Gibbs energy profiles in kcal mol⁻¹ for the Pauson–Khand reaction with 2-heptyne in (9,0)-SWCNT via the parallel methyl pathway. Blue and green lines respectively correspond to the alternative and generally-accepted pathways. The alternative pathway converges to the generally-accepted mechanism (black line).

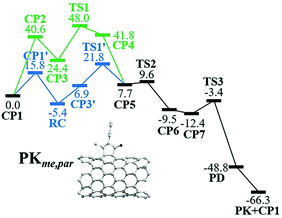
The nanotube insertion via the alternative pathway is an endergonic process requiring an energy gain from 13 to 28 kcal mol⁻¹ to form CP5 from RC. Energy barriers in this step range from 27 to 46 kcal mol⁻¹, being the lowest and highest ones through TS1′_me,par and TS1′*_bu,obl, respectively (details in Table S1†). As a result, the parallel methyl pathway is kinetically favored in the alternative mechanism. According to Fig. S1† and related discussion, the same result is obtained for the nanotube insertion of acetylene considering all possible reaction pathways. Therefore and because of the size of the systems, henceforth we only describe the parallel pathway which is the most reactive position (see Fig. 3).

The CO insertion is an exergonic process which releases 17.2 and 24.4 kcal mol⁻¹, respectively, to form CP6_me,par and CP6_bu,par from CP5_me,par and CP5_bu,par. The energy barrier in this step is small, ca. 2 kcal mol⁻¹. The reductive elimination viaTS3_me,par occurs with a lower energy barrier (9.0 kcal mol⁻¹) as compared to TS3_bu,par (12.0 kcal mol⁻¹); as a result, the parallel methyl pathway is still kinetically favored. The formation of PD and PK is given with an energy stabilization of at least 36 kcal mol⁻¹. In general, in both the methyl and butyl pathways, the TDI is RC and the TDTS is TS1′, being the lowest energy barrier viaTS1′_me,par, 27.2 kcal mol⁻¹. Then, in view of the effective energy barrier of 22.6 kcal mol⁻¹ for the PKR in (5,5)-SWCNT with 2-heptyne, we conclude that the armchair SWCNTs react faster than the semimetallic zig-zag ones.

Finally, in the case of the PKR considering acetylene, the TDTS is TS1′ in the alternative pathway and the energy barrier of 29.2 kcal mol⁻¹viaTS1′_par is at least 3.8 kcal mol⁻¹ lower than the ones in the oblique pathways; indeed, it is a more effective activation energy than that of 43.9 kcal mol⁻¹via the Magnus mechanism. Besides, since PK_par is the most stable adduct, it is concluded that the parallel pathway is the most kinetically and thermodynamically favored reaction mechanism. As a final remark, it should be noticed that the energy barrier of 29.2 kcal mol⁻¹viaTS1′_par in (9,0)-SWCNT is identical to that one viaTS1′_obl in (5,5)-SWCNT, 29.4 kcal mol⁻¹; therefore, both metallic armchair and semimetallic zig-zag SWCNTs may not be thermally functionalized with acetylene under laboratory conditions.

The PKR in semiconducting SWCNTs. Based on the results from the previous subsections, we study the PKR with 2-heptyne for semiconducting SWCNTs only at the TDTS of the alternative pathway, TS1′. The selected models are the 3-Clar unit cells (6,5)- and (8,0)-SWCNT with diameters of 7.47 and 6.26 Å, respectively. The energy barrier viaTS1′_me,obl for (6,5)-SWCNT and TS1′_me,par for (8,0)-SWCNT is 15.1 kcal mol⁻¹ in both cases; the TDTS is CP1′ since the energy cost for its formation is 15.8 kcal mol⁻¹. These results suggest that the semiconducting SWCNTs react faster than any other ones. Then, given that the diameters of the SWCNTs under study are almost identical, within a range of 1.3 Å, we conclude that electronic factors are more important than the effect of the curvature. However, a reduced reactivity is expected as the diameter increases.^67,94

Origin of the regioselectivity of the PKR in SWCNTs. Scheme 1 illustrates the dependence of the PKR on either structural conformations or electronic interactions. To explain the regioselectivity of the PKR in SWCNTs, we make use of the activation strain model (ASM),^95–98 also known as the distortion/interaction model.^99–102 The ASM is a helpful tool to better understand the origin of energy barriers. These barriers are analyzed in terms of strain and interaction energies between the fragments participating in the formation or rupture of chemical bonds. In the ASM, activation energies can be separated into strain and interaction energies, i.e., ΔE^‡ = ΔE^‡_strain + ΔE^‡_int. The strain energy ΔE^‡_strain is the energy required to deform reactants from their equilibrium geometry into the geometry they acquire in the activated complex; and the transition state interaction ΔE^‡_int is the interaction energy between the deformed reactants in the transition state. This model can be extended through all the structures along a reaction coordinate; but here in Table 2 we only focus on all the TDTS structures under study, that is TS1′.

Table 2 The activation strain model at the TDTS of the PKR with 2-heptyne in (5,5)-SWCNT (upper half) and (9,0)-SWCNT (bottom). The fragment f1 stands for the nanotube and f2 for the CP1 fragment. Electronic energies in kcal mol⁻¹

Structure	ΔE^‡str (f1)	ΔE^‡str (f2)	ΔE^‡str	ΔE^‡int	ΔE^‡
TS1′me,obl	12.6	62.9	75.5	−71.1	4.4
TS1′*me,obl	26.0	67.2	93.2	−78.8	14.4
TS1′me,per	21.5	67.2	88.7	−68.2	20.5
TS1′bu,obl	12.2	68.6	80.8	−70.4	10.4
TS1′*bu,obl	26.6	64.1	90.7	−80.4	10.3
TS1′bu,per	23.0	66.2	89.2	−71.7	17.5
TS1′me,par	24.8	63.2	88.0	−82.4	5.6
TS1′me,obl	11.5	63.2	74.7	−60.4	14.3
TS1′*me,obl	12.0	70.2	82.2	−64.2	18.0
TS1′bu,par	26.0	65.0	91.0	−84.6	6.4
TS1′bu,obl	11.2	76.9	88.1	−68.8	19.3
TS1′*bu,obl	14.3	70.8	85.1	−60.7	24.4

---

The ASM is firstly discussed for TS1′ with (5,5)-SWCNT. In the case of 2-heptyne, larger differences in ΔE^‡_strain(f1) are observed, yet the oblique pathway results in significantly smaller deformation (ca. 12 kcal mol⁻¹) in the nanotube by at least 9 kcal mol⁻¹. CP1 is distorted with ΔE^‡_strain(f2) ranging from 66 to 69 kcal mol⁻¹, except for TS1′*_bu,obl (64.1 kcal mol⁻¹) and TS1′_me,obl (62.9 kcal mol⁻¹). ΔE^‡_int results in −70 ± 2 kcal mol⁻¹ for all the cases with the exceptions of TS1′*_me,obl (−78.8 kcal mol⁻¹) and TS1′*_bu,obl (−80.4 kcal mol⁻¹). Despite ΔE^‡_int for TS1′*_me,obl and TS1′*_bu,obl are the most favored ones, their ΔE^‡_strain are the highest ones; in fact, even though ΔE^‡_int for TS1′_me,obl is not the most favored, ΔE^‡_strain is the lowest one so that it results in the lowest activation energy. These outcomes certainly suggest that strain is the main factor influencing the PKR in (5,5)-SWCNT.

In the case of the PKR in (9,0)-SWCNT with 2-heptyne, ΔE^‡_strain(f1) in the parallel cycloaddition is higher with a value of ca. 25 kcal mol⁻¹, ΔE^‡_strain(f1) is in the range from 11 to 15 kcal mol⁻¹. On the other hand, ΔE^‡_strain(f2) in the parallel cycloaddition is among the lowest ones (63.2 and 65.0 kcal mol⁻¹ for the methyl and butyl pathways, respectively). The total ΔE^‡_strain in the parallel cycloadditions are the highest ones (above 88 kcal mol⁻¹), but both pathways also result in the lowest ΔE^‡_int (−82.4 and −84.6 kcal mol⁻¹ for the methyl and butyl pathways, respectively) and the lowest activation energies. As a result, it is concluded that the interaction energy is the main factor controlling the course of the PKR in (9,0)-SWCNT. In fact, results in Table S2† and related discussion exactly lead to the same conclusions regarding acetylene for both types of SWCNTs. Moreover, in the case of the PKR in (9,0)-SWCNT with acetylene, an analysis of HOMO–LUMO energies and an energy decomposition analysis, both related to TS1′ (see Tables S3 and S4†), suggest that the orbital interaction term (better HOMO_nanotube–LUMO_CP1 interaction at the TDTS) is the main factor explaining the more stabilizing interaction energy for the parallel attack.

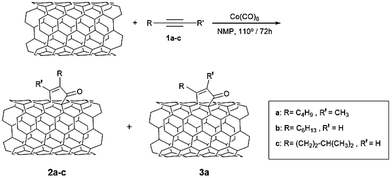
Experimental investigations

To confirm the theoretical predictions, we performed the PKR between three alkynes: 2-heptyne (1a), 1-octyne (1b), 5-methyl-1-hexyne (1c), Co₂(CO)₈ and two types of CNTs: HiPco SWCNTs (mixture of metallic and semiconducting SWCNTs in a 1 : 2 ratio, approximately) and (6,5) enriched SWCNTs (with a 95% content of semiconducting tubes) (Scheme 4).

Scheme 4 Chemical modification of SWCNTs under Pauson–Khand reaction.

Using HiPco tubes, no reaction was observed for alkyne 1a in N-methyl-2-pyrrolidone (NMP) at 70° C/72 h, neither at 110° C/24 h. Nevertheless, when the reaction was carried out at 110 °C during 72 h, the comparison of Raman spectra of pristine and PK-functionalized SWCNTs (vide infra) shows clear evidences of functionalization in the wall of carbon nanotubes. These reaction conditions were later used in all reactions with both, HiPco tubes and (6,5) enriched SWCNTs.

Thermogravimetric analysis (TGA) was used to confirm the functionalization of CNT samples by comparing the thermogravimetric profiles of the pristine and functionalized materials under inert atmosphere (Fig. S2†). PK-functionalized SWCNTs show an increase of the weight loss with respect to pristine SWCNT. The weight lost is lower for the hybrids formed from the less reactive alkyne 1a. This confirms the covalent reaction and support the higher reactivity of terminal alkynes; the absence of significant reaction of (6,5) SWCNT and alkyne 1a (Fig. S2b†) must be remarked.

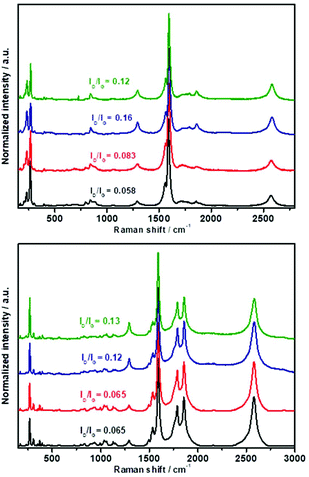
Raman spectroscopy clearly shows the degree of functionalization of HiPco and (6,5) enriched SWCNTs with the three alkynes 1a–c (Fig. 4). Firstly, for HiPco SWCNTs (Fig. 4, top), the low defect-related D-band to tangential G-band intensity ratio changes from 0.048 to 0.083 for 2a, 0.16 for 2b and 0.12 for 2c after functionalization; in case of (6,5) enriched SWCNT (Fig. 4, down) similar degree of functionalization changes was observed except for alkyne 1a confirming the observed by TGA (see above). The increase of D/G ratio confirms the increase of defects after PKR and the success of the reaction. Again, it is remarkable how the degree of functionalization is higher for terminal alkynes 1b and 1c rather than central alkyne 1a. It should be mentioned here that, after the PKR, the G-band of the functionalized carbon nanotubes is shifted to higher frequencies (3–6 cm⁻¹) in comparison with that of pristine SWCNTs (Fig. S3†), thus confirming the p-type doping of carbon nanotubes as consequence of the attached carbonyl moiety.¹⁰³ The higher shift is visible for the more functionalization materials. This shift can be also observed in the 2D band (Fig. S4†).¹⁰⁴ Moreover, analysis of the RBM zone (Fig. S5†) shows, for pristine HiPco SWCNT, two contributions, one at 231 cm⁻¹ and the other at 265 cm⁻¹ corresponding to a tube diameter of 1.03 nm and 0.89 nm respectively.¹⁰⁵ After PKR, the band ascribed to lower diameter reduces its intensity as a consequence of the high reactivity of smaller tubes. Same behaviour is observed for enriched (6,5) SWCNT, reduction of the lowest diameter tube (0.89 nm).

Fig. 4 Raman spectra (excitation wavelength 785 nm) of pristine HipCo (top) and (6,5) SWCNTs (—) (bottom) and PK-functionalized HiPco (top) and (6,5) (bottom) enriched SWCNTs with alkyne 1a (), 1b (), and 1c (). Intensities have been normalized to the G-band (highest peak).

Information derived from X-ray photoelectron spectroscopy is in agreement with Raman spectroscopy data. In XPS, comparison of the high-resolution C 1s spectra (Fig. S6–S9†) of pristine SWCNTs and PK-functionalized SWCNTs (HiPco and (6,5)) confirms the sidewall covalent functionalization due to appearance of new carbon component at 285.9 eV corresponding to sp³ C atoms,¹⁰⁴ which is visible in all CNT hybrids.

Covalent functionalization is known to quench carbon nanotubes photoluminescence;¹⁰⁵ so, the emission features of PK-functionalized SWCNTs were compared with those of pristine SWCNTs, both dispersed in sodium dodecylbenzene sulfonate (SDBS). Photoluminescence maps of pristine enriched (6,5) SWCNT and PK-functionalized SWCNT with 1b and 1c are shown in Fig. 5 and Fig. S10† respectively; red shift of 4–8 nm for (6,5) peak are observed after PK reaction, ascribed to the electron-withdrawing effect of the cyclopentenone ring. Also, new component at 1117 nm corresponded to E₁₁⁻ formation. These results confirmed the (6,5) SWCNTs reactivity and the formation of defects on the sidewall of CNTs.

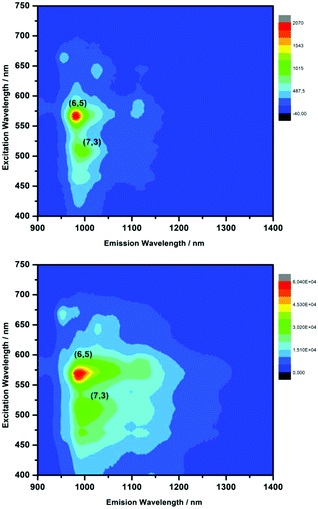Fig. 5 3D-photoluminescence plot of: (top) pristine (6,5) enriched SWCNTs and (bottom) PK-functionalized (6,5) enriched SWCNTs with 1b in D₂O at room temperature.

On the other hand, (Fig. S11†), from photoluminescence spectra for functionalized HiPco SWCNT with respect to pristine HiPco tubes, a remarkable intensity variation is evident despite not being homogeneous for all chiralities. Upon a more detailed inspection for the hybrids derived from reaction with 1a, red shifts of peak position are observed for PK-functionalized HiPco SWCNTs (Fig. S11†). In particular, the (10,2) and (8,4) are shifted from 1055 nm to 1062 nm and from 1113 nm to 1118 nm, respectively. Nevertheless, shift of only 0–1 nm is observed for (9,4) and (7,6) peaks. Similar shifts are observed for reaction with 1b and 1c. As a final remark, the results obtained by the experimental investigation corroborate the theoretical predictions: SWCNTs can be indeed chemically functionalized via the PKR with accessible energy barriers for the semiconducting and metallic types.

Conclusions

We theoretically and experimentally studied the Pauson–Khand reaction (PKR) catalyzed by Co₂(CO)₈ between carbon monoxide, several alkynes, and three types of single-walled carbon nanotubes (SWCNTs). Accurate and broad quantum chemical exploration of this [2 + 2 + 1] cycloaddition provided evidence for an alternative reaction mechanism operative in SWCNTs that appears to be more viable than the traditional mechanism proposed by Magnus. In the mechanism that we established, the turnover-frequency determining transition state (TDTS) of the PKR is given by the nanotube-insertion step, TS1′. For metallic and semimetallic SWCNTs reacting with acetylene, the associated Gibbs activation energy of 29 kcal mol⁻¹ is too high to be viable under laboratory conditions. On the other hand, the effective Gibbs energy barrier in the PKR with 2-heptyne amounts to 27.2 kcal mol⁻¹ for the semimetallic (9,0)-SWCNT, 22.6 kcal mol⁻¹ for the metallic (5,5)-SWCNT, and only 15.8 kcal mol⁻¹ for the semiconducting (6,5)- and (8,0)-SWCNT. These results suggest that semiconducting SWCNTs react faster than any other, although metallic ones are also prone to PK-functionalization because of the accessible energy barrier of 22.6 kcal mol⁻¹. Moreover, the cycloaddition is regioselective as it takes place exclusively at the oblique position of armchair SWCNTs and at the parallel position of zig-zag SWCNTs.

Finally, guided by our theoretical predictions, we were able to generate PK adducts of SWCNTs using one central and two terminal alkynes in the laboratory under simple heating. Both mixtures of metallic/semiconducting and enriched semiconducting SWCNTs were PK-functionalized in agreement with the theoretical results. The characterization based on Raman spectroscopy supported by XPS, TGA, and photoluminescence analyses confirmed the successful synthesis of PK adducts. Terminal alkynes showed a higher reactivity. In addition, the PKR did not proceed with alkynes of lower molecular weight, which is in accordance with the higher DFT energy barriers predicted for the PKR with acetylene. We envisage that our proposed mechanism for the PKR may help develop synthetic routes more efficiently.

Experimental details

A suspension of pristine HiPco SWCNTs or enriched (6,5) SWCNT (10 mg) in N-methyl-2-pyrrolidone (NMP) (25 mL) was sonicated for 15 minutes and then the alkyne (0.83 mmol) was added. On the other hand, a suspension of Co₂(CO)₈ (0.083 mmol) in NMP (25 mL) was sonicated for 15 minutes and then added to the suspension of pristine SWCNTs and alkyne 1a–c. The reaction mixture was stirred at 110 °C for 72 hours under inert atmosphere. After cooling to room temperature, the suspension was filtered with a PTFE membrane and the solid was washed successively with NMP and CH₂Cl₂. The black solid was dispersed in 3 mL of water/SDBS 5 wt%. The solution was first sonicated in bath sonicator for 30 minutes; next, the obtained solution was sonicated for 1 min using a tip sonicator. The PK-functionalized SWCNTs were exfoliated after these treatment, and the undissolved particles that correspond to the unreacted Co₂(CO)₈ were settle after centrifuged for 1 min under 3000 rpm. The obtained dark solution was then centrifuged at 14 000 rpm to deposit the PK-functionalized SWCNT. The black solid was washed subsequently with water and acetone to remove the excess of SDBS.

Computational details

All calculations were done with the Amsterdam Density Functional (ADF, 2013) program at the BP86-D₃BJ level of theory.^106–116 Molecular orbitals were expanded in uncontracted sets of Slater-type orbitals (STOs) of double-ζ (DZP: for H, C, O atoms) and triple-ζ quality (TZP: for Co) containing one set of polarization and diffuse functions. The frozen-core approximation (FCA) was employed for the 1s core of carbon and oxygen atoms, and the 1s2s2p core of Co.¹⁰⁶ The FCA has been shown to have a negligible effect on the geometry optimization procedure.^117,118 In addition, scalar relativistic corrections were added within the zeroth-order regular approximation (ZORA).¹¹⁹

All geometry optimizations were performed by the quantum regions interconnected by local descriptions (QUILD) code.¹²⁰ This latter works as a wrapper around the ADF program since it creates input files for ADF, then executes this program and collects energies and gradients. QUILD uses adapted delocalized coordinates and constructs model Hessians with the appropriate number of eigenvalues; which results in an advantage in the determination of transition state structures.¹²¹ All the stationary points were analyzed through analytical vibrational frequencies as calculated at the BP86(D₃-BJ)/DZP (TZP: for cobalt) including FCA and ZORA. Low frequencies were recalculated via the scanfreq keyword¹⁰⁶ since frequencies that have a small force constant are more sensitive to the numerical noise. For a more detailed description of the determination of stationary points, see the ESI.†

Electronic energies were corrected in a single-point approach at the O3LYP^122,123(D₃-BJ)/TZP//BP86(D₃-BJ)/DZP (TZP: for cobalt) level of theory including FCA and ZORA. Solvent effects due to N-methyl-2-pyrrolidone (with a dielectric constant of 33.0) were incorporated via the conductor-like screening model (COSMO)¹²⁴ as implemented in ADF. Gibbs energies were determined from the corrected electronic energies. Furthermore, corrections of the zero-point energy, thermal contributions to the internal energy, and the entropy term were computed from vibrational frequencies at 298.15 K considering an ideal gas in standard conditions. In a performance test of various functionals, we have verified that our O3LYP-corrected approach reproduces best the activation Gibbs energy obtained from kinetic studies based on ¹H nuclear magnetic resonance spectroscopy (complete details in Fig. S12 and Table S5†).¹²⁵

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

Excellent service by the Stichting Academisch Rekencentrum Amsterdam (SARA) and the Consorci de Serveis Universitaris de Catalunya (CSUC) is gratefully acknowledged. A. P. and F. L. thank the Spanish MINECO for projects CTQ2014-59832-JIN and CTQ2016-79189-R, respectively. M. S. thanks EU for a FEDER fund (UNGI08-4E-003), the Generalitat de Catalunya for project 2017SGR39, the Xarxa de Referència en Química Teòrica I Computacional, and ICREA Academia 2014 prize, and MINECO of Spain through project CTQ2017-85341-P. M. V. thanks CYTEMA-SANTANDER for a postdoctoral grant and L. M. A. thanks the Spanish MINECO for a FPI grant.

Notes and references

1. I. U. Khand, G. R. Knox, P. L. Pauson and W. E. Watts, J. Chem. Soc. D, 1971, 36a–36a.
2. I. U. Khand, G. R. Knox, P. L. Pauson and W. E. Watts, J. Chem. Soc., Perkin Trans. 1, 1973, 975–977.
3. I. U. Khand, G. R. Knox, P. L. Pauson, W. E. Watts and M. I. Foreman, J. Chem. Soc., Perkin Trans. 1, 1973, 977–981.
4. C. Exon and P. Magnus, J. Am. Chem. Soc., 1983, 105, 2477–2478.
5. P. Magnus, L. M. Principe and M. J. Slater, J. Org. Chem., 1987, 52, 1483–1486.
6. N. E. Schore and E. G. Rowley, J. Am. Chem. Soc., 1988, 110, 5224–5225.
7. M. E. Price and N. E. Schore, J. Org. Chem., 1989, 54, 5662–5667.
8. J. Castro, H. Sorensen, A. Riera, C. Morin, A. Moyano, M. A. Pericas and A. E. Greene, J. Am. Chem. Soc., 1990, 112, 9388–9389.
9. I. Nomura and C. Mukai, J. Org. Chem., 2004, 69, 1803–1812.
10. T. Kozaka, N. Miyakoshi and C. Mukai, J. Org. Chem., 2007, 72, 10147–10154.
11. Y. Hayashi, F. Inagaki and C. Mukai, Org. Lett., 2011, 13, 1778–1780.
12. K. Fujioka, H. Yokoe, M. Yoshida and K. Shishido, Org. Lett., 2012, 14, 244–247.
13. J. Blanco-Urgoiti, L. Añorbe, L. Pérez-Serrano, G. Domínguez and J. Pérez-Castells, Chem. Soc. Rev., 2004, 33, 32–42.
14. H.-W. Lee and F.-Y. Kwong, Eur. J. Org. Chem., 2010, 789–811.
15. J. Solà, A. Riera, X. Verdaguer and M. A. Maestro, J. Am. Chem. Soc., 2005, 127, 13629–13633.
16. M. Revés, T. Achard, J. Solà, A. Riera and X. Verdaguer, J. Org. Chem., 2008, 73, 7080–7087.
17. S. Kitagaki, F. Inagaki and C. Mukai, Chem. Soc. Rev., 2014, 43, 2956–2978.
18. S. P. Simeonov, J. P. M. Nunes, K. Guerra, V. B. Kurteva and C. A. M. Afonso, Chem. Rev., 2016, 116, 5744–5893.
19. N. Jeong, S. Lee and B. K. Sung, Organometallics, 1998, 17, 3642–3644.
20. K. H. Park, S. U. Son and Y. K. Chung, Tetrahedron Lett., 2003, 44, 2827–2830.
21. D. E. Kim, I. S. Kim, V. Ratovelomanana-Vidal, J.-P. Genêt and N. Jeong, J. Org. Chem., 2008, 73, 7985–7989.
22. T. Morimoto, N. Chatani, Y. Fukumoto and S. Murai, J. Org. Chem., 1997, 62, 3762–3765.
23. T. Kondo, N. Suzuki, T. Okada and T. Mitsudo, J. Am. Chem. Soc., 1997, 119, 6187–6188.
24. L.-J. Deng, J. Liu, J.-Q. Huang, Y. Hu, M. Chen, Y. Lan, J.-H. Chen, A. Lei and Z. Yang, Synthesis, 2007, 2565–2570.
25. T. Shibata and K. Takagi, J. Am. Chem. Soc., 2000, 122, 9852–9853.
26. T. Shibata, N. Toshida, M. Yamasaki, S. Maekawa and K. Takagi, Tetrahedron, 2005, 61, 9974–9979.
27. A. J. Pearson and R. A. Dubbert, J. Chem. Soc., Chem. Commun., 1991, 202–203.
28. A. J. Pearson and R. A. Dubbert, Organometallics, 1994, 13, 1656–1661.
29. T. R. Hoye and J. A. Suriano, J. Am. Chem. Soc., 1993, 115, 1154–1156.
30. C. Mukai, M. Uchiyama and M. Hanaoka, J. Chem. Soc., Chem. Commun., 1992, 1014–1015.
31. N. Jeong, S. J. Lee, B. Y. Lee and Y. K. Chung, Tetrahedron Lett., 1993, 34, 4027–4030.
32. T. R. Hoye and J. A. Suriano, Organometallics, 1992, 11, 2044–2050.
33. L. Jordi, A. Segundo, F. Camps, S. Ricart and J. M. Moreto, Organometallics, 1993, 12, 3795–3797.
34. F. Robert, A. Milet, Y. Gimbert, D. Konya and A. E. Greene, J. Am. Chem. Soc., 2001, 123, 5396–5400.
35. T. J. M. de Bruin, C. Michel, K. Vekey, A. E. Greene, Y. Gimbert and A. Milet, J. Organomet. Chem., 2006, 691, 4281–4288.
36. E. Fager-Jokela, M. Muuronen, M. Patzschke and J. Helaja, J. Org. Chem., 2012, 77, 9134–9147.
37. E. Fager-Jokela, M. Muuronen, H. Khaizourane, A. Vázquez-Romero, X. Verdaguer, A. Riera and J. Helaja, J. Org. Chem., 2014, 79, 10999–11010.
38. R. R. Torres, The Pauson–Khand Reaction: Scope, Variations and Applications, John Wiley & Sons, 2012.
39. N. Martín, M. Altable, S. Filippone and A. Martín-Domenech, Chem. Commun., 2004, 1338–1339.
40. N. Martín, M. Altable, S. Filippone, A. Martín-Domenech, A. Poater and M. Solà, Chem. – Eur. J., 2005, 11, 2716–2729.
41. S. Su, R. A. Rodriguez and P. S. Baran, J. Am. Chem. Soc., 2011, 133, 13922–13925.
42. N. Aiguabella, A. Pesquer, X. Verdaguer and A. Riera, Org. Lett., 2013, 15, 2696–2699.
43. A. Vázquez-Romero, L. Cárdenas, E. Blasi, X. Verdaguer and A. Riera, Org. Lett., 2009, 11, 3104–3107.
44. A. Vázquez-Romero, J. Rodríguez, A. Lledó, X. Verdaguer and A. Riera, Org. Lett., 2008, 10, 4509–4512.
45. A. Cabré, X. Verdaguer and A. Riera, Synthesis, 2017, 49, 3945–3951.
46. A. Cabré, H. Khaizourane, M. Garçon, X. Verdaguer and A. Riera, Org. Lett., 2018, 20, 3953–3957.
47. Y. H. Yang and W. Z. Li, Appl. Phys. Lett., 2011, 98, 041901.
48. M. M. J. Treacy, T. W. Ebbesen and J. M. Gibson, Nature, 1996, 381, 678–680.
49. E. Thostenson, C. Li and T. Chou, Compos. Sci. Technol., 2005, 65, 491–516.
50. E. Pop, D. Mann, Q. Wang, K. Goodson and H. Dai, Nano Lett., 2006, 6, 96–100.
51. M. Ouyang, J.-L. Huang and C. M. Lieber, Acc. Chem. Res., 2002, 35, 1018–1025.
52. M. E. Itkis, S. Niyogi, M. E. Meng, M. A. Hamon, H. Hu and R. C. Haddon, Nano Lett., 2002, 2, 155–159.
53. H. Kataura, Y. Kumazawa, Y. Maniwa, I. Umezu, S. Suzuki, Y. Ohtsuka and Y. Achiba, Synth. Met., 1999, 103, 2555–2558.
54. C. A. Dyke and J. M. Tour, J. Phys. Chem. A, 2004, 108, 11151–11159.
55. Y.-P. Sun, K. Fu, Y. Lin and W. Huang, Acc. Chem. Res., 2002, 35, 1096–1104.
56. M. Prato, K. Kostarelos and A. Bianco, Acc. Chem. Res., 2008, 41, 60–68.
57. J. G. Duque, A. N. G. Parra-Vasquez, N. Behabtu, M. J. Green, A. L. Higginbotham, B. K. Price, A. D. Leonard, H. K. Schmidt, B. Lounis, J. M. Tour, S. K. Doorn, L. Cognet and M. Pasquali, ACS Nano, 2010, 4, 3063–3072.
58. A. Criado, M. J. Gómez-Escalonilla, J. L. G. Fierro, A. Urbina, D. Peña, E. Guitián and F. Langa, Chem. Commun., 2010, 46, 7028–7030.
59. D. Tasis, N. Tagmatarchis, A. Bianco and M. Prato, Chem. Rev., 2006, 106, 1105–1136.
60. T. Yang, X. Zhao and S. Nagase, J. Comput. Chem., 2013, 34, 2223–2232.
61. A. Criado, M. Vizuete, M. J. Gómez-Escalonilla, S. García-Rodriguez, J. L. G. Fierro, A. Cobas, D. Peña, E. Guitián and F. Langa, Carbon, 2013, 63, 140–148.
62. V. O. Koroteev, L. G. Bulusheva, I. P. Asanov, E. V. Shlyakhova, D. V. Vyalikh and A. V. Okotrub, J. Phys. Chem. C, 2011, 115, 21199–21204.
63. P. Magnus, C. Exon and P. Albaugh-Robertson, Tetrahedron, 1985, 41, 5861–5869.
64. P. Magnus and L. M. Principe, Tetrahedron Lett., 1985, 26, 4851–4854.
65. M. Yamanaka and E. Nakamura, J. Am. Chem. Soc., 2001, 123, 1703–1708.
66. M. A. Pericàs, J. Balsells, J. Castro, I. Marchueta, A. Moyano, A. Riera, J. Vázquez and X. Verdaguer, Pure Appl. Chem., 2002, 74, 167–174.
67. J. P. Martínez, F. Langa, F. M. Bickelhaupt, S. Osuna and M. Solà, J. Phys. Chem. C, 2016, 120, 1716–1726.
68. Y. Matsuo, K. Tahara and E. Nakamura, Org. Lett., 2003, 5, 3181–3184.
69. M. Baldoni, A. Sgamellotti and F. Mercuri, Org. Lett., 2007, 9, 4267–4270.
70. M. Baldoni, D. Selli, A. Sgamellotti and F. Mercuri, J. Phys. Chem. C, 2009, 113, 862–866.
71. E. Clar, The Aromatic Sextet, Wiley, New York, 1972.
72. M. Solà, Front. Chem., 2013, 1, 22.
73. S. Osuna, M. Torrent-Sucarrat, M. Solà, P. Geerlings, C. P. Ewels and G. Van Lier, J. Phys. Chem. C, 2010, 114, 3340–3345.
74. F. J. Martín-Martínez, S. Melchor and J. A. Dobado, Phys. Chem. Chem. Phys., 2011, 13, 12844–12857.
75. M. Garcia-Borràs, S. Osuna, J. M. Luis, M. Swart and M. Solà, Chem. Soc. Rev., 2014, 43, 5089–5105.
76. F. J. Martín-Martínez, S. Melchor and J. A. Dobado, Org. Lett., 2008, 10, 1991–1994.
77. J. Zhao and P. B. Balbuena, J. Phys. Chem. C, 2008, 112, 3482–3488.
78. T. Pankewitz and W. Klopper, J. Phys. Chem. C, 2007, 111, 18917–18926.
79. F. Baert, A. Guelzim, J. M. Poblet, R. Wiest, J. Demuynck and M. Benard, Inorg. Chem., 1986, 25, 1830–1841.
80. C. M. Gordon, M. Kiszka, I. R. Dunkin, W. J. Kerr, J. S. Scott and J. Gebicki, J. Organomet. Chem., 1998, 554, 147–154.
81. S. M. Draper, C. Long and B. M. Myers, J. Organomet. Chem., 1999, 588, 195–199.
82. M. E. Krafft, I. L. Scott, R. H. Romero, S. Feibelmann and C. E. Van Pelt, J. Am. Chem. Soc., 1993, 115, 7199–7207.
83. X. Verdaguer, A. Moyano, M. A. Pericas, A. Riera, V. Bernardes, A. E. Greene, A. Alvarez-Larena and J. F. Piniella, J. Am. Chem. Soc., 1994, 116, 2153–2154.
84. S. A. Brusey, E. V. Banide, S. Dörrich, P. O'Donohue, Y. Ortin, H. Müller-Bunz, C. Long, P. Evans and M. J. McGlinchey, Organometallics, 2009, 28, 6308–6319.
85. M. K. Pallerla, G. P. A. Yap and J. M. Fox, J. Org. Chem., 2008, 73, 6137–6141.
86. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
87. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
88. Y. Gimbert, D. Lesage, A. Milet, F. Fournier, A. E. Greene and J.-C. Tabet, Org. Lett., 2003, 5, 4073–4075.
89. E. V. Banide, H. Müller-Bunz, A. R. Manning, P. Evans and M. J. McGlinchey, Angew. Chem., Int. Ed., 2007, 46, 2907–2910.
90. S. Kozuch and S. Shaik, J. Phys. Chem. A, 2008, 112, 6032–6041.
91. A. Uhe, S. Kozuch and S. Shaik, J. Comput. Chem., 2011, 32, 978–985.
92. S. Kozuch and J. M. L. Martin, ChemPhysChem, 2011, 12, 1413–1418.
93. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
94. J. Li, G. Jia, Y. Zhang and Y. Chen, Chem. Mater., 2006, 18, 3579–3584.
95. W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127.
96. F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128.
97. I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967.
98. L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343.
99. K. N. Houk, R. W. Gandour, R. W. Strozier, N. G. Rondan and L. A. Paquette, J. Am. Chem. Soc., 1979, 101, 6797–6802.
100. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647.
101. Y. Cao, Y. Liang, L. Zhang, S. Osuna, A.-L. M. Hoyt, A. L. Briseno and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 10743–10751.
102. F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
103. A. Jorio, A. G. Souza Filho, G. Dresselhaus, M. S. Dresselhaus, A. K. Swan, M. S. Ünlü, B. B. Goldberg, M. A. Pimenta, J. H. Hafner, C. M. Lieber and R. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155412.
104. T. I. T. Okpalugo, P. Papakonstantinou, H. Murphy, J. McLaughlin and N. M. D. Brown, Carbon, 2005, 43, 153–161.
105. M. S. Strano, C. A. Dyke, M. L. Usrey, P. W. Barone, M. J. Allen, H. Shan, C. Kittrell, R. H. Hauge and R. E. Smalley, Science, 2003, 301, 1519–1522.
106. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
107. S. J. A. van Gisbergen, J. G. Snijders and E. J. Baerends, Comput. Phys. Commun., 1999, 118, 119–138.
108. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
109. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
110. J. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
111. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
112. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
113. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
114. S. Osuna, M. Swart and M. Solà, J. Phys. Chem. A, 2011, 115, 3491–3496.
115. J. P. Martínez, D. E. Trujillo-González, A. W. Götz, F. L. Castillo-Alvarado and J. I. Rodríguez, J. Phys. Chem. C, 2017, 121, 20134–20140.
116. J. P. Martínez, E. Rivera-Avalos, S. Vega-Rodríguez and D. de Loera, Res. Chem. Intermed., 2018, 44, 2061–2073.
117. J. G. Snijders and M. Swart, Theor. Chem. Acc., 2003, 110, 34–41.
118. M. Swart and J. G. Snijders, Theor. Chem. Acc., 2004, 111, 56–56.
119. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597.
120. M. Swart and F. M. Bickelhaupt, J. Comput. Chem., 2008, 29, 724–734.
121. M. Swart and F. M. Bickelhaupt, Int. J. Quantum Chem., 2006, 106, 2536–2544.
122. N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412.
123. W.-M. Hoe, A. J. Cohen and N. C. Handy, Chem. Phys. Lett., 2001, 341, 319–328.
124. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
125. D. R. Hartline, M. Zeller and C. Uyeda, Angew. Chem., Int. Ed., 2016, 55, 6084–6087.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental evidence, detailed discussion of reaction mechanisms that are not included in the main manuscript, benchmarking methodology, structural analysis of some optimized geometries, and energies and cartesian coordinates of all located stationary points. See DOI: 10.1039/c8nr03480j

---