Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Lubricating properties of single metal ions at interfaces†
Clodomiro
Cafolla
 and
Kislon
Voïtchovsky
and
Kislon
Voïtchovsky
 *
*
Physics Department, Durham University, Durham DH1 3LE, UK. E-mail: kislon.voitchovsky@durham.ac.uk
First published on 19th June 2018
Abstract
The behaviour of ionic solutions confined in nanoscale gaps is central to countless processes, from biomolecular function to electrochemistry, energy storage and lubrication. However, no clear link exists between the molecular-level behaviour of the liquid and macroscopic observations. The problem mainly comes from the difficulty to interrogate a small number of liquid molecules. Here, we use atomic force microscopy to investigate the viscoelastic behaviour of pure water and ionic solutions down to the single ion level. The results show a glassy-like behaviour for pure water, with single metal ions acting as lubricants by reducing the elasticity of the nano-confined solution and the magnitude of the hydrodynamic friction. At small ionic concentration (<20 mM) the results can be quantitatively explained by the ions moving via a thermally-activated process resisted by the ion's hydration water (Prandtl–Tomlinson model). The model breaks down at higher salt concentrations due to ion-ion interaction effects that can no longer be neglected. The correlations are confirmed by direct sub-nanometre imaging of the interface at equilibrium. The results provide a molecular-level basis for explaining the tribological properties of aqueous solutions and suggest that ion-ion interactions create mesoscale effects that prevent a direct link between nanoscale and macroscopic measurements.
Introduction
Interfaces between solids and aqueous solutions are ubiquitous in nature,1 often confined to nano-gaps, inside or between solids.2 Examples range from biomolecules folding3 and microcirculation of metabolites in cells4 to the growth of minerals5 and geochemistry.6 In technology, the role played by this so-called nano-confined7 water is arguably even more central with applications in electrochemistry and energy science,8 colloidal science,9 biomedical sciences,10 heterogeneous catalysis,11 tribology and lubrication.12 Nano-confined water does not, generally, behave like its bulk counterpart; water molecules tend to be more ordered due to their interactions with the surface2,13 and reduced conformational entropy.14 This molecular ordering vanishes over a few molecular diameters (typically < 1–2 nm) in the bulk liquid,15 but the specific organisation and dynamics of the interfacial water molecules depend on the details of each system.2,15–17 Parameters such as the chemical nature and the geometry of the confining surfaces,8,15 as well as the presence of dissolved molecules and ions,18 can dramatically influence the behaviour of interfacial water.19 The importance of interfacial effects is further emphasised for nano-confined water in systems where every liquid molecule can be seen as belonging to one or more interfaces. Additionally, the pressure and the temperature within the nano-confined gap,19–21 as well as a possible relative motion of the confining surfaces,22 can influence both the molecular arrangement and the dynamics of the nano-confined solution.Numerous studies2,6,7,12–15,17,20–37 have examined the behaviour of nano-confined aqueous solutions in various systems and under different circumstances. Experimentally, the two main approaches are based on the surface force apparatus (SFA) and atomic force microscopy (AFM) with each family of methods offering different modes of operation. The SFA-related methods rely on a well-defined confinement geometry between atomically flat surfaces over a large area (typically several μm2).22,28,31,33,38–41 The distance between the confining surfaces can be measured in an absolute manner using interferometry, and dynamical measurements of the viscoelastic properties of confined aqueous solutions are possible over a range of frequencies (typically 1–3 Hz) using surface force balances (SFB),42 or SFA with resonance detection.33,38,40,41 In contrast, AFM-based methods probe a small number of liquid molecules, typically located between a nanometre sharp tip and an atomically surface.2,43,44 The exact confinement geometry is less well controlled, unless the tip radius is artificially increased.45 This is both a drawback and an advantage over SFA-based methods. On the one hand, AFM is able to probe systems locally, with minimal area averaging, and with sub-nanometre precision in all directions.24,44 AFM allows for molecular-level imaging of the confined liquid,44,46 direct identification of possible contaminant,47 and avoids mesoscale averaging effects. On the other hand, the small confinement area and poor control of the tip geometry can render interpretation of results challenging, especially in the absence of an absolute measurement of the confining gap's thickness.
Recently, both techniques have been used to investigate the effects of dissolved metal ions on the behaviour of nano-confined water.31,32,39,42,48–50 SFB studies indicate that ultrapure water remains mostly fluid even when confined to gaps <3.5 nm, resulting in a 3–5 fold increase in viscosity.22,28,42,49 This result is supported by some theoretical studies,51,52 and explained by a fast rotational and translational dynamics of water molecules under extreme confinement.51 In contrast, AFM measurements suggest anomalous behaviour of nanoconfined water, with an effective viscosity that increases by orders of magnitude for nanoscale gaps between hydrophilic surfaces.17,29 This is also supported by some theoretical studies: Monte Carlo simulations showed that water molecules in contact with mica's ditrigonal cavities exhibit a residence time almost 10 times greater than that of bulk water.30
Dissolving metal salts into the water does not reconcile the techniques. SFB studies show a general tendency for metal ions to increase the lubrication of water films confined between negatively charged mica surfaces, at least for ionic concentrations in the order of 100 mM NaCl.39,42,49 This was interpreted as due to the shear rate being smaller than the hydration shell relaxation rate:50 rapid exchange of water molecules between ions and the mica (in the order of 109 s−1) ensures that the surface-bound hydration layer remains fluid at the shear rates (up to 103 s−1).48 Different ions give rise to a wide range of lubricating properties, usually more effective for ions with a higher charge density39,42 suggesting a more robust Stern layer. In contrast, AFM experiments on various concentrations of NaCl suggest the confined ions act as pinning centres for water molecules, restricting their mobility and increasing the effective elasticity of the system.32
The discrepancies between techniques highlight gaps in our understanding of the behaviour of nano-confined aqueous solutions. The confining constraints and the spatial scale of observations are just but two potential factors responsible for the divergent findings, in particular when taking into account the observed molecular arrangement of the sheared liquid film.33 Ions do not necessarily arrange randomly at the surface of solids, but instead can form organised nanoscale clusters through water-mediated correlations,24 and with millisecond dynamics at the single ion level.23,53 While only a handful of reports evidence mesoscale order (1–100 nm),24,25 its origin would suggest mesoscale effects to be the rule rather than the exception. In nano-shearing experiments, mesoscale order could have significant consequences for the dynamics and lubrication properties of the system depending on the scale considered.23–25,54 Molecular-level measurements also need to address boundary effets55 and any surface singularities that prevent mean field simplifications.
The present study investigates the tribological properties of aqueous solutions confined between an AFM tip and a flat mica surface at the single ion level. We explore the impact of charge density and pH on the viscoelastic response of the nano-confined liquid. The results provide quantitative insights into the lubrication properties of nano-confined solution, including the conditions leading to the breakdown of the simple molecular-level descriptions that neglect system-specific effects.
Experimental
Sample preparation
High-quality V1 muscovite mica disc (SPI Supplies, West Chester, PA, USA) glued to a steel plate was freshly cleaved and rinsed copiously with ultra-pure water (Water AnalaR NORMAPUR, VWR International Ltd, Leicestershire, UK). All the solutions were prepared in ultrapure water with 99.9% pure salts (Sigma-Aldrich, St Louis, MO, USA). pH adjustment was done with a solution of fuming 37% hydrochloric acid (HCl, Merck Millipore, Billerica, MA, USA). No buffering agent was used to avoid interfering with the measurements.56,57 Testing of the pH was also conducted immediately after conducting experiments to ensure stability.Atomic force microscopy measurements
The measurements were performed using a commercial Cypher ES AFM system (Oxford Instruments, Santa Barbara, CA, USA), equipped with temperature control. All the experiments were conducted with silicon nitride cantilevers originating from a same wafer (Olympus RC800 PSA, Olympus, Tokyo, Japan) with a nominal flexural spring constant, kf = 0.39 N m−1. Each cantilever was calibrated using its thermal spectrum58 yielding a typical stiffness of 0.33 (±0.05) N m−1 in solution. Calibration of the torsional cantilever inverse optical lever sensitivity (InvOLS) and spring constant, kt, is a more demanding procedure59 and was hence performed only on 5 cantilevers. We found kt = 184 (±1) N m−1. The calibration procedure is described, in detail, in ESI.†At least, three full sets of measurement (>100 curves each) were obtained in any given solution. For a given series, measurements were first conducted in ultrapure water, followed by monovalent, and then divalent salts. The monovalent ion solutions were tested in no particular order between the different sets in order to minimize the risk of systematic errors. When exchanging solutions within a given series, the tip was thoroughly washed with pure water (20 times with 100 μl) and then with the new solution of interest (40 times with 100 μl). This ensured that only the metal ions of interest were present on the mica surface (see also ESI†). Particular attention was paid to avoid any possible sources of contamination (cleaning procedures detailed in ESI†).47
Imaging of the confined Stern layer and hydration landscape was conducted with sub-nanometre resolution. The AFM was operated in amplitude-modulation using photothermal excitation. The ratio A/A0, between the imaging amplitude and the free amplitude (away from the surface) was kept as high as possible,24 with A between 0.8–1.5 nm. When operating in this regime, atomic level resolution of the interface could be routinely achieved.25,47,60
Shear-force spectroscopy
The shearing measurements were acquired over typically five different locations in each solution (at least three) resulting in ∼100 shear-force curves that were subsequently averaged. The AFM effectively functions as a nanoscopic linear rheometer (1.1 kHz), with sub-nanometre lateral oscillation amplitudes of ∼0.5 nm chosen to equate the distance between two adjacent lattice sites for adsorbed ions.61,62 Standard force–distance curves are then acquired recording simultaneously three quantities: (i) the normal defection of the cantilever, directly related to the confining force/pressure, (ii) the measured shear amplitude, At, and (iii) the phase lag, φt, between the driving shear and the resulting tip motion (see ESI, Fig. S1,† for a representative example).63 The shear amplitude At is always taken as peak to peak throughout this study, and the approaching speed of the tip towards the surface set to 10 nm s−1. For small torsional amplitudes, the magnitude of the time-averaged shear-force, Fshear, can be directly calculated from At:| Fshear = Atkt, | (1) |
In contrast, if φt = 90°, the coupling is perfectly viscous. The average energy dissipated per shear cycle, Ediss, can be calculated from the viscous part of the work carried out by the tip over an oscillation cycle:
| Ediss = 2AtFshear sin(φt). | (2) |
It should be noted that eqn (2) relies on averaged quantities since the instantaneous (oscillating) shear forces and phases are not accessible with our setup. As such, the energy dissipated over a cycle is simply modelled as the product of the viscous component of the shear force and the total distance, 2At, travelled by the tip over a full shear cycle.
Accurate derivation of Fshear and Ediss hinges on a careful calibration of the system and the tip moving perfectly in phase with the driving signal. The system calibration is described, in detail, in ESI,† including control experiments with the tip pinned to the sample (perfectly elastic shear) to confirm that no additional phase lag, induced by possible delays in the mechanical motion of the oscillating scanner, occurs (see ESI, Fig. S2 and S3†).
Since At, φt, and hence Fshear and Ediss depend on the applied confining force, it is useful to present them as functions of the later. In this study, we consistently present Fshear, φt and Ediss as functions of the confining force. We note that if the confinement area is known (typically ∼10 nm2), Fshear and Ediss can also be expressed as functions of the confining pressure. Here, the confining pressure increases by ∼100 MPa for every nanonewton load (nN) applied.
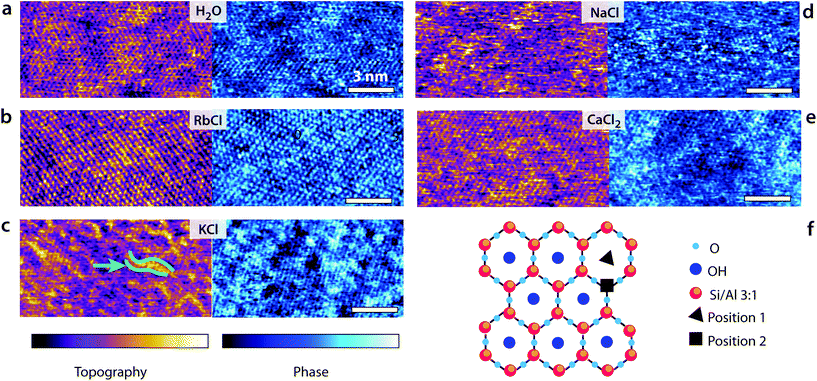
Controlling the confinement is difficult with AFM, and tip asperities can significantly affect the reproducibility of shear force measurements. To address this issue and remove unreproducible tip asperities, each tip was gently ‘blunted’ in a controlled manner at the beginning of the experiments. This resulted in typical tip radii of 15–20 nm (see ESI, Fig. S4†). The quality of the images (Fig. 1) collected with ‘blunted’ tips confirms the tips are still sharp enough for high-resolution imaging.
Analysis and calculations derived from the shear data was performed using homemade routines programmed in Igor Pro (Wavemetrics, Lake Oswego, OR, USA) and Python.
Results and discussion
High-resolution imaging of the confined interface
Fig. 1 presents some high-resolution images of the mica surface in the different solutions. In all cases, atomic-level details are visible, but the quality of the image and the existence of mesoscale order depends on each imaging solution. The mesoscale patterns for the different ions are reproducible over multiple independent experiments. In pure water, the pseudo-hexagonal crystal structure appears clearly both in the topography and phase images. Water molecules form well-ordered hydration layers that extend up to 1 nm in the bulk solution62 and follow the mica lattice arrangements. Adsorbed K+ and Rb+ ions tend to form small domains due to water-mediated attractive lateral interactions when at the interface,23,24 inducing near-uniform looking layer in 5 mM RbCl24 and ordered longitudinal domains in KCl at the same concentration. This is consistent with the hydration structures of Rb+ and K+ ions, with both ions adsorbing mainly in a single hydration state to the mica substrate. In contrast, Na+ ions can adopt different hydration states (inner and outer shell coordination),64 rendering the AFM images less uniform (Fig. 1d). Marked localised height variations are visible resulting in noisier images due to the higher mobility of adsorbed Na+ ions. Divalent Ca2+ ions can also adopt multiple hydration states and adsorb at both the centre of the ditrigonal cavities (position 1 the cartoon in Fig. 1f) and at interstitial sites64 (position 2 in Fig. 1f). Domains similar to those induced by K+ are visible, but Ca2+ ions are bound more strongly to the mica and cannot be easily removed.64Shear-spectroscopy: hard confinement
The high-resolution images shown in Fig. 1 highlight the importance of local hydration effects on the organisation and the behaviour of the different ions at the interface. Order can exist both at the molecular (single-ion) level and at the mesoscale, inducing variations in the hydration landscape of the interface. To single out the impact of single ions on the lubrication of the interface, we conducted shear-force spectroscopy measurements64 with a shearing amplitude At ∼ 0.5 nm, significantly smaller than mesoscale structures. At is also comparable to the smallest distance ions would diffuse when moving between adjacent lattice sites of the mica. Given the ion coverage of mica shown by the high resolution images, we expect, on average, at most one ion to be present between the confining tip and the mica surface, effectively conducting single ion-level nano-tribological measurements.The results, presented in Fig. 2, confirm the lubricating effect of the added ions on the system where they reduce Fshear for a given applied force. The magnitude of the effect depends on the ion's charge density, following a standard Hofmeister series. The phase information shows that while the ions reduce Fshear, they increase the viscosity of the sheared liquid, with φt moving closer to 90° (Fig. 2b). This and the fact that Ediss also decreases when ions are added to the solution suggest that pure water adopts a glassy-like behaviour. Substantial friction between ordered hydration water layers increases the energy dissipated in the system following a mechanism analogous to boundary friction. Consistently, the system exhibits a significant elastic response in pure water. Adding ions ruptures this order and decreases the friction through an increase in local viscosity. In other words, the system appears to evolve towards a more liquid-like behaviour of the interface, better described by hydrodynamic friction. Both theoretical65,66 and experimental studies67,68 have shown that water molecules on mica tend to acquire a crystalline, or ice-like arrangement in the first layer due to the approximate lattice matching between the mica surface and the hexagonal ice basal plane. When under nano-confinement, the diffusion of the water molecules decreases dramatically.23,65
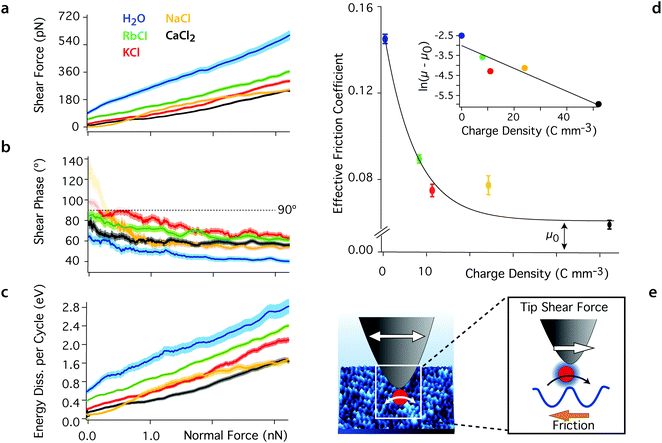 | ||
| Fig. 2 Averaged shear force (a), shear phase (b) and energy dissipated per shear cycle (c) as functions of the confining force for the different aqueous solutions. The thickness of the curves represents the standard error. Added ions decrease the magnitude of the shear force Fshear at any given confining force by comparison with pure water, and the phase, φt, increases to values closer to 90°, indicating a more viscous behaviour of the sheared liquid. At low confining forces (<0.2 nN), the shear amplitude and hence force are close to the experimental noise level and the phase becomes undefined (φt > 90°, semi-transparent region). The energy dissipation, Ediss, also decreases with added ions, indicating less friction. The effective friction coefficient derived from (a) are shown in (d) with their standard error (μwater = 0.142 ± 0.002, μRb = 0.089 ± 0.001, μK = 0.074 ± 0.003, μNa = 0.077 ± 0.004, and μCa = 0.059 ± 0.002). The magnitude of the coefficients decreases exponentially with the ion's charge density (inset in d) as expected from eqn (3) (see text). (e) The tip-driven shear motion of the ions at the surface of the mica lattice is captured by the Prandtl–Tomlinson model: the tip pulls ions between adjacent sites, over an energy barrier related to their hydration energy. All the solutions are at pH 5.38 and ionic solutions contain 5.0 mM salt. The temperature is 25 ± 0.1 °C. | ||
Added ions frustrate the otherwise highly structured hydrogen bond network, limiting the range of intermolecular correlations and competing with the ordered mica surface for water molecules. This results in an increase in mobility for the water molecule in the nano-confined gap,50,69 rendering the sheared solution more viscous. Ions with a larger charge density, ρ, exhibit a more cohesive hydration shell and tend to strongly restructure the water's hydrogen bond network,70–72 leading to better lubrication properties. This is obvious from the difference in the friction coefficients derived for Rb+ and Ca2+ (Fig. 2c). Na+ exhibits a slightly anomalous behaviour that partly challenges this simple description due to its complex adsorption profile.24,64,73,74 The contribution of anions can be neglected here given the important negative surface charge of both confining surfaces. Anions may gather in the upper hydration layers, but X-ray scattering and AFM show a rapid decrease of the degree of ordering in this region, indicating limited impact.75,76
The linear increase of Fshear with the confining force suggests that the system follows a simple hydrodynamic friction that can be characterised by a single, ion-dependent coefficient. Empirically, we find an exponential relationship between the hydrodynamic friction coefficient and the charge density of the cations in the solution:
| μ = μ0 + μHe−λρ, | (3) |
Conceptually, this interpretation is captured by the Prandtl–Tomlinson model77,78 that describes the atomistic friction between a single atom and a periodic surface. Here, this translates as the tip being assimilated to a point mass that pulls single hydrated ions via an elastic spring over the periodic mica lattice. Because of the small amplitude used, ions are repeatedly dragged back and forth between adjacent sites of the lattice. While the Prandtl–Tomlinson model has become famous for its description of the atomistic stick-slip friction, its theoretical framework can also describe smooth sliding friction. This occurs when the energy barrier experienced by the atom moving between two adjacent lattice sites is significantly lower than the energy provided by the pulling spring:
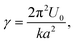 | (4) |
In the present case, the energy barrier, Ea, experienced by hydrated ions moving between adjacent lattice sites of the mica lattice can be deduced from the parameter λ in eqn (3). λ effectively captures the thermally-activated motion of the ions and must hence take the following form:
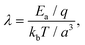 | (5) |
Overall, the model works remarkably well and provides a consistent interpretation of the molecular processes dominating the nano-shearing measurements. The applicability of the model also suggests a profound connection between the solid–solid boundary friction implicitly assumed by the Prandtl–Tomlinson model and the hydrodynamic friction observed here for ions at interfaces: at the nanoscale, hydrodynamic friction can be understood as an extreme case of boundary friction where ions and molecules are pulled across the interface in a low γ regime that enables smooth motion. In this framework, the friction force can then be understood in terms of local solvation effects and disruption of the hydrogen bond network that oppose the motion of the molecule considered at the interface, similarly to U0 in the Prandtl–Tomlinson model.
From a purely thermodynamics perspective, the same process can be explained by the reduced entropy of the confined system whereby the imposed shear force precludes ions from moving randomly at the interfaces and freely probe all the available configurational states. This explains the fact that, for a given applied force, a decrease in the charge density of the added ion increases Fshear and Ediss: ions with lower ρ exhibit a weaker solvation shell that can be easily disrupted by the confining tip. More work is hence needed to compensate for the associated tip-induced entropy reduction.
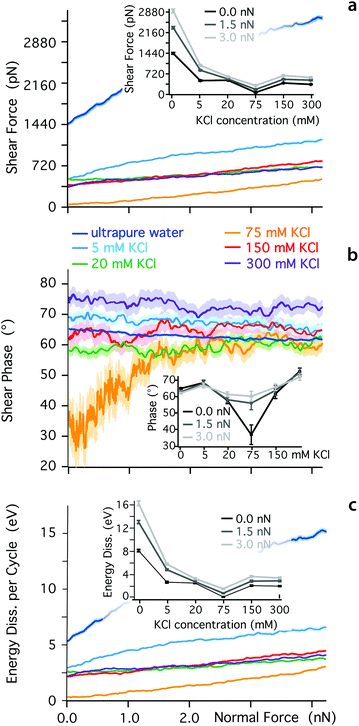
The ionic sequence found here for the effective friction coefficients contrasts with SFB findings.31 This discrepancy could suggest that the two techniques probe different physical phenomena, due to the different sizes in the nano-confined areas they explore. The mesoscale order visible for K+ ions in Fig. 1 is likely to influence SFB measurements, for example inducing local jamming and overlap during the lateral motion of ions and water molecules within the confined layer. Additionally, the ionic concentration probed here is relatively low, to ensure single ion level measurements. At higher concentrations, the confined hydrogen bond network becomes saturated with ions and other effects can take place such as ion-ion friction or the sliding past of dense Stern layers. To explore these effects, we quantified the dependence of Fshear, φt and Ediss on KCl concentration (Fig. 3). At low ionic concentration (<75 mM KCl), the adjunction of ions enhances the lubricating properties of the confined solution, but the solution becomes progressively more elastic under a given applied load already past 5 mM KCl (inset Fig. 3b). Around 75 mM KCl, the system reaches minimum of friction, but through an almost completely elastic behaviour. This could be interpreted as ‘dry’ boundary friction with the K+ ions arranged in such a manner that the confined hydrogen bond network plays a minimal role. At such high concentration, the mica is saturated with cations23,80 and multiple layers of ions may exist between the tip and the surface. Past 75 mM KCl, the lubrication properties of the solution deteriorate, and the response under shear becomes again more viscous. The ionic concentration corresponding to the friction minimum is only approximately identified but the results clearly indicate a non-monotonic behaviour, also confirming previous studies in NaCl.81 Qualitatively, this non-monotonicity should be expected since ions can no longer behave as dissolved ‘point perturbations’ to the hydrogen bond network past a certain concentration, but rather become the dominating feature with its own characteristics. Overall, these results highlight the importance of both spatial and temporal scales as well as ionic concentration when characterising the behaviour of confined fluids.
Shear-spectroscopy: soft confinement
The impact of the cations on the behaviour of the nano-confined water's hydrogen bond network can also be observed further away from the mica surface, with several layers of water and ions between the tip and the surface. This is done by examining changes in Fshear, φt and Ediss as functions of the tip–sample distance. The results of this experiment are shown in Fig. 4. In pure water, Fshear increases already when the tip is still ∼2 nm away from the mica surface. In contrast, Fshear increases only at distances smaller than ∼0.5 nm when salt is added to the solution. No clear trend links ρ and Fshear or Ediss except for an increase in the effective viscosity, consistent with better-ordered interfacial water layers. The effective viscosity ηeff of the nano-confined liquid under shear can be quantified as follows:29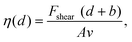 | (6) |
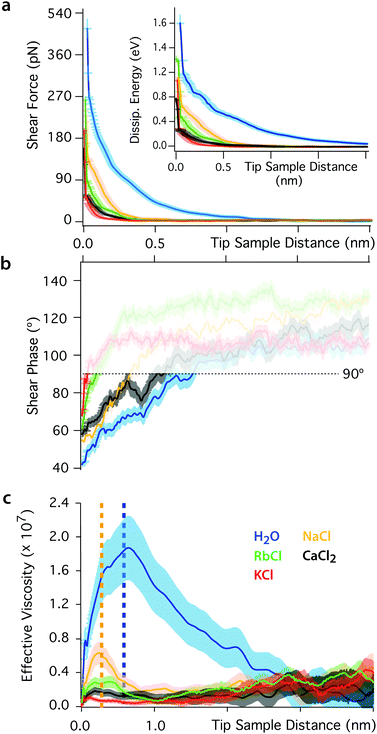 | ||
| Fig. 4 Shear force (a), phase (b) and effective viscosity (c) as functions of the tip–sample distance. The force increases below distances of ∼2 nm in pure water and ∼0.5 nm in ionic solution. The inset in (a) shows the evolution of the energy dissipated per shear cycle. The response of nano-confined water induces a greater dissipation of energy than in ionic solutions. In (b) the phase is undefined at large tip–sample distance due to the shear amplitude and force being close to the noise level (φt > 90°, semi-transparent region). (c) The effective viscosity of the interfacial liquid increases by orders of magnitude in pure water, but changes in ionic solutions are close to the noise limit (except for NaCl). The yellow and blue dotted lines indicate regions where the confinement is smaller than one or two water molecules, respectively. For such small nanogaps, the assumption of continuous fluid implicit to eqn (6) breaks down.17 In the non-contact region, the shearing area is A ∼ 10 nm2. The slip length of mica was taken to be zero.29 | ||
Eqn (6) implicitly assumes a continuous fluid, a hypothesis that tends to break down at very short tip–sample distances where the molecular nature of water can no longer be ignored.17 In pure water, this breakdown is observed for nano-confinement distances smaller than about two water molecules (dotted vertical blue line in Fig. 4b), characterised by a subsequent decrease of ηeff. Interestingly, a second step-like decrease of ηeff can be seen at a distance of ∼0.25 nm (dotted yellow line), the approximate thickness of a single water layer. These observations suggest that the apparent decrease of ηeff can be explained by the tip disrupting ordered, solid-like confined water layers. This is consistent with the significant elastic response of pure water, its glassy-like behaviour and the existence of long-range order in the hydrogen bond network.
The presence of ions dramatically reduces ηeff that decreases only for nano-gaps thinner than a single water layer. This highlights the fact that the ions’ lubricating properties originate from their ability to disrupt the ordered molecular arrangement of nano-confined water molecules, thereby inducing a greater fluidity of the liquid.50,69,70–72
Aside from calculating ηeff, it is also possible to derive the storage, G′, and loss, G′′, moduli of the confined liquid (ESI, Fig. S5†) and obtain an estimate of the system's relaxation time τ:17
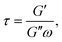 | (7) |
The effect of pH
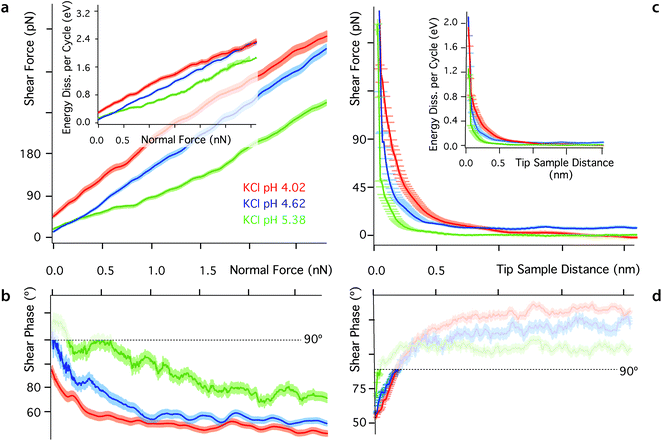
One key aspect of measurements involving nano-confined water is the solution's pH. The hydronium ions compete with dissolved metal cations23,80,84 and the dipole of the water molecules23 for neutralising mica's negative surface charge. As a result, changes in pH can have a dramatic effect on the molecular organisation and dynamics of interfacial water, often with consequences on the interface's tribological properties. At low pH, most of mica's surface charge is neutralised by strongly bound hydronium ions84 and metal ions tend to remain dissolved in the bulk solution due to their comparatively lower affinity for the mica surface.84 To test this interpretation, we conducted shear experiments at three different pH for each of the ionic solutions investigated. Representative results for the KCl solution are presented in Fig. 5. Results in the other solutions exhibit a similar trend and are hence presented in ESI for clarity (Fig. S6–S9†). As the pH decreases, both Fshear and Ediss, increase (Fig. 5a), confirming the replacement of metal cations by hydronium ions. Hydronium ions limit the cations’ ability to disrupt the ordered hydrogen bond network, but have a smaller impact on pure water (see ESI, Fig. S6†) given the similar hydration structures of H3O+ and pure water.35 Dissolved ions can alter the interfacial network, but this is dependent on the charge density of the confining surface itself, which is controlled by the pH.Conclusions
This study combines atomic-level resolution AFM imaging with sub-nanometre shear-force spectroscopy to examine the nano-tribological properties of aqueous solutions under shear down to the single ion level. Results obtained in five different aqueous solutions (ultrapure water, RbCl, KCl, NaCl, and CaCl2) and at different pH show that the behaviour of nano-confined water can be quantitatively interpreted in terms of the restructuring dynamics of its hydrogen bond network. Under strong confinement, the system is dominated by the thermally activated motion of ions between adjacent sites of the confining mica surface, with an energy barrier determined by the mica and the ions’ hydration structures. The ions disrupt the otherwise ordered hydrogen bond network of the liquid and act as lubricants, whose effectiveness follows a direct Hofmeister series. Under softer confinement, the ions still disrupt water's hydrogen bond network, but ion-specificity is no longer obvious. Lowering the pH of the solution tends to replace adsorbed metal ions by hydronium, thereby rendering the system more elastic and increasing the measured friction. High-resolution imaging reveals some mesoscopic ordering of ions within the Stern layer, suggesting that the nanoscale shear force measurements conducted here cannot be extrapolated directly from measurements involving larger confining areas and shear amplitudes. Further studies are needed to investigate the effect of the shearing velocity and extend the current findings to other ionic species, including for potential technological applications in the fields of energy and the design of the ‘ultimate green’ water-based lubricants.12Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the Engineering and Physical Sciences Council (ICASE studentship, grant EP/P510476/1) (CC), the European Council (MC-CIG grant 631186) (KV) and Durham University.References
- O. Björneholm, M. H. Hansen, A. Hodgson, L.-M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen, G. Tocci, E. Tyrode, M.-M. Walz, J. Werner and H. Bluhm, Chem. Rev., 2016, 116, 7698–7726 CrossRef PubMed
.
- T. D. Li, J. Gao, R. Szoszkiewicz, U. Landman and E. Riedo, Phys. Rev. B, 2007, 75, 115415 CrossRef
.
-
M. N. Levy, R. M. Berne, B. M. Koeppen and B. A. Stanton, Berne & Levy principles of physiology, Mosby, 2006 Search PubMed
.
- P. M. Wiggins, Microbiol. Rev., 1990, 54, 432–449 Search PubMed
.
- R. Milke, R. Dohmen, H. W. Becker and R. Wirth, Contrib. Mineral. Petrol., 2007, 154, 519–533 CrossRef
.
- M. Ricci, P. Spijker, F. Stellacci, J.-F. Molinari and K. Voïtchovsky, Langmuir, 2013, 29, 2207–2216 CrossRef PubMed
.
- S. Granick, S. Bae, S. Kumar and C. Yu, Physics, 2010, 3, 18–21 CrossRef
.
- R. J. Mashl, S. Joseph, N. R. Aluru and E. Jakobsson, Nano Lett., 2003, 3, 589–592 CrossRef
.
- F. Ridi, E. Fratini and P. Baglioni, J. Colloid Interface Sci., 2011, 357, 255–264 CrossRef PubMed
.
- H. E. Stanley, S. V. Buldyrev, G. Franzese, P. Kumar, F. Mallamace, M. G. Mazza, K. Stokely and L. Xu, J. Phys.: Condens. Matter, 2010, 22, 284101 CrossRef PubMed
.
- D. Bradshaw, A. Garai and J. Huo, Chem. Soc. Rev., 2012, 41, 2344–2381 RSC
.
- S. Liu, D. Guo and G. Xie, J. Appl. Phys., 2010, 108, 084315 CrossRef
.
- N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Phys. Rev. Lett., 2009, 102, 050603 CrossRef PubMed
.
- E. Tombari, G. Salvetti, C. Ferrari and G. P. Johari, J. Chem. Phys., 2005, 122, 104712 CrossRef PubMed
.
- R. Zangi, J. Phys.: Condens. Matter, 2004, 16, S5371–S5388 CrossRef
.
- T. Mitsui, M. K. Rose, E. Fomin, D. F. Ogletree and M. Salmeron, Science, 2002, 297, 1850–1852 CrossRef PubMed
.
- T. D. Li and E. Riedo, Phys. Rev. Lett., 2008, 100, 106102 CrossRef PubMed
.
- M. J. Dellostritto, J. D. Kubicki and J. O. Sofo, Langmuir, 2016, 32, 11353–11365 CrossRef PubMed
.
- N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Phys. Chem., 2012, 63, 179–200 CrossRef PubMed
.
- S. Smirnov, I. Vlassiouk, P. Takmakov and F. Rios, ACS Nano, 2010, 4, 5069–5075 CrossRef PubMed
.
- L. Liu, S.-H. Chen, A. Faraone, C.-W. Yen and C.-Y. Mou, Phys. Rev. Lett., 2005, 95, 117802 CrossRef PubMed
.
- W. H. Briscoe, S. Titmuss, F. Tiberg, R. K. Thomas, D. J. McGillivray and J. Klein, Nature, 2006, 444, 191–194 CrossRef PubMed
.
- M. Ricci, W. Trewby, C. Cafolla and K. Voïtchovsky, Sci. Rep., 2017, 7, 43234 CrossRef PubMed
.
- M. Ricci, P. Spijker and K. Voïtchovsky, Nat. Commun., 2014, 5, 4400 CrossRef PubMed
.
- K. Voitchovsky and M. Ricci, Proc. SPIE, 2012, 8232, 82320O CrossRef
.
- M. A. Ricci, V. Tudisca, F. Bruni, R. Mancinelli, E. Scoppola, R. Angelini, B. Ruzicka and A. K. Soper, J. Non-Cryst. Solids, 2015, 407, 418–422 CrossRef
.
- D. Argyris, D. R. Cole and A. Striolo, ACS Nano, 2010, 4, 2035–2042 CrossRef PubMed
.
- U. Raviv, S. Perking, P. Laurat and J. Klein, Langmuir, 2004, 20, 5322–5332 CrossRef PubMed
.
- D. Ortiz-Young, H.-C. Chiu, S. Kim, K. Voïtchovsky and E. Riedo, Nat. Commun., 2013, 4, 2482 CrossRef PubMed
.
- A. Malani and K. G. Ayappa, J. Chem. Phys., 2012, 136, 194701 CrossRef PubMed
.
- A. Gaisinskaya-Kipnis, L. Ma, N. Kampf and J. Klein, Langmuir, 2016, 32, 4755–4764 CrossRef PubMed
.
- A. Ulcinas, G. Valdre, V. Snitka, M. J. Miles, P. M. Claesson and M. Antognozzi, Langmuir, 2011, 27, 10351–10355 CrossRef PubMed
.
- G. Zhao, Q. Tan, L. Xiang, D. Cai, H. Zeng, H. Yi, Z. Ni and Y. Chen, J. Chem. Phys., 2015, 143, 104705 CrossRef PubMed
.
- I. Waluyo, C. Huang, D. Nordlund, U. Bergmann, T. M. Weiss, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2011, 134, 064513 CrossRef PubMed
.
- L. Cheng, P. Fenter, K. L. Nagy, M. L. Schlegel and N. C. Sturchio, Phys. Rev. Lett., 2001, 87, 156103 CrossRef PubMed
.
- S. Cerveny, J. Colmenero and A. Alegría, Eur. Phys. J., 2007, 141, 49–52 Search PubMed
.
- W. Qi, J. Chen, J. Yang, X. Lei, B. Song and H. Fang, J. Phys. Chem. B, 2013, 117, 7967–7971 CrossRef PubMed
.
- H. Sakuma, K. Otsuki and K. Kurihara, Phys. Rev. Lett., 2006, 96, 046104 CrossRef PubMed
.
- S. Perkin, R. Goldberg, L. Chai, N. Kampf and J. Klein, Faraday Discuss., 2009, 141, 399–413 RSC
.
- C. D. Dushkin and K. Kurihara, Colloids Surf., A, 1997, 129, 131–139 CrossRef
.
- H. Kawai, H. Sakuma, M. Mizukami, T. Abe, Y. Fukao, H. Tajima and K. Kurihara, Rev. Sci. Instrum., 2008, 79, 043701 CrossRef PubMed
.
- U. Raviv and J. Klein, Science, 2002, 297, 1540–1543 CrossRef PubMed
.
- S. H. Khan, G. Matei, S. Patil and P. M. Hoffmann, Phys. Rev. Lett., 2010, 105, 106101 CrossRef PubMed
.
- T. Fukuma, K. Kobayashi, K. Matsushige and H. Yamada, Appl. Phys. Lett., 2005, 87, 034101 CrossRef
.
- D. Naumenko, V. Snitka, E. Serviene, I. Bruzaite and B. Snopok, Analyst, 2013, 138, 5371–5383 RSC
.
- A. Shiotari and Y. Sugimoto, Nat. Commun., 2017, 8, 14313 CrossRef PubMed
.
- E. J. Miller, W. Trewby, A. Farokh Payam, L. Piantanida, C. Cafolla and K. Voïtchovsky, J. Visualized Exp., 2016, 118, e54924 Search PubMed
.
- J. Klein, U. Raviv, S. Perkin, N. Kampf, L. Chai and S. Giasson, J. Phys.: Condens. Matter, 2004, 16, S5437–S5448 CrossRef
.
- J. Klein, Friction, 2013, 1, 1–23 CrossRef
.
- A. Gaisinskaya, L. Ma, G. Silbert, R. Sorkin, O. Tairy, R. Goldberg, N. Kampf and J. Klein, Faraday Discuss., 2012, 156, 217–233 RSC
.
- Y. Leng and P. T. Cummings, Phys. Rev. Lett., 2005, 94, 026101 CrossRef PubMed
.
- A. Malani, K. G. Ayappa and S. Murad, J. Phys. Chem. B, 2009, 113, 13825–13839 CrossRef PubMed
.
- S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Nat. Commun., 2017, 8, 15826 CrossRef PubMed
.
- I. Siretanu, D. Ebeling, M. P. Andersson, S. L. S. Stipp, A. Philipse, M. C. Stuart, D. van den Ende and F. Mugele, Sci. Rep., 2015, 4, 4956 CrossRef PubMed
.
- F. H. J. Van Der Heyden, D. J. Bonthuis, D. Stein, C. Meyer and C. Dekker, Nano Lett., 2007, 7, 1022–1025 CrossRef PubMed
.
- W. Trewby, D. Livesey and K. Voïtchovsky, Soft Matter, 2016, 12, 2642–2651 RSC
.
- L. Piantanida, H. L. Bolt, N. Rozatian, S. L. Cobb and K. Votchovsky, Biophys. J., 2017, 113, 426–439 CrossRef PubMed
.
- H.-J. Butt and M. Jaschke, Nanotechnology, 1995, 6, 1–7 CrossRef
.
- N. Mullin and J. K. Hobbs, Rev. Sci. Instrum., 2014, 85, 113703 CrossRef PubMed
.
- K. Voitchovsky, J. J. Kuna, S. A. Contera, E. Tosatti and F. Stellacci, Nat. Nanotechnol., 2010, 5, 401–405 CrossRef PubMed
.
- M. Urbakh, J. Klafter, D. Gourdon and J. Israelachvili, Nature, 2004, 430, 525–528 CrossRef PubMed
.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101 CrossRef PubMed
.
- K. Voïtchovsky, Nanoscale, 2016, 8, 17472–17482 RSC
.
- K. Kobayashi, Y. Liang, S. Murata, T. Matsuoka, S. Takahashi, N. Nishi and T. Sakka, Langmuir, 2017, 33, 3892–3899 CrossRef PubMed
.
- Y. Leng and P. T. Cummings, J. Chem. Phys., 2006, 124, 074711 CrossRef PubMed
.
- M. Odelius, M. Bernasconi and M. Parrinello, Phys. Rev. Lett., 1997, 78, 2855 CrossRef
.
- A. Verdaguer, G. M. Sacha, H. Bluhm and M. Salmeron, Chem. Rev., 2006, 106, 1478–1510 CrossRef PubMed
.
- P. B. Miranda, L. Xu, Y. R. Shen and M. Salmeron, Phys. Rev. Lett., 1998, 81, 5876 CrossRef
.
- J. S. Kim and A. Yethiraj, J. Phys. Chem. B, 2008, 112, 1729–1735 CrossRef PubMed
.
- B. Hribar, N. T. Southall, V. Vlachy and K. A. Dill, J. Am. Chem. Soc., 2002, 124, 12302–12311 CrossRef PubMed
.
- I. A. Topol, G. J. Tawa, S. K. Burt, S. K. Burt and A. A. Rashin, J. Chem. Phys., 1999, 111, 10998–11014 CrossRef
.
- J. E. Combariza and N. R. Kestner, J. Phys. Chem., 1995, 99, 2717–2723 CrossRef
.
- S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Langmuir, 2012, 28, 8637–8650 CrossRef PubMed
.
- H. Sakuma and K. Kawamura, Geochim. Cosmochim. Acta, 2011, 75, 63–81 CrossRef
.
- S. Pintea, W. De Poel, A. E. F. De Jong, V. Vonk, P. Van Der Asdonk, J. Drnec, O. Balmes, H. Isern, T. Dufrane, R. Felici and E. Vlieg, Langmuir, 2016, 32, 12955–12965 CrossRef PubMed
.
- K. Kimura, S. Ido, N. Oyabu, K. Kobayashi, Y. Hirata, T. Imai and H. Yamada, J. Chem. Phys., 2010, 132, 194705 CrossRef PubMed
.
- E. Gnecco, R. Bennewitz, T. Gyalog and E. Meyer, J. Phys.: Condens. Matter, 2001, 13, 619–642 CrossRef
.
- R. Guerra, A. Vanossi and M. Urbakh, Phys. Rev. E, 2010, 78, 03611 Search PubMed
.
- A. Erbaş, D. Horinek and R. R. Netz, J. Am. Chem. Soc., 2011, 134, 623–630 CrossRef PubMed
.
- C. Park, P. A. Fenter, K. L. Nagy and N. C. Sturchio, Phys. Rev. Lett., 2006, 97, 016101 CrossRef PubMed
.
- S. H. Khan, E. L. Kramkowski and P. M. Hoffmann, Langmuir, 2016, 32, 10802–10807 CrossRef PubMed
.
- J. Kestin, M. Sokolov and W. A. Wakeham, J. Phys. Chem. Ref. Data, 1978, 71, 941–948 CrossRef
.
- T. D. Li, H. C. Chiu, D. Ortiz-Young and E. Riedo, Rev. Sci. Instrum., 2014, 85, 123707 CrossRef PubMed
.
- C. Park, P. A. Fenter, N. C. Sturchio and K. L. Nagy, Langmuir, 2008, 24, 13993–14004 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary methods and Fig. S1–S9. See DOI: 10.1039/c8nr02859a |
| This journal is © The Royal Society of Chemistry 2018 |