Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanisms behind the enhancement of thermal properties of graphene nanofluids†
M. R.
Rodríguez-Laguna
 *ab,
A.
Castro-Alvarez
*ab,
A.
Castro-Alvarez
 c,
M.
Sledzinska
c,
M.
Sledzinska
 a,
J.
Maire
a,
J.
Maire
 a,
F.
Costanzo
a,
F.
Costanzo
 a,
B.
Ensing
a,
B.
Ensing
 ad,
M.
Pruneda
ad,
M.
Pruneda
 a,
P.
Ordejón
a,
P.
Ordejón
 a,
C. M.
Sotomayor Torres
a,
C. M.
Sotomayor Torres
 ae,
P.
Gómez-Romero
ae,
P.
Gómez-Romero
 a and
E.
Chávez-Ángel
a and
E.
Chávez-Ángel
 *a
*a
aCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC and BIST, Campus UAB, Bellaterra, 08193 Barcelona, Spain. E-mail: rocio.rodriguez@icn2.cat; emigdio.chavez@icn2.cat
bDepartament de Química, Universitat Autònoma de Barcelona, Cerdanyola del Vallès, 08193 Barcelona, Spain
cOrganic Chemistry Section, Facultat de Química, Universitat de Barcelona, Av. Diagonal 645, 08028 Barcelona, Catalonia, Spain
dVan't Hoff Institute for Molecular Sciences, University of Amsterdam, 1098 XH Amsterdam, The Netherlands
eICREA, Pg. Lluís Companys 23, 08010 Barcelona, Spain
First published on 7th August 2018
Abstract
While the dispersion of nanomaterials is known to be effective in enhancing the thermal conductivity and specific heat capacity of fluids, the mechanisms behind this enhancement remain to be elucidated. Herein, we report on highly stable, surfactant-free graphene nanofluids, based on N,N-dimethylacetamide (DMAc) and N,N-dimethylformamide (DMF), with enhanced thermal properties. An increase of up to 48% in thermal conductivity and 18% in specific heat capacity was measured. The blue shift of several Raman bands with increasing graphene concentration in DMF indicates that there is a modification in the vibrational energy of the bonds associated with these modes, affecting all the molecules in the liquid. This result indicates that graphene has the ability to affect solvent molecules at long-range, in terms of vibrational energy. Density functional theory and molecular dynamics simulations were used to gather data on the interaction between graphene and solvent, and to investigate a possible order induced by graphene on the solvent. The simulations showed a parallel orientation of DMF towards graphene, favoring π–π stacking. Furthermore, a local order of DMF molecules around graphene was observed suggesting that both this special kind of interaction and the induced local order may contribute to the enhancement of the fluid's thermal properties.
Introduction
Heat transfer fluids (HTFs) play an important role in a wide range of applications. Vehicles, microelectronics and industrial processes require the use of coolants to dissipate the heat produced and thus prevent overheating. However, the functionality of HTFs is not limited to this single role: heat transfer plays a key part in energy conversion applications and thermal storage.Water, ethylene glycol, oils, etc. are widely used as HTFs,1 but a major problem with these conventional coolants is the low heat exchange rate and thermal conductivity (k), typically between 0.06–0.6 W m−1 K−1.1 These values are not high enough to meet the coming needs and challenges of the industry, such as in the field of microelectronics, where temperature control has become crucial for an adequate and reliable performance of the electronic components. The high demand for HTFs with superior performance in terms of heat transfer efficiency has led to the development of a variety of novel nanofluid (NF) materials, formed by solid nanoparticles (NPs) dispersed in a base fluid. Numerous studies have revealed that the thermal properties of a fluid can be improved remarkably by the dispersion of nanoparticles, such as specific heat capacity and thermal conductivity,2–9 and in the case of the latter by more than 20%.5–11
The enhancement of k has been commonly observed in NFs and there is still an ongoing debate to explain it. This work sheds some light on the possible causes of this enhancement. In previous studies, various mechanisms have been suggested to explain thermal conductivity enhancement, such as: (i) an increase in thermal transfer due to Brownian motion of nanoparticles;12,13 (ii) localized convection created in the fluid due to Brownian motion of nanoparticles;13–15 (iii) agglomeration of nanoparticles;12,16,17 (iv) enhanced thermal energy transfer due to increased interatomic interactions arising from the interatomic potential;15,18 (v) layer-like ordered liquid around the solid;12 and (vi) ballistic phonon transport of heat through solid nanoparticles.12
In this paper, all of these mechanisms are discussed and considered in the particular case of graphene–amide NFs. Herein, we report a simple NF system in which a surfactant free nanomaterial is dispersed in an organic fluid. This approach was chosen because the presence of a surfactant can result in additional complexity in modeling and interpreting the enhancement of the thermal properties.19,20 Consequently, the experimental and theoretical data obtained from this book-example system can provide valuable information regarding the interaction between a nano-solid and the fluid molecules. This work also seeks to address how the presence of a small concentration of nanomaterial is capable of modifying the macro-properties of the fluid. The solvents, N,N-dimethylacetamide (DMAc) and N,N-dimethylformamide (DMF), were used to prepare graphene NFs because they form highly stable graphene dispersions. Moreover, these fluids possess a higher boiling point than most coolants, e.g. water. Graphene was selected as the additive material due to its extraordinary thermal conductivity (above 2000 W m−1 K−1) and non-toxicity.21,22 Furthermore, graphene-based nanofluids have also attracted great attention due to the wide range of fields they can be applied in, including liquid electrodes for energy storage and flexible electronics, among others.23–26 We determined experimentally the influence of graphene concentration on thermal conductivity, heat capacity (Cp), sound velocity (vs) and Raman spectra. Additionally, molecular dynamics (MD) and density functional theory (DFT) were used to study the interaction between graphene and amide molecules and a possible local order close to the graphene flake, as previously done with other nanofluid systems.27 Our study provides considerable insight into the field of thermal transport in dynamic systems, such as liquids and NFs, thereby addressing a fundamental problem in NFs.
Results
Thermal conductivity and specific heat capacity studies
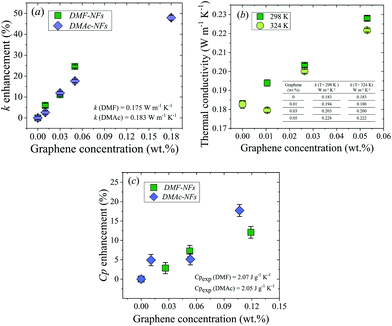
Thermal conductivity measurements of the DMAc and DMF graphene NFs were performed using the 3ω technique at 298 K and 324 K. In contrast to other techniques used for thermal conductivity characterization (e.g. hot transient wire), the three-omega method works in a very fast time window (10–200 Hz). Therefore, it mostly suppresses the interference from convection, for which the effect decreases with frequency.28 Three concentrations of DMF nanofluids ranging from 0.01 to 0.05 wt% of graphene dispersed in DMF and four concentrations of graphene dispersed in DMAc nanofluids ranging from 0.01 to 0.18 wt% were measured along with the bare fluids. Hereafter, for convenience, sample names will be shortened by omitting ‘wt% of graphene dispersed in’, for example: 0.01 wt% of graphene dispersed in DMAc will henceforth be written as 0.01% DMAc. The thermal conductivity enhancement of the NFs at room temperature compared to the bare fluids is shown in Fig. 1a as a function of graphene concentration. A progressive and almost linear enhancement can be observed in both sets of NFs as a function of graphene concentration. The largest enhancement (∼48%) was obtained with 0.18% DMAc NF. The thermal conductivity data are summarized in Tables S3 and S4 in the ESI.†The thermal conductivity as a function of graphene concentration for two different temperatures, T = 298 K (green solid squares) and 324 K (light green solid circles), is shown in Fig. 1b. As can be seen, the thermal conductivity of DMF-NFs tends to decrease as temperature increases, exhibiting the same temperature behavior as with common organic fluids.29
The specific heat capacities (Cp) of the base fluids and graphene–DMAc and –DMF NFs were measured using differential scanning calorimetry (DSC) at 293 K. The study of the influence of graphene concentration on the specific heat capacity of the nanofluids was carried out using concentrations in the range of 0.01–0.12% for both DMAc and DMF.
The progressive enhancement of the specific heat capacity as a function of graphene concentration for DMAc and DMF-based fluids is shown in Fig. 1c. The largest enhancement (∼18%) was obtained with 0.11% DMAc NF.
The viscosity of the NFs was also measured as a function of graphene concentration. A relevant increment of the viscosity was found on increasing graphene loadings (see the ESI†).
Analysis of vibrational spectra
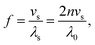 | (1) |
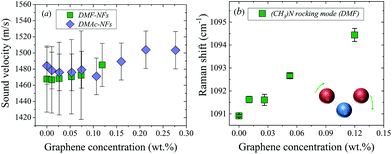
The Raman spectra of DMF NFs and the bare fluid were recorded, as shown in Fig. S4 in the ESI.† The peak position of the Raman mode at 1090 cm−1 is plotted in Fig. 2b as a function of graphene concentration. This band corresponds to an asymmetric bending vibration in a plane (rocking) of the bond ‘(CH3)N’ of the DMF molecule.36 The Raman spectra at 1090 cm−1 at different concentrations of graphene show a continuous displacement to higher frequencies and a broadening of the mode with increasing graphene concentration (see Fig. S4 in the ESI†). Similarly, the band centered at 1438 cm−1, v(C–N) stretching, undergoes a shift to higher frequencies with increasing graphene concentration, as shown in Table 1.
| Experimental frequencies [cm−1] | Theoretical frequencies [cm−1] | ||||
|---|---|---|---|---|---|
| B3LYP/6-311G(d, p) | ωB97X-D3/6-311G(d, p) | ||||
| DMF | 0.05 wt% | DMF | A | DMF | A |
| 1090.9 | 1092.6 | 1092.9 | 1096.3 | 1103.0 | 1108.5 |
| 1438.5 | 1439.8 | 1430.7 | 1443.7 | 1452.0 | 1448.2 |
Discussion
As the results show, the presence of graphene in the NFs impacts all the measured properties, i.e., thermal conductivity, specific heat capacity, sound velocity and vibrational Raman modes. The enhancement of k has been commonly observed in NFs and there is still an ongoing debate to explain it. Different mechanisms have been suggested, such as: (i) an increase in thermal transfer due to Brownian motion of nanoparticles;12,13 (ii) localized convection created in the fluid due to Brownian motion of nanoparticles;13–15 (iii) agglomeration of nanoparticles;12,16 (iv) enhanced thermal energy transfer due to increased interatomic interactions arising from the interatomic potential;15,18 (v) layer-like ordered liquid around the solid;12 and (vi) ballistic phonon transport of heat through solid nanoparticles.12Assuming that the Brownian motion mechanisms (i and ii) are correct, if the temperature increases, then the overall speed of the particles will be higher and consequently k should also increase. However, as shown in Fig. 1b, k decreases when the temperature increases, therefore such a mechanism does not explain our results. In addition, Keblinski et al.12 showed that the movement of nanoparticles, due to Brownian motion, is too slow to transport significant amounts of heat through a nanofluid, even in the case of extremely small particles. This conclusion is supported by molecular dynamics simulations.12 Similarly, a localized convection caused by Brownian motion can also be discarded.13 The NP agglomeration model (iii) can explain the enhancement of k in unstable NFs and is time dependent.16 The formation of large aggregates, up to a certain size, can enhance k even further due to local percolation behavior. In our case, the DLS results showed a constant particle size and concentration over time. Additionally, the average graphene size observed using TEM is in good agreement with the DLS results, demonstrating that no agglomeration occurred (see the ESI†). Moreover, a constant k was measured in different samples as a function of time (months), demonstrating that this mechanism cannot explain our results.
Raman spectroscopy was used as a tool to determine the plausibility of applying theory (iv) to our nanofluids. If graphene induces a modification of the interatomic interactions in the fluid, the Raman spectrum should be affected. As can be seen in Fig. 2b and Table 1, two Raman modes of DMF shifted to higher frequencies with increasing graphene concentration. Remarkably, the bands exhibiting larger displacements were the ones corresponding to carbon–nitrogen bonds: N–(CH3) (≈ 1090 cm−1) and C–N (≈ 1438 cm−1). The displacement of the band ≈1090 cm−1 was around 4 cm−1 for 0.12% graphene–DMF nanofluid. This band corresponds to an asymmetric rocking vibration from the bond ‘N–(CH3)’.36 The displacement of these bands to higher frequencies in the presence of graphene physically could be interpreted as the C–N bond becoming more rigid, needing more energy to vibrate, with increasing graphene concentration. This interpretation leads us to suggest that graphene somehow affects the interaction between the solvent molecules, resulting in a strong modification of the interatomic potential as a function of graphene concentration, as model (iv) suggests.
Some authors claim that the weak interplanar bonding in graphite is merely due to van der Waals interactions. However, graphite does not show the same behavior as typical molecular (van der Waals) crystals.37 Nevertheless, the delocalization of π electrons seems to play an important role in the interaction (stacking) between layers. Similarly, the nitrogen, oxygen and carbonyl carbon atoms in both DMF and DMAc all have sp2 hybridization, and hence p orbitals perpendicular to the O–C–N plane which allow electron delocalization.38 The quasi-planarity of the solvent molecules and the sp2 hybridization favor the π–π stacking if the solvent molecules are in a parallel orientation with respect to the graphene flakes. Therefore, it is reasonable to suggest that a π–π bond is formed between the solvent molecules and the graphene surface. This interaction would then increase the rigidity of C–N bonds of the molecules closest to the graphene, and consequently, modify their Raman spectra, as shown in Table 1. This table shows the calculated Raman frequencies of a simple system (A), consisting of three molecules of DMF parallel to a graphene flake and the experimental Raman frequencies of DMF and 0.05% DMF. As can be seen, the calculated Raman modes as a function of graphene concentration exhibit a consistent shift to higher frequencies by an amount in agreement with the experimental spectra.
Gong et al.39 reported a similar interaction, particularly a π–π+ stacking, between sp2 carbon in an amorphous carbon surface and imidazolium cation. The imidazolium ring is a delocalized π system and could adopt a parallel orientation to the solid substrate interacting with sp2 π electrons, as argued by Gong et al.39 Xu et al. described a comparable scenario where chemically converted graphene induced molecular flattening of a porphyrin-based molecule through electrostatic and π–π stacking cooperative interactions.40 However, this interaction does not explain the shift of the whole band at 1090 cm−1 with increasing graphene concentration.
In order to test our interpretation in terms of orientation of the solvent molecules to graphene surfaces, theoretical simulations using a combination of density functional theory (DFT) and molecular dynamics (MD) calculations were performed (see the ESI†). The MD calculations showed that the most frequent DMF orientation with respect to graphene was the parallel one. We found that three parallel configurations, labelled as A, B and C, presented the highest occurrence of 59.7%, 17.6% and 8.1%, respectively, compared to all other possible DMF orientations (see Fig. S12 in the ESI†). These configurations represent simple systems consisting of three (A and B) or two (C) DMF molecules around a graphene flake. Subsequently, these configurations were used as inputs for DFT simulations. It was found that these parallel configurations were the most energetically favorable, facilitating π–π stacking (see Fig. S10, and 12–14 in the ESI†).
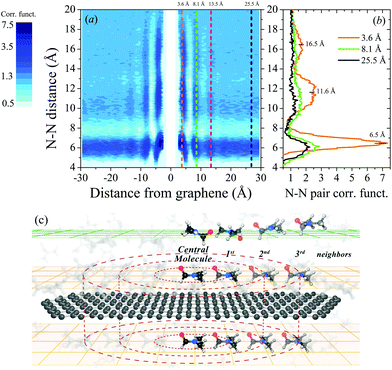
To investigate a possible order of DMF molecules near graphene (model v), the nitrogen–nitrogen (N–N) pair-correlation function (PCF) of DMF molecules was calculated. Fig. 3a shows the contour plot of the N–N PCF as a function of graphene distance and N–N pair distances. This plot represents the relative density of nitrogen atoms around a central nitrogen atom as a function of its distance to graphene. In this particular case, the plot provides information about the distance between DMF molecules (N–N distance) in all possible parallel planes with respect to graphene. Fig. 3c schematically illustrates the surroundings of a graphene flake, where layers of DMF at different distances from the graphene flake are represented. The scheme shows that in the nearest layers of DMF to the graphene flake (orange planes) DMF molecules are parallelly oriented towards the graphene flake. A central molecule of DMF and its first, second and third neighbors are represented in the layers on top and above the graphene flake.
Three vertical cuts of the contour plot (Fig. 3a) at 3.6, 8.1 and 25.5 Å distance from the graphene are displayed in Fig. 3b. These representative cuts were selected based on the relatively high density of DMF molecules at certain N–N distances as shown in Fig. 3a. At a distance of 3.6 Å from the graphene flake, DMF molecules show a large degree of ordering, similar to that of a crystal: the first (∼6.5 Å), second (∼11.6 Å) and third (∼16.5 Å) neighbors can be identified (also called coordination shells). At least three layers of ordered DMF can be observed at 3.6, 8.1 and 13.5 Å from the graphene flake, which is remarkable considering that the flake radius is only 16.5 Å; hence, on larger flakes even longer-ranged ordering may be expected. Fig. 3a clearly shows that these three layers of DMF molecules have a higher density of DMF molecules at different N–N distances, although the effect is lost thereafter (see the ESI† for details). As the distance of DMF molecules from the graphene flake increases, the dynamic solid-like behavior of DMF is lost and it starts to behave as a normal liquid (just the first neighbors can be identified). Akıner et al. reported a similar nanolayer formation of water in the vicinity of hexagonal boron nitride.41
The interaction between the graphene and DMF molecules also induces a shift in the maxima of peaks in PCF as shown in Fig. 3b. The first peak (first neighbors) corresponding to a plane of molecules of DMF at 3.6 Å of graphene is shifted compared to the first peaks corresponding to the planes at 8.1 and 25.5 Å from the graphene flake. This indicates a rearrangement of the molecules on the graphene flake. Close to graphene DMF molecules tend to lay parallel to the flake, as mentioned before, requiring a larger N–N distance in the first coordination shell (see orange solid line in Fig. 3b). A shifting of the second peak is also observed.
The above discussion suggests that the local order of solvent molecules near the graphene flake, the parallel configuration and the possible π–π stacking are plausible key factors to explain the high dispersibility of graphene in DMF and DMAc.42 The same mechanism can also explain the high dispersibility of graphene in other amides, such as N-methyl-2-pyrrolidone (NMP).42
Delving deeper into the experimental Raman spectra of DMF NFs, the associated symmetric shape of the band at ∼1090 cm−1, indicates that, to a greater or lesser extent, all DMF molecules are affected by the graphene flakes, in terms of the energy associated with this DMF vibrational mode. This unexpected result has been studied theoretically here; however, no explicit order was found beyond the third DMF layer above the graphene flake. If the DMF molecules near graphene were the only molecules affected by the presence of the graphene flake, the band at 1090 cm−1 should not shift and a weak shoulder would appear at higher frequencies as evidence of a fraction of DMF molecules acquiring a stronger bond.
Finally, our findings demonstrate that both this particular molecular interactions and local order mechanisms of the solvent molecules around graphene are present in the NFs as models (iv) and (v) suggested. Concerning model (vi), as the mean free path of phonons in graphene covers a large range (40–800 nm)43,44 and the size of our graphene flakes varies from 150 to 450 nm, it is conceivable that phonons with a certain range of mean free path also contribute to the enhancement of k.
In fact, flakes of such sizes have been reported to display very high thermal conductivity.45 As mentioned above, graphene flakes with those sizes were able to induce a liquid layering effect, in agreement with model (v), which in turn reduces the thermal boundary resistance between the flakes and the liquid.46 Shahil et al.47 separately showed that the thermal conductivity of a graphene-based nanocomposite increased with the graphene loading due to the low thermal boundary resistance between the flakes and the matrix. Both studies highlighted the fact that a strong enhancement of thermal conductivity requires the presence of thin flakes, albeit not exclusively. One of the reasons for the smaller thermal conductivity enhancement of nanofluids compared to nanocomposites might be attributed to the higher interface thermal resistance between graphene flakes and liquids, as can be seen on comparing the results from Shahil et al.47 and Alexeev et al.46
In a nanocomposite, the thermal conductivity enhancement can also be further improved by giving a specific orientation to the flakes,48 which might also occur in our nanofluids.
Regarding the enhancement of Cp exhibited by our NFs, similar enhancements in analogous NFs have been reported previously, e.g. for graphite nanoplatelets (NPts), Nelson et al.49 showed a 50% enhancement of Cp of polyalphaolefin with 0.6 wt% of graphite NPts with a thickness of ∼100 nm and diameters ∼20 μm. Xie et al.50 reported enhancements of ∼8% and 17% for molten salt-based NFs with concentrations of 0.5% and 1.0 wt% graphite NPts (thickness ∼2–5 nm and diameters ∼10–20 μm).
In the case of oxide nanoparticles (NPs), Shin and Banerjee also reported a 26%51 and 14.5%3 enhancement in molten salt using SiO2 NPs with a concentration of 1 wt%. Similarly, Qiao et al.52 found an enhancement of 15.7% in other molten salts with the same concentration and NPs. Sang and Liu53 also showed a huge enhancement of Cp in ternary-based NFs with different NPs. They measured enhancement of 79.9–113.7% for SiO2, 50.6–73.9% for CuO, 31.1–56.5% for TiO2 and 50.6–66.5% for Al2O3 nanoparticles with concentrations up to 1 wt%.
While it is well known that the addition of small amounts of nanomaterials (<1 wt%) could lead to the enhancement of Cp, the mechanism behind is still under debate. In certain simple cases it has been shown that the Cp of the NFs can be explained using the mixing theory of ideal gas mixtures.54 However, it has been demonstrated that this approach fails for some NFs, where the Cp of the NPs is lower or in the order of the bare fluids. Shin and Banerjee identified three mechanisms to understand the enhancement of Cp:3 (i) higher Cpof NPs in comparison with their bulk counterpart: this enhancement of Cp is well known and it comes from the discretization of the phonon spectra and the modification of the phonon density of states.55–58 (ii) High solid–fluid interaction: the high surface area per unit mass of the NPs induces an increase in the interfacial thermal resistance (ITR) between the NPs and the surrounding fluid molecules. The increase in the ITR acts as additional thermal storage.14,59 (iii) Nanolayering of the liquid molecules around the NPs: the existence of this solid-like layer is likely to have enhanced specific heat due to the smaller intermolecular spacing in comparison with the bare fluid.3
Mechanism (i) cannot explain completely the enhancement of Cp in our samples. Due to the lateral sizes of the graphene flakes, it is not small enough to see the “phonon confinement effect”, and we do not expect a strong modification in the phonon spectra. But, if we consider that as the thickness of the flakes is below 10 nm, the heat capacity can be affected by the emergence of new phonon modes, such as breathing and shear vibrations.60 However, due to these modes having a very low energy (∼20–80 cm−1, 2.5–10 meV) we do not expect an important contribution at room temperature.61,62
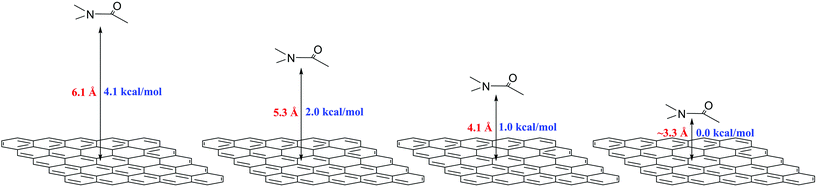
Regarding model (ii) (high solid-fluid interaction), Xue et al.63 demonstrated that for nanofluids characterized by weak atomic bonding (compared with solid–solid) at the particle–fluid interface, they exhibit high thermal resistance. In our case, the strength of the π–π interaction for the parallel configuration fluctuates between 4.1–1.0 [kcal mol−1] (see Fig. 4). The weak strength of the π–π stacking and the possible high thermal resistance together with the formation of the nanolayering (model iii) around the graphene flakes could explain the enhanced Cp observed in this work.
Recently, Hentschke64 discussed other possible mechanisms caused by mesolayers of the liquid molecules around the NPs and their interaction with other mesolayers. These mesolayers should have higher Cp compared with the bare fluid and they should extend far beyond the NPs with extensions about 4 times the diameters of the NPs. While this theory matches quite well with the cases presented in the work of Hentschke, our results did not show a layering beyond 18 Å, i.e., in the same order as the lateral size of the graphene flakes.
Conclusions
Highly stable graphene dispersions over time in DMAc and DMF with enhanced thermal properties were prepared. The influence of graphene concentration on thermal conductivity, specific heat capacity and speed of sound was measured showing an enhancement of all these properties with increasing graphene concentration. We measured a 48% enhancement in the thermal conductivity of 0.18% DMAc-based nanofluid, demonstrating that only a small amount of dispersed graphene is required to induce a large enhancement of the overall thermal properties compared with the base fluid. Furthermore, a 0.11 wt% of graphene in the same fluid resulted in an 18% improvement in specific heat capacity. Finally, the Raman scattering results and the simulations lend support to the idea of stronger intermolecular interaction between the solvent and the graphene flakes than initially thought.The Raman spectra analysis indicated that the intermolecular interaction between DMF molecules is modified when graphene is present, affecting the whole liquid. Furthermore, the theoretical studies suggested that the interaction between graphene and the nearest DMF molecules is stronger than initially thought. These molecules tend to lay parallel to the graphene flake favoring a possible π–π stacking. A local order of the DMF molecules up to three layers was also observed in the simulations.
These results represent an excellent initial step toward understanding the manner in which NPs modify the fluid arrangement directly affecting thermal transport. NFs are commonly highly diluted systems; therefore, it is the properties of the NPs and fluid molecule atoms at the points of intermolecular contact which are important in assessing the type of interaction. It clearly depends on the nature of the NPs and fluid molecules. It is also important to remark that the interaction between graphene and DMF is the key factor explaining the high dispersibility of graphene in DMF, DMAc and NMP.
Our results suggest that the presence of graphene produces important changes at the macroscopic level in organic base fluids, with the result that the dispersal of tiny concentrations of graphene produces a large improvement in the overall thermal properties of DMF and DMAc. This revealing finding demonstrates the applicability of these types of nanofluids as efficient, heat transfer materials. Furthermore, the small concentrations of graphene help to minimize contamination and can reduce possible sedimentation problems and the final costs of heat transfer fluids.
Methodology
Sample fabrication
Graphene flakes with lateral sizes ∼150–450 nm and thicknesses from 1 to 10 layers were prepared from graphite (Sigma-Aldrich, purity >99+% and size <20 μm) by a mechanical exfoliation method, similar to that used by Hermann et al.65 An extended explanation of sample preparation is included in the ESI.†Characterization
Several experimental techniques were used to obtain a complete structural, thermal and spectroscopic characterization of the fluids, including transmission electron microscopy (TEM), differential scanning calorimetry (DSC) and Raman and Brillouin spectroscopy. The thermal conductivity was obtained using a modified three-omega (3ω) method based on the work of Oh et al.66 (see the ESI†). Finally, the stability of the dispersions was studied over time by regular tests every month for four months using dynamic light scattering (DLS). An extended description of the preparation of the NFs and characterization techniques can be found in the ESI.†Author contributions
MRRL and PGR fabricated the samples. MRRL carried out DSC, DLS and TEM measurements and analyses. MRRL, ECA and MS fabricated 3ω devices and measured the thermal conductivities. MRRL and ECA performed the Raman analyses. MRRL, ECA and JM designed and performed the Brillouin measurements. ECA designed and performed the refractive index measurements. ACA carried out the Raman simulations, and studied the non-covalent interaction and orientation of the solvent molecules toward graphene. FC, BE, MP and PO calculated the N–N pair correlation function and provided support for the theoretical analysis. PGR and CMST supervised the work and discussed the experimental results. MRRL and ECA analysed and discussed the data and wrote the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Catalan Institute of Nanoscience and Nanotechnology (ICN2) acknowledges support from the Severo Ochoa Program (MINECO, Grant SEV-2013-0295) and funding from the CERCA Programme/Generalitat de Catalunya. Funding from the Spanish Ministry (MINECO/FEDER: MAT2015-68394-R NaCarFLOW, FIS2015-70862-P PHENTOM and FIS2015-64886-C5-3-P SIESTA) is also acknowledged. FC, BE, MP and PO acknowledge support from the EU Center of Excellence MaX-Materials Design at the Exascale (Grant No. 676598), Generalitat de Catalunya (Grant No. 2014SGR301) and supercomputing resources from the Red Española de Supercomputación (RES). ACA acknowledges Fundació Cellex de Barcelona for financial support. We would also like to thank Andrew Hudson for the assistance provided with the use of English in the manuscript and Dr Torres for designing Fig. 3c.References
- S. M. Sohel Murshed and C. A. Nieto de Castro, Renewable. Sustainable Energy Rev., 2017, 78, 821–833 CrossRef.
- P. Andreu-Cabedo, R. Mondragon, L. Hernandez, R. Martinez-Cuenca, L. Cabedo and J. Julia, Nanoscale Res. Lett., 2014, 9, 582 CrossRef PubMed.
- D. Shin and D. Banerjee, Int. J. Heat Mass Transfer., 2011, 54, 1064–1070 CrossRef.
- H. Tiznobaik and D. Shin, Int. J. Heat Mass Transfer., 2013, 57, 542–548 CrossRef.
- O. Manca, Y. Jaluria and D. Poulikakos, Adv. Mech. Eng., 2010, 1–2 Search PubMed.
- A. Turgut, I. Tavman, M. Chirtoc, H. P. Schuchmann, C. Sauter and S. Tavman, Int. J. Thermophys., 2009, 30, 1213–1226 CrossRef.
- D. Kwek, A. Crivoi and F. Duan, J. Chem. Eng. Data, 2010, 55, 5690–5695 CrossRef.
- S. Jana, A. Salehi-Khojin and W.-H. Zhong, Thermochim. Acta, 2007, 462, 45–55 CrossRef.
- M. M. Tawfik, Renewable Sustainable Energy Rev., 2017, 75, 1239–1253 CrossRef.
- B. T. Branson, P. S. Beauchamp, J. C. Beam, C. M. Lukehart and J. L. Davidson, ACS Nano, 2013, 7, 3183–3189 CrossRef PubMed.
- P. M. Sudeep, J. Taha-Tijerina, P. M. Ajayan, T. N. Narayanan and M. R. Anantharaman, RSC Adv., 2014, 4, 24887 RSC.
- P. Keblinski, S. R. Phillpot, S. U. S. Choi and J. A. Eastman, Int. J. Heat Mass Transfer, 2002, 45, 855–863 CrossRef.
- P. Keblinski and J. Thomin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 10502 CrossRef PubMed.
- R. Prasher, P. Bhattacharya and P. E. Phelan, J. Heat Transfer, 2006, 128, 588 CrossRef.
- S. Sarkar and R. P. Selvam, J. Appl. Phys., 2007, 102, 74302 CrossRef.
- R. Prasher, P. E. Phelan and P. Bhattacharya, Nano Lett., 2006, 6, 1529–1534 CrossRef PubMed.
- M. Liu, C. Ding and J. Wang, RSC Adv., 2016, 6, 3571–3577 RSC.
- N. H. Abou-tayoun, Molecular Dynamics Simulation of Thermal Conductivity Enhancement of Copper-water Nanofluid, American University of Sharjah, 2012 Search PubMed.
- Y. Xuan, Q. Li and P. Tie, Exp. Therm. Fluid Sci., 2013, 46, 259–262 CrossRef.
- G. Xia, H. Jiang, R. Liu and Y. Zhai, Int. J. Therm. Sci., 2014, 84, 118–124 CrossRef.
- K. P. Loh, Q. Bao, P. K. Ang and J. Yang, J. Mater. Chem., 2010, 20, 2277 RSC.
- A. A. Balandin, Nat. Mater., 2011, 10, 569–581 CrossRef PubMed.
- D. P. Dubal and P. Gomez-Romero, 2D Mater., 2016, 3, 31004 CrossRef.
- X. Han, Y. Chen, H. Zhu, C. Preston, J. Wan, Z. Fang and L. Hu, Nanotechnology, 2013, 24, 205304 CrossRef PubMed.
- Y. Liang, D. Wu, X. Feng and K. Müllen, Adv. Mater., 2009, 21, 1679–1683 CrossRef.
- K. V. Wong and O. De Leon, Adv. Mech. Eng., 2010, 2, 519659 CrossRef.
- V. V. Chaban and E. E. Fileti, Phys. Chem. Chem. Phys., 2016, 18, 26865–26872 RSC.
- Z. L. Wang, D. W. Tang, S. Liu, X. H. Zheng and N. Araki, Int. J. Thermophys., 2007, 28, 1255–1268 CrossRef.
- D. S. Viswanath and M. Bhagwant Rao, J. Phys. D: Appl. Phys., 1970, 3, 1444–1450 CrossRef.
- J. G. Dil, Rep. Prog. Phys., 1982, 45, 285–334 CrossRef.
- G. Benedek and T. Greytak, Proc. IEEE, 1965, 53, 1623–1629 Search PubMed.
- T. Yogi, K. Sakai and K. Takagi, J. Appl. Phys., 2006, 100, 23505 CrossRef.
- H. Bohidar, T. Jossang and J. Feder, J. Phys. D: Appl. Phys., 1988, 21, S53–S55 CrossRef.
- S. Nemoto, Appl. Opt., 1992, 31, 6690 CrossRef PubMed.
- T. M. Aminabhavi and B. Gopalakrishna, J. Chem. Eng. Data, 1995, 40, 856–861 CrossRef.
- V. Venkata Chalapathi and K. Venkata Ramiah, Proc. - Indian Acad. Sci., Sect. A, 1968, 68, 109–122 Search PubMed.
- F. Rozpłoch, J. Patyk and J. Stankowski, Acta Phys. Pol., A, 2007, 112, 557–562 CrossRef.
- C. R. Kemnitz and M. J. Loewen, J. Am. Chem. Soc., 2007, 129, 2521–2528 CrossRef PubMed.
- X. Gong, A. Kozbial, F. Rose and L. Li, ACS Appl. Mater. Interfaces, 2015, 7, 7078–7081 CrossRef PubMed.
- Y. Xu, L. Zhao, H. Bai, W. Hong, C. Li and G. Shi, J. Am. Chem. Soc., 2009, 131, 13490–13497 CrossRef PubMed.
- T. Akıner, J. K. Mason and H. Ertürk, J. Chem. Phys., 2017, 147, 44709 CrossRef PubMed.
- C.-J. Shih, S. Lin, M. S. Strano and D. Blankschtein, J. Am. Chem. Soc., 2010, 132, 14638–14648 CrossRef PubMed.
- H. Zhang, X. Chen, Y. D. Jho and A. J. Minnich, Nano Lett., 2016, 16, 1643–1649 CrossRef PubMed.
- J. Zou and B. Cao, Appl. Phys. Lett., 2017, 110, 103106 CrossRef.
- D. L. Nika and A. A. Balandin, Rep. Prog. Phys., 2017, 80, 36502 CrossRef PubMed.
- D. Alexeev, J. Chen, J. H. Walther, K. P. Giapis, P. Angelikopoulos and P. Koumoutsakos, Nano Lett., 2015, 15, 5744–5749 CrossRef PubMed.
- K. M. F. Shahil and A. A. Balandin, Nano Lett., 2012, 12, 861–867 CrossRef PubMed.
- J. Renteria, S. Legedza, R. Salgado, M. P. Balandin, S. Ramirez, M. Saadah, F. Kargar and A. A. Balandin, Mater. Des., 2015, 88, 214–221 CrossRef.
- I. C. Nelson, D. Banerjee and R. Ponnappan, J. Thermophys. Heat Transfer, 2009, 23, 752–761 CrossRef.
- Q. Xie, Q. Zhu and Y. Li, Nanoscale Res. Lett., 2016, 11, 306 CrossRef PubMed.
- D. Shin and D. Banerjee, J. Heat Transfer, 2011, 133, 24501 CrossRef.
- G. Qiao, M. Lasfargues, A. Alexiadis and Y. Ding, Appl. Therm. Eng., 2017, 111, 1517–1522 CrossRef.
- L. Sang and T. Liu, Sol. Energy Mater. Sol. Cells, 2017, 169, 297–303 CrossRef.
- J. Buongiorno, J. Heat Transfer, 2006, 128, 240 CrossRef.
- V. N. Likhachev, G. A. Vinogradov and M. I. Alymov, Phys. Lett. A, 2006, 357, 236–239 CrossRef.
- B.-X. Wang, L.-P. Zhou and X.-F. Peng, Int. J. Thermophys., 2006, 27, 139–151 CrossRef.
- M.-J. Huang, T.-M. Chang, C.-K. Liu and C.-K. Yu, Int. J. Heat Mass Transfer., 2008, 51, 4470–4479 CrossRef.
- E. Chávez, J. Cuffe, F. Alzina and C. M. Sotomayor Torres, J. Phys.: Conf. Ser., 2012, 395, 12105 CrossRef.
- L. Xue, P. Keblinski, S. R. Phillpot, S. U. S Choi and J. A. Eastman, Int. J. Heat Mass Transfer, 2004, 47, 4277–4284 CrossRef.
- C. H. Lui, Z. Ye, C. Keiser, X. Xiao and R. He, Nano Lett., 2014, 14, 4615–4621 CrossRef PubMed.
- E. Chávez-Àngel, Confined acoustic phonons in Si nanomembranes: impact on thermal properties, PhD thesis, Universitat Autònoma de Barcelona, 2014 Search PubMed.
- M. Mouis, in Beyond-CMOS Nanodevices 1, ed. F. Balestra, John Wiley, 2014, pp. 142–152 Search PubMed.
- L. Xue, P. Keblinski, S. R. Phillpot, S. U. S. Choi and J. A. Eastman, J. Chem. Phys., 2003, 118, 337–339 CrossRef.
- R. Hentschke, Nanoscale Res. Lett., 2016, 11, 88 CrossRef PubMed.
- H. Hermann, T. Schubert, W. Gruner and N. Mattern, Nanostruct. Mater., 1997, 8, 215–229 CrossRef.
- D.-W. Oh, A. Jain, J. K. Eaton, K. E. Goodson and J. S. Lee, Int. J. Heat Fluid Flow, 2008, 29, 1456–1461 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr02762e |
| This journal is © The Royal Society of Chemistry 2018 |