Open Access Article
Open Access ArticleReactivity of fluorographene is triggered by point defects: beyond the perfect 2D world†
Miroslav
Medveď
 *a,
Giorgio
Zoppellaro
*a,
Giorgio
Zoppellaro
 a,
Juri
Ugolotti
a,
Dagmar
Matochová
a,
Petr
Lazar
a,
Tomáš
Pospíšil
b,
Aristides
Bakandritsos
a,
Jiří
Tuček
a,
Juri
Ugolotti
a,
Dagmar
Matochová
a,
Petr
Lazar
a,
Tomáš
Pospíšil
b,
Aristides
Bakandritsos
a,
Jiří
Tuček
 a,
Radek
Zbořil
a,
Radek
Zbořil
 a and
Michal
Otyepka
a and
Michal
Otyepka
 *a
*a
aRegional Centre of Advanced Technologies and Materials, Department of Physical Chemistry, Faculty of Science, Palacky University in Olomouc, 17. listopadu 1192/12, 771 46 Olomouc, Czech Republic. E-mail: Miroslav.Medved@upol.cz; Michal.Otyepka@upol.cz
bCentre of the Region Haná for Biotechnological and Agricultural Research, Department of Chemical Biology and Genetics, Faculty of Science, Palacky University in Olomouc, 17. listopadu 1192/12, 771 46 Olomouc, Czech Republic
First published on 6th February 2018
Abstract
Preparation of graphene derivatives using fluorographene (FG) as a precursor has become a key strategy for the large-scale synthesis of new 2-D materials (e.g. graphene acid, cyanographene, allyl-graphene) with tailored physicochemical properties. However, to gain full control over the derivatization process, it is essential to understand the reaction mechanisms and accompanying processes that affect the composition and structure of the final products. Despite the strength of C–F bonds and high chemical stability of perfluorinated hydrocarbons, FG is surprisingly susceptible to reactions under ambient conditions. There is clear evidence that nucleophilic substitution on FG is accompanied by spontaneous defluorination, and solvent-induced defluorination can occur even in the absence of any nucleophilic agent. Here, we show that distributed radical centers (fluorine vacancies) on the FG surface need to be taken into account in order to rationalize the defluorination mechanism. Depending on the environment, these radical centers can react as electron acceptors, electrophilic sites and/or cause homolytic bond cleavages. We also propose a new radical mechanism of FG defluorination in the presence of N,N′-dimethylformamide (DMF) solvent. Spin-trap experiments as well as 19F NMR measurements unambiguously confirmed formation of N,N′-dimethylformyl radicals and also showed that N,N′-dimethylcarbamoyl fluoride plays a key role in the proposed mechanism. These findings imply that point defects in 2D materials should be considered as key factor determining their chemical properties and reactivity.
1. Introduction
The discovery of graphene1 in 2004 opened a route to a new class of carbon-based 2D materials with unique chemical, electronic and magnetic properties. Whereas graphene itself is chemically a low reactive semimetal with high electron conductivity, even dilute concentrations of chemisorbed impurities can dramatically change its band structure and induce local magnetic moments.2 Increasing the adsorbate concentration can further disrupt the π-conjugated network, transforming the conducting material to an insulator through a variety of intermediate states.3,4 Possibilities for tuning the band gap characteristics and associated electronic and magnetic properties by graphene derivatization provide an auspicious base for future technological advancements, including development of batteries,5–7 biosensoring,8 gas sensing on surfaces9 and solar cell technologies.10 Nevertheless, selective and controllable covalent graphene functionalization remains a challenging task due to the limited reactivity of graphene.11,12 Many proposed direct derivatization strategies suffer from a low degree of functionalization13–16 or require harsh reaction conditions that strongly affect the final stoichiometry and chemical structure of the resulting graphene derivative.17,18Fluorographene (FG)19–21 offers a promising alternative for graphene derivatization because (i) chemisorption of monovalent fluorine atoms prevents formation of complex (non-stoichiometric) structures; (ii) the material is thermally stable up to 400 K; (iii) the pristine 3D material, graphite fluoride, is available in large-scale as an industrial lubricant; and (iv) FG reacts readily as an electrophile under mild conditions.22–26 Owing to these features, FG has recently been used as a precursor for the synthesis of several graphene derivatives, including amino-graphenes,26–30 cyanographene,31 carboxygraphene (graphene acid),31 sulfur-linked derivatives25,32 and alkylated graphenes.33 During the chemical transformation of FG, substitution of fluorine atoms proceeds simultaneously with reductive defluorination. It has been suggested that bimolecular nucleophilic substitution SN2 is the preferred mechanism of substitution of the fluorine atoms.23 Also important is the role of the solvent, which can significantly affect the whole process, not only by the common (de)stabilization solvation effects but also by triggering and/or enhancing the defluorination process. Wang et al.34 has shown that FG spontaneously defluorinates in the presence of highly nucleophilic (dipolar) solvents, such as N,N′-dimethylformamide (DMF), dimethylacetamide (DMAc) and N-methyl-2-pyrrolidone (NMP). The authors rationalized the defluorination effect of these solvents in terms of strong dipolar–dipolar interactions of the solvent molecules with the electron-deficient carbon atom of the C–F bond. All these findings indicate that unusual chemistry drives the reactivity of FG, and its intricacies need to be deciphered in order to rationalize the process of graphene derivatization using FG.
In our work, we present a description of the mechanism of the reactivity of FG obtained by combining electron paramagnetic resonance (EPR) and 19F NMR experiments with theoretical calculations. We focus on FG in DMF, which is a widely used solvent for FG exfoliation and chemical treatment. EPR experiments confirmed the presence of radical centers (fluorine vacancies) in FG and allowed their distribution and time-evolution to be studied. We observed defluorination in DMF, despite the fact that it is not a sufficiently strong reducing agent for FG. Based on theoretical calculations, we suggest a new mechanism involving N,N′-dimethylformyl radicals (DMF˙), formation of which was evidenced by a series of spin-trap experiments. In addition, 19F NMR measurements unambiguously confirmed formation of N,N′-dimethylcarbamoyl fluoride, which plays a key role in the proposed mechanism. These findings show that defects present in FG determine the chemical behavior of this 2D material and make it susceptible to defluorination and subsequent substitution and addition reactions. Such defects may be important in determining the reactivity of other 2D materials because they may initiate reactions which then propagate on the surface of 2D materials.
2. Experimental setup & computational details
2.1 Chemicals
All chemicals and reagents were used as obtained from the suppliers without further purification. Graphite fluoride (GrF, C1F1.1), anhydrous DMF (99.8%, CAS number: 68-12-2), α-4-pyridyl-1-oxide-N-tert-butylnitrone (POBN, 99%, CAS number: 66893-81-0) and dry benzene (99.8%, CAS number: 71-43-2) were provided by Sigma-Aldrich. Fluorographene used for the experiments described in section 3.6 was obtained by exfoliation of GrF in DMF.35N,N′-Dimethylcarbamoyl fluoride (F-DMF) was obtained by fluorination of the corresponding N,N′-dimethylcarbamoyl chloride (Sigma-Aldrich) with KF/CaF2 (Sigma-Aldrich) in acetonitrile (Penta), following a procedure reported in the literature.362.2 Characterization
EPR spectra were recorded on a JEOL JES-X320 electron spin resonance spectrometer operating at the X-band frequency (∼9.16–9.17 GHz) and equipped with variable temperature control ES 13060DVT5 apparatus. The cavity Q quality factor was kept above 6000 in all measurements and signal saturation was avoided by working at low-applied microwave powers. Concentrated suspensions of GrF (15 mg GrF per mL solvent, DMF or benzene) thoroughly degassed under N2 were mechanically stirred at 40 °C without sonication and kept in airtight and oxygen-free vials, and EPR spectra of the resulting dense suspensions were recorded during a 10 day time-frame. Use of very concentrated suspensions of GrF was necessary for successful spin-trapping experiments with POBN (see ESI for details, section 1.2†). Generally, 0.1 mL of GrF suspension was loaded into the EPR tubes by using airtight syringes. In the case of GrF powder, 10 mg were used. For the spin-trap experiments, the reaction mixtures (GrF/solvent/POBN reacted together at RT for 40 min) were centrifuged prior to loading 0.1 mL of the supernatants into the EPR tubes. Discussion on the use of GrF instead of FG for the EPR studies and radical formation on the carbon lattice is available in the ESI.† Highly-pure quartz tubes were employed (Suprasil, Wilmad, ≤0.5 OD). Simulation of the EPR resonances were carried out using the WinEPR SimFonia software (V.1.25, Dr Ralph T. Weber. EPR Division. Bruker Instruments, Inc. Billerica, MA USA) with second-order perturbation theory. The frequency unit can be converted into magnetic fields units through the following relation: 0.1 mT equals to 2.8025 MHz. Nuclear magnetic resonance (19F) spectra were obtained with a JEOL ECA-500 NMR spectrometer (19F frequency 470 MHz, CFCl3 = 0 ppm). Further experimental details can be found in the ESI.†2.3 Computational details
The ground state (GS) structures of all the investigated species were optimized by the ωB97X-D method37 using 6-31+G(d) and 6-31++G(d,p) basis sets.38 Solvent effects were included by using the universal continuum solvation model based on solute electron density (SMD).39 Whereas the structures of small and medium size systems (F, F−, HF, DMF, F-DMF, etc.) were fully relaxed in geometry optimizations, to mimic the semilocal flexibility of FG sheets, FG-like structures were obtained by constrained geometry optimizations, keeping the edge carbon atoms frozen. All calculations were performed with the Gaussian09 program.403. Results and discussion
3.1 EPR spectra of GrF in benzene and DMF
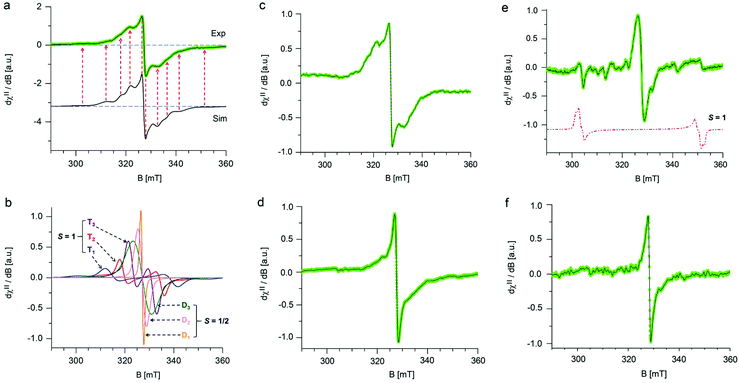
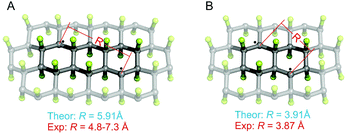
The stability of GrF dispersed in two model solvents (benzene and DMF) was probed using electron paramagnetic resonance (EPR) spectroscopy by monitoring the variation of the respective EPR envelopes over time. Fig. 1a shows the frozen matrix (T = 123 K) X-band EPR envelope recorded for the freshly prepared GrF/benzene suspension. Although the overall resonance line of the system in benzene was rather broad (∼30 mT field-spread), it exhibited several small resonances that developed symmetrically with respect to an intense narrow central line, a signature of overlapped contributions of triplet and doublet spin-states. The observed g-averaged (gavg) value was estimated to be 2.000 and validated by recording the spectrum together with the Mn(II)MgO standard (JEOL internal reference standard, Mn(II), geff = 2.00101 ± 0.00005, ESI, Fig. S5 and S6†). A comparable EPR spectrum was observed for the neat GrF powder (ESI, Fig. S1a and S3†). Similar EPR spectra have been previously reported around the g = 2 region (∼280–380 mT) by Panich and co-authors41 on polycrystalline graphite fluoride (CF)n obtained by fluorination of petroleum coke as well as by Giraudet and co-authors in a later report (∼310–380 mT region).42 However, we noticed that by recording the EPR signal of the GrF powder in a broader magnetic-sweep range (50–550 mT), a broad tail emerged in the high field region (360–550 mT) together with a broad resonance signal in the low field region (around g = 4) (ESI, Fig. S3†). These features became strongly weakened in the diluted systems (GrF/benzene and GrF/DMF). The ESI provides additional EPR spectra for GrF, including the EPR power-saturation behavior (Fig. S1a, S2–S4†). Panich and co-authors suggested that the fine structure observed around g = 2.00 in GrF was due to resolved hyperfine components (AF) with ∼5 mT of splitting value, originating from the interaction of an unpaired spin (S = 1/2) with six neighboring fluorine nuclei. The authors also found that these hyperfine lines were rather broad (ΔH = 30 G by simulation), a factor that pointed towards the joint effect of dipole–dipole and exchange interactions between paramagnetic centers. In the later work, Giraudet and co-authors took the similar approach in the simulation of the observed EPR envelope for GrF, but with the addition of two broad resonance lines. The simulation of the signal was obtained by adding the hyperfine contribution of six fluorine nuclei (A = 45 ± 2 G, line width of 36 ± 2 G, and g factor of 2.003 ± 0.001). As stated by the authors, and similar to the Panich's work, “the large line width is interpreted by the joint effect of dipole–dipole and exchange interactions between paramagnetic centers”. In the case of the GrF/benzene frozen matrix sample, we therefore tried to disentangle these effects previously anticipated by ref. 41 and 42 and carried out an EPR simulation of the resonance signal in the g = 2.0 region under the assumption of an overlapped contribution of different spin components (Fig. 1a, black line, Sim, and Fig. 1b showing the individual spin components with their relative weights). The observed EPR signal of GrF/benzene shown in Fig. 1a (Exp) can be interpreted as a superposition of three effective triplet states (S = 1) and three sets of spin-doublets (S = 1/2), i.e., in GrF exists a distribution of spin-carrying defects, some close enough (through-space distance) to show signatures of high-spin systems and others behaving as isolated S = 1/2 defects. This hypothesis is supported by the observation that the low field signal around g = 4.0 observed in neat GrF can still be observed in the dilute GrF/benzene suspension through signal accumulation (ESI, Fig. 1b,† GrF/benzene system, 133 K, 4 mW, 40 scan accumulated and averaged) and may represent the half-field transition (Δms = 2) of these high spin (S = 1) components. The triplet signatures (Fig. 1b, marked T1, T2, and T3, with g-tensor (x,y,z) of 2.000, 2.000, 2.000) gave from simulation the following axial values (D): one large with |D| of 701 MHz (marked as T1) and negligible 19F hyperfine contribution, one intermediate (marked as T2) with |D| of 462 MHz and with line broadening by hyperfine terms (four 19F nuclei, Ax,y,z of 56.0, 14.0, 14.0 MHz), and one much smaller (marked as T3) with |D| of 202 MHz, with similarly broadened resonances (two 19F nuclei, Ax,y,z of 38.0, 12.0, 12.0 MHz). From the point-dipole-approach, these triplet configurations (and D values) indicate a spread of through-space distances among the spin-carrying centers that are effectively magnetically coupled together, with S1/2–S1/2 through-space distances that lie within 4.8–7.3 Å. These distances are an estimate, assuming dominant 1/r3 dependence on the D value and a dominant spin–spin (SS) contribution.43 The biquadratic zero-field-splitting (ZFS) D-tensor comprised two contributions: (i) a first order term arising from direct magnetic dipoles SS interaction, and (ii) a second-order contribution arising from spin–orbit coupling (SOC). In organic based magnets, the first term usually dominates. It is known that the point-dipole approach gives rather poor estimation of inter-center radical distances (compared to X-ray radical distances) if the radical units interact via π-bond pathways. In contrast, when the interacting radicals are connected through an array of σ-bonds, which tends to hamper spin delocalization, the point dipole approach gives fairly accurate distances, comparable to those obtained by X-ray.44–46 The other types of spin active species are shown by the three sets of S = 1/2 signals in Fig. 1b, marked as D1, D2 and D3. One doublet (D1, line-width tensor Lxyz of 28.0, 28.0, 56.0 MHz) corresponded to the relatively sharp and slightly asymmetric central signal at geff = 2.000. This fingerprint indicates that the S = 1/2 spins experienced the strong exchange regime, i.e., the exchange energy (Hex) of the spin packet was much larger than Hdip (the dipolar interaction component), which in turn was greater than Hhf (the hyperfine component). Considering the upper limit of the strongest triplet obtained by simulation (701 MHz), this indicates that the exchange term (J) associated to these spins was stronger than 0.02 cm−1. Since the applied microwave power was kept low and under non-saturating conditions (≪1 mW), this sharp central line could not have arisen from a double-quantum transition and very unlikely originated from a quartet spin state (S = 3/2). The second broad doublet (D3, Fig. 1b) belonged to an ensemble of S = 1/2 spins that experienced weak dipolar interaction (<100 MHz) but still larger than 19F hyperfine (Hdip > Hhf). This effect resulted in a very broad line-width (Lxyz) of 250.0, 196.0, 196.0 MHz encoded in the electronic transition. The third doublet (D2, Fig. 1b) corresponded to S = 1/2 spins that experienced an intermediate regime with Hdip–Hhf and a relatively narrow line-width tensor in the frozen matrix (Lxyz) of 98.0, 98.0, 98.0 MHz. Overall, our observations support the earlier description of Grigorieva and co-authors on the dominant spin-half paramagnetism for GrF-based materials.47 Following GrF aging in benzene solution, we did not observe severe changes in the overall EPR resonance line, which remained after 6 days and 10 days similar to that shown at the beginning of the process (ESI, Fig. S8†). Thus, benzene can be considered a “nearly inert” solvent for GrF which does not induce substantial degradation of the paramagnetic centers. Chemical stability of GrF in benzene was also confirmed by measurement of the XPS spectrum for a 10-days aged GrF sample in benzene (Fig. S25 in ESI†). After dispersion of GrF in DMF, the freshly prepared suspension showed the same EPR fingerprints in a frozen matrix (Fig. 1c) as witnessed for GrF/benzene (Fig. 1a). Additional EPR spectra for GrF/DMF are given in the ESI† (power saturation behavior of the entire resonance line, from 50 to 550 mT, Fig. S9a–c†). The concentration of spin centers on the GrF surface at this stage was estimated to be 23.2 × 1018 spin per g, which corresponds to ca. 1 center per area of 5 nm × 5 nm (see ESI, section 1.2†). This value closely resembles the estimated spin concentration found to near stoichiometric C/F ratios in GrF (C/F0.9–1.0) by Grigorieva and co-authors, which were obtained from in-depth analysis of bulk magnetic susceptibility experiments (∼22–17 × 1018 spin per g).47 However, already after 6 h stirring at 40 °C, the GrF/DMF suspension darkened considerably. The X-band EPR spectrum (T = 123 K) observed after 6 h revealed some changes in the overall resonance line (Fig. 1d) compared to the initial spectrum. The doublet component (S = 1/2, D1 in the simulation shown in Fig. 1b) appeared to increase strongly in intensity (relative increase) at the expense of the T1, T2 and T3 triplet components (see S = 1 components, Fig. 1b and ESI, Fig. S10†) and the doublet component D2. After 7 days of stirring, the EPR spectrum of FG/DMF showed more significant changes (Fig. 1e). Besides still being centered at geff = 2.000, the doublet components D1 and D2 became dominant, several resonances appeared throughout the spectrum and a novel but very minor triplet emerged. The spin-Hamiltonian simulation of this species was very tentative (shown by the dotted red-line in Fig. 1e). This system should exhibit a large axial value (|D| of 1345 MHz, |E/D| of 0.04). In this case, the inter-spin (through-space) distance of the triplet configuration (S = 1, arising from two interacting S = 1/2) was estimated from the point-dipole approach to fall short, at about 3.87 Å. This value corresponded well with the minimum through-space spin–spin distance of the spin carrying defects estimated by theory (vide infra, Fig. 4b). It is important to note that at such later stage of the GrF aging process, an alternative explanation for the appearance of the large triplet signal reported above can be put forward. Namely, it may arise from voids in the GrF sheets, especially in the areas corresponding to sp2 islands that are formed upon extended defluorination. As discussed by Palacios and co-authors,48 the presence of voids, such as type A3B, can lead to non-vanishing local magnetic moments. Consequently, S = 1 signatures can arise in the EPR spectrum from the presence of these sublattice imbalances (NI = NA − NB). When the Hubbard repulsion is active, Lieb's theorem grants the S = 1 spin state to such defect structures.48,49 Further aging, and after 10 days of stirring, the dense GrF DMF solution became very dark brownish and the EPR spectrum revealed signatures of only S = 1/2 species (Fig. 1f and ESI, Fig. S11†), with no clear indications of remaining higher spin-states. The spin concentration decreased to 5.4 × 1018 spin per g, i.e. to 23% of the initial value. These results clearly indicate that, unlike benzene, DMF cannot be considered an inert solvent for GrF but rather a reactant for GrF, capable of inducing degradation of the spin carrying defects present in GrF.3.2 Origin of radical centers
The experimental evidence of radical centers in FG raises questions concerning their origin. Let us first assume a perfect perfluorinated graphene structure corresponding to an unperturbed domain on the FG surface and consider creation of radical centers on such an ideal structure. In spite of the outstanding stability of perfluorocarbons (PFCs) related to the high strength of C–F bonds,23 it was observed that defluorination of PFCs can be achieved by using strong reducing agents, such as metals (metal surfaces, amalgams or transition metal complexes as catalysts), electron rich organic donors (e.g., organic radical anions, thiolates, sulfonates)50–52 or photochemically.53 The partial sensitivity of PFCs to reduction is often explained in terms of enhanced reactivity of the most electron-deficient tertiary C–F bonds, which are therefore sometimes termed the “Achilles heel” of PFCs.54,55 Referring to works by Borden,56 which discuss that various phenomena of fluorocarbon chemistry can be explained by the ability of C–F σ* orbitals to act as electron acceptors, Sandford57 suggested that the defluorination of PFCs (e.g., perfluorodecalin) is initiated by transfer of an electron to the σ* orbital of a tertiary C–F bond to give a radical anion. To obtain a more detailed picture about the role of the C–F σ* orbitals and ability to accept an electron by larger PFC structures, we computed gas phase vertical (VEA) and adiabatic (AEA) electron affinities and the HOMO–LUMO gap at the ωB97X-D/6-31++G(d,p) level of theory for a series of medium-sized model fluorinated polycyclic hydrocarbons and their radical counterparts (see Table S1 in ESI†). We found that for the parent closed-shell systems, the VEA values were negative and even AEAs, taking into account geometry relaxation of the corresponding radical anions, were very small. Although the VEA values increased with increasing size of the fluorinated PHC systems, due to a possibility of larger delocalization of the negative charge, it can be expected that even for larger (perfect) FG structures, the electron affinity (EA) will be small, in line with the relatively large theoretically predicted band gap of FG varying from 3.1 to 7.5 eV (depending on the approach).58,59 Variation of the VEA values with the system size was in line with the qualitative picture provided by the HOMO/LUMO analysis. The positive LUMO energies and rather large HOMO–LUMO gap in closed-shell systems were consistent with their low electron acceptor strength. As anticipated by Sandford and others,57 the LUMO was predicted to have σ* character and was mainly located on the central tertiary carbon atom (Fig. S27 in ESI†). In line with our results on EA, the extent of its delocalization increased with the system size. To sum up, although the energetically low-lying C–F σ* orbital doubtlessly plays an important role in fluorine chemistry (e.g., through orbital mixing, as explained by Borden applying the second-order perturbation theory56), it is improbable that mild reducing agents could initiate a radical cascade process of defluorination by direct electron transfer to the C–F σ* orbital.Although formation of radical centers on an ideal C1F1 layer was expected to be hampered by the low EA, the experimental evidence of observable spin concentrations in C1F1 structures clearly proves the presence of isolated sp3 carbon sites. The origin of such centers depends largely on the preparation process. Recent experimental surface imaging techniques have shown that fluorination of CVD graphene with XeF2 leads to formation of highly ordered sizable (150 nm) CF, C2F chair and unfluorinated domains,60 whereas fluorination with CF4 plasma gives rise to inhomogeneous and disordered microscopic configurations.61 From a radical center formation point of view, in the former case, the carbon atoms at the boundary between these domains can remain unfluorinated as the attachment of fluorine on such sites would lead to a cis configurations, which would be energetically unfavorable.62 On the other hand, the inhomogeneous spatial distribution of fluorine on CVD graphene treated with CF4 plasma is accompanied by formation of multilayer islands and structural features such as folds, wrinkles, and ripples that are less fluorinated, which consequently increases the probability of spin center emergence.
3.3 Electron affinities of radical centers
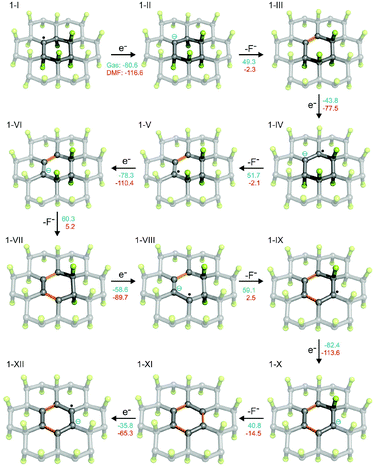
The presence of radical centers (even in very low concentrations) can obviously dramatically change the behavior of FG in the presence of reducing agents or nucleophilic species. As shown in Table S1 (see ESI†), the electron affinities of radical species derived from parent perfluorinated model systems are very high. For instance, AEA of a fluorinated coronene radical is 80.6 kcal mol−1, i.e., it is even larger than that of a fluorine atom (78.4 kcal mol−1). These extremely large values of EA of perfluorinated radicals are mainly due to the electron-withdrawing effect of highly electronegative fluorine atoms bound to the nearest carbon atoms but also increased delocalization of the negative charge with increasing size of the system. This delocalization is closely related to the presence of the already discussed C–F σ* orbitals on neighboring carbons, which can stabilize the SOMO orbital in a pyramidal configuration of the radical center by mutual orbital mixing.56,63 The extraordinary oxidizing power of highly fluorinated organic radicals can initiate the defluorination process in the presence of even mild reducing agents. Therefore, we probed a possible scenario of initial phases of the cascade reduction of FG in which defluorination spreads outwards from a radical center (Fig. 2).Although the total reaction enthalpies of the reduction steps depend on the strength of reducing agent as well as solvation enthalpies of the involved species, it can be seen that, in general, they are energetically favorable and polar solvents stabilize the charged intermediates. As expected, the oxidizing power of the radical species is much higher (by about a factor of 2) than that of closed-shell systems occurring in the reduction process. However, even for the latter, the EA is rather high as a consequence of the effect of highly polar C–F bonds on the neighboring carbon atoms. Note that EA of the final structure 1-IX, which is fully π-conjugated, is significantly lower than that of the other structures. It is therefore possible that depending on the power of the reducing agent, the cascade defluorination process may cease after formation of larger π-conjugated domains. Finally, let us consider possible formation of fluorine radicals by charge transfer from fluoride anions to the radical center. Although the gas phase value of the EA of 1-I is slightly larger than that of an F atom, the stability of a small fluoride anion is significantly increased in polar solvents (much more than 1-II), and therefore formation of F radicals by this mechanism would be unfavorable. Let us also underline that our results for model systems well reproduce those obtained for larger systems and are also in good correspondence with periodic calculations (see section 2.5 in ESI†).
3.4 Radical defluorination mechanism in DMF
We have shown that radical centers on FG act as efficient electron acceptors. Although such electron transfer can be a trigger for cascade defluorination, in the case of a sufficiently strong reducing agent, it does not explain the defluorination of FG observed in solvents with ionization potential in the liquid phase significantly higher than the EA of FG point defects. An example of such a solvent is DMF (discussed in section 3.1), which has an ionization potential in the liquid phase of 149 kcal mol−1, compared to the EA of a radical center 1-I of 117 kcal mol−1 in the same solvent. Let us recall that electron affinities of the subsequent species are even smaller. Clearly, DMF can hardly be considered a direct reductant of FG in the sense of direct electron transfer to such radical centers.To rationalize the observed spontaneous defluorination of FG in DMF, we suggest a mechanism initiated by hydrogen atom transfer from DMF to the FG radical center (Fig. 3). In this mechanism, the energetically favorable initiation step (1a) involves hydrogenation of a radical center and formation of a DMF˙ radical. In principle, a cis isomer of 2-II can also be formed, but the trans isomer is much more stable (by ca. 36 kcal mol−1). In the next step, a HF molecule can possibly be released forming a double bond in 2-III by reaction (1b), although this step is energetically less favorable and may require some activation energy.
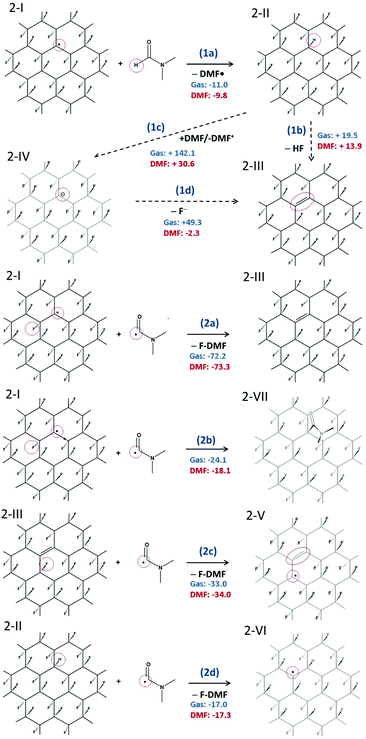 | ||
| Fig. 3 Radical mechanism of defluorination of FG in DMF. (1a–c) Initial phases of defluorination. (2a–d) Re-creation of FG radical center. The reaction energies are given in kcal mol−1. | ||
Nevertheless, the defluorinated structure 2-III can be formed via reaction (2a) of a DMF˙ radical with another FG radical, leading to formation of N,N′-dimethylcarbamoyl fluoride (F-DMF), which appears to be a significantly more favorable process than recombination of FG˙ and DMF˙ radicals by reaction (2b). Reactions (2c) and (2d) show possible ways of re-creating radical centers, the former leading to a cascade (radical) defluorination process. Note that subtraction of fluorine atoms from the FG surface by organic radicals (namely 2,2,6,6-tetramethylpiperidine-1-oxyl) triggering the defluorination process, which is in line with the proposed steps, has very recently been observed by Lai et al.64 Since it can be expected that the hydrogen atom in 2-II is moderately acidic due to the electron-withdrawing effect of fluorine atoms bound to the nearest carbons, we also considered the possibility of proton transfer to a DMF molecule (1c). Although the charged products are significantly stabilized in a polar environment compared to the gas phase, the reaction energy appears to be too large to accept this channel as a direct source of FG anions. However, taking into account the energetically advantageous release of the fluoride anion from 2-IV (cf. step 2 in Fig. 2), concerted transformation of 2-II to 2-III cannot be excluded under harsher conditions. Let us also underline that our model systems with fluorine atoms in the trans configuration represent the most stable (i.e. the least reactive) radical structures65 and less stable structures (e.g. radical centers on deformed domains or edges) can enhance the defluorination process by providing even more favorable thermodynamic and kinetic conditions.
As the EPR spectra of FG in DMF confirmed the presence of biradical centers (besides monoradical sites) on the FG surface, we also studied a radical mechanism of defluorination starting from structure 3-I (Fig. 4), for which the theoretical distance between the spin centers (3.91 Å) was in reasonable agreement with the experimentally derived value (3.87 Å). The energetics of the key reaction steps were very similar to those predicted for the monoradical case (see ESI, Fig. S29†). An important feature of this mechanism, which is in line with the experimental observations discussed in section 3.1, is the successive annihilation of the biradical centers. A critical step in this context appears to be reaction of 3-III with a DMF˙ radical, which could potentially lead to regeneration of biradicals (Fig. S29b†). Although such regeneration is energetically allowed, it is much less favorable than the formation of π-conjugated motifs (Fig. 5).
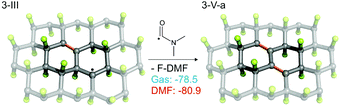 | ||
| Fig. 5 Reaction of 3-III with a DMF˙ radical. For alternative (less favorable) reactions see Fig. S13b in ESI.† | ||
3.5 Evidence of DMF˙ radical entrapment
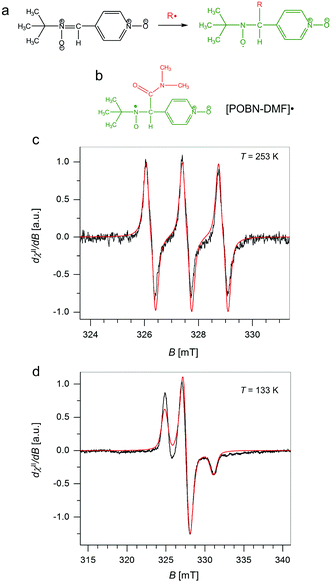
To validate the presence and chemical nature of the radical species (besides those residing on GrF) developing during the aging process of GrF in DMF, we employed the EPR technique in conjunction with spin-trapping experiments using α-4-pyridyl-1-oxide-N-tert-butylnitrone (POBN) as a chemical trapping agent (Fig. 6a). After addition of solid POBN to the GrF/DMF suspension, followed by incubation of these components at RT for 40 min, a large number of radical species were detected by EPR in the supernatant collected after centrifugation. The recorded solution EPR spectrum is shown in Fig. 6c and its frozen matrix in Fig. 6d. Additional EPR spectra are provided in the ESI (Fig. S14, S16 and S19†). The observed three-lines pattern (with ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity) shown in Fig. 6c is characteristic for nitroxide-radicals.66,67 The observed resonance envelope is here found very similar to that shown by TEMPO free radical (2,2,6,6-tetramethyl-piperidine 1-oxyl radical, ESI, Fig. S17†), and strongly suggests that the formed POBN radical adduct originated from entrapment of a tertiary-carbon radical, possibly the carbamoyl DMF˙ radical, with structure shown in Fig. 6b. Simulation of the EPR envelopes (Fig. 6c and d, red-line simulated spectra) with the WinEPR SimFonia software gave the following spin-Hamiltonian parameters: giso = 2.0049, 1AN = 1.340 mT (37.55 MHz), 1AH = 0.172 mT (4.82 MHz), Lw = 0.210 mT (5.88 MHz), Lorentzian/Gaussian ratio = 0.20 (Fig. 6c, red-line) and gxx = 2.0066, gyy = 2.0059, gzz = 2.0022, A(N)xx = 0.40 mT (11.21 MHz), A(N)yy = 0.50 mT (14.01 MHz), A(N)zz = 3.15 mT (88.28 MHz), Lw(x,y,z) = 0.70, 1.10, 0.80 mT (19.6, 30.83, 22.42 MHz), Lorentzian/Gaussian ratio = 0.63 (spherical integration using theta, phi of 200
1 intensity) shown in Fig. 6c is characteristic for nitroxide-radicals.66,67 The observed resonance envelope is here found very similar to that shown by TEMPO free radical (2,2,6,6-tetramethyl-piperidine 1-oxyl radical, ESI, Fig. S17†), and strongly suggests that the formed POBN radical adduct originated from entrapment of a tertiary-carbon radical, possibly the carbamoyl DMF˙ radical, with structure shown in Fig. 6b. Simulation of the EPR envelopes (Fig. 6c and d, red-line simulated spectra) with the WinEPR SimFonia software gave the following spin-Hamiltonian parameters: giso = 2.0049, 1AN = 1.340 mT (37.55 MHz), 1AH = 0.172 mT (4.82 MHz), Lw = 0.210 mT (5.88 MHz), Lorentzian/Gaussian ratio = 0.20 (Fig. 6c, red-line) and gxx = 2.0066, gyy = 2.0059, gzz = 2.0022, A(N)xx = 0.40 mT (11.21 MHz), A(N)yy = 0.50 mT (14.01 MHz), A(N)zz = 3.15 mT (88.28 MHz), Lw(x,y,z) = 0.70, 1.10, 0.80 mT (19.6, 30.83, 22.42 MHz), Lorentzian/Gaussian ratio = 0.63 (spherical integration using theta, phi of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200, Fig. 6d, red-line).
200, Fig. 6d, red-line).
The same trapped radical species by POBN was obtained when the GrF/DMF solution was aged for a longer time (1 day, 7 days), whereas negative results were consistently found for a GrF/benzene solution aged in the presence of POBN (see ESI, section 1.3, Fig. S13†). These findings suggest that DMF reacts with GrF via a radical mechanism. It is important to note that there is no clear report in literature of direct trapping of carbamoyl radical derived from DMF. However, in the recent study of cross-benzoin and Stetter-type reactions mediated by KOtBu-DMF by Massi et al., the authors observed generation of a weak EPR signal of difficult interpretation in the solution of KOtBu-DMF in presence of spin-trap agent PBN, signal that became well resolved into a doublet of triplet upon addition of diaryl α-diketone.68 The EPR signal encoded hyperfine splitting coupling constants similar to those observed here for the GrF/DMF/POBN trapped radical species, with AN = 1.33 mT and AH = 0.177 mT, which the authors attributed to the successful entrapment of benzil anion radical by PBN (Fig. 7a, trapped radical species). Furthermore, Aggarwal et al.69 recently reported the successful entrapment of a trifluoromethyl radical by PBN in DMF at 298 K (Fig. 7b), which exhibited g = 2.0044, AN = 1.411 mT, AH = 0.1664 mT, AF = 0.1781 mT, hence, similar giso, AN and AH as found for the GrF/DMF/POBN trapped radical system. Thus, because our system contains only GrF, and the POBN radical adducts can be trapped in DMF but not in benzene, the generation of the carbamoyl-radical trapped by POBN (POBN-DMF radical) as shown in Fig. 6b, is plausible.
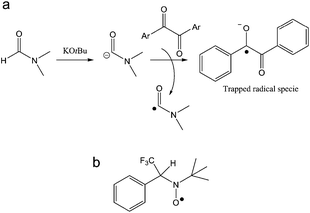 | ||
| Fig. 7 (a) Possible pathway of the trapped benzyl anion radical by PBN during the cross-benzoin like reaction as adapted from ref. 68. (b) The trifluoromethyl-PBN radical adduct from ref. 69. | ||
The use of other experimental setups, e.g., GrF sonication, as often employed for its fast dispersion in organic solvents, leads to generation of an admixture of radical species due to the fast temperature gradients induced in the solution. Due to the number of other experimental variables to dissect (e.g. sonication time, power applied) such study will be devoted for future work. As an example of other EPR signatures detected following the sequence of a specific sonication-time/applied power conditions (30 min, 40 kHz applied power) for the GrF/DMF/POBN mixture is given in the ESI (Fig. S20–S24†). However, the present findings wish to stress the notion that radical defluorination reactions of GrF occurs even under mild conditions in DMF.
3.6 Evidence of N,N′-dimethylcarbamoyl fluoride
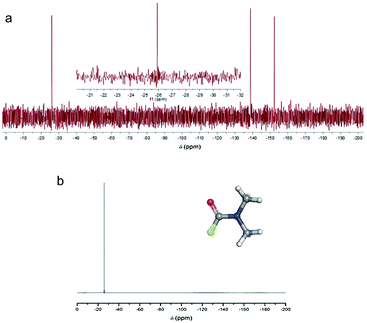
As can be seen in Fig. 3, N,N′-dimethylcarbamoyl fluoride (F-DMF) plays a key role in the proposed mechanism since its formation leads directly to defluorination and also generation of new radical centers. To confirm formation of F-DMF, we performed a series of 19F NMR measurements on FG/DMF samples treated in different ways (see details in ESI†). The first sample was sonicated for 2 hours at room temperature and stirred overnight. The day after, the suspension was still pale-grey, the color of the starting suspension. 19F NMR analysis of the supernatant solution did not show the presence of any F-containing compounds. A second sample of FG/DMF was treated at 120 °C for 5 hours and then left stirring overnight at room temperature. This time, the suspension appeared black, indicating that defluorination of FG had taken place. Using 19F NMR, the supernatant liquid showed the presence of one peak at −26 ppm, which was attributed to F-DMF (Fig. 8a). Two more peaks, at −138 and −152 ppm, were also visible, which could be attributed to some soluble FG fragments (cf., −135.85, −162.45 ppm for 1,2,3-trifluorobenzene, and −139.93, −157.07 ppm for 1,2,3,4-tetrafluorobenzene70) or to a product of reaction of fluoride ions with borosilicate glass (cf., −152.2 ppm for BF4− (ref. 71)). The peak at −26 ppm was confirmed to be due to the F-DMF compound by separately preparing F-DMF,36,72 whose 19F NMR spectrum in DMF also consisted of a peak at −26 ppm (Fig. 8b). The stability of F-DMF under the experimental conditions was also assessed by adding an aliquot of the compound to a FG/DMF suspension heated at 120 °C for 5 hours and then stirred overnight. In this case, the supernatant liquid showed again the presence of the compound peak at −26 ppm (see ESI, Fig. S26†). Although it cannot be fully excluded that F-DMF can be produced by recombining DMF˙ and F˙ radicals (possibly formed during sonication process), the presence of the F-DMF peak in 19F NMR spectrum supports our hypothesis that defluorination of FG in DMF results from the direct reaction between DMF˙ and FG. The requirement of higher temperature indicates that steps (2a, 2c, 2d) in the proposed mechanism require some activation energy.Finally, we will briefly comment on recent experimental work by Wang et al.,34 in which defluorination of FG in the presence of selected solvents was studied by various instrumental techniques, including XRD, FTIR, TEM, TGA and UV-vis reflectance spectroscopy. They found that highly polar (dipolar) solvents, including DMF, were able to facilitate the FG defluorination. They rationalized this capability in terms of high nucleophilicity, arguing that dipolar solvents can interact via dipole–dipole interactions with the electron-deficient carbon atom of a C–F bond, providing sufficient energy to rupture the C–F bond. To verify this hypothesis, we calculated the interaction energy of a DMF molecule with an ideal FG surface by using the implicit SMD model to account for the polar DMF environment (see ESI, Fig. S31†). Although the interaction energy was indeed found to be relatively high (4 kcal mol−1) compared to ordinary weakly interacting systems, it was still far below the dissociation energy of a C–F bond (∼100 kcal mol−1 for fluorinated coronene). Therefore, although we agree that the nucleophilicity of the solvent plays an important role in the later phases of defluorination, we believe that the proposed radical mechanism supported by the experimental evidence of the DMF˙ radical is a more plausible explanation of the initial steps of the FG defluorination process occurring in DMF.
3.7 Consequences for the reactivity of FG
We have shown that, depending on the chemical composition of the sample, the presence of radical centers on FG can initiate two important processes. On the one hand, direct reduction of FG (i.e., formation of anionic centers) can occur in the presence of mild reducing agents. On the other hand, a radical mechanism initiated by hydrogen atom transfer can take place provided that species sensitive to homolytic R—H bond dissociation are present in the environment. In both cases, a cascade defluorination process can commence, leading preferentially to compact motifs stabilized by π-conjugation of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. It can be expected that the defluorinated chains of carbons carrying partial positive charge due to surrounding C–F bonds will be highly sensitive to nucleophilic substitutions. In fact, the idea of competitive substitution and reductive defluorination has already been applied to account for experimental observations during the covalent functionalization of graphene based on reactions of FG with various nucleophilic agents, including OH−,23 CN−,31 Grignard reagents33 and others. In such reactions, the main indication of concurrent substitution and defluorination was the composition of the resulting material, which showed only partial functionalization of graphene (e.g., ca. 15% in the case of G-CN) with negligible fluorine content. Nevertheless, the presence of radical centers in FG opens possibilities for direct attack of nucleophilic species on the radical site (Fig. 9). Such attacks could play an important role in the initiation of SN reactions in solvents that are not able to trigger defluorination on their own (e.g., methanol, ethanol, chloroform). Our calculations showed that formation of a radical anion (4-II) is energetically highly favorable (ΔE = −70.4 kcal mol−1 for the gas phase), which strongly supports the idea that early-phase defluorination can be caused by direct interaction of a nucleophile with a radical center.
C double bonds. It can be expected that the defluorinated chains of carbons carrying partial positive charge due to surrounding C–F bonds will be highly sensitive to nucleophilic substitutions. In fact, the idea of competitive substitution and reductive defluorination has already been applied to account for experimental observations during the covalent functionalization of graphene based on reactions of FG with various nucleophilic agents, including OH−,23 CN−,31 Grignard reagents33 and others. In such reactions, the main indication of concurrent substitution and defluorination was the composition of the resulting material, which showed only partial functionalization of graphene (e.g., ca. 15% in the case of G-CN) with negligible fluorine content. Nevertheless, the presence of radical centers in FG opens possibilities for direct attack of nucleophilic species on the radical site (Fig. 9). Such attacks could play an important role in the initiation of SN reactions in solvents that are not able to trigger defluorination on their own (e.g., methanol, ethanol, chloroform). Our calculations showed that formation of a radical anion (4-II) is energetically highly favorable (ΔE = −70.4 kcal mol−1 for the gas phase), which strongly supports the idea that early-phase defluorination can be caused by direct interaction of a nucleophile with a radical center.
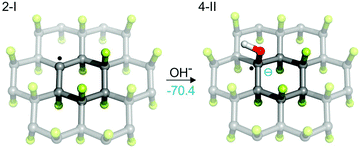 | ||
| Fig. 9 Direct attack of a nucleophilic species (here OH−) on a radical site is energetically very favorable (energy in kcal mol−1 in the gas phase). | ||
Conclusions
Defluorination of FG is a complex process involving direct reduction, nucleophilic substitution or radical substitution reactions depending on the reductive and nucleophilic strengths of the solvent environment and/or presence of dissolved reactive agents. By combining DFT calculations with spectroscopic (EPR and NMR) studies, we have shown that it is the imperfectness of the FG sheets that induces its observed reactivity, distinguishing this 2D material from unreactive perfluorinated hydrocarbons, such as Teflon. The low-lying C–F σ* orbitals in an ideal FG sheet could, in principle, render the structure susceptible to defluorination in the presence of strong reductants. However, it is improbable that mild reducing agents could initiate a cascade process of defluorination by direct electron transfer to the σ* orbital. On the other hand, FG radical centers recorded by EPR measurements exhibit much higher electron affinities, making them ideal reactive sites for mild reducing agents and/or nucleophilic species. Nevertheless, even the relatively large electron acceptor strength of FG spin centers does not explain defluorination of FG in weakly reductive environments, such as DMF. In such cases, point defects can trigger a radical mechanism, provided that species sensitive to homolytic R–H bond dissociation are present in the environment. The proposed mechanism was supported by spin-trap experiments as well as 19F NMR measurements, which suggested formation of DMF˙ radicals under mild reaction conditions (room temperature, simple stirring) and formation of F-DMF (under harsher conditions such as prolonged heating at 120 °C). To sum up, it is clear that point defects play a key role in the reactivity of FG. Understanding relationships between the reductive/nucleophilic strengths of the environment, possible formation of free radicals and point defect redox characteristics seems to be crucial for achieving full control over the functionalization of FG.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the Ministry of Education, Youth and Sports of the Czech Republic (grants LO1305, CZ.1.05/2.1.00/19.0377 and the Research Infrastructure NanoEnviCz: project no. LM2015073), the ERC (Consolidator grant 683024 from the European Union's Horizon 2020 research and innovation programme), and the Neuron fund. We also thank Martin Petr for measuring the XPS spectra and Martin Pykal for preparing the TOC.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- E. J. Duplock, M. Scheffler and P. J. D. Lindan, Phys. Rev. Lett., 2004, 92, 225502 CrossRef PubMed.
- S. H. Cheng, K. Zou, F. Okino, H. R. Gutierrez, A. Gupta, N. Shen, P. C. Eklund, J. O. Sofo and J. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys, 2010, 81, 205435 CrossRef.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- L. G. Bulusheva, V. A. Tur, E. O. Fedorovskaya, I. P. Asanov, D. Pontiroli, M. Riccò and A. V. Okotrub, Carbon, 2014, 78, 137–146 CrossRef CAS.
- A. Vizintin, M. Lozinsek, R. K. Chellappan, D. Foix, A. Krainc, G. Mali, G. Drazic, B. Genorio, R. Dedryvere and R. Dominko, Chem. Mater., 2015, 27, 7070–7081 CrossRef CAS.
- J. J. Xie, C. L. Li, Z. H. Cui and X. X. Guo, Adv. Funct. Mater., 2015, 25, 6519–6526 CrossRef CAS.
- V. Urbanova, F. Karlicky, A. Matej, F. Sembera, Z. Janousek, J. A. Perman, V. Ranc, K. Cepe, J. Michl, M. Otyepka and R. Zboril, Nanoscale, 2016, 8, 12134–12142 RSC.
- S.-Z. Liang, G. Chen, A. R. Harutyunyan, M. W. Cole and J. O. Sofo, Appl. Phys. Lett., 2013, 103, 233108 CrossRef.
- S. Das, P. Sudhagar, V. Verma, D. Song, E. Ito, S. Y. Lee, Y. S. Kang and W. Choi, Adv. Funct. Mater., 2011, 21, 3729–3736 CrossRef CAS.
- L. Liao, H. L. Peng and Z. F. Liu, J. Am. Chem. Soc., 2014, 136, 12194–12200 CrossRef CAS PubMed.
- J. Park and M. D. Yan, Acc. Chem. Res., 2013, 46, 181–189 CrossRef PubMed.
- S. P. Economopoulos, G. Rotas, Y. Miyata, H. Shinohara and N. Tagmatarchis, ACS Nano, 2010, 4, 7499–7507 CrossRef CAS PubMed.
- J. M. Englert, C. Dotzer, G. A. Yang, M. Schmid, C. Papp, J. M. Gottfried, H. P. Steinruck, E. Spiecker, F. Hauke and A. Hirsch, Nat. Chem., 2011, 3, 279–286 CrossRef CAS PubMed.
- S. D. Bian, A. M. Scott, Y. Cao, Y. Liang, S. Osuna, K. N. Houk and A. B. Braunschweig, J. Am. Chem. Soc., 2013, 135, 9240–9243 CrossRef CAS PubMed.
- G. Dubey, R. Urcuyo, S. Abb, G. Rinke, M. Burghard, S. Rauschenbach and K. Kern, J. Am. Chem. Soc., 2014, 136, 13482–13485 CrossRef CAS PubMed.
- A. Y. S. Eng, C. K. Chua and M. Pumera, Nanoscale, 2015, 7, 20256–20266 RSC.
- S. Gilje, S. Han, M. Wang, K. L. Wang and R. B. Kaner, Nano Lett., 2007, 7, 3394–3398 CrossRef CAS PubMed.
- R. R. Nair, W. C. Ren, R. Jalil, I. Riaz, V. G. Kravets, L. Britnell, P. Blake, F. Schedin, A. S. Mayorov, S. J. Yuan, M. I. Katsnelson, H. M. Cheng, W. Strupinski, L. G. Bulusheva, A. V. Okotrub, I. V. Grigorieva, A. N. Grigorenko, K. S. Novoselov and A. K. Geim, Small, 2010, 6, 2877–2884 CrossRef CAS PubMed.
- J. T. Robinson, J. S. Burgess, C. E. Junkermeier, S. C. Badescu, T. L. Reinecke, F. K. Perkins, M. K. Zalalutdniov, J. W. Baldwin, J. C. Culbertson, P. E. Sheehan and E. S. Snow, Nano Lett., 2010, 10, 3001–3005 CrossRef CAS PubMed.
- R. Zboril, F. Karlicky, A. B. Bourlinos, T. A. Steriotis, A. K. Stubos, V. Georgakilas, K. Safarova, D. Jancik, C. Trapalis and M. Otyepka, Small, 2010, 6, 2885–2891 CrossRef CAS PubMed.
- K. A. Worsley, P. Ramesh, S. K. Mandal, S. Niyogi, M. E. Itkis and R. C. Haddon, Chem. Phys. Lett., 2007, 445, 51–56 CrossRef CAS.
- M. Dubecky, E. Otyepkova, P. Lazar, F. Karlicky, M. Petr, K. Cepe, P. Banas, R. Zboril and M. Otyepka, J. Phys. Chem. Lett., 2015, 6, 1430–1434 CrossRef CAS PubMed.
- P. Lazar, C. K. Chua, K. Hola, R. Zboril, M. Otyepka and M. Pumera, Small, 2015, 11, 3790–3796 CrossRef CAS PubMed.
- V. Urbanova, K. Hola, A. B. Bourlinos, K. Cepe, A. Ambrosi, A. H. Loo, M. Pumera, F. Karlicky, M. Otyepka and R. Zboril, Adv. Mater., 2015, 27, 2305–2310 CrossRef CAS PubMed.
- K. E. Whitener, R. Stine, J. T. Robinson and P. E. Sheehan, J. Phys. Chem. C, 2015, 119, 10507–10512 CAS.
- R. Stine, J. W. Ciszek, D. E. Barlow, W. K. Lee, J. T. Robinson and P. E. Sheehan, Langmuir, 2012, 28, 7957–7961 CrossRef CAS PubMed.
- C. Bosch-Navarro, M. Walker, N. R. Wilson and J. P. Rourke, J. Mater. Chem. C, 2015, 3, 7627–7631 RSC.
- B. Y. Li, T. J. He, Z. M. Wang, Z. Cheng, Y. Liu, T. Chen, W. C. Lai, X. Wang and X. Y. Liu, Phys. Chem. Chem. Phys., 2016, 18, 17495–17505 RSC.
- X. Y. Ye, L. M. Ma, Z. G. Yang, J. Q. Wang, H. G. Wang and S. R. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 7483–7488 CAS.
- A. Bakandritsos, M. Pykal, P. Blonski, P. Jakubec, D. D. Chronopoulos, K. Polakova, V. Georgakilas, K. Cepe, O. Tomanec, V. Ranc, A. B. Bourlinos, R. Zboril and M. Otyepka, ACS Nano, 2017, 11, 2982–2991 CrossRef CAS PubMed.
- P. Kovaricek, Z. Bastl, V. Vales and M. Kalbac, Chem. – Eur. J., 2016, 22, 5404–5408 CrossRef CAS PubMed.
- D. D. Chronopoulos, A. Bakandritsos, P. Lazar, M. Pykal, K. Cepe, R. Zboril and M. Otyepka, Chem. Mater., 2017, 29, 926–930 CrossRef CAS PubMed.
- X. Wang, W. M. Wang, Y. Liu, M. M. Ren, H. N. Xiao and X. Y. Liu, Phys. Chem. Chem. Phys., 2016, 18, 3285–3293 RSC.
- J. Tuček, K. Holá, A. B. Bourlinos, P. Błoński, A. Bakandritsos, J. Ugolotti, M. Dubecký, F. Karlický, V. Ranc, K. Čépe, M. Otyepka and R. Zbořil, Nat. Commun., 2017, 8, 14525 CrossRef PubMed.
- J. Ichihara, T. Matsuo, T. Hanafusa and T. Ando, J. Chem. Soc., Chem. Commun., 1986, 793–794 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Wallingford CT, 2009 Search PubMed.
- A. M. Panich, A. I. Shames and T. Nakajima, J. Phys. Chem. Solids, 2001, 62, 959–964 CrossRef.
- J. Giraudet, M. Dubois, A. Hamwi, W. E. E. Stone, P. Pirotte and F. Masin, J. Phys. Chem. B, 2005, 109, 175–181 CrossRef CAS PubMed.
- R. Jain, M. B. Sponsler, F. D. Coms and D. A. Dougherty, J. Am. Chem. Soc., 1988, 110, 1356–1366 CrossRef CAS.
- C. Riplinger, J. P. Y. Kao, G. M. Rosen, V. Kathirvelu, G. R. Eaton, S. S. Eaton, A. Kutateladze and F. Neese, J. Am. Chem. Soc., 2009, 131, 10092–10106 CrossRef CAS PubMed.
- G. Zoppellaro, V. Enkelmann, A. Geies and M. Baumgarten, Org. Lett., 2004, 6, 4929–4932 CrossRef CAS PubMed.
- G. Zoppellaro, A. Geies, K. K. Andersson, V. Enkelmann and M. Baumgarten, Eur. J. Org. Chem., 2008, 1431–1440 CrossRef CAS.
- R. R. Nair, M. Sepioni, I. L. Tsai, O. Lehtinen, J. Keinonen, A. V. Krasheninnikov, T. Thomson, A. K. Geim and I. V. Grigorieva, Nat. Phys., 2012, 8, 199–202 CrossRef CAS.
- J. J. Palacios, J. Fernández-Rossier and L. Brey, Phys. Rev. B: Condens. Matter Mater. Phys, 2008, 77, 195428 CrossRef.
- E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201–1204 CrossRef PubMed.
- J. Burdeniuc and R. H. Crabtree, Science, 1996, 271, 340–341 CAS.
- J. L. Kiplinger and T. G. Richmond, Chem. Commun., 1996, 1115–1116 RSC.
- J. L. Kiplinger and T. G. Richmond, J. Am. Chem. Soc., 1996, 118, 1805–1806 CrossRef CAS.
- J. Burdeniuc, P. E. M. Siegbahn and R. H. Crabtree, New J. Chem., 1998, 22, 503–510 RSC.
- R. P. Hughes, T. LeHusebo, S. M. Maddock, A. L. Rheingold and I. A. Guzei, J. Am. Chem. Soc., 1997, 119, 10231–10232 CrossRef CAS.
- T. G. Richmond, Angew. Chem., Int. Ed., 2000, 39, 3241–3244 CrossRef CAS PubMed.
- W. T. Borden, Chem. Commun., 1998, 1919–1925 RSC.
- G. Sandford, Tetrahedron, 2003, 59, 437–454 CrossRef CAS.
- F. Karlický and M. Otyepka, J. Chem. Theory Comput., 2013, 9, 4155–4164 CrossRef PubMed.
- M. A. Ribas, A. K. Singh, P. B. Sorokin and B. I. Yakobson, Nano Res., 2011, 4, 143–152 CrossRef CAS.
- R. J. Kashtiban, M. A. Dyson, R. R. Nair, R. Zan, S. L. Wong, Q. Ramasse, A. K. Geim, U. Bangert and J. Sloan, Nat. Commun., 2014, 5, 4902 CrossRef CAS PubMed.
- B. Wang, J. J. Wang and J. Zhu, ACS Nano, 2014, 8, 1862–1870 CrossRef CAS PubMed.
- A. M. Suarez, Theory and Simulation of Atomic Hydrogen, Fluorine, and Oxygen on Graphene, The Pennsylvania State University, 2012 Search PubMed.
- D. M. Lemal, J. Org. Chem., 2004, 69, 1–11 CrossRef CAS PubMed.
- W. Lai, D. Xu, X. Wang, Z. Wang, Y. Liu, X. Zhang, Y. Li and X. Liu, Phys. Chem. Chem. Phys., 2017, 19, 24076–24081 RSC.
- D. K. Samarakoon, Z. Chen, C. Nicolas and X.-Q. Wang, Small, 2011, 7, 965–969 CrossRef CAS PubMed.
- G. R. Buettner, Free Radicals Biol. Med., 1987, 3, 259–303 CrossRef CAS PubMed.
- G. M. K. Humphries and H. M. McConnell, Nitroxide Spin Labels, in Methods in Experimental Physics, ed. C. Marton, Academic Press, New York, 1982, vol. 20, pp. 53–122 Search PubMed.
- R. Ragno, A. Zaghi, G. Di Carmine, P. P. Giovannini, O. Bortolini, M. Fogagnolo, A. Molinari, A. Venturini and A. Massi, Org. Biomol. Chem., 2016, 14, 9823–9835 Search PubMed.
- Y. Wang, A. Noble, C. Sandford and V. K. Aggarwal, Angew. Chem., Int. Ed., 2017, 56, 1810–1814 CrossRef CAS PubMed.
- N. Y. Adonin, S. A. Prikhod'ko, V. V. Bardin and V. N. Parmon, Mendeleev Commun., 2009, 19, 260–262 CrossRef CAS.
- H. Fenton, I. S. Tidmarsh and M. D. Ward, Dalton Trans., 2009, 4199–4207 RSC.
- R. P. Singh and J. n. M. Shreeve, Chem. Commun., 2001, 1196–1197 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr09426d |
| This journal is © The Royal Society of Chemistry 2018 |