Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Programming hierarchical self-assembly of colloids: matching stability and accessibility
Daniel
Morphew
and
Dwaipayan
Chakrabarti
 *
*
School of Chemistry, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK. E-mail: d.chakrabarti@bham.ac.uk
First published on 11th July 2018
Abstract
Encoding hierarchical self-assembly in colloidal building blocks is a promising bottom-up route to high-level structural complexity often observed in biological materials. However, harnessing this promise faces the grand challenge of bridging hierarchies of multiple length- and time-scales, associated with structure and dynamics respectively along the self-assembly pathway. Here we report on a case study, which examines the kinetic accessibility of a series of hollow spherical structures with a two-level structural hierarchy self-assembled from charge-stabilized colloidal magnetic particles. By means of a variety of computational methods, we find that for a staged assembly pathway, the structure, which derives the strongest energetic stability from the first stage of assembly and the weakest from the second stage, is most kinetically accessible. Such a striking correspondence between energetics and kinetics for optimal design principles should have general implications for programming hierarchical self-assembly pathways for nano- and micro-particles, while matching stability and accessibility.
Self-assembly of colloidal particles offers tremendous opportunities for fabricating three-dimensional structures in a bottom-up approach due to the scope for tuning the interparticle interactions.1,2 Recent advances in the synthesis of complex colloidal particles have made a wide variety of nano- and micro-scale building blocks available. Many of these colloidal building blocks involve anisotropic interparticle interactions, often due to either anisotropic shape or heterogeneous surface chemistry.2–5 These novel colloidal particles offer rich avenues for programming colloidal self-assembly.6,7
Hierarchical self-assembly of nano- and micro-particles is emerging as an attractive route to structural organization at a higher level, spanning multiple length scales.8,9 Notably, the hierarchical self-assembly of mono-disperse colloidal octapod-shaped nanocrystals resulted in a three-dimensional superlattice via the formation of linear chains of interlocked octapods.10 The assembly of binary and ternary patchy nanoparticles produced supracolloidal ordered structures in a hierarchical scheme.11 The ‘patchiness’ of colloidal triblock spherical particles was exploited to encode staged self-assembly triggered by stepwise changes of the ionic strength of the medium.12 A computational study demonstrated an alternative scheme for patchiness without engineered surfaces en route to a variety of complex superstructures via hierarchical self-assembly.13 A theoretical analysis was presented for programming self-assembly of octopus nanoparticles, which themselves may be self-assembled, into a target nanostructure.14 Recent work also demonstrated how the self-assembly of colloidal particles in confinement could lead to a complex hierarchical geometry that exhibited a rich variety of optical effects including structural coloration due to the interaction of light with the structural features at different length scales.15 We recently followed a biomimetic design route to hollow spherical structures, exploiting a hierarchical self-assembly scheme for charge-stabilized colloidal magnetic particles with an off-centered magnetic dipole.16,17 While a growing body of work in recent years has demonstrated the great promise of hierarchical colloidal self-assembly,10–18 a conceptual framework to reliably program hierarchical self-assembly of colloidal building blocks has proved to be elusive. Such a framework is crucially important to address the challenges of a multiscale design problem, arising from the requirement of bridging hierarchies of multiple length- and time-scales, associated with structure and dynamics respectively, along the self-assembly pathway.19
Harnessing the enormous potential for colloidal self-assembly to offer a bottom-up route to structure fabrication critically hinges on our ability to manipulate the interactions between the colloidal particles such that a target structure is not only thermodynamically favorable, but also kinetically accessible on experimental time scales.6,14,20 This task becomes even more formidable in the context of hierarchical self-assembly. In this case, a pertinent question is whether the pathway is staged – that is to say, whether the assembly itself follows a hierarchical pathway.17,21 Such a pathway for colloidal self-assembly would involve concerted movements of colloidal particles over the course of the assembly. In fact, the requirement of matching stability and accessibility draws a parallel between the target structure for programmed self-assembly and the native structure of a protein.22
In particular, hollow spherical structures at the nano- and micro-scale are attractive targets for a range of practical applications,23–25 especially as nanocapsules resembling viral capsids and microvesicles for drug delivery.26,27 Viral capsids of icosahedral symmetry are in fact marvelous examples of molecular self-assembly in nature, resulting in a remarkable structural hierarchy in terms of repeating subunits.28 While the structures of viral capsids are now known in great detail, the pathways for capsid assembly still remain poorly understood largely due to limitations on experimental characterization.29,30
In this contribution, we report on a case study where we employed a variety of computational methods to examine the kinetic accessibility of a series of hollow spherical structures self-assembled from charge-stabilized colloidal magnetic particles. The structures each show a fascinating two-level structural hierarchy. We demonstrate how an optimal design rule for hierarchical self-assembly in this case can be derived while satisfying both the thermodynamic and kinetic criteria. We find a striking correspondence between the energetics and kinetics, which we account for a staged assembly pathway. While our designer building blocks closely resemble recently synthesized colloidal magnetic particles,31 our results suggest design principles, which should have general implications for programming hierarchical self-assembly of nano- and micro-particles.19
While magnetic colloidal particles are classic examples of microscale building blocks with anisotropic interactions,32 recent years have experienced a surge in the synthesis of exotic colloidal magnetic particles.31,33 Having drawn motivation from these research activities, a number of computational studies have focused on spherical magnetic colloids with an additional anisotropy attribute in terms of an off-centered point-dipole.16,34,35 We considered charge-stabilized colloidal magnetic particles, which included a permanent point-dipole shifted away from the center,16 closely resembling those synthesized using a single-domain hematite cube inclusion underneath the surface of organopolymer spheres.31 However, there was uncertainty in the direction of the dipole moment within the magnetic cube in this experimental system.35 It was most likely that the direction of the dipole was not parallel to the radial shift vector to the position of the dipole.35 We introduced an additional model parameter θ, denoting the angle at which the direction of the point-dipole is inclined to the radial shift vector (see Fig. 1a).17
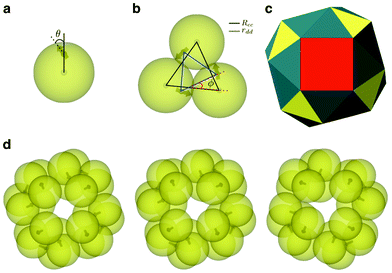 | ||
| Fig. 1 Two-level structural hierarchy emerging from the charge-stabilized colloidal magnetic particles under consideration. (a) A schematic representation of a single colloidal magnetic particle, showing the angle θ at which the direction of the point-dipole is inclined to the radial shift vector. (b) A representative global minimum for N = 3 charge-stabilized colloidal magnetic particles – the planar trimer formed at the intermediate level – showing the dipoles in a flux-closure arrangement. In addition, the parameters defining the structural features tabulated in Table 1 are shown: Rcc denotes the distance between the geometric centers of adjacent colloidal particles and rdd the distance between the corresponding point-dipoles; φ is the angular displacement between the triangles formed by the geometric centers and those by the point-dipoles on the plane. (c) A polyhedral representation of the snub cube structure of octahedral symmetry for θ = 5°, where distinct types of faces are color coded. The eight equilateral triangular faces, shown in yellow, are sustained by the colloidal magnetic particles; the remaining faces, namely six square faces (red) and twenty four triangular faces (blue), emerge from the assembly of these trimers. (d) The global minima for N = 24 charge stabilized colloidal magnetic particles corresponding to three sets of model parameters, where only the model parameter θ is varied. From the left to the right θ increases: 0°, 5° and 10°, respectively. All three structures are of octahedral symmetry and are topologically equivalent to the snub cube. | ||
We employed the basin-hopping global optimization method to identify the global minima on the potential energy landscapes for size-selected clusters.36,37 In the case of a cluster of N = 24 particles, a polyhedron of octahedral symmetry topologically equivalent to the snub cube was found to be the most favored structure on the potential energy landscape for a range of θ values from 0° to 10° (see Fig. 1), the rest of the model parameters remaining identical. Apart from the angle θ, the set of model parameters includes the inverse Debye screening length λ−1, the strength of the magnetic dipole μD and the separation d between the center of the colloidal particle and the location of the embedded point dipole; the latter is expressed in terms of the dimensionless parameter α = 2d/σ, σ being the unit of length. In the present study, we set α = 0.6, μD = 2 and λ−1 = 25. This choice of the parameter set, as identified in previous studies,16,17 ensured that the colloidal building blocks exclusively formed planar trimers in the first stage and subsequently the trimers formed the snub cube structure. The supracolloidal polyhedron thus exhibited a fascinating two-level structural hierarchy via the planar trimers with the dipoles in a flux-closure arrangement at the intermediate level (see Fig. 1b). Fig. 1c shows a polyhedral representation with color codes to distinguish distinct types of faces. The eight equilateral triangular faces, shown in yellow in Fig. 1c, are sustained by the colloidal magnetic particles; the remaining faces, namely six square faces (red) and twenty four triangular faces (blue) emerge from the assembly of these trimers. Hereafter, we refer to this structure as the snub cube structure or the hollow spherical structure. For θ = 15°, the snub cube structure was no longer the global minimum on the energy landscape. It is of interest to note that an analysis of the energetics for the snub cube structure revealed that an energetically favorable nearly anti-parallel arrangement of the dipoles in neighboring trimers, as apparent in Fig. 1d, was the key factor driving the second level of assembly into this hollow spherical structure.17 In the present study, we compared the kinetic accessibility of the snub cube structure for three different θ values over the range from 0° to 10°, in which this structure is the global minimum on the energy landscape.
Although the basin-hopping global optimization method relies upon a hypersurface deformation,36,37 which removes the barriers on the potential energy landscape, the success rate of this method in finding the global minimum reflects the complexity of the landscape, which would have some impact on the kinetics. It is noteworthy that a series of basin-hopping steps do not correspond to a physical dynamical process. As θ assumed a non-zero value, an indication for reduced complexity and improved kinetics was apparent in a significant enhancement of the success rate for the basin-hopping global optimization method to find the snub cube structure as the global minimum on the potential energy landscape within a certain pre-fixed number of basin-hopping steps. When identical sets of 20 random starting configurations were considered for half a million basin-hopping steps, the success of finding the global minimum was only 5% for θ = 0° as opposed to 100% for both θ = 5° and θ = 10°. The mean first encounter times differed only by approximately 4% between θ = 5° and θ = 10° – not significant enough for comparing their kinetic accessibility conclusively.
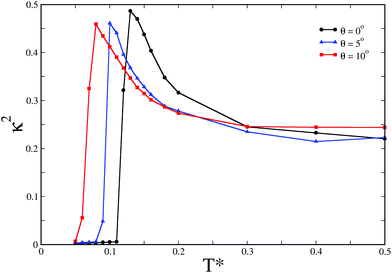
In order to draw a comparison of the hollow spherical structures for different θ values in terms of their kinetic accessibility when the underlying energy landscape is sampled at a non-zero temperature, we carried out Monte Carlo (MC) simulations. In a given MC run, the reduced temperature T*, defined by T* = kBT/εY, εY being the Yukawa contact potential chosen as the unit of energy, was gradually lowered. In the context of emerging structural hierarchy, single-particle Monte Carlo moves for the elementary building blocks were known to be inadequate.16 The dominant pathway for the hierarchical self-assembly into a structure topologically equivalent to the snub tetrahedron for N = 12 and θ = 10° was found by means of a rare event simulation technique to proceed stagewise via the formation of trimers.17 It was therefore reasonable to anticipate that a staged assembly pathway would most likely be followed for the emergence of structural hierarchy in this case. We thus performed Monte Carlo simulations with the trimers formed at the first level of the assembly, and carried out single-particle moves treating these secondary units as rigid bodies. The secondary units with dipoles in planar flux-closure arrangements, as shown in Fig. 1(b), were distinct for each value of θ. The distinct structural features are tabulated in Table 1. 10 independent Monte Carlo simulations were carried out with Nt = 8 rigid secondary units for all three θ values, each within an identical spherical container. The data shown in Fig. 2 are corresponding to the spherical container of radius 2.5 in the reduced unit, while the radius of gyration is 1.405 for the snub cube structure corresponding to the value of θ = 10°. The formation of a hollow spherical structure was monitored with the relative shape anisotropy parameter κ2 as shown in Fig. 2, and was also confirmed by visual inspection. For a hollow spherical structure such as the snub cube, κ2 ≈ 0. As evident in Fig. 2, for all three θ values we observed the formation of the snub cube structure. It was striking that the success rate varied considerably. The success rate was 10% for θ = 0°, increasing to 40% for θ = 5° and further to 80% for θ = 10°. It is clearly evident that an increase in the θ value from 0° to 10° gradually results in an improved kinetic accessibility of the snub cube structure, which shows a two-level structural hierarchy. In what follows, an explanation for this improved kinetic accessibility is provided. As a representative case, for θ = 0° for which the success rate was the least, we considered bigger spherical containers to investigate whether the snub cube structure was formed for a container size varying over a reasonable range; we indeed observed the formation of the snub cube structure up to a radius of 5 in the reduced unit.
| θ | 0° | 5° | 10° |
|---|---|---|---|
| R cc | 0.963 | 0.955 | 0.949 |
| r dd | 0.667 | 0.637 | 0.612 |
| φ | 30.92° | 30.42° | 29.67° |
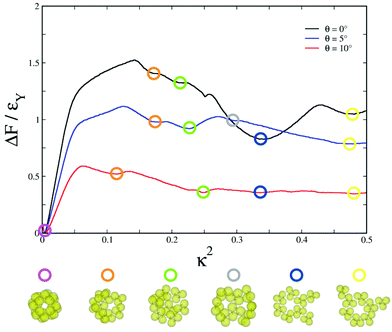
The free-energy profiles for the formation of the hollow spherical structures, as shown in Fig. 3, were found to be consistent with the gradual increase in their kinetic accessibility as θ was varied from 0° to 10°. The free-energy profiles were obtained by the umbrella sampling technique, where the order parameter κ2 was used as the reaction coordinate. For each θ value, the umbrella sampling simulations were undertaken around the respective temperatures at which the formation of the hollow spherical structures was first observed upon cooling. The biased Monte Carlo simulations were carried out with rigid secondary units, distinct for each θ value, with single-particle moves. The self-assembly of the colloidal particles into the snub cube structure, which is of octahedral symmetry, is expected to incur an entropy cost. Fig. 3 shows that the snub cube structure was indeed the global minimum on the free energy profile for all three θ values, despite the entropy cost. It is also evident in Fig. 3 that the free energy barrier to the formation of the snub cube structure gradually decreased as the model parameter θ was increased from 0°, thus leading to increased kinetic accessibility.
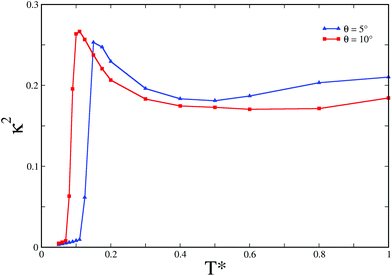
Since the aforementioned series of Monte Carlo simulations were performed with the rigid secondary units, these simulations could capture only the second stage of assembly. In order to garner a complete picture, we also performed Monte Carlo simulations of the primary building blocks for all three θ values, using the virtual-move Monte Carlo (VMMC) algorithm.38 The VMMC algorithm implements cluster moves, and thus promises to be effective for sampling with the primary building blocks in this case. We carried out 10 independent VMMC simulations of N = 24 colloidal magnetic particles within a fixed spherical container for each of the three θ values. As the temperature T* was gradually decreased for the VMMC simulations, the formation of the snub cube structure demonstrating a remarkable two-level structural hierarchy was observed for θ = 5° and 10°, as revealed by the evolution of the order parameter κ2 (Fig. 4). The desired snub cube structure was formed with a 30% success rate for θ = 5° and with a 60% success rate for θ = 10°. However, for θ = 0°, the snub cube structure was not obtained in any of these simulation runs. In fact, we did not observe even the formation of the requisite number of trimers (i.e. 8 trimers for a 24-particle system) in a single instance for θ = 0°, implying that the first stage of the assembly was not completed correctly in this case. The results of the VMMC simulations thus unequivocally provided evidence that the hollow spherical structure was most kinetically accessible for θ = 10°. A spherical container of radius 2.5 in the reduced unit was used for the data in Fig. 4. For the representative case of θ = 10°, additional data, not shown here, confirmed the formation of the snub cube structure with spherical containers up to the radius of 4 in the reduced unit. It is apparent that upon cooling the systems the relative shape anisotropy κ2 undergoes a rise before it falls rather sharply to values close to zero corresponding to the formation of the snub cube structure. It is plausible that entropically favorable open bowl-like structures, which are also stabilized by anti-parallel arrangements of the dipoles in the neighboring trimers,17 tend to form first upon gradual cooling before the closed snub cube structure was formed, resulting in such a non-monotonic behavior of κ2.
The hollow spherical structure, despite being thermodynamically favorable, proved elusive for θ = 0°. While a staged pathway was most likely, it was striking that the first stage of the self-assembly into the trimers could not be completed in terms of forming requisite number of trimers in our VMMC simulations. This observation, in particular, led us to analyze the energetics of the snub cube structure, which shows a two-level structural hierarchy, and compare the energetic stabilities gained at each level of the assembly for all three θ values, as shown in Table 2. The analysis revealed a remarkable correspondence between the relative energetic stabilities gained at successive levels of the assembly, as shown schematically in Fig. 5, and the kinetic accessibility of the hollow spherical structure as the model parameter θ was varied. It is clearly evident that the thermodynamic driving forces arising from the energetic stability gained through the formation of a trimer at the first level of the assembly increased as θ increased from θ = 0° to θ = 10°. This resulted in the formation of increasingly more stable secondary building units. The second stage of assembly brought together eight such secondary building units to form the snub cube structure. The difference in the potential energy between the snub cube structure and eight independent trimers, which appears in the column denoted by ΔE12 in Table 2, accounts for the energetic driving force behind the second stage of the assembly. It thus follows that the energetic driving force for the second stage of the assembly gradually decreased as θ was varied from θ = 0° to θ = 10°. The energetic stability was drawn from nearly anti-parallel arrangements for pairs of dipoles in neighboring secondary units emerging from the second stage of the assembly. Note that the formation of the closed snub cube structure would incur a reduction in entropy. The decrease in energetic driving force for the second stage of assembly as the parameter θ increases therefore also accounts for the corresponding decrease in the temperature at which the formation of the snub cube structure was first observed as the finite system was gradually cooled in both MC (Fig. 2) and VMMC (Fig. 4) simulations.
| θ | E 1 | E 2 | ΔE12 |
|---|---|---|---|
| 0° | −31.294 | −275.225 | −24.873 |
| 5° | −35.761 | −304.189 | −18.101 |
| 10° | −40.395 | −336.721 | −13.561 |
The striking correspondence between the energetics and kinetics of the self-assembly into a two-level structural hierarchy, as revealed here, called for an explanation. For the success of programmed self-assembly into a target structure, the microscale colloidal particles need to negotiate the so-called kinetic traps, which arise from the presence of metastable “wrong” structures in the free-energy landscape.39 Reversible association allows for facile annealing of defects, and hence removal of kinetic traps. Such reversibility is best achieved here at the expense of relatively weak thermodynamic driving forces for the second stage of assembly. In the present case, the hierarchical self-assembly followed a staged pathway, in which the trimers formed in the first stage of assembly served as the secondary building blocks in the course of the second stage of assembly while retaining their integrity. Such a pathway involved concerted movements of the colloidal particles over the course of the second stage of assembly, incurring an entropy contribution to the free energy barrier. The more energetically stable the secondary building blocks, the higher would be the energy penalty for any alternative pathway involving the loss of integrity of the secondary building blocks once they are formed, making such a pathway highly unlikely. A strong energetic driving force for the first stage of assembly therefore not only facilitates this stage from a thermodynamic consideration, but also promotes concerted movements in the next stage despite the entropy cost involved, and thus favor a staged assembly pathway from the perspective of the free energy barrier.
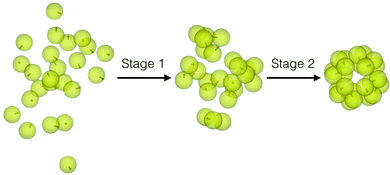
It follows from the results presented here that a hierarchy of interactions is crucial for a staged assembly pathway to structural hierarchy. Such a hierarchy of interactions allows us to consider also a staged disassembly into the secondary building blocks and their reassembly, as shown in Fig. 6 for the case of θ = 10°, by the application of a weak external magnetic field in the first place and then turning it off. The strength of the magnetic field was so chosen that it could open up the snub cube structure while retaining the integrity of the trimers. For the data shown in Fig. 6, B = 0.25 at T* = 0.07. This demonstration suggests that a weak magnetic field could, in principle, be also exploited to induce staged disassembly of any “wrong” structure obtained from the second stage of assembly. The ease of disassembly that such an operational hierarchy of interactions implies may have implications for disassembly observed for viral capsids.40
In the present study we employed a variety of computational methods to examine the kinetic accessibility of a series of hollow spherical structures, each displaying a remarkable two-level structural hierarchy, self-assembled from charge-stabilized colloidal magnetic particles. For these designer building blocks, which were modeled after recently synthesized colloidal magnetic particles,31 a model parameter was varied across the series, resulting in a gradual change in the energetics. We found that for a staged assembly pathway, the structure, which derived the strongest energetic stability from the first stage of the assembly and the weakest from the second stage, was most kinetically accessible. We accounted for such a striking correspondence between the energetics and kinetics for optimal design principles, which should have general implications for programming hierarchical self-assembly pathways for nano- and micro-particles, while matching stability and accessibility.19 The present scenario should be distinguished from those, where thermodynamic control or kinetic control prevails so that a structure is observed either because it is the most stable state or because the pathway leading to it has the lowest free energy barrier.39
We further note that it is quite likely that an experimental system would have some degree of dispersity in the dipole direction. Given the global stability of the hollow spherical structure for a range of θ values, one would expect that the formation of such structure would have some level of tolerance to this dispersity, though the symmetry of the structure would then be reduced. The study of a model system with the dispersity of the dipole direction was, however, beyond the scope of the present investigation.
Methods
Model
We modeled the charge-stabilized colloidal magnetic particles under consideration using a one-component description with an effective pairwise potential and the point-dipole approximation for the magnetic interactions. The point-dipole was off-centered, located at a distance d away from the center of a spherical particles and inclined with an angle θ to the radial shift vector. The Yukawa potential was used to describe the screened electrostatic repulsion giving rise to the charge-stabilization. In this description, the potential energy V for a finite-size system of N colloidal magnetic particles in the absence of any external magnetic field is then given by: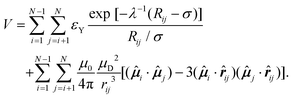 | (1) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i is the unit vector defining the orientation of the aforementioned point dipole, whose magnitude is given by μD, μ0 is the permeability of free space, and rij is the separation vector: rij = ri − rj with magnitude rij, so that the unit vector
i is the unit vector defining the orientation of the aforementioned point dipole, whose magnitude is given by μD, μ0 is the permeability of free space, and rij is the separation vector: rij = ri − rj with magnitude rij, so that the unit vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij = rij/rij. In the Yukawa description of screened electrostatic repulsion, λ−1 is the inverse Debye screening length and εY is the so-called contact potential. The chosen units of energy and length are the Yukawa parameters εY and σ, respectively. The model parameters are then the inverse Debye screening length λ−1, the strength of the magnetic dipole μD, the separation d between the center of the colloidal particle and the location of the embedded point dipole and the angle θ between the direction of the dipole moment
ij = rij/rij. In the Yukawa description of screened electrostatic repulsion, λ−1 is the inverse Debye screening length and εY is the so-called contact potential. The chosen units of energy and length are the Yukawa parameters εY and σ, respectively. The model parameters are then the inverse Debye screening length λ−1, the strength of the magnetic dipole μD, the separation d between the center of the colloidal particle and the location of the embedded point dipole and the angle θ between the direction of the dipole moment ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) i and the shift vector ri − Ri. The shift distance is expressed in terms of the dimensionless ratio α = 2d/σ, where σ is the length scale in terms of which the Yukawa potential is defined, proposing an estimate of the particle size in the absence of a hard core. The magnetic dipole μD is given in reduced units of (4πεYσ3/μ0)1/2. In the present study, α = 0.6, μD = 2 and λ−1 = 25; θ was varied. We treated the colloidal particles as rigid bodies, representing the translational coordinates of each rigid body by the Cartesian coordinates of the center of the spherical particle and the rotational coordinates by a unit quaternion, unless specified otherwise. An additional contribution to the potential energy is drawn in the presence of an external static magnetic field B and is given by
i and the shift vector ri − Ri. The shift distance is expressed in terms of the dimensionless ratio α = 2d/σ, where σ is the length scale in terms of which the Yukawa potential is defined, proposing an estimate of the particle size in the absence of a hard core. The magnetic dipole μD is given in reduced units of (4πεYσ3/μ0)1/2. In the present study, α = 0.6, μD = 2 and λ−1 = 25; θ was varied. We treated the colloidal particles as rigid bodies, representing the translational coordinates of each rigid body by the Cartesian coordinates of the center of the spherical particle and the rotational coordinates by a unit quaternion, unless specified otherwise. An additional contribution to the potential energy is drawn in the presence of an external static magnetic field B and is given by 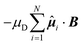 . The magnetic field strength B is given here in the units of [εYμ0/(4πσ3)]1/2.
. The magnetic field strength B is given here in the units of [εYμ0/(4πσ3)]1/2.
Global optimization
We used the basin-hopping (BH) global optimization method,36,37 as implemented in GlOSP, a program for Global Optimization for Structure Prediction developed in-house, to identify the global minimum of potential energy landscape and to calculate mean first-encounter times. A hypersurface deformation, which results in a reduced configuration space spanned by all the local minima of original landscape, underlies this method. This reduced configuration space is then explored by proposing random steps, followed by local geometry optimization to a minimum. The limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm was employed for local minimization.41 The proposed step from the current minimum is accepted or rejected by the application of the Metropolis criterion, using the relative energies of the two minima and a fictitious temperature. In our implementation of the method, the local minimization was performed using analytical gradients; an angle-axis representation was used for the rigid-body rotational coordinates due to certain numerical advantages associated with such a representation in the context of geometry optimization.42For each set of model parameters with a distinct value of θ, twenty independent BH global optimization runs were performed, undertaking 0.5 × 106 basin-hopping steps from an identical set of random initial configurations. The BH step at which the global minimum was first identified for each run, the first-encounter time, was recorded to calculate a mean first-encounter time for each θ.
Monte Carlo sampling
Monte Carlo simulations of a number of systems, each containing Nt = 8 rigid building blocks, were performed in the canonical ensemble, employing a constraining radius to avoid evaporation especially at high temperatures. For each set of model parameters with a distinct value of θ, 10 independent MC runs were undertaken. In a given run, starting from a random initial configuration, the system was gradually cooled. The number of MC steps carried out increased from 107 at high temperatures to 2 × 109 at low temperatures; the first half of the MC run at every temperature was used for the system to equilibrate. Each MC step involved Nt single-particle moves in both translational and rotational coordinates, where the step sizes were adapted to achieve a target acceptance ratio of 0.45. For the MC simulations, the reduced temperature T* was used.The formation of the spherical structure was monitored by calculating the relative shape anisotropy κ2 for the distribution of the particles in the system, which is given by:43
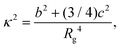 | (2) |
In order to compute the free energy profiles, we employed umbrella sampling,44 using the relative shape anisotropy κ2 as the order parameter. To this end, a series of Monte Carlo simulations of 8 rigid trimers were carried out employing additional biasing potentials, which were harmonic functions, centered on successive values of the order parameter. The biasing potentials ensured efficient sampling over several partially overlapping windows, spanning the range of the order parameter of interest. The unbiased probability distribution was then obtained using the weighted histogram analysis method.45,46 Finally, the free energy difference along the chosen order parameter was evaluated from this unbiased probability distribution, taking the hollow spherical structure, corresponding to κ2 ≈ 0, as the reference.
Virtual move Monte Carlo
We employed the virtual move Monte Carlo (VMMC) algorithm,38 as implemented in PaSSion, a Package for Soft Matter Simulation developed in-house, following a recent prescription.47 The VMMC algorithm prescribes cluster moves. It is necessary to consider cluster moves in the context of emergent structural hierarchy. Such an algorithm helps to overcome the non-physical kinetic traps that are encountered during MC simulations employing single-particle moves, leading to an enhanced sampling of the equilibrium distribution.We carried out VMMC simulations in the canonical ensemble for finite-size clusters of N = 24 particles, mostly contained within a spherical volume of radius 2.5 in the reduced unit. For each set of model parameters with a distinct value for θ, 10 independent VMMC simulations were performed starting from random initial configurations. For a given run, the system was gradually cooled. As the reduced temperature T* was decreased, the number of VMMC cycles undertaken was increased from 108 at high temperatures to 109 at low temperatures. Each VMMC cycle involved N translational moves or N collective rotational moves; the first half of the run at every temperature studied was used for equilibration. The steps sizes proposed within the translational and collective rotational VMMC moves were adjusted to secure an average acceptance ratio of 0.45. For the VMMC simulations, the reduced temperature T* was also given by T* = kBT/εY.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council of the UK via EP/M506461/1 and the University of Birmingham. The datasets presented here are available from the corresponding author on request.References
- G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774 CrossRef PubMed.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- S.-M. Yang, S.-H. Kim, J.-M. Lim and G.-R. Yi, J. Mater. Chem., 2008, 18, 2177–2190 RSC.
- F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388 CrossRef PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S.-H. Kim, D. Pine and G.-R. Yi, Nat. Commun., 2013, 4, 1688 CrossRef PubMed.
- L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2015, 14, 2–9 CrossRef PubMed.
- W. B. Rogers, W. M. Shih and V. N. Manoharan, Nat. Rev. Mater., 2016, 1, 16008 CrossRef.
- J. Zhang, E. Luijten and S. Granick, Annu. Rev. Phys. Chem., 2015, 66, 581–600 CrossRef PubMed.
- D. Morphew and D. Chakrabarti, Curr. Opin. Colloid Interface Sci., 2017, 30, 70–80 CrossRef.
- K. Miszta, J. de Graaf, G. Bertoni, D. Dorfs, R. Brescia, S. Marras, L. Ceseracciu, R. Cingolani, R. van Roij, M. Dijkstra and L. Manna, Nat. Mater., 2011, 10, 872–876 CrossRef PubMed.
- A. H. Gröschel, A. Walther, T. I. Löbling, F. H. Schacher, H. Schmalz and A. H. E. Müller, Nature, 2013, 503, 247–252 CrossRef PubMed.
- Q. Chen, S. C. Bae and S. Granick, J. Am. Chem. Soc., 2012, 134, 11080–11083 CrossRef PubMed.
- M. Grünwald and P. L. Geissler, ACS Nano, 2014, 8, 5891–5897 CrossRef PubMed.
- A. V. Tkachenko, Phys. Rev. Lett., 2011, 106, 255501 CrossRef PubMed.
- N. Vogel, S. Utech, G. T. England, T. Shirman, K. R. Phillips, N. Koay, I. B. Burgess, M. Kolle, D. A. Weitz and J. Aizenberg, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10845–10850 CrossRef PubMed.
- D. Morphew and D. Chakrabarti, Nanoscale, 2015, 7, 8343–8350 RSC.
- D. Morphew and D. Chakrabarti, Soft Matter, 2016, 12, 9633–9640 RSC.
- Y. Zhang, A. McMullen, L.-L. Pontani, X. He, R. Sha, N. C. Seeman, J. Brujic and P. M. Chaikin, Nat. Commun., 2017, 8, 21 CrossRef PubMed.
- D. Morphew, J. Shaw, C. Avins and D. Chakrabarti, ACS Nano, 2018, 12, 2355–2364 CrossRef PubMed.
- D. Frenkel and D. J. Wales, Nat. Mater., 2011, 10, 410–411 CrossRef PubMed.
- T. K. Haxton and S. Whitelam, Soft Matter, 2013, 9, 6851–6861 RSC.
- R. L. Baldwin, Nature, 1994, 369, 183–184 CrossRef PubMed.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef PubMed.
- C. H. J. Evers, J. A. Luiken, P. G. Bolhuis and W. K. Kegel, Nature, 2016, 534, 364–368 CrossRef PubMed.
- J. M. Fletcher, R. L. Harniman, F. R. H. Barnes, A. L. Boyle, A. Collins, J. Mantell, T. H. Sharp, M. Antognozzi, P. J. Booth, N. Linden, M. J. Miles, R. B. Sessions, P. Verkade and D. N. Woolfson, Science, 2013, 340, 595–599 CrossRef PubMed.
- T. Douglas and M. Young, Science, 2006, 312, 873–875 CrossRef PubMed.
- K. L. Thompson, M. Williams and S. P. Armes, J. Colloid Interface Sci., 2015, 447, 217–228 CrossRef PubMed.
- D. L. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef PubMed.
- M. F. Hagan, Adv. Chem. Phys., 2014, 155, 1–68 Search PubMed.
- S. Faez, Y. Lahini, S. Weidlich, R. F. Garmann, K. Wondraczek, M. Zeisberger, M. A. Schmidt, M. Orrit and V. N. Manoharan, ACS Nano, 2015, 12, 12349–12357 CrossRef PubMed.
- S. Sacanna, L. Rossi and D. J. Pine, J. Am. Chem. Soc., 2012, 134, 6112–6115 CrossRef PubMed.
- P. Tierno, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528 RSC.
- L. Baraban, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031407 CrossRef PubMed.
- M. Klinkigt, R. Weeber, S. Kantorovich and C. Holm, Soft Matter, 2013, 9, 3535–3546 RSC.
- A. A. Abrikosov, S. Sacanna, A. P. Philipse and P. Linse, Soft Matter, 2013, 9, 8904–8913 RSC.
- Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615 CrossRef.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 111, 5111–5116 CrossRef.
- S. Whitelam and P. G. Geissler, J. Chem. Phys., 2007, 127, 154101 CrossRef PubMed.
- S. Whitelam and R. L. Jack, Annu. Rev. Phys. Chem., 2015, 66, 143 CrossRef PubMed.
- D. Law-Hine, A. K. Sahoo, V. Bailleux, M. Zeghal, S. Prevost, P. K. Maiti, S. Bressanelli, D. Constantin and G. Tresset, J. Phys. Lett., 2015, 6, 3471–3476 Search PubMed.
- D. Liu and J. Nocedal, Mathematical Programming, 1989, vol. 45, pp. 503–528 Search PubMed.
- D. Chakrabarti and D. J. Wales, Phys. Chem. Chem. Phys., 2009, 11, 1970–1976 RSC.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1206–1214 CrossRef.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef.
- Š. Růžička and M. P. Allen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 033307 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |