Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A computational exploration of the crystal energy and charge-carrier mobility landscapes of the chiral [6]helicene molecule†
Beth
Rice
ab,
Luc M.
LeBlanc
 c,
Alberto
Otero-de-la-Roza
d,
Matthew J.
Fuchter
c,
Alberto
Otero-de-la-Roza
d,
Matthew J.
Fuchter
 be,
Erin R.
Johnson
be,
Erin R.
Johnson
 c,
Jenny
Nelson
c,
Jenny
Nelson
 ab and
Kim E.
Jelfs
ab and
Kim E.
Jelfs
 *be
*be
aDepartment of Physics, Imperial College London, South Kensington, London, SW7 2AZ, UK
bCentre for Plastic Electronics, Imperial College London, South Kensington, London, SW7 2AZ, UK. E-mail: k.jelfs@imperial.ac.uk; Web: www.twitter.com/JelfsChem
cDepartment of Chemistry, Dalhousie University, Halifax, Nova Scotia B3H 4R2, Canada
dDepartment of Chemistry, University of British Columbia, Okanagan, 3247 University Way, Kelowna, British Columbia V1V 1V7, Canada
eDepartment of Chemistry, Imperial College London, South Kensington, London, SW7 2AZ, UK
First published on 5th January 2018
Abstract
The potential of a given π-conjugated organic molecule in an organic semiconductor device is highly dependent on molecular packing, as it strongly influences the charge-carrier mobility of the material. Such solid-state packing is sensitive to subtle differences in their intermolecular interactions and is challenging to predict. Chirality of the organic molecule adds an additional element of complexity to intuitive packing prediction. Here we use crystal structure prediction to explore the lattice-energy landscape of a potential chiral organic semiconductor, [6]helicene. We reproduce the experimentally observed enantiopure crystal structure and explain the absence of an experimentally observed racemate structure. By exploring how the hole and electron-mobility varies across the energy–structure–function landscape for [6]helicene, we find that an energetically favourable and frequently occurring packing motif is particularly promising for electron-mobility, with a highest calculated mobility of 2.9 cm2 V−1 s−1 (assuming a reorganization energy of 0.46 eV). We also calculate relatively high hole-mobility in some structures, with a highest calculated mobility of 2.0 cm2 V−1 s−1 found for chains of helicenes packed in a herringbone fashion. Neither the energetically favourable nor high charge-carrier mobility packing motifs are intuitively obvious, and this demonstrates the utility of our approach to computationally explore the energy–structure–function landscape for organic semiconductors. Our work demonstrates a route for the use of computational simulations to aid in the design of new molecules for organic electronics, through the a priori prediction of their likely solid-state form and properties.
Introduction
Supramolecular materials consist of assemblies built from molecules packed through non-covalent interactions. The design of molecular materials with targeted properties is a long-standing goal, but, unfortunately, often thwarted by the inherent unpredictability of the supramolecular assembly.1 In the absence of strong directional non-covalent interactions (for example hydrogen bonds), small changes in molecular position or conformation can have a large impact on the crystal packing and consequent properties. Crystal structure prediction (CSP) techniques have been developed over the last few decades for the prediction of polymorphism in pharmaceuticals.2,3 Such techniques identify the most likely polymorphs of organic molecules by searching the potential energy landscapes and energetically ranking the structures. “Blind tests” of these methods have shown increasing success over the last decades, with successful predictions for increasingly complex systems, such as co-crystals, hydrates and larger, more flexible molecules.4–6 However, the application of these techniques to molecular materials is still relatively rare, with some recent exceptions including the comparison of two polymorphs of an acetylene molecule in organic electronics7 and in the prediction of porous molecular materials,8 including the generation in 2017 of “energy–structure–function” (ESF) maps for extrinsically porous materials.9 Very recently, Campbell et al. explored ESF maps for small molecule planar azapentacenes, demonstrating the influence of both intra- and intermolecular interactions in determining crystal packing and thus charge-carrier mobilities in the molecules.10 Through prediction of ESF maps, one can lay the basis for computational design, or rather, screening of molecules that will likely form structures with optimal properties, such as electronic transport properties. In this work, we explore the energy–structure–function relationships for charge-carrier mobilities in [6]helicene, a chiral molecule with high potential for novel organic electronic device applications.Helicenes are a class of chiral molecules where the chirality arises from the intrinsically helical nature of their twisted aromatic structure (see Fig. 1).11 Like all chiral molecules, they can exist in both left-handed or right-handed forms (so-called enantiomers) and single-handed (enantiopure) helicenes exhibit exceptionally strong chiroptical properties, such as circular dichroism and high optical rotatory power.11 Helicenes have been investigated for application in chemosensors, stereoselective charge transfer complexes, liquid crystals, organic light emitting diodes (OLEDs), asymmetric catalysis, molecular machines and in biological chemistry.11–14 Many of these applications depend on the presence of certain supramolecular assemblies of the molecular helicenes. For example, functionalized helicenes have been developed to form one-dimensional columnar aggregates, the fibres of which have then exhibited high non-linear optical susceptibility.15–17 Chemical modifications of such molecules have directed how they pack into mesophases as helical discotic liquid crystals,18 and studies of their assembly on surfaces have shed light on their chiral molecular recognition (see ref. 19 and 20 and references therein).
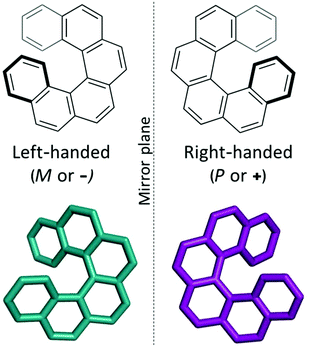 | ||
| Fig. 1 The two enantiomers of the chiral [6]helicene molecule, shown in a top-down view (bold bonds indicate bonds projecting towards the viewer). | ||
Given their conjugated aromatic framework, the solid-state structures of helicenes provide significant opportunities for use in organic electronic devices.11,14 Furthermore, the chirality of these materials allows for additional functionality in devices, such as OLEDs that emit circularly polarized light,21,22 and spintronic devices based on the chiral-induced spin-selectivity effect.23 Despite such high promise however, the application of helicenes to electronic devices is, to date, in its infancy. In part, this is due to a poor understanding of molecular packing and how this impacts device performance. Furthermore, chiral materials will pack differently depending on whether a single-handed (enantiopure), racemic (a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mix of left-handed and right-handed molecules), or some other mixture is employed. For example, Hatakeyama et al. reported a difference in the carrier type for azaboradibenzo[6]helicene between the racemic form, which exhibited higher mobility for holes, and the enantiopure form, which exhibited higher mobility for electrons.24 They rationalized this on the basis of the differences in molecular packing between the two forms, driven by molecular chirality. One of us has previously reported the use of aza[6]helicene in organic field effect transistors (OFETs), finding opposite enantiomers to have, as expected, a strong dependence of photogenerated current on the handedness of circularly polarized light.25 Recently, P3HT-helicene blend organic photovoltaics (OPVs) were reported, which showed a five-fold increase in power conversion efficiency when switching from a racemic to an enantiopure helicene additive as part of a polymer blend material.26 We have recently shown for aza[6]helicene that differences in molecular packing cause an 80-fold difference in charge mobility for OFET devices fabricated using enantiopure vs. racemate mixtures.27 Understanding the relationship between packing and electronic properties would enable control of useful properties for applications.
50 mix of left-handed and right-handed molecules), or some other mixture is employed. For example, Hatakeyama et al. reported a difference in the carrier type for azaboradibenzo[6]helicene between the racemic form, which exhibited higher mobility for holes, and the enantiopure form, which exhibited higher mobility for electrons.24 They rationalized this on the basis of the differences in molecular packing between the two forms, driven by molecular chirality. One of us has previously reported the use of aza[6]helicene in organic field effect transistors (OFETs), finding opposite enantiomers to have, as expected, a strong dependence of photogenerated current on the handedness of circularly polarized light.25 Recently, P3HT-helicene blend organic photovoltaics (OPVs) were reported, which showed a five-fold increase in power conversion efficiency when switching from a racemic to an enantiopure helicene additive as part of a polymer blend material.26 We have recently shown for aza[6]helicene that differences in molecular packing cause an 80-fold difference in charge mobility for OFET devices fabricated using enantiopure vs. racemate mixtures.27 Understanding the relationship between packing and electronic properties would enable control of useful properties for applications.
Thus far, attempts to control the solid-state assembly of helicenes have largely been based on a combination of chemical intuition and trial-and-error in the laboratory. The ability to control or predict the assembly of a given helicene, in particular towards helical columns, is tantalizing as this could help to dramatically improve properties related to a chiroptical response15 and therefore potential device performance in certain contexts. Detailed experimental studies into polymorphism in helicenes are, however, relatively rare. In this work, we use CSP to explore the lattice energy landscape for the carbohelicene, [6]helicene (see Fig. 1), allowing us to explore what drives the molecular packing of this molecule. Furthermore, through calculating the charge mobility of the energetically accessible hypothetical polymorphs, we are able to explore the energy–structure–function relationships for this material. The relationship between molecular structure and the macroscopic properties of relevance in organic electronics is a complex one. Charge-carrier mobility is influenced by molecular structure, conformation, molecular packing and the degree of order. There are often a wide range of mobilities reported for a single chemical structure, due to the various causes of heterogeneity. High mobility in the crystalline part is a condition for high mobility in the film, so we would like to understand both the relationship between crystal structure and mobility and the preference for given crystal structures.
We selected [6]helicene because it is well known and studied.28,29 It also expresses an interesting range of crystalline forms including homochiral structures and intergrowths. The solid-state form of enantiopure [6]helicene was reported by de Rango et al. in 1973 with the chiral P212121 space group.29 Interestingly, a racemate crystal structure has never been reported for [6]helicene. Instead, the racemic solutions of [6]helicene spontaneously crystallise as conglomerates of homochiral crystals in the chiral P212121 space group.30 Such preference for homochiral interactions is relatively rare (found with ∼19% of chiral compounds).31 However, further investigation has shown that the individual crystals with a chiral space group formed from a racemic [6]helicene solution are in fact racemic, with enantiomeric excesses (ee) of a few percent.30 In 1981, Thomas and co-workers suggested this was due to intergrowths with alternating layers of opposite helicene enantiomers forming, and using surface energy calculations they postulated a (100) intergrowth was most likely to form.30
A critical factor in the improvement of polymorph prediction, as observed in the blind tests,4–6 has been the use of electronic structure calculations as a final step in the reliable ranking of the hypothetical polymorphs. This is a particular challenge due to the requirement for an accurate description of the non-covalent interactions between molecules. These London dispersion interactions are fundamentally absent in standard density functional theory (DFT). In this work, we utilise the exchange-hole dipole moment (XDM) dispersion model32,33 for this reason. XDM is a non-empirical model of dispersion, in which the C6, C8, and C10 dispersion coefficients are calculated directly from properties of the electron density and therefore vary depending on the local chemical environment. When combined with the B86bPBE density functional,34 XDM has been shown to reproduce well the experimental sublimation enthalpies and geometries for molecular solids,35,36 predict experimental ee describing the relative stabilities of enantiopure and racemic crystals,36 and to produce reliable energy rankings for CSP.37 With knowledge of the crystal structure and molecular structures, non-adiabatic Marcus theory can be used to calculate the direction- and field-dependent rate of charge hopping between molecules in the non-adiabatic limit, and hence to predict the charge-carrier mobility.
Methods
Full methodological details are provided in the ESI.† For the CSP calculations, a molecular model of [6]helicene was constructed manually and geometry optimised in Gaussian09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 at the B3LYP/6-31G(d,p) level of theory. CrystalPredictor39,40 was used to generate the hypothetical crystal structures, with the search restricted to structures with a single molecule in the asymmetric unit (Z′ = 1) and using only common space groups that included both enantiopure and racemic packings. The structure search was conducted with the helicene treated as a rigid molecule and the electrostatic component of the intermolecular forces evaluated based upon a distributed multipole analysis41 (calculated using GDMA2)42 and the remaining intermolecular forces were calculated using the Williams potential.43 The unique structures from the search (∼10
38 at the B3LYP/6-31G(d,p) level of theory. CrystalPredictor39,40 was used to generate the hypothetical crystal structures, with the search restricted to structures with a single molecule in the asymmetric unit (Z′ = 1) and using only common space groups that included both enantiopure and racemic packings. The structure search was conducted with the helicene treated as a rigid molecule and the electrostatic component of the intermolecular forces evaluated based upon a distributed multipole analysis41 (calculated using GDMA2)42 and the remaining intermolecular forces were calculated using the Williams potential.43 The unique structures from the search (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) were then lattice energy minimised using DMACRYS.44 We constructed three intergrowth models manually (see Fig. S1†), finding the lowest-energy stable structure to be that with a (100) interface previously found by Thomas and co-workers.30 This structure was energy minimised as described above.
000) were then lattice energy minimised using DMACRYS.44 We constructed three intergrowth models manually (see Fig. S1†), finding the lowest-energy stable structure to be that with a (100) interface previously found by Thomas and co-workers.30 This structure was energy minimised as described above.
The 50 lowest-energy structures from the crystal structure search, along with the intergrowth structure, were then reoptimised using electronic structure calculations32,33 with the exchange-hole dipole moment (XDM) dispersion correction, B86BPBE density functional34,45 and a plane-wave/pseudopotentials approach46 in Quantum ESPRESSO,47 version 5.1. Crystal structure comparisons were performed using the COMPACK48 procedure in Mercury.49
Charge-carrier mobility calculations were performed on the 27 low energy structures, see the ESI† for full details. For each of these, the geometry of the first molecule in the unit cell was relaxed with hybrid DFT using the B3LYP functional and the 6-31G(d) basis set. It was necessary to reoptimise with B3LYP before performing the single point energy calculations to reduce the self-interaction error and localize charges on the molecules. B3LYP has been shown to give good results for the electronic structure of organic materials.50 This relaxed molecule was then projected onto its equivalent positions in the unit cell with symmetry operations, and translated by the lattice units to make up a 3 × 3 × 3 supercell. The transfer integrals between all molecules in the unit cell to all other molecules were calculated, subject to a distance cut-off of 18 Å, at which separation the transfer integrals were typically less than 1 × 10−9 eV. The symmetry of the supercell means that only a subset of all possible transfer integrals need to be calculated explicitly. The transfer integrals were calculated with a hybrid DFT molecular pair calculation and the projective method, which involves projecting the orbitals of a pair of molecules onto a basis set defined by the unperturbed orbitals of the individual molecules.51 The electron and hole transfer rates in a particular direction were calculated with non-adiabatic Marcus theory52 with a reorganisation energy of 0.46 eV, assuming no energetic disorder, and a master equation approach. As the absolute value for the outer sphere component of the reorganisation energy is not known, the calculated values of the charge mobility cannot be considered as absolute. However the calculated mobilities do allow direct comparison between different crystal structures and transport directions where the same reorganisation energy has been used. We calculated the anisotropy in the mobility by taking the normalized standard deviation (i.e. the standard deviation divided by the maximum value) of all of the mobilities in each of the directions. We further compared this to the ratio between the maximum and minimum mobility, as an alternative approach to considering anisotropy of the mobility.
Results and discussion
Crystal structure prediction
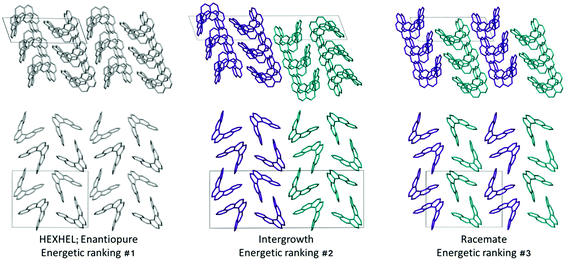
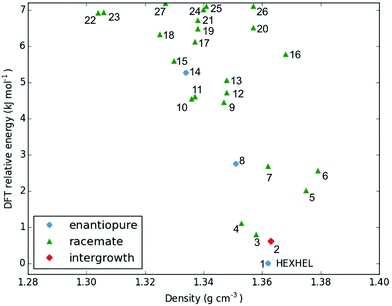
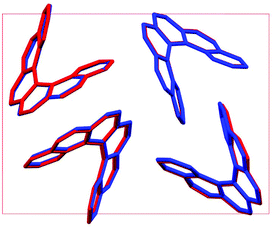
Throughout our results, structures are numbered according to the energetic ranking from the DFT calculations, with 1 being the lowest-energy polymorph found. Nyman and Day have previously calculated the lattice energies for 508 polymorphic organic molecules and found that the lattice energies of experimentally observed polymorphs fall within 7.2 kJ mol−1 of the absolute minimum in 95% of cases.53 Therefore, for further structural analysis and calculations of charge mobility calculations in the hypothetical helicene crystal structures, we included only those unique structures that lay within this energetic window from the XDM calculations, a total of 27 crystal structures. We found the lowest-energy stable intergrowth structure to be that with a (100) interface previously found by Thomas and co-workers.30Fig. 2 shows the intergrowth structure and how this relates to the enantiopure structure (the Cambridge Structure Database (CSD) reference for this structure is HEXHEL).The lattice energy landscape for [6]helicene is typical of an organic molecule, with an overall trend whereby more dense structures, that are packed more efficiently, have lower lattice energy. The lattice energy landscapes are shown in Fig. 3 for the DFT calculations, in Fig. S3† for the rigid-body search and the data for both is given in Table S2.† The reoptimization of the structures at the DFT level resulted in significant re-ranking of the predicted crystal structures, with the majority of structures being significantly stabilised (see comparison in Fig. S4†) relative to the global minimum structure. The most thermodynamically stable structure from the DFT calculations is an enantiopure structure in the chiral P212121 space group that is a match to the experimentally reported structure of de Rango et al. (CSD code HEXHEL),54 with a root-mean-square-displacement for a 15 molecule comparison (RMSD15) of 0.208 Å. The structural overlay of the experimentally observed and predicted structure 1 is shown in Fig. 4. The density of the predicted structure from the DFT calculations is 1.362 g cm−3, which is ∼6% more dense than the experimentally reported density of 1.289 g cm−3, leading to a very slight difference in the relative positions of helicenes in the experimental and theoretical structures shown in Fig. 4. This is to be expected given that we did not account for thermal expansion and zero-point-vibrational effects in these systems in our calculations, due to the large number of atoms in the unit cells.35
Whilst our calculations do correctly predict the experimentally observed HEXHEL enantiopure structure as the thermodynamically most stable structure, the difference in ranking across predicted structures 1, 2 and 3 is small, <1 kJ mol−1. The relative ranking of these structures is of particular interest, as 1 is the lowest enantiopure structure, 2 is the intergrowth structure and 3 is the lowest-energy racemate structure, with space group Pna21. Our final prediction regarding the order of thermodynamic stability is thus: enantiopure > intergrowth > racemate; suggesting [6]helicene defies the typical trend of racemates being favoured over conglomerates of homochiral crystals. Thus, not only do we correctly predict the observed enantiopure structure, we also predict that for a racemic mixture of [6]helicene, the intergrowth structure is more stable than a racemate structure, providing confirmation of the earlier suggestions30 that the lack of an observed racemate crystal structure for [6]helicene is the result of intergrowths preferentially forming. We do note that the ranking of these three structures was different in the rigid-body search (Fig. S3 and Table S2†) and that the errors introduced in neglecting thermal expansion are typically ∼1–2 kJ mol−1 at room temperature,55 which is greater than the lattice energy differences calculated herein. In a previous CSP study (without DFT level relaxation) of three spontaneously resolving systems by D'Oria et al.,56 the energy differences between the enantiopure and racemate structures were also found to be less than a few kJ mol−1 and therefore easily influenced by kinetic and entropic effects. In our case however, this means that lattice energy differences alone, although arguably within the margin of error, are sufficient to explain the experimental observations, as was the case with another previous CSP study that used hybrid DFT to predict spontaneous resolution.57
Predicted structures 1, 2 and 3 are highly interrelated, as can be seen from inspection of Fig. 2. The enantiopure structure 1 contains chains of homochiral pairs of helicenes that are interlocked, with each interlocked pair packed “back-to-back” with the next. Perpendicular to this, there run columns of homochiral helicenes with translational symmetry. The intergrowth structure 2, which was constructed as a (100) intergrowth of 1, has the same substructures, but in a larger cell where the unit cell of 1 is packed next to the same unit cell, but with helicenes of the opposite chirality. Finally, the racemate structure 3 again has the same substructure features, but it has alternating chains and columns of opposite chirality helicenes. Thus, from this we can hypothesise that these homochiral interlocked chains and translational symmetry chains are the low energy packings for [6]helicene. The differences in how these are packed together with adjacent homochiral or heterochiral chains is most likely all that is responsible for the subtle differences in their energetic rankings and consequently for their experimental observation. Comparing the two-dimensional (2D) fingerprint plots58 (see Fig. S7†) for these three structures, it can be seen that the alignment of exclusively homochiral chains in 1 results in the strongest C–H⋯π and π–π interactions across the three structures. This highlights how critical control of the interactions in all three dimensions would be in the “design” of a molecule with desired crystal packing features.
It is clear that there is a far greater number of racemic than enantiopure structures in the energetically low-lying region of the energy landscape we have investigated (<7.2 kJ mol−1), with 23 and 3 predicted structures, respectively. The predicted racemic structures are found in a range of space groups (see Fig. S5†), with P21/c being the most common of the lowest-energy structures. Structures 5 and 6 are particularly interesting, given that they are the two highest density structures found and yet are not lowest in energy. Structures 5 and 6 both feature interlocked heterochiral helicene pairings, rather than the interlocked homochiral helicene pairs in structures 1–3. However, 2D fingerprint plots of the non-covalent interactions of 5 and 6 (Fig. S7†) show that compared to the more thermodynamically stable structures, these lack C–H⋯π interactions. This shows that whilst inversion symmetry in a helicene structure can increase the density, this does not necessarily mean that favourable non-covalent interactions are maximised.
Classification of structure motifs
As the energy–structure relationships uncovered thus far had shown trends based on particular substructure features, we decided to investigate the crystal packing of the 27 lowest-energy structures further. We began by producing a packing similarity tree diagram (Fig. S2, Table S3†) and this allowed us to identify common substructures to search for throughout the predicted polymorphs. These results are shown in Fig. 5 and Table S1,† with the substructures displayed in Fig. 5b. We identified 10 common substructures, which can be listed in order of their frequency of appearance (given in brackets, together with a label of the substructure number):• a homochiral chain with translational symmetry (63%; I)
• a homochiral back-to-back pair (48%; II)
• a heterochiral interlocked pair (30%; III)
• a homochiral interlocked pair (26%; IV)
• a homochiral chain; consisting of alternating back-to-back and interlocked pairs (15%; V)
• a heterochiral back-to-back pair, “centre”; where the two central aromatic rings on each of the molecules are closest, although not at π–π stacking distances (15%; VI)
• a heterochiral back-to-back pair, “edge”; where the second and third aromatic rings on each of the molecules are closest, although not at π–π stacking distances or orientation (15%; VII)
• a heterochiral chain; consisting of alternating back-to-back and interlocked pairs (11%; VIII)
• a heterochiral chain; consisting of helicenes sitting adjacent to each other edge-to-edge (11%; IX)
• a homochiral chain with translational symmetry, arranged in a herringbone packing (11%; X)
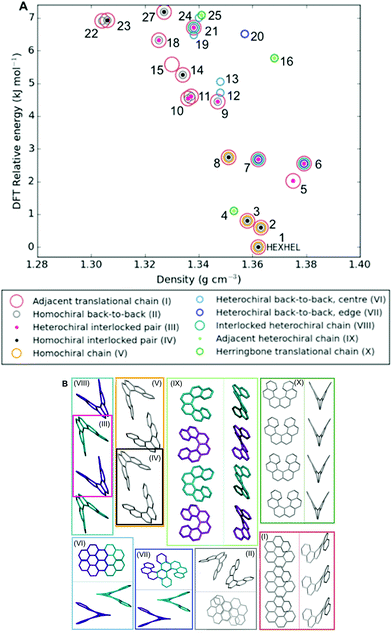 | ||
| Fig. 5 (a) Lattice energy landscape labelled according to which molecular substructures they contain. Substructures are ordered by decreasing frequency. Note, two predicted structures (17 and 26) do not appear on the plot as they contain none of these substructures, for their positions, refer back to Fig. 3; (b) the molecular substructures, with surrounding boxes coloured and labelled as per (a). Where necessary, two perpendicular views of the same substructure are shown within the box, divided by a line. Helicene molecules within homochiral substructures are shown grey and within heterochiral substructures opposite enantiomers are shown purple and cyan; no hydrogens are shown. Table S1† gives the substructures found in each of the 27 structures. | ||
Molecular structure files for these features are provided as ESI.† Some clear themes emerge from the results; firstly, chains of homochiral [6]helicenes (substructure V) are present in all but one of the eleven lowest-energy structures (1–11) and this is therefore a low energy packing feature, common to both enantiopure and racemate structures. Thus, whilst space groups change between enantiopure and racemate structures, key positioning of neighbouring molecules, i.e. substructures, are frequently retained. Secondly, crystal structure 4 exhibits completely different substructures; with a homochiral chain of molecules packed in a herringbone fashion with translational symmetry (substructure X), and in the perpendicular direction heterochiral chains with the helicenes adjacent to each other in an edge-to-edge fashion (substructure IX). Thirdly, for the densest racemate structures, a similar set of features to those in 1–3 is observed, except with the chains featuring alternating interlocked and back-to-back pairs that are hetero- (substructure VIII) rather than homochiral. Finally, higher in the energy landscape, it can be seen that a heterochiral back-to-back pair, aligned centrally (substructure VII), excludes any of the other common substructure features.
Charge-carrier mobilities
Among the most important properties of organic semiconductor crystals are the charge-carrier mobilities. Mobility is a particularly interesting property in the present context, because it can vary by orders of magnitude depending on the crystal polymorph, as well as crystal direction. To the best of our knowledge, there have not been any previous reports of experimental measurements of charge-carrier mobility for [6]helicene films. Here, we calculate direction-dependent electron and hole mobilities within the Marcus hopping model51 for all low energy structures and investigate the correlation between packing motif and calculated mobility. The relationship between the maximum transfer integral (J) and charge-carrier mobility is given in Table S4† for hole-mobility and Table S5† for electron-mobility and we find that a large maximum transfer integral does not necessarily mean a large mobility. This is because the large transfer integrals could be between adjacent pairs, so there is no extended high coupling pathway through the structure that can result in high charge-carrier mobility. We have also plotted histograms of the complete set of transfer integrals for the highest and lowest hole and electron-mobility structures (see Fig. S9†). If we consider a significant transfer integral as one that is greater than 1 meV, then the plots indicate that a greater number of transfer integrals above this threshold results in a larger mobility. These plots do not tell the whole story, as a high coupling pathway is still the most important factor in determining high mobility.The charge mobility obtained for the 27 low energy structures ranges from 0.0 to 2.0 cm2 V−1 s−1 for holes and 0.1 to 2.9 cm2 V−1 s−1 for electrons, using a reorganisation energy of 0.46 eV in both cases; the values are shown in Fig. 6, Fig. S10 and Tables S4, S5.† As the value of the outer component of the reorganisation energy cannot be calculated precisely, such calculations are best used for comparing relative carrier mobilities in a series of structures, as we have here, rather than absolute values. We can, however, compare the magnitude of our predicted mobilities to systems where the same method has been applied, although we note that the value for the reorganisation energy used in the calculations will influence the magnitude of the mobilities. In this context, the calculated carrier mobilities of [6]helicene structures are promising, with the maximum hole-mobility of 2.0 cm2 V−1 s−1 greater than that previously reported from calculations for (rac)-aza[6]helicene (0.058 cm2 V−1 s−1),27 (+)-aza[6]helicene (0.032),27 TIPS-pentacene (0.33),59 TES-pentacene (0.28),59 PCBM (0.0093),60 bis-PCBM (0.0005)60 and tris-PCBM (0.000009),60 all using similar values of reorganization energy (λ in the range 0.2 to 0.5 eV). We see that high hole-mobility structures within our energetically low-lying set of [6]helicenes polymorphs are a relatively rare feature; only 6 of the 27 structures have hole-mobility greater than 1 cm2 V−1 s−1. This suggests that whilst relatively high hole-mobility is achievable for [6]helicene, there would have to be some degree of serendipity for a high hole-mobility structure to be the one obtained experimentally. By comparison, high electron-mobility above 1 cm2 V−1 s−1 is relatively common for the [6]helicene structures, occurring in 17 of the 27 low-lying polymorphs, including the experimentally isolated structure, 1 (HEXHEL), for which a particularly high value of 2.1 cm2 V−1 s−1 was calculated. This finding suggests that [6]helicene is an ambipolar transport material and, since encouraging electron mobilities are seldom reported, [6]helicene may be a promising material class to investigate for electron-mobility.
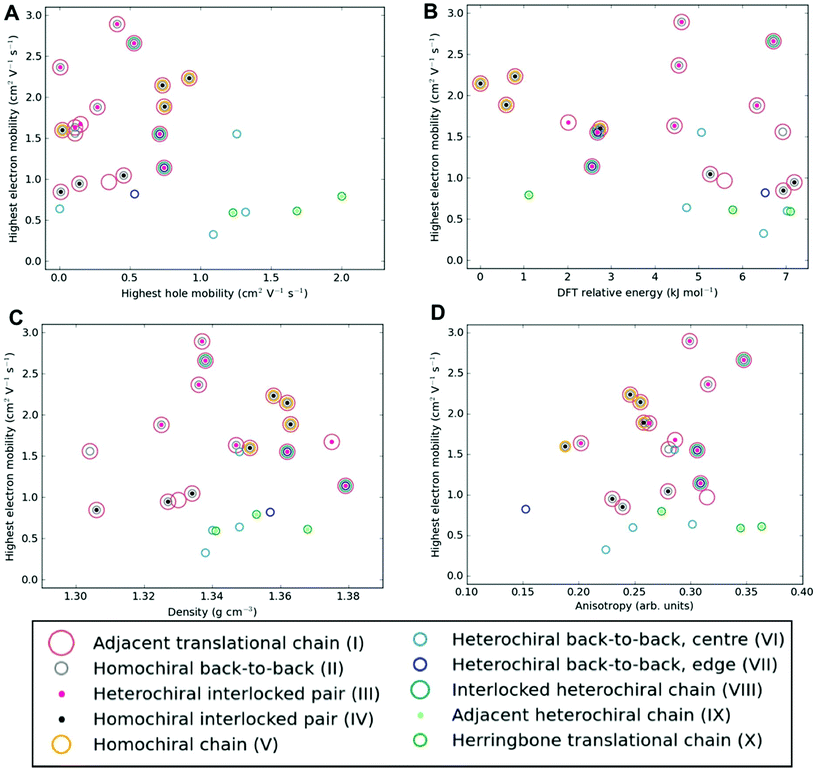 | ||
| Fig. 6 Electron-mobility for the energetically low-lying [6]helicene polymorphs compared to (a) hole-mobility, (b) DFT relative energy, (c) density and (d) anisotropy of electron-mobility. The data points are coloured according to the substructure type. The equivalent plots for hole-mobility are in Fig. S10.† | ||
No strong correlation between the electron and hole mobilities is observed for the various candidate structures (Fig. 6a). While the racemic structures tend to have higher hole mobilities and lower electron mobilities, relative to the enantiopure structures (in agreement with previous results from Hatakeyama et al. for azaboradibenzo[6]helicene24), the highest electron and hole mobilities are both obtained for racemic structures. Thus, it is clear that the specific packing is more important in determining the charge-carrier mobilities than the overall chirality of the crystal. Examining our results further for energy–structure–function relationships, we see that there is no strong correlation for highest charge-carrier mobility with relative energy, density or mobility anisotropy across the polymorphs (Fig. 6b–d and Fig. S10†). Examining the dependence of charge-carrier mobilities on the relative energies allows one to ascertain whether or not certain high hole-mobility structures are at least thermodynamically accessible. The structure with the highest hole-mobility, 4, is ranked only 1.1 kJ mol−1 above the global minimum, suggesting it is feasible that this polymorph could be crystallised from a thermodynamic perspective and display optimal hole-mobility. The structure with the highest electron-mobility, 11, is only 4.6 kJ mol−1 above the global minimum, and so might also be experimentally accessible.
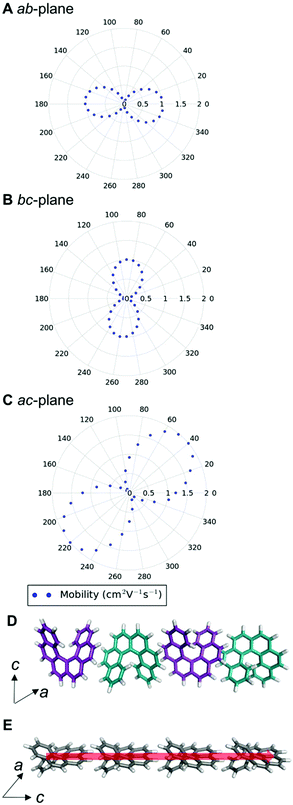
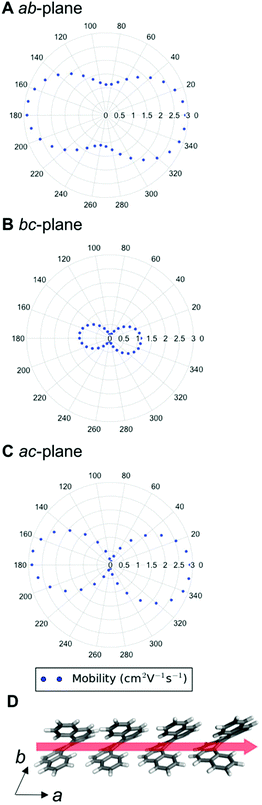
We can examine the highest hole-mobility racemic structure 4 to uncover the origin of this property. The angular-dependent mobility in each of the three orthogonal planes of 4 is shown in Fig. 7 and key data in Table 1. In terms of substructures, it contains both the adjacent heterochiral chain (substructure IX, Fig. 7d) and the herringbone translational homochiral chain (substructure X, Fig. 7e). These substructures are also found in structures 16 and 25, which have the second and fifth best hole-mobility respectively, thus they are clearly beneficial substructures for high hole-mobility. Within 4, the hole-mobility along the herringbone chain was 2.0 cm2 V−1 s−1, whereas it was lower, 0.01 cm2 V−1 s−1, along the adjacent heterochiral chain. The highest mobility direction in 4, 16 and 25 was always along the herringbone translational chain (substructure X). This high hole-mobility substructure was only found in 3 of the 27 (11%) low energy [6]helicene polymorphs, so is a relatively rare feature. Examination of the HOMOs and LUMOs for this substructure (see Fig. S8†) shows that it is not immediately obvious from either the inspection of these molecular orbitals, or the underlying molecular structures, as to why there would be high hole-mobility. This demonstrates the utility of our approach in calculating the charge-carrier mobility, which is not chemically intuitive to determine. The finding that a herringbone alignment leads to high mobility is consistent with evidence for high mobilities in crystal structures with a herringbone packing motif.61 However, the sign of the transfer integral,62 thermal vibrations63 and polarizability64 have been identified as factors that influence mobility in molecular crystals, meaning that structural motif is not the only contributions. These additional factors could be addressed in the future with more detailed studies of particular polymorphs.
| Structure | DFT relative energy (kJ mol−1) | Contributing substructures | Maximum hole-mobility (cm2 V−1 s−1) | Maximum electron-mobility (cm2 V−1 s−1) |
|---|---|---|---|---|
| Enantiopure (1, HEXHEL) | 0.0 | I, II, IV, V | 0.73 | 2.15 |
| Racemic (3) | 0.8 | I, II, IV, V | 0.92 | 2.24 |
| Intergrowth (2) | 0.6 | I, II, IV, V | 0.74 | 1.89 |
| 4 | 1.1 | IX, X | 2.00 | 0.80 |
| 11 | 4.6 | I, III | 0.41 | 2.90 |
The highest hole-mobility structures have relatively low electron-mobility, whereas the highest electron-mobility is found in the racemic structure 11. The angular-dependent mobility in each of the three orthogonal planes of 11 is shown in Fig. 8 and key data in Table 1. Structure 11 contains the adjacent translational homochiral chain substructure (I), and the direction of these chains corresponds to the highest electron-mobility. However, the presence of this substructure alone does not necessarily lead to a high electron-mobility, as it is also contained in many other structures, spanning a range of values. This is because the same substructure can exhibit different pair separations depending on the overall crystal structure. The homochiral chain substructure is particularly sensitive to the surrounding environment compared to the herringbone substructure, with the latter having very similar pair separations for all cases in which it appears. Again, as with the high hole-mobility structure, examination of the molecular orbitals for this substructure (see Fig. S8†) does not show an intuitively obvious hopping pathway for high electron-mobility.
The anisotropy of the charge-carrier mobility was calculated as the normalised standard deviation of the angular-dependent mobility by dividing the standard deviation of the values by the maximum value in that structure and additionally, the ratio between the maximum and minimum mobility was calculated (see Tables S4 and S5†). With both values, there was no strong trend in hole or electron-mobility with the anisotropy. In the remaining discussion, we use the normalised standard deviation of the mobility. The anisotropy values for the electron-mobility range from 0.18 to 0.37. There is no strong trend in electron-mobility with the anisotropy. More isotropic structures (with low calculated values for anisotropy) are desirable, as it means that slight changes in orientation or polymorphism give more robust performance in a device. The three structures with the highest charge-carrier mobility (4 and 11) do have relatively high anisotropy (0.27 and 0.32, respectively), indicating that the high charge-carrier mobility is principally in one direction in these cases.
Finally, in Table 1 we compare the charge-carrier mobilities for the lowest-energy enantiopure (1), racemic (3) and intergrowth structures (2), which have similar substructures in different arrangements (refer back to Fig. 2). All three structures have similar maximum electron mobilities, ranging from 1.9–2.2 cm2 V−1 s−1. Inspection of the origin of the high electron-mobility pathway shows that, for all three of these structures, high electron mobilities are along the same substructure – the homochiral chain with translational symmetry (substructure I). This is the same substructure as found in the maximum electron-mobility structure 11 (2.9 cm2 V−1 s−1). Thus, substructure I often results in high electron-mobility, notwithstanding the wider environment of other substructures influencing the exact magnitude of the electron-mobility. The three structures 1, 2 and 3 have a lower magnitude of hole-mobility, ranging from 0.7–0.9 cm2 V−1 s−1, with the high hole-mobility pathway running along the homochiral chain with alternating back-to-back and interlocked pairs (substructure V) for the intergrowth structure, but cutting diagonally across the same chains for the racemic and enantiopure structures, the latter not corresponding to a particular substructure.
Conclusions
In summary, we have used computational simulations to explore the energy–structure–function relationships for the [6]helicene molecule, considering its potential use as a material in organic semiconductor devices. Making use of CSP methods and DFT-XDM computations, we predicted the energetic ordering of possible crystal packings of [6]helicene. This approach correctly predicts the lowest-energy enantiopure structure that has been experimentally observed, as well as explaining why an intergrowth structure is preferentially formed over a racemate crystal structure. Energetically low-lying polymorphs of [6]helicene combine homochiral chains with translational symmetry (substructure I), as well as perpendicular chains with alternating pairs of interlocked and back-to-back homochiral helicenes (substructure V). The 3-dimensional arrangement of these chains, and the degree to which they maximise non-covalent interactions determines the observed forms.Through the use of charge-carrier mobility calculations, we determined that energetically low-lying [6]helicene polymorphs have promising carrier mobility, with the highest calculated hole-mobility of 2.0 cm2 V−1 s−1 and the highest electron-mobility of 2.9 cm2 V−1 s−1. Whilst these highest calculated mobilities are not found in the lowest-energy polymorphs, they are found in structures that are potentially observable on a thermodynamic basis, based on relative energies of 1.1 and 4.6 kJ mol−1 relative to the global minimum for the hole and electron carriers, respectively. Comparably high electron-mobility (exceeding 1.0 cm2 V−1 s−1) was found to occur in almost two-thirds of the structures, suggesting the experimental investigation of electron-mobility in [6]helicene is particularly promising.
We further explored how charge-carrier mobility relates to the energy–structure landscape of [6]helicene. We explored the relationship between hole and electron-mobility, with the relative energy, density and anisotropy of carrier mobility for the structure. There were no strong correlations for these properties, but we were able to identify certain substructures that are associated with high hole-mobility and high electron-mobility. The substructure that resulted in the highest hole-mobility was found to be a homochiral chain with translational symmetry, arranged in a herringbone packing (substructure X). This substructure was relatively rare across the energetically low-lying [6]helicene polymorphs, being found in only 11% of the structures sampled. The substructure that resulted in the highest electron-mobility was a chain of homochiral helicenes with translational symmetry (substructure I). It was the most frequently occurring substructure, being found in 63% of the polymorphs, including in the three lowest-energy structures.
We highlight the potential for our computational approach to be used in the future to help screen for molecules with desirable solid-state structures and/or properties. For example, if a synthetic chemist wishes to develop a chiral molecule that has a preferential type of packing combined with high, anisotropic hole-mobility, then our approach can help narrow the selection to the most promising candidates. Our insight into the relationship between packing and charge mobility for a single molecule has helped us to test or to go beyond intuitive assumptions about what types of molecular packing are desired for a given property. For example, for helicenes, chemical intuition might lead one to expect that helical columns would lead to high carrier mobility, however our calculations for [6]helicene suggested alternative, not intuitively obvious, substructures, to be the most promising charge-carriers. Beyond these lessons for the design of materials for organic semiconductors, we note that there may be lost opportunities in the laboratory, based upon the fact that the characterisation of the performance of a single crystal structure may neglect enhanced properties for alternative polymorphs of the materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge a Royal Society University Research Fellowship (KEJ), and the EPSRC (EP/M017257/1, EP/P005543/1, EP/P000525/1, EP/L014580/1, EP/R00188X/1) for funding and ARCHER time through the Materials Chemistry Consortium (EP/L000202). BR thanks the EPSRC CDT in Theory and Simulation of Materials (EP/L015579/1) for a PhD studentship. JN acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 742708). ERJ and LML thank the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Walter C. Sumner Foundation for funding, and Compute Canada for the use of computational resources. The authors thank Dr Louise Price, UCL, for assistance with the DMACRYS software and Profs. Sally Price and Graeme Day for discussions about the CSP calculations.References
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327 CrossRef CAS.
- S. Price, Science, 2014, 345, 619–620 CrossRef CAS PubMed.
- S. Price, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr., A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C. A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H. Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CAS.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551 CAS.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125 CAS.
- R. I. Goldstein, R. Guo, C. Hughes, D. P. Maurer, T. R. Newhouse, T. J. Sisto, R. R. Conry, S. Price and D. M. Thamattoor, CrystEngComm, 2015, 17, 4877–4882 RSC.
- J. T. A. Jones, T. Hasell, X. Wu, J. Bacsa, K. E. Jelfs, M. Schmidtmann, S. Y. Chong, D. J. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. M. Day and A. I. Cooper, Nature, 2011, 474, 367–371 CrossRef CAS PubMed.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657–664 CrossRef CAS PubMed.
- J. E. Campbell, J. Yang and G. M. Day, J. Mater. Chem. C, 2017, 5, 7574–7584 RSC.
- Y. Shen and C.-F. Chen, Chem. Rev., 2012, 112, 1463–1535 CrossRef CAS PubMed.
- M. Gingras, Chem. Soc. Rev., 2013, 42, 968–1006 RSC.
- M. Gingras, G. Félix and R. Peresutti, Chem. Soc. Rev., 2013, 42, 1007–1050 RSC.
- M. Gingras, Chem. Soc. Rev., 2013, 42, 1051–1095 RSC.
- C. Nuckolls, T. J. Katz and L. Castellanos, J. Am. Chem. Soc., 1996, 121, 79–88 CrossRef.
- A. J. Lovinger, C. Nuckolls and T. J. Katz, J. Am. Chem. Soc., 1998, 120, 264–268 CrossRef CAS.
- T. Verbiest, S. Van Elshocht, M. Kauranen, L. Hellemans, J. Snauwaert, C. Nuckolls, T. J. Katz and A. Persoons, Science, 1998, 282, 913–915 CrossRef CAS PubMed.
- L. Vyklický, S. H. Eichhorn and T. J. Katz, Chem. Mater., 2003, 15, 3594–3601 CrossRef.
- K.-H. Ernst, Acc. Chem. Res., 2016, 49, 1182–1190 CrossRef CAS PubMed.
- A. Mairena, L. Zoppi, J. Seibel, A. F. Tröster, K. Grenader, M. Parschau, A. Terfort and K.-H. Ernst, ACS Nano, 2017, 11, 865–871 CrossRef CAS PubMed.
- J. R. Brandt, X. Wang, Y. Yang, A. J. Campbell and M. J. Fuchter, J. Am. Chem. Soc., 2016, 138, 9743–9746 CrossRef CAS PubMed.
- Y. Yang, R. C. da Costa, D.-M. Smilgies, A. J. Campbell and M. J. Fuchter, Adv. Mater., 2013, 25, 2624–2628 CrossRef CAS PubMed.
- V. Kiran, S. P. Mathew, S. R. Cohen, I. Hernández Delgado, J. Lacour and R. Naaman, Adv. Mater., 2016, 28, 1957–1962 CrossRef CAS PubMed.
- T. Hatakeyama, S. Hashimoto, T. Oba and M. Nakamura, J. Am. Chem. Soc., 2012, 134, 19600–19603 CrossRef CAS PubMed.
- Y. Yang, R. C. da Costa, M. J. Fuchter and A. J. Campbell, Nat. Photonics, 2013, 7, 634–638 CrossRef CAS.
- J. Crassous, P. Josse, L. Favereau, C. Shen, S. Dabos-Seignon, P. Blanchard and C. Cabanetos, Chem. – Eur. J., 2017, 23, 6277–6281 CrossRef PubMed.
- Y. Yang, B. Rice, X. Shi, J. R. Brandt, R. Correa da Costa, G. J. Hedley, D.-M. Smilgies, J. M. Frost, I. D. W. Samuel, A. Otero-de-la-Roza, E. R. Johnson, K. E. Jelfs, J. Nelson, A. J. Campbell and M. J. Fuchter, ACS Nano, 2017, 11, 8329–8338 CrossRef CAS PubMed.
- M. S. Newman and D. Lednicer, J. Am. Chem. Soc., 1956, 78, 4765–4700 CrossRef CAS.
- G. Le Bas, A. Navaza, Y. Mauguen and C. de Rango, Cryst. Struct. Commun., 1976, 5, 357 CAS.
- S. Ramdas, J. M. Thomas, M. E. Jordan and C. J. Eckhardt, J. Phys. Chem., 1981, 85, 2421–2425 CrossRef CAS.
- A. Otero-de-la-Roza, J. E. Hein and E. R. Johnson, Cryst. Growth Des., 2016, 16, 6055–6059 CAS.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108 CrossRef PubMed.
- E. R. Johnson, in Non-covalent Interactions in Quantum Chemistry and Physics, ed. A. Otero-de-la-Roza and G. A. DiLabio, Elsevier, 2017, pp. 215–248 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1986, 85, 7184 CrossRef CAS.
- A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103–054111 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, B. H. Cao, I. K. Price, J. E. Hein and E. R. Johnson, Angew. Chem., Int. Ed., 2014, 53, 7879–7882 CrossRef CAS PubMed.
- S. R. Whittleton, A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Theory Comput., 2017, 13, 441–450 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. O. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ã. D. N. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 (Revision D.01), Gaussian Inc., Wallingford, CT, USA, 2009 Search PubMed.
- P. G. Karamertzanis and C. C. Pantelides, J. Comput. Chem., 2005, 26, 304–324 CrossRef CAS PubMed.
- P. G. Karamertzanis and C. C. Pantelides, Mol. Phys., 2007, 105, 273–291 CrossRef CAS.
- A. J. Stone, J. Chem. Theory Comput., 2005, 1, 1128–1132 CrossRef CAS PubMed.
- A. J. Stone, GDMA (Version 2.2.02), 2005 Search PubMed.
- D. E. Williams, J. Comput. Chem., 2001, 22, 1154–1166 CrossRef CAS.
- S. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr., A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901–465931 CrossRef CAS PubMed.
- J. A. Chisholm and S. Motherwell, J. Appl. Crystallogr., 2005, 38, 228–231 CrossRef.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. Van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2008, 4(2), 297–306 CrossRef CAS PubMed.
- J. Kirkpatrick, Int. J. Quantum Chem., 2007, 108, 51–56 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- C. de Rango, G. Tsoucaris, J. P. Declercq, G. Germain and J. P. Putzeys, Cryst. Struct. Commun., 1976, 2, 189–193 Search PubMed.
- Y. N. Heit and G. J. O. Beran, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 514–529 CAS.
- E. D'Oria, P. G. Karamertzanis and S. L. Price, Cryst. Growth Des., 2010, 10, 1749–1756 Search PubMed.
- J. Kendrick, M. D. Gourlay, M. A. Neumann and F. J. J. Leusen, CrystEngComm, 2009, 11, 2391–2399 RSC.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668 CrossRef PubMed.
- J. Wade, F. Steiner, D. Niedzialek, D. T. James, Y. Jung, D.-J. Yun, D. D. C. Bradley, J. Nelson and J.-S. Kim, J. Mater. Chem. C, 2014, 2, 10110–10115 RSC.
- F. Steiner, S. Foster, A. Losquin, J. Labram, T. D. Anthopoulos, J. M. Frost and J. Nelson, Mater. Horiz., 2014, 2, 113–119 RSC.
- H. Dong, X. Fu, J. Liu, Z. Wang and W. Hu, Adv. Mater., 2013, 25, 6158–6183 CrossRef CAS PubMed.
- S. Fratini, S. Ciuchi, D. Mayou, G. Trambly de Laissardière and A. Troisi, Nat. Mater., 2017, 16, 998–1003 CrossRef CAS PubMed.
- S. Illig, A. S. Eggeman, A. Troisi, L. Jiang, C. Warwick, M. Nikolka, G. Schweicher, S. G. Yeates, Y. Henri Geerts, J. E. Anthony and H. Sirringhaus, Nat. Commun., 2016, 7, 1–10 Search PubMed.
- N. A. Minder, S. Ono, Z. Chen, A. Facchetti and A. F. Morpugo, Adv. Mater., 2012, 24, 503–508 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details regarding the methods, additional tables and figures, as well as structure files for both the low-lying predicted structures and commonly occurring substructures. See DOI: 10.1039/c7nr08890f |
| This journal is © The Royal Society of Chemistry 2018 |