Open Access Article
Open Access ArticleUpconversion thermometry: a new tool to measure the thermal resistance of nanoparticles†
O. A.
Savchuk
a,
J. J.
Carvajal
 *a,
C. D. S.
Brites
*a,
C. D. S.
Brites
 b,
L. D.
Carlos
b,
L. D.
Carlos
 *b,
M.
Aguilo
*b,
M.
Aguilo
 a and
F.
Diaz
a and
F.
Diaz
 a
a
aUniversitat Rovira i Virgili, Departament Quimica Fisica i Inorganica, Fisica i Cristal·lografia de Materials i Nanomaterials (FiCMA-FiCNA)-EMaS, Campus Sescelades, E-43007, Tarragona, Spain. E-mail: joanjosep.carvajal@urv.cat
bDepartment of Physics, CICECO – Aveiro Institute of Materials, University of Aveiro, Campus Universitário de Santiago, 3810-193 Aveiro, Portugal. E-mail: lcarlos@ua.pt
First published on 5th March 2018
Abstract
The rapid evolution in luminescence thermometry in the last few years gradually shifted the research from the fabrication of more sensitive nanoarchitectures towards the use of the technique as a tool for thermal bioimaging and for the unveiling of properties of the thermometers themselves and of their local surroundings, for example to evaluate heat transport at unprecedented small scales. In this work, we demonstrated that KLu(WO4)2:Ho3+,Tm3+ nanoparticles are able to combine controllable heat release and upconversion thermometry permitting to estimate its thermal resistance (in air), a key parameter to model the heat transfer at the nanoscale.
Introduction
The emergence of luminescence nanothermometry during the last decade opened up the possibility of measuring thermal flows at spatial scales below 10 μm, unreachable by conventional electrical methods.1 In fact, diverse phosphors capable of providing a contactless thermal reading through their light emission properties have been examined, e.g., polymers,2 DNA or protein conjugated systems,3 organic dyes,4 quantum dots,5 Cr3+-based materials,6 and trivalent lanthanide (Ln3+) ions incorporated into organic–inorganic hybrids,7 multifunctional heater-thermometer nanoplatforms,8–10 and upconverting,11–13 downconverting14 and downshifting15,16 nanoparticles. The implementation of these Ln3+-based phosphors as ratiometric thermometers was extensively reviewed in the past five years for diverse applications.17–24In the last couple of years, the focus of luminescence thermometry has gradually shifted from the fabrication of more sensitive nanoarchitectures towards the use of the technique as a tool for thermal bioimaging (acquisition of in vivo thermal images25,26 and subcutaneous thermal videos27 and in vivo ischemia detection in small animals28) and for the unveiling of properties of the thermometers themselves and of their local surroundings, as, for instance, the heat transfer in heater-thermometer nanoplatforms,29 the absorption coefficient and thermal diffusivity of tissues,30 the instantaneous ballistic velocity of Brownian nanocrystals suspended in both aqueous and organic solvents,31 and the thermal conductivity of porous silica and titania nanostructures.32 Thermal heating of nanoparticles (nanoheaters), induced either by the application of an alternating magnetic field or by irradiation with a near infrared (NIR) laser, has found significant applications in nanomedicine, as, for instance, magnetic hyperthermia (or magnetothermal therapy)33,34 and photothermal therapy.35–37 Concerning the last two examples, in which malignant cells are destroyed by intracellular thermal ablation and the tumour microenvironment is thermally-modulated to have synergic effects with standard cancer treatments, the accurate measurement of the surface-temperature of nanoheaters by using a nanothermometer is crucial for regulating the heat released to the surroundings, allowing the adjustment of the irradiation parameters, thus assisting the therapy. Although distinct nanomaterials have been designed and fabricated as nanoheaters for magnetothermal and photothermal therapies,33,34,36,38 single heater-thermometer nanoplatforms operating in the biological spectral windows of the tissues where the absorption of water and biological specimens is minimal, and combining (i) efficient light-to-heat or magnetic field-to-heat energy conversion (>50%), (ii) high relative thermal sensitivity (>1% K−1), and (iii) low temperature uncertainty (<0.1 K) have not yet been realized, despite the numerous attempts reported in the last five years.8,29,39–42
Wawrzynczyk et al.,39 Debasu et al.40 and Piñol et al.29 were pioneers in combining heat generation and noncontact optical temperature sensing in single nanoplatforms using, respectively, heavily Nd3+-doped NaYF4 heater/thermometer nanoparticles metallic heaters combined with Yb3+/Er3+ luminescent thermometers and magnetic heaters combined with Eu3+/Tb3+ luminescent thermometers. The latter two examples operate using the visible emission lines of the Er3+ and Eu3+/Tb3+ ions, respectively, thus, out of the first biological window (I-BW, 700–980 nm (ref. 36)). In contrast, Nd3+-based nanostructures can simultaneously generate heating through photothermal conversion and temperature reading using intra-4f3 emissions with energies within the first, second and third biological spectral windows.35,39,51 However, the relative thermal sensitivity of the Nd3+-based nanostructures is generally one order of magnitude lower than the typical values reported for Yb3+/Er3+ and Eu3+/Tb3+ luminescent thermometers (Table 1 and ref. 20 and 51). Moreover, temperature uncertainties and photothermal conversion values were scarcely evaluated.50,52
| Material | ΔT (K) | λ exc (nm) | Δ | S m (% K−1) | δT min (K) | Ref. |
|---|---|---|---|---|---|---|
| a Emission wavelength out of the I-BW. b Excitation wavelength out of the I-BW. | ||||||
| Upconversion | ||||||
KLu0.94Ho0.01Tm0.05(WO4)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
300–333 | 808 | I 696/I755 | 1.86 | 0.3 | This work |
KLu0.84Ho0.01Tm0.15(WO4)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
300–333 | 808 | I 696/I755 | 2.84 | 0.2 | This work |
| GdVO4@SiO2:Tm3+,Yb3+ | 298–333 | 980 | I 700/I800 | 0.94 | 0.4 | 43 |
| LiNbO3:Tm3+,Yb3+ | 323–723 | 980 | I 700/I800 | 3.00 | — | 44 |
| Downshifting | ||||||
LiLaP4O12:Cr3+,Nd3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
123–473 | 665 | I 820–840/I1048 | 4.89 | — | 45 |
Gd2O3:Nd3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
288–323 | 580 | I 824/I892 | 1.75 | 0.1 | 15 |
| LaF3:Nd3+ | 283–333 | 808 | I 865/I885 | 0.26 | — | 42 |
| LiLaP4O12:Nd3+ | 80–600 | 808 | I 866/I870 | 0.22 | 1.1 | 46 |
| YAG:Nd3+ | 283–343 | 808 | I 938/I945 | 0.15 | — | 47 |
| NaYF4:Nd3+ | 273–423 | 830 | I 863/I870 | 0.12 | — | 39 |
SrF2:Gd3+,Nd3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
293–338 | 573 | I 859/I867 | 0.61 | 2.0 | 48 |
CaF2:Gd3+,Nd3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
293–338 | 573 | I 1058/I867 | 0.12 | 1.8 | 49 |
| NaNdF4@NaYF4@NaYF4:Nd3+ | 77–550 | 808 | I 857/I863 | 0.11 | — | 50 |
Here, we report the synthesis and thermal characterization of Ho3+, Tm3+ co-doped KLu(WO4)2 nanoparticles as new multifunctional heater-thermometer nanoplatforms operating in the I-BW with an unprecedented performance: relative thermal sensitivity of 2.8% K−1, temperature uncertainty of 0.2 K (both at 300 K) and photothermal efficiency of 34 ± 2% (integrating sphere method53) or 41 ± 3% (thermal relaxation method54). Moreover, as an added benefit, we demonstrate how upconversion thermometry can be used to calculate the thermal resistance of the nanoparticles in air through a full non-contact heating and temperature reading. The value obtained, 9.84 × 107 K W−1, is similar to those reported for Si nanorods and Si-based heterostructured nanowires using conventional techniques. The thermal resistance of a nanostructured material is a key parameter to understand thermal transport in a large variety of technologies, such as, micro- and nanoelectronic devices, thin-film thermoelectrics, and nanoparticle-based thermal interface materials.55
Experimental details
Photoluminescence
The emission spectra were acquired using an integrating sphere (Labsphere, 4P-GPS-020-SL), exciting with 0.100 W using a 200 × 10−6 m core diameter fiber-coupled laser diode (Apollo Instruments, F25-808-2) emitting at 808 nm. The laser was collimated to a spot diameter of 3.0 × 10−3 m on the sample. The emission was collected using an optical spectrum analyzer (OSA, Yokogawa, AQ6373). All the samples were measured after being compacted in the bottom of a borosilicate flat bottom vial.For the temperature-dependent experiments, the samples were in contact with a heating stage (Linkam, THMS 600) equipped with a boron disk (to obtain an improved temperature distribution). The nanoparticles were excited by the fiber-coupled diode laser with the beam focused on the sample using a 40× microscope objective (0.6 numerical aperture, spot size of ∼20 × 10−6 m). The emission was collected using the same objective and the optical spectrum analyzer, after eliminating the scattered excitation radiation by using a 800 nm shortpass dichroic filter (Edmund Optics).
Time-dependent photoluminescence experiments were implemented using a portable spectrometer (MAYA 2000Pro, Ocean Optics). The spectrometer is controlled by a homebuilt MatLab© interface to record the real-time dependence of the emission spectra and the 696 and 755 nm intensities, with a time step of 0.250 s. The laser power is 1.0 W and the spot size is 20 × 10−6 m, corresponding to a power density of 318 × 106 W m−2.
Transmission electron microscopy
Transmission electron microscopy (TEM) was performed in a JEOL JEM-1011 microscope placing a drop of the nanopowders, previously mixed in ethanol (Merck, pro analysis 99.8%), on a copper grid covered by a holey carbon film (HD200 Copper Formvar/carbon).Photothermal conversion efficiency
The photothermal conversion efficiency (η), e.g., the portion of light absorbed by the nanoparticles that is transformed into heat, has been determined by two different methods: (i) the thermal relaxation method,54 and (ii) the integrating sphere method.53 In the first method, 0.3 × 10−3 L of an aqueous suspension of nanoparticles (1 g L−1) were introduced in a glass cuvette (101-QS, Hellma Analytics). The suspension was irradiated with a Lumics fiber-coupled diode laser (LU0808 M250) emitting at 808 nm with an excitation power of 0.200 W. The laser beam was focused on the cuvette with a collimating lens, allowing a beam diameter of 5 × 10−3 m on the sample (corresponding to a power density of 10.2 × 103 W m−2). The temperature of the sample was recorded until the steady-state temperature was reached by means of a digital multimeter connected to a small Pt-100 thermo-resistor located inside the cuvette. When using the integrating method sphere, the cuvette containing the same suspension of nanoparticles was placed inside the integrating sphere, perpendicularly to the collimated 808 nm laser beam (again with a laser power density of 10.2 × 103 W m−2). A baffle was introduced inside the integrating sphere, between the sample and the detector, to prevent the direct reflections from the sample to the detector. The power values were measured by using a stabilized thermal power meter (S302C, Thorlabs).Synthesis
KLu1−x−yHoxTmy(WO4)2 nanoparticles with molar concentrations x = 0.01, 0.03, 0.05 and y = 0.05, 0.10, 0.15 were synthesized by the modified Pechini sol–gel method,56 following the methodology previously reported to prepare KLu(WO4)2:Yb3+,Ho3+ nanoparticles.57 Briefly, Ho2O3 (99.9999%), Tm2O3 (99.9%) and Lu2O3 (99.9999%), used as starting reagents, were dissolved in hot nitric acid in stoichiometric proportions to form the nitrate precursors that were subsequently dissolved in distilled water with citric acid (CA), as the chelating agent, in a molar ratio [CA]/[metals] = 1. Ammonium tungstate (NH4)2WO4 (99.99%) and potassium carbonate K2CO3 (99.99%) were added to the aqueous solution that was heated at 353 K under magnetic stirring during a day until the complete dissolution of the reagents. Then, ethylene glycol (EG), as the esterification agent, was added to the mixture in a molar ratio [EG]/[CA] = 2. The solution was heated at 373 K to evaporate water and generate the polymeric gel. The polymeric gel was then calcined at 573 K for 3 h to obtain the precursor powders that were again calcined at 1023 K for 2 h to eliminate the organic compounds and crystallize the desired nanoparticles.Structural and morphological characterization
The crystalline structure of the nanoparticles was investigated by powder X-ray diffraction (XRD) to confirm that the experimental procedure results in the same phase already reported.57 The XRD patterns of the KLu1−x−yHoxTmy(WO4)2 nanoparticles, x = 0.01, 0.03, 0.05 and y = 0.05, 0.10, 0.15, reveal that the nanoparticles crystallize in the monoclinic system with the C2/c spatial group (Fig. S1 in the ESI†). The Scherrer equation was used to calculate the crystallite size. In all cases a mean size of 155 ± 10 nm was obtained indicating that, within the error of the technique, different dopant concentrations produce non-measurable changes on the crystallite size. The concentration of dopants in the nanoparticles was measured by ICP-OES (Table S1 in the ESI†). As the nominal concentration of Ho3+ and Tm3+ in the precursor powders increased, the concentration in the synthesized nanoparticles increased. Keeping the Tm3+ concentration constant (y = 0.05), the emission intensity is maximized for an optimal Ho3+ content of x = 0.03.TEM micrographs (Fig. 1) show KLu1−x−yHoxTmy(WO4)2 nanoparticles with irregular shapes, typical of nanoparticles prepared using the Pechini sol–gel method,24 with sizes around 100–150 nm, that tend to appear aggregated in small clusters. Discrete smaller particles, with sizes below 50 nm can also be seen in the images, but in a small number. No dependence of the shape or size of the nanoparticles has been observed with the concentration of doping ions used.
 | ||
| Fig. 1 TEM micrographs of KLu1−x−yHoxTmy(WO4)2 nanoparticles with different Ho and Tm concentrations. (a) x = 0.01 and y = 0.05, (b) x = 0.01 and y = 0.15, and (c) x = 0.05 and y = 0.05. | ||
Results and discussion
Upconversion thermometry
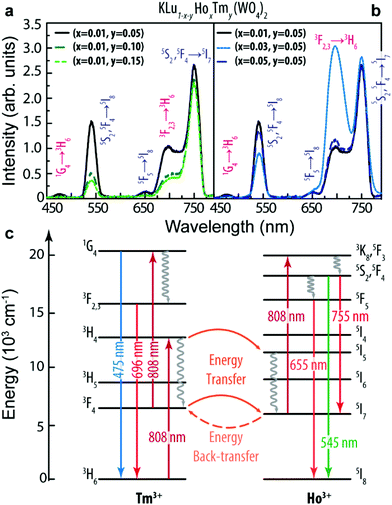
The upconversion emission spectra of the KLu1−x−yHoxTmy(WO4)2 (x = 0.01, 0.03, 0.05 and y = 0.05, 0.10, 0.15) nanoparticles are shown in Fig. 2a and b.The spectra consist of three separated bands located in the blue (1G4 → 3H6, Tm3+), green (5S2, 5F4 → 5I8, Ho3+), and red (5F5 → 5I8 and 5S2, 5F4 → 5I7, Ho3+, and 3F2,3 → 3H6, Tm3+) spectral regions. The Ho3+ bands may be generated by Tm3+-to-Ho3+ energy transfer processes, as previously reported.58–60Fig. 2c displays a simplified energy level diagram of the Ho3+ and Tm3+ ions where the represented absorption, emission and energy transfer processes are discussed in detail in the ESI.† When the molar concentration of Ho3+ was kept constant at x = 0.01, the intensity of all bands decreased as the concentration of Tm3+ increased, Fig. 2a. On the other hand, as the concentration of Ho3+ increased (and keeping the Tm3+ concentration constant at y = 0.05), the intensity of all bands increases until x = 0.03 (Fig. 2b).
Regarding the thermometric performance of the nanoparticles, it is clear from the temperature dependent emission spectra depicted in Fig. 3a–d that the emission intensity changes significantly in the 300–330 K range and thus it can be used to measure the temperature in the I-BW. The intensity ratio (Δ) between the Tm3+ line centered at 696 nm (I696, 3F2,3 → 3H6) and that of Ho3+ centered at 755 nm (I755, 5S2, 5F4 → 5I7) was calculated in the physiological range of temperatures for all the samples (Fig. 3e). For calculation simplicity we used the intensities at 696 and 755 nm (the calculus of the integrated area of the transitions gives the same result). In the absence of a complete physical model based on the rate equations of the populations of the levels involved in the energy transfer processes depicted in Fig. 2c, the experimental points were fitted to an empirical exponential growing equation:13,61
Δ = Δ0 + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(αT) exp(αT) | (1) |
 | (2) |
 | ||
| Fig. 4 (a) Relative thermal sensitivity (Sr) and (c) temperature uncertainty in the 300–330 K range of KLu1−x−yHoxTmy(WO4)2 nanoparticles. | ||
Comparing with examples of Tm3+, Yb3+ co-doped nanoparticles,43,44 the Sm value calculated here is of the same order of magnitude. Relatively to the downshifting Nd3+-doped nanoparticles,15,39,42,46–50 however, this work presents a sensitivity value that is generally one order of magnitude larger. Not using exclusively Ln3+ ions, the high Sm value of the LiLaP4O12 nanocrystal co-doped with Cr3+ and Nd3+, 4.89% K−1, is mentioned.45 Besides Sr, the temperature uncertainty δT is the other parameter used to characterize the nanothermometer's performance,20 being estimated as:
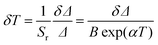 | (3) |
Photothermal heating efficiency
Fig. 5 displays the temperature profile of an aqueous dispersion of KLu0.84Ho0.01Tm0.15(WO4)2 (the sample with higher Sm value) recorded under illumination at 808 nm. In the steady-state regime (t > 600 s), we observe a maximum temperature increase (measured with the Pt-100 thermo-resistor immersed in the suspension) (Tm − Ta) = 8.60 ± 0.05 K (Tm and Ta are the maximum achieved temperature and the ambient temperature, respectively). As a control, the same experiment was repeated for pure water, reaching a smaller maximum temperature increment (about 1.0 K, Fig. 5). This validates that the temperature increment observed in the nanoparticle's aqueous suspension is majorly due to the heat dissipation by the nanoparticles themselves (and not by the water). | ||
| Fig. 5 Time-dependent temperature profiles of the aqueous dispersion of KLu0.84Ho0.01Tm0.15(WO4)2 nanoparticles (squares) and of pure water (circles). The line is the fit to the experimental data using eqn (6) (r2 > 0.994). The fit residuals are presented in the bottom graph. | ||
The nanoparticles’ photothermal conversion efficiency using the thermal relaxation method is evaluated by:54
 | (4) |
For comparison purposes, we also determine η of the same nanoparticles as a function of the excitation power density using the integrating sphere method, a methodology described in detail elsewhere.53 In this method η is calculated using:
 | (5) |
Thermal resistance of the nanoparticles through upconversion thermometry
Generally, the thermal resistance of a given material (defined as the ratio between the temperature increase and the heat flowing through it) has been measured by electric means, such as the thermal bridge and thermocouples (for instance in graphene layers62 or carbon nanotubes–Cu composites,63 respectively) or by null-point scanning thermal microscopy (for instance in graphene disks64). These methods, however, overestimate the thermal resistance, since they cannot decouple the thermal resistance from the parasitic contact resistance between the nanostructures and the heat source/sink, which can typically account for 50% of the measured thermal resistance.65 Moreover, the methods are complex, expensive and with significant limitations to be extended to other nanomaterials. Here we demonstrate that the upconversion of heater-thermometer nanoparticles can be used as a tool for the unveiling of the thermal properties of the particles themselves, in this case to determine the thermal resistance R. As an illustrative example, we use KLu0.94Ho0.01Tm0.05(WO4)2 powder nanoparticles in contact with air. We selected this sample because their Sr and δT values are almost constant in the tested temperature interval, contrary to those of the other examples in which larger variations are observed (Fig. 4).In a typical experiment, a laser beam is focused on the sample's surface inducing, simultaneously, upconversion emission and a temperature increment, ΔT(t), due to non-radiative deactivations. Then, the emission spectra are recorded with respect to the elapsed time being converted into temperature using eqn (1) (Fig. 6a). Fig. 6b presents the temperature increase of KLu1−x−yHoxTmy(WO4)2 (x = 0.01, y = 0.05 and x = 0.01, y = 0.15) induced by the irradiation with the 808 nm laser with power density values up to 400 × 106 W m−2. For the same laser power density, the temperature increment is smaller for the sample with a lower Tm3+ concentration, suggesting a positive correlation between the heat generated due to non-radiative Tm3+-to-Ho3+ energy transfer and Ho3+-to-Tm3+ back transfer and the Tm3+ content. Moreover, the plateau discerned for high power densities (>300 × 106 W m−2), and not observed in the PD range studied for the sample with a higher Tm3+ concentration, is related to a saturation effect on the Tm3+ absorption at 808 nm.
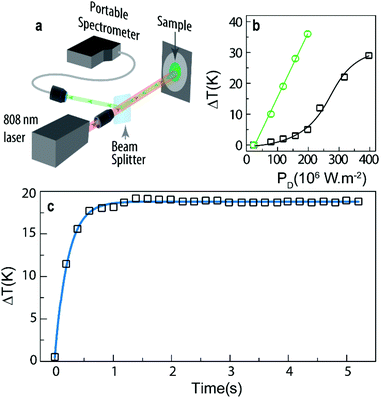 | ||
| Fig. 6 (a) Scheme of the experimental setup used to measure the real-time evolution of the emission spectra upon 808 nm excitation. The laser simultaneously heats and excites the sample providing the temperature dependent upconversion emission. A beam splitter was used to redirect a part of the emitted signal to the portable spectrometer that simultaneously records the emission spectra. (b) Temperature increase induced by distinct excitation power density (PD) for KLu0.94Ho0.01Tm0.05(WO4)2 (black squares) and KLu0.84Ho0.01Tm0.15(WO4)2 (green circles) powder nanoparticles in contact with air. (c) Heating curve of KLu0.94Ho0.01Tm0.05(WO4)2 (PD = 318 × 106 W m−2). The solid line corresponds to the best fit to experimental data using eqn (6) (r2 = 0.997). | ||
The thermal gradients within the nanoparticles are negligible when compared with the temperature change in their neighborhood (Biot number lower than 0.01, details in the ESI†). Thus, the heat dissipation follows the classical Fourier law, resulting in a temperature increase given by:66,67
 | (6) |
Fitting eqn (6) to the heating curve of KLu0.94Ho0.01Tm0.05(WO4)2 powder nanoparticles in contact with air, we obtain ΔTm = 18.3 ± 0.2 K and τ = 0.223 ± 0.004 s (r2 > 0.997), that corresponds to R = (9.50 ± 0.17) × 107 K W−1, considering c = 324 J kg−1 K−1 and m estimated by multiplying the area of the excitation beam, π × 10−10 m2, by the penetration length, 3 × 10−6 m, and the density ρ = 7686 kg m−3 (the c and ρ values are from the KLu(WO4)2 bulk crystal,68,69 Table S4, ESI†).
To the best of our knowledge, this is the first report of thermal resistance values for oxide nanoparticles. Nevertheless, the calculated value is of the same order of magnitude of the measured interfacial thermal resistance across the Si/NiSi2 interface in Si0.7Ge0.3/NiSi0.7Ge0.3 heterostructured nanowires, 6–12 × 107 K W−1,70 and of the estimated value for interfacial thermal resistance of a 1 μm Si nanowire on an Si substrate, 0.1–10 × 107 K W−1.55 Interestingly, it is well known that in all applications where nanoparticles are in physical contact with a substrate, the thermal transport in these systems is expected to be dominated by the thermal resistance at the interface formed between the nanostructure and the substrate.55
The calculus of the τ value allows the determination of the temporal resolution of the KLu0.94Ho0.01Tm0.05(WO4)2 thermometer (δt) which can be calculated by:20
 | (7) |
Conclusions
We demonstrated that KLu1−x−yHoxTmy(WO4)2 (x = 0.01–0.05 and y = 0.05–0.15) nanoparticles are tunable multifunctional heater-thermometer nanoplatforms under 808 nm excitation. Additionally, the upconversion emission lines at 696 and 755 nm (in the I-BW) can be used for luminescence thermometry, with a relative maximum thermal sensitivity of 2.8% K−1 and a minimum temperature uncertainty of 0.2 K at 300 K. The photothermal conversion efficiency was determined by both the thermal relaxation and the integrating sphere methods. The values obtained, 41 ± 3% and 34 ± 2%, respectively, although smaller than the values already reported for downshifting multishell Nd3+-based nanostructures are higher than those of semiconductor and metallic nanoparticles. The value recorded by the thermal relaxation method is slightly higher because the method neglects the light reflection and scattering from the sample and the cuvette in which the sample is contained. The thermal resistance of powder KLu0.94Ho0.01Tm0.05(WO4)2 nanoparticles in contact with air, (9.50 ± 0.17) × 107 K W−1, is of the same order of magnitude of that expected for interfacial thermal resistance Si nanorods and Si-based heterostructured nanowires. As the nanoparticles are in contact with each other, we can anticipate that the thermal resistance is dominated by the contact resistance at the interface between them. To study this effect, future work will be focused on the measurement of the dependence on the external pressure of the thermal resistance. Moreover, the role played by the medium in the thermal resistance can also be addressed by performing similar measurements in colloidal suspensions of the nanoparticles. In summary, all these new tools enlarge the application of luminescence thermometry paving the road to exploit the heat transfer processes occurring at the micro and nanoscale.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Ministerio de Economía, Industria y Competitividad, the Agencia Estatal de Investigación (AEI) and the European Regional Development Fund (ERDF) under Projects No. TEC2014-55948-R and MAT2016-75716-C2-1-R (AEI/FEDER, UE), Secretaria d'Universitats i Recerca del Departament d'Economia i Coneixement de la Generalitat de Catalunya, the European Union (EU) and the European Social Fund (ESF) under Project No. 2017SGR755, and CMST COST Action CM1403, and partially developed in the scope of the project CICECO − Aveiro Institute of Materials (Ref. FCT UID/CTM/50011/2013), financed by Portuguese funds through the Fundação para a Ciência e a Tecnologia/Ministério da Educação e Ciência (FCT/MEC) and when applicable co-financed by FEDER under the PT2020 Partnership Agreement. Financial support of FCT (PTDC/CTM-NAN/4647/2014 and POCI-01-0145-FEDER-016687) is also acknowledged. OAS was supported by the Catalan Government through the fellowship 2015FI_B 00136, CDSB thanks the individual grant financed by the SusPhotoSolutions project CENTRO-01-0145-FEDER-000005, and FD acknowledges additional support through the ICREA Academia awards 2010ICREA-02 for excellence in research.Notes and references
- L. D. Carlos and F. Palacio, Thermometry at the Nanoscale: Techniques and Selected Applications, Royal Society of Chemistry, Oxfordshire, 2016 Search PubMed.
- K. Okabe, N. Inada, C. Gota, Y. Harada, T. Funatsu and S. Uchiyama, Nat. Commun., 2012, 3, 705 CrossRef PubMed.
- J. S. Donner, S. A. Thompson, M. P. Kreuzer, G. Baffou and R. Quidant, Nano Lett., 2012, 12, 2107–2111 CrossRef CAS PubMed.
- G. Yang, X. Liu, J. Feng, S. Li and Y. Li, in Thermometry at the nanoscale: techniques and selected applications, ed. L. D. Carlos and F. Palacio, The Royal Society of Chemistry, 2016, vol. 38, ch. 6, pp. 167–189 Search PubMed.
- S. Kalytchuk, O. Zhovtiuk, S. V. Kershaw, R. Zboril and A. L. Rogach, Small, 2016, 12, 466–476 CrossRef CAS PubMed.
- M. Back, E. Trave, J. Ueda and S. Tanabe, Chem. Mater., 2016, 28, 8347–8356 CrossRef CAS.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2013, 5, 7572–7580 RSC.
- G. Jalani, R. Naccache, D. H. Rosenzweig, L. Haglund, F. Vetrone and M. Cerruti, J. Am. Chem. Soc., 2016, 138, 1078–1083 CrossRef CAS PubMed.
- M. L. Debasu, C. D. S. Brites, S. Balabhadra, H. Oliveira, J. Rocha and L. D. Carlos, ChemNanoMat, 2016, 2, 520–527 CrossRef CAS.
- X. Zhu, W. Feng, J. Chang, Y.-W. Tan, J. Li, M. Chen, Y. Sun and F. Li, Nat. Commun., 2016, 7, 10437 CrossRef CAS PubMed.
- O. A. Savchuk, P. Haro-González, J. J. Carvajal, D. Jaque, J. Massons, M. Aguiló and F. Diaz, Nanoscale, 2014, 6, 9727–9733 RSC.
- M. Bettinelli, L. D. Carlos and X. Liu, Phys. Today, 2015, 68, 38–44 CrossRef CAS.
- V. Lojpur, M. G. Nikolić and M. D. Dramićanin, J. Appl. Phys., 2014, 115, 203106 CrossRef.
- T. V. Gavrilović, D. J. Jovanović, V. Lojpur and M. D. Dramićanin, Sci. Rep., 2014, 4, 4209 CrossRef PubMed.
- S. Balabhadra, M. L. Debasu, C. D. Brites, L. A. Nunes, O. L. Malta, J. Rocha, M. Bettinelli and L. D. Carlos, Nanoscale, 2015, 7, 17261–17267 RSC.
- Ł. Marciniak, A. Bednarkiewicz, M. Stefanski, R. Tomala, D. Hreniak and W. Strek, Phys. Chem. Chem. Phys., 2015, 17, 24315 RSC.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301–4326 RSC.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799–4829 RSC.
- X. D. Wang, O. S. Wolfbeis and R. J. Meier, Chem. Soc. Rev., 2013, 42, 7834–7869 RSC.
- C. D. S. Brites, A. Millán and L. D. Carlos, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, B. V., Amsterdam, 2016, vol. 49, ch. 281, pp. 339–427 Search PubMed.
- M. Quintanilla, A. Benayas, R. Naccache and F. Vetrone, in Thermometry at the nanoscale: techniques and selected applications, ed. L. D. Carlos and F. Palacio, The Royal Society of Chemistry, Oxfordshire, 2016, vol. 38, ch. 5, pp. 124–166 Search PubMed.
- M. D. Dramićanin, Methods Appl. Fluoresc., 2016, 4, 042001 CrossRef PubMed.
- E. Hemmer, P. Acosta-Mora, J. Mendez-Ramos and S. Fischer, J. Mater. Chem. B, 2017, 5, 4365–4392 RSC.
- B. Liu, C. X. Li, P. P. Yang, Z. Y. Hou and J. Lin, Adv. Mater., 2017, 29, 1605434 CrossRef PubMed.
- T. Miyagawa, T. Fujie, Ferdinandus, T. T. V. Doan, H. Sato and S. Takeoka, ACS Appl. Mater. Interfaces, 2016, 8, 33377–33385 CAS.
- Ferdinandus, S. Arai, S. Takeoka, S. Ishiwata, M. Suzuki and H. Sato, ACS Sens., 2016, 1, 1222–1227 CrossRef CAS.
- E. C. Ximendes, U. Rocha, T. O. Sales, N. Fernández, F. Sanz-Rodríguez, I. R. Martín, C. Jacinto and D. Jaque, Adv. Funct. Mater., 2017, 1702249 CrossRef.
- E. C. Ximendes, U. Rocha, B. del Rosal, A. Vaquero, F. Sanz-Rodríguez, L. Monge, F. Ren, F. Vetrone, D. Ma and J. García-Solé, Adv. Healthcare Mater., 2017, 6, 1601195 CrossRef PubMed.
- R. Piñol, C. D. S. Brites, R. Bustamante, A. Martínez, N. J. O. Silva, J. L. Murillo, R. Cases, J. Carrey, C. Estepa, C. Sosa, F. Palacio, L. D. Carlos and A. Millán, ACS Nano, 2015, 9, 3134–3142 CrossRef PubMed.
- E. C. Ximendes, W. Q. Santos, U. Rocha, U. K. Kagola, F. Sanz-Rodriguez, N. Fernandez, A. D. Gouveia-Neto, D. Bravo, A. M. Domingo, B. del Rosal, C. D. S. Brites, L. D. Carlos, D. Jaque and C. Jacinto, Nano Lett., 2016, 16, 1695–1703 CrossRef CAS PubMed.
- C. D. Brites, X. Xie, M. L. Debasu, X. Qin, R. Chen, W. Huang, J. Rocha, X. Liu and L. D. Carlos, Nat. Nanotechnol., 2016, 11, 851–856 CrossRef CAS PubMed.
- C. D. S. Brites, M. C. Fuertes, P. C. Angelomé, E. D. Martínez, P. P. Lima, G. J. A. A. Soler-Illia and L. D. Carlos, Nano Lett., 2017, 17, 4746–4752 CrossRef CAS PubMed.
- J. Verma, S. Lal and C. J. F. Van Noorden, Int. J. Nanomed., 2014, 9, 2863–2877 Search PubMed.
- D. de Melo-Diogo, C. Pais-Silva, D. R. Dias, A. F. Moreira and I. J. Correia, Adv. Healthcare Mater., 2017, 6, 1700073 CrossRef PubMed.
- U. Rocha, K. U. Kumar, C. Jacinto, J. Ramiro, A. J. Caamano, J. G. Solé and D. Jaque, Appl. Phys. Lett., 2014, 104, 053703 CrossRef.
- D. Jaque, L. M. Maestro, B. Del Rosal, P. Haro-Gonzalez, A. Benayas, J. Plaza, E. M. Rodríguez and J. G. Solé, Nanoscale, 2014, 6, 9494–9530 RSC.
- A. K. Silva, A. Nicolas-Boluda, L. Fouassier and F. Gazeau, Nanomedicine, 2017, 12, 1213–1215 CrossRef CAS PubMed.
- N. Lee, D. Yoo, D. Ling, M. H. Cho, T. Hyeon and J. Cheon, Chem. Rev., 2015, 115, 10637–10689 CrossRef CAS PubMed.
- D. Wawrzynczyk, A. Bednarkiewicz, M. Nyk, W. Strek and M. Samoc, Nanoscale, 2012, 4, 6959–6961 RSC.
- M. L. Debasu, D. Ananias, I. Pastoriza-Santos, L. M. Liz-Marzán, J. Rocha and L. D. Carlos, Adv. Mater., 2013, 25, 4868–4874 CrossRef CAS PubMed.
- U. Rocha, C. Jacinto da Silva, W. Ferreira Silva, I. Guedes, A. Benayas, L. Martínez Maestro, M. Acosta Elias, E. Bovero, F. C. J. M. van Veggel, J. G. Solé and D. Jaque, ACS Nano, 2013, 7, 1188–1199 CrossRef CAS PubMed.
- E. Carrasco, B. del Rosal, F. Sanz-Rodríguez, Á. J. de la Fuente, P. H. Gonzalez, U. Rocha, K. U. Kumar, C. Jacinto, J. G. Solé and D. Jaque, Adv. Funct. Mater., 2015, 25, 615–626 CrossRef CAS.
- O. A. Savchuk, J. J. Carvajal, C. Cascales, M. Aguiló and F. Diaz, ACS Appl. Mater. Interfaces, 2016, 8, 7266–7273 CAS.
- L. L. Xing, Y. L. Xu, R. Wang, W. Xu and Z. G. Zhang, Opt. Lett., 2014, 39, 454–457 CrossRef CAS PubMed.
- L. Marciniak, A. Bednarkiewicz, D. Kowalska and W. Strek, J. Mater. Chem. C, 2016, 4, 5559–5563 RSC.
- L. Marciniak, K. Prorok, A. Bednarkiewicz, A. Kowalczyk, D. Hreniak and W. Strek, J. Lumin., 2016, 176, 144–148 CrossRef CAS.
- A. Benayas, B. del Rosal, A. Perez-Delgado, K. Santacruz-Gomez, D. Jaque, G. A. Hirata and F. Vetrone, Adv. Opt. Mater., 2015, 3, 687–694 CrossRef CAS.
- M. Pedroni, P. Cortelletti, I. X. Cantarelli, N. Pinna, P. Canton, M. Quintanilla, F. Vetrone and A. Speghini, Sens. Actuators, B, 2017, 250, 147–155 CrossRef CAS.
- P. Cortelletti, C. Facciotti, I. X. Cantarelli, P. Canton, M. Quintanilla, F. Vetrone, A. Speghini and M. Pedroni, Opt. Mater., 2017, 68, 29–34 CrossRef CAS.
- L. Marciniak, A. Pilch, S. Arabasz, D. Jin and A. Bednarkiewicz, Nanoscale, 2017, 9, 8288–8297 RSC.
- B. del Rosal, U. Rocha, E. C. Ximendes, E. M. Rodriguez, D. Jaque and J. G. Sole, Opt. Mater., 2017, 63, 185–196 CrossRef CAS.
- B. del Rosal, A. Perez-Delgado, E. Carrasco, D. J. Jovanovic, M. D. Dramicanin, G. Drazic, A. J. de la Fuente, F. Sanz-Rodriguez and D. Jaque, Adv. Opt. Mater., 2016, 4, 782–789 CrossRef CAS.
- O. A. Savchuk, J. Carvajal, J. Massons, M. Aguiló and F. Díaz, Carbon, 2016, 103, 134–141 CrossRef CAS.
- D. K. Roper, W. Ahn and M. Hoepfner, J. Phys. Chem. C, 2007, 111, 3636–3641 CAS.
- R. Prasher, Nano Lett., 2005, 5, 2155–2159 CrossRef CAS PubMed.
- M. Galceran, M. Pujol, M. Aguiló and F. Díaz, J. Sol-Gel Sci. Technol., 2007, 42, 79–88 CrossRef CAS.
- O. A. Savchuk, J. J. Carvajal, M. C. Pujol, E. W. Barrera, J. Massons, M. Aguilo and F. Diaz, J. Phys. Chem. C, 2015, 119, 18546–18558 CAS.
- S. A. Payne, L. K. Smith, W. L. Kway, J. B. Tassano and W. F. Krupke, J. Phys.: Condens. Matter, 1992, 4, 8525 CrossRef CAS.
- M. Guan, H. Zheng, L. Mei, Z. Huang, T. Yang, M. Fang and Y. Liu, Infrared Phys. Technol., 2014, 67, 107–110 CAS.
- Y. Li, Y. Wang, B. Yao and Y. Liu, Laser Phys. Lett., 2008, 5, 597 CrossRef CAS.
- A. C. Brandão-Silva, M. A. Gomes, S. M. V. Novais, Z. S. Macedo, J. F. M. Avila, J. J. Rodrigues and M. A. R. C. Alencar, J. Alloys Compd., 2018, 731, 478–488 CrossRef.
- Z. Wang, R. Xie, C. T. Bui, D. Liu, X. Ni, B. Li and J. T. Thong, Nano Lett., 2010, 11, 113–118 CrossRef PubMed.
- Z. An, M. Toda and T. Ono, Carbon, 2014, 75, 281–288 CrossRef CAS.
- G. Hwang and O. Kwon, Nanoscale, 2016, 8, 5280–5290 RSC.
- Y. K. Koh and D. G. Cahill, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075207 CrossRef.
- F. P. Incropera, D. P. DeWitt, T. L. Bergman and A. S. Lavine, Introduction to Heat Transfer, Wiley, New York, 5 edn, 2006 Search PubMed.
- J. H. Lienhard, A heat transfer textbook, Courier Corporation, 2013 Search PubMed.
- M. Pujol, X. Mateos, A. Aznar, X. Solans, S. Surinach, J. Massons, F. Díaz and M. Aguiló, J. Appl. Crystallogr., 2006, 39, 230–236 CAS.
- Ò. Silvestre, J. Grau, M. C. Pujol, J. Massons, M. Aguiló, F. Díaz, M. T. Borowiec, A. Szewczyk, M. U. Gutowska and M. Massot, Opt. Express, 2008, 16, 5022–5034 CrossRef PubMed.
- D. Liu, R. G. Xie, N. Yang, B. W. Li and J. T. L. Thong, Nano Lett., 2014, 14, 806–812 CrossRef CAS PubMed.
- E. Saïdi, N. Babinet, L. Lalouat, J. Lesueur, L. Aigouy, S. Volz, J. Labeguerie-Egea and M. Mortier, Small, 2011, 7, 259–264 CrossRef PubMed.
- J.-P. Tetienne, A. Lombard, D. A. Simpson, C. Ritchie, J. Lu, P. Mulvaney and L. C. Hollenberg, Nano Lett., 2016, 16, 326–333 CrossRef CAS PubMed.
- I. Sedmak, I. Urbancic, J. Strancar, M. Mortier and I. Golobic, Sens. Actuators, A, 2015, 230, 102–110 CrossRef CAS.
- V. V. Deshpande, S. Hsieh, A. W. Bushmaker, M. Bockrath and S. B. Cronin, Phys. Rev. Lett., 2009, 102, 105501 CrossRef PubMed.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Front. Chem., 2013, 1, 9 Search PubMed.
- R. A. S. Ferreira, C. D. S. Brites, C. M. S. Vicente, P. P. Lima, A. R. N. Bastos, P. G. Marques, M. Hiltunen, L. D. Carlos and P. S. André, Laser Photonics Rev., 2013, 7, 1027–1035 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: XRD, TEM, elemental analysis, upconversion, thermometric characterization, photothermal heating efficiency, and temperature-time dependence for the irradiated particles. See DOI: 10.1039/c7nr08758f |
| This journal is © The Royal Society of Chemistry 2018 |