Open Access Article
Open Access ArticleParticles with similar LET values generate DNA breaks of different complexity and reparability: a high-resolution microscopy analysis of γH2AX/53BP1 foci
Lucie
Jezkova
ab,
Mariia
Zadneprianetc
ac,
Elena
Kulikova
ac,
Elena
Smirnova
a,
Tatiana
Bulanova
ac,
Daniel
Depes
d,
Iva
Falkova
d,
Alla
Boreyko
ac,
Evgeny
Krasavin
ac,
Marie
Davidkova
e,
Stanislav
Kozubek
d,
Olga
Valentova
b and
Martin
Falk
 *d
*d
aJoint Institute for Nuclear Research, Dubna, Russia
bUniversity of Chemistry and Technology Prague, Prague, Czech Republic
cDubna State University, Dubna, Russia
dCzech Academy of Sciences, Institute of Biophysics, Brno, Czech Republic. E-mail: falk@ibp.cz; Tel: +420-541517116 Tel: +420-728084060
eCzech Academy of Sciences, Nuclear Physics Institute, Prague, Czech Republic
First published on 12th December 2017
Abstract
Biological effects of high-LET (linear energy transfer) radiation have received increasing attention, particularly in the context of more efficient radiotherapy and space exploration. Efficient cell killing by high-LET radiation depends on the physical ability of accelerated particles to generate complex DNA damage, which is largely mediated by LET. However, the characteristics of DNA damage and repair upon exposure to different particles with similar LET parameters remain unexplored. We employed high-resolution confocal microscopy to examine phosphorylated histone H2AX (γH2AX)/p53-binding protein 1 (53BP1) focus streaks at the microscale level, focusing on the complexity, spatiotemporal behaviour and repair of DNA double-strand breaks generated by boron and neon ions accelerated at similar LET values (∼135 keV μm−1) and low energies (8 and 47 MeV per n, respectively). Cells were irradiated using sharp-angle geometry and were spatially (3D) fixed to maximize the resolution of these analyses. Both high-LET radiation types generated highly complex γH2AX/53BP1 focus clusters with a larger size, increased irregularity and slower elimination than low-LET γ-rays. Surprisingly, neon ions produced even more complex γH2AX/53BP1 focus clusters than boron ions, consistent with DSB repair kinetics. Although the exposure of cells to γ-rays and boron ions eliminated a vast majority of foci (94% and 74%, respectively) within 24 h, 45% of the foci persisted in cells irradiated with neon. Our calculations suggest that the complexity of DSB damage critically depends on (increases with) the particle track core diameter. Thus, different particles with similar LET and energy may generate different types of DNA damage, which should be considered in future research.
1 Introduction
Ionizing radiation (IR) is one of the most effective cytotoxic agents. Due to its ability to ionize atoms or molecules, IR induces several types of DNA damage. Among these lesions, DNA double-strand breaks (DSBs) are the most critical. Cells have evolved sophisticated DNA damage repair systems capable of efficiently removing a vast majority of lesions to maintain genome integrity, which is permanently threatened by various exogenous and endogenous factors.1,2However, a unique attribute of IR is its ability to deposit energy within nanometre volumes and thus induce clustered/complex DNA damage containing various combinations of DSBs, single-strand breaks (SSBs), chemically modified or lost bases, DNA–DNA cross-links, DNA–protein cross-links, heat- and alkali-labile sites, and other potential impairments. These lesions pose a serious challenge for DNA repair systems, as in many instances, this damage is irreparable, may be repaired incorrectly or may lead to the formation of even more serious DNA damage.1–3 Hence, because clustered/complex DNA damage represents the main cause of cell death or mutagenesis upon irradiation, these types of damage have been considered key determinants of the radiobiological effectiveness of radiation.
The complexity of DNA damage depends on the radiation quality, and for radiobiological purposes, this quality is typically described in terms of linear energy transfer (LET).2,4 Two main groups of radiation have been distinguished based on LET and their mechanism of action and biological effects. Low-LET radiation sparsely and uniformly deposits energy within the whole volume of the cell nucleus. Hence, exposure to γ-rays or X-rays, two representatives of this category, typically leads to the formation of simple DNA lesions. In contrast, clustered or complex damage (multiple DSBs and other lesions within a few helical DNA turns) is the characteristic feature of high-LET irradiation.1–4 The phenomenon of clustered/multiple DNA damage is evoked by the nature of the energy transferred, and by definition, high-LET radiation densely releases energy along the track of the particle such that several types of damage form in a single localized spot volume.
The spatial structure of high-LET particle tracks depends on the physical parameters of the particle and chromatin structure. The distribution of energy deposited by high-LET radiation along the particle track is divided into two spatial components: the core and the penumbra, also known as the region of δ-rays.5,6 The core is typically referred as to the central region of extremely dense energy deposition, where biomolecules are directly damaged by the particle itself along with contributions from low-energy knock-on electrons that do not escape from the core volume. Secondary electrons of higher energy (δ-rays) subsequently radiate out from the core and form the penumbra. Although a generally accepted definition of these track components is not yet available,6 the microdosimetric characteristics of the track core and the penumbra together determine the initial complexity of DNA damage.6,7 This notion is also true for the relationship between these spatial track/streak components and relative biological effectiveness (RBE) of radiation.
LET is frequently calculated to definitively determine the RBE of radiation; however, this parameter cannot precisely predict how particle tracks will appear and behave in space and time. A considerable body of evidence has revealed the positive dependence of RBE on LET, where the biological endpoints of irradiation, such as cell killing,8–11 induction of mutations12–14 (reviewed in Yatagai et al.15), and formation of chromosomal aberrations,16–19 increase as the LET value increases. However, a certain LET value (approximately 100 keV μm−1) will correspond to the maximum peak RBE, and from this point, RBE decreases only with increasing LET. Moreover, the most biologically damaging LET value largely fluctuates between 100 and 200 keV μm−1 for different particles, depending on the cell type and endpoint studied.7,20–22 Hence, a reasonable hypothesis is that the particle generates tracks with different spatiotemporal characteristics according to specific sets of individual physical parameters (e.g., energy, charge, diameter, etc.), even if various combinations of these parameters show similar LET values.7 However, experimental studies focusing on the microstructure of DNA damage observed following the action of different high-LET particles with similar LET values are rare.
In addition to initial (static) structure of DNA damage, changes in the DNA dynamics over time after irradiation may also principally influence the reparability of DNA damage and therefore the RBE of radiation types. Chromatin fragmentation occurring in response to high-LET irradiation and chromatin decondensation that occurs during DSB repair (in response to both high-LET and low-LET irradiation) locally mobilizes damaged chromatin to some extent, generating clustered/complex DNA lesions.23–26 The extent of chromatin fragmentation and spatial density of DSBs depend on LET, and the spatiotemporal dynamics of DNA damage is also expected to rely on LET. Nevertheless, researchers have not determined whether and how chromatin dynamics vary for different particles with similar LET. The importance of particle LET/energy becomes particularly relevant for low-dose/particle fluences – the conditions addressed in the present study. The characterization of the particle tracks (DNA damage structure) in space and time thus emerges as a promising and necessary new approach to explain many aspects of the radiobiological effects of physically different radiation types.
Studies of spatiotemporal aspects of DNA damage have become feasible with the discovery of the focal accumulation of DSB repair proteins at DSB lesions.27 One of the first cell responses to DSB formation is the phosphorylation of histone H2AX on Ser-139, followed by the attraction of numerous downstream repair proteins to sites of DSB. Phosphorylated H2AX (referred as to γH2AX) rapidly spreads over 2 Mbps of damaged chromatin and becomes microscopically detectable as discrete nuclear (γH2AX) foci within minutes after irradiation.27–29 Subsequently, numerous repair factors, including p53-binding protein 1 (53BP1), accumulate at γH2AX foci in a time-dependent manner, resulting in the formation of discrete nuclear domains, which are generally referred to as IR-induced foci (IRIF).23,30
Importantly, the structural parameters and assembly and disassembly kinetics of γH2AX/IRIF foci reflect the physical characteristics of the damaging agent, chromatin structure, and overall (genetic and physiological) cell status. Microscopy of γH2AX/IRIF foci in situ enables complex studies on spatiotemporal aspects of DSB damage induction, repair, and misrepair in the context of intact or even living cells. Moreover, this method offers unprecedented sensitivity and the possibility of simultaneous visualization of multiple DSB repair proteins.30–32
The relationship between the number of DSBs and γH2AX foci is approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for low-LET radiation.28,33 However, high-LET radiation generates DSBs that are located so close to one another that these lesions cannot be further separated at the resolution of standard optical microscopy.29,34 Various super-resolution (nanoscopy) techniques have been proposed and more or less successfully implemented into research practice to overcome this problem35,36 (reviewed by Falk37); however, still these methods remain technically challenging and are typically applicable only to relatively small sample numbers. Two studies by Lorat and co-workers38,39 took advantage of transmission electron microscopy to precisely quantify DSB complexity upon high-LET irradiation at a single molecule level. However, despite the superior resolution power and undisputable advantages of this approach, it suffers from serious limitations that primarily result from the complicated sample preparation requirements and the inability to quantitatively analyse DSB damage in the entire (3D) volume of the cell nucleus.40 Hence, a method for the precise, reliable, high-throughput and complex (i.e., in 3D volumes) analysis of DSBs under physiological conditions is not currently available. Many fundamental questions therefore remain open. For example, the above discussed super-resolution study38 revealed up to approximately 500 DSBs per 1 μm3 volume of the carbon ion track (LET = 190 keV μm−1, energy E = 9.5 MeV per n). This result is surprising and prompts questions of how a single DSB is defined at the molecular level and what level of complexity do DSBs generated by different radiation types present.
1 for low-LET radiation.28,33 However, high-LET radiation generates DSBs that are located so close to one another that these lesions cannot be further separated at the resolution of standard optical microscopy.29,34 Various super-resolution (nanoscopy) techniques have been proposed and more or less successfully implemented into research practice to overcome this problem35,36 (reviewed by Falk37); however, still these methods remain technically challenging and are typically applicable only to relatively small sample numbers. Two studies by Lorat and co-workers38,39 took advantage of transmission electron microscopy to precisely quantify DSB complexity upon high-LET irradiation at a single molecule level. However, despite the superior resolution power and undisputable advantages of this approach, it suffers from serious limitations that primarily result from the complicated sample preparation requirements and the inability to quantitatively analyse DSB damage in the entire (3D) volume of the cell nucleus.40 Hence, a method for the precise, reliable, high-throughput and complex (i.e., in 3D volumes) analysis of DSBs under physiological conditions is not currently available. Many fundamental questions therefore remain open. For example, the above discussed super-resolution study38 revealed up to approximately 500 DSBs per 1 μm3 volume of the carbon ion track (LET = 190 keV μm−1, energy E = 9.5 MeV per n). This result is surprising and prompts questions of how a single DSB is defined at the molecular level and what level of complexity do DSBs generated by different radiation types present.
To our knowledge, the current study represents the first experimental research on the spatiotemporal aspects of DNA damage upon exposure to high-LET radiation with a similar LET and (low) energy. We used high-resolution immunofluorescence confocal microscopy to perform a detailed examination of the DNA damage generated by neon ions, which show potential to improve hadron therapy,41,42 and boron ions, which are common secondary particles produced by nuclear interactions between high-energy neutrons and protons.43 Surprisingly, only a few experimental6,30,44 or theoretical45,46 studies (reviewed in Hamada47) have more or less directly addressed the induction and distribution of DSBs in cell nuclei irradiated with different particles of similar (high) LET. In contrast to these studies, we modified the parameters of the accelerated ions to exhibit similar LET values close to the maximum RBE as well as similar low energies. We focused on lower-energy particles that although they are rarely studied, are attractive for several purposes: they may arise during radiation shielding or affect normal tissue in hadron therapy at the end of the Bragg peak. Moreover, low-energy ions induce more complex and persistent DNA damage than high-energy particles.6,30,48
20Ne ions generate DSBs of higher complexity and lower reparability than 11B ions, despite the similar LET values of both ions and slightly higher energy of neon. Besides other hypotheses, this result may be explained by the morphology and spatiotemporal dynamics of γH2AX/53BP1 focus streaks that also obviously differed for the two radiation types. Our detailed analysis of these streaks suggests that the particle track structure is the crucial determinant of the RBE of radiation, which roughly depends on LET and energy but might be largely modified by other particle parameters under conditions of similar LET/energy.
2 Materials and methods
2.1 Cell culture
Primary normal human neonatal dermal fibroblasts, NHDF-Neo (Lonza, CC-2509), were grown in Iscove's Modified Dulbecco's Medium (IMDM) supplemented with 10% foetal calf serum (FCS) and a 1% gentamicin–glutamine solution (all reagents from Sigma-Aldrich). Cells were maintained in T-25 cell flasks at 37 °C in a humidified atmosphere with 5% CO2. All experiments were performed using cells at passages 6–9.Prior to irradiation (16–18 h), cells were re-seeded on 14 mm glass coverslips (glued to the outer side of a 35 mm Petri dish with a microwell, MatTek Corporation, P35G-0.170-14-C) and cultivated to form an 80% confluent monolayer. For irradiation, dishes were aseptically closed and sealed with Parafilm M (Sigma-Aldrich) to prevent spillage and cell infection. All samples were irradiated at room temperature and immediately returned to the incubator (37 °C).
2.2 Low-LET and high-LET irradiation
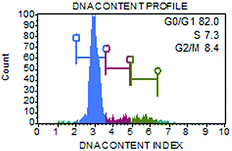
Non-synchronized cell populations with >80% of cells in G1-phase (Fig. 1) were irradiated with accelerated ions using a U-400 M isochronous cyclotron in the Flerov Laboratory of Nuclear Reaction at the Joint Institute for Nuclear Research (JINR, Dubna), and the Genome-M facility was used for the automatic fast irradiation of biological samples.49 According to the experiment, cells on glass coverslips (glued to a Petri dish as described above) were irradiated either at a perpendicular (90°) or sharp-angle (10°) geometry, i.e., with 90° or 10° angle between the ion beam and the plane of the cell monolayer. The coverslips were oriented towards the ion beam so that the cells were hit by the particles before the beam continued into the culture medium in the Petri dish. Samples that were irradiated in the perpendicular geometry were used to evaluate the kinetics of DSB repair and cell death (apoptosis) upon exposure to radiation. Cells irradiated in the sharp-angle geometry enabled detailed analyses of the morphology of γH2AX/53BP1 foci and structures of particle tracks (streaks) in space and time. In these experiments, cells were exposed to an average of three particles per nucleus, which corresponds to a dose of 1 Gy for 11B ions and 1.2 Gy for 20Ne ions (calculated as described by Jakob et al.29 for the average nuclear area of 186 μm2). The non-homogeneity within the irradiation field of 14 mm in diameter was less than 5%, as monitored using five identical flow-type ionization chambers; the central chamber served as the monitor of the radiation dose.49Fibroblasts were exposed to boron or neon beams with a dose rate of approximately 2 Gy min−1. The initial energy of 11B ions generated by the accelerator was 33 MeV per n. Due to the presence of different absorbers in the path of the ions in route to the sample (e.g., 1.842 mm-thick aluminium foil, 0.170 mm-thick borosilicate glass, etc.), this energy decreased to the final value of 8.1 MeV per n at the plane of the cell monolayer irradiated in the 90° setup, corresponding to a LET value of 138.1 keV μm−1. For the sharp-angle (10°) irradiation geometry, the energy of boron ions was further reduced to 7.5 MeV per n (the thickness of the glass at 10° was 0.979 mm) using an additional 1.006 mm-thick aluminium absorber, resulting in a LET value of 148.3 keV μm−1 (Table 1).
| Particle | Z | Geometry° | Energy, MeV per n | LET, keV μm−1 | Fluence*, 1 cm−2 | Particles per nucleus# |
|---|---|---|---|---|---|---|
| Z – charge, ○ – geometry of irradiation (the angle between the ion beam and the plane of the cell monolayer), * – fluence per 1 Gy absorbed in water, # – the number of particles per 1 Gy traversing a nucleus with an average area. The LET of Ne particles increased with increasing distance traversed along the glass at 10° irradiation, for which it was difficult to compensate. We cannot exclude minor influences on the results, but we consider this effect rather insignificant. Notably, identical conclusions to those drawn using 10° irradiation were obtained (though with lower precision) using 90° irradiation, where the LET values for B and Ne ions are much more similar. | ||||||
| 11B | 5 | 90 | 8.1 | 138.1 | 4.52 × 106 | 8.4 |
| 11B | 5 | 10 | 7.5 | 148.3 | 4.21 × 106 | 3.3 |
| 20Ne | 10 | 90 | 46.6 | 132.1 | 4.73 × 106 | 8.8 |
| 20Ne | 10 | 10 | 33.9 | 170.9 | 3.65 × 106 | 2.7 |
A beam of 20Ne ions accelerated to 50.0 MeV per n was used as the second type of high-LET radiation. The energy at the cell monolayer was 46.6 MeV per n in the 90° geometry and 33.9 MeV per n in the sharp-angle (10°) setup; the corresponding LET values were 132.1 keV μm−1 and 170.9 keV μm−1, respectively. For neon radiation, no additional absorbers (with the exception of mandatory absorbers, e.g., separating foils, electrodes, air, and glass coverslips) were used. The energy and corresponding LET values of ions at the plane of the cell monolayer were calculated using LISE++ software.50 The irradiation schemes and radiation characteristics are summarized in Table 1.
Gamma rays from a 60Co source were used as a low-LET radiation. The samples were irradiated at the Rokus-M facility in Dzhelepov Laboratory of Nuclear Problems (JINR, Dubna) with 1 Gy of γ-rays at a dose rate of 1 Gy min−1. Mock-irradiated cells were used as controls in all experiments.
2.3 Immunofluorescence assay
Irradiated cells were spatially (3D) fixed at different periods of time post-irradiation (PI), ranging from 5 min PI to 4 days PI, with 4% paraformaldehyde/PBS (10 min, room temperature (RT)) after a brief (2 × 2 min) wash with PBS (phosphate-buffered saline, 37 °C). Fixed cells were quickly rinsed (PBS), washed 3 × 5 min with PBS, and permeabilized with 0.2% Triton-X100/PBS (15 min at RT). After rinsing and washing (3 × 5 min) with PBS, cells were treated with the blocking solution I (5% inactivated FCS/2% bovine serum albumin/PBS) for 30 min at RT. The primary antibodies – mouse anti-γH2AX (ab22551, Abcam) and rabbit anti-53BP1 (ab21083, Abcam) – were diluted in the blocking solution I (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 and 1
700 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600, respectively) and applied to the cells for 10 min at RT and subsequently overnight at 4 °C. Cells were rinsed with PBS, washed 3 × 5 min (RT) with PBS, and blocked (30 min) with blocking solution 2 (5% inactivated goat serum/PBS) to inhibit nonspecific binding. The secondary antibodies – Texas Red-conjugated goat anti-rabbit (ab6719, Abcam) and FITC-conjugated goat anti-mouse (ab97239, Abcam) – were diluted in blocking solution 2 (1
600, respectively) and applied to the cells for 10 min at RT and subsequently overnight at 4 °C. Cells were rinsed with PBS, washed 3 × 5 min (RT) with PBS, and blocked (30 min) with blocking solution 2 (5% inactivated goat serum/PBS) to inhibit nonspecific binding. The secondary antibodies – Texas Red-conjugated goat anti-rabbit (ab6719, Abcam) and FITC-conjugated goat anti-mouse (ab97239, Abcam) – were diluted in blocking solution 2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 and 1
400 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200, respectively) and applied to the cells for 30 min (RT, in the dark). This step was followed by washes with PBS (a brief rinse + 3 × 5 min at RT), 2× saline sodium citrate (SSC) (2 min) and 4× SSC + 0.1% Igepal. The chromatin was counterstained with 600 nM 4′,6-diamidino-2-phenylindole dihydrochloride (DAPI, Sigma-Aldrich) in Vectashield antifade mounting medium (Vector Laboratories).
200, respectively) and applied to the cells for 30 min (RT, in the dark). This step was followed by washes with PBS (a brief rinse + 3 × 5 min at RT), 2× saline sodium citrate (SSC) (2 min) and 4× SSC + 0.1% Igepal. The chromatin was counterstained with 600 nM 4′,6-diamidino-2-phenylindole dihydrochloride (DAPI, Sigma-Aldrich) in Vectashield antifade mounting medium (Vector Laboratories).
2.4 Image acquisition and experimental data analysis
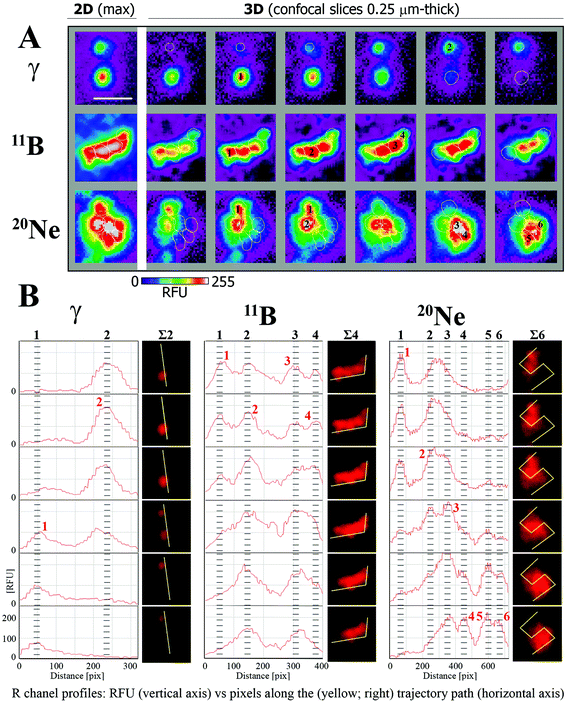
Images of the immunofluorescence staining were captured using an automated high-resolution Leica SP5 confocal laser-scanning fluorescence microscopy system equipped with a white laser for the excitation of multiple fluorochromes and sensitive hybrid detectors (Leica). Confocal slices of cells were obtained with a HCX PL APO lambda blue 63.0× 1.40 OIL UV immersion objective with 0.25 μm z-step increments across the nuclei, which were 2.7–3.4 μm-thick on average. Images were analysed using Acquiarium software,51 which enabled the three-dimensional reconstruction of images and inspection of individual γH2AX and 53BP1 foci in 3D space. For all analyses, only colocalized γH2AX/53BP1 foci were considered. There were 3 reasons for scoring only the colocalized signals: (1) to increase the precision of DSB detection in the early stages post-irradiation; (2) to increase the probability that unrepaired DSBs are still observed in later and very late periods of time PI; and (3) to partially increase the homogeneity of cells (i.e., the proportion of G1 cells) involved in the analyses. Notably, in early time periods post-irradiation, the γH2AX signal represents a mixture of small but more developed γH2AX foci (that colocalize with 53BP1) and similarly small or smaller γH2AX foci in very early stages, which could sometimes be difficult to distinguish from the background signal. In later periods of time PI, the persistence of the 53BP1 signal at γH2AX foci allowed us to legitimately presuppose that γH2AX/53BP1 foci present in nuclei still represent unrepaired DSBs and are not simply “relics” of previously repaired lesions. Finally, 53BP1 dissociates from γH2AX foci during late S-phase,52,53 G2-phase54 and mitosis;54 thus, the evaluation of colocalizing γH2AX foci alone may also increase the predominance of G1 cells in the present analyses.The foci were manually counted by eye (2 independent experienced evaluators) in three-dimensional images of approximately 100 nuclei per each experimental condition. In the 10° irradiation experiments, the software analyses described below supported this estimation. The mean numbers with the standard errors per group were calculated for pooled data from two independent experiments (additional experiments were not possible because of the limited beam time awarded to users and the specific settings required). The area and circularity of γH2AX/53BP1 foci and complexity of γH2AX/53BP1 focus clusters were measured in nuclei irradiated in the sharp-angle (10°) geometry, which ensured a sufficiently high microscopic resolution of individual foci. The area and circularity were measured on maximum images composed of all superimposed confocal slices using Adobe Photoshop CS6 Extended software; at least 200 γH2AX/53BP1 foci were scored per group to calculate the mean values with standard errors. The boundaries of individual γH2AX/53BP1 foci within the cluster and the complexity of 3D foci in the cluster (number of clustered foci) (Fig. 2) were semi-computationally determined by combining information obtained from (a) the cluster morphology (shape/size) characterized for each individual 0.25 μm-thick confocal slice of the image z-stack; (b) cluster fluorescence intensity heat maps computed for each individual confocal slice of the z-stack as well as for the maximum images composed of superimposed confocal slices; and (c) cluster red-channel fluorescence intensity profiles (R-profiles) measured for each individual confocal slice of the image z-stack along the path drawn to identify eventual fluorescence maxima and minima between foci in overexposed cluster areas. Since the 53BP1 signals precisely corresponded to γH2AX signals but presented better mutual separation in clusters, we used the 53BP1 (red) channel for image analyses. First (with the exception of morphologically clearly distinguishable foci), we determined the local fluorescence maxima (fluorescence foci centres; heat maps) of the clusters and compared their numbers per cluster and positions relative to the number and positions of putative foci defined according to cluster morphology. When all parameters were correlated, the number of foci per cluster was counted as the number of fluorescence centres. When two or more foci were identified according to cluster morphology but the number of fluoresce centres was lower (e.g., one large inseparable maximum existed for two putative foci), a fluorescence profile in the red channel (53BP1) was measured along the path intersecting putative foci in more peripheral areas, where the fluorescence signal was not overexposed. Decisions regarding the number of foci were made based on the number of local fluorescence maxima along the path. Alternatively (seemingly one focus contains two fluorescence centres), two foci were only scored under the following conditions: (a) both maxima were intensive, and (b) the focus was large and (c) sufficiently irregular to provide a legitimate impression of the existence of two foci (e.g., large elliptic focus with two intensive eccentrically located fluorescence maxima). The morphology of the clusters was studied in 3D with Acquiarium software, and R-profiles and heat maps were prepared with ImageJ55 and CellProfiler56 software, respectively. The line demarcating the area of each focus in the cluster (white circles in Fig. 2A) was manually drawn according to the focus heat map signal in the confocal slice showing the strongest fluorescence maximum. Typically, the signal of two levels above the heat map background (green signal in Fig. 2A) was used for this purpose. The described procedures were repeatedly performed for all individual confocal slices in the image z-stack, and the data were combined to obtain the final results. The procedure is demonstrated for illustrative foci (later introduced in Fig. 8, Results) generated by γ-rays, boron ions and neon ions in Fig. 2. Foci forming a spatial unit and connected at least by the “green” fluorescence level (heat maps) were considered to occupy one cluster. Statistical analyses were performed with the Sigma Plot statistical package.
2.5 Quantification of apoptosis by flow cytometry
The percentage of apoptotic cells after γ-ray or boron ion irradiation was determined via flow cytometry staining of Annexin V/7-amino actinomycin (7-AAD)-positive cells (Muse™ Annexin-V & Dead Cell Assay kit). Cells that had been irradiated with 1 or 4 Gy were assayed at 24 h and again at 48 h PI on the Muse™ Cell Analyzer, according to the manufacturer's instructions. Briefly, adherent cells and cells floating in the culture medium were collected, diluted to the required concentration (1 × 105 to 5 × 105 cells per ml) and consecutively incubated with the Muse Cell Dispersal Reagent (20 min at RT to prevent the formation of aggregates and clumps) and the Muse™ Annexin-V & Dead Cell Assay kit (20 min at RT in the dark). All reagents and the cell analyser were obtained from EMD Millipore Bioscience. Each sample was measured in triplicate, and the mean values with standard errors were calculated. Six thousand cells were acquired and analysed per sample. The proportions of apoptotic cells were determined using the Muse Cell Analyzer software.2.6 Core radius calculation
The radius rc of the particle track core was calculated based on the model reported by Chatterjee and Holley57 using the following formulas: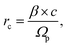 | (1) |
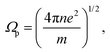 | (2) |
3 Results
3.1 DSB repair kinetics compared for low-LET γ-rays and two high-LET particles with similar LET values
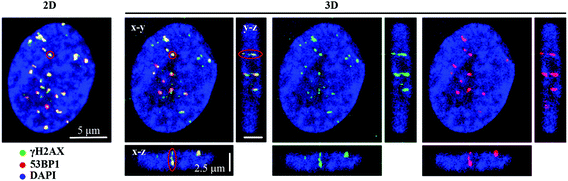
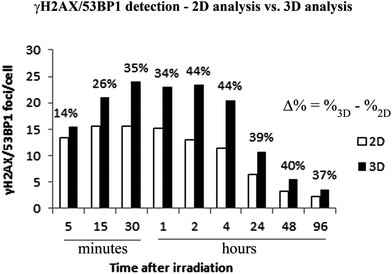
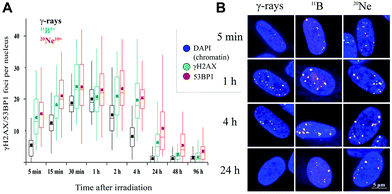
We examined the kinetics of γH2AX/53BP1 foci formation and characterized their decrease with time PI in normal human neonatal dermal fibroblasts (NHDF-Neo) exposed to three different types of radiation (section 2.2) to determine how radiation quality affects the induction of double-strand breaks (DSBs) in DNA molecules and assess the ability of human cells to repair this damage. Gamma rays from 60Co, representing low-LET radiation, are used in the present study as the standard for comparisons. However, the boron (11B) and neon (20Ne) ions facilitated an examination of the effects of two high-LET particles with comparable LET values (similar to the maximum relative biological efficiency, RBE) and only slightly different energies (Table 1). For kinetics studies, we irradiated cell monolayers with 1 Gy of a particular radiation in the perpendicular (90°) geometry to the beam axis. Consequently, we visualized DSBs using high-resolution immunofluorescence confocal microscopy of colocalization of γH2AX and 53BP1 foci, the markers of DSBs,58 in spatially (3D) fixed cells (Fig. 3). This approach currently provides the maximum sensitivity and fidelity for DSB detection59 and, upon reconstructing 3D images of cell nuclei (Fig. 3), also enables efficient discrimination between individual γH2AX or 53BP1 foci (Fig. 3 and 4). The human skin fibroblasts used in the present study (representing a widely accepted model for studying normal tissue radiosensitivity)60 are naturally flat cells with a height of approximately 2.8 μm.61 We measured highly similar thicknesses of the nuclei of the cells (2.7–3.4 μm) (Fig. 3), which excluded their significant flattening during 3D fixation. At least 3 closely spaced γH2AX/53BP1 foci could be distinguished in the z-direction in cells irradiated with 11B or 20Ne ions. Hence, we were able to precisely examine the qualitative and quantitative characteristics of chromatin damage and DSB repair following exposure to different radiation types. The enhancement of DSB resolution in the 3D analysis compared with the 2D analysis is quantified in Fig. 4.We quantified the colocalization of γH2AX and 53BP1 foci at numerous times PI, ranging from 5 min PI to 96 h PI, to evaluate the kinetics of DSB repair. The maximum number of individual radiation-induced γH2AX/53BP1 foci per cell was observed between 30 min PI and 1 h PI, and the value was higher for samples exposed to both types of accelerated ions (11B: 24.0 ± 1.1, 20Ne: 23.9 ± 1.3) than for samples exposed to γ-rays (20.1 ± 0.5) (Fig. 5).
Additionally, the dynamics of foci formation and elimination differed with the radiation type. The fastest production of γH2AX/53BP1 foci upon irradiation was observed in cells irradiated with 20Ne, whereas the slowest production was observed in cells subjected to γ-rays. The opposite situation emerged for foci elimination. For cells exposed to both types of high-LET ions, the foci disappeared more slowly than in cells subjected to γ-rays. Four hours after irradiating the cells with 20Ne or 11B ions, approximately 85% of the maximum numbers of γH2AX/53BP1 foci persisted in the cells, whereas this fraction was only 41% for cells irradiated with γ-rays (Table 2). Moreover, although the γH2AX/53BP1 foci per cell decreased to approximately 1 focus (6% of the maximum) at 24 h PI in γ-irradiated cells, approximately 6 (26%) and 11 (45%) foci remained in cells damaged by 11B and 20Ne ions, respectively (Fig. 5 and Table 2). Consistent with this observation, preliminary data for cells exposed to another accelerated charged particle, 12C (LET = 9.8 keV μm−1, E = 500 MeV per n, D = 0.3 Gy), revealed a similar delay in DSB repair; only a small number of foci disappeared from cells within the first 4 h PI, and 16% of these foci persisted in cells at 24 h PI (data not shown).
| Radiation type | Time after irradiation | ||||
|---|---|---|---|---|---|
| 2 h | 4 h | 24 h | 48 h | 96 h | |
| Mean percent values of pooled data from two experiments (approximately 100 counted cells) are shown. The data were normalized to the peak numbers for each radiation type, i.e., the maximum number of foci scored for the particular radiation type, irrespective of the time PI. | |||||
| γ-Rays (60Co) | 75.2 | 41.1 | 6.3 | 6.2 | 6.3 |
| 11B | 87.7 | 84.7 | 26.4 | 10.6 | 7.1 |
| 20Ne | 97.9 | 85.7 | 45.1 | 22.8 | 15.1 |
Interestingly, despite the similar LET values for 11B and 20Ne ions and similar maximum numbers of γH2AX/53BP1 foci induced by these radiation types, both the elimination kinetics of γH2AX/53BP1 foci and their residual amounts measured at long periods of time (96 h) PI differed for these two radiation types. The number of γH2AX/53BP1 foci persisting at this period of time in cells irradiated with boron ions (1.7 foci per nucleus) decreased to values typical for γ-irradiated cells (1.3 foci per nucleus), but approximately 4 foci per nucleus persisted in cells exposed to 20Ne ions (Fig. 5). These values were significantly higher than sham-irradiated (control) cells, with 0.1 foci per nucleus on average. These results demonstrate that the irradiation of NHDF cells with both 20Ne and 11B high-LET ions (as well as 12C) delays the repair kinetics of DSBs compared with γ-rays, based on the persistence of γH2AX/53BP1 foci in cells during PI periods. Although this finding was expected according to current theoretical knowledge (see Discussion), the surprising observation is that neon ions caused significantly more severe damage than boron ions with a very similar LET value. Therefore, we characterized the DNA damage resulting from boron and neon in more detail (next sections).
3.2 γH2AX/53BP1 focus streaks induced by high-LET ions with similar LET values and their changes with time post-irradiation
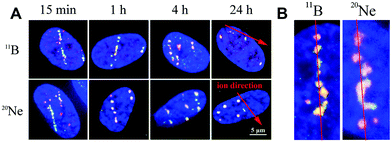
In contrast to individual DSBs dispersed throughout the whole volumes of nuclei upon γ-ray irradiation, the exposure of cells to high-LET ions produced γH2AX/53BP1 foci that were concentrated along the particle path (γH2AX/53BP1 focus streaks). We studied the morphology and dynamics of these streaks in cells irradiated at a sharp (10°) angle to the particle beam to maximize the resolution of separate foci using confocal microscopy. Doses of 1.0 and 1.2 Gy were used for 11B and 20Ne ions, respectively, to ensure that an average of 3 particles traversed the nucleus in both cases. As early as 5 min PI, the streaks of γH2AX and 53BP1 foci were detectable in cells and were mutually colocalized. At least three γH2AX/53BP1 foci were required to appear in a straight line parallel with the (known) direction of irradiating particles to be considered a streak. Streaks of both ions exhibited a grainy substructure and comprised closely spaced γH2AX/53BP1 foci with non-stained “gaps” (Fig. 6). Within 1 h PI, streaks exhibited fully developed structures and the particle trajectories across the cell nuclei were clearly identified. As expected, most cells contained 3 γH2AX/53BP1 focus streaks.Although the particles passed the nuclei along a linear path, some foci slightly deflected from this linear trajectory, particularly at longer periods of time PI (>2 h PI) (Fig. 6B). Beginning at 2 h PI, individual γH2AX/53BP1 foci in the streaks also began to disappear, indicating the on-going repair of some DSBs. However, 22 h later (24 h PI), approximately 40% and 30% of the nuclei that had been irradiated with neon and boron ions still contained focus streaks, with typically one streak in the nucleus (Fig. 6A). Within the next two days (96 h PI), all streaks had dissolved and only individual foci persisted in the nuclei. This observation highlights the successful repair of most DSBs and the existence of residual DNA damage. We also expect that seriously damaged cells died (see section 3.4), detached from the microscopic slides, and thus were undetectable in the confocal microscopy analyses.
3.3 Morphology of γH2AX/53BP1 foci as a function of radiation quality (evaluation of foci structure)
The γH2AX/53BP1 foci and focus streaks induced by high-LET boron and neon ions differed in morphology, specifically their sizes and shapes. Moreover, as described above, we recognized that some larger γH2AX/53BP1 foci (later referred as to the γH2AX/53BP1 clusters) comprised several smaller, closely spaced foci.Therefore, we also analysed γH2AX/53BP1 streaks in cells irradiated in the sharp-angle (10°) geometry prior to their spatial (3D) fixation in different periods of time PI to obtain more detailed insights (with better resolution power) into the morphology of γH2AX/53BP1 foci and compare the structure and complexity of their clusters following exposure to the radiation types studied here. We focused on the following parameters: (a) the size of γH2AX/53BP1 foci in the maximum images, (b) the circularity of γH2AX/53BP1 foci in the maximum images [4π*(area/perimeter2)], and (c) the complexity of γH2AX/53BP1 foci. All measurements were performed exactly as in the previous experiments with samples collected at 15 min and 1, 4, 24 and 96 h after irradiating cells with an average of 3 high-LET particles (1 Gy 11B and 1.2 Gy of 20Ne ions, respectively). Low-LET γ-rays administered at a dose of 1 Gy were used for comparison.
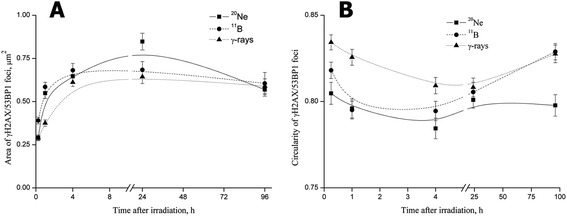
For all radiation types, the foci size rapidly increased beginning at 15 min PI, when the foci had not yet completely formed (Fig. 7A). The mean areas of γH2AX/53BP1 foci induced by boron ions and γ-rays subsequently rapidly increased to maximum levels at 4 h PI. Afterwards, the mean areas of foci, which were larger for boron ions and smaller for γ-rays, plateaued at the maximum (γ-rays) or slightly decreased (boron ions) by the end of the experiment (96 h PI). Interestingly, γH2AX/53BP1 foci induced by neon ions behaved differently, increasing to values markedly exceeding the maximum sizes measured for γ-rays or boron ions until 24 h (Fig. 7A). Afterwards, the size of 20Ne-induced foci also decreased slightly, reaching values comparable to the values measured for boron ions or γ-rays at the end of the experiment (96 h PI). Despite the differences in the growth dynamics and final area of the foci induced by 11B and 20Ne, we concluded that both high-LET ions evoked (a) the formation of DSB foci on a much more rapid timescale than low-LET γ-rays, and (b) these foci were also larger.
The second measured parameter, the circularity of γH2AX/53BP1 foci, also revealed significant quantitative differences between radiation types, reflecting their quality (Fig. 7B). Although the foci induced by γ-rays were mostly regular, with only small deviations from circularity, the foci showed marked irregularities in shape after neon and boron irradiation, leading to lower circularity values. Interestingly, the circularity of γH2AX/53BP1 foci changed over time PI, with the most prominent foci irregularity (deviation from the circularity) detected at 4 h PI for all radiation types. Specifically, we recognized three different profiles of changes in the circularity of the three radiation types studied (Fig. 7B). For γ-rays, the highest circularity was detected immediately after irradiation, after which it subsequently decreased and eventually returned to approximately the original values at the late (96 h PI) period PI. A similar profile was observed for neon ions, but both the initial (15 min PI) and the final (96 h PI) circularities were much lower than for γ-rays (and boron ions). Finally, for boron ions, the profile started with an intermediate initial circularity (lying between the values for neon ions and γ-rays) that decreased in the first hour PI, stagnated at lower values until 4 h PI, and subsequently started to increase, returning to the initial value at 24 h PI. However, in contrast to γ-rays and neon ions, the circularity of boron-induced foci increased compared with the initial value (measured upon irradiation) until it reached the value characteristic for γ-rays at 96 h PI.
The above-described analyses performed on the maximum images (2D superimpositions of individual confocal slices) clearly revealed the relationship between the radiation quality and morphology of γH2AX/53BP1 foci. Therefore, in the next step, we thoroughly analysed the spatiotemporal changes in foci morphology in the 3D space using individual consecutive confocal slices (0.25 μm-thick) from all 3D image stacks (25 slices per stack).
At all monitored periods of time PI (15 min to 96 h), fractions of foci comprising several smaller foci appeared for all radiation types studied (representative images are shown in Fig. 8A). The yields and complexity of these clusters of foci largely depended on the radiation quality and the period of time PI (Fig. 8B). As expected, clusters of γH2AX/53BP1 foci were rare upon exposure to low-LET γ-rays and these clusters exhibited low complexity: approximately 13% of foci appeared in clusters containing 2 (11%) or occasionally 3 foci (<2%). In contrast, one-half or almost three-quarters of all γH2AX/53BP1 foci formed clusters in cells irradiated with boron and neon ions, respectively. In both cases, the complexity and fraction of focus clusters increased with time; both parameters were elevated until 4 h PI and subsequently decreased. Within 15 min PI, only 19% and 36% of foci occurred in clusters after boron and neon irradiation, respectively, whereas these fractions reached 58% and 71%, respectively, at 4 h PI. At this time point, the focus clusters typically contained 2, 3 and 4 smaller foci; however, clusters comprising 5 to 8 foci were also detected, particularly in cells exposed to neon ions. Only insignificant changes in the focus cluster composition were observed between 4 and 24 h PI, followed by a marked reduction in both parameters, the foci complexity and proportion of focus clusters with a higher level of complexity, at 96 h PI. However, approximately 32% (boron ions) and 44% (neon ions) of foci were still located in clusters at that time point. In summary, neon ions induced the greatest incidence of the most complex clusters of foci. Compared with low-LET γ-rays and high-LET boron ions, a significantly greater proportion of γH2AX/53BP1 focus clusters persisted in the nuclei of cells exposed to high-LET neon ions, even at 96 h after irradiation (Fig. 8).
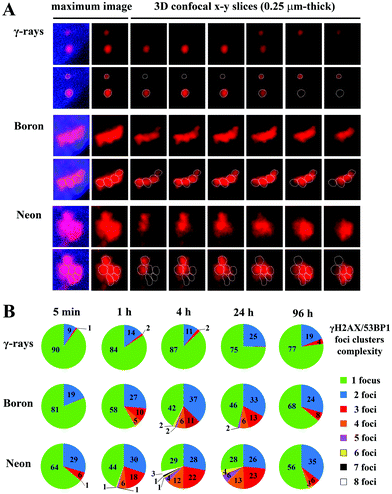 | ||
| Fig. 8 Comparison of the complexity of γH2AX/53BP1 focus clusters in spatially (3D) fixed NHDF-Neo fibroblasts irradiated with γ-rays, 20Ne ions, or 11B ions. The dose was 1.0 Gy for γ-rays, 1.0 Gy for boron ions, and 1.2 Gy for neon ions to ensure that an average of 3 particles traversed the nucleus in both high-LET radiation cases. Cells were irradiated in the sharp-angle (10°) geometry. (A) Representative γH2AX/53BP1 foci/focus clusters at the time period of their maximum complexity (4 h PI). The maximum (2D) images, shown on the left, comprise ∼25 confocal slices obtained with a z-step of 0.25 μm. Individual consecutive confocal slices through the γH2AX/53BP1 focus clusters (right columns) presented here subsequently show the composition of individual foci in the cluster and the ability to precisely describe their complexity. Only the 53BP1 signal is shown because this signal enables better discrimination of individual foci than the γH2AX signal. See Methods (chpt. 2.4) and Fig. 2 for details of the foci discrimination procedure. (B) The γH2AX/53BP1 foci complexity was quantitatively compared for the radiation types studied. For different periods of time PI, the percentages of γH2AX/53BP1 foci presented in clusters of a given complexity level are indicated. The mean values are calculated for pooled data from two experiments (>200 foci). | ||
3.4 Apoptosis induction after irradiation with γ-rays and boron particles
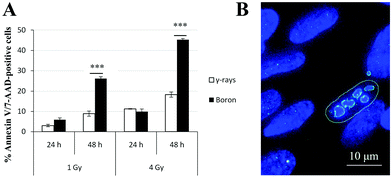
Based on the obtained results, the kinetics of γH2AX/53BP1 foci elimination were markedly slower and the complexity of foci was greater in cells irradiated with high-LET radiation types than in cells irradiated with γ-rays. Hence, we simultaneously quantified Annexin V- and 7-amino-actinomycin-positive irradiated cells using flow cytometry to determine whether these findings were also correlated with increased cell death. Because of limited beam time availability, only cells irradiated with boron ions and γ-rays were studied. The results for the two radiation types applied in two doses (1 Gy and 4 Gy) and scored at two different periods of time (24 h and 48 h) after irradiation are presented in Fig. 9. The values are expressed as the percentages of Annexin V-positive plus 7-AAD-positive or negative cells normalized to the background level in non-irradiated cells. For both the 1 and 4 Gy doses, similar apoptosis rates occurred for γ-rays and boron ions at 24 h PI, regardless of the different LET values for these radiation types. This finding strikingly contrasts with the situation observed at 48 h PI, when boron ions induced approximately 3-fold higher numbers of positive cells than γ-rays. This difference was particularly prominent for the higher dose of 4 Gy. For both radiation types, the number of apoptotic cells clearly depended on the dose.4 Discussion
To our knowledge, this study is the first to address the spatiotemporal aspects of DNA damage and repair after cells are exposed to different high-LET radiation types with similar low-energy and LET values. Previous experimental research on the biological effects of high-LET radiation types have primarily focused on ions with high energies (≥100 MeV per n), but results for low-energy (<50 MeV per n) ions are still rare. Moreover, the mutually compared radiation types (in the literature) have typically largely differed in energy or LET values, frequently by orders of magnitude.6,30,62 Although this experimental design enables useful analyses of DNA damage (or other biological endpoints) related to LET or radiation energy, large differences in these parameters mask possible effects of other radiation qualities. The mechanism by which different high-LET particles affect the DNA molecule under conditions of similar LET and energy values thus remains poorly understood. We evaluated the extent, spatiotemporal behaviour and repair of DSB damage in normal human neonatal dermal fibroblasts irradiated with either boron or neon ions that had been accelerated to similar lower energies and similar LET values (see Table 1) or γ-rays, a representative low-LET radiation, to address this current gap in knowledge.For many biological endpoints, the RBE increases with LET. However, for different radiation types, LET values oscillating between 100 and 200 keV μm−1 may correspond to the maximum RBE, depending on the physical parameters of the particle, cell type and biological endpoint studied.20–22,63 Alternatively, as shown in the present study, radiation types with similar LET values produce DNA damage with different complexities and spatiotemporal behaviours. Because increased DNA damage complexity was found to be correlated with slower DSB repair and increased cell death, our results confirm the hypothesis that the spatiotemporal characteristics of energy deposition and DNA damage, which cannot be simply described by LET, play a crucial role in determining the RBE of different radiation types.
Hence, micro-morphological analyses of DNA damage, as performed in the present study, significantly contribute to the current understanding of the mechanisms by which low-LET and high-LET radiation types kill cells and consequently the mystery of radiation RBE. To date, the knowledge in these areas is incomplete and optical microscopy approaches enabling detailed analyses of DSB damage under physiological conditions remain challenging.64 For example, recent works attempting to study DSB damage in cells exposed (90° geometry) to nitrogen ions (19.5 MeV per n, LET = 132 keV μm−1)65 or α particles (0.75 MeV per n, LET = 125 keV μm−1)66 using classical confocal microscopy failed to distinguish a substructure of γH2AX focus clusters, although they analysed cell nuclei in the 3D space. Therefore, various super-resolution ‘nanoscopy’ methods that increase the resolution power of optical microscopy up to several nanometres have high expectations.36,64,67 Unfortunately, studies taking advantage of optical super-resolution techniques remain rare and are extremely technically demanding (depending on the method); hence, studies have typically been limited to analyses of relatively small datasets.35,61,68 Electron microscopy offers a superior resolution power that enables the precise quantification of DSB complexity;38–40,69,70 however, the necessity of sample sectioning makes analyses of entire particle tracks in space and time difficult. Moreover, experimental artefacts might appear, reflecting (harmful) sample fixation steps, such as dehydration or freezing (reviewed by Winey et al.71).
Therefore, in the present study, we used dual-immunofluorescence high-resolution confocal microscopy on spatially (3D) fixed cells irradiated at a sharp angle.59 Based on this approach, we successfully visualized a detailed substructure of colocalized γH2AX and 53BP1 focus streaks along 11B and 20Ne particle tracks in situ and in large datasets. Selective scoring of colocalized γH2AX and 53BP1 foci improved the precision of these analyses and increased the probability of observing unrepaired DSBs, especially in later periods of time PI (see Methods, chapter 2.4 for explanation). The exclusion of cells with non-colocalizing signals (rare cases) also reduced the numbers of inefficiently immunostained cells and non-G1-cells52–54 included in the analyses (we studied non-synchronized cell populations to better reflect the situation in irradiated tissues; the cultures contained >80% G1 cells at the time of irradiation).
In contrast with the results reported by Costes et al.65 or Antonelli et al.,66 3D analyses of confocal image stacks performed in this study improved the detection of γH2AX/53BP1 (sub)foci by approximately 40% compared with a simple 2D analysis (see Fig. 4). Nevertheless, some potential and real limitations of the present study should be considered. First, cell fixation may influence chromatin structure. Therefore, we confronted the morphology of the cell nuclei (thickness and the maximal length vs. thickness ratio) of the fibroblasts (as a widely accepted model for exploring normal tissue radiosensitivity)60 after 3D fixation with the results of other studies.61,72,73 The measurements (nucleus thickness of approximately 2.7–3.4 μm) confirmed that the complexity of γH2AX/53BP1 focus clusters predominantly reflects the deposition of radiation energy, without a significant contribution of cell flattening. Indeed, closer approach of very tightly spaced γH2AX/53BP1 foci in the focus streaks of high-LET ions, potentially provoked by fixation-mediated cell flattening, would lead to overlapping foci and underestimation of focus cluster complexity, rather than to a dramatic increase in this parameter (e.g., because of fusions between foci located inside of and more distant from the main particle track). In any case, relative comparisons should be unaffected, as the same potential effect was detected for all cells.
Second, as previously reported by Jakob et al.,29 sharp-angle cell irradiation allowed us to substantially increase the resolution power; this strategy reduced limitations arising from fibroblast flatness and the insufficient resolution power of confocal microscopy in the vertical (z)-direction.74 To identify individual foci within clusters, we combined information on cluster morphology, fluorescence heat maps, and fluorescence intensity profiles along the paths intersecting putative foci in non-overexposed parts of the cluster (see Methods, Fig. 2). Although high precision of the spatiotemporal analysis was achieved, serious technical restrictions (low resolution power of confocal microscopy, leading to a certain amount of artificial overlap in complex arrangements of foci due to diffraction; reviewed in Waters74) as well as biological reality (spreading of H2AX phosphorylation over 1–2 Mb chromatin domains and overlapping signals) prevented the discrimination of individual DSBs in multiple lesions (≥2 DSBs within 1–2 helical turns). Hence, the precise boundaries and, thus, the numbers of very closely spaced DSB foci were only estimated. The biological nature of the complex γH2AX/53BP1 focus clusters observed in the present study and the precise numbers of DSBs present in γH2AX/53BP1 foci/focus clusters (in general) therefore remain uncertain and must be further studied. Several recent reports75–78 have suggested that super-resolution localization light microscopy offers an exciting but still challenging means of analysing the same biological specimens in parallel with confocal microscopy, but with much more detailed data. This strategy could be used to obtain answers to many questions discussed in this chapter in the near future.
Taking advantage of current approach, the microdosimetric complexity of γH2AX/53BP1 (DSB) repair foci differs not only for cells irradiated with low-LET γ-rays and high-LET radiation types, as expected, but also for cells irradiated with boron ions and neon ions, which have very similar LET and low-energy values. Mathematical modelling/simulations and novel ultra-sensitive immunogold-labelling transmission electron microscopy (TEM) provides clear evidence that high-LET radiation causes complex DSBs, and in contrast to low-LET radiation, the majority of γH2AX foci contain more than one DSB.32,38,39 As recently reviewed by Goodhead et al. (2015), approximately 20% (γ-rays) and 70% (high-LET ions) of DSB damage sites contain at least three DNA-chain breaks, according to simulations.7 Based on our direct measurements (1 h PI), approximately 16%, 42%, and 56% of γH2AX/53BP1 foci generated from γ-rays, boron ions, and neon ions, respectively, exist in clusters with additional foci. Nevertheless, these numbers were not able to be directly compared with other studies that typically quantify the proportion of simple foci to DSB clusters. In any case, consistent with previous findings,38,40,61 our 3D analysis revealed highly clustered (>3) γH2AX/53BP1 foci only after exposure to high-LET particles, whereas clusters observed after γ-irradiation comprised a maximum of two or occasionally (2%) three foci.
The difference between DSB complexity following the exposure of cells to γ-rays and high-LET ions (boron or neon) was primarily explained by the different characters of energy deposition (ionization density and distribution) by these radiation types. However, based on the present and previous results,24,67,79 we propose that not only the character of energy deposition per se but also the character of energy deposition in the context of higher-order chromatin structure80 (see Fig. 10F) significantly contributes to the increased complexity of DNA damage and RBE following exposure to high-LET radiation types. Specifically, high-LET radiation types attack condensed (hetero)chromatin, which contains a much higher density of potential DNA targets than decondensed (eu)chromatin, more efficiently than low-LET radiation types79 (reviewed in ref. 24 and 67). However, γ-rays preferentially damage low-density chromatin, since, in condensed (hetero)chromatin, more abundant (hetero)chromatin-binding proteins better shield the DNA from free radicals largely mediating the harmful effects of low-LET radiation. Therefore, it is important not only how, but also where the radiation energy is released in the cell nucleus (also see Fig. 10F).
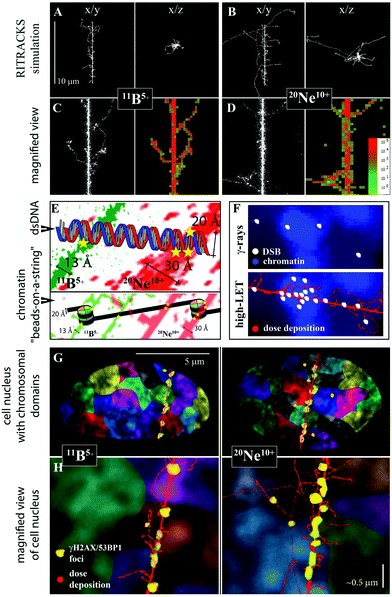 | ||
| Fig. 10 Relationships between radiation energy deposition, higher-order chromatin structure and DNA double-strand break induction for γ-rays and 11B and 20Ne ions (see Table 1 for radiation parameters). A, B. Simulations of 10 μm-long track structures for 11B and 20Ne ions using RITRACS software; the range and distribution of δ-electrons relative to the track core can be observed in x/y and x/z projections. C, D. Detailed views along the tracks, with emphasis on the core structure. Free radical tracks (left panel) are shown together with dose deposition tracks (right panels). Dose deposition decreases from red to green, as indicated. The simulations show that δ-electrons penetrate deeper with neon ions, while they are more concentrated along the track core with boron ions. Nevertheless, the combined action of the neon particle itself plus low-energy electrons (that do not escape from the track core) generates a thick track core, approximately twice as thick as the boron ion. E. Compared with 11B ions, a wider track core of 20Ne ions (which is still highly concentrated compared, for example, to particles of high energy) directly damages both strands of the DNA molecule with a higher probability/frequency. Moreover, 20Ne ions can more easily attack both DNA turns around the nucleosome at the same time (bottom image). Chromatin is shown at the organization level of “beads-on-a-string” for simplification. F. Relationships between dose deposition, higher-order chromatin structure and DSB induction. γ-rays (top image) induce DSBs randomly across the cell nucleus, with euchromatin being more sensitive than heterochromatin to free radicals (which largely mediate harmful effects of low-LET radiation), since heterochromatin is better protected by larger amounts of (hetero)chromatin-binding proteins.24,64,79 In contrast, high-LET radiation (bottom image) deposits energy in a concentrated manner along the particle track, which causes DNA damage that cannot be prevented by the chromatin structure. Condensed (hetero)chromatin provides more DNA targets per volume unit and is therefore more seriously damaged (fragmented) by high-LET particles.64 G, H. Relationships between the character of energy deposition, higher-order chromatin structure, and induction of chromosomal aberrations. The dose deposition (red) simulated for 11B and 20Ne ions by the RITRACKS code is overlaid onto the cell nucleus, with schematically illustrated chromosomal territories (various colours) and γH2AX/53BP1 foci (yellow). A slightly greater complexity of γH2AX/53BP1 foci in cells irradiated with 20Ne ions (compared with 11B ions) is indicated by their larger size. The higher-order chromatin structure is shown via DAPI staining (condensed chromatin is intensively stained). Both ions and kick-off electrons of low energy generate extensive damage along the particle path and thus complex chromosomal aberrations. In addition, 20Ne ions emit longer-range δ-electrons than 11B ions (panel A vs. B). These electrons radiate to sufficient distances from the track core to cause DSBs in the neighbouring chromosomal territories; nevertheless, these DSBs may still be sufficiently close to interact with DSBs along the particle core, particularly if we consider the chromatin fragmentation and decondensation caused by irradiation and the associated, though limited, chromatin movement. Typically, damaged chromatin (labelled with 53BP1-GFP in living cells) is displaced at a distance of approximately 1 μm in cells irradiated with accelerated ions, but the displacement of <2% foci occasionally exceeds 5 μm in the 12 h interval after Ni irradiation.93 Therefore, we propose that chromosomal aberrations formed with 20Ne ions may involve more chromosomes than those that appear with 11B ions, and their complexity in terms of the number of DNA breaks can be higher, as shown in the present study. Consider that human skin fibroblasts are flat cells (as shown on the image), and even more chromosomal territories may participate in chromosomal aberrations in spherical cells.17,94,95 Panel H: Section of panel G magnified approximately 10 times. Scale bar, approximately 0.5 μm (schematic illustration). | ||
The complexity of DSBs was inversely correlated with the disappearance of γH2AX/53BP1 foci from the cell nuclei, i.e., the kinetics and efficiency of DSB repair, and cell survival. Consistent with some earlier reports,31,61,64,66,79–81 simple (and on principle frequently euchromatic79) γH2AX/53BP1 foci generated by γ-rays were largely eliminated within the first (4 h) hours PI in the present study. Similar findings of the rapid repair and disappearance of non-clustered (smaller) individual γH2AX/53BP1 foci were observed in cells irradiated with high-LET ions (11B and 20Ne). However, large γH2AX/53BP1 foci, and particularly clusters of these foci, were repaired with difficulty irrespective of their origin in euchromatin or heterochromatin, and they persisted in the cell nuclei for much longer periods of 1 day (11B) or more (20Ne) after irradiation. For 20Ne ions that produced the most complex DSB lesions in this study, approximately 3/4 of DSB foci persisting at 24 h PI formed clusters. These results precisely correspond to an interesting study by Jakob et al.,48 who observed the slower repair of DSBs generated by carbon ions than of DSBs produced by γ-rays, and this delayed repair was even higher for heterochromatin-associated damage. Based on the evidence obtained in this and previous studies, we conclude that both DSB complexity and the chromatin environment surrounding DSBs significantly influence the repair of initially formed lesions (appearing as a consequence of energy deposition), which at least partially explains the higher RBE of high-LET ions.
The average complexity of clusters and number of clusters per cell gradually increased with time PI and started to decrease only after 24 h PI. This scenario suggests the gradual processing of less complex and individual DSBs within the clusters61 and highlights the long-term persistence of complex DSB clusters. An alternative, but not mutually exclusive possibility is that these repair kinetics may reflect the formation of DSB focus clusters over a longer time post-irradiation, due to chromatin movement provoked by DSB repair processes, as described below. The cells with unrepeatable DSB clusters (of either origin) are expected to die or undergo mutagenesis at later periods of time PI. Indeed, a much higher proportion of cells underwent apoptosis following irradiation with boron ions (almost 50% of cells exposed to a 4 Gy dose) compared with γ-rays (less than 20% of cells exposed to a 4 Gy dose), indicating that (a) DSBs produced by high-LET ions are repaired but only with difficulty and (b) the proportions of cells with complex γH2AX/53BP1 foci and the complexity of persistent DSBs at >24 h PI may be even greater than reported here (because the seriously damaged cells died, detached from the microscopic slides and escaped detection).
Moreover, concerning the long period of time examined post-irradiation (up to 96 h PI), a proportion of cells may also die due to mitotic catastrophe, since as was only recently shown,61,82 even cells with relatively high numbers (e.g., 10–15) of DSBs can enter mitosis under some circumstances. These conclusions are consistent with the combined results of previous studies of carbon and ferrous ions.38,39,61
Finally, we cannot exclude the possibility that previously repaired cells may overpopulate cells still harbouring damage and, thus, further decrease the average number of foci per nucleus observed in later time periods PI. Since the critical level of DSBs (<10–20)82 allowing cells to enter mitosis is reached more rapidly (within approximately 4 h PI) using γ-rays than using both high-LET ions (>24 h PI), this effect may eventually lead to underestimation of DSBs, especially in γ-irradiated cells. However, any significant effect of cell division on DSB repair kinetics and differences in such effects between the different types of radiation studied are unlikely since (a) only a small fraction of fibroblasts were dividing; (b) only background DSB numbers were detected in γ-irradiated cells at 24 h PI (and this number plateaued at later times); and (c) the most prominent differences in DSB repair kinetics were observed at PI times <4 h. We also calculated the average numbers of γH2AX/53BP1 foci per nucleus specifically in γH2AX/53BP1-positive cells (not shown), which resulted in the same trends/conclusions obtained from analyses performed for whole cell populations (γH2AX-positive + γH2AX-negative cells). Moreover, most cells exposed to γ-rays contained <20 DSB (mean = approximately 10 DSBs) foci per nucleus at 4 h PI, and damaged cells could therefore theoretically also undergo mitosis, similar to undamaged cells.
An additional level of DSB complexity that negatively influences DSB repair may paradoxically appear as a side effect of repair processes per se. First, the processing of complex (even non-DSB) lesions directly generates secondary DSBs.83,84 Second, the heterochromatin structure has consistently been reported to represent a barrier to DNA repair and thus DSBs in condensed heterochromatin are repaired but only with difficulty, with slower kinetics and lower efficiency than DSBs in euchromatin.38–40,48,79,85 The repair of heterochromatic DSBs requires extensive (hetero)chromatin decondensation, which in turn locally mobilizes damaged chromatin domains to some extent.25,81,86,87 This increased mobility of heterochromatic DSBs can result in collisions of two or more DSBs and the formation of secondary DSB clusters (the term ‘secondary’ distinguishes these clusters from the ‘primary’ clusters discussed above, which are directly formed by high-LET particles due to localized energy deposition). Although this phenomenon occurs occasionally upon irradiation with γ-rays, its importance has dramatically increased for cells exposed to high-LET radiation types, in which the local chromatin structure is highly fragmented and DSBs are concentrated along a relatively thin particle path, i.e., located in close proximity to one another. Indeed, the secondary DSB clusters observed after high-LET irradiation are in fact frequently higher order clusters comprising primary DSB clusters.67,85
Consistent with this scenario, we observed deflections of some foci from otherwise linear particle tracks and these ‘mobile’ foci mostly occurred at the border between condensed (hetero)chromatin and decondensed (eu)chromatin domains. The protrusion of heterochromatic DSBs into decondensed (eu)chromatin has also been reported in other studies upon high-LET26,48 and low-LET81,86,88 irradiation (reviewed by Falk et al.;24 Chiolo et al.89). Moreover, the highest numbers of clusters were detected between 4 and 24 h, i.e., when the DSB repair of non-complex lesions is mostly complete. During this PI period, the clusters also showed the greatest irregularity and complexity, with 2 to 5 smaller foci per cluster observed in boron-irradiated cells and up to 8 foci observed in neon-irradiated cells. Together, these results highlight the problematic spatiotemporal stabilization of complex γH2AX/53BP1 focus clusters, particularly in the initial phase and most active period of DSB repair. Conceivably, after high-LET irradiation, simultaneous chromatin fragmentation and dispersion supported by chromatin decondensation occurring in the frame of repair processes locally mobilize chromatin to a much greater extent than in cells exposed to low-LET γ-rays. This phenomenon dramatically increases the complexity of DSB lesions and the risk of repair errors or failure. Finally, these observations demonstrate that two phenomena – energy deposition, leading to primary chromatin fragmentation, and DNA repair, provoking secondary chromatin decondensation – contribute to (restricted) chromatin movement and formation of (complex/multiple) DSB clusters and chromosomal aberrations in cells exposed to high-LET ions.
The greater complexity and delayed repair of DSB lesions induced by neon ions compared with that induced by boron ions, which was observed in our morphological and kinetic studies, is harder to explain than the differences between high-LET and low-LET types of radiation. For low radiation energies, the δ-electrons emitted by the transversing particle are expected to significantly damage DNA inside or close to the track core since they do not have sufficient energy to escape. Consistently, for both boron and neon ions, we observed only occasional γH2AX/53BP1 foci (more frequent for neon ions) that were attributed to the activity of δ-electrons at sites located outside of γH2AX/53BP1 focus streaks. In the proximity of the track core, some large γH2AX/53BP1 foci diverged from the linearity of the streaks, in addition to small γH2AX/53BP1 foci produced by δ-electrons (see Fig. 6); these objects likely correspond to complex foci relocated from the track core or increased energy deposition at the ends of δ-electron tracks.90–92 Whether δ-electron ends can generate DSBs with a sufficient density to form multiple DSBs is unclear;90–92 in any case, such DSB clusters would be less complex than clusters inside the track core. Hence, based on the relatively large size of observed out-of-line foci and the gradually decreasing linearity of the particle tracks with the PI period, we consider the first scenario to be more likely/important. The track core therefore probably plays a crucial role in influencing the characteristics of DSB damage under the conditions of the present study, although long-range δ-electrons may also influence characteristics such as the complexity of chromosomal aberrations (see Fig. 10).
Therefore, we complemented our experiments with theoretical calculations on the track core (as described by Chatterjee, 1993,57 see the Methods) to determine potential factors that may explain why neon ions induce DNA damage of greater complexity than boron ions. The results revealed a core radius of only 13 Å for boron ions but 30 Å for neon ions. An approximately two-times wider track “core” for 20Ne ions was also observed in RITRACKS simulations (Fig. 10). Based on these results, we propose that neon ions generate a wider particle track core that is better able to cause complex DNA (DSB) lesions than the thinner track core of boron ions. This conclusion is not in disagreement with the findings of Saha et al. (2014),30 who associated a thinner track of low-energy ions (more concentrated energy deposition) with more efficient DNA damage induction than was associated with a wider track of high-energy ions – the tracks of the 11B and 20Ne ions used here are both much thinner than the tracks of high-energy ions.
The proposed relationships between the particle track structures of 11B and 20Ne ions, the higher-order chromatin architecture and the formation of (complex) DSBs and chromosomal aberrations (discussed here as the endpoint of irradiation most directly related to DSB induction) are illustrated in Fig. 10. Briefly, both high-LET ions (11B and 20Ne) and kick-off electrons of low energy generate extensive damage along the particle track core, which leads to complex chromosomal aberrations that may involve chromosomes whose (interphase) territories are intersected by the particle. A wider but still highly focused (dense energy deposition) track core of 20Ne ions can more efficiently induce DSBs than too narrow track core of 11B ions. In addition, 20Ne ions emit longer-range δ-electrons than 11B ions. These electrons radiate to sufficient distances from the track core and may cause numerous DSBs, mostly at the end of their tracks, i.e., in neighbouring (more distant) chromosomal territories. Nevertheless, these DSBs may be still sufficiently close to interact with DSBs along the particle core, particularly if we consider the chromatin fragmentation and decondensation caused by irradiation and the associated, though limited, chromatin movement. Typically, damaged chromatin (labelled with 53BP1-GFP in living cells) may be displaced by a distance of approximately 1 μm in cells irradiated with accelerated ions, although relocation occasionally (<2% foci) exceeds 5 μm during the 12 h interval after high-LET nickel ion exposure.93 Therefore, we propose that chromosomal aberrations formed with 20Ne ions may involve more chromosomes than appear in association with 11B ions, and their complexity in terms of the number of DNA breaks can be higher, as shown in the present study (Fig. 10G and H; note that more chromosomal territories may participate in chromosomal aberrations in spherical cells than in flat fibroblasts).17,94,95 Nevertheless, this hypothesis remains to be experimentally confirmed.
Moreover, the radiation types used in the present study differed in particle charge (20Ne = 10+, 11B = 5+), which was not considered in our calculations. Because the higher charge of Ne ions is reasonably expected to influence the microdosimetric distribution of ionization and thus significantly contribute to the track (core) structure,96,97 we can hypothesize that it also increases DNA damage complexity under conditions of similar LET and energy values for different radiation types. However, the physical quality of the particle, which primarily determines the characteristics of DNA damage under conditions of similar LET and energy values for the radiation types, should be further investigated.
The γH2AX/53BP1 foci/focus clusters generated by boron and neon ions and γ-rays differed not only in complexity but also in structural parameters and spatiotemporal behaviours. Neon ions provoked the most rapid formation of γH2AX/53BP1 foci in irradiated cells and neon ions also induced the largest and most irregular foci (the lowest circularity). The results for boron ions were generally more similar to neon ions than to γ-rays. Faster formation of DSB foci in cells irradiated with high-LET ions compared with low-LET γ-rays is not unprecedented in radiobiology,34,93 but negative observations65,98 leave the question open. We postulate that chromatin fragmentation by high-LET radiation types opens damaged chromatin sites for DSB sensors and repair factors, which is manifested in rapid focus formation, occurring faster and to greater extent than fragmentation induced by γ-rays. Alternatively, but not mutually exclusively, clustered DSBs (together with factors such as high local concentrations of radicals), which represent a serious threat to genome integrity, may induce a more severe shock to the cells than a comparable, or even higher, level of spatially separated DSBs, and the repair systems are therefore activated faster or at a higher level. Finally, reflecting the character of energy deposition (highly localized vs. dispersed, with high-LET and low-LET radiation, respectively), primary DSB clusters generated by high-LET ions appear in cells immediately following irradiation, whereas the formation of occasional secondary clusters induced by γ-rays requires additional time. As previously discussed, primary clusters originate from physico-chemical processes occurring immediately after irradiation, while secondary clusters form later, as a consequence of restricted chromatin movement provoked by DNA repair;25,26,79 reviewed in Falk et al. (2014).64 Based on the results from the present study, the complexity of DNA damage influences the speed of DSB recognition or γH2AX/53BP1 foci formation.
In summary, different particles with similar LET and energy values induce DSB damage with different microdosimetric (spatiotemporal) characteristics that are correlated with the efficiency of DSB repair and cell survival. We propose that the extent and character of DSBs induced by radiation types with similar LET and energy values critically depend on the particle track core diameter. However, the physical quality of the particle that primarily dictates this diameter requires further study. Hence, not only the physical characteristics of radiation types but also the spatiotemporal features and behaviours of induced DNA damage should be considered in future radiotherapy studies and investigations of the effects/risks of space missions.
Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
The authors thank Y. G. Teterev and A. A. Bezbakh from the Flerov Laboratory of Nuclear Reactions (JINR) and G. N. Timoshenko and V. A. Krylov from the Laboratory of Radiation Biology (JINR) for exposing the cells to radiation with accelerated heavy ions using the U400M cyclotron and V. N. Gaevskiy from the Dzhelepov Laboratory of Nuclear Problems (JINR) for performing the gamma irradiation using the Rokus-M unit.The work was supported by grants from the Czech Republic to the Joint Institute for Nuclear Research, Dubna (Projects of the Czech Plenipotentiary and the 3 + 3 Projects), the Czech Science Foundation (project 16-12454S), and the Ministry of Health of the Czech Republic (AZV grant no. 16-29835A, all rights reserved).
References
- S. Moore, F. K. T. Stanley and A. A. Goodarzi, DNA Repair, 2014, 17, 64–73 CrossRef CAS PubMed.
- E. Sage and N. Shikazono, Free Radicals Biol. Med., 2016, 107, 125–135 CrossRef PubMed.
- Z. Nikitaki, V. Nikolov, I. V. Mavragani, E. Mladenov, A. Mangelis, D. A. Laskaratou, G. I. Fragkoulis, C. E. Hellweg, O. A. Martin, D. Emfietzoglou, V. I. Hatzi, G. I. Terzoudi, G. Iliakis and A. G. Georgakilas, Free Radical Res., 2016, 50, S64–S78 CrossRef PubMed.
- R. Okayasu, Int. J. Cancer, 2012, 130, 991–1000 CrossRef CAS PubMed.
- F. A. Cucinotta, H. Nikjoo and D. T. Goodhead, Radiat. Res., 2000, 153, 459–468 CrossRef CAS PubMed.
- D. M. Sridharan, L. J. Chappell, M. K. Whalen, F. A. Cucinotta and J. M. Pluth, Radiat. Res., 2015, 184, 105–119 CAS.
- D. T. Goodhead, Radiat. Prot. Dosim., 2015, 166, 276–281 CrossRef CAS PubMed.
- M. Suzuki, C. Tsuruoka, T. Kanai, T. Kato, F. Yatagai and M. Watanabe, Biol. Sci. Space., 2003, 17, 302–306 CrossRef PubMed.
- C. Tsuruoka, M. Suzuki and K. Fujitaka, Biol. Sci. Space, 2004, 18, 188–189 Search PubMed.
- T. Takatsuji, I. Yoshikawa and M. S. Sasaki, J. Radiat. Res., 1999, 40, 59–69 CrossRef CAS PubMed.
- M. Niemantsverdriet, M.-J. van Goethem, R. Bron, W. Hogewerf, S. Brandenburg, J. A. Langendijk, P. van Luijk and R. P. Coppes, Int. J. Radiat. Oncol., Biol., Phys., 2012, 83, 1291–1297 CrossRef CAS PubMed.
- H. Tauchi, S. Endo, K. Eguchi-Kasai, Y. Furusawa, M. Suzuki, S. Matsuura, K. Ando, N. Nakamura, S. Sawada and K. Komatsu, J. Radiat. Res., 1999, 40 Suppl, 45–52 CrossRef CAS PubMed.
- Y. Kazama, K. Ishii, T. Hirano, T. Wakana, M. Yamada, S. Ohbu and T. Abe, Plant J., 2017, 38, 42–49 Search PubMed.
- P. Bláha, N. A. Koshlan, I. V. Koshlan, D. V. Petrova, Y. V. Bogdanova, R. D. Govorun, V. Múčka and E. A. Krasavin, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2017, 803–805, 35–41 CrossRef PubMed.
- F. Yatagai, Biol. Sci. Space, 2004, 18, 224–234 CrossRef PubMed.
- R. M. Anderson, D. L. Stevens, N. D. Sumption, K. M. S. Townsend, D. T. Goodhead and M. A. Hill, Radiat. Res., 2007, 167, 541–550 CrossRef PubMed.
- H. A. Foster, G. Estrada-Girona, M. Themis, E. Garimberti, M. A. Hill, J. M. Bridger and R. M. Anderson, Mutat. Res., Genet. Toxicol. Environ. Mutagen., 2013, 756, 66–77 CrossRef CAS PubMed.
- S. Ritter, E. Nasonova and E. Gudowska-Novak, Int. J. Radiat. Biol., 2002, 78, 191–202 CrossRef CAS PubMed.
- I. Testard, B. D. X. Utrillau and L. Sabatier, Int. J. Radiat. Biol., 1997, 72, 423–433 CrossRef CAS PubMed.
- K. A. M. Suzuki, Y. Kase, H. Yamaguchi and T. Kanai, Int. J. Radiat. Oncol., Biol., Phys., 2000, 48, 241–250 CrossRef.
- J. Kiefer, P. Schmidt and S. Koch, Radiat. Res., 2001, 156, 607–611 CrossRef CAS PubMed.
- M. C. Joiner, in Basic Clinical Radiobiology, ed. M. Joiner and A. van der Kogel, Hodder Arnold, 338 Euston Road, London, NW1 3BH, Great Britain, 4th edn, 2009, pp. 68–77 Search PubMed.
- J. A. Aten, J. Stap, P. M. Krawczyk, C. H. van Oven, R. A. Hoebe, J. Essers and R. Kanaar, Science, 2004, 303, 92–95 CrossRef CAS PubMed.
- M. Falk, E. Lukasova and S. Kozubek, Mutat. Res., 2010, 704, 88–100 CAS.
- M. J. Kruhlak, A. Celeste, G. Dellaire, O. Fernandez-Capetillo, W. G. Müller, J. G. McNally, D. P. Bazett-Jones and A. Nussenzweig, J. Cell Biol., 2006, 172, 823–834 CrossRef CAS PubMed.
- B. Jakob, J. Splinter and G. Taucher-Scholz, Radiat. Res., 2009, 171, 405–418 CrossRef CAS PubMed.
- E. P. Rogakou, D. R. Pilch, A. H. Orr, V. S. Ivanova and W. M. Bonner, J. Biol. Chem., 1998, 273, 5858–5868 CrossRef CAS PubMed.
- E. P. Rogakou, C. Boon, C. Redon and W. M. Bonner, J. Cell Biol., 1999, 146, 905–916 CrossRef CAS PubMed.
- B. Jakob, M. Scholz and G. Taucher-Scholz, Radiat. Res., 2003, 159, 676–684 CrossRef CAS PubMed.
- J. Saha, P. Wilson, P. Thieberger, D. Lowenstein, M. Wang and F. A. Cucinotta, Radiat. Res., 2014, 182, 282–291 Search PubMed.
- A. Asaithamby, N. Uematsu, A. Chatterjee, M. D. Story, S. Burma and D. J. Chen, Radiat. Res., 2008, 169, 437–446 CrossRef CAS PubMed.
- G. Du, G. A. Drexler, W. Friedland, C. Greubel, V. Hable, R. Krücken, A. Kugler, L. Tonelli, A. A. Friedl and G. Dollinger, Radiat. Res., 2011, 176, 706–715 CrossRef CAS PubMed.
- O. A. Sedelnikova, D. R. Pilch, C. Redon and W. M. Bonner, Cancer Biol. Ther., 2003, 2, 233–235 CrossRef CAS PubMed.
- S. V. Costes, A. Ponomarev, J. L. Chen, D. Nguyen, F. A. Cucinotta and M. H. Barcellos-Hoff, PLoS Comput. Biol., 2007, 3, e155 CrossRef PubMed.
- R. Lopez Perez, G. Best, N. H. Nicolay, C. Greubel, S. Rossberger, J. Reindl, G. Dollinger, K.-J. Weber, C. Cremer and P. E. Huber, FASEB J., 2016, 30, 2767–2776 CrossRef PubMed.
- Y. Zhang, G. Máté, P. Müller, S. Hillebrandt, M. Krufczik, M. Bach, R. Kaufmann, M. Hausmann and D. W. Heermann, PLoS One, 2015, 10, e0128555 Search PubMed.
- M. Falk, Biophys. J., 2016, 110, 872–873 CrossRef CAS PubMed.
- Y. Lorat, C. U. Brunner, S. Schanz, B. Jakob, G. Taucher-Scholz and C. E. Rübe, DNA Repair, 2015, 28, 93–106 CrossRef CAS PubMed.
- Y. Lorat, S. Timm, B. Jakob, G. Taucher-Scholz and C. E. Rübe, Radiother. Oncol., 2016, 121, 154–161 CrossRef CAS PubMed.
- C. E. Rübe, Y. Lorat, N. Schuler, S. Schanz, G. Wennemuth and C. Rübe, DNA Repair, 2011, 10, 427–437 CrossRef PubMed.
- F. Tommasino, E. Scifoni and M. Durante, Int. J. Part. Ther., 2015, 2, 428–438 CrossRef.
- E. C. Halperin, Lancet Oncol., 2006, 7, 676–685 CrossRef CAS PubMed.
- M. Wang, J. Saha and F. A. Cucinotta, Mutat. Res., Genet. Toxicol. Environ. Mutagen., 2013, 756, 108–114 CrossRef CAS PubMed.
- A. L. Ponomarev and F. A. Cucinotta, Radiat. Meas., 2006, 41, 1075–1079 CrossRef CAS.
- W. Friedland, E. Schmitt, P. Kundrát, M. Dingfelder, G. Baiocco, S. Barbieri and A. Ottolenghi, Sci. Rep., 2017, 7, 45161 CrossRef CAS PubMed.
- W. E. Wilson and T. L. Criswell, Adv. Space Res., 1986, 6, 75–81 CrossRef CAS PubMed.
- N. Hamada, J. Radiat. Res., 2009, 50, 1–9 CrossRef PubMed.
- B. Jakob, J. Splinter, S. Conrad, K.-O. Voss, D. Zink, M. Durante, M. Lobrich and G. Taucher-Scholz, Nucleic Acids Res., 2011, 39, 6489–6499 CrossRef CAS PubMed.
- A. A. Bezbakh, V. B. Zager, G. Kaminski, A. I. Krylov, V. A. Krylov, Y. G. Teterev and G. N. Timoshenko, Phys. Part. Nucl. Lett., 2013, 10, 175–178 CrossRef.
- O. B. Tarasov and D. Bazin, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 376, 185–187 CrossRef CAS.
- P. Matula, M. Maška, O. Daněk, P. Matula and M. Kozubek, in IEEE International Symposium on Biomedical Imaging, IEEE, 2009, pp. 1138–1141 Search PubMed.
- J. M. Daley and P. Sung, Mol. Cell. Biol., 2014, 34, 1380–1388 CrossRef PubMed.
- S. Pellegrino, J. Michelena, F. Teloni, R. Imhof and M. Altmeyer, Cell Rep., 2017, 19, 1819–1831 CrossRef CAS PubMed.
- A. J. Nakamura, V. A. Rao, Y. Pommier and W. M. Bonner, Cell Cycle, 2010, 9, 389–397 CrossRef CAS PubMed.
- W. S. Rasband, ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, 1997–2016, https://imagej.nih.gov/ij/ Search PubMed.
- T. R. Jones, I. Kang, D. B. Wheeler, R. A. Lindquist, A. Papallo, D. M. Sabatini, P. Golland and A. E. Carpenter, BMC Bioinf., 2008, 9, 482 CrossRef PubMed.
- A. Chatterjee and W. R. Holley, Adv. Radiat. Biol., 1993, 17, 181–226 CrossRef CAS PubMed.
- A. Asaithamby and D. J. Chen, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2011, 711, 87–99 CrossRef CAS PubMed.
- M. Hofer, M. Falk, D. Komůrková, I. Falková, A. Bačíková, B. Klejdus, E. Pagáčová, L. Štefančíková, L. Weiterová, K. J. Angelis, S. Kozubek, L. Dušek and Š. Galbavý, J. Med. Chem., 2016, 59, 3003–3017 CrossRef CAS PubMed.
- S. Tenhumberg, E. Gudowska-Nowak, E. Nasonova and S. Ritter, Int. J. Radiat. Biol., 2007, 83, 501–513 CrossRef CAS PubMed.
- N. I. Nakajima, H. Brunton, R. Watanabe, A. Shrikhande, R. Hirayama, N. Matsufuji, A. Fujimori, T. Murakami, R. Okayasu, P. Jeggo and A. Shibata, PLoS One, 2013, 8, e70107 CAS.
- D. M. Sridharan, A. Asaithamby, S. M. Bailey, S. V. Costes, P. W. Doetsch, W. S. Dynan, A. Kronenberg, K. N. Rithidech, J. Saha, a. M. Snijders, E. Werner, C. Wiese, F. A. Cucinotta and J. M. Pluth, Radiat. Res., 2015, 183, 1–26 CrossRef CAS PubMed.
- D. T. Goodhead, J. Radiat. Res., 1999, 40(Suppl), 1–13 CAS.
- M. Falk, M. Hausmann, E. Lukasova, A. Biswas, G. Hildenbrand, M. Davidkova, E. Krasavin, Z. Kleibl, I. Falkova, L. Jezkova, L. Stefancikova, J. Sevcik, M. Hofer, A. Bacikova, P. Matula, A. Boreyko, J. Vachelova, A. Michaelidesova and S. Kozubek, Crit. Rev. Eukaryotic Gene Expression, 2014, 24, 225–247 CrossRef CAS.
- S. V. Costes, A. Boissière, S. Ravani, R. Romano, B. Parvin and M. H. Barcellos-Hoff, Radiat. Res., 2006, 165, 505–515 CrossRef CAS PubMed.
- F. Antonelli, A. Campa, G. Esposito, P. Giardullo, M. Belli, V. Dini, S. Meschini, G. Simone, E. Sorrentino, S. Gerardi, G. A. P. Cirrone and M. A. Tabocchini, Radiat. Res., 2015, 183, 417–431 CrossRef CAS PubMed.
- M. Falk, M. Hausmann, E. Lukasova, A. Biswas, G. Hildenbrand, M. Davidkova, E. Krasavin, Z. Kleibl, I. Falkova, L. Jezkova, L. Stefancikova, J. Sevcik, M. Hofer, A. Bacikova, P. Matula, A. Boreyko, J. Vachelova, A. Michaelidesova and S. Kozubek, Crit. Rev. Eukaryotic Gene Expression, 2014, 24, 205–223 CrossRef CAS.
- J. Reindl, G. A. Drexler, S. Girst, C. Greubel, C. Siebenwirth, S. E. Drexler, G. Dollinger and A. A. Friedl, Phys. Biol., 2015, 12, 66005 CrossRef PubMed.
- Y. Lorat, S. Schanz, N. Schuler, G. Wennemuth, C. Rübe and C. E. Rübe, PLoS One, 2012, 7, e38165 CAS.
- Y. Lorat, S. Schanz and C. E. Rübe, Clin. Cancer Res., 2016, 22, 5300–5311 CrossRef PubMed.
- M. Winey, J. B. Meehl, E. T. O'Toole and T. H. Giddings, Mol. Biol. Cell, 2014, 25, 319–323 CrossRef PubMed.
- A. Bolzer, G. Kreth, I. Solovei, D. Koehler, K. Saracoglu, C. Fauth, S. Müller, R. Eils, C. Cremer, M. R. Speicher and T. Cremer, PLoS Biol., 2005, 3, e157 Search PubMed.
- D.-H. Kim, B. Li, F. Si, J. M. Phillip, D. Wirtz and S. X. Sun, J. Cell Sci., 2016, 129, 457–457 CrossRef CAS PubMed.
- J. C. Waters, J. Cell Biol., 2009, 185, 1135–1148 CrossRef CAS PubMed.
- M. Hausmann, N. Ilić, G. Pilarczyk, J.-H. Lee, A. Logeswaran, A. Borroni, M. Krufczik, F. Theda, N. Waltrich, F. Bestvater, G. Hildenbrand, C. Cremer and M. Blank, Int. J. Mol. Sci., 2017, 18, 2066 CrossRef PubMed.
- M. Krufczik, A. Sievers, A. Hausmann, J.-H. Lee, G. Hildenbrand, W. Schaufler and M. Hausmann, Int. J. Mol. Sci., 2017, 18, 1005 CrossRef PubMed.
- J. P. Eberle, A. Rapp, M. Krufczik, M. Eryilmaz, M. Gunkel, H. Erfle and M. Hausmann, Methods Mol. Biol., 2017, 1663, 1–13 Search PubMed.
- M. Bach, C. Savini, M. Krufczik, C. Cremer, F. Rösl and M. Hausmann, Int. J. Mol. Sci., 2017, 18, 1726 CrossRef PubMed.
- M. Falk, E. Lukášová and S. Kozubek, Biochim. Biophys. Acta, Mol. Cell Res., 2008, 1783, 2398–2414 CrossRef CAS PubMed.
- S. Kozubek, E. Lukásová, P. Jirsová, I. Koutná, M. Kozubek, A. Ganová, E. Bártová, M. Falk and R. Paseková, Chromosoma, 2002, 111, 321–331 CrossRef CAS PubMed.
- M. Falk, E. Lukasova, B. Gabrielova, V. Ondrej and S. Kozubek, Biochim. Biophys. Acta, Mol. Cell Res., 2007, 1773, 1534–1545 CrossRef CAS PubMed.
- D. Deckbar, P. A. Jeggo and M. Löbrich, Crit. Rev. Biochem. Mol. Biol., 2011, 46, 271–283 CrossRef CAS PubMed.
- N. Shikazono, M. Noguchi, K. Fujii, A. Urushibara and A. Yokoya, J. Radiat. Res., 2009, 50, 27–36 CrossRef CAS PubMed.
- S. K. Singh, M. Wang, C. Staudt and G. Iliakis, Nucleic Acids Res., 2011, 39, 8416–8429 CrossRef CAS PubMed.
- L. Ježková, M. Falk, I. Falková, M. Davídková, A. Bačíková, L. Štefančíková, J. Vachelová, A. Michaelidesová, E. Lukášová, A. Boreyko, E. Krasavin and S. Kozubek, Appl. Radiat. Isot., 2014, 83, 128–136 CrossRef PubMed.
- M. Falk, E. Lukášová, L. Štefančíková, E. Baranová, I. Falková, L. Ježková, M. Davídková, A. Bačíková, J. Vachelová, A. Michaelidesová and S. Kozubek, Appl. Radiat. Isot., 2014, 83, 177–185 CrossRef CAS PubMed.
- Y. Ziv, D. Bielopolski, Y. Galanty, C. Lukas, Y. Taya, D. C. Schultz, J. Lukas, S. Bekker-Jensen, J. Bartek and Y. Shiloh, Nat. Cell Biol., 2006, 8, 870–876 CrossRef CAS PubMed.
- I. Chiolo, A. Minoda, S. U. Colmenares, A. Polyzos, S. V. Costes and G. H. Karpen, Cell, 2011, 144, 732–744 CrossRef CAS PubMed.
- I. Chiolo, J. Tang, W. Georgescu and S. V. Costes, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2013, 750, 56–66 CrossRef CAS PubMed.
- W. Friedland, P. Jacob, H. G. Paretzke and T. Stork, Radiat. Res., 1998, 150, 170 CrossRef CAS PubMed.
- W. Friedland, P. Jacob, H. G. Paretzke, A. Ottolenghi, F. Ballarini and M. Liotta, Radiat. Prot. Dosimetry, 2006, 122, 116–120 CrossRef PubMed.
- B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660 CrossRef.
- B. Jakob, J. Splinter, M. Durante and G. Taucher-Scholz, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 3172–3177 CrossRef CAS PubMed.
- R. M. Anderson, D. G. Papworth, D. L. Stevens, N. D. Sumption and D. T. Goodhead, Cytogenet. Genome Res., 2006, 112, 35–44 CrossRef CAS PubMed.
- M. Durante, D. Pignalosa, J. A. Jansen, X. F. Walboomers and S. Ritter, Radiat. Res., 2010, 174, 20–26 CrossRef CAS PubMed.
- G. Kraft, M. Kramer and M. Scholz, Radiat. Environ. Biophys., 1992, 31, 161–180 CrossRef CAS PubMed.
- V. Conte, P. Colautti, B. Grosswendt, D. Moro and L. De Nardo, New J. Phys., 2012, 14, 93010 CrossRef.
- T. Neumaier, J. Swenson, C. Pham, A. Polyzos, A. T. Lo, P. Yang, J. Dyball, A. Asaithamby, D. J. Chen, M. J. Bissell, S. Thalhammer and S. V. Costes, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 443–448 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |