Percolation in networks of 1-dimensional objects: comparison between Monte Carlo simulations and experimental observations

Abstract

Planar networks composed of 1-dimensional nanometer scale objects such as nanotubes or nanowires have been attracting growing interest in recent years. In this work we directly compare the percolation threshold of silver nanowire networks to predictions from Monte Carlo simulations, focusing particularly on understanding the impact of real world imperfections on the percolation onset in these systems. This work initially determines the percolation threshold as calculated from an ideal system using Monte Carlo methods. On this foundation we address the effects of perturbations in length, angular anisotropy and radius of curvature of the 1-dimensional objects, in line with those observed experimentally in purposely fabricated samples. This work explores why two-dimensional stick models in the literature currently underestimate the percolation onset in real systems and identifies which of the network's features play the most significant role in that deviation.

---

Conceptual insights

This work provides insight into the impact of imperfections on the percolation of 1D objects in a 2D network. This work combines simulations, theory and real world networks to explore the onset of percolation in 2D networks of silver nanowires. Three imperfections are recognised: length distributions, angular anisotropy and wire curvature. This work extends the previous literature to explain the discrepancy between theoretically predicted percolation onset and that observed experimentally. In light of this work it is clear that the angular distribution has the highest impact on network formation and that in a counter intuitive observation a length distribution actually works to lower the required nanowire density to form a percolating network.

Introduction

The study of planar networks of randomly or periodically oriented 1-dimensional objects is currently of increasing interest.¹ The ongoing efforts by the community to better understand the underlying physical mechanisms occurring in these planar networks is notably driven by the growing desire for low-cost consumer electronics and thin-film photovoltaics. Recent developments in the production of conductive nano-systems such as nanotubes^2–4 or nanowires (made either from silicon or metallic materials)^5–7 have provided innovative solutions for new applications in these fields. From a practical point of view metallic nanowire networks have desirable properties for a broad range of device applications including information and communication technologies,^8,9 electronics and optoelectronics,¹⁰ as well as in the domain of energy harvesting¹¹ and sensors.¹²

Although the technological interest is relatively recent, stick percolation in two-dimensional (2D) systems has already been the subject of research for many years. In their seminal paper of 1974, Pike and Seager^13,14 addressed the general problem of percolation in a variety of systems. Their models involved the use of two main parameters which are the network density n, defined as the number of sticks per unit area, and the stick length L. In the process of building a denser network by increasing the number of wires with random orientation on a planar substrate, the percolation threshold is defined as the first occurrence of a set of intersecting sticks spanning the whole system and electrically connecting two parallel electrodes placed at opposite sides of the system. The network density for which the probability of finding a spanning cluster has the value of 0.5 is defined as the critical density n_c. Li and Zhang¹⁵ studied stick percolation by Monte Carlo simulations with much higher accuracy and showed, for system size much larger than L, that:

n_cL² = 5.63726. (1)

This approach was used to investigate by numerical computations the nature of percolation in the mechanism of building up the electrical conductivity of the system from a sparse collection of independent, randomly oriented, sticks to dense networks which form percolating paths. The theoretical calculation of the percolation threshold also predicts that the electrical conductivity of a network increases with n as described by a power scaling law:

σ ∝ (n − n_c)^γ (2)

with the universal conductivity exponent γ ∼ 1.29 for 2D systems.¹⁶ Lowering the percolation threshold is key to the achievement of light-weight, cost-effective, more transparent and more conductive composites where conducting entities are embedded within an insulating matrix. Balberg and Binenbaum investigated the percolation threshold in systems with a preferential stick orientation and a lognormal stick length distribution.¹⁷ Although their results showed that an increase of network anisotropy was responsible for a percolation threshold increase, the relatively small number of simulations, limited by the computational capabilities available at the time, restricted the scope of their conclusions. The effects of system size and network density on the electrical conductance in these 2D systems were also addressed by Kumar et al.¹⁸ Such an analysis can be useful to predict the conductance of the nanotube network as a function of wire/tube densities and channel lengths.¹⁸ The work on 2D stick percolation by Mutiso et al.¹⁹ also explored the interrelation between network density, electrical resistance and optical transparency. Their work is an excellent study of the percolative behavior of 1D nanoscale objects and combines simulations and experiments. This work also explored the use of long and short wires though not in a continuous distribution.

In the present work, we propose a more general approach, which incorporates the effects of three experimentally observed imperfections on the percolation onset. To achieve this, we develop a computational protocol based on Monte Carlo simulations and apply it to a network made of identical and randomly oriented sticks. In addition we explore the impact of imperfections that can be found in real nanowire networks on the percolation threshold. In real devices, imperfections can be observed as a non-uniform distribution of nanowire length, orientation and curvature. Our algorithms are based on the formalism proposed by Newman and Ziff^20,21 which describes the formation of nanowire clusters and the identification of the conducting paths, renumbering the smaller clusters rather than the percolating cluster, thus enabling much faster modelling of the system than previous approaches in the literature. In this work comparing the theoretical results to the experimental electrical behaviour of real systems then validates this formalism. From there, a comparative study between simulations and experiments based on Ag nanowire networks has been carried out, allowing us to explore the mechanisms responsible for the electrical resistance of 2D metallic nanowire networks and how it relates to the onset of percolation which was analysed as function of network density, nanowire length distribution, non-isotropic angular distributions as well as nanowire curvature. Such a study of the percolation in perfect and imperfect nanowire networks based on computer simulation and experimental observations aims at improving the understanding of percolation mechanisms of 1D objects in general.

Monte Carlo simulations of stick percolation, for perfect and non-perfect networks

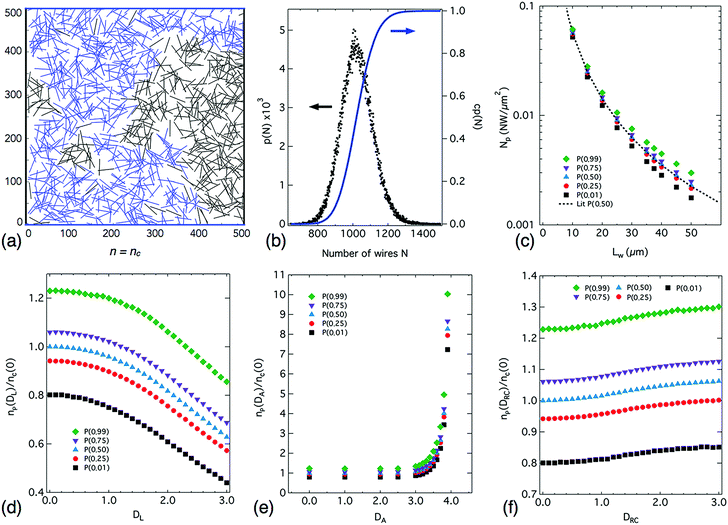
The motivation for this work is to explore the deviations observed in experimental systems from the behavior predicted by theory assuming perfect networks of identical straight sticks. Perturbations associated to length and angular orientation distribution and curvature of the wires were applied to the ideal system in the view of assessing which of these three parameters was most likely to play a dominant role in the percolation probability of a system. We conducted as well a quantitative assessment of the impact of any of these parameters in parallel. The algorithms for the simulations are based on the fast Monte Carlo method for stick percolation introduced by Newman and Ziff.²⁰ For the ideal case of perfectly straight sticks of uniform length and isotropic orientation, results obtained by this approach were validated against and found to be in agreement with the work of Li and Zhang,¹⁵ indicating that the algorithms have been applied in the correct manner. This work uses the same code implemented previously by Langley^22,23 to simulate ideal systems. Through our previous experimental observations of silver nanowire (AgNW) networks^23,24 we recognised that the ideal 2D stick percolation simulations, which are simplifications of the reality, do not appropriately represent the behaviour of many experimentally observed systems. Having validated our algorithms, additional modifications were introduced, leading to a new algorithm which incorporates curved nanowires, length distributions and angular distributions. All scripts were written and run using MATLAB R2014b.²⁵

Fig. 1a shows a typical layout of an ideal network of nanowires as generated by our algorithms. By definition, percolation in this system occurs when a cluster of sticks gets connected to both the top and bottom edges of the system. From a large number of simulations (typically 10⁵ or 10⁶) we can build up a statistical analysis of the network density at which the nanowires first span the system. This allows us to generate a percolation probability distribution function, as shown in Fig. 1b (black curve). In a subsequent step it is then possible to plot the cumulative probability distribution function (blue curve), from where the percolation threshold, defined as the network density at which the probability P of finding a network to be percolating is 0.5, can be extracted. This well-established definition is often used in the literature^3,5,13–15 and is indicative of a transition from a non-percolating to a percolating system.

Fig. 1 (a) An example of an ideal nanowire network generated in MATLAB (lengths are in microns). The AgNW denoted in blue belong to the percolating part of the network. Electrodes on the top edge and on the bottom edge are highlighted in blue. The AgNW length is 32.5 μm. (b) The probability distribution (p(N),black), associated to the percolation occurrence, as a result of 10⁶ simulations and the resulting cumulative probability distribution function (cp(N),blue) versus the number of AgNW within the studied network. (c) Parametric curves of the critical density as a function of nanowire length for a system 500 μm × 500 μm in size. (d)–(f) Real world imperfections added independently to the ideal simulation: (d) impact of length distribution (defined by D_L), (e) impact of angular distribution (D_A) and (f) impact of wire curvatures (D_RC).

In order to validate our simulations we compared our results to those of Li and Zhang¹⁵ and we determined that for the ideal system where all nanowires have the same length with completely isotropic angular distribution, identical conclusions could be drawn from our simulations. From this data set we also extracted the values of N_P corresponding to the number of nanowires at percolation probabilities of P = 0.1, 0.25, 0.75 and 0.99 on a specified area. This additional data is displayed in Fig. 1c and shows a small deviation as expected from the theoretical value for P = 0.5.

One of our objectives is to investigate further these probability distribution functions by extracting useful information on the densities required to achieve a broader range of percolation probabilities. For example, in industrial applications it is more realistic to consider networks with stick densities leading to a probability of percolation as high as 0.99. In this case, such a high threshold is more viable as the likelihood of having a percolating system will be much higher and devices will be more reliable and robust, knowing that the requirements related to AgNW networks physical properties depend strongly on the application.⁹

Each perturbation to the ideal system was then introduced in the form of a normal distribution for the corresponding variable. The width of these distributions is defined by a distribution parameter D_L, D_A and D_RC for the length, angular and radius of curvature distributions, respectively. These distribution parameters are used to generate normal distributions of length D_L and of radius of curvature D_RC as defined in eqn (S1)–(S3) (ESI†) where increasing the distribution parameter leads to an increase in the width of the distribution and results in a transition from the delta function of the ideal simulation towards an increasingly wide normal distribution. In contrast, an increase of the angular distribution parameter D_A results in a smooth transition from a uniform distribution of angles to a delta function (i.e. from the isotropic case where all wires are randomly oriented to the case where they would be all parallel to each other). As the values of the distribution parameters increase, the system deviates further from that of the ideal case.

The average wire length was kept constant. Yet, as D_L increases, the width of the normal distribution increases such that 4 standard deviations fall within D_LL of the average wire length (L) and the critical density n_c decreases as shown in Fig. 1d. As D_A increases the allowed angle range gets restricted, resulting in an increase in the anisotropy of the system and an increase in the percolation threshold as seen in Fig. 1e. The parameter D_RC is applied as a perturbation on the radius of curvature with three simple assumptions: (i) a 37.5 μm long nanowire with a radius of curvature of 10 000 μm is a fair approximation of a straight nanowire, (ii) from direct observation of fabricated networks, wires are very unlikely to form a curve tighter than a semicircle, thus the minimum allowed radius was fixed to L/π, and (iii) very short nanowires (less than 10 μm) do not appear to bend, hence short wires were restricted to high radius of curvature. Therefore the perturbation is applied in such a way that the nanowires are initially assumed to be effectively straight with a radius of curvature of 10 000 μm. Fig. 1f reports the influence of AgNW curvature on the critical density: a slight increase of n_c is observed when the curvature is increased although AgNW curvature does not appear as a prevailing parameter compared to the two others. A full definition of the distributions applied to the system can be found in the ESI† along with some representative images of the systems generated under such conditions (Fig. S1–S3, ESI†). For a fair comparison between real networks and the simulations reported in Fig. 1 our experimental work focused on the quantitative determination of the three distribution parameters mentioned above and on the experimental observation of the percolative nature of real networks by measuring their electrical resistance as function of network density for different AgNW sizes (average length and diameter).

Experimental observations

In order to experimentally identify the critical density of real 2D stick systems and compare with theory, AgNW networks with different densities were fabricated with spin coating on Corning glass. The nanowires were purchased from Seashell Technology (see Fig. S4, ESI†) and network density series were made for different nanowire types, each nanowire type having different average length and diameter, and being designated by its average diameter for simplicity. For instance nanowires having a diameter of 117 nm in average will be referred to as Ag117. Scanning Electron Microscopy (SEM) was used to determine the network morphology and to perform a network density calculation based on a previously published image analysis.²⁴ A post-deposition thermal annealing was performed on every sample as it is known to optimize the resistance of AgNW networks by a process of organic desorption and local sintering.²⁶Fig. 2a reports the electrical resistance behaviour of AgNW networks with various densities (with constant nanowire type), measured in situ during a ramped thermal annealing with a rate of 2 °C min⁻¹. From these measurements, it was possible to extract a minimum resistance R_min associated with each network. We assume that when this value is reached, the sample is optimized and that almost all nanowire junctions are electrically efficient. The minimum resistances were only reached in percolating networks, i.e. those having a sufficiently high density of wires. The networks presenting non-measurable resistance (>10⁷ Ω), after thermal treatment, were defined as non-percolating. Since a rather large range of densities was considered in this study, we could find an approximate value of the experimental critical density close to the lowest density leading to electrical percolation.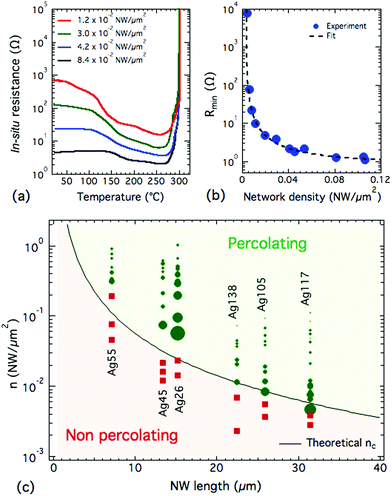

Fig. 2 (a) Variation of the electrical resistance of AgNW-based networks of different densities measured in situ during a thermal annealing in air, operated from room temperature with a heating ramp rate of 2 °C min⁻¹ (nanowire type: Ag117). (b) Minimum experimental resistance values associated to percolating networks made of Ag117, during thermal ramp as function of the network density. The fitting curve is calculated with eqn (3). (c) Silver nanowire networks density versus nanowire length diagram. The square red symbols are associated with non-percolating networks (i.e. as-measured non-conductive networks) while circle green markers are associated with conductive networks. The green markers sizes are proportional to the natural logarithmic values of the measured minimum electrical resistance R_min. The continuous line corresponds to the critical density n_c for uniform, perfect and infinite networks (eqn (1)).

The experimental minimum resistance R_min measured during a thermal ramp can be obtained for a series of similar specimen with different network densities n. These values, reported in Fig. 2a, were measured in situ at elevated temperatures. For the proper comparison of network resistances it is better to compare resistance values at room temperature. To determine the minimum resistance at room temperature, one can extrapolate from the high temperature using the thermal coefficient as reported previously.^24,26 The extrapolated values at room temperature are reported in Fig. 2b. From eqn (2) it can be shown that R_min depends on n and can be written as follows:

R_min(n) = R_inst + K·(n − n_c)^−γ (3)

where R_inst is the instrumental resistance, which was evaluated experimentally with an approximate value of 0.8 Ω, K is a fitting parameter related to the nanowires diameter,²⁴ and n_c was calculated from eqn (1). This equation was used to fit Fig. 2b and a fairly good agreement is found with a value of γ = 1.33 for the conductivity exponent and the value of K = 0.015.

The data shown in Fig. 2a and b are associated to networks composed of the same nanowires type (Ag117). Experimental data were similarly extracted from networks made from the other nanowire types. These results are plotted in Fig. 2c, which represents the network densities of both percolating and non- percolating networks versus the average length (as determined by SEM image analysis) of the nanowires used. The full line illustrates eqn (1), which corresponds to the characteristic of a perfect theoretical network. This theoretical curve divides the diagram in two parts: above the line, the networks have a density higher than the theoretical critical density n_c and should be therefore conducting, whereas below it, the opposite case holds.

Fig. 2c shows a weak deviation of the experimental data with respect to the theory. These results indicate that the critical density for real systems is not perfectly predicted by eqn (1), as some non-percolating networks stand above the line and some percolating networks fall below it.

The fact that the theoretical onset is predicated on the probability of percolation being 0.5 suggests that experimentally some networks could begin to percolate well below that value and some above that threshold may not necessarily be percolating. However the fact that with a small number of samples we were readily able to measure percolating networks close to and below the predicted threshold density indicates a deviation from the theory. This observation however is in agreement with the data derived from Monte Carlo simulations of theoretical networks in Fig. 1d–f. We ascribe this deviation to the existence of imperfections within the experimental network as compared to the ideal networks used to determine eqn (1): the presence of a length distribution, the curvature of the nanowires and a non-isotropy in the angular orientation of the nanowires might play a role. It is now interesting to define the contribution of each of these imperfections on the critical density deviation. At short nanowire lengths the angular distribution clearly dominates resulting in an increase in the percolation threshold. This is likely due to the narrower length distributions experimentally observed for short wires and the dependence of the critical density on the square of the length of the wire as shown in eqn (1). As the length increases the width and influence of the length distribution also increase, resulting in a transition across the theoretical boundary as the longer nanowires start dominating the formation of percolating clusters.

Comparison of the effects of imperfections for modelled real world networks

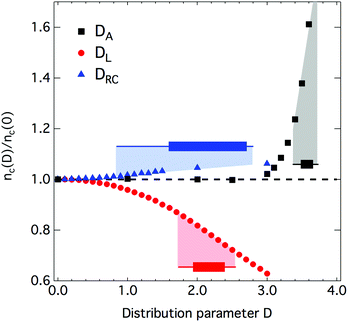
In order to determine whether the perturbations that we applied to the simulated nanowire networks were realistic we extracted values for each distribution parameter from experimental SEM images of actual nanowire networks. This allowed us to determine the actual expected range of each parameter (through the D_A, D_RC and D_L values) for real world samples. This is represented in Fig. 3 through the overlaid boxplots that indicate the as-observed ranges of the distribution parameter functions in real networks. Clearly it appears that the influence of the non-isotropic distribution has the most important effect, when compared with the length or curvature distributions, at least for the fabrication conditions considered in this work.

Fig. 3 Comparison between experimental results and simulations. Plots of the individual effects of network imperfections on the critical density associated to the percolation occurrence. The simulated distribution parameters used are plotted on the same axis with typical ranges determined experimentally and overlaid as box plots.

We then generated a network with the three extracted experimental parameters D_A, D_RC and D_L. Such a generated network, which incorporates each of the three imperfections, is reported in the (Fig. S4, ESI†). This allows to mimic fairly well the experimental results as observed by SEM images. Comparison with the generated network suggests qualitatively that the restrictions imposed in the simulations and the premise on which the perturbations were applied to the system are reasonable.

The analysis of Fig. 3 allows us to assess the relative effects of the three imperfections for the considered experimental conditions and AgNW sizes. The dominant parameter is the non-isotropic distribution of AgNW orientations which increases n_c of about 40–60%. Then the length distribution can have a certain influence with a decrease of n_c of about 20% while the AgNW curvature would only account for a few percentages of n_c increase. Therefore if one would consider an experimental method to deposit AgNW in a perfectly isotropic manner, a larger length distribution would lead to a lower critical density. This constitutes an interesting result which calls for further experimental tests. The curvature of the AgNWs appears to play a minor role most likely due to the fact that any reduction in length due to curvature results in an extension of the wire perpendicular to the long axis, therefore effectively increasing the interaction cross section of the wire and increasing the likelihood of cluster formation. The data suggests a slight increase in percolation threshold, which indicates that the shortening effect is not entirely mitigated by the increase in the excluded volume.

Conclusions

This paper identifies real world imperfections in silver nanowire networks through a combined approach using Monte Carlo simulations and experimental observations and we have included them into an expansion of the idealized 2D stick percolation problem. This system enables the calculation of the percolation threshold for any ensemble of 1D objects including length distributions, angular distributions and object curvature. The original algorithm was founded on the ideal stick system and shows excellent agreement with the literature, which allowed its validation before it is expanded to include real world imperfections. When comparing networks generated with the new algorithm and distribution parameters extracted experimentally we found networks that closely resembled those observed experimentally. This result practically allows a more accurate prediction of the percolation threshold and therefore the density required to achieve the optimal conductivity and optical transparency in such 2D networks of percolating 1D sticks.

Critically this work highlights that the imperfection which has the most impact on the electrical properties of nanowire networks is angular anisotropy. However, this does not appear to be the dominant defect in all systems experimentally. Reduction in the critical density caused by the length distributions appear to start dominating as the nanowire length increases and for wires longer than 20 μm we observe percolating networks below the percolation threshold. The introduction of wire curvatures was found to have a small impact on the network resulting in a moderate increase in the critical density, this is somewhat counter intuitive as the curvature effectively reduces the wire length so one might have expected that it would result in a significant increase. It is likely that the effective loss of length due to the wire curvature is partially mitigated by the increased excluded volume of the wire, increasing the likelihood that the wire will connect with others. These observations are important for future research in 2D networks of 1D objects as it is clear that for optimal network formation the isotropic orientation of the objects is important confirming that spray deposition is preferable over techniques that result in alignment such as meyer rod and spin coating. Additionally this research demonstrates it is not critical to achieve monodisperse object lengths. Finally this work reinforces that the length of the nanowires is likely the most critical factor in the formation of a percolating network and ultimately on the performance of such conductive networks.

Conflicts of interest

The authors declare there are no conflicts of interest.

Acknowledgements

This work was supported by the FICHTRE ANR-13-RMNP-0015-01 project, the European Joint Doctorate FunMAT program (H2020-MSCA-ITN-2014, Project ID 641640) and the J.0119.14 project (F.R.S-FNRS, Belgium). The authors would like to warmly thank Y. Bréchet, C. Celle, C. Jiménez, C. Mayousse and J. P. Simonato for fruitful discussions as well as M. Anikin for his help during experimental measurements. Additionally D. L. would like to acknowledge, Dr Barry Halstead and Dr Brad Stringer as friends and colleagues both of whom passed away during the production of this paper, you are missed. He would also like to thank Dr C. Liu, S. De Leon Vergara and R. E. Langley for their support.

References

1. A. Ono, J.-I. Kato and S. Kawata, Phys. Rev. Lett., 2005, 95, 267407.
2. B. Vigolo, C. Coulon, M. Maugey, C. Zakri and P. Poulin, Science, 2005, 309, 920–923.
3. J. N. Coleman, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R7492.
4. S. Xu, O. Rezvanian, K. Peters and M. A. Zikry, Nanotechnology, 2013, 24, 155706.
5. S. De, P. J. King, P. E. Lyons, U. Khan and J. N. Coleman, ACS Nano, 2010, 4, 7064–7072.
6. G. A. Gelves, B. Lin, U. Sundararaj and J. A. Haber, Adv. Funct. Mater., 2006, 16, 2423–2430.
7. S. Ye, A. R. Rathmell, Z. Chen, I. E. Stewart and B. J. Wiley, Adv. Mater., 2014, 26, 6670–6687.
8. D. Langley, et al. , Nanotechnology, 2013, 24, 452001.
9. T. Sannicolo, et al. , Small, 2016, 12, 6052–6075.
10. X. Lan, et al. , Adv. Mater., 2013, 25, 1769–1773.
11. J. A. Spechler, K. A. Nagamatsu, J. C. Sturm and C. B. Arnold, ACS Appl. Mater. Interfaces, 2015, 7, 10556–10562.
12. C.-H. Song, C. J. Han, B.-K. Ju and J.-W. Kim, ACS Appl. Mater. Interfaces, 2016, 8, 480–489.
13. G. E. Pike and C. H. Seager, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 10, 1421–1434.
14. C. H. Seager and G. E. Pike, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 10, 1435–1446.
15. J. Li and S.-L. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 40104.
16. M. Žeželj and I. Stanković, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134202.
17. I. Balberg and N. Binenbaum, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 3799–3812.
18. S. Kumar, J. Murthy and M. Alam, Phys. Rev. Lett., 2005, 95, 066802.
19. R. M. Mutiso, M. C. Sherrott, A. R. Rathmell, B. J. Wiley and K. I. Winey, ACS Nano, 2013, 7, 7654–7663.
20. M. E. J. Newman and R. M. Ziff, Phys. Rev. Lett., 2000, 85, 4104–4107.
21. M. E. J. Newman and R. M. Ziff, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 16706.
22. D. P. Langley, Silver nanowire networks: effects of percolation and thermal annealing on physical properties, PhD thesis, Université de Grenoble, Université de Liège, 2014.
23. D. P. Langley, et al. , Sol. Energy Mater. Sol. Cells, 2014, 125, 318–324.
24. M. Lagrange, et al. , Nanoscale, 2015, 7, 17410–17423.
25. Matlab Available at: http://www.mathworks.com, accessed: 10th September 2016.
26. D. P. Langley, et al. , Nanoscale, 2014, 6, 13535–13543.

---

Footnotes

† Electronic supplementary information (ESI) available: Matlab scripts for 1D object simulations, extended explanation of imperfection distributions with examples. See DOI: 10.1039/c8nh00066b

‡ These authors contributed equally to this work.

---