Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
4D visualisation of in situ nano-compression of Li-ion cathode materials to mimic early stage calendering†
S. R.
Daemi
 a,
X.
Lu
a,
D.
Sykes
b,
J.
Behnsen
b,
C.
Tan
a,
X.
Lu
a,
D.
Sykes
b,
J.
Behnsen
b,
C.
Tan
 a,
A.
Palacios-Padros
c,
J.
Cookson
c,
E.
Petrucco
c,
P. J.
Withers
b,
D. J. L.
Brett
a,
A.
Palacios-Padros
c,
J.
Cookson
c,
E.
Petrucco
c,
P. J.
Withers
b,
D. J. L.
Brett
 a and
P. R.
Shearing
a and
P. R.
Shearing
 *a
*a
aElectrochemical Innovation Lab, Department of Chemical Engineering, UCL, London, WC1E 7JE, UK. E-mail: p.shearing@ucl.ac.uk
bHenry Moseley X-ray Imaging Facility, Photon Science Institute, The University of Manchester, Manchester, M13 9PY, UK
cJohnson Matthey, Technology Centre, Blounts Court Road, Sonning Common, Reading, RG4 9NH, UK
First published on 18th December 2018
Abstract
Lithium-ion (Li-ion) batteries operate via electrochemical reactions between positive and negative electrodes, formed by complex porous microstructures. An improved understanding of these materials can lead to a greater insight into the link between microscopic electrode morphology and macroscopic performance. The practice of calendering electrodes after manufacturing has been widely used to increase the volumetric energy density and improve the electrical contact between electrode material particles and with the foil substrate. In this paper we present, for the first time to the authors’ knowledge, a technique to image battery electrodes in situ and in 3D whilst undergoing uniaxial compression with the intent of emulating the calendering process. This technique allows the tracking of electrode strain during compression and its further application will lead to a thorough understanding of crack initiation and propagation mechanisms within electrode particles, ultimately optimising their design and performance.
Conceptual insightsLi-ion battery electrodes are ‘calendered’, a process whereby these are pressed to improve packing density and enhance electrical conductivity. Whilst this process is universally adopted, there remains a lack of fundamental understanding of the influence of calendering on the resulting microstructure. This study presents a novel technique that allows the imaging of Li-ion battery electrodes during uniaxial compression with X-ray nano-computed tomography to emulate calendering. By combining novel sample preparation techniques, a nano-mechanical stage and digital volume correlation, we were able to map the strain evolution within an electrode during compression. Our study differs from previous literature as the imaging is done in situ: this is the only study to our knowledge which looks at nano-scale microstructure evolution in response to an applied mechanical load. We uniquely observe how different areas of the same electrode react to a compressive force offering unparalleled insight into the mechanical behaviour of electrodes and their constituent particles. Our work is not only a significant advance in battery characterisation, but offers a technique that could be applicable to a wide range of functional porous materials, leading to a further understanding of their mechanical properties and optimisation of their design. |
Li-ion batteries are ubiquitous in daily life, powering a range of devices, from consumer electronics to electric vehicles.1 A range of characterisation and computational techniques have been applied to understand and improve the design of the electrodes that underpin the reactions in the device.2–6 Concurrently, a variety of manufacturing procedures have been developed and optimised to tailor electrode energy and power. Specifically, calendering is a widely adopted technique to improve the energy density of electrode sheets by compressing the printed electrodes prior to their assembly in different battery designs.7 Conversely, compression may lead to particle cracking which exposes additional surfaces to electrochemical reactions and whilst this may improve reaction kinetics, it can also lead to accelerated degradation.8 Furthermore, compression increases the tortuosity of the porous channels and hence affects the rate capability of battery electrodes. Therefore, a delicate balance between power and energy density can be established by tailoring compression according to the required application.
A range of ex situ studies have investigated the effect that compression has on electrodes and successfully established a link between calendering and its effect on the electrochemical performance of the electrode.7,9–11 A recent study for example, has examined slices of LiNi0.33Mn0.33Co0.33O2 (NMC) electrodes compressed to different porosities with a scanning electron microscope (SEM), linking the change in the porous network to the electrochemical performance.12 One of the main limitations of this approach is that a 2D characterisation technique is applied to a complex 3D microstructure. Consequently there is a lack of understanding of how a compressive force is distributed within these porous networks and how this causes particle displacement. Furthermore, the role of particle cracking and fragmentation and its effect in long term capacity degradation has not been explored thoroughly in previous literature.
To address these shortcomings, we have devised a technique to mimic calendering in situ whilst imaging the electrode on the nano-scale by using a combination of X-ray nano-tomography, a novel sample preparation technique and an in situ nano-mechanical stage. In this work, we have been able to directly track secondary particle movement and visualise the development of strain hotspots throughout an electrode during uniaxial compression. We have also applied physical characterisation and computational tools to further the understanding of the material and quantify microstructural change within the electrode.
Advances in lab-based X-ray computed tomography (CT) instruments have paved the way for sub-micron resolution imaging of energy materials obtained via a transmission X-ray microscopy (TXM) architecture.4,13–15 In conventional lab-based micro-CT instruments, the optical magnification requires the sample to be as close as possible to the source and detector for the highest resolution. The TXM architecture leads to a sufficient increase in the distances between the sample, source and detector to allow for certain in situ rigs to be installed.16 Specifically, a nano-mechanical in situ loading stage has been developed and used to gauge the effect of compression on materials in the nano-scale.17 To fully utilise the sub-micron resolution offered by the nano-CT instrument and reduce artefacts during imaging, a novel sample preparation technique has been developed that consists in laser-milling electrode pillars below 100 μm.18
Results
Indentation stage setup
A ca. 80 μm NMC-type electrode pillar was fabricated from a printed electrode using a laser micro-machining instrument: this technique allows registration of the directional structure formed by electrode particles deposited onto a current collector.18 A modified sample holder was manufactured to accommodate the sample, as shown in Fig. 1a, and this was inserted in the nano-mechanical stage, viewed in Fig. 1b. The relevance of the overall sample size is discussed in the ESI.† Two SEM images of the electrode surface and a whole pillar are presented for reference in Fig. 1c and d respectively. A superficial burn zone can be observed on the surface of the pillar but as evident in the radiographs and virtual slices this is only a few μm thick and does not compromise the inner sections of the pillar. The pillar imaged is not the same pillar used for compression but is taken from the same batch.After mounting and manually aligning the sample holder to the compression flat head tip, indicated in Fig. 1b, the assembly was inserted in the chamber of the X-ray nano-CT instrument and allowed to thermally equilibrate. Compression was then continuously applied by controlling the sample displacement in the z-axis until the load stage reached the maximum displacement of 500 μm with two pause steps for imaging. A piezo actuator controls the sample displacement in the z-axis, pressing the sample upon the compression flat head. These two compression steps are named step A and B respectively. The full force-stage displacement graph can be found in the ESI.†
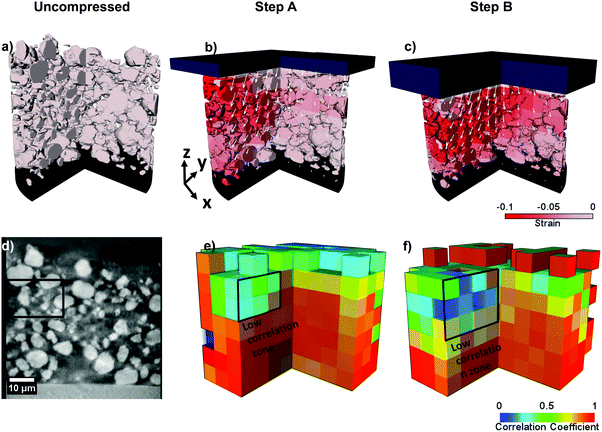
Fig. 2a–c present sequential radiographs of the sample taken in its uncompressed and post-compression states, whereas Fig. 2d–f present a virtual slice taken from the fully registered and aligned 3D tomographic dataset. The collected radiographs are reconstructed into a 3D volume for analysis by using a filtered back projection algorithm.19
Digital volume correlation analysis
The volumes at different loads were registered by using the particle highlighted by the 8 μm box in Fig. 2c as a reference, and used to run the DVC module in the subset-based mode in Avizo 9.4. DVC algorithms have been widely used in the literature to quantify displacements and microstructural evolution for a diverse range of applications.20–23 An edge length of 8 μm as the sub-volume edge length was selected as this provides an adequate compromise between feature detection and second highest average correlation coefficient (CC) of 0.81. Further information on how the sub-volume edge length was chosen and background information on the DVC algorithm can be found in the ESI.†Fig. 3a–c represent the volume renderings of each tomographic dataset overlaid by the respective strain map, along with the vector slice in the z direction. The compression flat head is also added for ease in visualisation. Fig. 3e and f represent the CC spatially mapped onto the entire dataset. A direct comparison between the particles presented in Fig. 3a–c and the corresponding spatially mapped CC presented in Fig. 3e and f can be achieved. The opacity of the subvolume cubes is gradually decreased as the CC approaches zero to aid in the visualisation on the sides of the dataset.
The first step in this analysis consists in decoupling the areas of poor correlation: namely those located on the sides or top of the full dataset volume, and those with a higher displacement and smaller particle size. From the CC map, it is possible to observe that the majority of areas of low correlation belong to the side and top edges of the dataset, where the pixel values are attributed to noise due to the presence of the compression flat head, or to edge pixels having null values. These can be viewed by the “empty” cubes in Fig. 3d and e. Typically, the strain calculated for these areas is either positive indicating tension or an outlying value of a negative compressive strain. As values below −0.10 are identified as belonging to the latter, the strain is capped at −0.10 for ease in visualisation.
From step A, it is possible to observe that the highest valid displacement occurs in a hotspot in the top section of the electrode, below the compression flat head. By comparing the strain and CC maps, a zone with low correlation can be identified within an area of high strain, highlighted by the recurring black outline in Fig. 3. This is thought to be due to the presence of a high displacement of small particle fragments with size below the correlation window. This may indicate that smaller particles, along with fragments that may be formed by particles crushing during calendering may act as strain hot-spots. Examining the compression of the upper layer of the electrode may also lead to a further understanding of how the uppermost porosity varies and how this affects the interpenetration of electrolyte within the electrode. The remaining regions of the electrode have a higher CC indicating the reliability of the result. This is confirmed by comparing the CC and the grayscale data: as the displacement increases, the correlation decreases in areas where particles are small but a strong correlation persists in the rest of the dataset.
With step B, the strain can be seen as concentrating throughout the top part of the electrode whilst spreading towards the lower half. The vector field also highlights that the particles are moving laterally within the electrode. This behaviour could be attributed to the different stress–strain propagation mechanisms within the electrode particles according to their morphology, local heterogeneity or dimensions. Lateral movement could also be emphasized by the fact that the edge of the sample is in close proximity the bulk. The above considerations indicate that by analysing all the outputs of the DVC calculation, it is possible to obtain an excellent representation of particle movement and strain evolution within an electrode.
Continuous pore size distribution
A continuous pore size distribution (CPSD) is run on the binarised image.24 This operates by inscribing spheres of increasing diameter in the pore space and measuring their volume and is ideal for porous networks with irregular shapes. It is important to note that the effective pore size distribution of the electrode is given by the contribution of the macroscale electrode pores and the nano-scale carbon and binder pores.25–27 Electrolyte transport occurs through the macro-scale electrode pores and nano-scale carbon and binder pores but these cannot be resolved at this length-scale with nano-CT due to their highly different attenuation. Running this calculation, however, can be used to quantify how compression is affecting the morphology and size of inter-particle channels as a whole.Fig. 4a and b present a binarised slice of the electrode and the corresponding CPSD can be viewed in Fig. 4c. The average radius size decreases from ca. 2 μm to 1.7 μm and 1.5 μm for step A and step B respectively. While the overall pore volume can be seen as decreasing between the two compression steps, most of this decrease occurs with the first compression step: this indicates that as the particles are reducing their separation, a major resistance to compression is taking place and in the context of increased loads, could indicate the onset of particle cracking. The inactive phase fraction was also calculated as 68% for the uncompressed sample, 58% for compression step A and 55% for compression step B. These results highlight the potential in the technique to shed light on the effect of compression on the microstructural evolution of the electrode particles and porous phases.
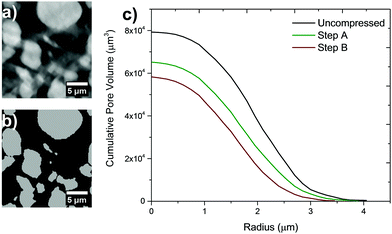 | ||
| Fig. 4 (a) Sample grayscale slice taken from reconstructed dataset and (b) its binarised equivalent. (c) Cumulative CPSD of porous networks and overall pore size and volume. | ||
Discussion
It is important to note that the sample size plays an important role in determining the effect of compression. Compared to an industrial manufacturing scenario, in which the electrode bulk dimensions are larger by several orders of magnitude compared to the edges of the electrode, in the present sample the edge zones occupy ca. 10% of the total electrode volume and this could accentuate lateral movements and spilling of particles. It is also important to consider that in an industrial setting, calendering is typically performed with pressure rollers. A link could be established between the samples obtained via roll-press calendering and the technique presented here by comparing microstructural metrics such as porosity, pore size and crack distributions for in and ex situ samples and this could allow direct relation of the load obtained with the nano-mechanical stage to the pressure exerted by the rollers.The potential implications of further application of this technique range from understanding the mechanical behaviour of battery electrodes to generating compressed electrode datasets that can be used for further modelling and the validation of novel electrochemical and microstructural models. An example application could be the study of species transport within an electrode, where diffusion within all phases could be considered to understand how inhomogeneous zones generated by compression can affect Li+ concentration gradients, electrical conduction, and the related local current density.28
In conclusion, we have used a nano-mechanical stage to compress micro-machined NMC pillars of ca. 80 μm diameter whilst performing nano-scale 3D imaging. A first analysis of two compression steps have been conducted to track the early-stage displacement, which has demonstrated that the combination of this setup along with DVC is a promising technique to understand the mechanisms of the Li-ion battery electrode microstructural evolution under compression. We have been able to accurately track the movement of secondary particles through the electrode as a function of applied load, as well as apply computational characterisation techniques to quantify how the inter-particle separation is decreasing.
This could potentially provide new insights into the industrial calendering process. Further work will be carried out to understand the particle cracking mechanisms using higher compressive loads. We believe that developing this technique can benefit the study of battery electrodes by bridging the knowledge between the microstructural evolution within electrode particles and the resulting effect on battery performance and capacity degradation.
Methods
Electrode production
The NMC electrode utilized was prepared as follows: 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 mass ratios were utilized for LiNi0.33Mn0.33Co0.33O2 (NMC333, Targray), conductive carbon black (Super C65, Imerys) and polyvinylidene fluoride (PVDF). A dual asymmetric centrifuge system (SpeedMixer DAC 150.1 FVZ-K) was used to homogenize the powders and NMP as a solvent. The slurry was dried overnight at 80 °C after being cast on aluminum foil.
5 mass ratios were utilized for LiNi0.33Mn0.33Co0.33O2 (NMC333, Targray), conductive carbon black (Super C65, Imerys) and polyvinylidene fluoride (PVDF). A dual asymmetric centrifuge system (SpeedMixer DAC 150.1 FVZ-K) was used to homogenize the powders and NMP as a solvent. The slurry was dried overnight at 80 °C after being cast on aluminum foil.
SEM imaging
SEM images were recorded on a Zeiss EVO 10 (Carl Zeiss Inc.) at 15 kV using the secondary electron detector.Pillar preparation
The electrode pillar was machined into a micro-scale pillar by using a laser instrument (A Series/Compact Laser Micromachining System, Oxford Lasers): a 1 mm electrode disk was cut out and glued onto a 1 mm dowel pin using a two-part epoxy. This was milled down with the aforementioned instrument to ca. 80 μm. An exhaustive description of this sample preparation technique can be found in the literature.18X-ray nano-CT
The adapted holder containing the sample was mounted on the nano-mechanical stage (Carl Zeiss, Inc.) and aligned manually according to the standard operating procedure. The stage was then installed within the lab-based nano-CT instrument (Xradia Ultra 810, Carl Zeiss Inc.). This uses a Chromium anode with a beam energy of 5.4 keV. The samples were scanned using absorption mode, with the tube voltage set at 35 kV and current at 25 mA. A pixel binning of 2 in large field-of-view (FOV) mode was used and a resultant effective pixel size of ca. 128 nm was achieved across a FOV of 65 μm. An initial continuous scan at no angular increments was performed to ensure that no thermal drift was taking place. The exposure time was set to 20 s and 801 projections were taken over the angular range of ±70° (rather than the default ±90°). This is to accommodate the mechanical stage crossing the path of the beam. A filtered back projection algorithm, implemented in the Zeiss XMReconstructor (Carl Zeiss Inc.), was used to reconstruct the radiographs into a 3D volume. The single-slice mosaic radiographs were taken in mosaic mode in XMController with each 3 × 3 mosaic component taken with an edge length of 65 μm and an exposure time of 1 s. The first mosaic was taken before compressing the sample and the remaining were taken after each compression step and before the full tomographic scan.Compression
Compression was carried out by moving the sample towards the compression flat head tip after aligning the sample and allowing for the sample to stabilize from thermal drift. Two compression steps were achieved with continuous compression between them. The relative stage displacement was zeroed at the first contact between the sample and the compression tip. Scans were taken at a relative stage displacement of 65 and 80 μm respectively. The sample was let set for 30 min before each scan to mitigate any sample movement that might have arisen because of force relaxation.Image analysis
All radiographs were processed with ImageJ. All 3D volume analysis was carried out in Avizo 9.4 (Thermo Fisher Scientific). The reconstructed datasets were imported into Avizo and their contrast was matched with the “Match Contrast” module. A 3D median filter was run with one iteration to gently de-noise the datasets and these were then registered and aligned spatially. The Avizo DVC algorithm was run by using the subset based (local) approach with sub-volume sizes ranging from 16 to 4 μm in 2 μm increments. The maximum displacement was set to 10 μm. The datasets were binarised with a combination of thresholding tools. The CPSD algorithm was run in ImageJ as part of the Beat add-on package.24Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors would like to acknowledge the EPSRC for funding under grants EP/R020973/1, EP/N032888/1 and EP/K005030/1, the funding from the Henry Moseley X-ray Imaging Facility which has been made available through the Royce Institute for Advanced Materials through grants (EP/F007906/1, EP/F001452/1, EP/I02249X, EP/M010619/1, EP/F028431/1, EP/M022498/1 and EP/R00661X/1), and the ISCF Faraday Challenge Fast Start project on “Degradation of Battery Materials” made available through grant EP/S003053/1. PRS acknowledges funding from the Royal Academy of Engineering for financial support under the Chair in Emerging Technologies scheme.References
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2014, 18, 252–264 CrossRef.
- D. Chen, S. Indris, M. Schulz, B. Gamer and R. Mönig, J. Power Sources, 2011, 196, 6382–6387 CrossRef CAS.
- M. Ebner, F. Geldmacher, F. Marone, M. Stampanoni and V. Wood, Adv. Energy Mater., 2013, 3, 845–850 CrossRef CAS.
- P. R. Shearing, L. E. Howard, P. S. Jørgensen, N. P. Brandon and S. J. Harris, Electrochem. Commun., 2010, 12, 374–377 CrossRef CAS.
- L. Zielke, T. Hutzenlaub, D. R. Wheeler, C.-W. Chao, I. Manke, A. Hilger, N. Paust, R. Zengerle and S. Thiele, Adv. Energy Mater., 2015, 5, 1401612 CrossRef.
- S. J. Cooper, D. S. Eastwood, J. Gelb, G. Damblanc, D. J. L. Brett, R. S. Bradley, P. J. Withers, P. D. Lee, A. J. Marquis, N. P. Brandon and P. R. Shearing, J. Power Sources, 2014, 247, 1033–1039 CrossRef CAS.
- H. Zheng, L. Tan, G. Liu, X. Song and V. S. Battaglia, J. Power Sources, 2012, 208, 52–57 CrossRef CAS.
- J. R. Wilson, J. S. Cronin, S. A. Barnett and S. J. Harris, J. Power Sources, 2011, 196, 3443–3447 CrossRef CAS.
- A. van Bommel and R. Divigalpitiya, J. Electrochem. Soc., 2012, 159, A1791–A1795 CrossRef CAS.
- Y. Sheng, C. R. Fell, Y. K. Son, B. M. Metz, J. Jiang and B. C. Church, Front. Energy Res., 2014, 2, 1–8 Search PubMed.
- W. Haselrieder, H. Seeba and A. Kwade, Meet. Abstr., 2012, 50, 59–70 Search PubMed.
- D. Schmidt, M. Kamlah and V. Knoblauch, J. Energy Storage, 2018, 17, 213–223 CrossRef.
- B. Yan, C. Lim, L. Yin and L. Zhu, J. Electrochem. Soc., 2012, 159, A1604–A1614 CrossRef CAS.
- S. Komini Babu, A. I. Mohamed, J. F. Whitacre and S. Litster, J. Power Sources, 2015, 283, 314–319 CrossRef CAS.
- D. S. Eastwood, R. S. Bradley, F. Tariq, S. J. Cooper, O. O. Taiwo, J. Gelb, A. Merkle, D. J. L. Brett, N. P. Brandon, P. J. Withers, P. D. Lee and P. R. Shearing, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 324, 118–123 CrossRef CAS.
- B. M. Patterson, N. L. Cordes, K. Henderson, J. C. E. Mertens, A. J. Clarke, B. Hornberger, A. Merkle, S. Etchin, A. Tkachuk, M. Leibowitz, D. Trapp, W. Qiu, B. Zhang, H. Bale, X. Lu, R. Hartwell, P. J. Withers and R. S. Bradley, Exp. Mech., 2016, 56, 1585–1597 CrossRef CAS.
- B. Hornberger, H. Bale, A. Merkle, M. Feser, W. Harris, S. Etchin, M. Leibowitz, W. Qiu, A. Tkachuk, A. Gu, R. S. Bradley, X. Lu, P. J. Withers, A. Clarke, K. Henderson, N. Cordes and B. M. Patterson, X-Ray Nanoimaging Instruments Methods Ii, 2015, vol. 9592, p. 95920Q.
- J. J. Bailey, T. M. M. Heenan, D. P. Finegan, X. Lu, S. R. Daemi, F. Iacoviello, N. R. Backeberg, O. O. Taiwo, D. J. L. Brett, A. Atkinson and P. R. Shearing, J. Microsc., 2017, 1–13 Search PubMed.
- A. C. Kak and M. Slaney, Algorithms for Reconstruction with Nondiffracting Sources, Society for Industrial and Applied Mathematics, 2001 Search PubMed.
- L. Wang, J. Y. Ooi and I. Butler, Procedia Eng., 2015, 102, 240–248 CrossRef.
- D. S. Eastwood, V. Yufit, J. Gelb, A. Gu, R. S. Bradley, S. J. Harris, D. J. L. Brett, N. P. Brandon, P. D. Lee, P. J. Withers and P. R. Shearing, Adv. Energy Mater., 2014, 4, 1300506 CrossRef.
- N. Lenoir, M. Bornert, J. Desrues, P. Bésuelle and G. Viggiani, Strain, 2007, 43, 193–205 CrossRef.
- S. A. Hall, N. Lenoir, G. Viggiani and P. Besuelle, 1st Int. Symp, 2009.
- B. Münch and L. Holzer, J. Am. Ceram. Soc., 2008, 91, 4059–4067 CrossRef.
- L. Zielke, T. Hutzenlaub, D. R. Wheeler, I. Manke, T. Arlt, N. Paust, R. Zengerle and S. Thiele, Adv. Energy Mater., 2014, 4, 1301617 CrossRef.
- S. Vierrath, L. Zielke, R. Moroni, A. Mondon, D. R. Wheeler, R. Zengerle and S. Thiele, Electrochem. Commun., 2015, 60, 176–179 CrossRef CAS.
- S. R. Daemi, C. Tan, T. Volkenandt, S. J. Cooper, A. Palacios-Padros, J. Cookson, D. J. L. Brett and P. R. Shearing, ACS Appl. Energy Mater., 2018, 1, 3702–3710 CrossRef CAS.
- D. Kehrwald, P. R. Shearing, N. P. Brandon, P. K. Sinha and S. J. Harris, J. Electrochem. Soc., 2011, 158, A1393 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh01533c |
| This journal is © The Royal Society of Chemistry 2019 |