Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crystalline silicon solar cells with tetracene interlayers: the path to silicon-singlet fission heterojunction devices†
Rowan W.
MacQueen
 *a,
Martin
Liebhaber
a,
Jens
Niederhausen
a,
Mathias
Mews
b,
Clemens
Gersmann
a,
Sara
Jäckle
cd,
Klaus
Jäger
e,
Murad J. Y.
Tayebjee
*a,
Martin
Liebhaber
a,
Jens
Niederhausen
a,
Mathias
Mews
b,
Clemens
Gersmann
a,
Sara
Jäckle
cd,
Klaus
Jäger
e,
Murad J. Y.
Tayebjee
 fg,
Timothy W.
Schmidt
fg,
Timothy W.
Schmidt
 h,
Bernd
Rech
b and
Klaus
Lips
*ai
h,
Bernd
Rech
b and
Klaus
Lips
*ai
aInstitute for Nanospectroscopy, Helmholtz-Zentrum Berlin für Materialen und Energie GmbH, Berlin, Germany. E-mail: rowan.macqueen@helmholtz-berlin.de; lips@helmholtz-berlin.de
bInstitute for Silicon Photovoltaics, Helmholtz-Zentrum Berlin für Materialen und Energie GmbH, Berlin, Germany
cNanoscale Structures and Microscopic Analysis, Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, Berlin, Germany
dMax-Planck-Institute for the Science of Light, Günther-Scharowsky-Straße 1, 91058, Erlangen, Germany
eYoung Investigator Group Nano-SIPPE, Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, Berlin, Germany
fCavendish Laboratory, University of Cambridge, Cambridge CB3 0HE, UK
gSchool of Photovoltaic and Renewable Energy Engineering, The University of New South Wales, Sydney, NSW 2052, Australia
hARC Centre of Excellence in Exciton Science, School of Chemistry, The University of New South Wales, Sydney, NSW 2052, Australia
iBerlin Joint EPR Laboratory (BeJEL), Fachbereich Physik, Freie Universität Berlin, Germany
First published on 13th August 2018
Abstract
Singlet exciton fission is an exciton multiplication process that occurs in certain organic materials, converting the energy of single highly-energetic photons into pairs of triplet excitons. This could be used to boost the conversion efficiency of crystalline silicon solar cells by creating photocurrent from energy that is usually lost to thermalisation. An appealing method of implementing singlet fission with crystalline silicon is to incorporate singlet fission media directly into a crystalline silicon device. To this end, we developed a solar cell that pairs the electron-selective contact of a high-efficiency silicon heterojunction cell with an organic singlet fission material, tetracene, and a PEDOT:PSS hole extraction layer. Tetracene and n-type crystalline silicon meet in a direct organic–inorganic heterojunction. In this concept the tetracene layer selectively absorbs blue-green light, generating triplet pairs that can dissociate or resonantly transfer at the organo-silicon interface, while lower-energy light is transmitted to the silicon absorber. UV photoemission measurements of the organic–inorganic interface showed an energy level alignment conducive to selective hole extraction from silicon by the organic layer. This was borne out by current–voltage measurements of devices subsequently produced. In these devices, the silicon substrate remained well-passivated beneath the tetracene thin film. Light absorption in the tetracene layer created a net reduction in current for the solar cell, but optical modelling of the external quantum efficiency spectrum suggested a small photocurrent contribution from the layer. This is a promising first result for the direct heterojunction approach to singlet fission on crystalline silicon.
Conceptual insightsSilicon photovoltaics dominate the solar cell market, but their best-performing designs are approaching the Auger recombination efficiency limit. Singlet fission is attractive for improving the conversion efficiency of silicon cells beyond this limit by generating two charge carrier pairs from high-energy photons. Unlike two-terminal tandem cells, singlet fission cells require no current matching between light absorbers, which confers a considerable performance advantage in real-world applications. Solar cells employing singlet fission layers have been reported in the past, in proof-of-concept organic or hybrid donor–acceptor architectures. But the most impactful use of a singlet fission layer, working within an efficient low-band gap device as a selective downconverting absorber, has yet to be achieved. We report a device structure that marks a significant step in this direction, bringing an organic singlet fission layer within the layer stack of a high-efficiency silicon heterojunction solar cell. We found that silicon remained well-passivated and electrically functional after the organic layer was added. While more efficient transfer from the organic layer must be engineered in subsequent work, this result opens a new line of investigation into singlet exciton fission-augmented silicon solar cells, allowing study of the crucial organo-silicon interface inside of a functioning silicon photovoltaic device. |
I. Introduction
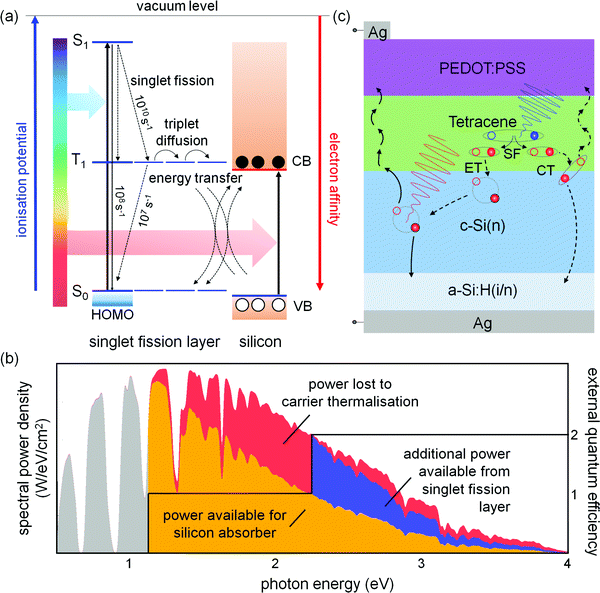
Crystalline silicon (c-Si) solar cells dominate the high-efficiency photovoltaic device landscape.1 Their conversion efficiency is fast approaching the inflexible limits set by Auger recombination and thermodynamics,2–4 so the question of how to overcome these limits is increasingly important. For c-Si, a band gap of 1.12 eV at 300 K means carrier thermalisation is the largest energy loss mechanism acting between incident photon absorption and charge carrier extraction.5 Thermalisation occurs when charge carriers generated at energies greater then the band gap emit phonons and approach the band edge. Photon energy in excess of the band gap energy is thereby turned to waste heat.The addition of a singlet fission (SF) layer to the front surface of a c-Si device can redress carrier thermalisation loss.6 SF is a spin-allowed multiple exciton generation process that takes place in dense assemblies of organic chromophores in which the energy of the first excited singlet state is approximately twice that of the first triplet state.7 In such systems, photoexcitation to S1 typically results in rapid decay of the singlet state, via an intermediate state with multiexciton character, resulting in the formation of two T1 states on adjacent chromophores.8–11 In solar energy converters, SF can recoup some of the energy normally lost to thermalisation, as long as the triplet excitons can be efficiently converted to charge carriers. SF is a particularly attractive means of multiple exciton generation for high-efficiency concepts, because unlike nanocrystalline downconverters, the optical gap of SF materials is equal to the onset energy of efficient carrier multiplication. SF materials are thus ideal selective light absorbers for combining with conventional high-efficiency semiconductors, absorbing higher-energy photons while transmitting photons with energy insufficient to create multiple excitons. The limiting efficiency of a single-threshold PV cell equipped with a SF layer under AM1.5G radiation has been calculated as 45.9%, compared to 33.7% for an unaugmented single-threshold cell.12
Xia and coworkers have prepared a comprehensive review of recent progress in SF materials and devices.13 Reports of SF have been made for many material systems: in thin films,14–17 nanoparticles,18–20 crystals,7,21,22 dimers of SF-capable chromophores,23,24 in concentrated solutions,25 and in chromophoric polymers26 – in general, where interchromophore interactions are significant on the timescale of the singlet lifetime. Aspects of the SF process, particularly concerning the nature of the intermediate multiexciton state and the SF rate dependence on morphology, are still under investigation.16,23,27,28 From the perspective of a photovoltaics application, however, the utility of SF as a means of increasing photocurrent by reducing thermalisation is clear.
Over the past decade, a number of groups have reported solar cells incorporating SF materials.26,29–39 A smaller number of works document the use of a SF layer working in conjunction with a second light absorber, which absorbs in the range between the T1 and S1 energy levels of the SF layer.40–45 This is critical for deriving a benefit to the conversion efficiency of a solar cell.
Moving beyond the proof-of-concept and implementing SF within c-Si cell architecture is an appealing prospect. Few investigations into SF-augmented c-Si devices have been reported, however. Piland and coworkers studied the interactions between thin film tetracene (Tc), a prototypical SF molecule, on c-Si substrates, but did not construct a device.46 Campbell and Crone reported a photodiode consisting of pentacene (Pc), another common SF molecule, on c-Si, but did not consider SF in an analysis of the device.47 Renshaw, Panda and coworkers included a device with Pc on InP, a semiconductor with band gap 1.35 eV, within a set of real and virtual devices constructed to model the electrical characteristics of organic–inorganic heterojunctions. No apparent consideration was given to SF and its effect on this device, however.48,49 Ehrler and coworkers have reported a voltage-matched tandem device comprising a SF-capable Pc/C60 heterojunction cell electrically connected in parallel to a rear-contacted c-Si cell.50 We report devices that differ from this tandem design in that the SF layer is incorporated directly into the c-Si device.
In an ideal SF-augmented c-Si cell, photons with energy greater than twice the c-Si band gap would be absorbed within a SF material on the cell surface, producing two triplet excitons per absorbed photon.6 Each triplet exciton would be harvested to generate free charge carriers, doubling the photocurrent generated from these photons. Photons with energy between the optical gaps of the SF absorber and the c-Si would be absorbed in the c-Si, generating single carrier pairs. Fig. 1(a) depicts an energy level diagram of the SF process and the SF-augmentation of a c-Si absorber. The depiction of energy levels in this figure is adapted from Zhu.51Fig. 1(b) shows the available gain in solar power for such a device. There are two modes by which the SF layer could generate electrical power, leading to different device designs. In the first, the SF layer forms a heterojunction with c-Si, and triplet excitons decay here by charge injection or resonant energy transfer. In the second design, the SF and c-Si layers couple only optically, and triplet excitons are converted to bright states in an emitter layer and transmitted to c-Si by electric dipole-allowed processes.52,53 A conceptual counterpart to SF-augmented c-Si PV is tandem c-Si PV devices.54,55 While these are a more mature technology, one comparative strength of the SF-PV concept is a lack of current matching, hence a robust spectral stability.
We have fabricated and characterised solar cells which contain a heterojunction formed between an evaporated film of tetracene (Tc) and n-type Si(111), as depicted in Fig. 1(c). This configuration harvests triplet excitons from the SF layer by exciton dissociation or transfer at the organo-silicon interface, while the organic acts concurrently as the silicon hole-selective contact. Tc is a p-type organic semiconductor with an S0–S1 energy gap of 2.43 eV, and a T1 energy of 1.24 eV, close to that of the c-Si band gap (1.12 eV). The fission process in Tc is endothermic, which is favourable for maximising the energy conversion yield.12 The S1 state of Tc decays predominantly via SF in evaporated polycrystalline films, on a timescale of 10–100 ps, and the triplet lifetime is around 500 ns.15,46 The limiting efficiency of a Tc/c-Si hybrid solar cell similar to those reported here has been calculated to be 35.8%,56 while the Auger limit of a normal silicon cell is 29.4%.3 This demonstrates the potential for singlet fission to improve an already-efficient solar cell technology.
A quirk of the solar cell design reported here is that the one structure permits two mechanisms by which excitons in tetracene may produce photocurrent. Dissociation of an exciton at the heterojunction yields a charge carrier in each layer, while resonant energy transfer of the exciton across the interface yields a pair of carriers in silicon. The selective contacts employed in the device support both mechanisms. The phenomenon of competing charge- and energy-transfer processes is common in hybrid inorganic–organic systems,57,58 where the rates of the two processes depend critically on the energy level alignment (ELA) at the interface, along with a host of other factors.59 The present hybrid interface, where c-Si abuts a triplet exciton-bearing organic film, makes for a complicated system that is yet to be fully understood. Our work is intended to begin addressing this.
Our report starts with a UV photoemission study of the silicon-tetracene interface, where we identify a type-I interface formed between the polaron transport levels of Tc and c-Si, and offsets well-aligned for favourable charge transport. We then describe the electrical and optical characterisation of functioning solar cells constructed about this organic–inorganic heterojunction. We find that the deposition of tetracene directly onto hydrogen-passivated silicon does not degrade the silicon passivation, and that p-type carriers are selectively extracted through the organic layer. Light absorbed in the tetracene does not make a net positive contribution to the photocurrent, and we show via an optical simulation of the device that the exciton-to-photocurrent conversion yield may be in the vicinity of 8%, of a possible maximum of 200%. We discuss why this yield may be suppressed and put forward design strategies for improvement. Finally, we simulate the optical behaviour of the heterojunction and identify a cell design that minimises reflection losses.
II. Results and discussion
A. Interface energy levels
We conducted ultraviolet photoemission measurements of Tc films thermally evaporated in-system onto hydrogen-passivated c-Si(111), using the synchrotron end station SurICat (BESSY II, Berlin).61 The key data are shown in Fig. 2(a)–(c). All samples exhibited a constant work function (Φw) of (4.3 ± 0.05) eV, determined by the intercept of linear fits to the signal edge and to the background. A Tc ionization energy of 5.4 eV was measured, consistent with literature values.38,40,62–64 The Tc HOMO level is located at (1.1 ± 0.1) eV relative to EF for both Tc samples. The valence band leading edge of the c-Si reference sample is at (0.95 ± 0.10) eV relative to EF, as determined by the indicated fit in the figure. This suggests a 150 meV barrier exists for hole extraction from silicon into the Tc. Barriers of this magnitude are present in other high-efficiency silicon concepts, including at the a-Si/c-Si interface on the rear of the device,65,66 and our device results, shown later, suggest the device is not hindered by this. Using literature values for the Tc LUMO38,40 and Eg of c-Si,67 we constructed the device energy level diagram shown in Fig. 2(d). The polaron transport levels align in a type-I (straddling) configuration. A 1.7 eV barrier blocks electron transport from c-Si to the organic layer and hence forms a good selective blocking contact for the electron.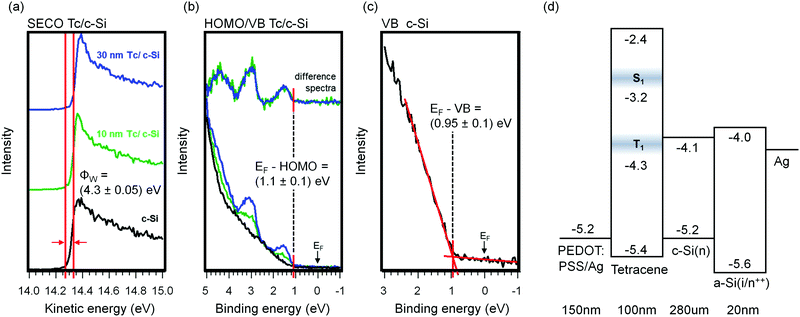 | ||
| Fig. 2 Results of an in-system UV photoelectron study of the Tc/c-Si(111) interface for three Tc thicknesses: (a) secondary electron cutoff (SECO) spectra; (b) valence band spectra, with normalised difference spectra displayed; (c) valence band onset for uncoated c-Si(111):H. (d) Energy level diagram of Tc-bearing solar cells, derived from the UPS data and literature values (see text). The energy of the Tc triplet exciton level is taken from Chan et al. and reflects the maximum of the feature;60 our Tc HOMO value is defined from the low binding energy onset of emission. The shaded boxes on the Tc exciton levels signify morphology-induced spreading of the energy levels. Layer thicknesses for the 100 nm Tc device are shown. | ||
An important quality influencing the probability of charge transfer between the Tc T1 exciton level and the c-Si conduction band is the alignment of these energy levels. To estimate the T1-conduction band alignment we refer to the work of Zhu and coworkers, who used pump–probe two-photon photoemission spectroscopy (2PPE) to measure a Tc T1 ionisation potential of 4.3 eV.60 For a c-Si electron affinity of 4.1 eV, and assuming vacuum level alignment, this leads to the prediction of a 0.2 eV barrier for electron injection from the Tc triplet to the c-Si interface. But the substrate and growth conditions used in the measurement by Zhu and coworkers are different to those of the present devices, presumably leading to changes in film structure.68 Ionization energies can show a strong morphology-dependence.69 In addition, exposure of the vacuum-deposited Tc films to nitrogen atmosphere or air during further processing steps can give rise to structural and chemical changes of the film itself and the hybrid interface.61 To estimate such post-growth effects, we also measured the ELA at the hybrid interface for samples in which Tc growth took place in the same setup used for solar cell production, and which were subsequently handled under nitrogen atmosphere and transferred to the UPS setup with a vacuum suitcase. Compared to the in situ deposition study, the offset between the Fermi level and the Tc HOMO level increased in magnitude by 0.1–0.2 eV. These UPS spectra can be found in Fig. S1 of the ESI.† Accordingly, the size of a possible barrier to electron injection from the Tc T1 level to the c-Si conduction band is currently not known. Attempts to measure the offset for the present system are underway.
The binding energy of any charge-transfer intermediate states formed at the hybrid interface should be much smaller than for all-organic heterojunctions, due to the large dielectric index and electron delocalisation in c-Si.48 As noted previously, a heterojunction SF device may also exploit the resonant transfer of energy from triplet excitons into c-Si, in a process akin to Dexter energy transfer. Although a mechanism is yet to be formulated for this system, recent evidence suggests that such a process may occur.70 The link between the rate of triplet exciton transfer at organic–inorganic interfaces and the ELA of the system is not yet firmly established. Further discussion on this topic is given below.
B. Device measurements
Devices with Tc thicknesses of 100 nm, 10 nm, and 0 nm (control device) were prepared according to the device scheme in Fig. 2(d). Current–voltage measurements of three such devices are shown in Fig. 3(a). The three devices showed very similar electrical characteristics, as presented in Table 1. The open circuit voltage (Voc) is within the range (645 ± 5) mV for all three devices.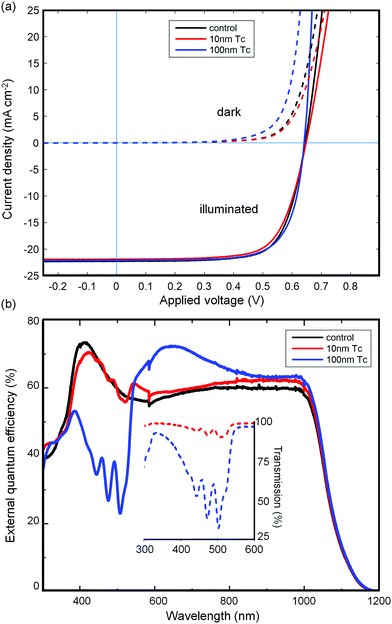 | ||
| Fig. 3 (a) Current–voltage measurements of three solar cells under illumination (solid lines) and in the dark (dashed lines). Parameters extracted from the curves are given in Table 1. (b) External quantum efficiency spectra of the three devices indicated. Transmission spectra of thin Tc films deposited on quartz glass during the same evaporation run as the corresponding devices are shown in the inset. Clear correlation between the absorption spectra and dips in the EQE indicates that a net photocurrent loss is incurred by light absorption in the tetracene layer. Determination of the actual exciton to photocurrent conversion yield requires a more detailed analysis, carried out below. | ||
| V oc (mV) | J sc (mA cm−2) | R s (Ω cm−2) | R p (kΩ cm−2) | FF | PCE (%) | |
|---|---|---|---|---|---|---|
| Control | 644 | 22.3 | 2.99 | 4.15 | 0.7 | 10.0 |
| 10 nm Tc | 648 | 21.9 | 3.71 | 4.83 | 0.7 | 9.9 |
| 100 nm Tc | 641 | 22.1 | 1.78 | 4.34 | 0.7 | 9.9 |
Since passivation of the silicon interface is directly reflected in Voc, this indicates that c-Si(111):H is passivated by thermally evaporated Tc to an extent comparable to PEDOT:PSS. This finding supports the potential of the organo-silicon heterojunction singlet fission-silicon cell, which would not be viable if such an interface gave rise to high surface recombination velocities. Likewise, a consistent fill factor with increasing Tc thickness suggests that the small hole extraction barrier at the Tc/c-Si interface, as found in the UPS study, is not a hindrance to the device.
Since evaporated polycrystalline Tc films have high roughness, there is the potential to form pinhole contacts between PEDOT:PSS and the c-Si substrate. Pinhole contacts could explain the apparent insensitivity of fill factor and Voc to the Tc thickness. To rule out pinhole contacts, we used atomic force microscopy and X-ray photoelectron spectroscopy to determine an upper limit for the presence of voids in the Tc surface, which could allow pinhole contacts to form. Then we calculated the expected series resistance for this pinhole density using a literature value of 50 mΩ cm2 for the contact resistance of PEDOT:PSS.71 For the 100 nm Tc device, PEDOT:PSS point contacts over the estimated surface coverage upper limit of 0.1% would yield a series resistance Rs of 50 Ω cm2, a factor of 10 greater than that of the measured devices. Hence we conclude that Tc is indeed acting as a hole-selective membrane on c-Si, at least in the thicker Tc layer device. Details of the measurement of the Tc surface roughness and coverage, derivation of the estimated upper pinhole density, and calculation of the Rs and Rp values are given in Section S2 of the ESI.† Compared to the control device, we assign the reduced Rs of the 100 nm Tc device to a slightly thicker PEDOT:PSS layer. The higher Rs of the 10 nm device is likely due to the roughness of the Tc film leading to poorer contact with the PEDOT:PSS layer.
The short circuit current densities of the three devices are within 2% of 22 mA cm−2, despite their differences in absorption and reflectivity. The external quantum efficiency (EQE) spectra of the devices in Fig. 3(b) suggest an explanation. The addition of an increasingly thick Tc layer causes two notable changes in the spectrum: enhanced photocurrent production for red-NIR photons, and a decrease for photons in the absorption range of tetracene. The former effect we ascribe to reduced reflectance due to the thicker organic overlayer. The latter we assign to parasitic absorption by the Tc layer, since the spectra clearly contain an imprint of the inverted Tc absorption spectrum. These two phenomena have opposite effects on Jsc, and result in the apparently steady current density as Tc is added to the device.
An EQE greater than 100% is a definitive indication of carrier multiplication, but the counterfactual is not true. Modelling the expected EQE spectrum for a low but non-zero yield of exciton-photocurrent conversion at the heterojunction is complicated. Adding tetracene to the c-Si surface changes four aspects of the optical system simultaneously: the reflectance of the interface, the absorption of the organic layer, the morphology of the PEDOT:PSS overlayer, which is birefringent,72,73 and scattering from the rough Tc layer. Consequently, with no control sample for a zero yield of triplet harvesting available, we turned to modelling to determine the extent of any photocurrent generation from the organic layer, as discussed below.
Two additional EQE measurements were conducted to test for barriers to exciton and charge transfer exciton dissociation. In one, a bias voltage was applied across the device, while in the other, cells were heated to 350 K. No signs of barriers or frustrated dissociation were seen from these experiments. The spectra and the experimental details are provided in Section S3 of the ESI.†
C. Optical modelling
Optical simulations of the control device and the 100 nm Tc device are shown in Fig. 4(a) and (b), respectively. These charts depict the relative coefficients of reflection and absorption for photons incident on the devices at each calculated wavelength, and the photocurrent density in each simulated layer once these coefficients are integrated over the AM1.5G spectrum. The simulated short circuit current density for the two devices is 10–15% greater than that of the measured devices. This difference is consistent with current loss due to reflections off the front contact grid of the devices, as the contact grid occupies 12% of the cell active area. Details of the contact grid are given in Section S4 of the ESI.†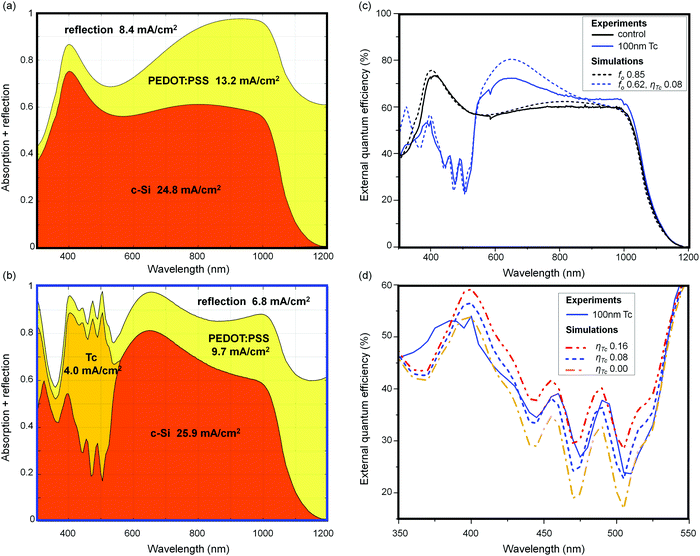 | ||
| Fig. 4 The optical absorption data of a simulated control device (a) and 100 nm Tc device (b) generated using GenPro4.74 Current densities are calculated for each device layer, including reflections to air. Model EQE spectra in (c) were constructed using the optical data on (a and b) folded with an internal quantum efficiency for the each active layer. The best fit to the measured 100 nm Tc spectrum is obtained for ηTc = 0.08, suggesting some exciton harvesting is occurring. A detailed view of the Tc absorption region is shown in (d); alongside the two spectra from (a) there are two otherwise-identical simulations with ηTc of 0 and 0.16. The fit is consistent with a non-zero yield of exciton harvesting from Tc. | ||
Measured and modelled EQE spectra of the 100 nm Tc device and the control device are shown in Fig. 4(c). The model EQE spectra were constructed by folding the optical data in Fig. 4(a) and (b) with three parameters: the internal quantum efficiencies for the active layers of each device, denoted ηTc (nm) and ηSi (nm), and fo, which represented the fraction of the birefringent PEDOT:PSS overlayer presenting the ordinary optical axis to the surface normal. This parameter had a strong effect on the red-NIR portion of the simulated EQE spectrum, but only a weak effect in the region of Tc absorption, as demonstrated in Fig. S6 of the ESI.† The thickness of the PEDOT:PSS and Tc films was allowed to vary during fit optimisation; the optimised thicknesses agreed well with those measured for the real devices. The fitted values are given in Table S2 of the ESI.† We did not model the 10 nm Tc device because the simulation's assumption of device layers with uniform thickness broke down for that system. We made a simplification to the internal quantum yields, assuming ηTc (nm) and ηSi (nm) to be flat across the measured spectrum, hence these are presented as single values from here on.
For the 100 nm Tc device, the optimised ηTc value is 0.08, of a possible maximum of 2.0 (due to exciton multiplication by SF). In Fig. 4(d) we show model EQE spectra for the same device with ηTc set to 0.0 and 0.16, as an indicative confidence interval to this finding. The discrepancies between the fit and the measured spectrum in Fig. 4(c) are most likely due to spatial variation in fo due to the rough Tc layer affecting the PEDOT:PSS orientation. No such discrepancy is seen in the Tc-free control device, and the deviation is within the red-NIR portion of the spectrum where the birefringence of PEDOT:PSS becomes significant. Critically, the model EQE spectrum is largely unaffected by fo in the Tc absorption region, which strengthens the finding of non-zero exciton harvesting despite these discrepancies in the EQE spectrum fitting.
The potential small photocurrent contribution from the Tc layer is approximately 0.3 mA cm−2. Further measurements would be necessary to corroborate this finding of a non-zero ηTc value. An ideal method would be a magnetic field-dependent photocurrent measurement, which could tease out a Tc photocurrent contribution by the characteristic effect of a magnetic field on the rate of non-geminate triplet pair recombination.75 Our setup presently lacks the sensitivity to perform this measurement for this low current density.
To bolster the veracity of the non-zero ηTc result, we performed two additional EQE simulations in an attempt to reproduce the measured 100 nm Tc EQE spectrum without a contribution from the Tc layer. These model spectra are depicted in Section S5 of the ESI.† In brief, we allowed fo, layer thicknesses, and ηSi to vary freely while constraining ηTc to zero. We also modelled a device which permitted photocurrent generation from the PEDOT:PSS layer. None of these simulated EQE spectra reproduced the magnitude of the Tc absorption imprints, undershooting the measured peaks in a way that closely resembles the ηTc = 0.0 scenario in Fig. 4(d).
We compare our result of a small but non-zero ηTc to that of Piland et al., who found no clear evidence of exciton harvesting at the Tc/c-Si:H interface using time-resolved photoluminescence measurements.46 The photoluminescence dynamics of Tc in the vicinity of c-Si are complicated, with coupled singlet and triplet exciton channels, proximity-dependent dielectric effects of the bulk silicon, and polymorphism affecting rates. While an efficient exciton quenching effect would be readily apparent in this measurement, we contend that a quenching effect of the size suggested by our simulations may be difficult to detect. On the other hand, our use of a working device allows a measurement of exciton harvesting that is insensitive to all processes not involved in photocurrent generation.
For the control and the 100 nm Tc devices, parasitic absorption in the PEDOT:PSS layer is significant, consuming the equivalent of 13.2 mA cm−2 in the former, and 9.7 mA cm−2 in the latter. Reducing this figure through re-engineering of the top contact is a clear path for device improvement. Reflections consume 8.4 and 6.8 mA cm−2 in the control and Tc devices, respectively. The high reflectivity of the device stems from the large refractive index step at the planar organo-silicon interface. Conventional silicon anti-reflection coatings are not feasible for the SF heterojunction design, which requires direct contact of the organic and silicon materials. Geometric or nanophotonic light-management schemes are a better prospect. To this end, using GenPro4 we simulated a device with a standard KOH-etched pyramidally-textured front surface on the c-Si wafer, and an otherwise-unchanged layer structure. The simulation charts and surface texture profile are supplied in the ESI.† Reflection losses for this device decreased to 1.6 mA cm−2, while parasitic PEDOT:PSS absorption increased slightly to 8.3 mA cm−2. When the least-parasitic conformation of the PEDOT:PSS overlayer was selected, by setting fo = 0, reflection loss increased slightly but was more than compensated by a reduction in parasitic absorption. These results show that by engineering the optical structure of the device, it should be possible to overcome the intrinsically high reflectivity of a planar organo-silicon heterojunction.
D. Overcoming hindered exciton harvesting
There are a number of possible explanations for the low exciton to photocurrent conversion yield of the 100 nm Tc device. Through examining these, a body of work for further device developments is made clear. The reported organo-silicon heterojunction device provides a stable cell architecture in which these and other SF-silicon experiments may be implemented.The deposition of organic chromophores onto c-Si:H may result in the formation of covalent bonds between the c-Si surface and the first organic monolayer, degrading the Tc and forming a barrier that prevents the approach of excitons to the heterointerface. Campbell and Crone propose this mechanism for their hybrid device, discussed earlier.47 However, reports of the decomposition of Tc on c-Si surfaces have, to our knowledge, used reconstructed Si surfaces, rather than the hydrogen-passivated c-Si surfaces used in our devices, which have greatly reduced surface reactivity.76 Another factor weighing against this argument is the effective hole extraction from c-Si by Tc. Hole extraction requires short-ranged interaction across the heterointerface akin to an exciton dissociation process. Disruption of hole extraction by a degraded interface monolayer may therefore cause a degradation of the fill factor, as is seen in c-Si/PEDOT:PSS devices with sub-oxide growth at the hybrid interface.77 No such effect is seen in the electrical measurements of these devices. In any case, chemical passivation of the c-Si surface using covalently-bound organic chromophores may be one method to address issues of residual reactivity, while potentially improving other aspects of the device.
The indirect band gap of c-Si suggests the prospect of momentum conservation impeding the efficient conversion of triplet excitons to photocurrent. If exciton dissociation was to occur by electron injection to the c-Si conduction band minimum, with hole retention in the Tc layer, a change in linear momentum is required. But the momentum required for a non-vertical transition could be taken up by recoil of the donor molecule, as suggested by Dexter.6 In fact, the size of the triplet exciton in a polyacene was measured to be 3.8 Å,78 similar to the silicon lattice constant of 3.6 Å. Thus the triplet exciton is localized on the scale of the Si band-structure, and extensively delocalized in k-space. Hence momentum arguments may not play an important role in triplet exciton harvesting at the silicon–organic interface. Our temperature-dependent EQE measurements yielded no evidence of increased temperatures modifying the EQE of the organic layer, which is consistent with this idea.
Another possibility for a low exciton-to-photocurrent conversion yield is the potential mismatch between the Tc triplet ionisation potential and the c-Si conduction band, inferred from literature 2PPE data.60 This would entail a lack of driving force for exciton dissociation. If so, the addition of a molecular dipole layer at the organic–inorganic interface might be used to produce a more staggered ELA between the organic and silicon materials, making exciton dissociation more favourable.79 Thin inorganic interlayers might also be implemented to achieve the same result. New SF chromophores with a slightly higher triplet energy compared to Tc, or a smaller ionisation potential, may also be interesting in this respect.
Given the complexity of the organo-silicon heterointerface, some combination of the above factors may be responsible for the low exciton conversion yield. Further device development is likely to shed light on the details of this system. The device structure reported is a robust platform that will allow many such investigations to be undertaken.
The potential for triplet excitons to resonantly transfer to silicon also warrants further study. The interplay between the ELA and the rate of triplet energy transfer (TET) at organic–inorganic interfaces is yet to be fully elucidated. Recent work on organic–inorganic TET focuses heavily on nanocrystalline metal chalcogenide particles functionalised with linear acene derivatives.80–84 Efficient TET between these components in both directions has been demonstrated,58,85 although no systematic study of the effect of ELA on TET has been conducted. However, an argument based on exciton binding energies points towards TET being insensitive to the ELA at donor–acceptor interfaces. For TET between an acene molecule such as pentacene and a lead chalcogenide nanoparticle, it is well-established that the donor and acceptor state energies should be in resonance.58 If alignment between the frontier energy levels of the donor and acceptor is also required for efficient TET, it follows that the exciton binding energy in the donor and acceptor must be similar. However, the exciton binding energy in small lead chalcogenide quantum dots is around 100 meV86 and exceeds 1 eV for the first triplet level in pentacene.87 Since efficient TET occurs between these materials, type-I alignment of the frontier energy levels is presumably not a precondition for efficient TET.
III. Experimental
A. UPS measurements
Ultraviolet photoemission spectroscopy (UPS) was performned at the synchrotron end station SurICat (BESSY II, Berlin). RCA-cleaned c-Si(111) substrates were evacuated in the load lock approximately 10 minutes after HF treatment. Tc was deposited by thermal evaporation at 380 K in a sample preparation chamber with base pressure 5 × 10−7 mbar, then the sample was transferred to the analysis chamber (base pressure 5 × 10−9 mbar) without breaking vacuum. Three samples were investigated: (i) a hydrogen-passivated c-Si reference surface, and (ii) 10 nm and (iii) 30 nm evaporated Tc on an identical surface. Excitation was by 35 eV photons in a low fluence configuration. Samples were biased at −10 V to clear the analyzer work function. Spectra were recorded at a 45° take-off angle to increase surface sensitivity, with the exception of the spectrum employed for determining the valence band maximum for H-passivated c-Si, which was recorded in normal emission geometry.B. Device fabrication
Device fabrication started with a 4-inch diameter 280 μm thick, (111)-oriented, 3 Ω cm−1 resistivity, phosphorus-doped float zone-grown Si wafer, polished on both sides and cleaned using the RCA method. The rear, electron contact was fabricated first. The design of the electron contact was based on the high-efficiency silicon heterojunction concept, and was fabricated as described in ref. 88, omitting the conventional indium-doped tin oxide layer to reduce the device complexity. The result is a structure consisting of the crystalline silicon wafer, a thin intrinsic amorphous Si layer (5 nm) and a thicker highly-doped n-type amorphous silicon layer (15 nm). After fabrication of the rear contact, the substrate was cut into a series of 1 cm2 half-cells.The organic SF layer and front contact were deposited next. In a clean-room environment, each half-cell was immersed in dilute hydrofluoric acid (1%, 2 min). After removal of the acid in a nitrogen gas stream, the substrates were immediately placed in a nitrogen-filled glovebox, then loaded into a thermal evaporator housed within it. Polycrystalline Tc layers were grown by thermal evaporation of Tc (sublimed grade, 99.99% purity, Sigma-Aldrich) at 380 K and base pressure of 10−6 mbar. The deposition rate was 1 Å s−1, determined by a quartz crystal microbalance. After Tc deposition, samples were moved back into the nitrogen glovebox, and a commercial pre-mixed dispersion of PEDOT:PSS (Clevios F HC solar, Heraeus) was spin-coated over the Tc layer at 1500 rpm for 10 s. Samples were then annealed for 90 min in a vacuum oven at 330 K. This resulted in a PEDOT:PSS layer thickness of approximately 150 nm, determined using scanning electron microscopy measurements of cleaved samples.
Metallisation of the front and rear contacts was carried out using thermal evaporation. The rear of each device was coated with 750 nm of silver, and the front with a 300 nm silver contact grid evaporated through a shadow mask. Devices controlling for the absence of a SF layer were prepared by omitting the Tc deposition step, spin-coating PEDOT:PSS directly onto hydrogen-passivated c-Si.
C. Electrical measurements
Dark and illuminated IV curves were measured in a four-point probe setup employing a source-measure unit (Keithley). Devices were pneumatically fixed on a temperature-stabilised metal chuck, held at 25 °C, which also served as the electron back contact. The hole contact was made using gold wires pressed onto the front contact grid. For calibration of the Class AAA solar simulator a certified c-Si reference cell was employed. AM1.5G test conditions with 1000 W m−2 light intensity were achieved by matching the short-circuit current density of the reference cell to its certified value by adjusting the electrical power of the light source, which consisted of a Xe lamp and a halogen lamp.External quantum efficiency spectra were measured using a home-built setup utilising a 300 W xenon lamp, a monochromator (CS260, Newport), a lock-in amplifier, and mechanical chopping of the incidient beam. A calibrated silicon solar cell was used to establish reference values. Device measurements were carried out in air, and repeated measurements showed no indications of device degradation over the timescale of the measurements.
The reported device results were reproduced over three independent device fabrication and measurement runs.
D. EQE spectrum model
Model EQE spectra were produced in two steps: first, optical simulations of the device structure were conducted using the MATLAB optical simulations package GenPro4, developed at Delft University of Technology.74 The program is based on the transfer-matrix algorithm. Device structures are divided into coherent and incoherent layers, then the program calculates Absx (nm), the fraction of the incident radiation absorbed in device layer x, for each device layer, across a user-specified wavelength range. The equivalent short circuit current density absorbed in each layer is also calculated assuming AM1.5G conditions.Input parameters are, for a planar device, the one-dimensional device structure and the complex refractive indices of each layer material. We added a PEDOT:PSS birefringence parameter, fo, to tune the complex refractive index of the PEDOT:PSS layer to respond to the layer morphology changing with the addition of Tc. fo represents the proportion of PEDOT:PSS which presents the ordinary optical axis to normally-incident radiation. Device structure inputs were as-measured for the manufactured devices, while the refractive index data were sourced from a reference database, with the exception of PEDOT:PSS and Tc. For Tc, transmission and reflection spectra of reference films evaporated onto glass were measured, then the complex refractive index was back-calculated. For PEDOT:PSS, values from a previous study were used, as detailed in ref. 77.
From the simulated optical data, EQE spectra were constructed as follows: EQE (nm) = ηTcAbsTc (nm) + ηSiAbsSi (nm), where ηTc and ηSi are the internal quantum efficiencies of photocurrent generation for the silicon and Tc layers of the device, assuming for simplified modelling that the quantum efficiencies were constant across the spectrum. For devices omitting Tc, AbsTc and ηTc are zero.
To fit an EQE spectrum, the thickness of the Tc and PEDOT:PSS layers, the birefringence parameter fo, and ηTc were allowed to vary to optimise the fit. The value of ηSi was fixed at 0.99, standard for silicon devices. The layer thicknesses from the optimised fits are supplied in Table S2 of the ESI,† and agree well with the experimentally-determined values.
Simulation of the effect of an etched, textured c-Si front surface on the Tc device was accomplished by loading a height map of such a textured surface, as shown in Fig. S5 of the ESI.† Scattering by non-planar interfaces are treated in GenPro4 by separately calculating scatter matrices and sub-fluxes for each scattered component.
IV. Conclusion
Singlet fission is an attractive method for reducing thermalisation losses in silicon solar cells, which in their best-performing manifestation are approaching the Auger recombination conversion efficiency limit. We produced and characterised solar cells that incorporate tetracene, a singlet fission material, into a direct heterojunction with crystalline silicon. This device configuration aims to harvest triplet excitons from the singlet fission layer by exciton dissociation or resonant energy transfer at the organo-silicon interface, while the organic layer acts concurrently as the hole-selective contact for the c-Si absorber. Device performance indicates that this is a promising device design for augmenting c-Si with singlet fission. The c-Si remains well-passivated by the organic film, and the energy level alignment allows excellent charge transport and blocking, allowing Tc to effectively extract holes from c-Si while maintaining a high fill factor. Exciton harvesting from the Tc layer is not efficient in the devices reported, with simulation suggesting an 8% exciton to photocurrent conversion efficiency. While Tc is thus acting as an overall parasitic absorber, the reported device structure is a robust platform for efforts to increase this value beyond 100%. Many pathways exist by which exciton harvesting may be enhanced in this solar cell design. Primarily, these consist of altering the energy level alignment at the heterojunction, increasing the triplet exciton energy of the singlet fission layer, or designing interlayers that enhance the exciton-photocurrent conversion yield. Realisation of a break-even conversion yield from the organic layer would mark the arrival of a new technology in the space of multi-threshold silicon solar cells with potential to break the Shockley–Queisser limit.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support was provided by the German Federal Ministry for Research and Education (BMBF) through the project “Silicon In-situ Spectroscopy at the Synchrotron” (SISSY), Grant No. BMBF-03SF0403, and the Deutscher Akademischer Austauschdienst (DAAD). RWM thanks the Helmholtz Association for funding and support. T. W. S acknowledges funding from the Australian Research Council (FT130100177, CE170100026). This work was supported by a Marie Sklodowska-Curie Individual Fellowship (705113). We gratefully acknowledge Lars Korte of Helmholtz-Zentrum Berlin, for assistance with device preparation and organic deposition, and the Norbert Koch group of Humboldt University of Berlin, for providing access to their UPS setups.References
- F. I. for Solar Energy Systems, Photovoltaics Report, published online, updated: 06-06-2016.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510 CrossRef.
- A. Richter, M. Hermle and S. W. Glunz, IEEE J. Photovolt., 2013, 3, 1184 Search PubMed.
- K. Yoshikawa, H. Kawasaki, W. Yoshida, T. Irie, K. Konishi, K. Nakano, T. Uto, D. Adachi, M. Kanematsu, H. Uzu and K. Yamamoto, Nat. Energy, 2017, 2, 17032 CrossRef.
- L. C. Hirst and N. J. Ekins-Daukes, Prog. Photovoltaics Res. Appl., 2011, 19, 286 CrossRef.
- D. L. Dexter, J. Lumin., 1979, 18, 779 CrossRef.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891 CrossRef PubMed.
- S. Singh, W. J. Jones, W. Siebrand, B. P. Stoicheff and W. G. Schneider, J. Chem. Phys., 1965, 42, 330 CrossRef.
- A. F. Schwerin, J. C. Johnson, M. B. Smith, P. Sreearunothai, D. Popovic, J. Cerny, Z. Havlas, I. Paci, A. Akdag, M. K. MacLeod, X. Chen, D. E. David, M. A. Ratner, J. R. Miller, A. J. Nozik and J. Michl, J. Phys. Chem. A, 2010, 114, 1457 CrossRef PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361 CrossRef PubMed.
- N. Monahan and X.-Y. Zhu, Annu. Rev. Phys. Chem., 2015, 66, 601 CrossRef PubMed.
- M. J. Y. Tayebjee, A. A. Gray-Weale and T. W. Schmidt, J. Phys. Chem. Lett., 2012, 3, 2749 CrossRef.
- J. L. Xia, S. N. Sanders, W. Cheng, J. Z. Low, J. P. Liu, L. M. Campos and T. L. Sun, Adv. Mater., 2017, 29, 11 CrossRef PubMed.
- M. J. Y. Tayebjee, R. G. C. R. Clady and T. W. Schmidt, Phys. Chem. Chem. Phys., 2013, 15, 14797 RSC.
- D. H. Arias, J. L. Ryerson, J. D. Cook, N. H. Damrauer and J. C. Johnson, Chem. Sci., 2016, 7, 1185 RSC.
- L. R. Weiss, S. L. Bayliss, F. Kraffert, K. J. Thorley, J. E. Anthony, R. Bittl, R. H. Friend, A. Rao, N. C. Greenham and J. Behrends, Nat. Phys., 2017, 13, 176 Search PubMed.
- J. L. Ryerson, J. N. Schrauben, A. J. Ferguson, S. C. Sahoo, P. Naumov, Z. Havlas, J. Michl, A. J. Nozik and J. C. Johnson, J. Phys. Chem. C, 2014, 118, 12121 CrossRef.
- M. J. Y. Tayebjee, K. N. Schwarz, R. W. MacQueen, M. Dvorák, A. W. C. Lam, K. P. Ghiggino, D. R. McCamey, T. W. Schmidt and G. J. Conibeer, J. Phys. Chem. C, 2016, 120, 157 CrossRef.
- R. D. Pensack, C. Grieco, G. E. Purdum, S. M. Mazza, A. J. Tilley, E. E. Ostroumov, D. S. Seferos, Y.-L. Loo, J. B. Asbury, J. E. Anthony and G. D. Scholes, Mater. Horiz., 2017, 4, 915 RSC.
- A. Thampi, H. L. Stern, A. Cheminal, M. J. Y. Tayebjee, A. J. Petty, J. E. Anthony and A. Rao, J. Am. Chem. Soc., 2018, 140, 4613 CrossRef PubMed.
- A. Ryasnyanskiy and I. Biaggio, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 193203 CrossRef.
- T. Zhu, Y. Wan, Z. Guo, J. Johnson and L. Huang, Adv. Mater., 2016, 28, 7539 CrossRef PubMed.
- M. J. Y. Tayebjee, S. N. Sanders, E. Kumarasamy, L. M. Campos, M. Y. Sfeir and D. R. McCamey, Nat. Phys., 2017, 13, 182 Search PubMed.
- E. Kumarasamy, S. N. Sanders, M. J. Y. Tayebjee, A. Asadpoordarvish, T. J. H. Hele, E. G. Fuemmeler, A. B. Pun, L. M. Yablon, J. Z. Low, D. W. Paley, J. C. Dean, B. Choi, G. D. Scholes, M. L. Steigerwald, N. Ananth, D. R. McCamey, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2017, 139, 12488–12494 CrossRef PubMed.
- B. J. Walker, A. J. Musser, D. Beljonne and R. H. Friend, Nat. Chem., 2013, 5, 1019 CrossRef PubMed.
- A. B. Pun, S. N. Sanders, E. Kumarasamy, M. Y. Sfeir, D. N. Congreve and L. M. Campos, Adv. Mater., 2017, 29, 1701416 CrossRef PubMed.
- C. Grieco, G. S. Doucette, R. D. Pensack, M. M. Payne, A. Rimshaw, G. D. Scholes, J. E. Anthony and J. B. Asbury, J. Am. Chem. Soc., 2016, 138, 16069 CrossRef PubMed.
- N. R. Monahan, D. Sun, H. Tamura, K. W. Williams, B. Xu, Y. Zhong, B. Kumar, C. Nuckolls, A. R. Harutyunyan, G. Chen, H.-L. Dai, D. Beljonne, Y. Rao and X. Y. Zhu, Nat. Chem., 2017, 9, 341 CrossRef PubMed.
- S. Yoo, B. Domercq and B. Kippelen, Appl. Phys. Lett., 2004, 85, 5427 CrossRef.
- A. K. Pandey, S. Dabos-Seignon and J.-M. Nunzi, Appl. Phys. Lett., 2006, 89, 113506 CrossRef.
- J. Lee, P. Jadhav and M. A. Baldo, Appl. Phys. Lett., 2009, 95, 033301 CrossRef.
- A. Rao, M. W. B. Wilson, J. M. Hodgkiss, S. Albert-Seifried, H. Bässler and R. H. Friend, J. Am. Chem. Soc., 2010, 132, 12698 CrossRef PubMed.
- P. D. Reusswig, D. N. Congreve, N. J. Thompson and M. A. Baldo, Appl. Phys. Lett., 2012, 101, 113304 CrossRef.
- M. Tabachnyk, B. Ehrler, S. Bayliss, R. H. Friend and N. C. Greenham, Appl. Phys. Lett., 2013, 103, 153302 CrossRef.
- N. J. Thompson, D. N. Congreve, D. Goldberg, V. M. Menon and M. A. Baldo, Appl. Phys. Lett., 2013, 103, 263302 CrossRef.
- J. Lee, P. Jadhav, P. D. Reusswig, S. R. Yost, N. J. Thompson, D. N. Congreve, E. Hontz, T. V. Voorhis and M. A. Baldo, Acc. Chem. Res., 2013, 46, 1300 CrossRef PubMed.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334 CrossRef PubMed.
- T. C. Wu, N. J. Thompson, D. N. Congreve, E. Hontz, S. R. Yost, T. Van Voorhis and M. A. Baldo, Appl. Phys. Lett., 2014, 104, 193901 CrossRef.
- N. J. Thompson, E. Hontz, D. N. Congreve, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Adv. Mater., 2014, 26, 1366 CrossRef PubMed.
- P. J. Jadhav, A. Mohanty, J. Sussman, J. Lee and M. A. Baldo, Nano Lett., 2011, 11, 1495 CrossRef PubMed.
- P. J. Jadhav, P. R. Brown, N. Thompson, B. Wunsch, A. Mohanty, S. R. Yost, E. Hontz, T. Van Voorhis, M. G. Bawendi, V. Bulovic and M. A. Baldo, Adv. Mater., 2012, 24, 6169 CrossRef PubMed.
- B. Ehrler, M. W. B. Wilson, A. Rao, R. H. Friend and N. C. Greenham, Nano Lett., 2012, 12, 1053 CrossRef PubMed.
- B. Ehrler, K. P. Musselman, M. L. Böhm, R. H. Friend and N. C. Greenham, Appl. Phys. Lett., 2012, 101, 153507 CrossRef.
- B. Ehrler, B. J. Walker, M. L. Böhm, M. W. B. Wilson, Y. Vaynzof, R. H. Friend and N. C. Greenham, Nat. Commun., 2012, 3, 1019 CrossRef PubMed.
- L. Yang, M. Tabachnyk, S. L. Bayliss, M. L. Böhm, K. Broch, N. C. Greenham, R. H. Friend and B. Ehrler, Nano Lett., 2015, 15, 354 CrossRef PubMed.
- G. B. Piland, J. J. Burdett, T.-Y. Hung, P.-H. Chen, C.-F. Lin, T.-L. Chiu, J.-H. Lee and C. J. Bardeen, Chem. Phys. Lett., 2014, 601, 33 CrossRef.
- I. H. Campbell and B. K. Crone, J. Appl. Phys., 2009, 106, 113704 CrossRef.
- C. K. Renshaw and S. R. Forrest, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045302 CrossRef.
- A. Panda, C. K. Renshaw, A. Oskooi, K. Lee and S. R. Forrest, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045303 CrossRef.
- L. M. Pazos-Outón, J. M. Lee, M. H. Futscher, A. Kirch, M. Tabachnyk, R. H. Friend and B. Ehrler, ACS Energy Lett., 2017, 2, 476 CrossRef PubMed.
- X. Y. Zhu, J. Phys. Chem. Lett., 2014, 5, 2283 CrossRef PubMed.
- A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 17063 CrossRef.
- S. W. Tabernig, B. Daiber, T. Wang and B. Ehrler, J. Photonics Energy, 2018, 8, 022008 Search PubMed.
- S. Albrecht, M. Saliba, J. P. Correa Baena, F. Lang, L. Kegelmann, M. Mews, L. Steier, A. Abate, J. Rappich, L. Korte, R. Schlatmann, M. K. Nazeeruddin, A. Hagfeldt, M. Grätzel and B. Rech, Energy Environ. Sci., 2016, 9, 81 RSC.
- K. A. Bush, A. F. Palmstrom, Z. J. Yu, M. Boccard, R. Cheacharoen, J. P. Mailoa, D. P. McMeekin, R. L. Z. Hoye, C. D. Bailie, T. Leijtens, I. M. Peters, M. C. Minichetti, N. Rolston, R. Prasanna, S. Sofia, D. Harwood, W. Ma, F. Moghadam, H. J. Snaith, T. Buonassisi, Z. C. Holman, S. F. Bent and M. D. McGehee, Nat. Energy, 2017, 2, 17009 CrossRef.
- M. J. Y. Tayebjee, A. Mahboubi Soufiani and G. J. Conibeer, J. Phys. Chem. C, 2014, 118, 2298 CrossRef.
- F. Bianchi, S. Sadofev, R. Schlesinger, B. Kobin, S. Hecht, N. Koch, F. Henneberger and S. Blumstengel, Appl. Phys. Lett., 2014, 105, 233301 CrossRef.
- M. Tabachnyk, B. Ehrler, S. Gelinas, M. L. Böhm, B. J. Walker, K. P. Musselman, N. C. Greenham, R. H. Friend and A. Rao, Nat. Mater., 2014, 13, 1033 CrossRef PubMed.
- R. Schlesinger, F. Bianchi, S. Blumstengel, C. Christodoulou, R. Ovsyannikov, B. Kobin, K. Moudgil, S. Barlow, S. Hecht, S. R. Marder, F. Henneberger and N. Koch, Nat. Commun., 2015, 6, 6754 CrossRef PubMed.
- W.-L. Chan, M. Ligges and X.-Y. Zhu, Nat. Chem., 2012, 4, 840 CrossRef PubMed.
- A. Vollmer, O. D. Jurchescu, I. Arfaoui, I. Salzmann, T. T. M. Palstra, P. Rudolf, J. Niemax, J. Pflaum, J. P. Rabe and N. Koch, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 17, 339 CrossRef PubMed.
- M. Kochi, Y. Harada, T. Hirooka and H. Inokuchi, Bull. Chem. Soc. Jpn., 1970, 43, 2690 CrossRef.
- Y. Tomkiewicz, R. P. Groff and P. Avakian, J. Chem. Phys., 1971, 54, 4504 CrossRef.
- K. R. Graham, P. Erwin, D. Nordlund, K. Vandewal, R. Li, G. O. Ngongang Ndjawa, E. T. Hoke, A. Salleo, M. E. Thompson, M. D. McGehee and A. Amassian, Adv. Mater., 2013, 25, 6076 CrossRef PubMed.
- M. Liebhaber, M. Mews, T. F. Schulze, L. Korte, B. Rech and K. Lips, Appl. Phys. Lett., 2015, 106, 031601 CrossRef.
- M. Mews, M. Liebhaber, B. Rech and L. Korte, Appl. Phys. Lett., 2015, 107, 013902 CrossRef.
- S. M. Sze and K. N. Kwok, Physics of Semiconductor Devices, John Wiley & Sons, Hoboken, New Jersey, 2007.
- R. K. Nahm and J. R. Engstrom, J. Chem. Phys., 2017, 146, 052815 CrossRef PubMed.
- J. Niederhausen, S. Duhm, G. Heimel, C. Bürker, Q. Xin, A. Wilke, A. Vollmer, F. Schreiber, S. Kera, J. P. Rabe, N. Ueno and N. Koch, J. Chem. Phys., 2014, 140, 014705 CrossRef PubMed.
- B. Ehrler, Personal correspondence, 2018.
- J. Bullock, Y. Wan, M. Hettick, J. Geissbühler, A. J. Ong, D. Kiriya, D. Yan, T. Allen, J. Peng, X. Zhang, C. M. Sutter-Fella, S. D. Wolf, C. Ballif, A. Cuevas and A. Javey, IEEE conference proceedings PVSEC43, 2016, 210.
- L. A. A. Pettersson, F. Carlsson, O. Inganäs and H. Arwin, Thin Solid Films, 1998, 313–314, 356 CrossRef.
- L. A. A. Pettersson, S. Ghosh and O. Inganäs, Org. Electron., 2002, 3, 143 CrossRef.
- R. Santbergen, T. Meguro, T. Suezaki, G. Koizumi, K. Yamamoto and M. Zeman, IEEE J. Photovolt., 2017, 7, 919 Search PubMed.
- J. J. Burdett, G. B. Piland and C. J. Bardeen, Chem. Phys. Lett., 2013, 585, 1 CrossRef.
- H. Mao, D. Guan, M. Chen, W. Dou, F. Song, H. Zhang, H. Li, P. He and S. Bao, J. Chem. Phys., 2009, 131, 044703 CrossRef PubMed.
- S. Jäckle, M. Liebhaber, C. Gersmann, M. Mews, K. Jäger, S. Christiansen and K. Lips, Sci. Rep., 2017, 7, 2170 CrossRef PubMed.
- S. L. Bayliss, A. D. Chepelianskii, A. Sepe, B. J. Walker, B. Ehrler, M. J. Bruzek, J. E. Anthony and N. C. Greenham, Phys. Rev. Lett., 2014, 112, 238701 CrossRef PubMed.
- M. Timpel, M. V. Nardi, G. Ligorio, B. Wegner, M. Patzel, B. Kobin, S. Hecht and N. Koch, ACS Appl. Mater. Interfaces, 2015, 7, 11900 CrossRef PubMed.
- D. M. Kroupa, D. H. Arias, J. L. Blackburn, G. M. Carroll, D. B. Granger, J. E. Anthony, M. C. Beard and J. C. Johnson, Nano Lett., 2018, 18, 865 CrossRef PubMed.
- J. A. Bender, E. K. Raulerson, X. Li, T. Goldzak, P. Xia, T. Van Voorhis, M. L. Tang and S. T. Roberts, J. Am. Chem. Soc., 2018, 140, 7543 CrossRef PubMed.
- L. Nienhaus, M. F. Wu, N. Geva, J. J. Shepherd, M. W. B. Wilson, V. Bulovic, T. Van Voorhis, M. A. Baldo and M. G. Bawendi, ACS Nano, 2017, 11, 7848 CrossRef PubMed.
- S. Garakyaraghi, C. Mongin, D. B. Granger, J. E. Anthony and F. N. Castellano, J. Phys. Chem. Lett., 2017, 8, 1458 CrossRef PubMed.
- Z. Y. Huang, X. Li, M. Mahboub, K. M. Hanson, V. M. Nichols, H. Le, M. L. Tang and C. J. Bardeen, Nano Lett., 2015, 15, 5552 CrossRef PubMed.
- M. Wu, D. N. Congreve, M. W. B. Wilson, J. Jean, N. Geva, M. Welborn, T. Van Voorhis, V. Bulovic, M. G. Bawendi and M. A. Baldo, Nat. Photonics, 2016, 10, 31 CrossRef.
- J. J. Choi, J. Luria, B.-R. Hyun, A. C. Bartnik, L. Sun, Y.-F. Lim, J. A. Marohn, F. W. Wise and T. Hanrath, Nano Lett., 2010, 10, 1805 CrossRef PubMed.
- K. Hummer and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 4 CrossRef.
- M. Mews, L. Korte and B. Rech, Sol. Energy Mater. Sol. Cells, 2016, 158, 77 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh00853a |
| This journal is © The Royal Society of Chemistry 2018 |