Open Access Article
Open Access ArticleAdditive manufacturing of complex micro-architected graphene aerogels†
Ryan M.
Hensleigh
 a,
Huachen
Cui
a,
James S.
Oakdale
b,
Jianchao C.
Ye
b,
Patrick G.
Campbell
b,
Eric B.
Duoss
b,
Christopher M.
Spadaccini
a,
Huachen
Cui
a,
James S.
Oakdale
b,
Jianchao C.
Ye
b,
Patrick G.
Campbell
b,
Eric B.
Duoss
b,
Christopher M.
Spadaccini
 b,
Xiaoyu
Zheng
*a and
Marcus A.
Worsley
*b
b,
Xiaoyu
Zheng
*a and
Marcus A.
Worsley
*b
aVirginia Polytechnic Institute and State University, Blacksburg, VA 24061, USA. E-mail: raynexzheng@vt.edu
bLawrence Livermore National Laboratory, Livermore, CA 24060, USA. E-mail: worsley1@llnl.gov
First published on 13th August 2018
Abstract
3D graphene foams exhibit immense degradation of mechanical properties. Micro-architecture can alleviate this problem, but no current technique meets the manufacturing requirements. Herein we developed a light-based 3D printing process to create hierarchical graphene structures with arbitrary complexity and order-of-magnitude finer features, showing enhanced mechanical properties at decreasing density.
Conceptual insightsPristine graphene is one of the stiffest materials ever measured, yet graphene foams experience such massive degradation in mechanical properties that they are worse than polymer foams at low densities. (Z. Qin, G. S. Jung, M. J. Kang and M. J. Buehler, Sci. Adv., 2017, 3, e1601536). 3D printed mechanical metamaterials have shown the unprecedented ability to alleviate such degradation, but all current graphene foam 3D printing techniques are unable to produce such complex metamaterial architectures due to insufficient resolution and toolpath limitations. Here we demonstrate high-resolution graphene foams incorporating hierarchical architecture which reduces mechanical degradation of graphene foams with decreasing density. Our technique achieves an order-of-magnitude finer resolution and far more intricate structures than any previous method. This technique opens new possibilities not only to enhance graphene foam mechanical properties, but to explore complex architectures and mesoscale effects for other graphene applications including energy storage and conversion, separations, and catalysis. |
Graphene is an atomically thin, two-dimensional (2D) carbon material with exceptional properties including a large specific surface area (2600 m2 g−1)1 and impressive electrical conductivity (8000 S m−1)2 all while being one of the stiffest materials ever measured (1 TPa).3 However, to fully exploit these properties for applications including catalysis,4 and energy storage,5 translation of 2D graphene into three-dimensional (3D) structures which maintain its exceptional properties has been particularly challenging. 3D graphenes (3DGs) largely consist of randomly interconnected sheets with no topological control, resulting in a sharp degradation of mechanical properties compared to pristine graphene, anywhere from a factor of 105 to 108 for elastic modulus (E).6,7 Understanding and overcoming this massive loss in mechanical properties is critical for 3DG application and development.
Following Maxwell's stability criterion in cellular structures, 3DGs’ mechanical degradation arises from their stochastic, bending-dominated cellular layout, carrying load by flexure of the sheets instead of tension and compression.8–10 The severity of degradation intrinsically depends on the density (ρ), and follows the proportion, E ∝ρn, where the scaling factor n for 3DGs is approximately 2.73, worse than stochastic polymer foams with n = 2.10
3D printing has been utilized to fabricate polymer foams with arbitrary, high-resolution architectures for a variety of advanced applications, and in particular, with stretch-dominated layouts. Stretch-dominated polymer architectures overcome traditional mechanical degradation and scale nearly linearly, n = 1.1, with decreasing density. Techniques which utilize 3D printing including extrusion,7,11–13 ice-templating,14,15 laser templating,16 and casting17 have been used to create 3DGs with moderate structural control. However, they have all failed to achieve a truly arbitrary design space due to limitations in both the printing technique (e.g. toolpath requirement and serial writing) and feedstock materials which are largely not self-supporting. The resulting 3DGs are still limited in design to only a few bending-dominated geometries (wood-pile, square array etc.) and relatively large ligament feature sizes (>100 μm) precluding the vast design freedom to create 3D graphene mesoscale architectures for applications in energy storage and conversion.4,5
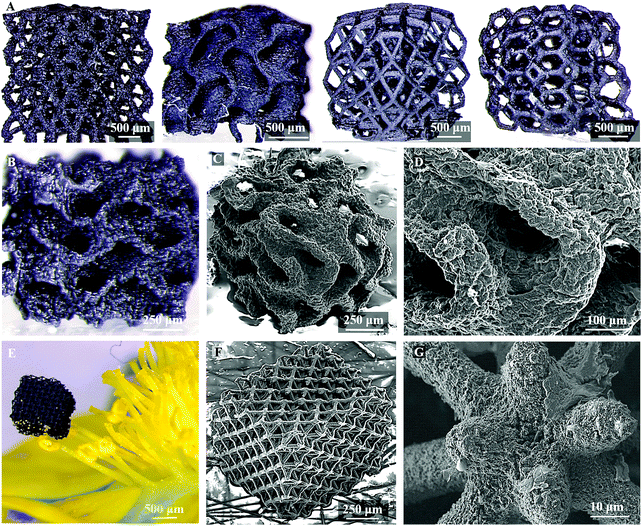
Herein, we report a process to create 3DGs with essentially any desired architecture with feature resolutions an order-of-magnitude finer to apply the benefits of micro-architecture to 3DGs. We designed and synthesized photocurable graphene oxide (GO) resins that can be sequentially patterned through a light-based 3D printing technique called projection micro-stereolithography (PμSL). The complex hierarchical 3D micro-architected graphene (MAG) assemblies, Fig. 1, have high surface area and are electrically conductive bringing all the desirable properties of 3DGs to a much broader design space. We utilize this ability to incorporate hierarchical stretch-dominated micro-architectures which mitigate the degradation in mechanical properties with decreasing density. Our process enables the fabrication of any designed 3D topologies with interconnected graphene foam as a base material, thereby enabling the use of design principles to incorporate structural hierarchies into the 3DGs. The resulting MAGs are lightweight, Fig. 1, and can be designed and created with intricate 3D topologies having hierarchical structural features from a few microns to hundreds of microns, not achievable in previous state-of-the-art 3D printed 3DGs.7,18
The main challenge to realizing MAGs was the development of a photocurable resin that (i) rapidly solidifies by light-initiated polymerization, and (ii) is sufficiently low viscosity to allow dipping and recoating for its layer-by-layer processing, Fig. 2.18 The resin we developed is a dilute (1 wt%) graphene oxide (GO) dispersion in concert with a dilute amount of photocurable acrylates (12 wt%) and photoinitiator (2 to 4 wt%). We call it “XGO resin” as it consists of crosslinked GO particles (XGO) made by ultrasonically dispersing a GO hydrogel monolith.2,19,20 It was presumed that crosslinking GO in the XGO resin would lead to a MAG with textural properties (e.g. surface area) more similar to traditional aerogels than simply using neat GO flakes. The acrylates and initiator allow PμSL printing by forming a temporary “green” structure that traps the XGO in the desired 3D architecture. The majority of the resin is solvent, N,N-dimethylformamide, DMF, as it maintains high quality GO dispersions, and solubilizes most acrylates and the photoinitiator.21 Our addition of DMF eliminates excessive amorphous carbon which could otherwise be introduced by using neat acrylates.22 The green structures are kept in solvent until dried either by supercritical or freeze-drying processes to maintain surface area. Pyrolysis of the “green” structures removes the majority of the photopolymer and reduces the GO green structure into a MAG.
The GO concentration was selected to meet the viscosity requirements for PuSL printing and appropriate light absorption for high resolution printing. Optical microscopy of XGO revealed that after 24 hours of sonication, the dispersion consists largely of particles below 5 μm, with a few larger particles and agglomerates also present, (Fig. S1, ESI†). The acrylic photopolymers, bisphenol A ethoxylate dimethacrylate (BisA-EDMA), and polyethylene glycol diacrylate (PEGDA700), were chosen through simple empirical tests. Using only BisA-EDMA at 12 wt% produced a macroscopically brittle dust, while using only PEGDA700 produced a weak, solvent-logged gel. Equal amounts of each provided a relatively robust material considering the low overall amount of polymer. Increasing photopolymer concentration above 20 wt% created excessive carbon filling the voids between the graphene sheets. (Fig. S2, ESI†). Therefore, a polymer concentration of 12 wt% was established as the minimum required to print 3D structures.
We investigated MAG's hierarchical morphology through scanning electron microscopy (SEM). There is an approximate 50–60% shrinkage (Table S1, ESI†) in feature size due to polymer burn off and densification which is consistent with the expected uniform shrinkage of the printed structure. We have been able to attain high-resolution features with our smallest MAG features sizes on the order of 10 μm (Fig. 1G), an order-of-magnitude finer than previous state-of-the-art 3D printed graphene aerogels whose finest features sizes are on the order of 100 μm.7,12 Importantly these structures maintain their printed architecture and integrity through the pyrolysis process, Fig. 1.
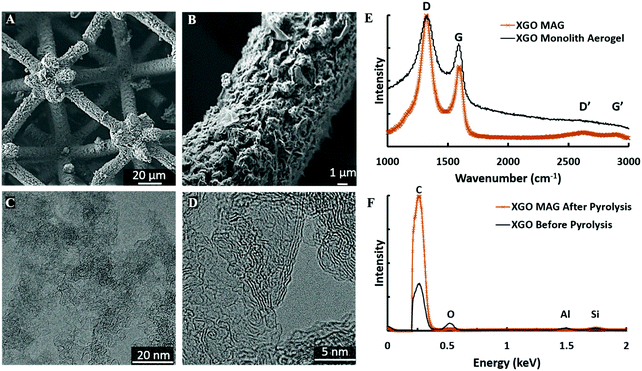
Fig. 3A and B show the porous microstructure of an XGO MAG consistent with traditional graphene aerogels. XGO exhibits markedly more pore structure than samples using neat flake GO (FGO, Fig. S3, ESI†), providing evidence that the GO crosslinks survive pyrolysis and help form the 3DG structure within the MAG struts. XGO also has much higher surface area (130 m2 g−1) than FGO (47 m2 g−1), as determined by gas adsorption, due to the pre-crosslinked GO, and fine pores. Though smaller than their monolith counterparts, the surface area is an order-of-magnitude higher than previously reported graphene lattices.17 The hierarchically porous nature of MAGs, with a 60 nm average pore diameter (Fig. S4, ESI†) and their large surface areas are consistent with other reported monolith and 3D printed 3DGs, though with an order-of-magnitude finer resolution and far more intricate architecture.7,11–16
Transmission electron microscopy (TEM) shown in Fig. 3C and D shows extensive wrinkling in the graphene sheets, as well as largely incomplete stacking of the sheets in-line with previous results.29Fig. 3D does show some sheet stacking is occurring, on the order of 4–5 layers, indicating graphene crosslink breakdown during resin synthesis is the likely cause for the degradation of MAG surface area, compared to bulk monoliths.28
To further investigate the microstructure of the as-fabricated MAGs from our light sensitive resins, we performed Raman Spectroscopy on an XGO MAG, and an XGO monolith aerogel2,19,20 without photopolymer (Fig. 3E). There are four peaks of concern for carbons, the G band (1582 cm−1) and D band (1350 cm−1), and their overtone G′ (3248 cm−1) and D′ (2700 cm−1) bands.2,20,23–29 The XGO aerogel monolith is typical of many 3DGs, exhibiting strong, broad G and D band peaks due to the many flake edges, and no noteworthy D′ or G′ peaks from the lack of well-ordered graphite-like layers.2,20,23–29 The XGO MAG spectra is nearly identical, indicative of porous, aerogel structure within the struts. The lower G band intensity of XGO MAG indicates a decrease in graphene sheet defects compared to the monolith.24
The elimination of acrylate and reduction of XGO were confirmed via SEM energy dispersive X-ray spectroscopy (EDS), Fig. 3F. XGO dispersions with no polymer were dried via vacuum and compared to dried and annealed XGO MAGs. Dried XGO showed an atom percentage (at%) of 20 at% for oxygen, typical for the highly oxidized nature of the GO precursor.2,19,20 After pyrolysis, XGO MAGs reveal a significant loss in oxygen to 5 at%, which is very similar to previous reports of XGO monoliths.2,19,20 This is indicative of the reduction of GO and burnout of the majority of the acrylate during furnace treatment to leave a largely pure graphene network within the MAG struts.
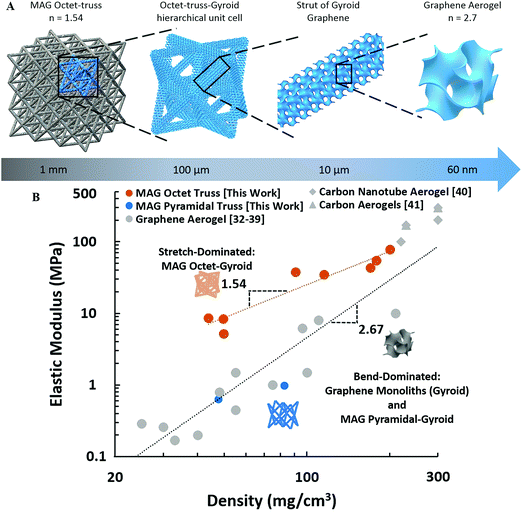
The ability to assemble graphene sheets into complex, three-dimensional architectures opens up new opportunities to incorporate designed topologies into 3D graphene assemblies. We utilize this ability to test architectural effects in 3DGs mechanical degradation by printing a class of octet-truss graphene lattice from 9–42% relative density and conducting uni-axial compression tests. The octet-truss is a stretch-dominated micro-architecture, satisfying Maxwell's Criterion,30 and has previously been demonstrated in polymer, ceramic, and metallic systems to provide exceptionally high elastic moduli at decreasing densities.8,31 Our octet-truss MAGs represent a hierarchical structure, Fig. 4A, consisting of the porous graphene foam within the overall octet-truss struts. The graphene foam can be approximated as a gyroid,10 with an average pore diameter of 60 nm (Barrett–Joyner–Halenda method).
The octet-truss MAGs are compared to previously reported graphene,32–39 carbon nanotube (CNT),40 and carbon aerogels41 on a log–log plot of density versus elastic modulus.8,10,28 Our hierarchical MAGs exhibit a scaling factor of n = 1.54, Fig. 4B, significantly improved over that of 3D porous carbon materials including graphene with n ∼ 2.67. It is also superior to previous 3D printed graphene aerogels, which due to material and printing limitations, could only achieve bend-dominated structures with scaling similar to that of bulk graphene aerogels (n = 2.5).10
Unstructured porous graphene aerogels have an architecture which can be represented by a gyroid (n = 2.73)10 deforming by mechanically inefficient flexure or bending of the sheets.9,42 The superior scaling of MAGs is a direct result of the beneficial hierarchical 3D architecture,6,31,43 confining the graphene gyroid, to the lowest level of hierarchy, with the second order stretch-dominated octet-truss providing sheet alignment, to cause predominate deformation by mechanically efficient in-plane tension and compression. The mechanical property and density scaling of the second order 3D architected graphene lattice can be approximated as (full derivation in ESI†):
E/Es ∼ (![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) )αN1+(1−α)N2 )αN1+(1−α)N2 |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ) of the hierarchical 3D MAGs by primarily reducing the relative density of the octet micro-architecture enables a superior scaling constant closer to the octet lattice architecture as compared to unstructured graphene aerogel. If one tunes the density by varying gyroid density, then the scaling of typical graphene aerogels results, ∼2.67.
) of the hierarchical 3D MAGs by primarily reducing the relative density of the octet micro-architecture enables a superior scaling constant closer to the octet lattice architecture as compared to unstructured graphene aerogel. If one tunes the density by varying gyroid density, then the scaling of typical graphene aerogels results, ∼2.67.
To further establish that the improved scaling is result of incorporation of octet microstructure, bending-dominated hierarchical pyramidal-gyroid microstructures were also tested. Pyramidal trusses are similar to octets trusses, but with lesser connectivity, deforming primarily by bending.8 The stiffness of the pyramidal structures is significantly less than octet, performing similarly to graphene monoliths Fig. 4B, due to the structures inefficient deformation by strut flexure.9 The incorporation of stretch-dominated octet truss micro-architecture gives rise to new property scaling law not seen in graphene aerogels. Previous studies have noted that at low density polymer foams will outperform graphene foams mechanically, despite graphene having base material properties orders-of-magnitude higher than any polymer.10 Through micro-architecture, the improved scaling relationship of MAGs, eliminates this tradeoff further expanding the applicability of low-density graphene assemblies.
MAG's electrical conductivity was probed through resistive testing revealing a high conductivity of 64 S m−1 for a MAG density of 92 mg cm−3 (refer to Table S2, ESI† for more samples). Previous literature reports have established the need for covalently crosslinked graphene foams to achieve high electric conductivity.2 MAGs excellent conductivity approaches the value of bulk crosslinked graphene aerogels (100 S m−1), and is indicative of their highly connected nature.2,19
MAGs open the desirable properties of 3DGs to many new possible applications with designed mesoscale architectures. In particular, MAG's high surface area, electrical conductivity, significantly improved mechanical properties at low density, and the ability to be manufactured into arbitrary form factors, makes them compelling electrode materials for energy storage. Graphene has significant potential as an electrode material,45 and electrode architecture has shown important performance effects as demonstrated by Zhu et al. with 3DG supercapacitors.5 While previous works were limited to relatively simple structures, MAGs open arbitrarily complex electrode architectures for exploration.
MAG's enhanced mechanical properties at low density is highly desirable for electrode materials which can experience severe mechanical stress during energy storage cycling. Swelling, on the order of 300–400%, can pulverize some battery electrodes.46 MAG's significantly improved low-density mechanical performance, can help drive graphene electrode performance, reducing density, while maintain mechanical integrity. The exploration of MAGs for energy storage will be explored in future works.
Conclusions
This work demonstrates an efficient pathway to optically print 3D graphene aerogels with complex, hierarchical 3D architectures of interconnected graphene sheets. The photo-activated graphene oxide resin can be precisely patterned by light into any desirable shape with 3D spatial features sizes of ∼10 micron, and the strut microstructure having pore sizes on the order of 60 nm. The method can be utilized by any lithographic based technique to open new opportunities for complex free-form 3D graphene assemblies. 3DG fabrication has been limited to relatively simple structure due to intrinsic limits in the manufacturing techniques. The high-resolution, intricate structures demonstrated here not only allow the fabrication of arbitrary form factors for a plethora of applications but can improve graphene foam properties at increasingly low densities. MAG's essentially unlimited design space, high surface area and electrical conductivity paves the way for exploring mesoscale architectures for advanced 3DG applications including catalysis and separation platforms, tunable thermal conductivity, and fluid flow among others.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Lawrence Livermore National Laboratory under the auspices of the U.S. Department of Energy under Contract DE-AC52-07NA27344, through LDRD award 16-ERD-051 (LLNL-JRNL-749080). The authors would like to acknowledge NSF CMMI 1727492, Air Force Office of Scientific Research (AFOSR) Young Investigator Program with Program Manager Dr Jaimie S. Tiley, Grant No. FA9550-18-1-0299 and ICTAS Junior Faculty Award for funding support. We would like to sincerely thank Christopher Winkler, of the Virginia Tech Nanoscale Characterization and Fabrication Laboratory, for his work taking the Transmission Electron Microscopy micrographs in this manuscript. We would like to sincerely thank Dr Thomas Staley and Dr Hesham Elmkharram for assistance in pyrolysis of the samples in this work.Notes and references
- A. Peigney, C. Laurent, E. Flahaut, R. R. Bacsa and A. Rousset, Carbon, 2001, 39, 507–514 CrossRef.
- M. A. Worsley, P. J. Pauzauskie, T. Y. Olson, J. Biener, J. H. Satcher and T. F. Baumann, J. Am. Chem. Soc., 2010, 132, 14067–14069 CrossRef PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef PubMed.
- B. F. Machado and P. Serp, Catal. Sci. Technol., 2011, 2, 54–75 RSC.
- C. Zhu, T. Liu, F. Qian, T. Y.-J. Han, E. B. Duoss, J. D. Kuntz, C. M. Spadaccini, M. A. Worsley and Y. Li, Nano Lett., 2016, 16, 3448–3456 CrossRef PubMed.
- X. Zheng, W. Smith, J. Jackson, B. Moran, H. Cui, D. Chen, J. Ye, N. Fang, N. Rodriguez, T. Weisgraber and C. M. Spadaccini, Nat. Mater., 2016, 15, 1100 CrossRef PubMed.
- C. Zhu, T. Y.-J. Han, E. B. Duoss, A. M. Golobic, J. D. Kuntz, C. M. Spadaccini and M. A. Worsley, Nat. Commun., 2015, 6, 6962 CrossRef PubMed.
- X. Zheng, H. Lee, T. H. Weisgraber, M. Shusteff, J. DeOtte, E. B. Duoss, J. D. Kuntz, M. M. Biener, Q. Ge, J. A. Jackson, S. O. Kucheyev, N. X. Fang and C. M. Spadaccini, Science, 2014, 344, 1373–1377 CrossRef PubMed.
- A. Nieto, B. Boesl and A. Agarwal, Carbon, 2015, 85, 299–308 CrossRef.
- Z. Qin, G. S. Jung, M. J. Kang and M. J. Buehler, Sci. Adv., 2017, 3, e1601536 CrossRef PubMed.
- S. Barg, F. M. Perez, N. Ni, P. do, V. Pereira, R. C. Maher, E. Garcia-Tuñon, S. Eslava, S. Agnoli, C. Mattevi and E. Saiz, Nat. Commun., 2014, 5, 4328 CrossRef PubMed.
- E. García-Tuñon, S. Barg, J. Franco, R. Bell, S. Eslava, E. D’Elia, R. C. Maher, F. Guitian and E. Saiz, Adv. Mater., 2015, 27, 1688–1693 CrossRef PubMed.
- Y. Jiang, Z. Xu, T. Huang, Y. Liu, F. Guo, J. Xi, W. Gao and C. Gao, Adv. Funct. Mater., 2018, 28, 170724 Search PubMed.
- Y. Lin, F. Liu, G. Casano, R. Bhavsar, I. A. Kinloch and B. Derby, Adv. Mater., 2016, 28, 7993–8000 CrossRef PubMed.
- Q. Zhang, F. Zhang, S. P. Medarametla, H. Li, C. Zhou and D. Lin, Small, 2016, 12, 1702–1708 CrossRef PubMed.
- J. Sha, Y. Li, R. Villegas Salvatierra, T. Wang, P. Dong, Y. Ji, S.-K. Lee, C. Zhang, J. Zhang, R. H. Smith, P. M. Ajayan, J. Lou, N. Zhao and J. M. Tour, ACS Nano, 2017, 11, 6860–6867 CrossRef PubMed.
- Q. Zhang, F. Zhang, X. Xu, C. Zhou and D. Lin, ACS Nano, 2018, 12, 1096–1106, DOI:10.1021/acsnano.7b06095.
- X. Zheng, J. Deotte, M. P. Alonso, G. R. Farquar, T. H. Weisgraber, S. Gemberling, H. Lee, N. Fang and C. M. Spadaccini, Rev. Sci. Instrum., 2012, 83, 125001 CrossRef PubMed.
- M. A. Worsley, S. O. Kucheyev, H. E. Mason, M. D. Merrill, B. P. Mayer, J. Lewicki, C. A. Valdez, M. E. Suss, M. Stadermann, P. J. Pauzauskie, J. H. Satcher, J. Biener and T. F. Baumann, Chem. Commun., 2012, 48, 8428–8430 RSC.
- M. A. Worsley, T. Y. Olson, J. R. I. Lee, T. M. Willey, M. H. Nielsen, S. K. Roberts, P. J. Pauzauskie, J. Biener, J. H. Satcher and T. F. Baumann, J. Phys. Chem. Lett., 2011, 2, 921–925 CrossRef PubMed.
- J. I. Paredes, S. Villar-Rodil, A. Martínez-Alonso and J. M. D. Tascón, Langmuir, 2008, 24, 10560–10564 CrossRef PubMed.
- H. Korhonen, L. H. Sinh, N. D. Luong, P. Lehtinen, T. Verho, J. Partanen and J. Seppälä, Phys. Status Solidi A, 2016, 213, 982–985 CrossRef.
- D. Graf, F. Molitor, K. Ensslin, C. Stampfer, A. Jungen, C. Hierold and L. Wirtz, Nano Lett., 2007, 7, 238–242 CrossRef PubMed.
- A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095–14107 CrossRef.
- A. C. Ferrari, Solid State Commun., 2007, 143, 47–57 CrossRef.
- F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126–1130 CrossRef.
- X. Xie, Y. Zhou, H. Bi, K. Yin, S. Wan and L. Sun, Sci. Rep., 2013, 3, 2117 CrossRef PubMed.
- M. A. Worsley, S. Charnvanichborikarn, E. Montalvo, S. J. Shin, E. D. Tylski, J. P. Lewicki, A. J. Nelson, J. H. Satcher, J. Biener, T. F. Baumann and S. O. Kucheyev, Adv. Funct. Mater., 2014, 24, 4259–4264 CrossRef.
- M. A. Worsley, T. T. Pham, A. Yan, S. J. Shin, J. R. I. Lee, M. Bagge-Hansen, W. Mickelson and A. Zettl, ACS Nano, 2014, 8, 11013–11022 CrossRef PubMed.
- J. C. Maxwell, London Edinburgh Dublin Philos. Mag. J. Sci., 1864, 27, 294–299 CrossRef.
- L. R. Meza, S. Das and J. R. Greer, Science, 2014, 345, 1322–1326 CrossRef PubMed.
- S. Barg, F. M. Perez, N. Ni, P. do Vale Pereira, R. C. Maher, E. Garcia-Tuñon, S. Eslava, S. Agnoli, C. Mattevi and E. Saiz, Nat. Commun., 2014, 5, 4328 CrossRef PubMed.
- Z. Han, Z. Tang, P. Li, G. Yang, Q. Zheng and J. Yang, Nanoscale, 2013, 5, 5462–5467 RSC.
- Y. Li, J. Chen, L. Huang, C. Li, J.-D. Hong and G. Shi, Adv. Mater., 2014, 26, 4789–4793 CrossRef PubMed.
- L. Lv, P. Zhang, H. Cheng, Y. Zhao, Z. Zhang, G. Shi and L. Qu, Small, 2016, 12, 3229–3234 CrossRef PubMed.
- H. Sun, Z. Xu and C. Gao, Adv. Mater., 2013, 25, 2554–2560 CrossRef PubMed.
- Z. Tang, S. Shen, J. Zhuang and X. Wang, Angew. Chem., Int. Ed., 2010, 49, 4603–4607 CrossRef PubMed.
- Q. Zhang, X. Xu, D. Lin, W. Chen, G. Xiong, Y. Yu, T. S. Fisher and H. Li, Adv. Mater., 2016, 28, 2229–2237 CrossRef PubMed.
- X. Zhang, Z. Sui, B. Xu, S. Yue, Y. Luo, W. Zhan and B. Liu, J. Mater. Chem., 2011, 21, 6494–6497 RSC.
- M. A. Worsley, S. O. Kucheyev, J. H. Satcher, A. V. Hamza and T. F. Baumann, Appl. Phys. Lett., 2009, 94, 073115 CrossRef.
- R. W. Pekala, C. T. Alviso and J. D. LeMay, J. Non-Cryst. Solids, 1990, 125, 67–75 CrossRef.
- S. N. Khaderi, V. S. Deshpande and N. A. Fleck, Int. J. Solids Struct., 2014, 51, 3866–3877 CrossRef.
- R. Lakes, Nature, 1993, 361, 511–515 CrossRef.
- H. Cui, R. Hensleigh, H. Chen and X. Zheng, J. Mater. Res., 2018, 33, 360–371 CrossRef.
- R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, Nat. Mater., 2015, 14, 271–279 CrossRef PubMed.
- P. V. Braun and J. B. Cook, ACS Nano, 2018, 12, 3060–3064 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh00668g |
| This journal is © The Royal Society of Chemistry 2018 |