Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bioinspired hierarchical composite design using machine learning: simulation, additive manufacturing, and experiment†
Grace X.
Gu
ab,
Chun-Teh
Chen
 a,
Deon J.
Richmond
a and
Markus J.
Buehler
a,
Deon J.
Richmond
a and
Markus J.
Buehler
 *a
*a
aLaboratory for Atomistic and Molecular Mechanics (LAMM), Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, MA 02139, USA. E-mail: mbuehler@mit.edu; Tel: +1-617-452-2750
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, MA 02139, USA
First published on 27th July 2018
Abstract
Biomimicry, adapting and implementing nature's designs provides an adequate first-order solution to achieving superior mechanical properties. However, the design space is too vast even using biomimetic designs as prototypes for optimization. Here, we propose a new approach to design hierarchical materials using machine learning, trained with a database of hundreds of thousands of structures from finite element analysis, together with a self-learning algorithm for discovering high-performing materials where inferior designs are phased out for superior candidates. Results show that our approach can create microstructural patterns that lead to tougher and stronger materials, which are validated through additive manufacturing and testing. We further show that machine learning can be used as an alternative method of coarse-graining – analyzing and designing materials without the use of full microstructural data. This novel paradigm of smart additive manufacturing can aid in the discovery and fabrication of new material designs boasting orders of magnitude increase in computational efficacy over conventional methods.
Conceptual insightsWe demonstrate a new machine learning-based design approach for hierarchical materials. The new designs created by our machine learning model, which is trained with a database of hundreds of thousands of geometries from finite element analysis, are validated using additive manufacturing and experimentation. Whereas most of the previous work applying machine learning in materials science is solely focused on predicting material properties, we aim to go beyond property prediction to optimize specific properties. This is achieved by further augmenting a convolutional neural network model with our self-learning algorithm; the goal being to learn patterns from sampled top-performing geometries to create even better designs, phasing out inferior designs for superior candidates. The result is a suite of new designs that outperform the training set. Additionally, for the first time in literature, we show that machine learning can be used as an alternative method for coarse-graining – analyzing and designing materials without the use of full microstructural data. The coarse-graining is realized by condensing a collection of building blocks into a single unit cell – significantly reducing the number of parameters needed in our machine learning model. Thus, this new approach accelerates the search for high-performing hierarchical materials by orders of magnitude and is widely applicable to other material systems to optimize a variety of properties. |
Introduction
The natural world contains an arsenal of materials with mechanical properties ranging across a broad spectrum of toughness and strength. Yet, virtually none of the basic building blocks in nature are monolithically tough or strong. This surprising insight is reconciled by examining the microscopic composition of natural materials. These emergent superior properties are encoded in the intricate and sophisticated hierarchical structures of natural materials.1–3 Motivated by such insights from nature, much research has been devoted to deconstructing the engineering rationales embedded in natural materials, aptly referred to as biomimicry.3–5 Superior mechanical properties and hierarchy in natural materials come at a cost, however, because the requisite microstructures consist of assemblages of sophisticated geometries. The progress of three-dimensional (3D)-printing enables researchers to recreate and emulate complex structures, facilitating novel fabrication techniques boasting higher resolution and more precise control when compared to traditional synthetic engineering methods.6–13 Many research groups have harnessed the power of 3D-printing to print hierarchical structures, such as auxetic materials, characterized by negative Poisson's ratio, and lightweight cellular materials.14–17Biomimicry offers a first-order, static approximation to replicating natural materials. Species, on the other hand, are constantly evolving and optimizing the architectures of biomaterials that constitute their anatomies, subject to their continued survival. Of more practical interest is surpassing biomimetic prototypes, in terms of mechanical properties, and more readily adapting these structures for engineering applications over an extremely condensed time horizon compared to the millennia of evolution in nature. This is done in practice by augmenting biomimicry using optimization with application-specific objective functions.18–22 Optimization, however, does not come without high computational expense as the necessary design space to be considered is vast. Specifically, there are many potential structures that can be arranged in numerous ways over various length scales, and so the number of possible configurations rapidly approaches astronomical values.
Machine learning (ML), a branch of artificial intelligence for discerning patterns from complex data sets, has proven to be a valuable method in various fields of research over the past few decades.23 ML algorithms have found great utility in several applications including, but certainly not limited to, image and speech recognition, spam detection, and drug discovery, as well as search engines.24–30 Recently, ML techniques have been utilized in the search for new materials, exploring different material properties such as elasticity, plasticity, fatigue life, wear performance, and buckling.31–36 While these studies demonstrate possible applications of using ML in materials design, they were mostly focused on using ML models to predict properties of materials or structures rather than designing new materials with desired properties. Furthermore, very little validation of such ML approaches has been done with experimental analysis.
In this work, we aim to study hierarchical structures like those found in nature and to accelerate the evolutionary process occurring in natural materials using ML. In a way, the natural process of evolution is cast into a computational framework under the guise of ML to study bioinspired hierarchical structures. Natural materials, which must survive with the material constituents available in their surroundings, instigate novel material response without introducing new materials by leveraging hierarchical assemblies. Nature makes do with what is at hand. Similarly, we aim to create better materials by building hierarchical structures made up of various symmetric and asymmetric unit cells. Convolutional neural networks (CNN) are employed to predict composite material properties and show that our ML model can generate high-performance designs with much better material properties than those of the training data. CNN allows us to study a hierarchical system without complete characterization of its microstructure, accelerating the material property prediction process. Our ML-predicted designs are validated through 3D-printing and testing. Thus, we propose a new ML-based paradigm of smart additive manufacturing, while demonstrating its capabilities of discovering new material designs with orders-of-magnitude speedup compared to conventional methods.
Results and discussion
Hierarchical design of systems
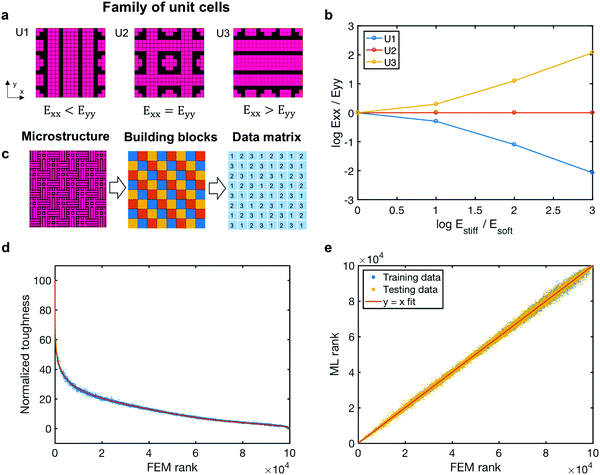
The prototypical model used is a composite system with a distinct set of unit cells. This composite structure departs from the conventional fiber/ply arrangement since nature, at sufficiently small length scales, is comprised of a limited set of soft and stiff building blocks. A similarly constrained suite of unit cell configurations is considered, as shown in Fig. 1a. The building blocks of unit cells are made up of stiff (pink color) and soft (black color) materials. The unit cells are constructed to achieve symmetric and asymmetric mechanical behavior, which is determined by their stiffness in the two in-plane directions (i.e., x and y-directions). For the unit cell 1 (U1), the stiffness in the x-direction is lower than that in the y-direction (i.e., Exx < Eyy). For the unit cell 2 (U2), the stiffness in the two in-plane directions is the same (i.e., Eyy = Exx) due to the symmetric geometry. For the unit cell 3 (U3), the geometry is 90-degrees rotated from that of U1, and thus the stiffness in the x-direction is higher than that in the y-direction (i.e., Exx > Eyy). The boundaries of all unit cells satisfy continuity, by which each type (i.e., stiff and soft) of element in one unit cell is connected to the same type of elements in adjoining unit cells when they are assembled. This continuity is satisfied by a specific design of interlocking edges, which allows for smooth load transfer between the unit cells. Additionally, each soft element is connected to no more than two stiff elements to prevent stress concentration. Fig. 1b depicts the orthogonal stiffness ratios of each unit cell (composed of 324 building blocks) as a function of the modulus ratios of the building blocks (soft to stiff) plotted on a log–log scale. The three unit cells exhibit different responses due to their geometrical configurations, as shown in Fig. 1a. Furthermore, the degree of isotropy can be tuned by changing the stiffness ratio of building blocks. These unit cells are assembled to create the entire microstructure (Fig. 1c), where different colors are used to signify the different unit cells (U1: blue, U2: orange, U3: yellow).Training and validation process
Inspired by biological neurons, the development of convolutional neural networks (CNN) provides an alternative to the stochastic process of evolution in a form that can be encapsulated in a parallel computing environment. CNN is adopted in our ML model to predict mechanical properties of a hierarchical composites system where the data matrix of 1, 2, 3's, enumerating the unit cells (Fig. 1c), is taken as an input to the ML model. A total of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random microstructures are generated as the training data (80
000 random microstructures are generated as the training data (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and testing data (20
000) and testing data (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), which correspond to 5.4 × 10−9% of all the possible combinations of three unit cells on an 8 by 8 lattice after taking symmetry into consideration. Those microstructures are subjected to tension in the x-direction and have an edge crack with initial length equal to 25% of the sample edge length. Their mechanical properties are calculated using finite element method (FEM) and considered as the ground truth. We aim to optimize the toughness of the hierarchical composite system, with details defined in ESI.† Even with less than 10−8% of the entire design space information available, the agreements between the FEM results and the ML-predicted toughness (Fig. 1d), and the FEM ranking and the ML-predicted ranking (Fig. 1e) are excellent. Note that the toughness value in Fig. 1d is scaled within a range of 0 to 100 (unitless value). All points lie very close to the line of y = x, as shown in Fig. 1e, signifying high accuracy in the ML model. Additionally, the normalized root-mean-square deviation (NRMSD) values of the training data and testing data for the normalized toughness are very close (i.e., NRMSD = 0.2978 for the training data and NRMSD = 0.4926 for the testing data), showing that the ML model has, indeed, learned the patterns from the training data, and there is no overfitting problem. Moreover, even with incomplete geometry information (i.e., only the unit cell numbers), the ML model can accurately predict the mechanical properties of the microstructures.
000), which correspond to 5.4 × 10−9% of all the possible combinations of three unit cells on an 8 by 8 lattice after taking symmetry into consideration. Those microstructures are subjected to tension in the x-direction and have an edge crack with initial length equal to 25% of the sample edge length. Their mechanical properties are calculated using finite element method (FEM) and considered as the ground truth. We aim to optimize the toughness of the hierarchical composite system, with details defined in ESI.† Even with less than 10−8% of the entire design space information available, the agreements between the FEM results and the ML-predicted toughness (Fig. 1d), and the FEM ranking and the ML-predicted ranking (Fig. 1e) are excellent. Note that the toughness value in Fig. 1d is scaled within a range of 0 to 100 (unitless value). All points lie very close to the line of y = x, as shown in Fig. 1e, signifying high accuracy in the ML model. Additionally, the normalized root-mean-square deviation (NRMSD) values of the training data and testing data for the normalized toughness are very close (i.e., NRMSD = 0.2978 for the training data and NRMSD = 0.4926 for the testing data), showing that the ML model has, indeed, learned the patterns from the training data, and there is no overfitting problem. Moreover, even with incomplete geometry information (i.e., only the unit cell numbers), the ML model can accurately predict the mechanical properties of the microstructures.
High performing designs predicted by ML model
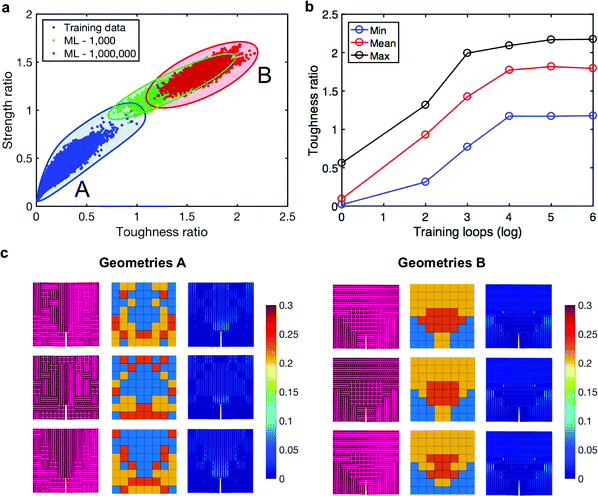
Fig. 2a shows the comparison of the training data and the high-performance designs identified by the ML model using a self-learning-based sampling method (discussed in ESI†) in the coordinate space of strength and toughness alone. To assess the performance of the ML model as a function of training time, we show two sets of designs: one is trained for 1000 loops only and another one is trained for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 loops. Most of the training data reside in the lower toughness and strength range, whereas most of the designs obtained by the ML models lie in the higher toughness and strength range. The designs from the ML model with a shorter training time (i.e., 1000 loops) have some overlap with the training data, while the designs from the ML model with a longer training time (i.e., 1
000 loops. Most of the training data reside in the lower toughness and strength range, whereas most of the designs obtained by the ML models lie in the higher toughness and strength range. The designs from the ML model with a shorter training time (i.e., 1000 loops) have some overlap with the training data, while the designs from the ML model with a longer training time (i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 loops) do not, showing that with more training loops, better designs can be obtained. The fact that the ML outputs reside outside of the range of the training data set indicates that the ML models have indeed learned the patterns of the top performing designs, even when only trained for 1000 loops. In this work, toughness ratio and strength ratio are defined as the toughness and strength values normalized by the highest toughness and strength value in the training data, respectively. The mean value of toughness ratio of the designs obtained from the ML model with 1
000 loops) do not, showing that with more training loops, better designs can be obtained. The fact that the ML outputs reside outside of the range of the training data set indicates that the ML models have indeed learned the patterns of the top performing designs, even when only trained for 1000 loops. In this work, toughness ratio and strength ratio are defined as the toughness and strength values normalized by the highest toughness and strength value in the training data, respectively. The mean value of toughness ratio of the designs obtained from the ML model with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 loops is approximately 13 times higher than the average value of the training data. Results for modulus ratio vs. toughness ratio are shown in Fig. S1 (ESI†), where modulus ratio is defined as the modulus normalized by the highest modulus value in the training data.
000 loops is approximately 13 times higher than the average value of the training data. Results for modulus ratio vs. toughness ratio are shown in Fig. S1 (ESI†), where modulus ratio is defined as the modulus normalized by the highest modulus value in the training data.
Fig. 2b shows that the toughness ratio, which is a function of training loops, starts to converge as training loops increase for minimum, mean, and maximum values. Two partitions, A and B, emerge as distinct regions in Fig. 2a and warrant further study of the geometrical patterns in those regions. Partition A contains the lowest performing designs from the training set and partition B contains the highest performing designs from the ML outputs. The partition A designs exhibit a strip of U1 unit cells (blue color in Fig. 2c) situated at the crack tip, which indicates that low performing designs cannot sustain tension load applied in the x-direction. Having U1 unit cells all along the crack tip is equivalent to placing a strip of soft, compliant material in that location, accounting for the weak performance of the partition A designs. As for the partition B designs, there are three key zones, [1 – at the crack tip]: there exists a band of U2 unit cells (orange color in Fig. 2) for all the top three designs to spread out the stress equally and have less preferred direction of damage, [2 – in the wake of the crack]: there are many U1 unit cells (blue color in Fig. 2c) which act to alleviate the stress around the crack tip, and [3 – around the crack tip]: there are patches of U3 unit cells (yellow color in Fig. 2c) to negate the loss of stiffness due to the presence of the crack. The strain distributions for each corresponding design from the partitions A and B are shown in Fig. 2c. It can be noted that the strain concentration at the crack tip for the lowest-performing designs is not evident in the highest-performing designs. Thus, the ML-generated designs exhibit a more disperse strain field, allowing for greater energy dissipation.
Patterns discovered from high-performing designs
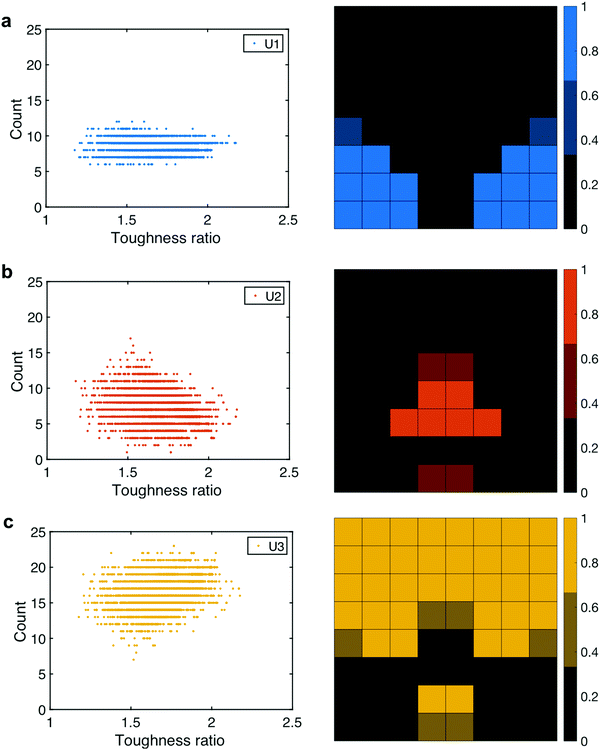
Geometrical elemental representation of the probability of a specific unit cell showing up in the top 100 designs identified by the ML model is shown in Fig. 3. For U1, U2, and U3 unit cells, there is an apparent pattern of locations where they have the most positive effect on the top designs, which further validates the patterns discussed in the previous paragraph. A critical question is how important each type of unit cell is and whether this constructed suite of U1, U2, and U3 unit cells maximizes effective composite material properties. Fig. 3 shows a plot counting the number of times each unit cell appears in designs generated by the ML model as a function of effective composite toughness modulus. It can be seen that all three types of unit cells are equally important when it comes to designing tougher materials, as there needs to be a collection of the three unit cells with different isotropic or anisotropic properties and that cannot be achieved using only one or two types of unit cells. This is consistent with different natural materials whose microstructures consist of distinct unit cells. Neural networks can mimic the evolutionary approach of nature using efficient parallel computing, leading us in the direction of tougher microstructural patterns.Additive manufacturing and tensile testing experiments
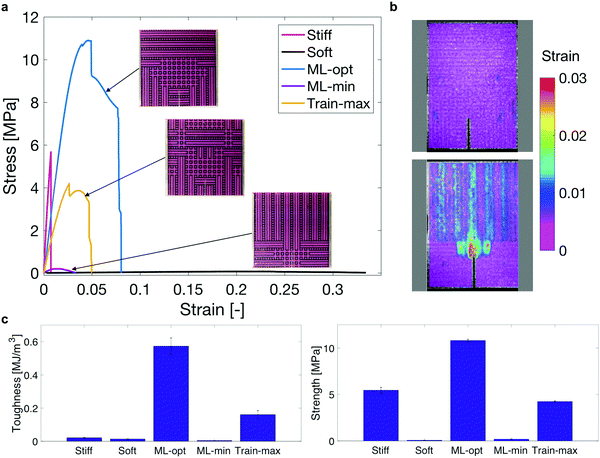
To evaluate the performance of the ML-generated designs, the best design identified by the ML model (denoted as ML-opt) is 3D-printed and its performance is measured from the stress–strain curve obtained from the tensile experiment (Fig. 4a). The details of the additive manufacturing and testing component are discussed in ESI.† The result is compared to homogeneous samples of the soft and stiff materials and other benchmark designs. One of the benchmark designs is the lowest-toughness design generated by the ML model, denoted as ML-min. The ML approach allows for optimizing with the objective to minimize toughness. From this optimization, the ML-min design can also shed some light on how to make a hierarchical composite weak. The ML-min design shows that a strip of compliant unit cells in the x-direction (U1) at the crack tip will diminish toughness. Another benchmark design is the best design in the training data, denoted as Train-max. The 3D-printed samples of ML-opt, ML-min, and Train-max are shown in Fig. 4a. The strain fields of the ML-opt sample (top) and the ML-min sample (bottom) obtained from digital image correlation are shown in Fig. 4b. The strain field of the ML-opt sample is more uniform and distributed compared to that of the ML-min sample, which has a high strain concentration at the crack tip. This shows that the optimized design can store more elastic energy before it breaks and that the ML model has learned the patterns that lead to high and low toughness scores, respectively.In this work, toughness is defined as the area underneath the stress–strain curve. Strength is defined as the failure stress of the sample obtained from the stress–strain curve. Fig. 4c shows the values with error bars for toughness and strength of different designs. The results show that the ML-designed optimal hierarchical composite is approximately 25 times tougher than the stiff material and approximately 40 times tougher than the soft material. Additionally, the ML-opt design is approximately 2 times stronger than the stiff material and greater than 100 times stronger than the soft material. The ML-opt design is also approximately 4 times tougher than the Train-max design, which shows that the ML model can learn from the training data and generate better designs significantly stronger and tougher than the training data. It can also be seen in Fig. 4c that the ML-min design has the lowest toughness of all the other tested samples, showing the efficacy in minimizing toughness using ML; the ML approach can generate designs across a broad spectrum of toughness. This approach demonstrates the merits of a machine learning-driven design combined with additive manufacturing for printing high-performance functional materials.
Discussion
In terms of computational cost, calculating the mechanical properties of the 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 microstructures using FEM took approximately 5 days. As for our ML approach, the training process took from 30 seconds to 10 hours (for 1000 to 1
000 microstructures using FEM took approximately 5 days. As for our ML approach, the training process took from 30 seconds to 10 hours (for 1000 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 loops), and the predictive phase took less than a minute to solve for the same amount of data. Once the training process is finished, the predictive phase is used to screen billions of designs in hours, which for FEM would take years to solve. Furthermore, we show that ML can be used as an alternative method of coarse-graining in the context of materials design since the inputs to the ML model do not consist of the full microstructural design, but rather just the unit cell types. The coarse-graining is realized by condensing a collection of building blocks into a single unit cell – significantly reducing the number of weights needed in our ML model. Thus, we propose a new ML-based paradigm of smart additive manufacturing, while demonstrating its capabilities in discovering new material designs boasting orders-of-magnitude increases in speed compared with conventional methods. We want to make a note here that additive manufacturing and testing is used as a proof-of-concept and not as a quantitative comparison with our FEM results, but as a qualitative comparison. This is due to the simplifications used in our simulations (discussed in ESI†) to balance computational costs. Additionally, instead of using the exact mechanical properties of the 3D-printing materials in our FEM model, we aim to highlight a simplified material model where one material is stiff and the other material is soft. Future work can use more rigorous finite element models to achieve quantitative comparisons. This method of using ML and additive manufacturing to design and fabricate materials can be applied to a broad range of materials to study any property. For example, materials of interest can be ceramics, metals, or polymers and the desired properties could be thermal, electrical, or mechanical. This framework will find applications in tissue engineering, drug delivery, and a multitude of other new materials design search endeavors.
000 loops), and the predictive phase took less than a minute to solve for the same amount of data. Once the training process is finished, the predictive phase is used to screen billions of designs in hours, which for FEM would take years to solve. Furthermore, we show that ML can be used as an alternative method of coarse-graining in the context of materials design since the inputs to the ML model do not consist of the full microstructural design, but rather just the unit cell types. The coarse-graining is realized by condensing a collection of building blocks into a single unit cell – significantly reducing the number of weights needed in our ML model. Thus, we propose a new ML-based paradigm of smart additive manufacturing, while demonstrating its capabilities in discovering new material designs boasting orders-of-magnitude increases in speed compared with conventional methods. We want to make a note here that additive manufacturing and testing is used as a proof-of-concept and not as a quantitative comparison with our FEM results, but as a qualitative comparison. This is due to the simplifications used in our simulations (discussed in ESI†) to balance computational costs. Additionally, instead of using the exact mechanical properties of the 3D-printing materials in our FEM model, we aim to highlight a simplified material model where one material is stiff and the other material is soft. Future work can use more rigorous finite element models to achieve quantitative comparisons. This method of using ML and additive manufacturing to design and fabricate materials can be applied to a broad range of materials to study any property. For example, materials of interest can be ceramics, metals, or polymers and the desired properties could be thermal, electrical, or mechanical. This framework will find applications in tissue engineering, drug delivery, and a multitude of other new materials design search endeavors.
Conclusions
In this paper, a new approach to designing hierarchical materials using machine learning and finite element analysis is proposed. Results show that our model can accurately predict mechanical properties of hierarchical systems and generate new microstructural patterns that lead to tougher and stronger materials. Furthermore, the optimal designs outputted from our machine learning model are validated using additive manufacturing and experimental tensile testing. Additionally, this work shows that machine learning can be used as an alternative method of coarse-graining, with the ability to analyze and design materials without the use of full microstructural data. The coarse-graining is realized by condensing a collection of building blocks into a single unit cell – significantly reducing the number of weights needed in our machine learning model. Thus, this new approach has orders of magnitude speedup compared to conventional methods, making the search for high-performing materials in a vast design space possible. In addition to FEM, this ML approach can also be incorporated with other simulation methods such as density functional theory or molecular dynamics in order to capture material properties at different length and time scales.Funding sources
This research was supported by ONR (N000141612333), AFOSR (FATE MURI FA9550-15-1-0514), and a National Defense Science & Engineering Graduate (NDSEG) fellowship.Conflicts of interest
There are no conflicts to declare.References
- R. O. Ritchie, Nat. Mater., 2011, 10, 817 CrossRef PubMed.
- P. Fratzl and R. Weinkamer, Prog. Mater. Sci., 2007, 52, 1263–1334 CrossRef.
- U. G. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2015, 14, 23–36 CrossRef PubMed.
- C. Sanchez, H. Arribart and M. M. G. Guille, Nat. Mater., 2005, 4, 277 CrossRef PubMed.
- C.-T. Chen, F. J. Martin-Martinez, S. Ling, Z. Qin and M. J. Buehler, Nano Futures, 2017, 1, 011003 CrossRef.
- W. Gao, Y. Zhang, D. Ramanujan, K. Ramani, Y. Chen, C. B. Williams, C. C. Wang, Y. C. Shin, S. Zhang and P. D. Zavattieri, Comput.-Aided Des., 2015, 69, 65–89 CrossRef.
- G. X. Gu, F. Libonati, S. Wettermark and M. J. Buehler, J. Mech. Behav. Biomed. Mater., 2017, 76, 135–144 CrossRef PubMed.
- F. Libonati, G. X. Gu, Z. Qin, L. Vergani and M. J. Buehler, Adv. Eng. Mater., 2016, 18, 1354–1363 CrossRef.
- G. X. Gu, I. Su, S. Sharma, J. L. Voros, Z. Qin and M. J. Buehler, J. Biomech. Eng., 2016, 138, 021006 CrossRef PubMed.
- E. Lin, Y. Li, C. Ortiz and M. C. Boyce, J. Mech. Phys. Solids, 2014, 73, 166–182 CrossRef.
- G. X. Gu, M. Takaffoli and M. J. Buehler, Adv. Mater., 2017, 29, 1700060 CrossRef PubMed.
- G. X. Gu, M. Takaffoli, A. J. Hsieh and M. J. Buehler, Extreme Mech. Lett., 2016, 9, 317–323 CrossRef.
- L. Wen, J. C. Weaver and G. V. Lauder, J. Exp. Biol., 2014, 217, 1656–1666 CrossRef PubMed.
- B. G. Compton and J. A. Lewis, Adv. Mater., 2014, 26, 5930–5935 CrossRef PubMed.
- X. Ren, J. Shen, A. Ghaedizadeh, H. Tian and Y. M. Xie, Smart Mater. Struct., 2015, 24, 095016 CrossRef.
- J. Shen, S. Zhou, X. Huang and Y. M. Xie, Phys. Status Solidi B, 2014, 251, 1515–1522 CrossRef.
- Y. Sun and N. Pugno, Materials, 2013, 6, 699–712 CrossRef PubMed.
- D. Brackett, I. Ashcroft and R. Hague, Proceedings of the solid freeform fabrication symposium, 2011, pp. 348–362 Search PubMed.
- G. X. Gu, L. Dimas, Z. Qin and M. J. Buehler, J. Appl. Mech., 2016, 83, 071006 CrossRef.
- G. X. Gu, S. Wettermark and M. J. Buehler, Addit. Manuf., 2017, 17, 47–54 CrossRef.
- A. T. Gaynor, N. A. Meisel, C. B. Williams and J. K. Guest, J. Manuf. Sci. Eng., 2014, 136, 061015 CrossRef.
- M. P. Bendsøe, O. Sigmund, M. P. Bendsøe and O. Sigmund, Topology optimization by distribution of isotropic material, Springer, 2004 Search PubMed.
- R. S. Michalski, J. G. Carbonell and T. M. Mitchell, Machine learning: an artificial intelligence approach, Springer Science & Business Media, 2013 Search PubMed.
- I. H. Witten, E. Frank, M. A. Hall and C. J. Pal, Data mining: Practical machine learning tools and techniques, Morgan Kaufmann, 2016 Search PubMed.
- A. L. Blum and P. Langley, Artif. Intell., 1997, 97, 245–271 CrossRef.
- M. S. Bartlett, J. R. Movellan and T. J. Sejnowski, IEEE Trans. neural networks, 2002, 13, 1450–1464 CrossRef PubMed.
- G. X. Gu, C.-T. Chen and M. J. Buehler, Extreme Mech. Lett., 2017, 18, 19–28 CrossRef.
- N. Lubbers, T. Lookman and K. Barros, Phys. Rev. E, 2017, 96, 052111 CrossRef PubMed.
- B. J. Kim, Phys. Rev. Lett., 2004, 93, 168701 CrossRef PubMed.
- S. Lafon and A. B. Lee, IEEE transactions on pattern analysis and machine intelligence, 2006, 28, 1393–1403 Search PubMed.
- A. Agrawal and A. Choudhary, APL Mater., 2016, 4, 053208 CrossRef.
- G. B. Goh, N. O. Hodas and A. Vishnu, J. Comput. Chem., 2017, 38, 1291–1307 CrossRef PubMed.
- G. Pilania, C. Wang, X. Jiang, S. Rajasekaran and R. Ramprasad, Sci. Rep., 2013, 3, 2810 CrossRef PubMed.
- Z. Zhang and K. Friedrich, Compos. Sci. Technol., 2003, 63, 2029–2044 CrossRef.
- R. Liu, A. Kumar, Z. Chen, A. Agrawal, V. Sundararaghavan and A. Choudhary, Sci. Rep., 2015, 5, 1551 Search PubMed.
- C. Bisagni and L. Lanzi, Compos. Struct., 2002, 58, 237–247 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh00653a |
| This journal is © The Royal Society of Chemistry 2018 |