How to interpret absorption and fluorescence spectra of charge transfer states in an organic solar cell†
Frank-Julian
Kahle
 a,
Alexander
Rudnick
a,
Heinz
Bässler
b and
Anna
Köhler
a,
Alexander
Rudnick
a,
Heinz
Bässler
b and
Anna
Köhler
 *ab
*ab
aSoft Matter Optoelectronics, University of Bayreuth, 95440 Bayreuth, Germany. E-mail: anna.koehler@uni-bayreuth.de
bBayreuth Institute of Macromolecular Science (BIMF), University of Bayreuth, 95440 Bayreuth, Germany
First published on 27th June 2018
Abstract
The aim of the present work is to identify the appropriate framework for analyzing photoluminescence and photocurrent (EQE) spectra of charge transfer (CT) states in donor–acceptor blends used as active materials for organic solar cells. It was stimulated by the work of Vandewal et al. (J. Am. Chem. Soc., 2017, 139(4), 1699–1704) who analyzed EQE spectra of CT states of a series of blend systems in terms of Marcus theory assuming that, first, the spectral shape reflects the reorganization energy of the donor upon ionization and, second, that disorder effects are unimportant. To test this assumption we applied gated photoluminescence (PL) spectroscopy within a temperature range from 5 to 295 K combined with EQE as well as electroluminescence (EL) experiments on 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Me-LPPP
1 Me-LPPP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCBM blends by weight. We find that the PL spectra are virtually temperature independent and the temporal decay of the emission features a power law with an exponent close to −3/2 as Hong and Noolandi predicted for distributed geminately bound electron-holes pairs. The EL spectrum reveals a red-shift by 100 meV relative to the PL spectrum. The results are inconsistent with both Marcus’ electron transfer theory and the original Marcus–Levich–Jortner (MLJ) theory, and they prove that disorder effects are crucial. Both PL and EQE spectra can be rationalized in terms of the classic Franck–Condon picture of electronic transitions that couple to intra-molecular vibrations as well as low frequency modes of the donor–acceptor pair that forms the CT state.
PCBM blends by weight. We find that the PL spectra are virtually temperature independent and the temporal decay of the emission features a power law with an exponent close to −3/2 as Hong and Noolandi predicted for distributed geminately bound electron-holes pairs. The EL spectrum reveals a red-shift by 100 meV relative to the PL spectrum. The results are inconsistent with both Marcus’ electron transfer theory and the original Marcus–Levich–Jortner (MLJ) theory, and they prove that disorder effects are crucial. Both PL and EQE spectra can be rationalized in terms of the classic Franck–Condon picture of electronic transitions that couple to intra-molecular vibrations as well as low frequency modes of the donor–acceptor pair that forms the CT state.
Conceptual insightsThe generation of charges in organic solar cells occurs by the dissociation of interfacial charge transfer (CT) states. It is therefore crucial to understand the properties of these states. Spectroscopy of CT state emission and absorption (inferred from the photocurrent) can yield pertinent information, provided one knows how to extract it. We demonstrate that the interpretation of CT spectra in thin films requires due consideration of the inhomogeneously broadened density of states. If energetic disorder is included, the spectra can be analysed in a conventional Franck–Condon or a Marcus–Levich–Jortner type picture, with the Stokes’ shift between the maxima of absorption and emission reflecting the reorganization energy of the donor–acceptor pair. This advances beyond the currently applied method, where a classical Marcus-type approach is used without consideration of the energetic inhomogeneity of the film, and where the Stokes’ shift is associated predominantly with the intramolecular reorganization energy of the donor. In contrast to the classical Marcus-type approach, our model correctly reproduces the spectra over the entire temperature range from 5 to 300 K. Conceptually, it implies that the CT state emission or absorption can be described as a process dominated by quantum mechanical tunnelling rather than by strong thermal activation. |
1. Introduction
Research into the spectroscopy of charge transfer (CT) states is basically an old subject1–4 but it receives currently a renaissance. The reason is related to the current endeavor to convert light to electrical power using an organic solar cell (OSC). The active material in an OSC is either a blend or a bilayer of two components that act as electron donors and electron acceptors. When the donor – or equivalently the acceptor – is optically excited, there is charge transfer in whose course a pair of free charge carriers is generated. Understanding how this process proceeds is the subject of current research. There is firm evidence that the process is sequential. Upon exciting the donor (or the acceptor) phase an exciton is created that diffuses towards the acceptor and transfers an electron. This interfacial transfer is an ultra-fast process, completed within typically 100 fs.5–11 Meanwhile there is growing evidence that the initial electron transfer step creates first a – more or less delocalized – CT state at the donor–acceptor interface.12–20 To contribute to a photocurrent, this CT state has to escape from the coulomb well to be converted into a charge-separated state. It turns out that in efficient OSCs this escape process is quite effective. The reason for this is currently heavily disputed.15,21–28 Evidently, the dynamics of the CT state plays a crucial role. Other factors include the magnitude of the charge carrier mobility, the delocalization of charge carriers comprising the CT state, the topology of interface and the entropy of the diffusive random walk that the geminately bound electron–hole pair execute prior to complete dissociation.Usually the CT state at the donor–acceptor interface of an OSC is generated by optically exciting the donor (or, equivalently, the acceptor) to the first singlet state. The electron in the LUMO of the donor is then transferred to the acceptor. Since this is an electron transfer process, it appeared straightforward to apply Marcus’ electron transfer theory for quantitative description. However, Marcus theory is based on thermal equilibrium assuming that the quantum nature of the vibrations that drive the thermally activated transition from the precursor state to the final state does not need to be considered explicitly. Our recent study showed that this assumption is indeed questionable, notably on a time scale of 100 fs that is typical for photo-induced electron transfer in thin films of donor–acceptor composites.5 There is growing evidence that fast electron transfer is accomplished via quantum tunneling.
Energetically, the CT state of the donor–acceptor complex is the lowest state in the system. It can also be generated optically by photons below the absorption edge of either donor or acceptor, yet the oscillator strength of such a transition is quite low. This precludes simple absorption spectroscopy of CT states, though more sophisticated techniques such as photothermal deflection measurements can reveal its absorption spectrum.24,29 Similarly, the low energy tail of the action spectrum of the photocurrent is a reflection of optical CT state generation. It is usually manifested as weak feature, usually of Gaussian character, in the low energy tail of the external quantum efficiency (EQE) spectrum. In principle, a direct optical formation of a CT state, i.e. not via an excited donor or acceptor state, is also an electron transfer process, as is the emission of the CT state. This led Gould et al.30 to use the Strickler–Berg relationship to connect the intensity of the reduced emission spectrum rPL(E) to the transfer rate for electron transfer by
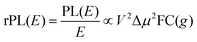 | (1) |
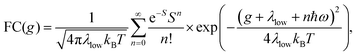 | (2) |
This work prompted Vandewal et al. to apply a similar formalism to analyze OSCs with different donor materials combined with PCBM as an acceptor that feature Gaussian tails below the dominant absorption of both donor and acceptor.37–40 Analogous to Gould, Vandewal used a modified Marcus expression taking an energy dependence of the electronic transition moment M into account, i.e.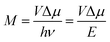 , thus arriving at the expressions for the reduced external quantum efficiency rEQE(E) and the reduced emission spectra rEL(E) of the OSCs, that is,37,38
, thus arriving at the expressions for the reduced external quantum efficiency rEQE(E) and the reduced emission spectra rEL(E) of the OSCs, that is,37,38
 | (3a) |
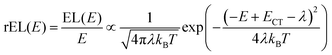 | (3b) |
The analysis of the CT spectra according to Gould et al. [eqn (1) + (2)] and according to Vandewal et al. [eqn (3)] differs from the approach usually taken in the spectroscopy of thin amorphous organic films. To describe the shape of absorption or emission spectra, it is common to consider a Franck–Condon progression in form of a Poisson-distribution of high-energy vibrational modes, that is multiplied by a Gaussian linewidth function, e.g. to account for the inhomogeneous broadening that is characteristic for amorphous thin films. This results in expressions such as41
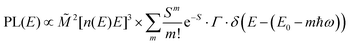 | (4a) |
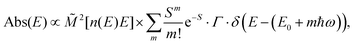 | (4b) |
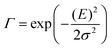 | (5) |
![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) is usually considered to be constant. In this representation, the effect of low-frequency modes is usually subsumed in the linewidth function. PL(E) and Abs(E) are given in photons per unit energy. Here, the relaxation energy associated with the transition is λhigh = S·ħω. n(E) is the refractive index of the medium. To allow for facile comparison with the work of Gould, we shall also consider the electronic transition moment to be energy dependent in this work. Eqn (4) can then be rewritten in a reduced form:
is usually considered to be constant. In this representation, the effect of low-frequency modes is usually subsumed in the linewidth function. PL(E) and Abs(E) are given in photons per unit energy. Here, the relaxation energy associated with the transition is λhigh = S·ħω. n(E) is the refractive index of the medium. To allow for facile comparison with the work of Gould, we shall also consider the electronic transition moment to be energy dependent in this work. Eqn (4) can then be rewritten in a reduced form: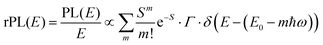 | (6a) |
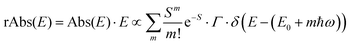 | (6b) |
2. Experimental section
Bulk heterojunction solar cells devices using MeLPPP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCBM blends (1
PCBM blends (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by weight) were fabricated on structured ITO-coated glass substrates. A 15 nm thick layer of MoO3 was used on top of the ITO to improve hole extraction. The active blend layer was spun from chloroform solution (15 mg ml−1) and had a thickness of 110 nm. Finally, a 100 nm thick aluminum cathode was evaporated. For reference, solar cells with pristine MeLPPP (in chloroform, 7.5 mg ml−1) and PCBM layers (in chloroform, 15 mg ml−1), respectively, were fabricated accordingly. The thickness of MeLPPP and PCBM were 60 nm and 30 nm, respectively. The thicknesses of the active layer of the solar cells were controlled with a Dektak (Veeco) profilometer directly on a device. Structure formulas and relevant literature values for the energy levels (ionisation potential Ip, electron affinity Ea, S1 energy) of MeLPPP and PCBM are summarized in Table 1. For ease of reference, the absorption and emission of both compounds are shown in the ESI.†
1 by weight) were fabricated on structured ITO-coated glass substrates. A 15 nm thick layer of MoO3 was used on top of the ITO to improve hole extraction. The active blend layer was spun from chloroform solution (15 mg ml−1) and had a thickness of 110 nm. Finally, a 100 nm thick aluminum cathode was evaporated. For reference, solar cells with pristine MeLPPP (in chloroform, 7.5 mg ml−1) and PCBM layers (in chloroform, 15 mg ml−1), respectively, were fabricated accordingly. The thickness of MeLPPP and PCBM were 60 nm and 30 nm, respectively. The thicknesses of the active layer of the solar cells were controlled with a Dektak (Veeco) profilometer directly on a device. Structure formulas and relevant literature values for the energy levels (ionisation potential Ip, electron affinity Ea, S1 energy) of MeLPPP and PCBM are summarized in Table 1. For ease of reference, the absorption and emission of both compounds are shown in the ESI.†
EQE measurements were performed using a Lock-In-Amplifyer (SR830) at a reference frequency of 130 Hz and monochromatic illumination from a 150 W tungsten lamp (Osram). For EL measurements, the solar cells were biased at 3 V using a Keithley source-measure unit (SMU 237). The luminescence of the sample was recorded by a CCD-camera (Andor iDus) coupled to a monochromator (Oriel). For both EQE and EL measurements, the sample was kept in a sample holder under vacuum at room temperature.
For time-gated emission spectroscopy, the sample was excited at 355 nm, using the frequency-tripled output from a Nd-YAG laser with variable pulse frequency. To record spectra with distinct delay and integration time an intensified charged coupled device camera from Andor was used. For exact time correlation the iCCD camera was triggered by the laser. All experiments were done with the sample being kept under vacuum in a temperature controlled cryostat.
3. Results
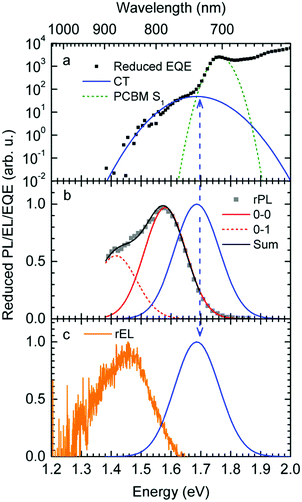
Fig. 1a shows gated photoluminescence spectra of a Me-LPPP:PCBM blend with zero delay and integration time of 10 ns excited at 3.49 eV and recorded in a temperature range of 5 K to 295 K. The spectra reveal two main features with maxima at 1.68 eV and near 1.55 eV.Spectra recorded with a variable delay time indicate that the higher energy feature gradually disappears (Fig. 1b). It is straightforward to associate the 1.68 eV feature with fluorescence from large PCBM domains that are formed during the spin coating process based on comparison with emission spectra from neat PCBM films (shown in the ESI,† Fig. S1). Evidently, domains with a size that exceeds the exciton diffusion lengths are being formed at such a high PCBM loading (≥50 wt%) in MeLPPP. We note that the PCBM emission is still noticeable after a delay time of 30 ns although the lifetime of C60 is known to be around 1 ns. In the following discussion only the 1.55 eV feature of the PL spectrum will be considered that we assign to the CT emission of a Me-LPPP:PCBM complex. This is consistent with the fact that the energy difference between the Ea of the acceptor and the Ip of the donor is about 1.5 eV (cf.Table 1).
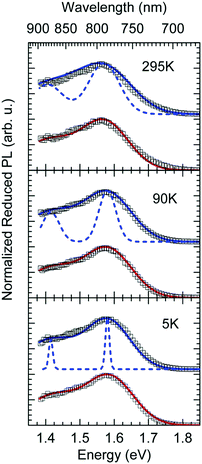
In Fig. 1c we show how the CT emission spectra, recorded after a delay time of 90 ns, evolve as a function of temperature. The key observation is that there is a 5-fold increase in intensity when lowering the temperature from 295 K to 5 K while the shape of the emission spectrum is preserved (see also Fig. S2, ESI†). There is only a marginal hypsochromic shift of the spectra upon cooling. The high energy wing of the spectrum is close to a Gaussian lineshape.
Next we measured the temporal decay of the CT emission. It turns out the decay is highly non-exponential and extends into μs range. This is documented by Fig. 2(a and b), in which the emissions, recorded at 295 K with a gate width of 10 ns (at 5 K with a gate width of 500 ns) are plotted on a double logarithmic scale. The decay follows a power law with an exponent very close to −3/2.
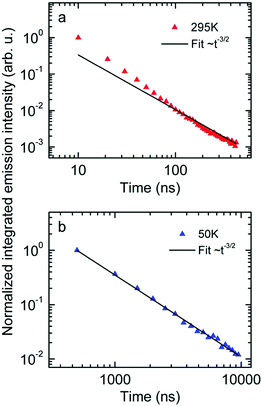 | ||
| Fig. 2 Normalized emission intensity at (a) 295 K and (b) 50 K along with fits following a t−3/2 power law. | ||
Finally we measured the EQE as well as the electroluminescence (EL) of the diode with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 blend of Me-LPPP
1 blend of Me-LPPP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
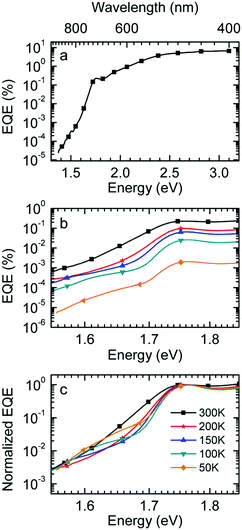
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCBM at selected temperatures. The EQE spectra, shown in Fig. 3a, reveal a broad tail with a weak shoulder below 1.7 eV that is associated with the generation of CT states, followed by a weak local maximum at the S1–S0 0–0 transition of PCBM at about 1.75 eV (cf.Table 1) and a smooth increase at higher photon energies. Upon sample cooling from the 300 K to 50 K the EQE decreases by two orders of magnitude (Fig. 3b), yet the character of the spectra is largely retained. Normalization of the EQE to the PCBM S1 energy (1.75 eV) identifies two small spectral changes (Fig. 3c). First, the linewidth close to S1 increases with temperature, and second, the relative intensity of the EQE signal at the CT energy reduces, so that the tail of S1 and the CT state merge into one indistinguishable feature.
PCBM at selected temperatures. The EQE spectra, shown in Fig. 3a, reveal a broad tail with a weak shoulder below 1.7 eV that is associated with the generation of CT states, followed by a weak local maximum at the S1–S0 0–0 transition of PCBM at about 1.75 eV (cf.Table 1) and a smooth increase at higher photon energies. Upon sample cooling from the 300 K to 50 K the EQE decreases by two orders of magnitude (Fig. 3b), yet the character of the spectra is largely retained. Normalization of the EQE to the PCBM S1 energy (1.75 eV) identifies two small spectral changes (Fig. 3c). First, the linewidth close to S1 increases with temperature, and second, the relative intensity of the EQE signal at the CT energy reduces, so that the tail of S1 and the CT state merge into one indistinguishable feature.
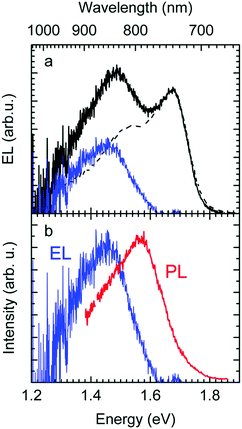
The EL spectrum (Fig. 4a), is a superposition of the electroluminescence from the CT state (ELCT) and the EL-spectrum of PCBM. By subtracting the EL-spectrum of pristine PCBM, know from the literature,40 the ELCT spectrum can be recovered. It is noteworthy that the ELCT spectrum is bathochromically shifted relative to the PLCT spectrum (Fig. 4b).
4. Analysis
Before embarking on an analysis and discussion of results it is appropriate to summarize the essential experimental facts: (i) upon lowering the temperature from 295 K to 5 K the intensity of the CT emission increases by a factor of 5 while the spectrum shifts slightly to the blue, yet it retains its spectral shape (Fig. 1c). (ii) When cooling from 295 K to 50 K, the EQE-decreases by two orders of magnitude while the spectral shape is preserved (Fig. 3b). (iii) The electroluminescence spectrum is off-set from the PL spectrum by roughly 100 meV (Fig. 4b). (iv). The decay of the optically generated CT spectrum features a power law and extends into the μs range (Fig. 2).We shall first argue that there is not a single, well-defined CT state, but rather a broad distribution of them that gives rise to significant energetic disorder.46 In general, OSCs are made of disordered materials as evidenced by the inhomogeneous broadening of the absorption and photoluminescence spectra of the singlet excited states. Likewise, charge transport occurs via incoherent hopping among energetically disordered chromophores or conjugated segments of a polymer chain. Therefore, CT spectra are likely to be affected by disorder.43,46 There are two features in the experimental data that testify to it.
First, the CT-emission decays in power law fashion rather than exponentially (Fig. 2). This is firm evidence that there is a broad distribution of states that have their own transition rates and emission energies. The observation that the CT decay follows a power law with an exponent of −3/2 up to a microsecond is suggestive of geminate recombination as has been described by Hong and Noolandi.52 In their original work these authors calculated how an electron–hole pair within its Coulomb capture radius recombines with constant, temperature dependent, diffusivity, and they found that the recombination rate follows a power law with exponent −3/2. Later on they extended their formalism by including the possibility that the recombination event is a tunneling process that does not require thermal activation, yet the functional dependences are the same.53 It is a straightforward conjecture that this formalism can explain the observed non-exponential decay of optically generated CT states evidenced in Fig. 2. Since donor and acceptor moieties are distributed in energy it is likely that CT states also form a distribution. It is also likely that the hole that has been transferred from an excited PCBM molecule can make another jump to a nearby but energetically lower state at the expense of electron–hole separation. Considering that the recombination of the pair depends exponentially on their distance this gives rise to a broad distribution of recombination rates and the premises for the Hong–Noolandi formalism are fulfilled.
Second, the observation that the EL spectrum is red-shifted relative to the PL spectrum of CT states is also a signature of the importance of disorder. If one generates an exciton or a charge carrier in a bulk organic solid in which the distribution of sites is inhomogeneously broadened, it will execute a random walk and thereby, on average, jump to lower states of the distribution. Such a spectral relaxation of an exciton is amenable by time resolved fluorescence spectroscopy. In an EL experiment, the recombining electrons and holes are injected from the electrodes, and thus experience a long journey until their decay during which significant energetic relaxation in the DOS occurs. However, when a CT state is generated by direct optical excitation, electron and hole are correlated. In addition, the transition dipole moment and overlap integral, controlling the rate of energy transfer, are low. Thus, spectral diffusion is greatly reduced. Accordingly, EL spectra are red-shifted relative to PL spectra of CT states, and this redshift is a signature of the broadened DOS. This implies, by the way, that the Stokes shift between absorption and EL emission includes a contribution from spectral relaxation.54–56
Having confirmed that the CT states form a broad DOS, we now proceed to analyze the spectra in terms of the classic Franck–Condon picture. In this concept, absorption and fluorescence spectra of a chromophore are vibronic progressions of high-frequency intramolecular modes built on a resonant 0–0 origin. The coupling strength is controlled by a Huang–Rhys factor S. In rigid chromophores S is usually <1. In this case, the 0–0 transitions in absorption and emission are the dominant spectral features, and they are resonant. If the chromophore is embedded in a solid or liquid environment both, absorption and emission, experience a bathochromic shift because the excited state polarizes its environment. If the environment is non-crystalline, the inter-molecular distances, and concomitantly the polarization energies, vary randomly, and this effect leads to inhomogeneous line broadening and an associated Gaussian lineshape.42 Nevertheless, the 0–0 features in absorption and emission remain being resonant provided that S ≤ 1 and that there is no spectral diffusion, e.g. due to energy transfer. In a condensed medium, such as a thin film, there is an additional coupling of the excited state to low energy modes of the molecular environment, i.e. phonons. As a consequence, each vibronic (high-frequency) transition carries a so-called phonon wing. This wing can be described by a Poisson distribution characterized by Huang–Rhys factor Slow and an average (low-frequency) phonon energy ħωlow. If Slow > 2, the maxima of the 0–0 transition are no longer resonant as evidenced by the appearance of a Stokes shift.57 For large values of Slow, e.g. Slow ≳ 4 the Poisson distribution merges into a Gaussian distribution (cf. ESI,† Fig. S3). In consequence, a Gaussian lineshape results that adds to the Gaussian linewidth obtained by the inhomogeneous broadening.
The reduced EQE spectrum (Fig. 5a), plotted on a logarithmic scale, is composed of a Gaussian low energy tail and a strong feature that is associated with S1–S0 0–0 transition of PCBM. The width of the PCBM feature decreases upon sample cooling which facilitates spectral deconvolution (Fig. 3c). For this reason and since at lower temperatures thermal broadening plays a lesser role, we present an analysis of the reduced PL and EQE spectra recorded at 90 K. At that temperature, the origin of the PCBM feature is at 1.77 eV with a standard deviation of 20 meV. The rPL spectra of the CT state show a Gaussian high energy edge followed by a low energy tail that we interpret as a vibrational overtone (Fig. 5b). In the rEQE spectra, the vibrational overtone cannot be differentiated from those pertaining to the S1 state of the PCBM.
We therefore analyze the rEQE and rPL spectra with eqn (6) for only the 0–0 and, in the case of the rPL, also the 0–1 peak, i.e. m = 0 to 1. As already mentioned, the Gaussian linewidth function Γ usually includes contributions from both, the inhomogeneous line broadening as well as the low-frequency phonon wing. Here, we wish to explicitly differentiate between the two contributions. Focusing first only on the 0–0 transition of the CT state (m = 0), we thus use the product of the Poisson distribution for the low-frequency intermolecular modes with the Gaussian lineshape function of variance σ2 characterizing the inhomogeneous broadening to fit the 0–0 peak. This corresponds to using eqn (6) with S = Slow and ω = ωlow (and m = 0).
To fit both, rEQE and rPL, E0 = ECT is determined by the intersection of the rEQE and rPL spectra. It may, at first, seem that with 3 parameters, Slow, ħωlow and σ, the problem is overparametrized. However, the high energy tail of the rPL (the low energy tail of the rEQE) needs to be reproduced, thus determining the inhomogeneous broadening captured in σ2, and the maxima of rEQE and rPL are at fixed positions, which defines combination of Slow and ħωlow. (We recall that any contribution to the PL at energies above the 0–0 transition can only arise from inhomogeneous broadening and not from a phonon wing that, by definition, is below the 0–0 transition.)
The rPL spectrum can be reproduced by invoking a 0–0 feature of the CT transition at ECT = 1.62 eV and an inhomogeneous broadening (standard deviation σ) of 67 meV. The coupling to low-frequency phonons can be expressed, e.g., by considering 10 meV phonons with a Huang Rhys factor of Slow = 4.0, corresponding to a reorganization energy of λlow = Slow·ħωlow = 40 meV. Equally good fits can be obtained by considering phonons of a lower or higher energy, with correspondingly higher or lower Huang–Rhys parameter (in the range of S = 3–7), as long as the reorganization energy is kept at 40 meV.‡ The peaks pertaining to rPL and rEQE are not fully mirror-symmetric but differ slightly. However, the pertinent parameters to fit the rEQE are kept at a σ of 67 meV, and a ECT of 1.62 eV. For the rEQE, a reorganization energy of λlow = 60 meV results, e.g. obtained by Slow = 4 and ħωlow = 15 meV. The sum of both reorganization energies is 40 meV + 60 meV = 100 meV. This is the observed Stokes’ shift. The parameters used for the fits of rEQE and rPL are summarized in Table 2.
| E CT (eV) | σ (meV) | λ low (meV) | S low | ħω (meV) | |
|---|---|---|---|---|---|
| rEQE | 1.62 | 67 | 60 | 4 | 15 |
| rPL | 1.62 | 67 | 40 | 4 | 10 |
We can now continue to also include the first vibrational overtone observed in the PL. The easiest way to do this is to shift the obtained rPL fit by an effective high frequency mode, here ħωhigh = 165 meV, multiply it by an appropriate high-frequency Huang–Rhys factor, here Shigh = 0.58, and add the two peaks (0–0 and 0–1). The excellent match of the fit to the experimental data is shown in Fig. 5b. Mathematically, this is equivalent to performing one multi-mode fit, taking both modes into account simultaneously, according to41
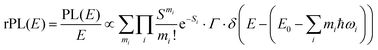 | (7) |
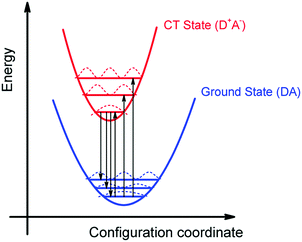
We can summarize the result of our analysis as follows. The rPL and rEQE of the CT state can be modelled as a Franck–Condon progression with a 0–0 transition at ECT = 1.62 eV. It is characterized by an inhomogenous broadening of 67 meV. The Stokes’ shift of 100 meV between the peaks of CT emission and rEQE arises only due to low-frequency phonon modes. The asymmetry between the CT part of the rEQE and the rPL results in a higher reorganization energy for the CT state D+A− than for the associated ground state pair DA. This is illustrated in Fig. 6. It implies a steeper curve of the potential energy for D+A− than for DA, in agreement with the intuitive notion that there should be a stronger bonding, i.e. force constant k, for the ionic pair where coulomb forces prevail than for the neutral pair that is only held together by van der Waals forces. We suggest that the low-frequency modes be predominantly of inter-molecular nature. The transfer of an electron from donor to acceptor creates an inter-molecular coulomb attraction that is likely to couple strongly to inter-molecular motion. Moreover, coupling of the rigid MeLPPP or the fullerene to low-frequency torsional or librational modes can only be weak due to their geometric constraints.
The above analysis is consistent with all experimentally observed features. In Fig. 1, we noticed a surprisingly long-lived fluorescence from PCBM that still prevails after 30 ns at room temperature, and concomitantly, the CT emission increases upon cooling by a factor of 5. Given the moderately small energy difference between the 0–0 peaks of the CT state (1.62 meV) and that of the PCBM S1 state (1.77 meV) of 150 meV, the part of PCBM emission that we still observe at 30 ns after excitation is likely to arise from thermally activated delayed fluorescence (TADF), and this is also the most likely non-radiative decay channel of the CT state that is frozen out upon cooling. The power-law decay with exponent −3/2 we reported in Fig. 2 testifies to the existence of a broad DOS of CT states. Our analysis shows that the CT DOS (σ = 67 meV) is about 3.5 times as broad as that of the S1 state of PCBM (σ = 20 meV). This broad CT DOS is fully consistent with the observed energy difference between EL and PL (Fig. 4b), as detailed above. The fact that the EQE of the diode decreases strongly upon cooling as documented by Fig. 3b can be understood by considering that the EQE is the product of the probability for creating a CT state, the probability that it dissociates into a pair of free charge carriers, and the probability that these free carriers are extracted at the electrode. From earlier work we know that the dissociation probability of the MeLPPP-fullerene CT state under short-circuit conditions depends only weakly on temperature.58 This is because the degree of delocalization of the hole on the conjugated polymer of Me-LPPP is large, which substantially reduces the binding energy of the CT state with fullerenes.58 The probability for charge extraction is controlled by the mobility of the charge carriers, which has a strong dependence on temperature.25,59,60 Thus, the overall decrease of the EQE reflects mostly the charge transport properties of the film. The subtle change in shape of the EQE reflects mostly the increase in inhomogeneous line broadening for the S0–S1 transition of the PCBM with temperature.
5. Discussion
It appears appropriate to briefly comment on the results of the analysis of the rEQE that Vandewal et al. carried out on a series of donor–acceptor systems with C60 as an acceptor.39 Using the Marcus-formalism [eqn (3)], they identified the standard deviation of the Gaussian tail of the reduced EQE spectrum with the structural relaxation of the CT state thus ignoring inhomogeneous spectral broadening. They suggest (i) that the most important contributor to the line-shape be low-frequency intramolecular vibrations and that static disorder played no role, and (ii) that these vibrations be thermally activated, so that the lineshape be reasonably well described in terms of a Marcus-type expression. In their definition, “low-frequency” reaches up to 125 meV, which differs from the range e.g. Jortner35 refers to as “low-frequency”, which is up to about 10 meV. Moreover, they compared the inferred reorganization energy with that of the donor upon ionization thus arguing (iii) that the EQE spectrum is an experimental probe of this intramolecular reorganization energy.In certain cases, it can indeed be useful to consider the optical excitation as a charge-transfer reaction,30,61 and this approach, cast into eqn (1) by Gould, is undoubtedly valid. However, we question whether the use of a classical Marcus expression [eqn (3)] is appropriate, and whether the neglect of inhomogeneous broadening can be justified, and we doubt to the direct association of the Stokes’ shift with a reorganization energy that mostly reflects the intramolecular reorganization energy of the donor cation.
We first point out that the observations presented in Fig. 2 and 4 cannot be accounted for when presuming a single CT-state energy without energetic disorder. Moreover, when using the rEL instead of the rPL to obtain a simultaneous fit of reduced emission and reduced EQE, a different Stokes’ shift is obtained, which would suggest a different reorganization energy, depending on the mode of excitation, which is unphysical. When using the rPL spectra, the Gaussian shape of the 0–0 peak at room temperature can readily be reproduced using the classical Marcus expression of eqn (3), which is also a Gaussian function, albeit with ECT = 1.71 and λ = 160 meV at 295 K, as shown in Fig. 7a. However, neither the low-energy tail of the rPL nor the experimental rEQE are reproduced. Rather, the fit suggests the absorption of the CT state to peak at an energy above the S1 energy of PCBM, which is also unphysical. More important, however, is that the temperature evolution of the rPL spectra of Fig. 1c cannot be rendered correctly in the classical Marcus framework of eqn (3). When reducing the temperature, eqn (3) predicts a narrowing of the Gaussian shape that is not observed experimentally, as evident in Fig. 7b. Fig. 7c compares the intensity-normalized rPL spectra with the fit to eqn (3) for different temperatures. In the same way, the shape of the EQE around the CT transition hardly narrows upon cooling (Fig. 3 and 7b), and is thus not compatible with the Marcus-type description.
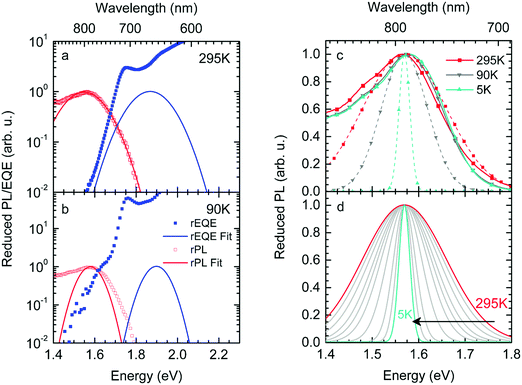 | ||
| Fig. 7 (a) Reduced PL and EQE recorded at (a) 295 K and (b) 90 K (squares), along with a fit (blue solid lines) to the rPL according to the Marcus model, i.e.eqn (3b). The concomitant resulting curve for the rEQE (blue curve) according to eqn (3a) is also shown. The fit parameters are at ECT = 1.71 (1.74) meV and λ = 160 meV at 295 K (90 K). (c) Comparison of the rPL data at 295 K, 90 K and 5 K (solid lines) with the spectra calculated (dashed lines) according to Marcus’ theory [eqn (3)] at corresponding temperatures. (d) Spectra calculated according to Marcus theory [eqn (3)] over a temperature range from 295 K down to 5 K. | ||
To understand why the classical Marcus expression falls short here, it is worthwhile reconsidering eqn (1). As Jortner pointed out some time ago,35 the Franck–Condon-weighted density of states, FC(g), can be evaluated for different limiting cases, such as at low, intermediate and high temperature, where the thermal energy is compared to the energy of the vibrational modes involved. The classical Marcus expression that is used for eqn (3), with λ = λlow + λhigh, presumes that the thermal energy be large compared to both low-frequency and high-frequency phonons, i.e. kBT ≫ ħω. For MeLPPP and PCBM, the dominant high-frequency mode is associated with the CC stretching motion and is around 160 meV. The highest temperature, at which the measurements are carried out, is room temperature, where kBT is about 25 meV. Thus, the requirements for the classic case are not fullfilled. kBT is even smaller than the “low-frequency” cut-off of 125 meV of Vandewal et al.
In his evaluation of CT-states, Gould used the MLJ-expression to account for FC(g). This is the intermediate case, where the thermal energy is large compared to the low-frequency modes, yet small compared to the high-frequency modes, ħωlow ≪ kBT ≪ ħω. Given that for organic thin films, low frequency modes usually range from about 1–10 meV,35 and high-frequency ones from about 50–300 meV, this appears to be the appropriate range for a description at room temperature. To test whether this works, we have fitted the PL and EQE using the MLJ expression, multiplied with a Gaussian lineshape function of standard deviation σ to account for inhomogeneous broadening. The pertinent expression is thus
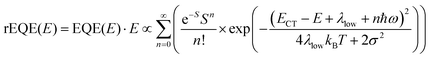 | (8a) |
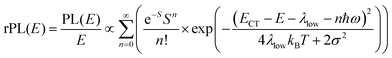 | (8b) |
| σ (meV) | ħω (meV) | S | λ low (meV) | E CT (eV) | E CT (eV) | E CT (eV) | |
|---|---|---|---|---|---|---|---|
| (295 K) | (90 K) | (5 K) | |||||
| FC-Fit | 67 | 165 | 0.58 | 40 | 1.61 | 1.62 | 1.625 |
| MLJ-Fit with σ | 65 | 165 | 0.58 | 40 | 1.61 | 1.62 | 1.62 |
| MLJ-Fit σ = 0 meV | 0 | 165 | 0.58 | 40 | 1.61 | 1.62 | 1.62 |
What do we learn from this? Evidently, a FC-Fit and a MLJ-Fit work equally well, as long as inhomogeneous line broadening due to energetic disorder is taken into account. In fact, the large degree of disorder (σ = 65 meV) compared to the reorganization energy of the low-frequency phonons (40 meV) makes it impossible to differentiate between two fits.
Formally, at very low temperatures where kBT ≪ ħωlow, according to Jortner's work it would be necessary to use a different expression for the Franck–Condon-weighted density of states instead of eqn (2) or (8). It is
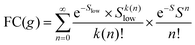 | (9) |
6. Conclusion
Thus, in summary we find that the lineshape of the CT state, in PL and EQE, is determined by the effects of static disorder and low-frequency vibrations by about equal contributions. Vandewal et al. attribute the modes involved in the reorganization process entirely to an intramolecular origin. We question this and suggest that the transfer of a charge, that changes a neutral DA pair into a charged D+A− pair, is likely to couple strongly to inter-molecular vibrations, so that the low-frequency reorganization energy is predominantly an inter-molecular quantity that reflects the structural displacement between donor and acceptor upon excitation like in an excimer state. Even so, Vandewal et al. have convincingly shown that the Gaussian linewidth, and thus the Stokes'shift, correlate linearly with the reorganization energy calculated for the formation of the donor cation. It is conceivable that this correlation is accidental. We suspect that the static disorder, which contributes to about half of the Gaussian linewidth, may actually correlate with the flexibility or rigidity of the chromophores. For a satisfying description of the CT state spectra, we found that the inclusion of static disorder is essential. As already noted by Burke et al., the neglect of disorder in the treatment of CT states leads to values that implicitly contain a contribution from disorder, and the associated values for λ, ECT and the Stokes’ shift need to be viewed with some caution, keeping this implication in mind.46,62 With disorder included, the spectra may be modelled using a MLJ-based or a FC-based fit [eqn (8) or (7), respectively]. In our interpretation, the resulting Stokes’ shift gives the reorganization energy associated with low-frequency phonons.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support by the German Science Foundation DFG through the doctoral training center “Photophysics of Synthetic and Biological Multichromophoric Systems” (GRK 1640) and the Bavarian State Ministry of Education, Science and the Arts through the Collaborative Research Network “Solar Technologies go Hybrid” (SolTech). Furthermore, F.-J. K. was supported by the Elite Network Bavaria (ENB) in the framework of the Elite Study Program “Macromolecular Science”. We thank S. Athanasopoulos for critical reading of the manuscript.Notes and references
- H. Leonhardt and A. Weller, Ber. Bunsen-Ges., 1963, 67, 791–795 CrossRef.
- D. Rehm and A. Weller, Z. Phys. Chem., 1970, 69, 183–200 CrossRef.
- A. Weller, Z. Phys. Chem., 1982, 130, 129–138 CrossRef.
- A. Weller, Z. Phys. Chem., 1982, 133, 93–98 CrossRef.
- T. Unger, S. Wedler, F. J. Kahle, U. Scherf, H. Bässler and A. Köhler, J. Phys. Chem. C, 2017, 121, 22739–22752 CrossRef.
- S. M. Falke, C. A. Rozzi, D. Brida, M. Maiuri, M. Amato, E. Sommer, A. De Sio, A. Rubio, G. Cerullo, E. Molinari and C. Lienau, Science, 2014, 344, 1001–1005 CrossRef PubMed.
- J. L. Brédas, E. H. Sargent and G. D. Scholes, Nat. Mater., 2017, 16, 35–44 CrossRef PubMed.
- E. R. Bittner and C. Silva, Nat. Commun., 2014, 5, 3119 CrossRef PubMed.
- H. Tamura, I. Burghardt and M. Tsukada, J. Phys. Chem. C, 2011, 115, 10205–10210 CrossRef.
- H. Tamura, R. Martinazzo, M. Ruckenbauer and I. Burghardt, J. Chem. Phys., 2012, 137, 22A540 CrossRef PubMed.
- H. Tamura and I. Burghardt, J. Phys. Chem. C, 2013, 117, 15020–15025 CrossRef.
- G. Grancini, M. Maiuri, D. Fazzi, A. Petrozza, H. J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Nat. Mater., 2013, 12, 29–33 CrossRef PubMed.
- J. M. Szarko, B. S. Rolczynski, S. J. Lou, T. Xu, J. Strzalka, T. J. Marks, L. P. Yu and L. X. Chen, Adv. Funct. Mater., 2014, 24, 10–26 CrossRef.
- A. C. Jakowetz, M. L. Bohm, J. B. Zhang, A. Sadhanala, S. Huettner, A. A. Bakulin, A. Rao and R. H. Friend, J. Am. Chem. Soc., 2016, 138, 11672–11679 CrossRef PubMed.
- M. Gerhard, A. P. Arndt, M. Bilal, U. Lemmer, M. Koch and I. A. Howard, Phys. Rev. B, 2017, 95, 195301 CrossRef.
- C. Schwarz, S. Tscheuschner, J. Frisch, S. Winkler, N. Koch, H. Bässler and A. Köhler, Phys. Rev. B, 2013, 87, 155205 CrossRef.
- B. Bernardo, D. Cheyns, B. Verreet, R. D. Schaller, B. P. Rand and N. C. Giebink, Nat. Commun., 2014, 5, 3245 CrossRef PubMed.
- V. Abramavicius, V. Pranculis, A. Melianas, O. Inganäs, V. Gulbinas and D. Abramavicius, Sci. Rep., 2016, 6, 32914 CrossRef PubMed.
- X. Liu, K. Ding, A. Panda and S. R. Forrest, ACS Nano, 2016, 10, 7619–7626 CrossRef PubMed.
- B. W. Larson, O. G. Reid, D. C. Coffey, S. M. Avdoshenko, A. A. Popov, O. V. Boltalina, S. H. Strauss, N. Kopidakis and G. Rumbles, Adv. Energy Mater., 2016, 6, 1601427 CrossRef.
- S. N. Hood and I. Kassal, J. Phys. Chem. Lett., 2016, 7, 4495–4500 CrossRef PubMed.
- S. Albrecht, K. Vandewal, J. R. Tumbleston, F. S. U. Fischer, J. D. Douglas, J. M. J. Frechet, S. Ludwigs, H. Ade, A. Salleo and D. Neher, Adv. Mater., 2014, 26, 2533–2539 CrossRef PubMed.
- D. C. Coffey, B. W. Larson, A. W. Hains, J. B. Whitaker, N. Kopidakis, O. V. Boltalina, S. H. Strauss and G. Rumbles, J. Phys. Chem. C, 2012, 116, 8916–8923 CrossRef.
- K. Vandewal, S. Albrecht, E. T. Hoke, K. R. Graham, J. Widmer, J. D. Douglas, M. Schubert, W. R. Mateker, J. T. Bloking, G. F. Burkhard, A. Sellinger, J. M. J. Frechet, A. Amassian, M. K. Riede, M. D. McGehee, D. Neher and A. Salleo, Nat. Mater., 2014, 13, 63–68 CrossRef PubMed.
- T. Hahn, J. Geiger, X. Blase, I. Duchemin, D. Niedzialek, S. Tscheuschner, D. Beljonne, H. Bässler and A. Köhler, Adv. Funct. Mater., 2015, 25, 1287–1295 CrossRef.
- C. Deibel, A. Wagenpfahl and V. Dyakonov, Phys. Status Solidi RRL, 2008, 2, 175–177 CrossRef.
- W. Tress, K. Leo and M. Riede, Phys. Rev. B, 2012, 85, 155201 CrossRef.
- J. Liu, S. S. Chen, D. P. Qian, B. Gautam, G. F. Yang, J. B. Zhao, J. Bergqvist, F. L. Zhang, W. Ma, H. Ade, O. Inganas, K. Gundogdu, F. Gao and H. Yan, Nat. Energy, 2016, 1, 16089 CrossRef.
- N. A. Ran, J. A. Love, C. J. Takacs, A. Sadhanala, J. K. Beavers, S. D. Collins, Y. Huang, M. Wang, R. H. Friend, G. C. Bazan and T. Q. Nguyen, Adv. Mater., 2016, 28, 1482–1488 CrossRef PubMed.
- I. R. Gould, D. Noukakis, L. Gomezjahn, R. H. Young, J. L. Goodman and S. Farid, Chem. Phys., 1993, 176, 439–456 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef.
- R. A. Marcus, Discuss. Faraday Soc., 1960, 21–31 RSC.
- V. G. Levich, Adv. Electrochem. Electrochem. Eng., 1966, 4, 249–371 Search PubMed.
- R. R. Dogonadze, in Reactions of Molecules at Electrodes, ed. M. S. Hush, Wiley-Interscience, London, 1971 Search PubMed.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867 CrossRef.
- M. Bixon and J. Jortner, Faraday Discuss., 1982, 74, 17–29 RSC.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Phys. Rev. B, 2010, 81, 125204 CrossRef.
- K. Vandewal, Annu. Rev. Phys. Chem., 2016, 67, 113–133 CrossRef PubMed.
- K. Vandewal, J. Benduhn, K. S. Schellhammer, T. Vangerven, J. E. Rückert, F. Piersimoni, R. Scholz, O. Zeika, Y. L. Fan, S. Barlow, D. Neher, S. R. Marder, J. Manca, D. Spoltore, G. Cuniberti and F. Ortmann, J. Am. Chem. Soc., 2017, 139, 1699–1704 CrossRef PubMed.
- K. Tvingstedt, K. Vandewal, A. Gadisa, F. L. Zhang, J. Manca and O. Inganas, J. Am. Chem. Soc., 2009, 131, 11819–11824 CrossRef PubMed.
- P. K. H. Ho, J. S. Kim, N. Tessler and R. H. Friend, J. Chem. Phys., 2001, 115, 2709–2720 CrossRef.
- A. Köhler and H. Bässler, Electronic Processes in Organic Semiconductors: An Introduction, Wiley, 2015 Search PubMed.
- R. A. Street, K. W. Song, J. E. Northrup and S. Cowan, Phys. Rev. B, 2011, 83, 165207 CrossRef.
- N. Jain, N. Chandrasekaran, A. Sadhanala, R. H. Friend, C. R. McNeill and D. Kabra, J. Mater. Chem. A, 2017, 5, 24749–24757 RSC.
- A. N. Brigeman, M. A. Fusella, Y. X. Yan, G. E. Purdum, Y. L. Loo, B. P. Rand and N. C. Giebink, Adv. Energy Mater., 2016, 6, 1601001 CrossRef.
- T. M. Burke, S. Sweetnam, K. Vandewal and M. D. McGehee, Adv. Energy Mater., 2015, 5, 1500123 CrossRef.
- R. A. Marcus, J. Phys. Chem., 1989, 93, 3078–3086 CrossRef.
- C. Schwarz, H. Bässler, I. Bauer, J. M. Koenen, E. Preis, U. Scherf and A. Köhler, Adv. Mater., 2012, 24, 922–925 CrossRef PubMed.
- J. J. Benson-Smith, L. Goris, K. Vandewal, K. Haenen, J. V. Manca, D. Vanderzande, D. D. C. Bradley and J. Nelson, Adv. Funct. Mater., 2007, 17, 451–457 CrossRef.
- D. Hertel, S. Setayesh, H. G. Nothofer, U. Scherf, K. Müllen and H. Bässler, Adv. Mater., 2001, 13, 65–70 CrossRef.
- W. J. D. Beenken, F. Herrmann, M. Presselt, H. Hoppe, S. Shokhovets, G. Gobsch and E. Runge, Phys. Chem. Chem. Phys., 2013, 15, 16494–16502 RSC.
- K. M. Hong and J. Noolandi, J. Chem. Phys., 1978, 68, 5163–5171 CrossRef.
- K. M. Hong, J. Noolandi and R. A. Street, Phys. Rev. B, 1981, 23, 2967–2976 CrossRef.
- S. T. Hoffmann, H. Bässler, J. M. Koenen, M. Forster, U. Scherf, E. Scheler, P. Strohriegl and A. Köhler, Phys. Rev. B, 2010, 81, 115103 CrossRef.
- R. Jankowiak, B. Ries and H. Bässler, Phys. Status Solidi B, 1984, 124, 363–371 CrossRef.
- B. Movaghar, M. Grünewald, B. Ries, H. Bässler and D. Wurtz, Phys. Rev. B, 1986, 33, 5545–5554 CrossRef.
- R. F. Mahrt and H. Bässler, Synth. Methods, 1991, 45, 107–117 CrossRef.
- S. Tscheuschner, H. Bässler, K. Huber and A. Köhler, J. Phys. Chem. B, 2015, 119, 10359–10371 CrossRef PubMed.
- J. Kurpiers and D. Neher, Sci. Rep., 2016, 6, 26832 CrossRef PubMed.
- T. Hahn, S. Tscheuschner, F. J. Kahle, M. Reichenberger, S. Athanasopoulos, C. Saller, G. C. Bazan, T. Q. Nguyen, P. Strohriegl, H. Bässler and A. Köhler, Adv. Funct. Mater., 2017, 27, 1604906 CrossRef.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH, Weinheim, 3rd edn, 2011 Search PubMed.
- N. A. Ran, S. Roland, J. A. Love, V. Savikhin, C. J. Takacs, Y. T. Fu, H. Li, V. Coropceanu, X. F. Liu, J. L. Brédas, G. C. Bazan, M. F. Toney, D. Neher and T. Q. Nguyen, Nat. Commun., 2017, 8, 79 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh00564h |
| ‡ As a criterion for the appropriateness of a fit, we choose a maximum deviation from the experimental data of 5% (significance level) at half of the maximum peak height at the high energy edge of the spectrum. To determine the according parameter range we varied the Huang–Rhys-parameter S while keeping the reorganization energy fixed. |
| This journal is © The Royal Society of Chemistry 2018 |