Open Access Article
Open Access ArticleChaotic printing: using chaos to fabricate densely packed micro- and nanostructures at high resolution and speed†
Grissel
Trujillo-de Santiago
 abcd,
Mario Moisés
Alvarez
abcd,
Mario Moisés
Alvarez
 *abcd,
Mohamadmahdi
Samandari
abe,
Gyan
Prakash
ab,
Gouri
Chandrabhatla
ab,
Pamela Inés
Rellstab-Sánchez
abd,
Batzaya
Byambaa
ab,
Parisa
Pour Shahid Saeed Abadi
*abcd,
Mohamadmahdi
Samandari
abe,
Gyan
Prakash
ab,
Gouri
Chandrabhatla
ab,
Pamela Inés
Rellstab-Sánchez
abd,
Batzaya
Byambaa
ab,
Parisa
Pour Shahid Saeed Abadi
 ab,
Serena
Mandla
ab,
Serena
Mandla
 abf,
Reginald K.
Avery
abf,
Reginald K.
Avery
 abg,
Alejandro
Vallejo-Arroyo
abd,
Amir
Nasajpour
abg,
Alejandro
Vallejo-Arroyo
abd,
Amir
Nasajpour
 abkn,
Nasim
Annabi
abkn,
Nasim
Annabi
 abhk,
Yu Shrike
Zhang
abhk,
Yu Shrike
Zhang
 ab and
Ali
Khademhosseini
ab and
Ali
Khademhosseini
 *abfijklmn
*abfijklmn
aBiomaterials Innovation Research Center, Division of Engineering in Medicine, Department of Medicine, Brigham and Women's Hospital, Harvard Medical School, Cambridge 02139, MA, USA
bHarvard-MIT Division of Health Sciences and Technology, Cambridge 02139, MA, USA
cMicrosystems Technologies Laboratories, MIT, Cambridge, 02139, MA, USA
dCentro de Biotecnología-FEMSA. Escuela de Ingeniería y Ciencias, Tecnologico de Monterrey, Monterrey, 64849, Nuevo León, Mexico. E-mail: mario.alvarez@itesm.mx
eSchool of Mechanical Engineering, College of Engineering, University of Tehran, Tehran 11155-4563, Iran
fWyss Institute for Biologically Inspired Engineering, Harvard University, Boston 02115, MA, USA
gDepartment of Biological Engineering, Massachusetts Institute of Technology, Cambridge, 02139, MA, USA
hDepartment of Chemical Engineering, Northeastern University, Boston, 02115-5000, MA, USA
iCenter for Nanotechnology, King Abdulaziz University, Jeddah 21569, Saudi Arabia
jKU Convergence Science and Technology Institute, Department of Bioindustrial Technologies, College of Animal Bioscience and Technology, Konkuk University, Seoul 05029, Republic of Korea
kDepartment of Bioengineering, Department of Chemical and Biomolecular Engineering, Henry Samueli School of Engineering and Applied Sciences, University of California-Los Angeles, Los Angeles, CA, USA
lDepartment of Radiology, David Geffen School of Medicine, University of California-Los Angeles, Los Angeles, CA, USA
mCenter for Minimally Invasive Therapeutics (C-MIT), University of California-Los Angeles, Los Angeles, CA, USA
nCalifornia NanoSystems Institute (CNSI), University of California-Los Angeles, Los Angeles, CA, USA. E-mail: khademh@ucla.edu
First published on 3rd July 2018
Abstract
Nature generates densely packed micro- and nanostructures to enable key functionalities in cells, tissues, and other materials. Current fabrication techniques, due to limitations in resolution and speed, are far less effective at creating microstructures. Yet, the development of extensive amounts of surface area per unit volume will enable applications and manufacturing strategies not possible today. Here, we introduce chaotic printing—the use of chaotic flows for the rapid generation of complex, high-resolution microstructures. A simple and deterministic chaotic flow is induced in a viscous liquid, and its repeated stretching and folding action deforms an “ink” (i.e., a drop of a miscible liquid, fluorescent beads, or cells) at an exponential rate to render a densely packed lamellar microstructure that is then preserved by curing or photocrosslinking. This exponentially fast creation of fine microstructures exceeds the limits of resolution and speed of the currently available 3D printing techniques. Moreover, we show that the architecture of the microstructure to be created with chaotic printing can be predicted by mathematical modelling. We envision diverse applications for this technology, including the development of densely packed catalytic surfaces and highly complex multi-lamellar and multi-component tissue-like structures for biomedical and electronics applications.
Conceptual insightsThis communication presents a simple, effective, and novel printing technique—one that is rooted in chaos theory and, more precisely, in the physics of chaotic mixing in a laminar regime. The main strength and differential attribute of this novel microfabrication strategy is its ability to create a densely packed microstructure at high resolution and speed in a predictable manner. Moreover, chaotic flows are deterministic, therefore, they are amenable to rigorous modeling and the microstructure resulting from them can be predicted using computational fluid dynamics platforms. In chaotic printing, a drop of “ink” (i.e., a drop of a miscible liquid, nanoparticles, or cells) is injected into a viscous and Newtonian soldifiable liquid. A chaotic flow is then applied to generate a very complex microstructure at an exponential rate, which is then preserved by a crosslinking or curing step. This exponentially fast creation of a linear structure (meters), and the accompanying rapid decrease in the length scales of the micro- and even nano-structure, is not currently achievable by any other 3D printing technique. We envision the use of this platform for many relevant applications such as the fabrication of complex tissues, catalytic surfaces, supercapacitors, and highly reinforced materials, among others. |
Introduction
Complex microstructures are one of the signatures of nature.1,2 In natural phenomena and in many relevant applications, the microstructure of a material defines its macroscale functionality.3–6 The local rates of reaction,7,8 heat and mass transfer,1 ion and electron fluxes,9,10 material strength,2,5,11 and other important properties, depend on the extent of the interface between materials. Therefore, controlling the amount of surface area between materials is a key design criterion for the development of artificial tissues,12 biomimetic structures,13,14 reinforced constructs,11 energy harvesting systems,15–17 permeable membranes,18 sensors and supercapacitors,10,19,20 micro- or nano-sheets21,22 and super-catalytic surfaces.7,8,23 State-of-the-art three-dimensional (3D) printing (and bioprinting) technologies have shown their potential to create complex architectures for a wide range of applications, including electronics, microfluidics, biomedicine, and art,24–27 and their resolution has reached the order of tens of microns.28,29 However, these technologies fail to fabricate high resolution multi-layered microstructures efficiently. Most 3D printing platforms rely on the use of printing heads (mini- or micro extruders of polymers) that move in the X, Y, and Z space to deposit streams of a material at a constant rate in a layer-by-layer fashion.26–29 Therefore, they are only capable of creating fine microstructures at a linear rate. Bioprinting technologies are even more limited in their resolution (hundreds to tens of microns).26,29,30 Moreover, the precise control of the position of each printed particle is another limitation of the current bioprinting technologies.25,30Here, we introduce chaotic printing: the use of simple chaotic flows to fabricate complex, aligned, and high-resolution 3D microstructures in a controllable, predictable, and reproducible manner in solidifiable materials. We exploit the inherent and well-studied property of chaotic processes of producing the structure at an exponentially fast rate,31–33 and use it, for the first time, for micro-fabrication purposes.
Using chaos to fabricate fine microstructures
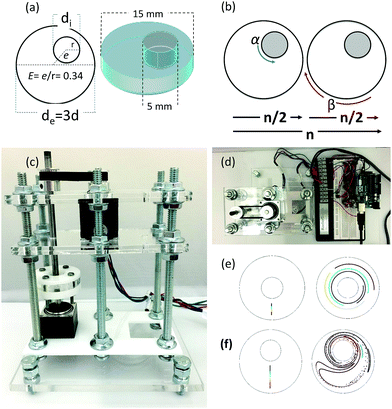
Chaotic printing adheres to the general definition of printing; namely, a process to reproduce a pattern based on a predetermined template. However, it challenges the paradigms of additive manufacturing. Instead of using moving printing heads and/or a layer-by-layer deposition strategy, chaotic printing relies on the flow itself to do the drawing, much as flow creates a highly convoluted structure when we add cream to our coffee. The choice of materials with high viscosities coupled with low speed mixing enables laminar flow conditions. The selection of specific iterative operational protocols (mixing protocols) originates chaotic flows (Fig. S1 and S2, ESI†) and develops high resolution, predictable, and complex structures that can then be solidified.Many chaotic flows have been described in the literature; some of these are only theoretical,33 while others are physically feasible.34,35 Our demonstrative model is a finely controlled and miniaturized version of the journal bearing (miniJB) flow, modified from the one reported by Swanson and Ottino34 (Fig. 1). Our miniJB consists of a cylindrical reservoir (outer cylinder) and an eccentrically located shaft (inner cylinder) (Fig. 1a); these slowly rotate alternately (one at the time), and in opposite directions according to a given mixing protocol or recipe (Fig. 1b). A mixing protocol [α°, β°] is fully defined by the counter-clockwise angle of rotation of the external cylinder (α), a momentary stop, and the clockwise angle of rotation of the internal cylinder (β). In this system, we mix at least two components—a viscous fluid polymer and the ink(s)—to generate a simple or regular (Fig. 1e) or complex (Fig. 1f) lamellar microstructure.
A drop of ink (i.e., a pregel drop, a suspension of fluorescent particles, nanoparticles, or cells) is injected into the viscous fluid contained inside the outer cylinder, and the flow [α°, β°] is applied for a number of flow cycles (n) (Fig. 2a and b).
A chaotic flow exponentially deforms and elongates the drop, increasing the interface between the ink and the viscous fluid, and creating a microstructure at an exponential rate33,36,37 (Fig. 1f and Movies S1 and S2; ESI†). The process of creation of the microstructure is guided by an intrinsic flow template (flow manifold) that is characteristic and unique for each mixing protocol33,38,39 (Fig. S2, ESI†). The resulting microstructure can be stabilized within the polymer by curing or crosslinking after any given number of flow cycles (Fig. 2b). In our experiments, we used gelatin methacryloyl40 (GelMA) and polydimethylsiloxane (PDMS) as liquid polymers.‡
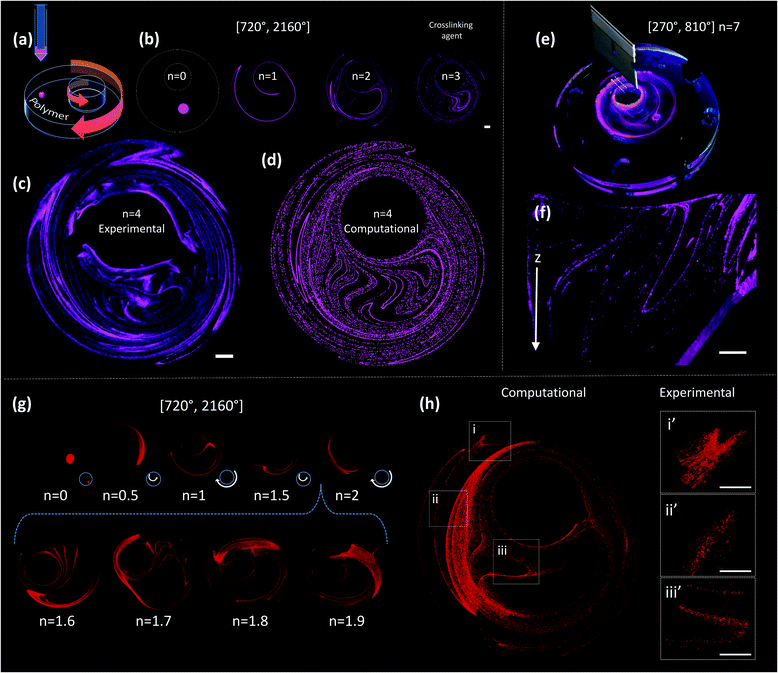
Fig. 2c shows a construct fabricated by injecting fluorescent microparticles into a liquid GelMA pre-polymer and allowing the flow to operate for 4 complete flow cycles (n = 4). A chaotic flow was induced by a clockwise rotation of 720° of the outer cylinder, followed by a counter-clockwise rotation of 2160° of the inner cylinder [720°, 2160°]. For the specific miniJB geometry that we used, this protocol induces a globally chaotic flow (Fig. S2, ESI†) that creates a structure by the repeated reorientation and deformation of the fluid that promotes stretching and folding.33,41 Such a simple iterative process drives the development of complex structures, and enables the creation of progressively finer patterns, moving from macro to micro and even nano-scales. The final structure was then solidified by simply exposing the GelMA pre-polymer to UV light for 30 seconds.
Since the chaotic flows that we used to print are deterministic (i.e., they are governed by the Navier–Stokes equations of motion), the process of particle convection and the generation of structures can be modelled (Fig. 2). Our simulations closely reproduce the behaviour of the actual experimental systems; therefore, they enable the prediction of microstructures with specific desired characteristics. For instance, the simple 2D simulations presented in Fig. 2b and d allow an accurate prediction, at a low computing investment, of the structure observed at the top layer of the experimentally obtained construct (Fig. 2c).
The sole observation of this top layer of the microstructure may convey the idea of the existence of a surface 2D flow. However, our miniJB flow is capable, by design, of producing highly complex 3D flows (and therefore 3D microstructures). The asymmetry in the boundary conditions at the top and bottom fluid layers—the top layer is a free surface while the bottom one is solid and rotates—creates a fully 3D flow.
Fig. 2e and f show a cross-sectional image of a PDMS-based construct fabricated through chaotic 3D printing (protocol [270°, 810°], n = 7)‡; the structure is evidently 3D, and a membrane-like structure is clearly depicted in the Z plane. Each layer of material, from top to bottom, is topologically different and the geometric features of the entire construct are continuous. The 3D nature of the microstructure generated by our miniJB flow system is described by the computational solution of the equations of motion in 3D (Fig. 2g and h). Fig. 2g shows the evolution of the shape of a drop of ink (a cylindrical array of 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 massless particles) into a highly convoluted 3D continuous micro-sheet that rapidly invades the flow domain. Our simulations are capable of reproducing, with high accuracy, the characteristic features observed in the experimentally obtained constructs (Fig. 2h).
000 massless particles) into a highly convoluted 3D continuous micro-sheet that rapidly invades the flow domain. Our simulations are capable of reproducing, with high accuracy, the characteristic features observed in the experimentally obtained constructs (Fig. 2h).
Printing at high resolution and speed
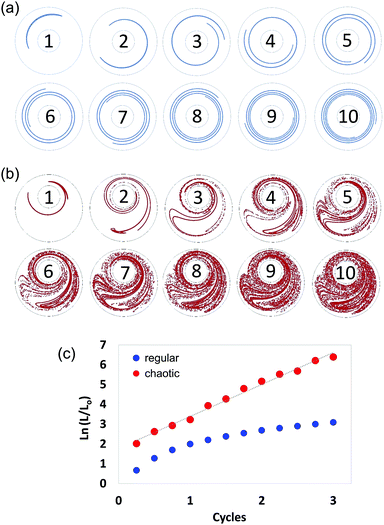
In chaotic flows, stretching proceeds at an exponential rate. Consequently, whereas regular flows produce interfaces that grow linearly (Fig. 3a), chaotic flows develop the structure at an exponential rate (Fig. 3b); in a chaotic flow, any material filament grows exponentially in time, closely following the following model:| (L/Lo) = exp (Λn), | (1) |
The Λ value36,37,42 is a quantity that can be used to estimate the speed of advance of the chaotic process. Therefore, Λ conveys a profound physical meaning for a chaotic flow: it describes, within a single value, the overall potential for the flow to stretch the material, cause elongation, and generate the structure. Fig. 3 describes the determination of Λ, based on 2D numerical simulations.
We calculated and recorded, every quarter-a-cycle, the evolution of the length of a filament initially located at the centre line between the two cylinders as they rotated at 5 rpm—this was done both for a globally chaotic miniJB case [270°, 810°] and for a regular flow case [270°, 810°] (centred JB configuration). A Lyapunov exponent value of 1.61 cycle−1 was determined from the slope of the linear version of eqn (1) (Fig. 3c).
Once the Λ is known,§ some simple additional calculations can be done. For example, Fig. 4a shows an estimation of the length of a progressively deformed filament that was produced by the repeated stretching and folding of a fluid segment of 1000 μm in a 2D model chaotic flow characterized for Λ = 1.61 cycle−1. This segment could be elongated into a fibre of 3.13 m length after only 5 flow cycles (equivalent to 3 min at our operational speed of 5 rpm). By comparison, an extrusion-3D professional printer prints at a maximum speed of 1.2 cm s−1 for resolutions of 200 μm.43 The currently available nozzle-based bioprinting techniques exhibit a speed limit between 10 and 50 μm s−1 for resolutions between 50 and 200 μm.29 At maximum speed, an average professional 3D printer, and a nozzle-based 3D bioprinter, will print the same segment (3.13 m long) in 43.47 min and 17.38 h, respectively (Tables S1 and S2, ESI†).
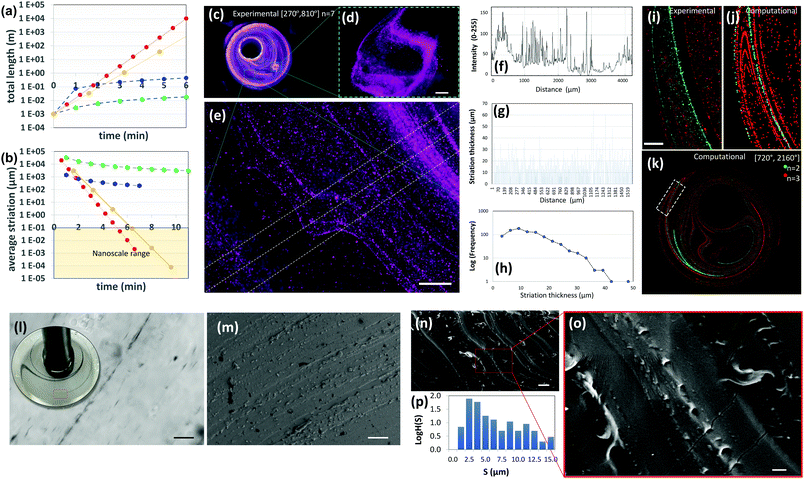 | ||
| Fig. 4 Highly aligned micro and nano structures produced by chaotic printing. (a) The growth of surface area and, (b) the reduction in striation thickness achievable by a chaotic printing process characterized by Λ = 1.61 cycle−1 = 2.68 min−1 at 5 rpm (red symbols); by chaotic printing characterized by Λ = 3.50 cycle−1 = 2.18 min−1 at 5 rpm (yellow symbols); by a state-of-the-art extrusion 3D printer43 (blue symbols), and by a state-of-the-art extrusion bioprinter29 (green symbols). (c) Fluorescent microparticles (2–15 μm in diameter), chaotically printed in PDMS using the protocol [270°, 810°] n = 7, are aligned to the chaotic flow manifold to reveal a complex 3D microstructure; (d and e) close-ups of two regions within the construct. After seven flow iterations, repeated folding and stretching yields alignment at the micro scale, and (e and f) develop a densely packed microstructure composed of parallel lamella; (g) in some regions of the flow, after three flow iterations, this separation is on the order of tens of microns. (h) The striation thickness distribution (STD) can be calculated from the estimation of the space between neighbour striations using image analysis techniques. (i) The microstructure resulting from the injection of two different types of microparticles at two different time points (n = 2, green; n = 3, red) and locations; both particle sets are aligned to the flow manifold to produce a highly aligned microstructure, as revealed by experiments and (j and k) CFD simulations. Scale bars: 500 μm. (l) The injection of a drop of a silver nanowire suspension into GelMA under a chaotic miniJB flow [270°, 810°] n = 4. The chaotic flow rapidly stretches the pointwise injection into strings of nanowires aligned on the micro-scale. A close-up of a particular region of the construct reveals a high level of alignment and resolution. Individual nanowires rotate and align to the flow manifold. (m) Parallel strains of carbon nanoparticles in a PDMS construct [720°, 2160°] n = 4. Similarly, (n and o) gold nanoparticles chaotically printed in PDMS align to the flow manifold [720°, 2160°] n = 4. (p) STD (logH(S)) of the microstructure as determined by image analysis techniques. Scale bars: (l) 50 μm; (m) 20 μm; (n) 10 μm; (o) 2 μm. | ||
Our calculations also suggest that chaotic printing can generate finer features faster than conventional linear printers. In our chaotic printing system, any growing segment of interface has to be accommodated within the finite volume between cylinders, which results in a densely packed microstructure.
Therefore, this exponential growth rate implies the creation of a great expanse of interface33,37 in a small area and in a few flow cycles (Fig. 2c and Fig. S3, ESI†).¶
In Fig. 4b, we have calculated the evolution in time of the average striation thickness resulting from the repeated operation of an ideal 2D chaotic printer characterized by Λ§ = 2.68 min−1, an average speed professional 3D printer printing at 1.2 mm s−1,43 and a nozzle-based state of the art 3D bioprinter printing at 50 μm s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 on a square section of 1 cm2. Remarkably, our simple chaotic printer will produce an average striation thickness of 10 nm after 10 flow cycles (6 minutes) (Fig. 4b; Fig. S3 and Table S1, ESI†).
29 on a square section of 1 cm2. Remarkably, our simple chaotic printer will produce an average striation thickness of 10 nm after 10 flow cycles (6 minutes) (Fig. 4b; Fig. S3 and Table S1, ESI†).
Fig. 4c–e show a PDMS construct obtained by 3D chaotic printing using an ink composed of fluorescent microparticles suspended in PDMS. The multiple sheets of particles were observed in remarkable alignment and packed in a nearly parallel fashion (Fig. 4e).
Based on a simple image analysis conducted by measuring the sum of the length of particle lines per unit of surface area in that particular plane, ∼7.10 m per cm2 of interface was developed in a few flow periods (n = 7). The resolution of this microstructure is exceptionally fine. In agreement with our theoretical estimates, in some regions of the flow, the distance between adjacent lamellae (striation thickness) is less than 10 μm (Fig. 4e–h), a value that equals or exceeds the resolution of any 3D printer currently available today. The best resolution achievable with a state of the art commercial 3D printer (i.e., Raise 3D N2) and bioprinter (i.e., Inkredible+ from Cellink) is still on the order of 10 and 50 μm, respectively.
We calculated the distribution of distances between neighbouring lines (striation thickness distribution or STD) using image analysis techniques (Fig. 4f–h). Most striation thicknesses reside in the range of 5–20 μm, with a mode peak at 10 μm, following the application of the mixing protocol [270°, 810°] n = 7. The shape of the STD, which deviates from that of a normal distribution and is significantly skewed towards low striation values, is a signature feature in chaotic flows.33,37
The STD is not homogeneous throughout the entire chaotic flow domain, with some regions of the flow showing more densely packed structures and the distance between striations much lower or higher than the expected average (Fig. 4e, g and h).
The process of creation of the microstructure in a chaotic flow is governed by a property called asymptotic directionality (AD),38,44 which induces a rapid alignment of all the flow vectors in a chaotic flow to the invariant manifold template of the flow.39,42,45
This natural, strong, and flow-induced alignment results in the creation of very complex and fine (micro) structures, replicated in time and space, with robust and reproducible statistical properties.33,37 The added length of the filament aligns to the previously developed structure, thereby creating, at each flow period, a more complicated microstructure composed of a nested family of parallel curves (Fig. 4i–k). Fig. 4i shows the microstructure generated by the injection of green and red particles at two different times and locations using the miniJB system. Since all injections align to the same flow manifold, we obtained a set of intimately nested curves of different colours. Importantly, our simulations closely predicted this complex microstructure (Fig. 4j and k) resulting from the injection of more than one ink, confirming the predictability of the architecture of these highly convoluted nested surfaces.
Chaotic printing could be a versatile nanofabrication platform as well. Our results of simple calculations in 2D systems suggest that the use of chaotic flows will allow us to fabricate at the nanoscale (Fig. S3, ESI†). We investigated this hypothesis further by injecting inks, composed of silver nanowires (200 nm in diameter and 25 μm in length), and carbon and gold nanoparticles (50 nm in diameter), into PDMS in a chaotic miniJB flow, and then curing the resulting structure. The distances between the strings of nanoparticles (striation thicknesses) approached values in the nanoscale neighbourhood in a vast portion of the flow domain after n = 4. Inspection by optical imaging and/or scanning electron microscopy (SEM) revealed a fine alignment of the sets of nanoparticles under chaotic flows (Fig. 4l–o). For example, individual nanowires rotate, similar to fluid vectors, orient and align themselves to the flow template after 4 cycles (Fig. 4l). We also observed alignment of gold nanoparticles to the flow manifold in chaotically printed PDMS constructs (Fig. 4m–o), and we measured the STD of the microstructure generated within these constructs. To do this, we cut the PDMS constructs to expose and observe a 2D plane using SEM. We used image analysis techniques to measure the distances between parallel strings of nanoparticles within that plane (Fig. 4p). The main population of striation distances resides in the order of microns (with a peak at ∼2.5 μm) in constructs produced by 4 flow cycles.
Taken together, our experimental results and simple calculations demonstrate that the use of chaotic flows will allow us to “draw” parallel convoluted nanoparticle lines (or surfaces) at the micro- and nanoscale (Fig. S3, ESI†). We envision one application of chaotic printing to be the fabrication of highly packed arrays of nanoparticles. Conceptually, the sheets of conductive nanoparticles can be packed at high density within a dielectric or non-conductive material (i.e. PDMS) to enable the fabrication of supercapacitors or simply constructs with tuneable or localized conductivity. In addition, the use of high nanowire concentrations can yield long cables (or conductive sheets) fully embedded within polymer constructs.46
Chaotic bioprinting
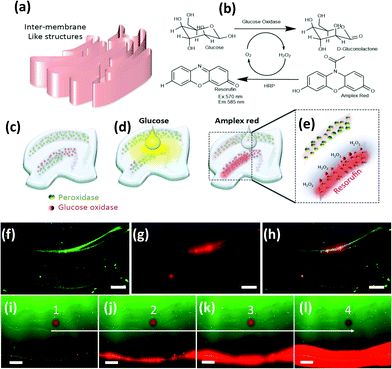
Next, we briefly explore chaotic bioprinting applications. Nature presents us with many examples of highly efficient catalytic surfaces where multiple enzymes are arranged in high density and proximity. This is one of the strategies that cells use to conduct high efficiency conversion processes, such as photosynthesis in thylakoids, energy production in mitochondria, or glycosylation in the endoplasmic reticulum.47–49 We used 3D chaotic printing for the fabrication of convoluted bioinspired bio-catalytic surfaces (Fig. 5a), similar to those presented in Fig. 2f. A system of two sequential reactions, glucose oxidation and hydrogen peroxide conversion, was taken as our model (Fig. 5b–e).We independently immobilized biotinylated horseradish peroxidase and glucose oxidase on polymer nanoparticles, and co-imprinted them in a GelMA40 pregel construct in order to fabricate a convoluted multi-lamellar structure containing both enzymes immobilized in close proximity (Fig. 5c–h).
The addition of glucose to the construct then triggers an oxidation reaction mediated by the glucose oxidase to produce hydrogen peroxide. This is then used as a substrate by the peroxidase. The reaction is indicated by the development of red fluorescence due to the oxidation of Amplex™ red (Fig. 5e). The reaction front is localized in the regions where the second enzyme, the peroxidase, was immobilized (Fig. 5f–h). The extent of the reaction, as revealed by the intensity of red fluorescence, is proportional to the density of the nanoparticles functionalized with peroxidase (Fig. 5b). The progression of the reaction in time can be followed by taking successive snapshots (Fig. 5i–l).
The facile creation of convoluted and fine tissue-like structures is an on-going challenge in tissue engineering.50 Current bioprinting techniques enable the printing of simple cell-laden constructs, where one cell type at a time is printed in one matrix.
A one-step fabrication of fine cell (or tissue) multilayers with an accurate control of alignment and position is not achievable with the currently available bioprinting techniques, but this level of precise control is an indispensable requirement for the creation of multilayered tissue-like constructs. Our miniJB flow allows the printing of multi-layers of one or more particle type (single or multiple bio-inks), within the same matrix and in a single operation (Fig. 6a–c and Fig. S4, ESI†). Each injection rapidly aligns to the manifold of the flow, due to the property of AD. We used inks composed of HUVEC suspensions and GelMA-VEGF (GelMA covalently functionalized with vascular endothelial growth factor or VEGF51) to print layers of cells in GelMA matrices. This alignment yields a highly ordered structure that closely resembles the multi-layered tissue structures of complex mammalian tissues (e.g., skin, cancerous tissue encapsulated in healthy organs, pancreatic tissue, and brain pathways).52 Chaotic bioprinting is cell friendly. The cells are minimally exposed to shear forces during injection with conventional pipettes and later during exposure to laminar flows. We observed mammalian cell viability in the range of 90 to 97% after printing. Cells preserved their original seeding position during the first 96 hours of culture (Fig. 6a and b), spread at later times, using the flow structural template, and reached across lines to establish connections between neighbouring lamellae to develop complex tissue-like structures (Fig. 6d, e and Fig. S4, S5, ESI†). As shown earlier, the resulting structure can be accurately predicted by CFD simulations (Fig. 6c).
The microstructure fabrication strategy proposed here can be applied to many relevant biological and biomedical engineering scenarios, ranging from the study of fundamental questions related to cell–cell interactions at microbial communities or tissue interfaces to the development of organ-on-a-chip platforms.
Fig. 6f shows a 3D printed construct containing both MCF7 (breast cancer cells, red stained) and MCF10A (noncancerous breast tissue fibroblasts, green stained). A significant amount of interface between the cancerous and normal cells develops after 3 flow cycles. At low cycles, the different degrees of intimacy between cancerous and normal tissue can be observed at different locations within the same construct (Fig. 6f–h). This enables the study of the effect of a variety of degrees of spatial interaction between cancerous and healthy tissue under the same experimental conditions. Greater intimacy between different types of cells can also be achieved simply by increasing the number of flow applications. For example, we printed bacterial communities of red (the producers of red fluorescent proteins [RFP]) and green (the producers of green fluorescent proteins [GFP]) Escherichia coli with different degrees of proximity by varying the number of printing cycles. At n = 3, E. coli-GFP and E. coli-RFP are planted along different branches of the flow manifold. At n = 4, sections populated by the lines of GFP-bacteria are flanked by RFP-bacterial lamella. At higher cycles, a great amount of interface is shared between both cell types (Fig. 6k). Also, the STD (and the degree of intimacy between cell types) can be tuned by selecting different mixing protocols; protocols with higher Λ generate greater intimacy in fewer cycles (Fig. 6l). The results can be anticipated through simulations or experiments using simpler model systems, such as particles and PDMS. The use of two or more polymers to fabricate composites with long embedded sheets (and therefore high interfacial surfaces) might also have diverse and relevant applications. We conducted chaotic printing experiments in which a drop of gelatin was dispensed in the GelMA pregel in our miniJB flow. In these constructs, only the GelMA fluid pregel is crosslinked after exposure to UV light; the gelatin sheet, rhodamine stained, remains as a soft gel and serves as a sacrificial component that melts rapidly at 37 °C, leaving a convoluted empty space in the form of an embedded continuous microstructure (Fig. S4, ESI†). We envision the use of this simple technique for the fabrication of convoluted sacrificial microstructures that might improve the mass transfer within thick cell-laden constructs or for the design and fabrication of micro-vasculature in tissue engineering applications.
Since the chaotic flows we used are deterministic, the dynamics of the printing processes is governed by the equations of motion that are solvable numerically for laminar regime conditions. Therefore, the outcome of the printing process, the resulting microstructure, is predictable for any given chaotic flow system.
Chaotic printing might be a powerful enabler. Remarkably complex microstructures can be fabricated, in a predictable manner, within solidifiable polymers and hydrogels, using chaotic flows generated in a simple “lab-made” printer composed of stepper motors and an Arduino-based controller (Fig. 1 and Fig. S6, ESI†). We conducted experiments and simulations using another chaotic flow. In principle, any research group would easily be able to produce a version of a chaotic printer with a minimum investment. We have mainly presented 3D printing experiments and simulations using different JB protocols. However, in principle, any realizable chaotic flow could be used as a chaotic printer.
We envision chaotic printing as a versatile micro- and nanofabrication platform that can be applied for the facile creation of constructs with unique properties: composites containing hundreds of meters of interface per area unit between materials, long filaments or sheets with a highly defined geometry embedded within hydrogels, thin and conductive sheets within insulating polymeric matrices, catalytic surfaces bioinspired in the architecture of internal cellular membranes, and tissue-like living structures.
Conclusions
Chaotic printing is a technological platform rooted in strong fundamental concepts. Chaotic flows exhibit an ability to create a self-similar microstructure at an exponential rate33,36 due to their inherent properties, which include the existence of a unique flow intrinsic template and AD. The iterative character of a chaotic flow enables the creation of progressively finer patterns, moving from macro to micro and nano-scales. Ink drops will rapidly elongate by the action of the chaotic flow to produce 3D sheets with a total length that will grow exponentially and rapidly to reach hundreds of centimetres after a few flow cycles. In volume preserving systems, this exponential increase in length aligned to the flow manifold will necessarily imply a contraction in other dimensions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
GTdS acknowledges the funding received from CONACyT (scholarship 234713) and Fundación México en Harvard in the form of postdoctoral scholarships. MMA acknowledges the institutional funding received from Tecnológico de Monterrey (GEE-002EICIN01), and funding provided by CONACyT (Consejo Nacional de Ciencia y Tecnología, México) in the form of a sabbatical scholarship (262130, SNI-26048). AK acknowledges funding from the National Science Foundation (EFRI-1240443), IMMODGEL (602694), and the National Institutes of Health (EB012597, AR057837, DE021468, HL099073, AI105024 and AR063745). NA acknowledges the support from the American Heart Association (AHA, 16SDG31280010), FY17 TIER 1 Interdisciplinary Research Seed Grants, the Northeastern University, and the startup fund provided by the Department of Chemical Engineering, College of Engineering at Northeastern University. YSZ acknowledges funding from the National Cancer Institute of the National Institutes of Health (K99CA201603). This research has been partially funded by the Tecnológico de Monterrey and the Massachusetts Institute of Technology (MIT) Nanotechnology Program, and the MIT International Science and Technology Initiatives (MISTI). We gratefully acknowledge the experimental contribution of Patrick Boisvert, Research Specialist in the Electron Microscopy Facilities at the Centre for Material Sciences and Engineering (CMSE) at MIT, and Sara Cristina Pedroza-González, Everardo González-González, Alan Roberto Márquez-Ipiña, Brenda Giselle Flores-Garza, David Choy-Buentello, Felipe López-Pacheco, and Ricardo García-Ramírez at Tecnológico de Monterrey. We sincerely thank Professor Troy Shinbrot, at Rutgers University, for repeatedly reading and extensively commenting on this work.Notes and references
- X. Zheng, G. Shen, C. Wang, Y. Li, D. Dunphy, T. Hasan, C. J. Brinker and B.-L. Su, Nat. Commun., 2017, 8, 14921 CrossRef PubMed.
- Y. Zhang and X. Li, Nano Lett., 2017, 17, 6907–6915 CrossRef PubMed.
- K.-I. Jang, H. U. Chung, S. Xu, C. H. Lee, H. Luan, J. Jeong, H. Cheng, G.-T. Kim, S. Y. Han, J. W. Lee, J. Kim, M. Cho, F. Miao, Y. Yang, H. N. Jung, M. Flavin, H. Liu, G. W. Kong, K. J. Yu, S. Il Rhee, J. Chung, B. Kim, J. W. Kwak, M. H. Yun, J. Y. Kim, Y. M. Song, U. Paik, Y. Zhang, Y. Huang and J. A. Rogers, Nat. Commun., 2015, 6, 6566 CrossRef PubMed.
- T. Lingham-Soliar, Sci. Rep., 2017, 7, 45162 CrossRef PubMed.
- H.-L. Gao, Y.-B. Zhu, L.-B. Mao, F.-C. Wang, X.-S. Luo, Y.-Y. Liu, Y. Lu, Z. Pan, J. Ge, W. Shen, Y.-R. Zheng, L. Xu, L.-J. Wang, W.-H. Xu, H.-A. Wu and S.-H. Yu, Nat. Commun., 2016, 7, 12920 CrossRef PubMed.
- B. Zhang, X. Li, T. Wang and Z. Liu, Mater. Sci. Eng., A, 2016, 674, 242–249 CrossRef.
- C. M. A. Parlett, M. A. Isaacs, S. K. Beaumont, L. M. Bingham, N. S. Hondow, K. Wilson and A. F. Lee, Nat. Mater., 2015, 15, 178–182 CrossRef PubMed.
- H. J. Cui, H. M. Yu, J. F. Zheng, Z. J. Wang, Y. Y. Zhu, S. P. Jia, J. Jia and Z. P. Zhu, Nanoscale, 2016, 8, 2795–2803 RSC.
- A. Hauke, L. S. Selva Kumar, M. Y. Kim, J. Pegan, M. Khine, H. Li, K. W. Plaxco and J. Heikenfeld, Biosens. Bioelectron., 2017, 94, 438–442 CrossRef PubMed.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P.-L. Taberna, C. P. Grey, B. Dunn and P. Simon, Nat. Energy, 2016, 1, 16070 CrossRef.
- J. Visser, F. P. W. Melchels, J. E. Jeon, E. M. van Bussel, L. S. Kimpton, H. M. Byrne, W. J. A. Dhert, P. D. Dalton, D. W. Hutmacher and J. Malda, Nat. Commun., 2015, 6, 6933 CrossRef PubMed.
- K. R. Stevens, M. A. Scull, V. Ramanan, C. L. Fortin, R. R. Chaturvedi, K. A. Knouse, J. W. Xiao, C. Fung, T. Mirabella, A. X. Chen, M. G. McCue, M. T. Yang, H. E. Fleming, K. Chung, Y. P. de Jong, C. S. Chen, C. M. Rice and S. N. Bhatia, Sci. Transl. Med., 2017, 9, eaah5505 CrossRef PubMed.
- M. Gou, X. Qu, W. Zhu, M. Xiang, J. Yang, K. Zhang, Y. Wei and S. Chen, Nat. Commun., 2014, 5, 3774 CrossRef PubMed.
- M. R. Gullo, S. Takeuchi and O. Paul, Adv. Healthcare Mater., 2017, 6, 7 Search PubMed.
- C.-H. Chang, S.-H. Chung and A. Manthiram, Mater. Horiz., 2017, 4, 249–258 RSC.
- G. Zhu, Y. Su, P. Bai, J. Chen, Q. Jing, W. Yang and Z. L. Wang, ACS Nano, 2014, 8, 6031–6037 CrossRef PubMed.
- Z. Wen, M.-H. Yeh, H. Guo, J. Wang, Y. Zi, W. Xu, J. Deng, L. Zhu, X. Wang, C. Hu, L. Zhu, X. Sun and Z. L. Wang, Sci. Adv., 2016, 2, 1–8 Search PubMed.
- H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Science, 2017, 356, eaab0530 CrossRef PubMed.
- F. Han, G. Meng, F. Zhou, L. Song, X. Li, X. Hu, X. Zhu, B. Wu and B. Wei, Sci. Adv., 2015, 1, e1500605 Search PubMed.
- Q. Cheng, J. Duan, Q. Zhang and L. Jiang, ACS Nano, 2015, 9, 2231–2234 CrossRef PubMed.
- T. Fujie, Polym. J., 2016, 48, 773–780 CrossRef.
- J. N. Coleman, M. Lotya, A. O’Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H.-Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571 CrossRef PubMed.
- A. Nel, L. Mädler, D. Velegol, T. Xia and E. Hoek, Nat. Mater., 2009, 8, 543 CrossRef PubMed.
- N. Bhattacharjee, A. Urrios, S. Kang and A. Folch, Lab Chip, 2016, 16, 1720–1742 RSC.
- C. Mandrycky, Z. Wang, K. Kim and D.-H. Kim, Biotechnol. Adv., 2016, 34, 422–434 CrossRef PubMed.
- H.-W. Kang, S. Jin Lee, I. Kap Ko, C. Kengla, J. J. Yoo and A. Atala, Nat. Biotechnol., 2016, 34, 312 CrossRef PubMed.
- T. J. Hinton, Q. Jallerat, R. N. Palchesko, J. H. Park, M. S. Grodzicki, H.-J. Shue, M. H. Ramadan, A. R. Hudson and A. W. Feinberg, Sci. Adv., 2015, 1, e1500758 Search PubMed.
- W. Liu, Y. S. Zhang, M. A. Heinrich, F. De Ferrari, H. L. Jang, S. M. Bakht, M. M. Alvarez, J. Yang, Y.-C. Li, G. Trujillo-deSantiago, A. K. Miri, K. Zhu, P. Khoshakhlagh, G. Prakash, H. Cheng, X. Guan, Z. Zhong, J. Ju, G. H. Zhu, X. Jin, S. R. Shin, M. R. Dokmeci and A. Khademhosseini, Adv. Mater., 2017, 29, 3 Search PubMed.
- S. V. Murphy and A. Atala, Nat. Biotechnol., 2014, 32, 773–785 CrossRef PubMed.
- J. L. Connell, E. T. Ritschdorff, M. Whiteley, J. B. Shear and L. Harry Swinney, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18380–18385 CrossRef PubMed.
- J. P. Crutchfield, Nat. Phys., 2011, 8, 17 Search PubMed.
- S. L. Brunton, B. W. Brunton, J. L. Proctor, E. Kaiser and J. N. Kutz, Nat. Commun., 2017, 8, 19 Search PubMed.
- M. M. Alvarez, F. J. Muzzio, S. Cerbelli, A. Adrover and M. Giona, Phys. Rev. Lett., 1998, 81, 3395–3398 CrossRef.
- P. Swanson and J. Ottino, J. Fluid Mech., 1990, 213, 227–249 CrossRef.
- A. Stroock, S. Dertinger, A. Ajdari and I. Mezić, Science, 2002, 295, 647–651 CrossRef PubMed.
- A. Adrover, M. Giona, F. Muzzio, S. Cerbelli and M. Alvarez, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58(1), 447 CrossRef.
- F. Muzzio, M. Alvarez, S. Cerbelli and M. Giona, Chem. Eng. Sci., 2000, 55, 1497–1508 CrossRef.
- M. Giona, A. Adrover, F. J. Muzzio, S. Cerbelli and M. M. Alvarez, Phys. D, 1999, 132, 298–324 CrossRef.
- T. Shinbrot, M. Alvarez, J. Zalc and F. Muzzio, Phys. Rev. Lett., 2001, 86, 1207 CrossRef PubMed.
- K. Yue, G. Trujillo-De Santiago, M. M. Alvarez, A. Tamayol, N. Annabi and A. Khademhosseini, Biomaterials, 2015, 73, 254–271 CrossRef PubMed.
- T. Ma, N. Ouellette and E. Bollt, Chaos, 2016, 26(2), 23112 CrossRef PubMed.
- M. W. Beims and J. A. C. Gallas, Sci. Rep., 2016, 6, 37102 CrossRef PubMed.
- J. Go, S. N. Schiffres, A. G. Stevens and A. J. Hart, Addit. Manuf., 2017, 16, 1–11 CrossRef.
- S. Cerbelli, M. Giona, A. Adrover, M. M. Alvarez and F. J. Muzzio, Chaos, Solitons Fractals, 2000, 11, 607–630 CrossRef.
- D. Beigie, A. Leonard and S. Wiggins, Chaos, Solitons Fractals, 1994, 4, 749–868 CrossRef.
- D. J. Lipomi, M. Vosgueritchian, B. C.-K. Tee, S. L. Hellstrom, J. A. Lee, C. H. Fox and Z. Bao, Nat. Nanotechnol., 2011, 6, 788–792 CrossRef PubMed.
- S. Flori, P.-H. Jouneau, B. Bailleul, B. Gallet, L. F. Estrozi, C. Moriscot, O. Bastien, S. Eicke, A. Schober, C. R. Bártulos, E. Maréchal, P. G. Kroth, D. Petroutsos, S. Zeeman, C. Breyton, G. Schoehn, D. Falconet and G. Finazzi, Nat. Commun., 2017, 8, 15885 CrossRef PubMed.
- Y. Wu, C. Whiteus, C. Shan Xu, K. J. Hayworth, R. J. Weinberg, H. F. Hess, P. De Camilli, K. M. Harris and G. Voeltz, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E4859–E4867 CrossRef PubMed.
- Y.-F. Jiang, S.-S. Lin, J.-M. Chen, H.-Z. Tsai, T.-S. Hsieh and C.-Y. Fu, Sci. Rep., 2017, 7, 45474 CrossRef PubMed.
- T. Dvir, B. Timko, D. Kohane and R. Langer, Nat. Nanotechnol., 2011, 6, 13 CrossRef PubMed.
- B. Byambaa, N. Annabi, K. Yue, G. Trujillo-de Santiago, M. M. Alvarez, W. Jia, M. Kazemzadeh-Narbat, S. R. Shin, A. Tamayol and A. Khademhosseini, Adv. Healthcare Mater., 2017, 6, 16 Search PubMed.
- V. J. Wedeen, D. L. Rosene, R. Wang, G. Dai, F. Mortazavi, P. Hagmann, J. H. Kaas and W.-Y. I. Tseng, Science, 2012, 335, 1628–1634 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh00344k |
| ‡ Gelatine methacryloyl (GelMA) is a UV cross-linkable material that has been widely used in tissue engineering applications; it contains cell binding domains, and it is biodegradable, and amenable to microfabrication. Polydimethylsiloxane (PDMS) is arguably the most widely used silicon-based organic polymer. In our PDMS experiments, solidification was achieved by slowly curing on a vibration-free surface at room temperature overnight. |
| § The units of the Lyapunov exponent (Λ) can be converted from cycles to seconds simply by considering the speed of rotation of the cylinders [rpm] and the angle of rotation of the mixing protocol. For instance, at 5 rpm (the rotational speed used in our experiments), Λ = 1.61 cycle−1 = 2.68 s−1 for the mixing protocol [270°, 810°]. At 5 rpm, Λ = 3.50 cycles−1 = 2.18 s−1 for the mixing protocol [720°, 2160°]. |
| ¶ For example, in an ideal chaotic flow occurring on a surface, the mean distance between consecutive lamellae (striation thickness) decreases proportionally to S0.5/Ln, where S is the surface area of the system and Ln is the length of the stretched and folded filament at any given flow cycle (Fig. S3, ESI†). |
| This journal is © The Royal Society of Chemistry 2018 |