Striping modulations and strain gradients within individual particles of a cathode material upon lithiation†
Luis R.
De Jesus‡
 a,
Peter
Stein‡
b,
Justin L.
Andrews
a,
Peter
Stein‡
b,
Justin L.
Andrews
 a,
Yuting
Luo
a,
Bai-Xiang
Xu
a,
Yuting
Luo
a,
Bai-Xiang
Xu
 *b and
Sarbajit
Banerjee
*b and
Sarbajit
Banerjee
 *a
*a
aDepartment of Chemistry and Department of Materials Science and Engineering, Texas A&M University, College Station, TX 77843-3012, USA. E-mail: banerjee@chem.tamu.edu
bInsititute of Materials Science, Mechanik funktionaler Materialien, Technische Universität Darmstadt, Jovanka-Bontschits-Str. 2, 64287 Darmstadt, Germany. E-mail: xu@mfm.tu-darmstadt.de
First published on 27th February 2018
Abstract
The insertion of Li-ions within cathode materials during the discharging of a battery oftentimes brings about one or more structural transformations. The spatiodynamic propagation of phase transformations within a matrix of particles is determined by highly localized intercalation phenomena rather than the global voltage profile. Multiscale inhomogeneities resulting from variations in electrode reactions strongly influence the proportion of actively intercalating electrode materials, define local “hot-spots” wherein the current is greatly amplified during charge/discharge processes, and consequently dictate localized energy dissipation profiles. Multiphasic domains further give rise to localized stress gradients that can induce electrode degradation. However, a clear picture of chemical and stress inhomogeneities remains to be developed for most cathode materials. Here we demonstrate compositional striping modulations between Li-rich and Li-poor domains along the edges of individual nanowires of Li-ion-intercalated V2O5 based on analysis of hyperspectral X-ray microscopy data. Analysis of scanning transmission X-ray microscopy data using singular value decomposition and principal component analysis provides a means to map compositional inhomogenieties across individual nanowires and ensembles of nanowires alike. The compositional maps are further transformed to stress and strain maps, which depict the localization of tensile stress and strain within individual nanowires of LixV2O5. The core–shell and compositional striping modulations manifested here and the resulting strain gradients point to the need to design cathode materials and electrode architectures to mitigate such pronounced local inhomoegeneities in Li-ion intercalation and diffusion.
Conceptual insightsThe submitted article presents the first direct visualization of patterns of compositional inhomogeneities within cathode materials during electrochemical discharge processes based on statistical analysis of hyperspectral X-ray microscopy data. Two distinct patterns are evidenced within individual particles: (a) core–shell separation; (b) striping modulations of Li-rich and Li-poor domains within individual particles. 3D compositional maps are developed and translated to stress and strain maps, providing a hitherto unprecedented direct visualization of stress and strain inhomogenieties generated within single particles as a result of lithiation processes. In addition to single-particle inhomogeneities, we observe multiscale inhomogeneities across ensembles of particles. The consequences of compositional inhomogeneities introduced as a result of uneven lithiation are profound, ranging from localized current “hot spots” to build up of massive localized stress leading to fracture and uneven power densities. |
Introduction
The fundamental mechanism of operation of a Li-ion battery involves the reversible migration of Li ions between an anode and a cathode, typically solid-state materials that provide a large difference in the chemical potential of inserted Li-ions.1–3 Electrode materials are most often porous particulate networks bound together within a conductive matrix. Insertion of Li-ions within electrode materials can occur with continuous compositional modulation stabilizing a solid-solution across a broad range of stoichiometries,4,5 or alternatively, involve one or more discontinuous phase transformations.6–10 The insertion and extraction of Li-ions is inevitably accompanied by an alteration of lattice parameters and change of volume, which has substantial consequences for retention of the mechanical integrity of the electrodes.11–14 The progressive deterioration of the accessible capacity of electrodes upon prolonged cycling is a major impediment to the broader utilization of intercalation batteries in large-area formats. Such deterioration appears to derive in some measure from inhomogeneous strain that causes mechanical pulverization of the electrode particles and results in loss of conduction pathways across the particulate network.15,16 Delineating multiscale strain and compositional inhomogeneities in electrode materials has thus emerged as an urgent imperative but is not readily accessible given the intrinsic limitations of most local structure probes although coherent diffraction imaging, Raman microprobe analysis, neutron radiography, in situ powder X-ray diffraction, and high-resolution electron microscopy methods have each provided insight into aspects of intercalation phenomena at specific length scales.15,17–26 In this work, we demonstrate that principal component analysis of hyperspectral soft-X-ray scanning transmission X-ray microscopy (STXM) data allows for the “standard-free” delineation of local state of charge in individual V2O5 particles as well as ensembles of particles upon Li-ion intercalation. The compositional profiles are furthermore converted to strain maps, thereby providing a means of elucidating local inhomogeneities in stress and strain at phase boundaries.It is increasingly apparent that the progression of intercalation-induced structural transformations within a matrix of particles is determined by highly localized intercalation phenomena rather than the global voltage profile.27–31 The specific spatiodynamic propagation of phase transformations depends on the atomistic diffusion pathways defined by the crystal structure of the electrode material, variations in the surface state of the particle, the relative positioning of particles with respect to the current collector, desolvation reactions at the electrolyte interface, and the dynamics of lithiation of adjacent particles.17,27–29,31–34 Such inhomogeneities have profound consequences for determining the proportion of actively intercalating electrode materials, define local “hot-spots” wherein the current is greatly amplified during charge/discharge processes, and consequently dictate localized energy dissipation profiles.29,35,36 From the perspective of coupling of electrochemistry and mechanics, phase inhomogeneities give rise to substantial stress at interfaces and such local stresses can indeed be large enough to induce fracture and electrode pulverization.11,12,14,37–40 Several approaches have been developed as remedies to this problem including the synthesis and development of smart template anode materials,41–44 the synthesis of dichalcogenide/anode composites,45 and the preparation of anode/carbonaceous-nanomaterial composites,46–49 in order to mitigate of deterioration of the active anode material.
Elucidating compositional and phase inhomogeneities across electrodes is a considerable challenge since it requires examination not just of morphological variations but necessitates high-resolution mapping of chemical and structural speciation. Indeed, coherent diffraction imaging methods capture structural distortions but since they are limited to probing variations of the lattice constant do not directly map the state of charge or chemical composition. Hyperspectral X-ray imaging has emerged as a valuable tool for this purpose and allows for simultaneous examination of variances in atomistic and electronic structure.29,30,32,50,51 In scanning transmission X-ray microscopy (STXM), raster scanned transmission images are acquired across a range of soft X-ray energies, allowing for evaluation of heterogeneities based on acquisition of an element-specific X-ray absorption near-edge structure spectrum at every pixel. X-ray microscopy has contributed to evaluation of intercalation mechanisms and hysteresis in LiFePO4;29,51–53 polaron formation and phase separation in LixV2O5 particles;30,34,50,54 and spatial distribution of discharged products in Li–O batteries.55 In recent work, Weker and collaborators have visualized the formation of cracks upon lithiation of Ge particles using operando transmission X-ray microscopy.38 Statistical deconvolution of hyperspectral STXM data using methods such as principal component analysis (PCA)56–58 can provide a powerful means to map chemical speciation with high spatial resolution but have not been hitherto used for mapping electronic-structure, compositional, or phase profiles of electrode materials. PCA provides a means to orthogonalize the hyperspectral dataset to eigenspectra and allows for mapping of discrete chemical components without requiring a priori knowledge of standard spectra, which oftentimes are unavailable for intercalated phases. Herein, we demonstrate the use of PCA to evaluate electronic structure and phase inhomogeneities across nanowires of lithiated V2O5 based on STXM imaging at the V L- and O K-edges. We further demonstrate a method to develop compositional maps and to subsequently render such maps as stress and strain profiles across the nanowires. The methods demonstrated here provide a means to elucidate the spatial variances in chemical and phase speciation as well as strain generated as a result of intercalation-induced phase transformations. The multiscale evaluation of compositional and strain inhomogeneities provides mechanistic insight into the lithiation process and suggests the complex evolution of multiphasic domains within individual nanowires involving considerable differences between the core and the surface and compositional striping modulations along the surface contours of the nanowires.
Results and discussion
Intercalation-induced structural transformations upon chemical lithiation of a cluster of V2O5 wires
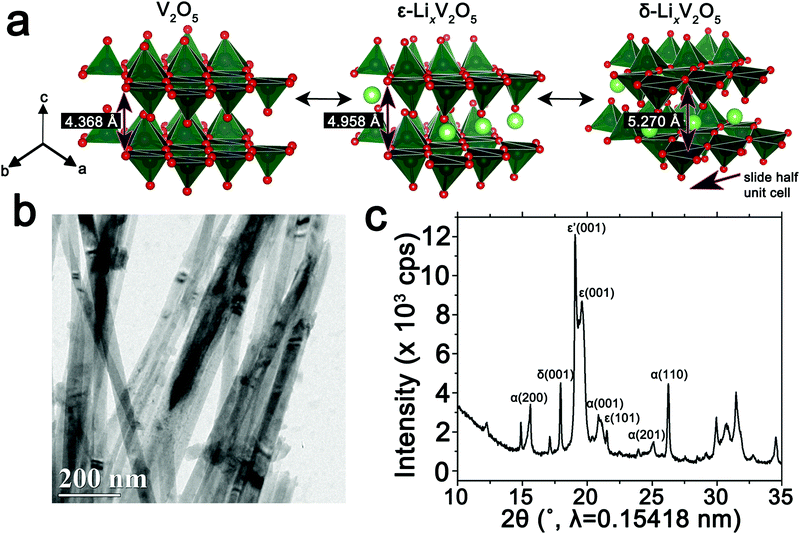
The orthorhombic phase of vanadium pentoxide (V2O5) depicted in Fig. 1a is a canonical intercalation host with an abundance of interstitial sites and a readily accessible redox couple that allows for charged ionic species to be accommodated with accompanying reduction of vanadium sites.59–61 Li-ion insertion within V2O5 initiates a series of phase transformations that bring about substantial structural distortions as depicted in Fig. 1a.60–63 Initial lithiation results in transformation to a slightly distorted α-LixV2O5 phase, which is stabilized within a concentration range of x < 0.1 in LixV2O5. Upon increasing incorporation of Li-ions, ε-LixV2O5 is stabilized in the concentration range between 0.3 < x < 0.85 (an incommensurate ε′-phase can be distinguished above x > 0.53); this structure is characterized by pronounced puckering of the apical oxygens as a result of electrostatic interactions with the inserted Li-ions as well as an expansion of the interlayer spacing in order to accommodate the increased concentrations of Li-ions. With further insertion of Li-ions, in the range 0.88 < x < 1.0, δ-LixV2O5 is stabilized with a highly puckered structure characterized by the layers sliding by half a unit cell length along the b direction. Increasing the Li-ion concentration still further, beyond x > 1, brings about two irreversible phase transformations to highly distorted γ and ω phases. Herein, we focus on the reversible regime of Li-ion incorporation where structural modifications are anisotropic but less pronounced than upon stabilization of the γ- and ω-phases.8 Previous STXM mapping results showed surprising phase segregation and intercalation gradients within individual nanowires of chemically lithiated V2O5.50 Based on spectroscopic studies of electronic structure and density functional theory modeling, phase heterogeneities in this system have been attributed to two primary origins: (i) stage-ordering phenomena, i.e., the preferential insertion of Li-ions into an already expanded layer;10,64 and (ii) the formation of small polarons, which correspond to the coupling of an electron in the V2O5 framework with a local structural distortion.50,54 Given the distinctive spectroscopic signatures of different LixV2O5 phases50 at V L- and O K-edges, arising from modifications to the electronic structure of V2O5 induced by lithiation, STXM is expected to be an effective probe not just of individual nanowires but ensembles of particles where heterogeneities are a result of multiscale intercalation gradients.34Fig. 1b depicts a transmission electron microscopy (TEM) image of a LixV2O5 nanowires prepared by chemical lithiation of hydrothermally grown V2O5 nanowires in n-butyllithium as per:6,65| V2O5 + xC4H9Li → LixV2O5 + x/2C8H18(g) | (1) |
Details of the synthesis and chemical lithiation of V2O5 nanowires are provided in the Methods section.6,50 Chemical lithiation eliminates the directionality inherent in electrochemical lithiation experiments, allows for exposure to a globally invariant Li-ion flux, and furthermore can be performed without use of a binder. As such, it is a useful model for electrode processes and allows for examination of fundamental mechanisms underpinning intercalation phenomena. The powder X-ray diffraction (XRD) pattern in Fig. 1c corresponds to V2O5 nanowires subject to chemical lithiation with a large molar excess of n-butyllithium for 15 min (an average composition of Li0.30±0.08V2O5 is deduced based on ICP-MS analysis); considerable local phase-coexistence and heterogeneity is discernible with reflections from α-, ε-, ε′-, and δ-phases, as indexed in the pattern.6,66–68 The performance of V2O5 as a cathode material is reflected in the first discharge cycle (Fig. S1, ESI†) with a capacity of 355 mA h g−1 at a constant 0.2C rate. The transformation between the lithiated phases of V2O5 can be observed as plateaus at 3.4, 3.2, and 2.3 V for α–ε, ε–δ, and δ–γ phases, respectively, reflecting the sequence of transformations shown in Fig. 1a. Transformation to the γ-phase is irreversible and further cycling retains the distorted γ′ structure.
Elucidation of compositional inhomogeneities in LixV2O5 by singular value decomposition (SVD) and PCA analysis of STXM images
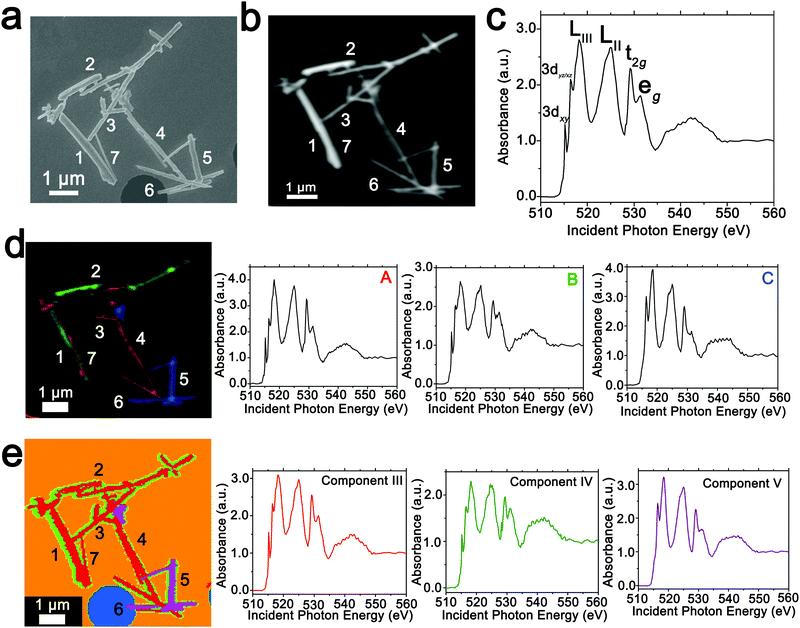
In order to spatially resolve phase inhomogeneities observed in ensemble XRD measurements, a cluster of interconnected chemically lithiated V2O5 nanowires has been examined using scanning electron and scanning transmission X-ray microscopy as shown in Fig. 2. Fig. 2a depicts a high-resolution scanning electron microscopy image, whereas Fig. 2b shows the corresponding integrated STXM image constructed by scanning across the V L- and O K-edges from 508 to 560 eV. Fig. 2c depicts the integrated X-ray absorption spectrum acquired for these nanowires. X-ray absorption spectroscopy involves the excitation of core electrons to unoccupied and partially occupied states, and thus principally maps the atom-projected unoccupied density of states of the excited solid.30,69,70 Rigorous spectral assignments are now available for V L-edge and O K-edge absorption features of V2O5 based on first-principles simulations of excited state spectra and angle-resolved X-ray absorption spectroscopy measurements.50,71–73 The V L-edge spectrum of V2O5 comprises V LIII and V LII absorption features, corresponding to transitions from V 2p3/2 → V 3d (ca. 518 eV) and V 2p1/2 → V 3d (ca. 525 eV) states, respectively;71,72 these features are separated by a spin–orbit splitting of ca. 7 eV. As a result of the operation of Coster–Kronig Auger decay processes, the V LII absorption is subject to considerable spectral broadening and is consequently less informative as a probe of local electronic structure. In contrast, the V LIII absorption has well-resolved fine structure corresponding to transitions from singlet V 2p63d0 to V 2p53d1 states split by crystal field and multiplet effects.50,72,74 The first two sharp features correspond to distinct transitions from V 2p states to states of fairly “pure” V 3dxy (ca. 515.6 eV) and V 3dxz/yz (ca. 516.8 eV) character as labelled in Fig. 2c. The O K-edge corresponds to transitions from O 1s states to states with O 2p character. As a result of the substantial hybridization between the O 2p and V 3d derived states, two distinct features can be resolved, reflecting the distorted octahedral crystal field splitting of the V 3d-derived states (denoted as t2g and eg in Fig. 2c). The features correspond to transitions of O 1s electrons to (i) O 2px and 2py states engaged in π interactions with the V 3d t2g states (529.7 eV); and (ii) O 2px and 2py states engaged in direct σ interactions with V 3dx2−y2 (at ca. 531.6 eV), and 2pz states engaged in σ-interactions with V 3dz2 states (at ca. 533.1 eV).The intercalation of Li-ions within V2O5 is coupled with redox chemistry at the vanadium sites, specifically the local reduction of V5+ sites to V4+ sites; the added electron occupies the lowest-lying states at the bottom of the conduction band, which in the case of V2O5 corresponds to a split-off conduction band that has primarily V 3dxy character.71–73,75 Li-ion insertion thus results in a significant diminution, or even disappearance, of the V LIII absorption feature at 515.6 eV as a result of Pauli blocking (owing to filling of the V 3dxy state). Furthermore, the polarization, lattice distortion, and lifting of spin degeneracy in the V 3d1 system strongly modifies the ratio of the t2g and eg* features at the O K-edge; the intensity of the t2g feature is gradually diminished as a function of increasing Li-ion concentration.50 These two spectral modifications, which are directly correlated to Li-ion content, are of particular significance for statistical deconvolution of hyperspectral stacks.
Two distinct methods have been used to map spatial inhomogeneities. In the first case, based on examining integrated spectra across different regions of the image and given prior knowledge of evolution of V LIII and O K-edge X-ray absorption spectra with increasing Li-ion content,30,34,50,54 three different components (A–C) are identified as plotted in Fig. 2d. Notably, these components are spectra integrated within discrete regions of the image. Next, the spectral data at each pixel across the entire image is deconvoluted into a combination of the three component spectra using SVD. Spatial maps are then constructed reflecting the relative weights of each of the three components at each pixel as depicted in the left panel of Fig. 2d. The components herein correspond to spectra characteristic of specific regions of the image. However, they do not represent “pure” spectra of individual phases and furthermore are based on approximations of spectral signatures of potential species used to facilitate selection.
Fig. 3 maps the intensity of each of the three components individually across the region of interest. Components A–C depict stark differences with respect to the intensity of the transition to the V 3dxy final state at the V LIII edge and the ratio between t2g and eg* components at the O K-edge, indicating a successive increase of lithiation from A–C (Fig. 2d). As a first finding, mapping of the spectral components clearly delineates that the ensemble XAS spectrum plotted in Fig. 2c does not accurately depict the remarkable spatial inhomogeneity of lithiation (state-of-charge) prevalent across this cluster of nanowires. Component A is assigned to a relatively low Li-content α-phase, Component B represents the intermediate Li-content ε-phase, whereas Component C represents a substantially higher degree of lithiation. The almost complete loss of the V 3dxy absorption feature at 515.6 eV and the appearance of a strong 3dxz/yz absorption feature at 516.8 eV are suggestive of a more substantial rearrangement of the crystal structure to accommodate a higher concentration of Li-ions; these spectral features are attributed to the substantially more distorted δ-LixV2O5 phase characterized by sliding of the layers along the b direction.
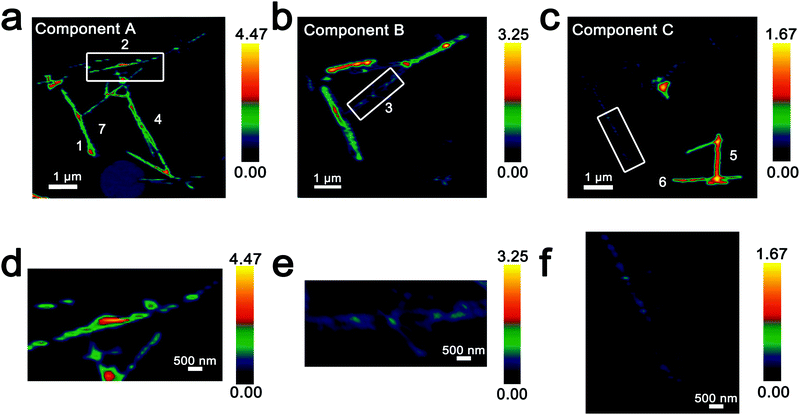 | ||
Fig. 3 Intensity maps derived from region-of-interest singular value decomposition analysis of an ensemble of V2O5 nanowires lithiated for 15 min (resulting in an average composition of Li0.30±0.08V2O5 based on ICP-MS analysis). (a–c) Intensity maps depict the localization of the spectral signatures of components A–C in Fig. 2d. Component A corresponds to the lowest extent of lithiation, whereas Component C corresponds to the highest lithiation, as determined by the relative intensity of the 3dxy resonance and the t2g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eg* ratio. (d–f) Modulations of spectral intensities within the boxed regions of the upper panels corresponding to the distribution of Li-rich and Li-poor domains within individual nanowires. eg* ratio. (d–f) Modulations of spectral intensities within the boxed regions of the upper panels corresponding to the distribution of Li-rich and Li-poor domains within individual nanowires. | ||
Seven individual nanowires have been labelled 1–7 as depicted in the images. Based on Fig. 2 and 3, the nanowires on the top and left are relatively less lithiated, whereas the nanowires on the bottom right of the image are relatively more lithiated. No clear correlation is observed between the nanowire dimensions and the extent of lithiation. For instance, the nanowire labelled 5 is much more extensively lithiated as compared to the nanowire labelled 7 even though Fig. 2a shows that it is much thicker. Considering nanowires 1–3, the SEM image suggests that these are individual faceted nanowires; Fig. 2d and 3 suggest that these nanowires show considerable compositional variations, domain formation, and the coexistence of both Components A and B within each of the nanowires. Similarly, nanowire 6 shows the coexistence of Components A and C. While component B, which represents a relatively greater extent of lithiation is generally more predominant at the edges of the nanowires and along the nanowires at the apex of the region of interest, an alternating interleaved domain structure is observed suggestive of the stabilization of a complex domain structure upon cation insertion. Fig. S2 (ESI†) depicts high-resolution SEM images of various segments of the cluster of nanowires shown in Fig. 2a. A consistent morphology is retained along the length of individual wires suggesting that the observed modulations in the intensities of spectral components observed in Fig. 2 and 3 result from compositional and not topographical variations. Fig. 3d–f depicts an alternation of intensity along the length of select nanowires for each of the three components. Fig. 3d indicates stripes of Li-poor Component A in nanowire 2, whereas Fig. 3f depicts stripes of the Li-rich Component C along nanowire 1. Such stripe formation observed here is likely a result of the spinodal decomposition to Li-rich and Li-poor domains at the particle boundaries.76,77 Intercalation of Li-ions within thin wires occurs faster laterally (along the edges) rather than transversally (through the nanowire) due to sluggish diffusion of ions; this results in pronounced compositional “stripes”. Striping resulting from compositional heterogeneity has been indirectly evidenced in coherent diffraction imaging based on mapping of lattice constants and has been predicted by numerous phase field models.15,31,65 However, to the best of our knowledge the images here represent the first direct evidence of compositional modulation along the length of Li-ion intercalated nanowires. Indeed, similar behaviour with compositional heterogeneities and modulations is observed in electrochemically lithiated samples extracted from samples discharged at 2.75 V in a coin cell configuration (Fig. S3, ESI†). In the imaged ensemble of nanowires, core–shell behaviour and the formation of stripes is observed along the length of the nanowires.
Next, we examine an alternative “standard-free” treatment of the hyperspectral STXM data. PCA methods can be applied without a priori knowledge of spectral components and yield eigenspectra that maximize the variances within the spectral data integrated across the sample. Fig. 2e depicts the three components, denoted as III–V derived from such analysis. Components I and II correspond to the background. PCA analysis clearly distinguishes the background signal from a hole (depicted in blue in Fig. 2e) and the signal of the underlying silicon nitride grid (depicted in orange). Utilizing an angle distance cutoff or normalized scalar to specify a radius below which pixels are not included mitigates differences arising primarily from thickness variations.58 Fig. S4 (ESI†) depicts spatial maps of the principal components reflecting their weights at each pixel; Table S1 (ESI†) summarizes the cluster weight percentage as evaluated in each of the dimensions. Fig. S5 (ESI†) depicts the separation of the pixels along three distinct pairs of component axes. Each pixel is classified (and thus colored) according to its position in the scatter plot, which shows effective separation along the component axes. In contrast to the overlapping coloration of different components in Fig. 2d, in the PCA map of Fig. 2e, each pixel is colored to reflect just the majority component. Even though eigenspectra are principally representative of the total spectral variances and do not directly correspond to experimental spectra, their lineshapes embed chemical information. While the single coloration at each pixel does not provide as granular of a compositional map as in Fig. 2d (and thus modulations are not as clearly observed), they nevertheless delineate distinct compositional (and thus phase) gradients. Based on the intensity of the feature at 515.6 eV corresponding to the transition to the V 3dxy state and the relative intensities of the t2g and eg absorptions at the O K-edge, Component III is a spectrum representative of V2O5 with a relatively low degree of lithiation; the higher weighting of this component at the nanowire cores is consistent with the slower lithiation of the core6 albeit it is clear that as also observed in Fig. 2d a clear core–shell structure is not established. Similarly, component IV reflects a higher degree of lithiation based on the relatively lower intensity of the V 3dxy absorption at the V L-edge and the lower ratio of t2g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eg* intensities at the O K-edge; this component is weighted substantially at the edges of the nanowires. This component thus is analogous to component B in Fig. 2d. The distribution of this component is discontinuous along the nanowire surfaces consistent with the compositional modulation noted in Fig. 3. Remarkably, component V accurately captures the relatively highly lithiated δ-LixV2O5 spectral signature and such nanowires are clearly distinguishable from the rest of the cluster in the PCA analysis. PCA analysis thus provides a standard-free means of orthogonalizing the STXM dataset and can delineate lithiation gradients and phase segregation in a chemically meaningful manner.
eg* intensities at the O K-edge; this component is weighted substantially at the edges of the nanowires. This component thus is analogous to component B in Fig. 2d. The distribution of this component is discontinuous along the nanowire surfaces consistent with the compositional modulation noted in Fig. 3. Remarkably, component V accurately captures the relatively highly lithiated δ-LixV2O5 spectral signature and such nanowires are clearly distinguishable from the rest of the cluster in the PCA analysis. PCA analysis thus provides a standard-free means of orthogonalizing the STXM dataset and can delineate lithiation gradients and phase segregation in a chemically meaningful manner.
Generation of compositional, stress, and strain maps from PCA analysis of STXM data
The ability to deconvolute hyperspectral X-ray microscopy data further facilitates the mapping of compositional, stress, and strain profiles across an individual particle. Fig. 4a depicts the PCA map derived from STXM imaging of an individual particle with a diameter of ca. 3 μm upon chemical lithiation for 1 min (an average composition of Li0.28±0.07V2O5 is deduced based on ICP-MS analysis). Fig. 4b depicts the integrated V L- and O K-edge X-ray absorption spectrum and three eigenspectral components obtained from PCA analysis of the hyperspectral stack. Fig. S6a–c (ESI†) depicts the scatter plots illustrating the scores of the spectrum at each pixel with respect to the three different components (the respective component weights are summarized in Table S2, ESI†); the selected principal components are seen to allow for effective classification of each of the pixels, which are mapped in Fig. 4a. Components I–III correspond to increasing levels of lithiation based on the intensity of the V 3dxy feature at the V LIII edge and the ratio of t2g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eg* intensities at the O K-edge. Notably, the extent of lithiation is lower as compared to Fig. 2 given the reduced immersion time here. The components can be attributed to approximate values of Li-ion content based on the intensities of the V 3dxy feature and the ratio of t2g
eg* intensities at the O K-edge. Notably, the extent of lithiation is lower as compared to Fig. 2 given the reduced immersion time here. The components can be attributed to approximate values of Li-ion content based on the intensities of the V 3dxy feature and the ratio of t2g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eg* intensities. The yellow core is sparsely lithiated whereas the surface indicates modulation of Li-rich and Li-poor domains.
eg* intensities. The yellow core is sparsely lithiated whereas the surface indicates modulation of Li-rich and Li-poor domains.
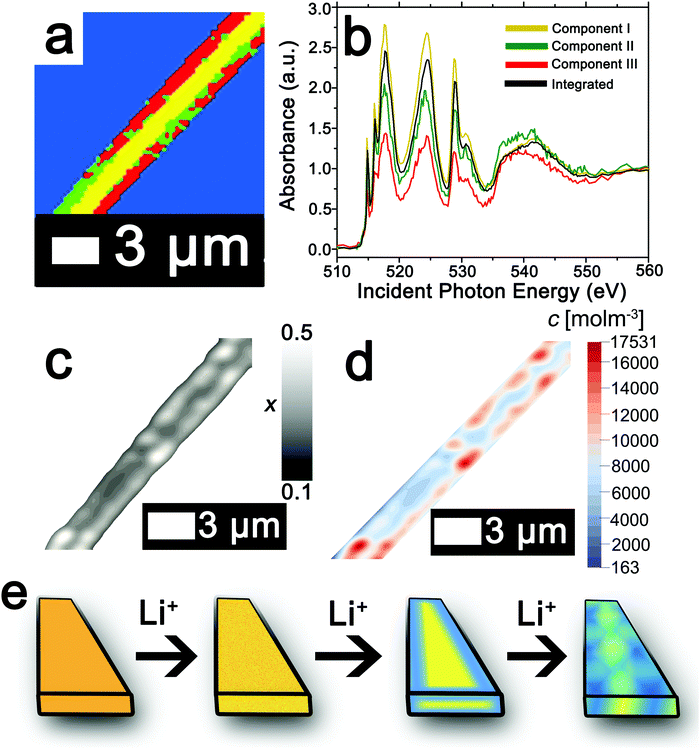 | ||
| Fig. 4 Mapping of the composition map onto a concentration distribution from PCA analysis of STXM data. (a) PCA map defining domains with varying extents of lithiation obtained from deconvolution of a STXM hyperspectral image acquired for an individual particle of V2O5 chemically lithiated for 1 min (an average composition of Li0.28±0.07V2O5 is deduced based on ICP-MS analysis). (b) Integrated V L- and O K-edge spectrum and eigenspectra obtained from PCA analysis. Component I (yellow) is the least lithiated, followed by component II corresponding to an intermediate extent of lithiation (green), and finally component III, which corresponds to the highest extent of lithiation (the corresponding pixel-weighted scatterplots are plotted in Fig. S3, ESI†). (c) Using the nanowire contours, a finite element mesh has been created onto which the composition (x) data have been mapped. (d) Linear transformation of the composition by corresponding average phase concentrations then yields the concentration distribution over the nanowire. (e) Schematic depiction of the progression of Li-intercalation within V2O5 to the formation of stripes with Li-poor (yellow) and Li-rich (blue) domains. | ||
While STXM provides detailed compositional maps of electrode materials,32,34,50,51 a major constraint is that it is a 2D imaging method whereas in order to obtain stress and strain maps, such as required to evaluate inhomogeneous coherent strain at phase boundaries, the thickness of the sample is required. Indeed, the thickness of the nanowire in Fig. 4a can be estimated based on a quantitative measurement of the absorption cross-section; Fig. S7 (ESI†) indicates that the nanowire (ca. 245 nm in diameter) has a uniform thickness of ca. 79 nm along the diameter as delineated by the consistent height at two different regions spaced ca. 400 nm apart. The concentration of Li-ions (state of charge) in each cluster is furthermore required in order to precisely develop a compositional map; these values can be approximated based on the ratio between the t2g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eg* absorbances, which serve as a direct probe for the amount of Li intercalation in α-V2O5. The weights of the individual clusters (as delineated in Table S2, ESI†) provide a means to weight the contribution of the composition-specific components at each pixel, thereby enabling the development of a detailed composition map.
eg* absorbances, which serve as a direct probe for the amount of Li intercalation in α-V2O5. The weights of the individual clusters (as delineated in Table S2, ESI†) provide a means to weight the contribution of the composition-specific components at each pixel, thereby enabling the development of a detailed composition map.
The composition map plotted in Fig. 4c has been obtained from weighted superposition of the respective pixel-wise intensity data as described in the Methods section. Li-rich and Li-poor domains are clearly evidenced at the edges denoting clear segregation. The concentration map in Fig. 4d maps the concentration of Li-ions across the particle. Domains demarcated in red denote regions of a locally enhanced ion concentration reaching 1.75 × 104 mol m−3 (x = 0.41 in LixV2O5, corresponding to the ε-phase) at the edges of the nanowires, whereas the core is substantially less lithiated with a concentration of ca. 6.00 × 103 mol m−3 (x = 0.15 in LixV2O5, corresponding to the α-phase). Since the lattice parameters of LixV2O5 vary continuously as a function of Li-ion content (in ε-V2O5, a = 11.420–11.377 Å; b = 3.558–3.570 Å),78–80 the inhomogeneous compositional profile induces localized lattice mismatch and straining of the active material. Fig. 4e depicts a schematic of the progression of Li-ion intercalation within V2O5 showing core–shell segregation followed by segregation of Li-poor and Li-rich domains as stripes as observed in Fig. 4c.
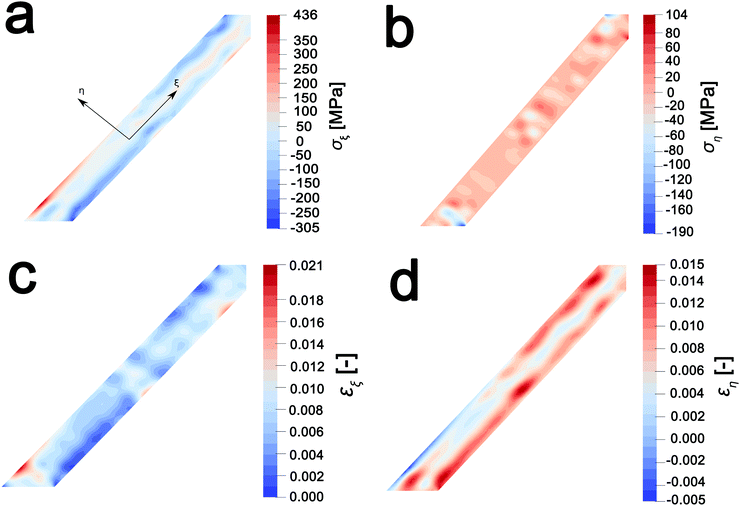
In order to map stress and strain gradients resulting from compositional inhomogeneities, the nanowire geometry has been extracted from this map by the Marching Squares algorithm, yielding the outline curves of the nanowire. These data have been used to generate a planar finite element mesh. The corresponding spatial composition data have been mapped onto its nodes. A finite element simulation of the coupled chemo-mechanical behavior81 yields stress and strain maps in the Cartesian reference frame. The stress and strain maps have been transformed onto the nanowire-aligned along the xi-eta coordinate system in order to facilitate interpretation. The incurred stress gradients have been mapped in a nanowire-aligned coordinate system, as depicted in Fig. 5a and b. These maps depict the anisotropic deformation induced by the insertion of Li ions. The stress maps suggest that it is, in particular, the regions of high heterogeneity that exhibit high levels of stress. Clusters of high local ion concentrations tend to expand isotropically but are hindered by the surrounding material. This can be observed in Fig. 5a where the bands of high compressive longitudinal stress σξ with magnitude of ca. 305 MPa are correspondent with bands of Li-rich domains (Fig. 4d). As illustrated in Fig. 5c, the material in the outer layers of the nanowire is compressively strained along the longitudinal direction. In contrast, the core of the nanowire is subjected to tensile stresses of around 100 MPa, which is brought about by the expanding Li-rich edges “pulling” at the core of the nanowire. The lateral expansion of the nanowire is comparatively unconstrained, as is demonstrated by the low lateral stresses ση depicted in Fig. 5b. The expansion of the V2O5 layers in order to accommodate Li-ions at the edges of the particles is expected to create tensile stresses that further induce significant compressive stress within the nanowire interiors as a result of the anisotropic distortion of the layered structure upon Li-ion intercalation (Fig. 1a). The inhomogeneity in direction and magnitude of stress establishes strain gradients across the particle as mapped in Fig. 5c and d. Indeed, such strain gradients considerably alter intercalation and diffusion in active material,81,82 and can underpin electromechanical degradation.39,83 Such degradation can result in fracture of the particle and loss of capacity.84,85 In contrast, recent studies suggest that tensile strain can induce modulation of electrochemical potentials by ca. 40 mV and bring about a doubling of Li-ion diffusion coefficients within V2O5.83 The ability to extract concentration, stress, and strain profiles further renders STXM a valuable probe of intercalation phenomena. The pronounced strain gradients at phase boundaries provide a direct visualization of the implications of compositional inhomogeneities.
Conclusions
In conclusion, the initiation and progression of Li-ion intercalation within electrode materials is dominated by local phenomena and results in considerable inhomogeneity both within individual particles and across ensembles of adjacent particles. STXM serves as an effective element-specific probe of electronic structure, and since electronic structure is greatly modulated by cation intercalation, provides a spatially resolved view of distinct domains stabilized upon lithiation of transition metal oxides. Upon chemical lithiation of V2O5 nanowires, longitudinal and lateral domain formation is evidenced within individual nanowires and is reflective of surface lithiation phenomena as well as compositional striping corresponding to separation of Li-rich and Li-poor domains at particle boundaries. Considerable compositional inhomogeneity is evidenced within an ensemble and appears to reflect selective deep lithiation of specific particles whereas adjacent particles are lithiated to a much lower extent. A principal component analysis treatment of STXM hyperspectral data allows for deconvolution of V L-edge and O K-edge spectra to principal components reflective of different lithiated phases and allows for reconstruction of domain maps without a priori knowledge of spectral profiles. Such an analysis allows for elucidation of intercalation gradients within individual nanowires. Mapping compositional and phase inhomogeneities is greatly consequential for determining the actively intercalating regions and localized current profiles. The compositional information gleaned from PCA analysis of STXM data in conjunction with determination of the nanowire thickness based on quantitative evaluation of the X-ray absorption cross-section as well as knowledge of lattice parameters of intercalated phases allows for mapping of stress gradients and strain across an individual particle. The significant disparity between domains subjected to compressive and tensile stress as a result of inhomogeneous lithiation is thought to underpin capacity loss. Mitigating such inhomogeneities requires the development of cathode materials that are able to accommodate Li-ions with less of a structural distortion and that can mitigate polaronic bottlenecks to Li-ion diffusion or structuring of electrodes to facilitate more homogeneous lithiation. Future work will focus on in situ and in operando STXM and ptychography studies of intercalation phenomena within cathode and anode architectures in realistic device configurations in conjunction with electron microscopy such as to combine the excellent spatial resolution accessible from the latter methods with the energy resolution and high chemical sensitivity of synchrotron-based X-ray imaging.24,25 Inhomogeneities will further be explored for “beyond Li” energy storage vectors such as multivalent cations.86Materials and methods
Chemical lithiation of V2O5 nanowires
Single-crystalline V2O5 nanowires were prepared by air oxidation of hydrothermally grown V3O7 nanowires as described in previous work.6 Chemical lithiation of the nanowires was performed within a glove box filled with argon by immersion of powders in a solution of 2.5 M n-butyllithium (Sigma-Aldrich) in hexanes diluted to 0.025 M in heptane for a specific time interval (0.025 M of n-butyllithium to 0.55 mM of V2O5, corresponding to a ca. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar excess of Li
1 molar excess of Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V2O5). The samples were then washed within the glove box with copious amounts of hexanes to remove any unreacted lithium precursor. The recovered powder was allowed to dry under argon.
V2O5). The samples were then washed within the glove box with copious amounts of hexanes to remove any unreacted lithium precursor. The recovered powder was allowed to dry under argon.
Inductively-coupled plasma mass spectrometry (ICP-MS)
The average Li-ion concentration of the solid lithiated V2O5 samples was determined by ICP-MS using a PerkinElmer NexION 300D instrument. Powder samples lithiated for a specific time were dissolved to achieve overall concentrations of 5–7 ppm in a 1 vol% aqueous solution of HNO3 solution (15 M).Powder X-ray diffraction
Powder X-ray diffraction (XRD) measurements were performed using a Bruker D8-Focus Bragg–Brentano X-ray powder diffractometer with a Cu Kα radiation source (λ = 0.15418 nm).Microscopy characterization
Transmission electron microscopy (TEM) images were obtained using a JEOL JEM-2010 instrument operated at an accelerating voltage of 200 kV. SEM images were acquired using a JEOL JSM-7500F FE-SEM operated at 2 kV.STXM data were collected at the spectromicroscopy (SM) beamline 10ID-1 of the Canadian Light Source, Saskatoon, SK. The beamline is equipped with an elliptically polarized undulator source; incident soft X-rays were focused onto the sample of interest using a Fresnel zone-plate, which includes an order-sorting aperture to eliminate undesired diffraction orders. A plane grating monochromator with 500 line mm−1 was used for hyperspectral imaging at V L- and O K-edges. A dwell time of 1 ms was used for signal acquisition at each pixel. The image stacks were analyzed using the Principal Components Analysis (PCA) suite developed by Jacobsen and co-workers and aXis2000 (http://unicorn.mcmaster.ca/aXis2000.html).87 Region of interest (ROI) maps were obtained by a SVD of the image stack and by using as a reference, spectral components identified within different regions of the stack. This procedure yields a set of composition maps where intensities represent the signal strength of each of the selected components. Thickness maps were developed by linearly scaling the V L- and O K-edge stack to a reference spectrum of LixV2O5 (spectrum scaled to a calculated elemental X-ray absorption spectrum of a 1 nm thick material). Principal component analysis was performed to orthogonalize the data and reduce the noise of the spectral features. The hyperspectral stack was deconvoluted into components representing a linear combination of spectral signatures. The graded contributions of the orthogonalized spectral components at each pixel were subsequently determined, allowing for the construction of maps indicating the relative abundance of each of the orthogonalized components at each pixel within the area of interest.57,58 Application of this analysis method allows for reconstruction of spatially resolved images from eigenspectra of complex samples without requiring a priori knowledge of reference spectra. The angle dependence cutoff was set to the point just before the highest pixel contribution; this substantially mitigates the effects of thickness variations and allows for mapping of variations in chemical signatures.
Electrochemical cycling
Galvanostatic cycling of V2O5 was carried out in a coin cell configuration against a Li metal anode using a Landt battery testing system (CT2001A) at a 0.2C rate. The cathode was prepared by casting a mixture of active material (V2O5 nanowires), conductive carbon material (C45), and binder (polyvinylidene fluoride) in a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, respectively, on the Al foil current collector. The electrolyte used was a 1.0 M solution of LiPF6 in a (1
1 ratio, respectively, on the Al foil current collector. The electrolyte used was a 1.0 M solution of LiPF6 in a (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v)) mixture of diethyl carbonate and ethylene carbonate (Sigma Aldrich).
1 (v/v)) mixture of diethyl carbonate and ethylene carbonate (Sigma Aldrich).
Compositional & strain maps
Compositional and strain maps were generated by defining meshes using the PCA separated component maps. The starting points for the mesh generation procedure are the maps shown in Fig. S8 (ESI†). These normalized intensities in images space represent intensities xi; x = 0.2 (a and d); x = 0.4 (b and e); and x = 0.5 (c and f) corresponding to various phases of LixV2O5. First, these images were subjected to a Gaussian filter to remove noise; subsequently, superposition of the pixel intensities, as weighted by the corresponding stoichiometric fraction xi, yields a composition map in image space as shown in Fig. S9a (ESI†). This image exhibits a relatively low resolution of 75 × 65 pixels. A continuous representation can be achieved by bilinear interpolation of the pixel data, resulting in the smooth composition map shown in Fig. S9b (ESI†). In order to extract the nanowire geometry from image space, the Marching Square algorithm was applied with a user-defined threshold for the stoichiometric fraction x. The resulting nanowire outline curves, shown in Fig. S9b (ESI†), were then used as input for the Finite Element mesh generator GMSH. The local stoichiometric fraction was mapped onto the nodes of the planar triangle mesh, was and scaled by the ion concentration (state-of-charge). The resulting finite element model was used to solve for the distribution of stresses and strains using the software package FEAP. To that end, linear isotropic material behavior was assumed together with a chemical eigenstrain model: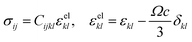 | (2) |
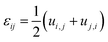 | (3) |
Author contributions
LDJ prepared the materials. LDJ and JLA performed STXM experiments and LDJ carried out the analysis. LDJ and JLA performed SEM experiments. YL performed the electrochemical cycling experiments. PS designed the calculations and performed phase-field modeling. BX and SB conceptualized the experiments and interpreted the data. LDJ, PS, BX, and SB contributed to writing the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We gratefully acknowledge assistance from Dr Jian Wang (Canadian Light Source). This study is based on work supported by the National Science Foundation (NSF) under DMR 1627197. L. D. J. acknowledges support under a NSF Graduate Research Fellowship under Grant No. 1252521. J. L. A. acknowledges support from a NASA Fellowship under grant number 80NSSC17K0182. P. S. and B. X. acknowledge the Adolf Messer Foundation for financial support through award of the Adolf Messer Prize to B. X. The funding DFG STE2350/1-1 by Deutsche Forschungsgemeinschaft is gratefully acknowledged. A. portion of the research described in this article was performed at the Canadian Light Source, which is supported by the Natural Sciences and Engineering Research Council of Canada, the National Research Council Canada, the Canadian Institutes of Health Research, the Province of Saskatchewan, Western Economic Diversification Canada, and the University of Saskatchewan.Notes and references
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 CAS.
- J. B. Goodenough, J. Solid State Electrochem., 2012, 16, 2019–2029 CrossRef CAS.
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- P. Bai, D. A. Cogswell and M. Z. Bazant, Nano Lett., 2011, 11, 4890–4896 CrossRef CAS PubMed.
- D. Zeng, J. Cabana, J. Bréger, W.-S. Yoon and C. P. Grey, Chem. Mater., 2007, 19, 6277–6289 CrossRef CAS.
- G. A. Horrocks, M. F. Likely, J. M. Velazquez and S. Banerjee, J. Mater. Chem. A, 2013, 1, 15265–15277 CAS.
- L. Laffont, C. Delacourt, P. Gibot, M. Y. Wu, P. Kooyman, C. Masquelier and J. M. Tarascon, Chem. Mater., 2006, 18, 5520–5529 CrossRef CAS.
- C. Delmas, M. Maccario, L. Croguennec, F. Le Cras and F. Weill, Nat. Mater., 2008, 7, 665–671 CrossRef CAS PubMed.
- G. Brunetti, D. Robert, P. Bayle-Guillemaud, J. L. Rouvière, E. F. Rauch, J. F. Martin, J. F. Colin, F. Bertin and C. Cayron, Chem. Mater., 2011, 23, 4515–4524 CrossRef CAS.
- Y. Guo, R. B. Smith, Z. Yu, D. K. Efetov, J. Wang, P. Kim, M. Z. Bazant and L. E. Brus, J. Phys. Chem. Lett., 2016, 7, 2151–2156 CrossRef CAS PubMed.
- C.-F. Chen, P. Barai and P. P. Mukherjee, J. Electrochem. Soc., 2014, 161, A2138–A2152 CrossRef CAS.
- W. H. Woodford, Y.-M. Chiang and W. C. Carter, J. Electrochem. Soc., 2010, 157, A1052–A1059 CrossRef CAS.
- Y.-T. Cheng and M. W. Verbrugge, Electrochem. Solid-State Lett., 2010, 13, A128–A131 CrossRef CAS.
- C.-F. Chen and P. P. Mukherjee, Phys. Chem. Chem. Phys., 2015, 17, 9812–9827 RSC.
- A. Ulvestad, A. Singer, H. M. Cho, J. N. Clark, R. Harder, J. Maser, Y. S. Meng and O. G. Shpyrko, Nano Lett., 2014, 14, 5123–5127 CrossRef CAS PubMed.
- M. S. Whittingham, Chem. Rev., 2014, 114, 11414–11443 CrossRef CAS PubMed.
- J. Nanda, J. Remillard, A. O'Neill, D. Bernardi, T. Ro, K. E. Nietering, J. Y. Go and T. J. Miller, Adv. Funct. Mater., 2011, 21, 3282–3290 CrossRef CAS.
- A. Ulvestad, A. Singer, J. N. Clark, H. M. Cho, J. W. Kim, R. Harder, J. Maser, Y. S. Meng and O. G. Shpyrko, Science, 2015, 348, 1344–1347 CrossRef CAS PubMed.
- H. Zhou, K. An, S. Allu, S. Pannala, J. Li, H. Z. Bilheux, S. K. Martha and J. Nanda, ACS Energy Lett., 2016, 1, 981–986 CrossRef CAS.
- Y. Yuan, K. Amine, J. Lu and R. Shahbazian-Yassar, Nat. Commun., 2017, 8, 15806 CrossRef CAS.
- B. Li, X. Li, J. Zai and X. Qian, Nano-Micro Lett., 2016, 8, 174–181 CrossRef.
- B. Li, R. Qi, J. Zai, F. Du, C. Xue, Y. Jin, C. Jin, Z. Ma and X. Qian, Small, 2016, 12, 5281–5287 CrossRef CAS PubMed.
- X. Li, J. Zai, S. Xiang, Y. Liu, X. He, Z. Xu, K. Wang, Z. Ma and X. Qian, Adv. Energy Mater., 2016, 6, 1601056 CrossRef.
- J. Song, F. Xia, M. Zhao, Y. L. Zhong, W. Li, K. P. Loh, R. A. Caruso and Q. Bao, Chem. Mater., 2015, 27, 3471–3482 CrossRef CAS.
- W. Li, D. Chen, F. Xia, J. Z. Y. Tan, J. Song, W.-G. Song and R. A. Caruso, Chem. Commun., 2016, 52, 4481–4484 RSC.
- W. Li, F. Xia, J. Qu, P. Li, D. Chen, Z. Chen, Y. Yu, Y. Lu, R. A. Caruso and W. Song, Nano Res., 2014, 7, 903–916 CrossRef CAS.
- B. Orvananos, T. R. Ferguson, H.-C. Yu, M. Z. Bazant and K. Thornton, J. Electrochem. Soc., 2014, 161, A535–A546 CrossRef CAS.
- T. R. Ferguson and M. Z. Bazant, J. Electrochem. Soc., 2012, 159, A1967–A1985 CrossRef CAS.
- J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin, Y. Yu, N. J. Salmon, D. A. Shapiro, M. Z. Bazant, T. Tyliszczak and W. C. Chueh, Science, 2016, 353, 566–571 CrossRef CAS PubMed.
- G. A. Horrocks, L. R. De Jesus, J. L. Andrews and S. Banerjee, JOM, 2017, 69, 1469–1477 CrossRef CAS.
- Y. Yu, M. Farmand, C. Kim, Y. Liu, C. P. Grey, F. C. Strobridge, T. Tyliszczak, R. Celestre, P. Denes, J. Joseph, H. Krishnan, F. R. N. C. Maia, A. L. D. Kilcoyne, S. Marchesini, T. P. C. Leite, T. Warwick, H. Padmore, J. Cabana and D. A. Shapiro, arxiv.org/abs/1711.01525v1, 2017, 1–36.
- W. C. Chueh, F. El Gabaly, J. D. Sugar, N. C. Bartelt, A. H. McDaniel, K. R. Fenton, K. R. Zavadil, T. Tyliszczak, W. Lai and K. F. McCarty, Nano Lett., 2013, 13, 866–872 CrossRef CAS PubMed.
- H. D. Yoo, Y. Liang, H. Dong, J. Lin, H. Wang, Y. Liu, L. Ma, T. Wu, Y. Li, Q. Ru, Y. Jing, Q. An, W. Zhou, J. Guo, J. Lu, S. T. Pantelides, X. Qian and Y. Yao, Nat. Commun., 2017, 8, 339 CrossRef PubMed.
- L. R. De Jesus, Y. Zhao, G. A. Horrocks, J. L. Andrews, P. Stein, B.-X. Xu and S. Banerjee, J. Mater. Chem. A, 2017, 5, 20141–20152 CAS.
- W. Dreyer, C. Guhlke and R. Huth, Phys. D, 2011, 240, 1008–1019 CrossRef CAS.
- Y. Li, F. El Gabaly, T. R. Ferguson, R. B. Smith, N. C. Bartelt, J. D. Sugar, K. R. Fenton, D. A. Cogswell, A. L. D. Kilcoyne, T. Tyliszczak, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2014, 13, 1149–1156 CrossRef CAS PubMed.
- J. R. Croy, D. Kim, M. Balasubramanian, K. Gallagher, S.-H. Kang and M. M. Thackeray, J. Electrochem. Soc., 2012, 159, A781–A790 CrossRef CAS.
- J. N. Weker, N. Liu, S. Misra, J. C. Andrews, Y. Cui and M. F. Toney, Energy Environ. Sci., 2014, 7, 2771–2777 CAS.
- P. Barai and P. P. Mukherjee, Mater. Res. Express, 2016, 3, 104011 Search PubMed.
- F. Hao and D. Fang, J. Electrochem. Soc., 2013, 160, A595–A600 CrossRef CAS.
- X. Li, G. Wu, X. Liu, W. Li and M. Li, Nano Energy, 2017, 31, 1–8 CrossRef CAS.
- X. Li, Y. Feng, M. Li, W. Li, H. Wei and D. Song, Adv. Funct. Mater., 2015, 25, 6858–6866 CrossRef CAS.
- L. S. Zhang, L. Y. Jiang, C. Q. Chen, W. Li, W. G. Song and Y. G. Guo, Chem. Mater., 2010, 22, 414–419 CrossRef CAS.
- W. Li, Y.-X. Yin, S. Xin, W.-G. Song and Y.-G. Guo, Energy Environ. Sci., 2012, 5, 8007–8013 CAS.
- X. Li, W. Li, M. Li, P. Cui, D. Chen, T. Gengenbach, L. Chu, H. Liu and G. Song, J. Mater. Chem. A, 2015, 3, 2762–2769 CAS.
- Y. Liu, L. Si, Y. Du, X. Zhou, Z. Dai and J. Bao, J. Phys. Chem. C, 2015, 119, 27316–27321 CAS.
- X. Zhou, L. Yu and X. W. (David) Lou, Nanoscale, 2016, 8, 8384–8389 RSC.
- X. Zhou, L. Yu and X. W. (David) Lou, Adv. Energy Mater., 2016, 6, 1600451 CrossRef.
- Z. Chen, Y. Yan, S. Xin, W. Li, J. Qu, Y. G. Guo and W. G. Song, J. Mater. Chem. A, 2013, 1, 11404–11409 CAS.
- L. R. De Jesus, G. A. Horrocks, Y. Liang, A. Parija, C. Jaye, L. Wangoh, J. Wang, D. A. Fischer, L. F. J. Piper, D. Prendergast and S. Banerjee, Nat. Commun., 2016, 7, 12022 CrossRef CAS PubMed.
- M. Wolf, B. M. May and J. Cabana, Chem. Mater., 2017, 29, 3347–3362 CrossRef CAS.
- F. Yang, Y. Liu, S. K. Martha, Z. Wu, J. C. Andrews, G. E. Ice, P. Pianetta and J. Nanda, Nano Lett., 2014, 14, 4334–4341 CrossRef CAS PubMed.
- U. Boesenberg, F. Meirer, Y. Liu, A. K. Shukla, R. Dell’Anna, T. Tyliszczak, G. Chen, J. C. Andrews, T. J. Richardson, R. Kostecki and J. Cabana, Chem. Mater., 2013, 25, 1664–1672 CrossRef CAS PubMed.
- G. A. Horrocks, E. J. Braham, Y. Liang, L. R. De Jesus, J. Jude, J. M. Velázquez, D. Prendergast and S. Banerjee, J. Phys. Chem. C, 2016, 120, 23922–23932 CAS.
- M. Olivares-Marín, A. Sorrentino, R. C. Lee, E. Pereiro, N. L. Wu and D. Tonti, Nano Lett., 2015, 15, 6932–6938 CrossRef PubMed.
- L. R. De Jesus, R. V. Dennis, S. W. Depner, C. Jaye, D. A. Fischer and S. Banerjee, J. Phys. Chem. Lett., 2013, 4, 3144–3151 CrossRef CAS PubMed.
- M. Lerotic, C. Jacobsen, T. Schäfer and S. Vogt, Ultramicroscopy, 2004, 100, 35–57 CrossRef CAS PubMed.
- M. Lerotic, C. Jacobsen, J. B. Gillow, A. J. Francis, S. Wirick, S. Vogt and J. Maser, J. Electron Spectrosc. Relat. Phenom., 2005, 144–147, 1137–1143 CrossRef CAS.
- P. M. Marley, T. A. Abtew, K. E. Farley, G. A. Horrocks, R. V. Dennis, P. Zhang and S. Banerjee, Chem. Sci., 2015, 6, 1712–1718 RSC.
- N. A. Chernova, M. Roppolo, A. C. Dillon and M. S. Whittingham, J. Mater. Chem., 2009, 19, 2526–2552 RSC.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301 CrossRef CAS PubMed.
- P. M. Marley, G. A. Horrocks, K. E. Pelcher and S. Banerjee, Chem. Commun., 2015, 51, 5181–5198 RSC.
- D. W. Murphy, P. A. Christian, F. J. DiSalvo and J. V. Waszczak, Inorg. Chem., 1979, 18, 2800–2803 CrossRef CAS.
- K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y. S. Meng, A. van der Ven, V. Srinivasan, R. Kostecki and G. Ceder, J. Phys. Chem. Lett., 2010, 1, 1176–1180 CrossRef CAS.
- M. S. Whittingham and M. B. Dines, J. Electrochem. Soc., 1977, 124, 1387–1388 CrossRef CAS.
- R. Enjalbert and J. Galy, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 1467–1469 CrossRef.
- C. Satto, P. Sciau, E. Dooryhee, J. Galy and P. Millet, J. Solid State Chem., 1999, 109, 103–109 CrossRef.
- J. Galy, J. Solid State Chem., 1992, 100, 229–245 CrossRef CAS.
- H. Ade and A. P. Hitchcock, Polymer, 2008, 49, 643–675 CrossRef CAS.
- S. G. Urquhart, A. P. Hitchcock, A. P. Smith, H. W. Ade, W. Lidy, E. G. Rightor and G. E. Mitchell, J. Electron Spectrosc. Relat. Phenom., 1999, 100, 119–135 CrossRef CAS.
- J. M. Velazquez, C. Jaye, D. A. Fischer and S. Banerjee, J. Phys. Chem. C, 2009, 113, 7639–7645 CAS.
- D. Maganas, M. Roemelt, M. Hävecker, A. Trunschke, A. Knop-Gericke, R. Schlögl and F. Neese, Phys. Chem. Chem. Phys., 2013, 15, 7260–7276 RSC.
- C. Kolczewski and K. Hermann, Surf. Sci., 2004, 552, 98–110 CrossRef CAS.
- J. L. Andrews, L. R. De Jesus, T. M. Tolhurst, P. M. Marley, A. Moewes and S. Banerjee, Chem. Mater., 2017, 29, 3285–3294 CrossRef CAS.
- T. M. Tolhurst, B. Leedahl, J. L. Andrews, P. M. Marley, S. Banerjee and A. Moewes, Phys. Chem. Chem. Phys., 2016, 18, 15798–15806 RSC.
- D. A. Cogswell and M. Z. Bazant, ACS Nano, 2012, 6, 2215–2225 CrossRef CAS PubMed.
- Y. Zhao, L. R. De Jesus, P. Stein, G. A. Horrocks, S. Banerjee and B.-X. Xu, RSC Adv., 2017, 7, 41254–41264 RSC.
- E. A. Meulenkamp, W. van Klinken and A. R. Schlatmann, Solid State Ionics, 1999, 126, 235–244 CrossRef CAS.
- R. Baddour-Hadjean, E. Raekelboom and J. P. Pereira-Ramos, Chem. Mater., 2006, 18, 3548–3556 CrossRef CAS.
- P. G. Dickens, S. J. French, A. T. Hight and M. F. Pye, Mater. Res. Bull., 1979, 14, 1295–1299 CrossRef CAS.
- P. Stein and B. Xu, Comput. Methods Appl. Mech. Eng., 2014, 268, 225–244 CrossRef.
- P. Stein, Y. Zhao and B.-X. Xu, J. Power Sources, 2016, 332, 154–169 CrossRef CAS.
- N. Muralidharan, C. N. Brock, A. P. Cohn, D. Schauben, R. E. Carter, L. Oakes, D. G. Walker and C. L. Pint, ACS Nano, 2017, 11, 6243–6251 CrossRef CAS PubMed.
- B.-X. Xu, Y. Zhao and P. Stein, GAMM-Mitteilungen, 2016, 39, 92–109 CrossRef.
- Y. Zhao, B.-X. Xu, P. Stein and D. Gross, Comput. Methods Appl. Mech. Eng., 2016, 312, 428–446 CrossRef.
- J. L. Andrews, A. Mukherjee, H. D. Yoo, A. Parija, P. M. Marley, D. Prendergast, J. Cabana, R. F. Klie and S. Banerjee, Chem, 2018 DOI:10.1016/j.chempr.2017.12.018.
- C. Jacobsen, S. Wirick, G. Flynn and C. Zimba, J. Microsc., 2000, 197, 173–184 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh00037a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |