Mechanically triggered composite stiffness tuning through thermodynamic relaxation (ST3R)†
Abstract
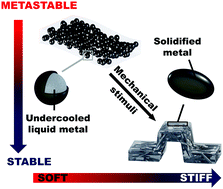
Recent developments in smart responsive composites have utilized various stimuli including heat, light, solvents, electricity, and magnetic fields to induce a change in material properties. Here, we report a thermodynamically driven mechanically responsive composite, exploiting irreversible phase-transformation (relaxation) of metastable undercooled liquid metal core shell particle fillers. Thermal and mechanical analysis reveals that as the composite is deformed, the particles transform from individual liquid droplets to a solid metal network, resulting in a 300% increase in Young's modulus. In contrast to previous phase change materials, this dramatic change in stiffness occurs autonomously under deformation, is insensitive to environmental conditions, and does not require external energy sources such as heat, light, or electricity. We demonstrate the utility of this approach by transforming a flat, flexible composite strip into a rigid, 3D structure that is capable of supporting 50× its own weight. The ability for shape change and reconfiguration are further highlighted, indicating potential for multiple pathways to trigger or tune composite stiffness.
- This article is part of the themed collection: Materials Horizons Most Popular Articles


 Please wait while we load your content...
Please wait while we load your content...