Unidirectional water delivery on a superhydrophilic surface with two-dimensional asymmetrical wettability barriers†
Hui
Geng
a,
Haoyu
Bai
a,
Yangyang
Fan
a,
Shaoyu
Wang
a,
Teer
Ba
a,
Cunming
Yu
b,
Moyuan
Cao
 *a and
Lei
Jiang
*a and
Lei
Jiang
 b
b
aSchool of Chemical Engineering and Technology, State Key Laboratory of Chemical Engineering, Tianjin University, Tianjin, 300072, P. R. China. E-mail: moyuan.cao@tju.edu.cn
bTechnical Institute of Physics and Chemistry, Key Laboratory of Bio-inspired Materials and Interfacial Science, Chinese Academy of Sciences, Beijing, 100190, P. R. China
First published on 2nd February 2018
Abstract
A superhydrophilic surface decorated with 2D hydrophobic water barriers is proven to be a potential platform for unidirectional liquid transport. Differing from the existing systems based on 3D micro-structures, this functional surface features a simplified structure and high adaptiveness that provide more possibilities for the development of fluid manipulating materials.
Conceptual insightsIn nature, a unidirectional liquid transporting process can guarantee efficient water uptake and specific functions of organisms. Unlike the common industrial methods, the external energy input is insignificant to such bio-inspired liquid delivery processes. With respect to successful spontaneous liquid delivery, the structure and wettability of an anisotropic surface have been regarded as effective factors for driving the liquid motion via capillary forces, Laplace pressure, etc. However, the current materials for long-range fluid delivery mainly depend on complicated 3D micro-/nano-structures, which may restrict their potential integration and applications in the real world. Through the incorporation of asymmetric 2D water barriers into a flat superhydrophilic surface, we demonstrate that liquid can actively spread and continuously move in one specific direction. This unidirectional liquid delivery is regulated by the anisotropic motion resistance arising from the patterns, and offers a facile, adaptive, and reliable strategy for long-range liquid transport on an open surface. Our method remarkably simplifies the design and fabrication of these functional interface materials, providing a convenient way to manipulate fluid delivery on a 2D surface. |
The anisotropic wetting phenomenon, which is ubiquitous in nature, exhibits crucial functions to help organisms survive in harsh environments.1–3 As a famous desert animal, the lizard (Moloch horridus) is able to actively guide water by means of its asymmetrically arranged hydrophilic skin.4–6 Through oriented capillarity (viz. Taylor rise), lubricated liquid in the Pitcher plant (Nepenthes alata) can be spontaneously uplifted to the peristome, resulting in a slippery surface for trapping small insects.7–10 Taking advantage of the directional droplet motion on its conical spines, the cactus (Opuntia microdasys) can effectively harvest extra water from the morning fog in arid regions.11,12 These fantastic water transporting processes can serve as an inspiration for the development of current fluid manipulating systems for liquid collection/separation, mass/heat transfer, micro-fluidics, etc.13–17
A chemistry gradient and structural asymmetry are key factors for fabricating directional liquid transporting interfaces. The self-propelled running of a water droplet has been widely proven on flat surfaces with gradient wettability or Janus materials.18–22 A droplet is able to move from a hydrophobic site to a hydrophilic site without any external energy;23–26 however, the moving distance of the droplet and the sustainability of liquid transport are unsatisfactory due to irreversible energy loss. With respect to asymmetric geometry, substrates of triangular/conical shape can also realize directional droplet motion.27–29 The imbalance of the Laplace pressure of the droplet propels it from the tip-site to the root-site of a substrate. Compared with the wettability gradient surfaces, shaped substrates can be applied to droplet delivery on a centimetre scale, exhibiting promising performances in fog collection and oil-spill clean-up.
The peristome structure of a Picher plant represents another kind of directional surface, viz. a unidirectional wetting surface.30–32 The incorporation of oriented 3D micro-/nano-structures, e.g. nano-needles, micro-ratchets and micro-cavities, can endow the surface with unidirectional liquid wetting ability.33–36 Liquid preferentially spreads toward the direction with least motion resistance, whereas the liquid is pinned in the opposite direction. Differing from the above-mentioned surfaces, this unidirectional wetting surface is suitable for long-range liquid delivery without external energy consumption, which is extremely important in real-world applications. The previous reports have suggested that a well-defined 3D micro-structure may be indispensable to successful unidirectional liquid spreading.37–41 In accordance with the requirements of tilted micro-structures, complicated micro-machining processes, such as photolithography,30 replica molding38etc., have been the focus of fabrication methods. Simplicity would be the ultimate sophistication.42 If unidirectional water spreading could be fulfilled by a simple 2D surface, fluid manipulating surfaces would be highly adaptive to optimization and application to current interface materials.
Here we show that unidirectional water delivery can be achieved on the basis of a superhydrophilic 2D surface possessing asymmetrical hydrophobic barriers. The hydrophobic water barriers could be directly drawn on the surface with superhydrophilic properties. An asymmetric spreading resistance is generated by the different interaction modes between the liquid and the hydrophobic barriers, i.e., water tends to spread against the tilt direction of the linear pattern. Accordingly, versatile water delivery surfaces were designed to facilitate a series of directional water transporting/gating processes. We envision that these 2D liquid delivery surfaces should open a new avenue for investigating the unidirectional wetting phenomenon and for promoting research into, and applications of, fluid controlling interfaces.
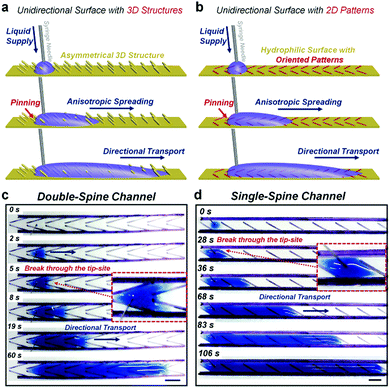
The essence of unidirectional liquid spreading is the difference in resistance between the front and the rear of the fluid motion. For a 3D unidirectional surface, oriented micro-structures, such as re-entrant and cilia structures, can generate a remarkable difference in the length of the solid/liquid/gas three-phase contact line (TCL), resulting in distinguishable advancing angles (Fig. 1a). In general, a small advancing angle reveals that there is a relatively low resistance to the liquid spreading; therefore the direction with the smallest advancing angle is regarded as the “spreading direction”. In contrast, the opposite direction with a higher resistance can be noted as the “pinning direction”.
A similar design principle can be applied to a 2D surface via the rational incorporation of wettability patterns (Fig. 1b). To minimize the additional resistance from the substrate, a TiO2 micro-particle coated superhydrophilic surface, which has a negligible advancing angle of spreading fluid, was selected as the delivery substrate.43 With the assistance of a drawing robot, a waterproof marker pen with a tip-diameter of 0.2 mm was used to pattern the superhydrophilic surface with a specific hydrophobic ink stain in a facile procedure. A typical unidirectional 2D channel contains two parallel walls and tilted water barriers. The detailed morphology of the patterned surface is shown in Fig. S1 (ESI†); the final width of the linear water barrier is approximately 300 μm due to the slight diffusion of ink. The contact angle of the ink stain is 73.2° ± 1.5°, and the TiO2 particle coated surface shows superhydrophilicity with an advancing contact angle near 0° (Fig. S1c and S2, ESI†). When water is continuously supplied to the surface, significant unidirectional spreading is observed both on single-spine and double-spine channels (Fig. 1c, d and Movie S1 (ESI†), liquid injection velocity of 8 ml h−1). The spreading water can easily break though the tip-site of the hydrophobic barrier and move to the next joint. During the transporting process, the rear surface of the liquid remains pinned. The transporting velocity of the liquid on the 2D surface is lower than that previously reported for a channel with a groove-structure, due to the absence of the additional propulsion of capillary force. However, the volume of liquid transported is greatly improved from microliters to milliliters.38 Because the liquid transport is confined in a channel with hydrophobic walls, a continuous water supply can efficiently propel the directional delivery without any liquid leakage. In our experiment, the optimized 2D channel is able to realize directional and massive water delivery with an injection velocity of over 300 ml h−1 (Movie S2, ESI†), which is practicable for applications in surface heat/mass transfer. Without the titania coating, the directional liquid spreading might also proceed in one or more joints; however, the overlarge resistance would resist long-distance liquid delivery (Fig. S3, ESI†). The orientation of each joint of channel keeps the direction of liquid spread consistent (Fig. S4, ESI†). Water always spreads against the barrier tilt, irrespective of the injection point. The incorporation of TiO2 particles with photo-catalysis ability can guarantee the durability of the surface hydrophilicity, and the hydrophobic silica particles can enhance the water repellence of the barriers. As a result, the liquid channel with this optimal design can repeatedly achieve unidirectional transport for a long period of time.
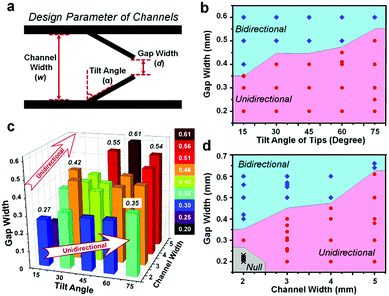
A systematic investigation into the design parameters of the unidirectional channel should provide more information for the control of fluid behaviour. Three parameters are considered decisive to unidirectional water delivery: the width of the channel (w), the tilt angle of the water barriers (α), and the width of the gap between two barriers (d) (Fig. 2a). The phase diagrams of liquid spreading are plotted to reveal the relationship between these parameters and delivery behaviour. The critical gap width is at the boundary between unidirectional delivery (below the boundary) and bidirectional delivery (above the boundary). According to our experiment, the control of gap width is accurate to 0.1 mm. The actual width is measured using a microscope, and the critical width is set as the average value of the boundary widths between two directionalities. For the channel with a width of 4 mm, the critical gap width increases from 0.35 to 0.5 mm as the tilt angle varies from 15° to 75°, indicating that a large tilt angle is preferred for unidirectional spreading (Fig. 2b). At a tilt angle of 60°, the channel with 5 mm width exhibits a large critical gap width of over 0.6 mm (Fig. 2d). In similar conditions, the critical gap width is only 0.3 mm for the 2 mm channel. Furthermore, the 2 mm channel with a 0.2 mm gap width does not guide the liquid motion at all owing to the over-large motion resistance. The overall critical gap widths with varied parameters are displayed in Fig. 2c. The clear trend is that a large tilt angle of the hydrophobic barriers and a wide channel for liquid transport are highly desired for unidirectional water delivery. More details on the design parameters are listed in the ESI† (Fig. S5 and S6).
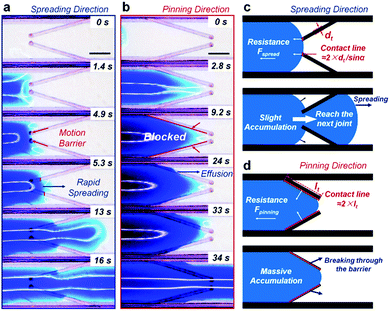
The detailed process by which liquid penetrates across the water barriers was recorded using a microscope (Fig. 3). Water is continuously charged onto a single joint until the barriers are broken through. The front edge of the liquid flow maintains an arc-shape during the continuous spreading (Fig. S7, ESI†). It can be seen that the spine easily stabs into the front surface of the liquid in the spreading direction (Fig. 3a). Once in contact with the superhydrophilic surface at the next joint, liquid rapidly moves forwards. In contrast, it is hard for the liquid to cross the barrier from the opposite direction, and so the liquid can only effuse from the barrier after massively accumulating (Fig. 3b). This in-plane water motion is mainly dependent on spontaneous spreading on a resistance-free superhydrophilic surface; this is different from previous reports on 3D grooved structures which show strong capillary effects. Therefore, the mechanism behind the directional wettability of this 2D surface can be explained based on the above observation.
To the best of our knowledge, asymmetric motion resistance of water determines the direction of liquid transport.32–34 The superhydrophilic surface can promote the spontaneous spread of a droplet, indicating its ultralow resistance for water infusion.44–46 To regulate the pathway of water delivery, the hydrophobic pattern should be chosen to generate oriented resistance on the superhydrophilic surface.47 The motion resistance of a droplet sliding upon a flat surface can be expressed according to eqn (1):48
f = γ·(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − cos θ − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe) θe) | (1) |
Fspread = 2·dt·γ·(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θadv − cos θadv − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe)/sin θe)/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α | (2) |
Fpinning = 2·lt·γ·(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θadv − cos θadv − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe)·cos θe)·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α | (3) |
lt = 0.5·(w − d)/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α | (4) |
Therefore, Fpinning can also be expressed as eqn (5):
Fpinning = γ·(w − d)·(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θadv − cos θadv − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe) θe) | (5) |
A brief estimation of the resistance difference between the two directions can be conducted. For a channel with parameters w = 5 mm, d = 0.5 mm and α = 75°, Fpinning is about 7 times larger than Fspread, demonstrating an obvious asymmetric resistance. The model can also illustrate the trend in Fig. 2c, i.e., an increase of w and α can enhance the difference between Fpinning and Fspread. A significant resistance difference and a relatively high Fpinning contribute to successful unidirectional water delivery. The mechanisms of directional wettability between single- and double-spine channels are slightly distinct, i.e., the motion resistance of a single spine channel is generated by both the wall and the spine. As a result, the overall resistance may not be parallel to the spreading direction. To illustrate this process clearly, we herein select the double-spine channel as the model.
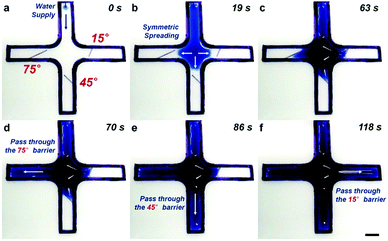
On the basis of an understanding of the spreading resistance, we fabricated a smart fluid distributing surface with three channels for controlling the order of liquid spread. The mechanism reveals that the larger the tilt angle of the water barrier, the lower the resistance to the water spreading. As shown in Fig. 4 and Movie S3 (ESI†), each channel on the surface possesses a tilted water barrier, and the tilt angles are set at 15°, 45°, and 75°. Water is continuously supplied from the barrier-free channel and consistently moves toward the centre. After reaching the fork of the channels, water firstly passes through the channel with the 75° tilted barrier (Fig. 4d). A continuous water supply next propels the water across the 45° barrier and then the 15° barrier. As a consequence, the ordered distribution of the water flow can be conveniently achieved through a pen-drawn fluid delivery surface.
The 2D unidirectional surface with its simplified structure can unlock more possibilities and options for integration into complex fluid controlling systems. Taking advantage of a single-spine channel, unidirectional water transport on curved and polygonal channels can be successfully fabricated, showing the high adaptiveness and universality of our method. A pattern of two circular channels with different directionality can be made on the superhydrophilic surface (Fig. 5a). With continuous liquid injection, water flows anticlockwise in the outer circle; on the contrary, the inner circular channel guarantees clockwise unidirectional spreading (Movie S4, ESI†). This coupled directional liquid transport demonstrates a valuable and handy method for regulating the moving train of surface fluids. In addition, stepwise unidirectional water transport can be achieved via a polygonal channel with oriented water barriers (Fig. 5b). Wherever the droplet is discharged, liquid always runs toward the destination of the channel. More importantly, liquid which is discharged at a later time-point can spread ahead and connect with the front liquid flow, facilitating a continuous and programmable process for liquid transferring and mixing.
Conclusions
In conclusion, a simplified strategy for achieving unidirectional liquid spreading is proposed on the basis of a wettability patterned superhydrophilic surface. An asymmetric arrangement of hydrophobic water barriers can be conveniently drawn on the surface, resulting in a 2D unidirectional water channel. With a continuous water supply, the liquid tends to spread against the tilt direction of the water barrier, arising from the lower motion resistance. The design parameters and the mechanism were systematically investigated, revealing that the anisotropic interaction between the hydrophobic barriers and the liquid is essential to the directional liquid transport. This contribution provides a facile, scalable, and adaptive strategy for achieving unidirectional water delivery without complicated 3D micro-structures. It should offer more options for the development of novel materials in the fields of liquid transport/separation, micro-fluidics, etc.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Fund for Fundamental Key Projects (2013CB933000), the State High-Tech Development Plan (2012AA030305), the National Natural Science Foundation (21504098), and the State Key Laboratory of Chemical Engineering (SKL-ChE-16B04).Notes and references
- K. Koch and W. Barthlott, Philos. Trans. R. Soc., A, 2009, 367, 1487–1509 CrossRef CAS PubMed.
- L. Feng, S. H. Li, Y. S. Li, H. J. Li, L. J. Zhang, J. Zhai, Y. L. Song, B. Q. Liu, L. Jiang and D. B. Zhu, Adv. Mater., 2002, 14, 1857–1860 CrossRef CAS.
- M. Qu, S. Liu, J. He, C. Yu, X. Liu, Y. Yao and J. Feng, RSC Adv., 2016, 6, 93403–93409 RSC.
- P. J. Bentley and W. F. C. Blumer, Nature, 1962, 194, 699 CrossRef CAS PubMed.
- P. Comanns, C. Effertz, F. Hischen, K. Staudt, W. Bohme and W. Baumgartner, Beilstein J. Nanotechnol., 2011, 2, 204–214 CrossRef CAS PubMed.
- W. C. Sherbrooke, A. J. Scardino, R. de Nys and L. Schwarzkopf, Zoomorphology, 2007, 126, 89–102 CrossRef.
- T. S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477, 443–447 CrossRef CAS PubMed.
- H. W. Chen, P. F. Zhang, L. W. Zhang, H. L. L. Iu, Y. Jiang, D. Y. Zhang, Z. W. Han and L. Jiang, Nature, 2016, 532, 85–89 CrossRef CAS PubMed.
- P. F. Zhang, H. W. Chen, L. Li, H. L. Liu, G. Liu, L. W. Zhang, D. Y. Zhang and L. Jiang, ACS Appl. Mater. Interfaces, 2017, 9, 5645–5652 CAS.
- X. Yao, Y. H. Hu, A. Grinthal, T. S. Wong, L. Mahadevan and J. Aizenberg, Nat. Mater., 2013, 12, 529–534 CrossRef CAS PubMed.
- J. Ju, H. Bai, Y. M. Zheng, T. Y. Zhao, R. C. Fang and L. Jiang, Nat. Commun., 2012, 3, 1247 CrossRef PubMed.
- F. T. Malik, R. M. Clement, D. T. Gethin, M. Kiernan, T. Goral, P. Griffiths, D. Beynon and A. R. Parker, Philos. Trans. R. Soc., A, 2016, 374, 20160110 CrossRef PubMed.
- M. Y. Cao and L. Jiang, Surf. Innovations, 2016, 4, 180–194 CrossRef.
- P. P. Zhang, J. J. Zhang, Z. X. Xue, J. M. Wang and L. Jiang, Mater. Horiz., 2017, 4, 665–672 RSC.
- J. W. Chen, Y. M. Liu, D. W. Guo, M. Y. Cao and L. Jiang, Chem. Commun., 2015, 51, 11872–11875 RSC.
- M. Y. Cao, J. S. Xiao, C. M. Yu, K. Li and L. Jiang, Small, 2015, 11, 4379–4384 CrossRef CAS PubMed.
- M. Y. Cao, K. Li, Z. C. Dong, C. M. Yu, S. Yang, C. Song, K. S. Liu and L. Jiang, Adv. Funct. Mater., 2015, 25, 4114–4119 CrossRef CAS.
- Z. X. Wang, X. B. Yang, Z. J. Cheng, Y. Y. Liu, L. Shao and L. Jiang, Mater. Horiz., 2017, 4, 701–708 RSC.
- F. Lugli, G. Fioravanti, D. Pattini, L. Pasquali, M. Montecchi, D. Gentili, M. Murgia, Z. Hemmatian, M. Cavallini and F. Zerbetto, Adv. Funct. Mater., 2013, 23, 5543–5549 CrossRef CAS.
- K. Ichimura, S. K. Oh and M. Nakagawa, Science, 2000, 288, 1624–1626 CrossRef CAS PubMed.
- B. S. Gallardo, V. K. Gupta, F. D. Eagerton, L. I. Jong, V. S. Craig, R. R. Shah and N. L. Abbott, Science, 1999, 283, 57–60 CrossRef CAS PubMed.
- X. L. Tian, H. Jin, J. Sainio, R. H. A. Ras and O. Ikkala, Adv. Funct. Mater., 2014, 24, 6023–6028 CrossRef CAS.
- S. C. Hernandez, C. J. C. Bennett, C. E. Junkermeier, S. D. Tsoi, F. J. Bezares, R. Stine, J. T. Robinson, E. H. Lock, D. R. Boris, B. D. Pate, J. D. Caldwell, T. L. Reinecke, P. E. Sheehan and S. G. Walton, ACS Nano, 2013, 7, 4746–4755 CrossRef CAS PubMed.
- M. K. Chaudhury and G. M. Whitesides, Science, 1992, 256, 1539–1541 CAS.
- H. Zhou, H. X. Wang, H. T. Niu and T. Lin, Sci. Rep., 2013, 3, 2964 CrossRef PubMed.
- P. Liu, W. He, G. Lu, H. Zhang, Z. Wang and X. Yao, J. Mater. Chem. A, 2017, 5, 16344–16351 CAS.
- C. M. Yu, M. Y. Cao, Z. C. Dong, J. M. Wang, K. Li and L. Jiang, Adv. Funct. Mater., 2016, 26, 3236–3243 CrossRef CAS.
- K. C. Park, P. Kim, A. Grinthal, N. He, D. Fox, J. C. Weaver and J. Aizenberg, Nature, 2016, 531, 78–82 CrossRef CAS PubMed.
- E. Lorenceau and D. Quéré, J. Fluid Mech., 2004, 510, 29–45 CrossRef.
- H. W. Chen, L. W. Zhang, Y. Zhang, P. F. Zhang, D. Y. Zhang and L. Jiang, J. Mater. Chem. A, 2017, 5, 6914–6920 CAS.
- H. W. Chen, L. W. Zhang, P. F. Zhang, D. Y. Zhang, Z. W. Han and L. Jiang, Small, 2017, 13, 1601676 CrossRef PubMed.
- Y. Y. Zhu, D. S. Antao, R. Xiao and E. N. Wang, Adv. Mater., 2014, 26, 6442–6446 CrossRef CAS PubMed.
- N. A. Malvadkar, M. J. Hancock, K. Sekeroglu, W. J. Dressick and M. C. Demirel, Nat. Mater., 2010, 9, 1023–1028 CrossRef CAS PubMed.
- K. H. Chu, R. Xiao and E. N. Wang, Nat. Mater., 2010, 9, 413–417 CrossRef CAS PubMed.
- W. G. Bae, S. M. Kim, S. J. Choi, S. G. Oh, H. Yoon, K. Char and K. Y. Suh, Adv. Mater., 2014, 26, 2665–2670 CrossRef CAS PubMed.
- T. Q. Wang, H. X. Chen, K. Liu, S. L. Wang, P. H. Xue, Y. Yu, P. Ge, J. H. Zhang and B. Yang, ACS Appl. Mater. Interfaces, 2015, 7, 376–382 CAS.
- M. Y. Cao, X. Jin, Y. Peng, C. M. Yu, K. Li, K. S. Liu and L. Jiang, Adv. Mater., 2017, 29, 1606869 CrossRef PubMed.
- C. X. Li, N. Li, X. S. Zhang, Z. C. Dong, H. W. Chen and L. Jiang, Angew. Chem., Int. Ed., 2016, 55, 14988–14992 CrossRef CAS PubMed.
- C. Y. Huang, M. F. Lai, W. L. Liu and Z. H. Wei, Adv. Funct. Mater., 2015, 25, 2670–2676 CrossRef CAS.
- C. M. Yu, X. B. Zhu, M. Y. Cao, C. L. Yu, K. Li and L. Jiang, J. Mater. Chem. A, 2016, 4, 16865–16870 CAS.
- P. H. Xue, J. J. Nan, T. Q. Wang, S. L. Wang, S. S. Ye, J. H. Zhang, Z. C. Cui and B. Yang, Small, 2017, 13, 1601807 CrossRef PubMed.
- Leonardo da Vinci's logion cited from C. F. Barbas, Angew. Chem., Int. Ed., 2008, 47, 42–47 CrossRef CAS PubMed.
- J. Yong, F. Chen, M. Li, Q. Yang, Y. Fang, J. Huo and X. Hou, J. Mater. Chem. A, 2017, 5, 25249–25257 CAS.
- J. Drelich, E. Chibowski, D. D. Meng and K. Terpilowski, Soft Matter, 2011, 7, 9804–9828 RSC.
- Z. P. Zhu, S. Zheng, S. Peng, Y. Zhao and Y. Tian, Adv. Mater., 2017, 29, 5720–5724 Search PubMed.
- Z. P. Zhu, Y. Tian, Y. P. Chen, Z. Gu, S. T. Wang and L. Jiang, Angew. Chem., Int. Ed., 2017, 56, 5720–5724 CrossRef CAS PubMed.
- E. Ueda and P. A. Levkin, Adv. Mater., 2013, 25, 1234–1247 CrossRef CAS PubMed.
- P.-G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, Springer, 2004 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7mh01138e |
| This journal is © The Royal Society of Chemistry 2018 |