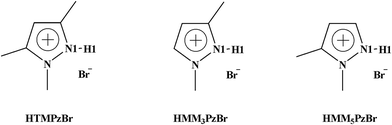
Protic pyrazolium ionic liquids for efficient chemical fixation of CO2: design, synthesis, and catalysis†
Danning
Zheng
a,
Tengfei
Wang
ab,
Xinrui
Zhu
a,
Ci
Chen
a,
Tiegang
Ren
*ab,
Li
Wang
 *a and
Jinglai
Zhang
*a and
Jinglai
Zhang
 *a
*a
aCollege of Chemistry and Chemical Engineering, Henan University, Kaifeng, Henan 475004, P.R. China. E-mail: rtg@henu.edu.cn; chemwangl@henu.edu.cn; zhangjinglai@henu.edu.cn
bEngineering Laboratory for Flame Retardant and Functional Materials of Henan Province, Henan University, Kaifeng, Henan 475004, P.R. China
First published on 15th December 2017
Abstract
The conversion of carbon dioxide into organic products under benign conditions is still challenging. Ionic liquids are regarded as efficient and “green” catalysts from a sustainability view point. However, little attention has been focused on pyrazolium ILs although they are structural isomers of imidazolium ILs. Even fewer studies have been performed on protic pyrazolium ILs. In this work, three new protic pyrazolium ILs, HTMPzBr, HMM3PzBr, and HMM5PzBr, have been synthesized to explore their catalytic activity for the coupling reaction of carbon dioxide and propylene oxide. Both theoretical calculations and experimental characterization have verified that HTMPzBr and HMM5PzBr have similar catalytic activity, which is higher than that of HMM3PzBr. The role of various weak interactions, especially hydrogen bonds, in the reaction is elucidated by detailed theoretical analysis. The sequence of catalytic activity predicted by the Double-IL theoretical model is totally consistent with the experimental result. It is reasonable to design ionic liquids from a molecular level if a suitable theoretical model is applied, and this would provide some guidance for further experimental study.
Design, System, ApplicationIt is still challenging to develop efficient and single component catalysts for fixation of CO2 under benign conditions. In this work, three protic pyrazolium-based ILs, HTMPzBr, HMM3PzBr, and HMM5PzBr, are firstly designed with computer assistance. Next, their catalytic activity for the coupling reaction of CO2 and propylene oxide is investigated by molecular dynamics simulation and quantum chemistry. Finally, they are synthesized and the corresponding catalytic activity is determined in experiment. The experimentally determined catalytic activity is totally consistent with the theoretical estimated result. HTMPzBr and HMM5PzBr have similar catalytic activity, which is higher than that of HMM3PzBr. The lower catalytic activity of HMM3PzBr is caused by the absence of methyl substitution in the C5 position. There are three highlights that deserved to be noted: (1) the Double-IL model is more reliable for predicting the sequence of catalytic activity than the Single-IL model; (2) the role of weak interactions, especially hydrogen bonds, in the catalytic cycle is elucidated; and (3) it is reasonable to explore new ionic liquids with desired properties from computer-assisted design to experimental synthesis rather than through experimental trial and error. Our final goal is to develop new ionic liquids from the molecular level. |
1. Introduction
The capture and utilization of carbon dioxide (CO2) have attracted considerable attention in the past few decades,1 since CO2 is one of the most pivotal factors associated with climate change.2 It is also a cheap, abundant, and non-toxic C1 resource, which could be converted into various useful chemicals, such as urea, polycarbonates, salicylic acid,3 carboxylic acids, and others.4 The conversion of CO2 to useful chemical products would not only ameliorate its negative effect on the environment but also solve the problem induced by the depletion of fossil fuels. The cycloaddition of CO2 with propylene oxide (PO) into propylene carbonate (PC)5 is regarded as one of the most attractive routes for CO2 fixation, because it has 100% atomic utilization and negligible by-products.6 Moreover, PC has been widely applied in many fields, such as in aprotic polar solvents, electrolytes in lithium-ion batteries, and precursors for polymer synthesis including polycarbonates.7 However, the activation of CO2 under benign conditions is still difficult because CO2 is in its highest oxidized state. Although various catalysts have been developed for the fixation of CO2˙ such as metal oxides,8 alkali metal salts,9 and transition metal complexes,10 they have some common disadvantages including being polluting to the environment, requiring harsh reaction conditions, and others. Ionic liquids (ILs) are outstanding because of their unique properties, including easy separation, negligible vapor pressure, recyclability, and solvation capability.11A product yield over 92.1% has been achieved on the basis of 1-methylimidazole along with ZnCl2 as the synergistic catalyst.12 In 2012, Zhang employed 1-ethyl-3-methyl imidazolium bromine [EMImBr] loaded on chitosan (CS) as the catalyst leading to a product yield as high as 96%.13 In another study, the reaction conditions were greatly optimised with [BMIm]Br (1-butyl-3-methylimidazolium bromine salt) as the catalyst along with ZnCl2.14 Compared to a system with a co-catalyst or heterogeneous catalysis, the catalytic performance of a single IL is still not satisfactory. Although a series of imidazolium ILs have been used as the catalyst as early as 2001,15 studies on single IL catalysts without a co-catalyst and organic solvent are still scarce. On the basis of theoretical study,16–18 three basic steps are included in the title reaction: ring-opening of PO, CO2 insertion, and ring closure, resulting in PC and generation of the catalyst again. Among them, the ring-opening of PO is the rate-determining step, which is promoted by both electrophilic attack from the active hydrogen atom in the cation and nucleophilic attack from the anion. Inspired by this, some task-functionalized ILs, hydroxyl-functionalized imidazolium ILs, hydroxyl-functionalized ammonium,19 and carboxylic acid-functionalized imidazolium ILs,20 have been developed with better catalytic activity compared to the corresponding room temperature ILs with the same cation. This is attributed to the fact that they have a more active hydrogen atom.
According to the same analysis, ILs with better catalytic activity can be developed by combination of a suitable cation and anion. How to select a suitable cation and anion is still a perplexing problem. Currently, the development of a new catalyst basically depends on experimental trial and error, which is time-consuming and expensive. Designing ILs with desired properties from the molecular level has not been accomplished. Since the involvement of an active hydrogen atom is helpful to improve the electrophilic attack, it is easy to infer that the performance of protic ILs is better than that of inert ILs. However, less attention has been focused on protic ILs. Moreover, imidazolium ILs have better catalytic activity than other ILs, which is attributed to the distinct five-membered ring structure. As a structural isomer of imidazolium, pyrazolium ILs would also have similar properties. However, no pyrazolium ILs have been applied as a catalyst for the coupling reaction of CO2. Perhaps pyrazolium ILs, especially protic pyrazolium ILs, have a better catalytic performance than imidazolium ILs.
In this work, three protic pyrazolium ILs, 1,3,5-trimethylpyrazolium bromide (HTMPzBr), 1,3-dimethylpyrazolium bromide (HMM3PzBr), and 1,5-dimethylpyrazolium bromide (HMM5PzBr) (Fig. 1, schematic structures of the three designed protic pyrazolium ILs with the key atoms labelled), are firstly designed. Next, their catalytic activity for the fixation of CO2 is explored by both quantum chemistry and molecular dynamics (MD) methods. To ensure the reliability of the theoretical predication, the catalytic activity and mechanism are studied using not only the Single-IL model but also the Double-IL model. Finally, the designed protic pyrazolium ILs are synthesized in experiment and are employed to catalyze the reaction of PO with CO2. Recently, Wang21 successfully predicted the performance of protic 1,8-diazabicyclo[5.4.0]undec-7-ene benzimidazole [HDBU][BenIm] by means of density functional theory (DFT) calculation. This theoretical assumption has been verified by the consequent experimental result. Inspired by this, it is reasonable to believe that the theoretical result could provide helpful guidance for the development of new ILs. We expect that this work would open an express pathway to explore new ILs from the molecular level and finally to realize the efficient fixation of CO2.
2. Results and discussion
2.1. Single-IL model
According to experiences from our work and previous literature,17,22 the ring-opening of PO is the rate-determining step in the whole catalytic cycle. Therefore, only the ring-opening step is considered in this work. The ring-opening of PO is promoted by both electrophilic activation from the H atom in the cation and nucleophilic activation from the Br− anion. The H atom with more positive charge would be favorable for enhancing electrophilic activation resulting in a more reactive substrate. The catalytic activity of the hydroxyl-functionalized imidazolium IL is better than that of the room temperature imidazolium IL, which is attributed to the fact that the H atom from the hydroxyl group has more positive charge.23 On the basis of natural bond orbital (NBO) analysis,24,25 the H1 atom in HTMPzBr has the largest positive charge, and would act as an electrophile to activate the O1 atom of PO. Additionally, hydrogen bonds of N1–H1⋯O1 and C2–H2⋯Br are formed, not only to stabilize the whole system but also to promote the ring-opening of PO. The other two designed protic pyrazolium ILs, HMM3PzBr and HMM5PzBr, have similar ring-opening steps. The corresponding energy profiles are plotted in Fig. 2. The barrier heights decrease in the order of route 3 ([HMM5PzBr] 16.58 kcal mol−1) > route 1 ([HTMPzBr] 15.61 kcal mol−1) > route 2 ([HMM3PzBr] 14.46 kcal mol−1) (Table S1†), indicating that the catalytic activity of HMM3PzBr is the best. The predicted sequence by the Single-IL model is not one hundred percent credible since the interaction between ILs is neglected, and this has been determined to be an important aspect affecting the catalytic activity.26 The Single-IL model has failed to predict the catalytic activity for a series of hydroxyl-functionalized quaternary ammonium ILs.27 To ensure reliability, the above-mentioned transition states are further studied using the Double-IL model.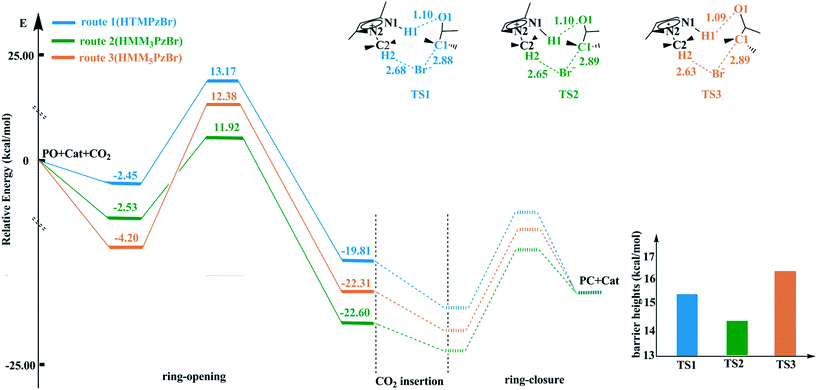 | ||
| Fig. 2 Potential energy profiles and schematic structures of the transition states for the ring-opening step along routes 1–3 calculated at the M06/6-311+G(2d,2p) (PCM)//B3PW91/6-31G(d,p) level. | ||
2.2. Double-IL model
When two HTMPzBr molecules are involved as a catalyst, it is easy to speculate that both of them are utilized to activate PO to enhance the electrophilic activation. To clearly distinguish the two HTMPzBr molecules, they are named as HTMPzBr-1 and HTMPzBr-2, respectively. In TS4 (route 4, Fig. S1†), both the H1 atom from HTMPzBr-1 and H2 atom from HTMPzBr-2 activate the O1 atom and the Br1− anion activates the C1 atom leading to ring-opening of PO with a barrier height of 19.09 kcal mol−1 (Table S2†). After that, the C1–O bond of PO is broken along with the H1 atom transferring from the N1 to O1 atom. Two hydrogen bonds, C3–H3⋯Br2 and C4–H4⋯Br2, are formed in TS4 to stabilize the Br2− anion. Alternatively, the Br2− anion is stabilized by H4 and H6 atoms to form hydrogen bonds, C4–H4⋯Br2 and C6–H6⋯Br2 in TS5 (route 5). The corresponding barrier height is 22.81 kcal mol−1. The schematic structures of TS4 and TS5 are plotted in Fig. S1† with the associated key atoms labelled. In TS4 and TS5, two hydrogen atoms act as the electrophilic reagent to activate PO, which should be better compared to activation by one hydrogen atom. However, the barrier heights of TS4 and TS5 are even higher than that of TS1 catalyzed by only one HTMPzBr molecule. One hand, the steric bulk is large if two HTMPzBr molecules are utilized to activate PO simultaneously. On the other hand, no hydrogen atom is used to stabilize the Br1− anion in TS4 and TS5, which is not favorable for stabilizing the whole system.To decrease the steric bulk and to stabilize the Br1− anion, the other situation is considered, i.e. HTMPzBr-1 plays a major role to directly activate PO and HTMPzBr-2 plays a minor role to stabilize the Br1− anion. The H1 atom from HTMPzBr-1 activates the O1 atom of PO and the Br1− anion activates the C1 atom of PO to form TS17 (HTMPzBr, route 17) with a barrier height of 8.47 kcal mol−1 (Table S2†). The H4 atom and H7 atom are employed to stabilize the Br1− anion to form hydrogen bonds, C4–H4⋯Br1 and C7–H7⋯Br1, and both the H2 atom and H3 atom are employed to stabilize the Br2− anion to form hydrogen bonds, C3–H3⋯Br2 and N2–H2⋯Br2. The latter two hydrogen bonds are kept and the former hydrogen bonds are formed between the H5 atom (H8 atom) and Br1− anion on the other side of HTMPzBr-2. As a result, TS16 (route 16) is formed with a barrier height of 15.92 kcal mol−1 (Table S2†). The only difference between TS17 and TS16 is that different hydrogen atoms are employed to stabilize the Br1− anion. However, their barrier heights deviate by as much as 7.45 kcal mol−1 indicating that the formation of hydrogen bonds is an important aspect to determine the barrier height. Other routes are designed according to the different hydrogen bonds formed between different H atoms and Br− anions (including the Br1− and Br2− anions). The schematic structures of the transition states for the ring-opening step of routes 4–17 are plotted in Fig. S1.† The corresponding barrier heights are tabulated in Table S2.† Among all studied routes, route 17 is the most favorable with the lowest barrier height.
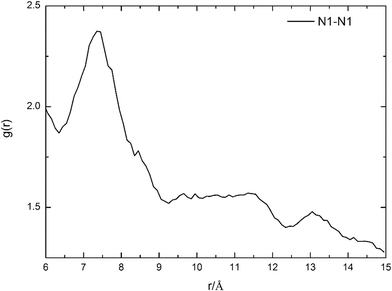
To further confirm the accuracy of route 17, the most feasible distance between two HTMPzBr ion pairs is evaluated by MD simulations. The distance between two protonated nitrogen atoms in two HTMPzBr ion pairs is analyzed by site–site radial distribution functions (RDFs), which are plotted in Fig. 3. The first peak is located at 7.4 Å, which is the most feasible distance between two protonated nitrogen atoms in two neighboring HTMPzBr ion pairs. The calculated distance between two protonated nitrogen atoms in TS17 is 6.4 Å, which is in good accordance with the distance determined by MD simulation. It is also confirmed that the most favorable model is reliable.
On the basis of the same pattern, the transition states for the ring-opening step are located for routes 18 and 19 catalyzed by HMM3PzBr and HMM5PzBr, respectively. The corresponding energy profiles are plotted in Fig. 4. The barrier heights decrease in the sequence of route 18 (HMM3PzBr, 10.60 kcal mol−1) → route 17 (HTMPzBr, 8.47 kcal mol−1) → route 19 (HMM5PzBr, 7.84 kcal mol−1). The difference in catalytic activity between route 17 and route 19 should be small because of their similar barrier height. In contrast, the difference between route 18 and route 17 is much larger. All three transition states have the same electrophile and the same hydrogen bonds to stabilize the Br1− and Br2− anions. However, the presence of a methyl group in the C5 position shortens the distance between H7 and the Br1− anion. As a result, a stronger hydrogen bond, C7–H7⋯Br1, is formed in TS17 and TS19, which is a vital aspect to lower the barrier heights. In contrast, the hydrogen bond C5–H7⋯Br1 in TS18 is weaker since the methyl group in the C5 position is replaced by a hydrogen atom, leading to a longer distance between the H7 atom and Br1− anion (2.96 Å). Consequently, the catalytic activity of HMM5PzBr is the best, and that of HMM3PzBr is the worst. The catalytic activity predicted by the Single-IL and Double-IL models is different. From experience, the result predicted by the Double-IL model is more reliable since more interactions are considered. The weak interactions, especially hydrogen bonds, play a critical role in determining the final catalytic activity, and so it is necessary to further explore them carefully before the final experimental synthesis.
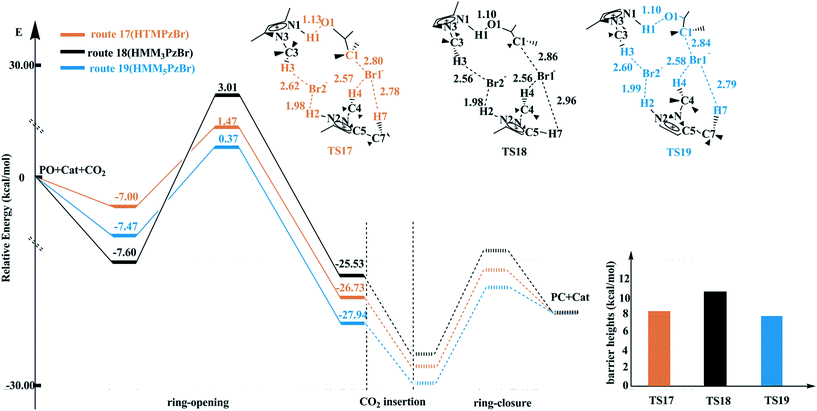 | ||
| Fig. 4 Potential energy profiles and schematic structures of the transition states for the ring-opening step along routes 17–19 calculated at the M06/6-311+G(2d,2p) (PCM)//B3PW91/6-31G(d,p) level. | ||
2.3. Reactivity analysis
To cast light onto the role non-covalent interactions (NCI) play in the reaction, TS17 (HTMPzBr), TS18 (HMM3PzBr), and TS19 (HMM5PzBr) are analyzed by means of NCI developed by Yang's group.28 The NCI index is based on a 2D plot of s versus sign(λ2)ρ, where λ2 is the second derivative of electronic density in the perpendicular direction of the bond and s is defined as follows:29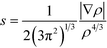 | (1) |
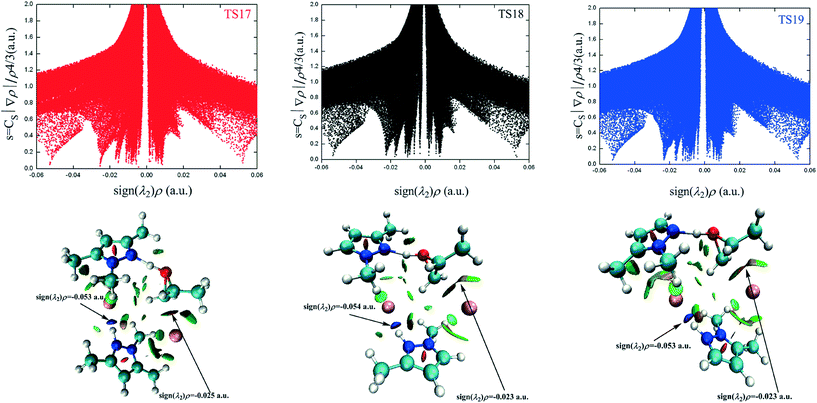
The different types of NCI are distinguished by the sign of the λ2 eigenvalue. The bonding interactions, non-bonding interactions, and van der Waals interactions correspond to the negative, positive, and around zero λ2 value, respectively. The NCI plots of TS17, TS18, and TS19 are presented in Fig. 5 and the corresponding 3D plots are displayed below. The surfaces are colored on a continuous blue-green-red scale according to the values of sign(λ2)ρ ranging from −0.06 to 0.06 a.u. Strong attractive interactions are shown in blue; more dispersive attractive interactions are shown in green; and strong repulsive interactions are shown in red. There are two prominent sign(λ2)ρ values in the negative region for TS17, which correspond to N2–H2⋯Br2 (−0.05286 a.u.) interaction and C1–Br1 (−0.02547 a.u.) interaction, respectively. The N2–H2⋯Br2 interaction is even stronger than the C1–Br1 interaction. However, the former is far away from the reaction center. Therefore, its contribution to the ring-opening is neglected in the following discussion. The NCI plots of the other two transition states present similar features. The difference between the three transition states is that there are some green-colored regions between the H7 atom and Br1− anion in TS17 and TS19, which corresponds to the hydrogen bonds of C7–H7⋯Br1 (TS17) and C7–H7⋯Br1 (TS19), respectively. However, the green-colored regions almost disappear in TS18 indicating that the hydrogen bond C5–H7⋯Br1 is weak. The C–Br interaction of TS17 is the strongest, which is in contrast to the above-determined catalytic activity. Besides the nucleophilic activation from the anion, the electrophilic activation from the cation is the other vital impetus to promote the ring-opening of PO. However, the presence of the electrophilic interaction is not conclusive in the NCI plot.
The atoms in molecule (AIM) analysis30 is further studied to gain more insight into the nature of weak interactions, especially the electrophilic activation from the H1 atom in the three protic pyrazolium ILs. The Laplacian value of the electron density, ∇2ρ (the fifth column in Table 1), is used to characterize the nature of bonds, in which a negative ∇2ρ value refers to a covalent bond and a positive ∇2ρ value refers to an ionic bond, hydrogen bond, or van der Waals interaction. The negative values of ∇2ρ verify the formation of a covalent bond between H1 and O1, i.e. the H1 atom has transferred from N1 to O1. Furthermore, the covalent nature of the interaction between the H1 and O1 atoms could be confirmed by the ratio of G/|V|. G and V are defined by the following relationships:31
| (1/4)∇2ρ = 2G + V | (2) |
| H = G + V | (3) |
| Transition state | X–Y⋯Z | Sign(λ2)ρ | ρ | ∇ 2 ρ | G | V | H | G/|V| |
|---|---|---|---|---|---|---|---|---|
| TS17 | N1–H1⋯O1 | −0.21316 | 0.21316 | −0.73977 | 0.08886 | −0.36267 | −0.27380 | 0.245 |
| C1⋯Br1 | −0.02547 | 0.02547 | 0.06064 | 0.01476 | −0.01436 | 0.00040 | 1.028 | |
| N–C–H4⋯Br1 | −0.01689 | 0.01689 | 0.04361 | 0.01023 | −0.00956 | 0.00067 | 1.070 | |
| C7–H7⋯Br1 | −0.01130 | 0.01130 | 0.03067 | 0.00669 | −0.00571 | 0.00098 | 1.171 | |
| TS18 | N1–H1⋯O1 | −0.23161 | 0.23161 | −0.90118 | 0.08568 | −0.39666 | −0.31098 | 0.216 |
| C1⋯Br1 | −0.02279 | 0.02279 | 0.05696 | 0.01343 | −0.01261 | 0.00082 | 1.065 | |
| N–C–H4⋯Br1 | −0.01756 | 0.01756 | 0.04459 | 0.01054 | −0.00993 | 0.00061 | 1.061 | |
| H7⋯Br1 | −0.01023 | 0.01023 | 0.03244 | 0.00648 | −0.00484 | 0.00163 | 1.337 | |
| TS19 | N1–H1⋯O1 | −0.23268 | 0.23268 | −0.90251 | 0.08658 | −0.39878 | −0.31220 | 0.217 |
| C1⋯Br1 | −0.02336 | 0.02336 | 0.05826 | 0.01383 | −0.01309 | 0.00074 | 1.056 | |
| N–C–H4⋯Br1 | −0.01682 | 0.01682 | 0.04380 | 0.01024 | −0.00953 | 0.00071 | 1.074 | |
| C7–H7⋯Br1 | −0.01115 | 0.01115 | 0.03051 | 0.00663 | −0.00562 | 0.00100 | 1.178 |
2.4. Experimental catalytic activity
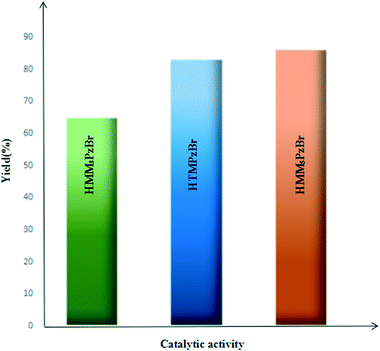
For the studied three protic pyrazolium ILs, the coupling reaction of PO and CO2 to form PC is carried out under identical reaction conditions (catalyst loading 1 mol%, CO2 pressure 1.5 MPa, 130 °C, 4.0 h) and the corresponding results are summarized in Fig. 6. The catalytic activity is influenced by the different substitution position. Taking the catalytic activity of HTMPzBr as the standard, HMM5PzBr is more active with a yield of 86.2%. However, HMM3PzBr is the least active with the lowest yield (65%) of all three studied ILs. The experimentally measured sequence is solidly consistent with the theoretical study. The substituted methyl in the C5 position is a vital aspect to determine the final activity for HTMPzBr, HMM3PzBr, and HMM5PzBr. Although the substituted methyl in the C5 position does not directly activate PO, it is helpful to stabilize the Br− anion by formation of a hydrogen bond, which is also favorable for promoting the ring-opening of PO. If the methyl in the C5 position is replaced by a hydrogen atom, the catalytic activity decreases greatly. The small difference in activity between HMM5PzBr and HTMPzBr is attributed to the larger steric hindrance of the latter.Due to the experiment equipment limitations, the yield of PC is obtained by a weighing method rather than gas chromatography (GC). Additionally, a small amount of PC is retained on the inner wall of the stainless steel reactor. Correspondingly, the product yield is reduced. Therefore the yield obtained by a weighing method is lower than that obtained by GC even if the reaction is carried out under the same conditions. Although the absolute yield could not be compared with that measured by GC, the relative sequence is still reliable under the same experimental conditions.
Compared with the common ILs reported in the literature,19,32–35 the new developed protic pyrazolium ILs have two distinct advantages. One is that the synthetic condition is easy to achieve. The other one is that the catalytic activity is comparable with that of other reported ILs. Three new designed protic pyrazolium ILs are synthesized at 40 °C in a yield above 96%. The lower reaction temperature is also beneficial for suppressing the occurrence of side reactions and appearance of by-products. Moreover, the cheap raw materials along with the simple and easy separation and purification of the product are another two advantages of the new designed protic pyrazolium ILs. The reaction conditions for synthesizing some ionic liquids are listed in Table S3.† Both a higher reaction temperature and longer reaction time are required to synthesize imidazolium ILs. Higher temperatures along with harsher reaction conditions are required for the synthesis of other ILs, especially for quaternary ammonium ILs. The product yield and reaction conditions for the coupling reaction catalyzed by the aforementioned ILs are listed in Table S4.† Although the product yield of PC catalyzed by 1,5-dimethylpyrazolium bromide (HMM5PzBr) is comparable with that of 1-ethylimidazolium bromide (HEimBr), the required reaction temperature for the former is higher than that for the latter. Thus, it is difficult to determine whether the catalytic activity of HMM5PzBr is better than that of the latter. However, the catalytic performance of HMM5PzBr is better than that of 1-ethyl-3-methylimidazolium bromine (EMImBr) and triethylammonium bromide (HTeaBr). When the reaction temperature is further increased, the product yields with EMImBr and HTeaBr as catalysts would be correspondingly improved. However, it is difficult to reach 86.2%.
3. Conclusions
Three protic pyrazolium ILs have been designed and synthesized in this study. Moreover, their catalytic activity in the coupling reaction of CO2 and PO is explored. The mechanism is investigated by both the Single-IL and Double-IL models. Only the catalytic activity predicted by the Double-IL model is consistent with the experimental measurement. The Double-IL model is more reliable for predicting both the mechanism and activity. With a combination of NCI and AIM analysis, it is discovered that the electrophilic activation plays a more important role in promoting the ring-opening step as compared with the nucleophilic activation. Both the theoretical and experimental studies indicate that methyl substituted in the C5 position is beneficial for improving the catalytic activity. In contrast, methyl substituted in the C3 position has a negligible influence on the activity. As a result, the catalytic activity of HMM5PzBr and HTMPzBr is similar, and is much higher than that of HMM3PzBr.4. Computational details
4.1. Quantum chemistry
The geometric parameters of all stationary points were obtained by Becke's three-parameter exact exchange functional combined with the Perdew and Wang (B3PW91)36,37 method with the 6-31G(d,p) basis set.38 Starting from the transition state, the minimum energy path (MEP) was constructed by the intrinsic reaction coordinate (IRC) method39 to confirm that two desired minima were connected with the transition state. On the basis of the optimized structures, the energy profiles were further refined at the M06/6-311+G(2d,2p) level40 associated with the polarized continuum model (PCM) in ethyl ether (Et2O) solvent.41,42 The above-mentioned electronic calculations were performed by the Gaussian 09 program.434.2 Molecular dynamics simulations
All MD simulations were carried out using the GROMACS 5.1.2 software package.44 Detailed information about the ionic liquids has been obtained from the aforementioned calculation, including bond lengths, angles, and other information. A cubic box with a size of 5 × 5 × 5 nm was built. The number of ILs in the cubic box was set to 256, which would be put into the cubic box. The initial configurations of the molecules in the simulation box were obtained by means of PACKMOL.45 All atoms belonging to different molecules were required to keep safe pair-wise distances. Each ionic pair is considered as a single unit in the calculation.After the initial box was generated, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 energy minimization steps were performed using the steepest descent method and then allowed to equilibrate for 2 ns. The periodic boundary condition (PBC) was applied to all three dimensions of a cubic simulation box, and a 1.5 nm cut-off was applied to the non-bonding interactions. The long-range electrostatic interactions were handled with the particle mesh Ewald (PME) method associated with long-range dispersion corrections.46 These MD trajectories ran under the isothermal and isobaric ensemble at T = 298 K and P = 0.1 MPa, where the V-rescale thermostat and Parrinello–Rahman barostat were used with relaxation constants of 1.0 and 4.0 ps, respectively. The molecule was described by the General Amber Force Field (GAFF).47 Next, the system was heated temporarily up to 700 K for 1000 ps, and then the temperature was gradually lowered to 298 K to ensure ion mobility. Finally, the production simulations were carried out for 5 ns, using a time-step of 2 fs and saving a configuration every 500 time-steps.
000 energy minimization steps were performed using the steepest descent method and then allowed to equilibrate for 2 ns. The periodic boundary condition (PBC) was applied to all three dimensions of a cubic simulation box, and a 1.5 nm cut-off was applied to the non-bonding interactions. The long-range electrostatic interactions were handled with the particle mesh Ewald (PME) method associated with long-range dispersion corrections.46 These MD trajectories ran under the isothermal and isobaric ensemble at T = 298 K and P = 0.1 MPa, where the V-rescale thermostat and Parrinello–Rahman barostat were used with relaxation constants of 1.0 and 4.0 ps, respectively. The molecule was described by the General Amber Force Field (GAFF).47 Next, the system was heated temporarily up to 700 K for 1000 ps, and then the temperature was gradually lowered to 298 K to ensure ion mobility. Finally, the production simulations were carried out for 5 ns, using a time-step of 2 fs and saving a configuration every 500 time-steps.
5. Experimental section
5.1. General information
The pyrazoles were purchased from Shanghai Macklin Biochemical Co. Ltd. PO and other organic compounds were purchased from Sinopharm Chemical Reagent Co. Ltd. CO2 (99.9%) was produced by Kaifeng Xinri Gas Co. Ltd. All of them were used directly without further purification.1H NMR (400 MHz) and 13C NMR (100 MHz) spectroscopy was performed on a Bruker AVANCE III HD 400 MHz spectrometer in D2O or DMSO-d6 with TMS as the internal standard. The 1H and 13C NMR chemical shifts (δ) are given in ppm relative to TMS. 1H and 13C positive chemical shifts (δ) in ppm were downfield from TMS (DMSO-d6: δC – 39.6 ppm; residual DMSO in DMSO-d6: δH – 2.5 ppm). MS (ESI) spectra were measured using an amaZon SL spectrometer.
5.2. Preparation and characterization of protic pyrazolium ILs
On the basis of previous literature,48 HTMPzBr was prepared by the following method (Scheme 1): HBr (3.102 g, 18 mmol) was added dropwise to 1,3,5-trimethylpyrazole (1.65 g, 15 mmol), and the mixture was stirred for 15 h at 40 °C to ensure that all of the base reacted to obtain a high yield (>90%). Then, water was removed by cyclohexane under heating conditions. Finally, the residue was washed repeatedly with ethyl acetate and dried in a vacuum to obtain HTMPzBr.A series of other protic pyrazolium ILs, such as HMM3PzBr and HMM5PzBr, were synthesized by a similar procedure to that used for HTMPzBr.
The structures of the protic pyrazolium ILs were determined by NMR and MS (ESI). The data from NMR and MS (ESI) are provided as follows:
HMM3PzBr: 1H NMR (400 MHz, DMSO-d6) δ (ppm): 7.83 (d, 1H), 6.22 (d, J = 2.6 Hz, 1H), 3.85 (s, J = 2.0 Hz, 3H), 2.23 (s, 3H). 13C NMR (100 MHz, D2O) δ (ppm): 146.04, 136.48, 107.18, 37.31, 10.26. MS (ESI): m/z 97.50 [M–Br]+.
HMM5PzBr: 1H NMR (400 MHz, DMSO-d6) δ (ppm): 7.47 (d, 1H), 6.14 (d, J = 1.9 Hz, 1H), 3.75 (d, J = 2.1 Hz, 3H), 2.27 (d, J = 2.6 Hz, 3H). 13C NMR (100 MHz, D2O) δ (ppm): 146.08, 132.88, 107.70, 34.86, 10.19. MS (ESI): m/z 97.51 [M–Br]+.
HTMPzBr: 1H NMR (400 MHz, DMSO-d6) δ (ppm): 6.27 (s, J = 3.9 Hz, 1H), 3.82 (s, J = 1.9 Hz, 3H), 2.31 (s, 3H), 2.27 (s, 3H). 13C NMR (100 MHz, D2O) δ (ppm): 144.36, 137.55, 106.94, 35.53, 12.33, 10.95. MS (ESI): m/z 111.09 [M–Br]+.
5.3. Procedure for the synthesis of PC
The synthesis of PC through the cycloaddition of CO2 and PO was chosen as a model reaction to evaluate the catalytic activity of protic pyrazolium ILs. In a typical experiment (Scheme 2), PO (5.0 mL, 71.5 mmol) and IL (0.71 mmol) were loaded in a 100 mL stainless steel reactor with a magnetic stirrer and heating equipment. The reactor was placed under a desired pressure of CO2 and heated to 130 °C for 4.0 h. Then the reactor was cooled to ambient temperature and the resulting mixtures were transferred to a 50 mL round-bottom flask. By distillation under vacuum, the product PC was obtained. The purified product was identified by NMR.Spectral characteristics of PC: 1H NMR (400 MHz, CDCl3) δ (ppm): 4.89 (m, 1H), 4.59 (d, J = 8.4 Hz, 1H), 4.05 (d, J = 8.4 Hz, 1H), 1.50 (d, J = 6.3 Hz, 3H). 13C NMR (100 MHz, CDCl3) δ (ppm): 155.15, 73.76, 70.67, 19.03.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Supercomputing Center in Shenzhen (Shenzhen Cloud Computing Center) for providing computational resources and software. This work was supported by the National Natural Science Foundation of China (21376063, 21476061, 21503069, and 21676071) and the Program for the Henan Innovative Research Team at the university (15IRTSTHN005).References
- R. Barker, Y. Hua and A. Neville, Int. Mater. Rev., 2017, 62, 1–31 CrossRef CAS.
- S. Chu, Y. Cui and N. Liu, Nat. Mater., 2017, 16, 16–22 CrossRef PubMed.
- Y. H. Li, X. J. Cui, K. W. Dong, K. Junge and M. Beller, ACS Catal., 2017, 7, 1077–1086 CrossRef CAS.
- R. Martin and A. W. Kleij, ChemSusChem, 2011, 4, 1259–1263 CrossRef CAS PubMed.
- A. W. Kleij, M. North and A. Urakawa, ChemSusChem, 2017, 10, 1–4 CrossRef.
- D. F. Monica, A. Buonerba, A. Grassi, C. Capacchione and S. Milione, ChemSusChem, 2016, 9, 3457–3464 CrossRef PubMed.
- P. Gautam, P. Kathe and B. M. Bhanage, Green Chem., 2017, 19, 823–830 RSC.
- D. W. Tian, B. Y. Liu, Q. Y. Gan, H. R. Li and D. J. Darensbourg, ACS Catal., 2012, 2, 2029–2035 CrossRef CAS.
- L. P. Guo, C. M. Wang, X. Y. Luo, G. K. Cui and H. R. Li, Chem. Commun., 2010, 46, 5960–5962 RSC.
- A. Decortes, R. M. Haak, C. Martín, M. M. Belmonte, E. Martin, J. Benet-Buchholz and A. W. Kleij, Macromolecules, 2015, 48, 8197–8207 CrossRef CAS.
- G. K. Cui, J. J. Wang and S. J. Zhang, Chem. Soc. Rev., 2016, 45, 4307–4339 RSC.
- D. Kim, Y. Moon, D. Ji, H. Kim and D. Cho, ACS Sustainable Chem. Eng., 2016, 4, 4591–4600 CrossRef CAS.
- J. Sun, J. Q. Wang, W. G. Cheng, J. X. Zhang, X. H. Li, S. J. Zhang and Y. B. She, Green Chem., 2012, 14, 654–660 RSC.
- F. W. Li, L. F. Xiao, C. G. Xia and B. Hu, Tetrahedron Lett., 2004, 49, 8307–8310 CrossRef.
- J. J. Peng and Y. Q. Deng, New J. Chem., 2001, 25, 639–641 RSC.
- L. Wang, P. Li, Y. Li, H. Q. He and J. L. Zhang, Theor. Chem. Acc., 2015, 134, 75 CrossRef.
- L. Wang, P. Li, X. F. Jin, J. L. Zhang, H. Y. He and S. J. Zhang, J. CO2 Util., 2015, 10, 113–119 CrossRef CAS.
- D. H. Lan, N. Fan, Y. Wang, X. Gao, P. Zhang, L. Chen, C. T. Au and S. F. Yin, Chin. J. Catal., 2016, 37, 826–845 CrossRef CAS.
- J. Sun, S. J. Zhang, W. G. Cheng and J. Y. Ren, Tetrahedron Lett., 2008, 49, 3588–3591 CrossRef CAS.
- Z. F. Fei, D. B. Zhao, T. J. Geldbach, R. Scopelliti and P. J. Dyson, Chem. – Eur. J., 2004, 10, 4886–4893 CrossRef CAS PubMed.
- K. H. Chen, G. L. Shi, W. D. Zhang, H. R. Li and C. M. Wang, J. Am. Chem. Soc., 2016, 138, 14198–14201 CrossRef CAS PubMed.
- S. Foltran, R. Mereau and T. Tassaing, Catal. Sci. Technol., 2014, 4, 1585–1597 CAS.
- L. Wang, X. F. Jin, P. Li, J. L. Zhang, H. Y. He and S. J. Zhang, Ind. Eng. Chem. Res., 2014, 53, 8426–8435 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. J. Weinhold, Chem. Phys., 1985, 83, 735–746 CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- C. Chen, Y. Ma, D. N. Zheng, L. Wang, J. F. Li, J. L. Zhang, H. Y. He and S. J. Zhang, J. CO2 Util., 2017, 18, 156–163 CrossRef CAS.
- H. Q. Yang, X. Wang, Y. Ma, L. Wang and J. L. Zhang, Catal. Sci. Technol., 2016, 6, 7773–7782 CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- R. F. W. Bader, Atoms in molecules, John Wiley & Sons, Ltd, 1990 Search PubMed.
- C. Q. Yuan, H. M. Wu, M. Y. Jia, P. F. Su, Z. X. Luo and J. N. Yao, Phys. Chem. Chem. Phys., 2016, 18, 29249–29257 RSC.
- J. S. Wilkes, J. A. Levisky, R. A. Wilson and C. L. Hussey, Inorg. Chem. Commun., 1982, 21, 1263–1264 CrossRef CAS.
- L. F. Xiao, D. Su, C. T. Yue and W. Wu, J. CO2 Util., 2014, 6, 1–6 CrossRef CAS.
- R. E. Buckles and L. Harris, J. Am. Chem. Soc., 1957, 79, 886–889 CrossRef CAS.
- W. G. Cheng, B. Xiao, J. Sun, K. Dong, P. Zhang, S. J. Zhang and F. T. T. Ng, Tetrahedron Lett., 2015, 56, 1416–1419 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
- P. M. W. Gill, B. G. Johnson, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1992, 197, 499–505 CrossRef CAS.
- K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- S. Miertus and J. Tomasi, Chem. Phys., 1982, 65, 239–245 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- J. M. Wang, R. M. Wolf, J. W. Caldwel, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. Chiappe, S. Rajamani and F. D'Andrea, Green Chem., 2013, 15, 137–143 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7me00068e |
| This journal is © The Royal Society of Chemistry 2018 |