Open Access Article
Open Access ArticleEnhanced ion transport using geometrically structured charge selective interfaces†
Anne M.
Benneker
 a,
Burcu
Gumuscu‡
b,
Ernest G. H.
Derckx
a,
Rob G. H.
Lammertink
a,
Burcu
Gumuscu‡
b,
Ernest G. H.
Derckx
a,
Rob G. H.
Lammertink
 a,
Jan C. T.
Eijkel
b and
Jeffery A.
Wood
a,
Jan C. T.
Eijkel
b and
Jeffery A.
Wood
 *a
*a
aSoft Matter, Fluidics and Interfaces, MESA+ Institute for Nanotechnology, University of Twente, The Netherlands. E-mail: j.a.wood@utwente.nl
bBIOS Lab-on-a-Chip Group, MESA+ Institute for Nanotechnology, MIRA institute for Biomedical Technology and Technical Medicine, University of Twente, The Netherlands
First published on 17th May 2018
Abstract
A microfluidic platform containing charged hydrogels is used to investigate the effect of geometry on charge transport in electrodialysis applications. The influence of heterogeneity on ion transport is determined by electrical characterization and fluorescence microscopy of three different hydrogel geometries. We found that electroosmotic transport of ions towards the hydrogel is enhanced in heterogeneous geometries, as a result of the inhomogeneous electric field in these systems. This yields higher ionic currents for equal applied potentials when compared to homogeneous geometries. The contribution of electroosmotic transport is present in all current regimes, including the Ohmic regime. We also found that the onset of the overlimiting current occurs at lower potentials due to the increased heterogeneity in hydrogel shape, owing to the non-uniform electric field distribution in these systems. Pinning of ion depletion and enrichment zones is observed in the heterogeneous hydrogel systems, due to electroosmotic flows and electrokinetic instabilities. Our platform is highly versatile for the rapid investigation of the effects of membrane topology on general electrodialysis characteristics, including the formation of ion depletion zones on the micro-scale and the onset of the overlimiting current.
1 Introduction
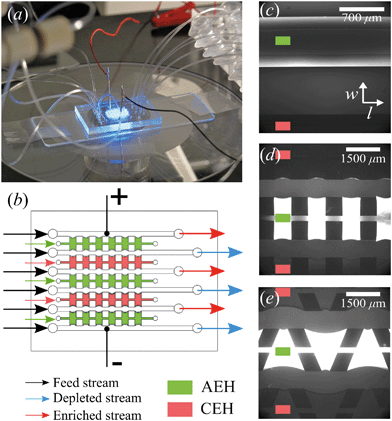
Electrodialysis (ED) is an established technique in water deionization, using a stack of alternating anion and cation selective membranes.1 Under the application of an electrical potential, ions migrate towards their counter electrode and are selectively blocked by cation and anion exchange membranes (CEM/AEM), resulting in the formation of desalinated and concentrated streams. Ion transport towards the membrane often limits the currents at which these processes are being operated in industry. At increasing field strengths diffusional transport becomes limiting, causing concentration polarization. The current reaches a limiting value, which reduces the efficiency of the process and prohibits economic operation. At elevated field strengths, the well-known overlimiting current regime arises as a result of induced electrokinetic flows at the membrane interface.2–4 In this overlimiting current regime, current starts increasing again because the concentration polarization layer is broken down by the convective movement of the fluid.Ions migrate along the electric field lines because of their charge. In systems with a homogeneous charge selective interface, electric field lines are homogeneously distributed as well. In systems with local conductivity or permselectivity gradients an inhomogeneous field arises. This can happen due to heterogeneous charge selective interfaces, for example patterned5,6 or structured7 membranes. Since a driving force for ion transport tangential to the membrane arises, the distorted electric field gives rise to the formation of electroosmotic flows (EOF) at the charged walls of the system, starting from the Ohmic regime. In the overlimiting current regime, this tangential component acts on the emerging extended space charge and enhances the formation of electrokinetic instabilities (EKI).8 The increased rate of ion transport can potentially yield a higher overall efficiency in ED processes in the Ohmic regime or reduce the limiting current plateau region by reducing the onset voltage for the overlimiting current regime. The influence of membrane geometry on the efficiency of ED systems has been of interest for several studies9,10 with the purpose of yielding more energy-efficient processes. Most of these studies have focused on the macro-scale effects of membrane topology on ED performance parameters, such as resistance and the onset of the limiting and overlimiting current regime in large scale systems.11,12 For fundamental understanding of the influence of membrane geometry on charge transport, visualization of the ion concentration profiles adjacent to the membrane is crucial.13,14 Pinning of ion depletion zones and vortices at heterogeneities on the membrane has been experimentally observed15 and numerically studied.16 Microfluidic platforms enable optical access to the membrane surface and can be manipulated easily for the investigation of several aspects of charge transport adjacent to a charge selective surface.17–25
We have previously reported a microfluidic platform using charge selective hydrogels for the microscopic investigation of ion transport in electrodialysis systems.26 Hydrogels are versatile materials that can easily be patterned with different geometries on the micro-scale. Therefore, hydrogels can be used to build micro-electrodialysis systems for rapid investigation of the influence of geometry on ion transport which can be applied in large scale electrodialysis systems. In our micro-scale electrodialysis system, six adjacent microchannels are separated by alternating anion exchange hydrogels (AEH) and cation exchange hydrogels (CEH). This allows us to microscopically observe concentration profiles and depletion zones adjacent to the hydrogel compartments. The previous work26 was a proof of principle of using patterned and charged hydrogels for microfluidic investigation of ion transport phenomena in electrodialysis. In this work, we investigate the influence of hydrogel geometry on the development of ion depletion zones and the current–voltage characteristics. Fluorescence microscopy and fluorescence lifetime microscopy (FLIM) are used for the visualization of ion concentration profiles. This demonstrates the role of hydrogel geometry on the formation and pinning of depletion zones. These experiments give insight into the interplay of membrane topology and performance. We show that transport of ions through the hydrogel is enhanced with increasing heterogeneity in hydrogel shape, as was predicted based on numerical simulations.16
2 Experimental details
2.1 Microchip fabrication
The microchips consist of a polydimethylsiloxane (PDMS, Dow Corning) layer on a microscope slide (see Fig. 1a). The PDMS layer contains microfluidic channels, capillary barriers, inlets and outlets and was fabricated using standard soft lithography techniques. Microchip designs included three different geometrical shapes: (1) Continuous hydrogel compartments (Fig. 1c) supported with capillary barriers with dimensions of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 × 1720 μm (length, width), which will be referred to as full, homogeneous hydrogels. (2) Pillars (700 μm in length) and five hydrogel compartments with dimensions of 700 × 1720 μm (Fig. 1d), which will be referred to as symmetric or rectangular heterogeneous hydrogels. (3) Five trapezoidal, asymmetric heterogeneous hydrogel compartments (length varying from 300 μm to 1725 μm) generated by PDMS pillars with 600 × 500 μm (length, width) placed with a zigzag pattern at angles of 20° (Fig. 1e). The height of microchannels and capillary barriers was 75 μm and 7.5 μm, respectively, while the width was 700 μm for all geometries. For the heterogeneous geometries, the capillary barriers are curved to ensure the pinning of the hydrogels in their compartments.27 We make use of the curvature in the analysis of our experimental results. To achieve the fabrication of microchannels and capillary barriers of different heights, two SU-8 layers were fabricated on a silicon wafer. The first SU-8 layer contained the pillar layout while the second SU-8 layer contained both capillary barrier and pillar layouts. The silicon wafer with patterned SU-8 structures served as a mold for the following PDMS patterning step.
100 × 1720 μm (length, width), which will be referred to as full, homogeneous hydrogels. (2) Pillars (700 μm in length) and five hydrogel compartments with dimensions of 700 × 1720 μm (Fig. 1d), which will be referred to as symmetric or rectangular heterogeneous hydrogels. (3) Five trapezoidal, asymmetric heterogeneous hydrogel compartments (length varying from 300 μm to 1725 μm) generated by PDMS pillars with 600 × 500 μm (length, width) placed with a zigzag pattern at angles of 20° (Fig. 1e). The height of microchannels and capillary barriers was 75 μm and 7.5 μm, respectively, while the width was 700 μm for all geometries. For the heterogeneous geometries, the capillary barriers are curved to ensure the pinning of the hydrogels in their compartments.27 We make use of the curvature in the analysis of our experimental results. To achieve the fabrication of microchannels and capillary barriers of different heights, two SU-8 layers were fabricated on a silicon wafer. The first SU-8 layer contained the pillar layout while the second SU-8 layer contained both capillary barrier and pillar layouts. The silicon wafer with patterned SU-8 structures served as a mold for the following PDMS patterning step.
The ingredients of a Sylgard 184 silicone elastomer kit were mixed at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (PDMS to curing agent), and the mixture was degassed for at least an hour in a vacuum chamber set to 7 kPa. The degassed solution was transferred onto the silicon wafer molds patterned with SU-8 structures and cured in an oven set at 60 °C for 4 hours. The microchips were cut to size using a blade. The microchannel inlet and outlet were opened using a hole puncher with 0.75 mm diameter. The patterned surface of the cured PDMS layer and a clean microscope slide were then treated with oxygen plasma at 500 mTorr for 45 seconds (Harrick Plasma Cleaner, USA) and assembled immediately after the plasma treatment. Assembled microchips were kept in a dark and dry place for at least a week or placed in an oven at 60 °C overnight before hydrogel patterning process. This step is necessary for the hydrophobic recovery of PDMS after the oxygen plasma treatment, and aids for easier hydrogel patterning.
1 ratio (PDMS to curing agent), and the mixture was degassed for at least an hour in a vacuum chamber set to 7 kPa. The degassed solution was transferred onto the silicon wafer molds patterned with SU-8 structures and cured in an oven set at 60 °C for 4 hours. The microchips were cut to size using a blade. The microchannel inlet and outlet were opened using a hole puncher with 0.75 mm diameter. The patterned surface of the cured PDMS layer and a clean microscope slide were then treated with oxygen plasma at 500 mTorr for 45 seconds (Harrick Plasma Cleaner, USA) and assembled immediately after the plasma treatment. Assembled microchips were kept in a dark and dry place for at least a week or placed in an oven at 60 °C overnight before hydrogel patterning process. This step is necessary for the hydrophobic recovery of PDMS after the oxygen plasma treatment, and aids for easier hydrogel patterning.
Positively and negatively charged hydrogels were prepared in a nitrogen environment by blending 20% v/v of acrylamide/bis (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (BioRad), 15% w/v N,N′-bis(2-hydroxyethyl) ethylenediamine (bis, Sigma-Aldrich), 10% w/v of DMPA (Invitrogen), and 5% w/v of ammonium per sulfate (Invitrogen) solutions. For the AEHs, 1% v/v METC solution (Sigma-Aldrich), and for the CEHs, 1% w/v SPAP salt (Sigma-Aldrich) were added to the acrylamide/bis mixture. Characterization of the hydrogels and their swelling behavior in microchip was reported earlier.26 As the cross-linking reaction is inhibited by oxygen, patterning and polymerization processes were performed in a nitrogen environment. Hydrogel precursors were degassed in a vacuum chamber set at 7 kPa for 15 minutes and used immediately after degassing. There are five hydrogel blocks separating the six parallel microchannels in all geometries, mimicking an electrodialysis stack. Three of these blocks (the outer two and the middle) are filled with the anion exchange hydrogel and the other two are filled with the cation exchange hydrogel using individual inlets and outlets, see Fig. 1b. Hydrogels were patterned in microchips using capillary line pinning to ensure the local confinement of the charged hydrogels between the microchannels. A detailed explanation of hydrogel patterning using capillary pinning was previously reported by Gumuscu et al.27 After hydrogel patterning, the microchip was kept in 0.1 mM NaCl solution. Redistribution of charges inside the hydrogels as a result of an applied potential was considered in the previous work, but no significant deviations from the expected hydrogel behavior were found and therefore the possible influence of this was neglected in the analysis in this work.26
1) (BioRad), 15% w/v N,N′-bis(2-hydroxyethyl) ethylenediamine (bis, Sigma-Aldrich), 10% w/v of DMPA (Invitrogen), and 5% w/v of ammonium per sulfate (Invitrogen) solutions. For the AEHs, 1% v/v METC solution (Sigma-Aldrich), and for the CEHs, 1% w/v SPAP salt (Sigma-Aldrich) were added to the acrylamide/bis mixture. Characterization of the hydrogels and their swelling behavior in microchip was reported earlier.26 As the cross-linking reaction is inhibited by oxygen, patterning and polymerization processes were performed in a nitrogen environment. Hydrogel precursors were degassed in a vacuum chamber set at 7 kPa for 15 minutes and used immediately after degassing. There are five hydrogel blocks separating the six parallel microchannels in all geometries, mimicking an electrodialysis stack. Three of these blocks (the outer two and the middle) are filled with the anion exchange hydrogel and the other two are filled with the cation exchange hydrogel using individual inlets and outlets, see Fig. 1b. Hydrogels were patterned in microchips using capillary line pinning to ensure the local confinement of the charged hydrogels between the microchannels. A detailed explanation of hydrogel patterning using capillary pinning was previously reported by Gumuscu et al.27 After hydrogel patterning, the microchip was kept in 0.1 mM NaCl solution. Redistribution of charges inside the hydrogels as a result of an applied potential was considered in the previous work, but no significant deviations from the expected hydrogel behavior were found and therefore the possible influence of this was neglected in the analysis in this work.26
All microchips consist of six parallel microchannels connected through alternating AEH and CEH, as depicted in Fig. 1b. The liquid flow is supplied to the individual channels using three programmable Harvard Picoplus syringe pumps connected to Tygon flexible plastic tubing (0.01′′ inner diameter) and Braun Omnifix-F 1 mL syringes.
Two gold-coated copper electrodes are placed in the two outside microchannels and electrical characterization of the system is performed using an Autolab PGSTAT204 potentiostat (Metrohm, the Netherlands). To avoid bubble formation at the electrodes and minimize water splitting, the maximum applied potential was limited to 10 V. For the electrical characterization of the system, IV-sweeps are performed with steps of 0.05 V and a scan rate of 0.01 V s−1. In all microchannels a cross flow (with a channel flow rate between 2 and 9 μL min−1) is applied for all IV-sweeps. This yields a linear flow velocity between ∼635 μm s−1 and ∼2900 μm s−1, corresponding to fluid residence times between 10 and 2.2 seconds in the part of the microchip containing charge selective hydrogels. The total residence time in the microchip is ∼three times larger due to in- and outlet sections that do not contain any hydrogel surface. Chronoamperometric (measuring the current as a function of time at a fixed potential) and chronopotentiometric (measuring the potential as a function of time at a fixed current) measurements are done at these flow conditions as well. For visualization experiments, chronoamperometric and chronopotentiometric measurements are conducted while microscopy images are taken, without the application of flow in the microchannels.
2.2 Fluorescence microscopy
All six microchannels were flushed with electrolyte solutions of NaCl. For the fluorescence experiments, solutions with 0.1 mM NaCl were used, containing 5 μM Alexa Fluor 488 Cadaverine (ThermoFisher Scientific) as a fluorescent dye (ex/em 490/525 nm). The Alexa dye is pH insensitive in the range applied (pH 4–10),28 has a negative charge and therefore qualitatively mimics the behavior of negative ions yielding information on the formation of ion depletion zones in the system. Prior to visualization experiments, the electrolyte flow through all microchannels was stopped to enable investigation of ion depletion in a stagnant system, where concentration polarization is maximized. The fluorescent dye was visualized using a Hamamatsu ORCA-Flash4.0 LT camera mounted on an inverted Zeiss Axiovert 40 MAT microscope.2.3 Fluorescence-lifetime imaging microscopy
For quantification of the local ion concentrations as a function of time, fluorescence-lifetime imaging (FLIM) was used. The fluorescence-lifetime of a dye can be dependent on the environmental conditions such as pH, local electric potential or solute concentration,29 however independent on the concentration of the dye. The lifetime of the dye used in our study, lucigenin (ThermoFisher Scientific), is dependent on the local Cl− concentration,30 and we are therefore able to quantify the local ion concentrations inside the microchannels. The lifetime of lucigenin is linearly dependent on the Cl− concentration between 0.2 mM and 1 mM (see ESI† S1 for calibration curve). We used a background electrolyte concentration of 0.5 mM NaCl, enabling quantification in both the concentrated and the diluted microchannels.Fluorescence lifetime was measured using a LI-FLIM system (Lambert Instruments, Groningen, The Netherlands) working in the frequency domain at a modulation frequency of 5 MHz and a phase angle of 30 degrees, equipped with a modulated TRiCAM and a modulated LED of wavelength 460 nm (3 W). The equipment is mounted on a Zeiss Axio Vert.A1 inverted microscope (Zeiss, Gemrany). An identical light path was used in all measurements to ensure the validity of the measurements. The lifetime is calculated based on a reference measurement of the lifetime of lucigenin without a background electrolyte, measured in the same light path configuration.
3 Results and discussion
3.1 Electrical characterization
IV-sweeps were performed using 0.1 mM NaCl at a feed flow rate of 3 μL min−1 in at least two different microchips for all geometries and at least three experimental runs per chip. As seen in Fig. 2a, current is the highest when the trapezoidal heterogeneous hydrogels are used, and lowest for the full homogeneous hydrogels. On chip reproducibility was high (standard deviation <5%), but the reproducibility between different chips was lower, yielding large standard deviations for the IV characteristics observed in Fig. 2a. In the Ohmic regime (up to ∼IV, see inset of Fig. 2a), the highest currents are measured for both heterogeneous hydrogels, even though they have a lower total area. We attribute this to the presence of electroosmotic contributions to the flow (EOF) at even the lowest voltages in heterogeneous systems. This EOF is a result of the tangential component in the electric field, shown in Fig. 3. The positive ions in the solution screen the fixed negative wall charge of the PDMS,31,32 resulting in a positively charged electric double layer (EDL) adjacent to the microchannel walls. The tangential component of the electric field acts on the charged EDL, causing electroosmotic flows towards the location of lower potential. As a result of this no stagnant ion depletion zone forms at the interface, which in turn explains the absence of a clear limiting current regime in our IV-sweeps. Apart from that, in the heterogeneous structures, the depletion zone is not growing into the microchannel to the same extent as at the homogeneous hydrogel. Due to the channel heterogeneity, the depletion zone is discontinuous along the channel wall, breaking down the growth of the depleted area into the channel. Inside the depletion zone, the potential drop is much larger than in the ion rich zones as a result of the lower conductivity. When the depletion zone is larger, this thus requires a larger driving potential to induce the same total current. At moderate voltages, the resistance of the system to charge transport seems to reduce as a when the applied potential is increased (especially for the trapezoidal hydrogels), which is surprising when compared to traditional electrodialysis systems. On average, we do not measure any current rectification33,34 in the trapezoidal hydrogels, as the asymmetry of the hydrogel structures alternation over the different patches, which results in the cancelling out of the potential rectification effect. For future investigations, it is interesting to pattern the asymmetric hydrogels in such a way that current rectification might be enhanced in the system. At higher voltages, the variance in the measurements for the trapezoidal hydrogels is large. We attribute this behavior to transitioning into the overlimiting current regime and the variable onset of this regime between different microchips that were tested. For the trapezoidal hydrogels, the sensitivity of the electrical response is large. In this geometry, more than in the others, the initial contribution of EOF along the channel walls influences the development of the ion depletion zones. The slightest change in configuration is expected to yield a deviation in IV-curve characteristics. This effect is less pronounced for the symmetric heterogeneous and homogeneous hydrogels, as the initial component of the EOF is smaller. The onset for the overlimiting current regime for these geometries is then at a higher voltage.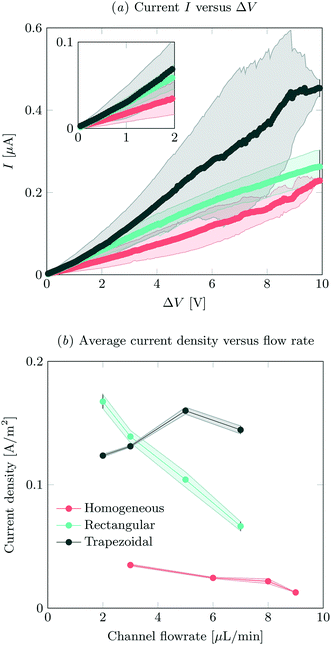 | ||
| Fig. 2 (a) IV-sweeps for all different geometries, at a flow rate of 3 μL min−1 and an inlet concentration of 0.1 mM NaCl. Error bars indicate standard deviation between measurements, where the average of at least two different chips was analyzed. (b) Average steady state current density at an applied potential of 8 V as a function of flow rate, obtained by dividing the total current by the active hydrogel area for the different geometries. For the measured absolute currents and the calculation of hydrogel areas, see ESI† S2. | ||
Current was measured as a function of time at different feed flow rates and a feed concentration of 0.1 mM NaCl. The current was averaged over 180 s for all systems, after reaching a steady state. In our system, we defined the onset of steady state as the time after which the current was not monotonically increasing or decreasing. The highest currents were measured for the asymmetric trapezoidal hydrogels. The absolute current as a function of flow rate is measured at an applied potential of 8 V, and is shown in ESI† S2. The asymmetric trapezoidal hydrogels show the highest absolute current for all flow rates and are less prone to a reduction in current as a function of flow rate. We attribute the decrease in current as a function of flow rate to not overcoming the limiting current regime at higher flow rates when homogeneous and rectangular heterogeneous hydrogels were used. The overlimiting current regime is reached at all flow rates using the asymmetric trapezoidal hydrogels. To make a more fair comparison, the current per hydrogel area (A m−2) in the different microchips should be compared, as shown in Fig. 2b. For the asymmetric trapezoidal hydrogels, the average length of the hydrogel is taken as a reference for the active hydrogel area (see ESI† S2 for calculations of the area). Since the full homogeneous hydrogels have the highest surface area per channel, the current density in this geometry is lowest. For both heterogeneous (trapezoidal and rectangular) hydrogels, the total exchange area is lower, resulting in higher current densities when compared to the full homogeneous hydrogel. This indicates a more efficient use of hydrogel area in these configurations.
For all electrical measurements it is confirmed that the supply of ions is larger than the theoretical removal of ions as a result of the electric field and the obtained currents. Even for the lowest flow rates (2 μL min−1) and hypothetical currents up to 0.6 μA (which is the highest current measured in this work) at this flow rate, not all ions will be removed from the feed, so this is not a limiting factor in our experiments.
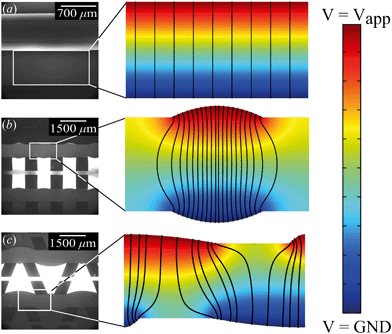
From the combined IV and chronopotentiometric measurements, we conclude that the asymmetric trapezoidal hydrogels enhance charge transport when compared to full homogeneous hydrogels. This enhancement occurs in all regimes: sublimiting, limiting and overlimiting regime. To explain this behavior, the potential distribution in the microchannels is modeled for all geometries. The results are shown in Fig. 3. These plots are obtained using COMSOL Multiphysics, in which the electric field is solved using the Poisson equation. For the homogeneous geometry (Fig. 3a), there is no initial gradient of the electric field in the direction tangential to the hydrogel surface, while for both heterogeneous geometries there is a tangential component present immediately after applying a potential (Fig. 3b and c). The tangential component gives rise to an electroosmotic flow (EOF) adjacent to the microchannel wall, yielding an additional transport of ions towards the hydrogel. Using the local electric field strength Ex obtained from these simulations, the magnitude of this EOF can be estimated for both heterogeneous geometries, using the Smoluchowski equation,35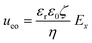 . With a ζ-potential of −100 mV,31,32 a viscosity η of 8.9 × 10−4 Pa s and a relative permittivity εrε0 = 7 × 10−10 F m−1 the expected velocity of EOF is estimated to be between ∼100 μm s−1 and ∼200 μm s−1 at the PDMS pillars between the hydrogel patches for an overall applied potential of 5 V. This EOF is enhanced by the heterogeneous nature of the surface charge as well, as PDMS is negatively charged and the AEH is positively charged this will also drive EOF mixing. Any contrast between the CEH and PDMS surface charge will also play a role in driving EOF.16,36,37 Electric-field distortion from the geometric patterning then couples to this and can enhance the overall EOF mixing in the system. A simple simulation illustrating this is provided in ESI† S3.
. With a ζ-potential of −100 mV,31,32 a viscosity η of 8.9 × 10−4 Pa s and a relative permittivity εrε0 = 7 × 10−10 F m−1 the expected velocity of EOF is estimated to be between ∼100 μm s−1 and ∼200 μm s−1 at the PDMS pillars between the hydrogel patches for an overall applied potential of 5 V. This EOF is enhanced by the heterogeneous nature of the surface charge as well, as PDMS is negatively charged and the AEH is positively charged this will also drive EOF mixing. Any contrast between the CEH and PDMS surface charge will also play a role in driving EOF.16,36,37 Electric-field distortion from the geometric patterning then couples to this and can enhance the overall EOF mixing in the system. A simple simulation illustrating this is provided in ESI† S3.
The local field strength is higher for the trapezoidal hydrogels than for the rectangular heterogeneous hydrogels (∼10%), resulting in slightly higher EOF velocities for this geometry. This EOF is present in all regimes, including the Ohmic and limiting. Already in the Ohmic regime, this yields a contribution of EOF to the charge transport in the heterogeneous geometries increasing the transport of ions towards the hydrogels. The direction of EOF is dependent on the local direction of the electric field at the and is thus of opposite sign on either side of the hydrogels. This induces electroosmotic mixing in the boundary layer, reducing concentration polarization and enhancing the effective ion transport. Additionally, the tangential component of the electric field and the presence of EOF enhances the onset of EKI and microfluidic mixing in the ion depletion zones after the development of an extended space charge.
3.2 Ion concentration profiles
To gain more understanding of the influence of geometry on ion transport, ion concentration profiles are monitored as a function of time and applied potential or current. All concentration profiles shown here are measured without the application of external cross flow, in order to decouple the effect of concentration polarization from the imposed flow. | ||
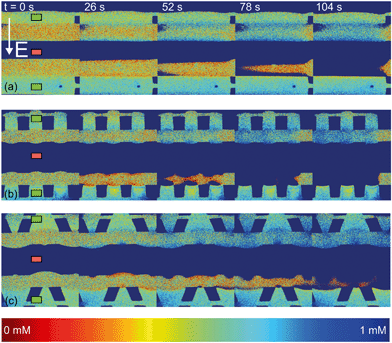
| Fig. 4 Fluorescence intensity profiles for three different hydrogel geometries as a function of time with an applied potential of 9 V, without the application of cross flow, (a) for homogeneous hydrogels, (b) for rectangular heterogeneous hydrogels and (c) for trapezoidal heterogeneous hydrogels. See ESI† for corresponding movies. Anion exchange hydrogels (indicated by the green markers) are bright as a result of the negatively charged fluorescent dye, cation exchange hydrogels (red markers) are less bright. Depletion zones are developing adjacent to the hydrogels after the application of an electric field, yielding different patterns for the three geometries. | ||
The ion depletion zones form in a different manner because the geometry of the hydrogel has an influence on the distribution of the electric field and thus alters the behavior of charge transport for the different geometries. For the homogeneous hydrogels (Fig. 4a), initially a depletion boundary layer forms at the hydrogel interface and grows into the microchannel until breaking down in small circular ion depletion zones moving along the hydrogel interface (from 27.5 s, see the ESI† S4). Then, the smaller depletion zones merge into larger zones that are still moving (with no preferential direction) along the hydrogel interface. The direction of this movement is dependent on the local charge distribution in the solution. Concentrated solution plugs remain between the large depletion zones (from t = 100 s). There is no initial heterogeneity in the electric field distribution in homogeneous geometries and thus no initial contribution of EOF on the ion transport occurs. Therefore, initially a stagnant concentration polarization layer forms and covers the entire membrane interface. Upon the development of ion depletion zones and an extended space charge adjacent to the hydrogel interfaces, the electric field is distorted in the homogeneous system as well, resulting in EKI and the movement of fluid and depletion zones at the hydrogel interface. Our experimental observations are in general agreement with the numerical predictions reported by Davidson et al. for similar geometric configurations.16
In both microchips with a heterogeneous hydrogel geometry, depletion zones form in a more controlled manner as pinning of depletion zones occurs at the hydrogel edges. A local zone of increased concentration is formed at both edges between the PDMS pillar and the hydrogel (see ESI† S5 and S6), while the depletion zone continues growing at the hydrogel interface. Near rectangular heterogeneous hydrogels, first small depletion zones form adjacent to the hydrogel interface, and merge into two larger depletion zones that are pinned at the hydrogel surface. These depletion zones grow as a function of time, until ions are fully depleted in the entire microchannel. The outer part of the hydrogels (beginning and ends of the microchannel, as can be seen from Fig. 4b at 210 s), still contains a higher concentration of ions when compared to the depletion zones. The zones of high concentration are locally pinned to the edge between the hydrogel and the PDMS. At this point, the current is reduced to a lower steady value, indicating a steady flux of ions through the hydrogels. Similar behavior can be observed in the heterogeneous trapezoidal hydrogels, where a local pinning of high concentration at the hydrogel edges and depletion zones form as a function of time. However, at the smaller hydrogel borders, there is only one depletion zone forming while at the larger border multiple smaller depletion zones are formed. These small zones merge into larger depletion zones (around t = 40 s) until the ions in entire microchannel are fully depleted at t = 100 s.
From the experiments with fluorescent dye, we can observe some of the fluid movement, especially at the planes of discontinuous conductivity (the edges between the hydrogel and the PDMS pillars) and we can compare the ion depletion zones to numerical predictions of similar systems that also included the development of fluid flow.16,38 Particle seeding of the flow was not successful as the polystyrene beads stick to the hydrogel surface and can move electrophoretically through the hydrogels and with that distort the system under investigation. We expect, based on these numerical predictions and previous experiments in microfluidic systems13,39 that vortex formation occurs also within the depletion zones observed in the current system.
The observed movement of the enriched zones pinned to the hydrogel edge can be explained by the combined effect of EOF adjacent to the microchannel walls and the electric field working on the extended space charge adjacent to the hydrogel surface. As was explained in section 3.1, EOF is present in our system as a result of the negative surface charge of PDMS and a tangential electric field. The surface is screened by cations present in the Debye layer. These cations migrate along the electric field lines towards the low potential sink, and drag along the liquid which results in an electro-osmotic flow (EOF) in the microchannels. For this EOF to establish itself, there should be a component of the electric field in the direction along the channel walls. As was shown, this component arises in systems with a heterogeneous distribution of hydrogels, since the electric field is non-homogeneous through local changes in conductivity and permittivity at the wall in such systems. Electrokinetic instabilities (EKI) can also occur from the development of a local space charge that is a result of the selective charge transport through the hydrogel,40 which is also influenced by the shape of the electric field lines. At the cation selective interface, a negative space charge develops and results in a fluid movement inside the electric field, directed towards the middle of the microchannel. The combination of this EOF and EKI lead to the pinning of high concentration plugs at the interface between the PDMS and the hydrogel in both heterogeneous geometries.
For all geometries, the Cl− concentration increases in the upper channel, while it is decreasing in the lower channel, as is expected based on the configuration of the electric field (Fig. 5). The negatively charged fluorescent dye was eventually depleted in the depleted channel, resulting in the loss of signal from this channel (most pronounced at the longest times). The behavior observed in the FLIM measurements is similar to the results of fluorescence microscopy measurements, which confirms that fluorescence measurements are a good indicator for qualifying ion concentration profiles inside microfluidic systems. However, both the spatial and time resolution of our FLIM system is not sufficient to detect the development of local depletion zones in our relatively small system in sufficient detail to draw firm conclusions. Fluorescence microscopy has shown that the time scale of this development is in the order of seconds while recording one FLIM frame takes 13 seconds in our system.
The increase of ion concentration in the enriched microchannels can be measured as a function of time for all different geometries. An example of such a result is shown in ESI† S7. However, the space and time resolution of the FLIM method yield a high variance in the measurements, resulting in uncertainties in the actual local value of concentration. In general, as observed in the electrical characterization, the system with the heterogeneous trapezoidal hydrogels shows the fastest charge transport and the highest final concentrations inside the enriched channel. As expected, the enrichment is most pronounced at high potentials and currents, yielding the highest final concentrations in the enriched channel.
4 Conclusion
In this study, we investigated the effect of geometry on ion transport through charge selective interfaces. Our platform is versatile and can be easily adjusted to test various geometries, as the PDMS molds can be designed in any desired shape and size. Using capillary line pinning of hydrogels we are able to produce charge selective interfaces in a large variety of shapes which are of interest for determination of the influence of geometry on ED stack performance.Comparing quantitative (FLIM) and qualitative (fluorescence) concentration measurements, we have found that the use of fluorescence microscopy as an indication for the ion concentration yields a good description of the local concentrations in microfluidic systems. Fluorescence imaging generally yields better time and space resolution than FLIM and is a more simple experimental method yielding advantages for the investigation of fast developing systems such as our platform.
By electrical characterization and imaging of concentration profiles of systems with different hydrogel geometries, we found that a heterogeneous charge selective interface can enhance the charge transport in the system, as the heterogeneity induces tangential components to the electric field acting on charges in the solution and causing an electroosmotic flow in the microchannels. This electroosmotic flow is present in all current regimes, including the under-limiting current regime and thus enhances ion transport to the hydrogels even in this regime. This electroosmotic contribution to the flow induces an enhanced vortex fluid movement in heterogeneous hydrogel systems, mixing the depletion boundary layer and supplying additional ions to the interface. When comparing two different heterogeneous geometries, the trapezoidal hydrogels show a higher charge transport as a result of the larger tangential electric field in this system when compared to the rectangular heterogeneous hydrogels.
Our results are relevant for systems in which selective charge transfer is of importance, for instance electrodialysis and fuel cell applications. However, the influence of the interface geometry on other system parameters such as fouling, scaling and long-term stability are of high importance. These are interesting future studies on the coupling of these effects by topology.
Shifting the relative location of the rectangular heterogeneous hydrogels between the different channels (to obtain a zigzag pattern of charged hydrogels) would possible enhance the charge transport in these heterogeneous systems further by and is of interest for further investigation. Preliminary numerical modeling shows that in this geometry the distortion of the electric field lines is enhanced and therefore the charge transport should be enhanced. In systems containing homogeneous charge selective interfaces, initially there is no tangential component in the electric field. After the development of an extended space charge at the membrane interface, a tangential component does occur. This means that there is a delayed mixing of the boundary layer when compared to the heterogeneous systems. Our results are in agreement with theoretical predictions on the formation of ion depletion zones in similar systems.6,16 We also found that in heterogeneous systems, pinning of the ion depletion zones and vortexes occurs at the plane of discontinuous conductivity, showing a local increase in ion concentration in the microchannel above the non-permeable pillars.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was financially supported by the European Research Council, under the ERC starting grant 307342-TRAM awarded to R. G. H. Lammertink. The authors wish to thank A. Sander Haase and Mark A. Hempenius for their contributions in setting up this work.References
- H. Strathmann, Desalination, 2010, 264, 268–288 CrossRef.
- I. Rubinstein and L. Shtilman, J. Chem. Soc., Faraday Trans. 2, 1979, 75, 231 RSC.
- J. J. Krol, M. Wessling and H. Strathmann, J. Membr. Sci., 1999, 162, 145–154 CrossRef.
- V. V. Nikonenko, A. V. Kovalenko, M. K. Urtenov, N. D. Pismenskaya, J. Han, P. Sistat and G. Pourcelly, Desalination, 2014, 342, 85–106 CrossRef.
- S. A. Mareev, V. S. Nichka, D. Y. Butylskii, M. K. Urtenov, N. D. Pismenskaya, P. Y. Apel and V. V. Nikonenko, J. Phys. Chem. C, 2016, 120, 13113–13119 Search PubMed.
- V. I. Zabolotskii, V. V. Nikonenko, M. K. Urtenov, K. A. Lebedev and V. V. Bugakov, Russ. J. Electrochem., 2012, 48, 692–703 CrossRef.
- J. Balster, M. H. Yildirim, D. F. Stamatialis, R. Ibanez, R. G. H. Lammertink, V. Jordan and M. Wessling, J. Phys. Chem. B, 2007, 111, 2152–2165 CrossRef PubMed.
- I. Rubinstein and B. Zaltzman, Phys. Rev. E, 2000, 62, 2238–2251 CrossRef.
- S. Pawlowski, V. Geraldes, J. G. Crespo and S. Velizarov, J. Membr. Sci., 2016, 502, 179–190 CrossRef.
- V. S. Pham, Z. Li, K. M. Lim, J. K. White and J. Han, Phys. Rev. E, 2012, 86, 046310 CrossRef PubMed.
- M. Wessling, L. G. Morcillo and S. Abdu, Sci. Rep., 2014, 4, 4294 CrossRef PubMed.
- M. C. Martí-Calatayud, D. C. Buzzi, M. García-Gabaldón, A. M. Bernardes, J. A. S. Tenório and V. Pérez-Herranz, J. Membr. Sci., 2014, 466, 45–57 CrossRef.
- J. C. De Valença, R. M. Wagterveld, R. G. H. Lammertink and P. A. Tsai, Phys. Rev. E, 2015, 92, 031003(R) CrossRef PubMed.
- S. M. Rubinstein, G. Manukyan, A. Staicu, I. Rubinstein, B. Zaltzman, R. G. H. Lammertink, F. Mugele and M. Wessling, Phys. Rev. Lett., 2008, 101, 236101 CrossRef PubMed.
- J. de Valença, M. Jõgi, R. M. Wagterveld, E. Karatay, J. A. Wood and R. G. H. Lammertink, Langmuir, 2018, 34, 2455–2463 CrossRef PubMed.
- S. M. Davidson, M. Wessling and A. Mani, Sci. Rep., 2016, 6, 22505 CrossRef PubMed.
- P. Kim, S. J. Kim, J. Han and K. Y. Suh, Nano Lett., 2010, 10, 16–23 CrossRef PubMed.
- I. Cho, G. Y. Sung and S. J. Kim, Nanoscale, 2014, 6, 4620–4626 RSC.
- R. Kwak, G. Guan, W. K. Peng and J. Han, Desalination, 2013, 308, 138–146 CrossRef.
- S. J. Kim, Y.-C. Wang, J. H. Lee, H. Jang and J. Han, Phys. Rev. Lett., 2007, 99, 044501 CrossRef PubMed.
- S. Hanasoge and F. J. Diez, Lab Chip, 2015, 15, 3549–3555 RSC.
- J. de Jong, R. G. H. Lammertink and M. Wessling, Lab Chip, 2006, 6, 1125–1139 RSC.
- S. Yu, T.-J. Jeon and S. M. Kim, Chem. Eng. J., 2012, 197, 289–294 CrossRef.
- T. A. Zangle, A. Mani and J. G. Santiago, Chem. Soc. Rev., 2010, 39, 1014–1035 RSC.
- H.-C. Chang, G. Yossifon and E. A. Demekhin, Annu. Rev. Fluid Mech., 2012, 44, 401–426 CrossRef.
- B. Gumuscu, A. S. Haase, A. M. Benneker, M. A. Hempenius, A. van den Berg, R. G. H. Lammertink and J. C. T. Eijkel, Adv. Funct. Mater., 2016, 26, 8685–8693 CrossRef.
- B. Gumuscu, J. G. Bomer, A. van den Berg and J. C. T. Eijkel, Lab Chip, 2015, 15, 664–667 RSC.
- N. Panchuk-Voloshina, R. P. Haugland, J. Bishop-Stewart, M. K. Bhalgat, P. J. Millard, F. Mao, W. Y. Leung and R. P. Haugland, J. Histochem. Cytochem., 1999, 47, 1179–1188 CrossRef PubMed.
- J. R. Lakowicz, H. Szmacinski, K. Nowaczyk, K. W. Berndt and M. Johnson, Anal. Biochem., 1992, 202, 316–330 CrossRef PubMed.
- J. Biwersi, B. Tulk and A. S. Verkman, Anal. Biochem., 1994, 219, 139–143 CrossRef PubMed.
- X. Ren, M. Bachman, C. Sims, G. P. Li and N. Allbritton, J. Chromatogr. B: Biomed. Sci. Appl., 2001, 762, 117–125 CrossRef.
- A. Sze, D. Erickson, L. Ren and D. Li, J. Colloid Interface Sci., 2003, 261, 402–410 CrossRef PubMed.
- E. Choi, C. Wang, G. T. Chang and J. Park, Nano Lett., 2016, 16, 2189–2197 CrossRef PubMed.
- Z. Guo, J. Wang, J. Ren and E. Wang, Nanoscale, 2011, 3, 3767–3773 RSC.
- C. J. van Oss, Interfacial Forces Aqueous Media, Second Ed., CRC Press, 2006, pp. 51–69 Search PubMed.
- A. D. Stroock and G. M. Whitesides, Acc. Chem. Res., 2003, 36, 597–604 CrossRef PubMed.
- F. Tian, B. Li and D. Y. Kwok, Langmuir, 2005, 21, 1126–1131 CrossRef PubMed.
- C. L. Druzgalski, M. B. Andersen and A. Mani, Phys. Fluids, 2013, 25, 110804 Search PubMed.
- A. M. Benneker, J. A. Wood, P. A. Tsai and R. G. H. Lammertink, Sci. Rep., 2016, 6, 37236 CrossRef PubMed.
- M. Bazant and T. Squires, Phys. Rev. Lett., 2004, 92, 066101 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7lc01220a |
| ‡ Present address: Department of Bioengineering, University of California, Berkeley, California, USA. |
| This journal is © The Royal Society of Chemistry 2018 |