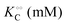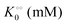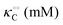DOI:
10.1039/C8IB00099A
(Paper)
Integr. Biol., 2018,
10, 587-597
Effect of macromolecular crowding on the kinetics of glycolytic enzymes and the behaviour of glycolysis in yeast†
Received
30th May 2018
, Accepted 22nd July 2018
First published on 3rd September 2018
Abstract
Water is involved in all aspects of biological activity, both as a solvent and as a reactant. It is hypothesized that intracellular water is in a highly structured state due to the high concentrations of macromolecules in the cell and that this may change the activity of intracellular enzymes due to altered binding affinities and allosteric regulations. Here we first investigate the kinetics of two glycolytic enzymes in artificially crowded aqueous solutions and show that crowding does indeed change their kinetics. Based on our kinetic measurements we propose a new model of oscillating glycolysis that instead of Michaelis–Menten or Monod–Wyman–Changeux kinetics uses the Yang–Ling adsorption isotherm introduced by G. Ling in the frame of the Association-Induction (AI) hypothesis. Using this model, we can reproduce previous experimental observations of the coupling of glycolytic oscillations and intracellular water dynamics, e.g., (i) during the metabolic oscillations, the latter variable oscillates in phase with ATP activity, and (ii) the emergence of glycolytic oscillations largely depends on the extent of intracellular water dipolar relaxation in cells in the resting state. Our results support the view that the extent of intracellular water dipolar relaxation is regulated by the ability of cytoplasmic proteins to polarize intracellular water with the assistance of ATP, as suggested in the AI hypothesis. This hypothesis may be relevant to the interpretation of many other biological oscillators, including cell signalling processes.
Insight, innovation, integration
Traditionally, metabolic pathways and signalling networks have been modelled using classical enzyme kinetic approaches (Michaelis–Menten and Monod–Wyman–Changeux kinetics). However, such kinetics, which is derived from studies of enzymes in dilute aqueous solutions may not hold in the crowded environment inside the cell, due to high concentrations of macromolecules and restrictions in the mobility of water. Here we first study the kinetics of two enzymes from glycolysis in artificially crowded aqueous solutions and demonstrate that models based on the Association-Induction hypothesis developed by G. N. Ling fit the data better than classical enzyme kinetic models. We then go on to show that such alternative models can be used to simulate and understand the coupling between metabolism and the dynamics of water in yeast cells with an oscillating glycolysis.
|
Introduction
All known forms of life depend on the presence of water. Water acts as an essential reactant or product in many metabolic processes, and it has long been known that its unusual properties as a polar solvent influence all biological processes. While water constitutes the most abundant component in cells, the high concentration of biological macromolecules, estimated to be approximately 200–350 mg mL−1,1,2 amounts for a volume fraction of 40%. This high concentration of macromolecules and the large polar surface areas of intracellular lipid membranes may bind water molecules and restrict their motion, substantially altering the state and dynamics of water in the cytoplasm compared with bulk water.3 Work done as early as the 1960s4,5 and later in the 1980s6–8 on the status of water in cells has led to a view of the cytoplasm as a crowded, reversible, non-covalent gel network, as opposed to a more classical view where cytoplasmic water is considered to be in a fluid state.9 This view has since been corroborated by a number of experiments (e.g., ref. 10–12). Additionally, recent studies using molecular dynamics (MD) simulations have indicated that the mobility of water molecules is very heterogeneous, and a large fraction of intracellular water molecules is essentially immobilized in long-lived water bridges between proteins.13 Despite this body of knowledge on the state of intracellular water, its importance in biological processes is still frequently overlooked or ignored, presumably due to the simplicity in assuming that water can be treated as a dielectric continuum with properties similar to bulk water.14 As a result, there seems to be a gap between the current view of metabolism and its regulation as determined for enzymes in dilute solutions and the properties of the same enzymes in the crowded environment inside a cell.15,16
In addition to the effect of the entire cytosol, there has been a recent interest in understanding the properties of so-called biomolecular condensates. A subset of these are sometimes referred to as membraneless organelles, such as e.g., the nucleolus or P granules.17,18 These condensates are thought to be intracellular areas of very high protein concentration, which may contain specific proteins and metabolites. Not only is this vital for compartmentalization of cellular processes, but the very nature of the increased crowding has been proposed to affect molecular function such as reaction kinetics.19
It has been known for more than seven decades that when glucose is added to a dense suspension of yeast cells glycolysis will start to oscillate.20 These glycolytic oscillations manifest themselves as temporal oscillations in e.g. NADH fluorescence,20,21 glycolytic intermediates,22 and mitochondrial membrane potential.23 In recent studies,24,25 we have shown that during glycolytic oscillations in yeast26 there is a tight coupling between the dynamics of glycolytic intermediates, particularly ATP, and the dynamics of intracellular water, measured as the fluorescence of the probes ACDAN (6-acetyl-2-(dimethylamino)naphthalene), PRODAN (6-propionyl-2-(dimethylamino)naphthalene) and LAURDAN (6-dodecanoyl-2-(dimethylamino)naphthalene). These probes are responsive to water dipolar relaxation phenomena in their local milieu.27–29 Using the generalized polarization (GP) function for these probes,30 which is a way to quantify the extent of the dipolar relaxation of intracellular water, we showed that the GP oscillates in phase with the intracellular concentration of ATP (Fig. S1, ESI†).24,25 Furthermore, we found for a wild type strain and 24 additional strains with null mutations in proteins involved in glycolysis, ATP synthesis, vacuolar H+ transport, actin polymerization and microtubule formation that the only parameter linking the amplitudes and frequencies of glycolytic oscillations was the GP function for ACDAN (the most hydrophilic probe of the DAN probes) measured in the resting state of the cells.25 In addition, using these mutant strains, we presented evidence for a critical region of ACDAN GP in which oscillations occur. This critical region is flanked by two supercritical Hopf bifurcations, and glycolytic oscillations do not occur outside this region (Fig. S2, ESI†).
We proposed that our results can be explained using the Association-Induction (AI) hypothesis developed by Gilbert Ling.10 Briefly, this hypothesis proposes that in resting living cells, the high affinity for K+ is dictated by its interaction with fibrillar cytoplasmic proteins with the assistance of high levels of ATP through an inductive effect. In addition, this inductive effect affects the dynamic state of intracellular water, which is polarized by its adsorption to these proteins. A decrease in ATP levels can transiently depolarize water, affecting the extent of water dipolar relaxation and the ionic balance in the intracellular space, as observed during cell function (for more details, see ref. 10).
In the current work, we investigate if the AI hypothesis can be used to develop alternative descriptions of enzyme action in the crowded intracellular environment of eukaryotic cells to the classical Michaelis–Menten approach for enzyme activity. In this description, we use the Yang–Ling adsorption isotherm,31,32 which may exhibit both Michaelis–Menten and more complicated cooperative enzyme kinetics without the need for specific requirements for enzyme structure or subunit number. The Yang–Ling isotherm is based on the AI hypothesis and builds on equilibrium statistical mechanics. We use the enzymes hexokinase (HK) and pyruvate kinase (PK) as our test enzymes by measuring their kinetic behaviour in artificially crowded aqueous solutions. We have used polyethylene glycol (PEG) as a crowding agent because it binds and immobilizes at least two water molecules per monomer33 and because it increases the GP value of ACDAN, suggesting that water is, at least partially, polarized.24 In this new description we introduce a variable  , which refers to the order or polarization of intracellular water. For bulk aqueous water, where the dipole vectors of the water molecules are randomly oriented in space we take
, which refers to the order or polarization of intracellular water. For bulk aqueous water, where the dipole vectors of the water molecules are randomly oriented in space we take 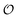 as equal to zero. On the other hand, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction,10,34 and here
as equal to zero. On the other hand, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction,10,34 and here 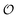 must be greater than 0. Furthermore, following Bagatolli and Stock27 we may assume that the experimentally determined ACDAN GP value is a measure of
must be greater than 0. Furthermore, following Bagatolli and Stock27 we may assume that the experimentally determined ACDAN GP value is a measure of 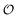 . Finally, inspired by previous work by Teusink et al.,35 who demonstrated that it is possible to construct models of in vivo metabolic process from in vitro kinetic studies, we use our in vitro studies of HK and PK to construct a simple model of glycolysis, based on Yang–Ling isotherms for glycolytic enzymes. We show that this model may exhibit oscillations in intracellular ATP coupled to oscillations in
. Finally, inspired by previous work by Teusink et al.,35 who demonstrated that it is possible to construct models of in vivo metabolic process from in vitro kinetic studies, we use our in vitro studies of HK and PK to construct a simple model of glycolysis, based on Yang–Ling isotherms for glycolytic enzymes. We show that this model may exhibit oscillations in intracellular ATP coupled to oscillations in 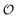 . The model is capable of reproducing all our previously observed observations of the coupling of glycolysis to polarization of water, including the phase relationship between ATP concentration and water dynamics as well as the narrow region of water dynamics flanked by two supercritical Hopf bifurcations giving rise to oscillations in glycolysis. We strongly believe that our model represents a paradigm shift in the perception of intracellular water and its role in cell physiology.
. The model is capable of reproducing all our previously observed observations of the coupling of glycolysis to polarization of water, including the phase relationship between ATP concentration and water dynamics as well as the narrow region of water dynamics flanked by two supercritical Hopf bifurcations giving rise to oscillations in glycolysis. We strongly believe that our model represents a paradigm shift in the perception of intracellular water and its role in cell physiology.
Methods
Chemicals
The aptamer switch probe S10 developed to measure ATP concentration36 was synthesized by VBC Biotech (Vienna); 6-acetyl-2-(dimethylamino)naphthalene (ACDAN) was purchased from Santa Cruz Biotechnology, Inc. (Dallas, TX). Hexokinase (99 U mg−1) from yeast was purchased from USB Products (OH, USA); ADP, ATP, phospho(enol)pyruvic acid (PEP), pyruvate kinase (575 U mg−1) from rabbit muscle, polyethylene glycol (PEG) 8000 (average mass), and chemicals for the ATP buffer were obtained from Sigma-Aldrich (Munich, Germany). All water used was of Milli-Q quality.
Synthesis of fluorescent ATP nanosensor
A polyacrylamide fluorescent nanosensor based on the aptamer switch probe S10 was synthesized as described previously.36 This sensor uses fluorescence to determine the ATP concentration and has successfully been used to measure ATP concentration both in vitro and in vivo as the fluorescence signal can be converted directly to ATP concentration using an in vitro calibration curve.36,37
Measurement of hexokinase kinetics
ATP concentrations were measured using the aptamer-based ATP nanosensor, as previously described.36 The experiments were performed using a SPEX spectrofluorometer. The sample was excited at 480 nm, and fluorescence emission was measured at 520 nm with both excitation and emission slits set to 4.5 nm. Prior to the experiments, the sensor signal was calibrated using a 2 mg mL−1 solution of ATP sensor in either ATP buffer (10 mM KH2PO4, pH 6.8, 25 mM K2SO4, 5 mM MgCl2 and 10 mM glucose) or in a PEG–ATP buffer mixture (ATP buffer containing 10% or 30% (w/w) PEG) with a series of ATP concentrations (0–6 mM ATP). In each experiment, the aptamer-based ATP sensor was added to a solution (ATP buffer or PEG–ATP buffer) to a final concentration of 2 mg mL−1. Then, 1 mL of the solution was placed in a quartz cuvette and measured by the spectrofluorometer. After a baseline was established, ADP was added to a concentration of 10 mM; 60 s later, PEP was added to a concentration of 10 mM. After an additional 60 s, pyruvate kinase (PK) was added to a final concentration of 16 U mL−1. Mechanical stirring was performed after each addition. Measurements were continued until the ATP concentration had reached a constant level. Then, hexokinase (HK) was added to a final concentration of 1 U mL−1 and stirred. Measurements were continued until the ATP concentration had dropped to the level obtained after ADP addition. The kinetic parameters were obtained from the transient value of [ATP] versus time, either as initial rates or as transient rates, as described in the following sections.
Statistical analysis of kinetic data and numerical simulations
Experimental transient rates (ve,i) were obtained by calculating the slope of the graphs of [ATP] versus time and compared to theoretical rates from the various models (vt,i) (Michaelis–Menten or Yang–Ling isotherm models) and the best fit was obtained by minimizing the term:| | 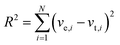 | (1) |
Statistical analysis and simulations of the various models were performed using MatLab (MathWorks, Natick, MA) and Berkeley Madonna software (Berkeley Madonna, Berkeley, CA).
Theoretical models
Kinetics of enzyme-catalyzed reactions in artificially crowded environments
Traditionally, mathematical models of enzyme-catalyzed reactions in cells have been constructed using mass-action kinetic methods, i.e. Michaelis–Menten or Monod–Wyman–Changeux (MWC) equations of the form:| | 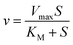 | (2) |
or| | 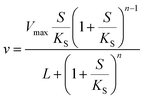 | (3) |
where Vmax is the maximum rate of the enzyme-catalyzed reaction, S is the substrate concentration and KM, KS and L are constants related to the binding of the substrate to the enzyme (KM and KS) or the equilibrium constant for the interconversion of active and inactive conformations of the enzyme (L). n in eqn (3) represents the number of subunits in the enzyme. Eqn (2) and (3) have mainly been used to fit data of initial velocity v0 against initial substrate concentration S0 to obtain values of Vmax and KM/KS, but also integrated forms of these equations (S against time) have been used to determine these parameters.38,39 Mass action and enzyme kinetics have been enormously successful in describing the kinetics of enzymes in dilute solutions, but also in setting up mathematical models of metabolic and signaling pathways in intact cells.26,40 Nevertheless, these descriptions may be less accurate for enzymes in the crowded intracellular milieu. In such an environment an alternative description based on statistical mechanical methods may be more appropriate. Such a description, based on the Association-Induction hypothesis proposed by G. N. Ling,10,41 is presented in the following section.
Several reports have proposed that water in the cytoplasm is in a polarized or gel-like state.10,11,42,43 In this new model, we therefore also introduce the variable  , which we will refer to as the order of the intracellular water. For bulk aqueous water, where the dipole vector of each water molecule is randomly oriented in space,
, which we will refer to as the order of the intracellular water. For bulk aqueous water, where the dipole vector of each water molecule is randomly oriented in space, 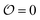 . In contrast, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction10,34 corresponding to
. In contrast, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction10,34 corresponding to 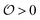 . According to the AI hypothesis4 (and as found in MD simulations13) this water, in addition to a preferred direction, has a reduced rotational velocity. Since dipolar relaxation is affected by the dipolar strength, average dipolar direction and rotational correlation times,44,45 we treat the GP function as a measure of
. According to the AI hypothesis4 (and as found in MD simulations13) this water, in addition to a preferred direction, has a reduced rotational velocity. Since dipolar relaxation is affected by the dipolar strength, average dipolar direction and rotational correlation times,44,45 we treat the GP function as a measure of 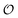 , such that a low GP value (i.e., high extent of dipolar relaxation) corresponds to a small
, such that a low GP value (i.e., high extent of dipolar relaxation) corresponds to a small 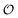 value, and a high GP value (low extent of dipolar relaxation) corresponds to a large
value, and a high GP value (low extent of dipolar relaxation) corresponds to a large  value. As we shall demonstrate below we may assume that the order of intracellular water has a regulatory effect on enzymatic reactions.
value. As we shall demonstrate below we may assume that the order of intracellular water has a regulatory effect on enzymatic reactions.
Yang–Ling isotherm for adsorption
To describe the kinetics of enzymes in crowded environments we use the Yang–Ling adsorption isotherm from the AI hypothesis.31,32 As opposed to Michaelis–Menten, the MWC or the related Koshland–Némethy–Filmer (KNF) models, the Yang–Ling adsorption isotherm has a statistical–mechanical origin and is general. For example, unlike the MWC and KNF models of allosteric enzymes, the Yang–Ling isotherm does not rely on the existence of multiple catalytic and regulatory subunits and yet the model is capable of showing both positive and negative cooperativity38 as demonstrated below, (see also Fig. S5, ESI†). Coupling of the isotherm to the dynamic state of water is carried out using the theoretical framework of Ling's AI hypothesis,10 which builds on the following assumptions: (i) intracellular water and various solutes are adsorbed on fibrillar proteins in the intracellular milieu (e.g., actin); (ii) this adsorption is cooperative as a result of the interactions of neighbouring adsorption sites; and (iii) the cooperative adsorptions are largely controlled by a smaller number of molecular species (e.g., relevant metabolites, such as ATP) referred to as cardinal adsorbents, which exert their control by interacting with key sites (cardinal sites) on the same proteins.10 Here, we will briefly explain the Yang–Ling adsorption isotherm31,32 for cooperative adsorption to a linear polymer, where two species (i and j) can both adsorb to the same adsorption sites, f, on a protein. The concentration of the adsorbed ith species, [pi]ad, is given by:31,32| | 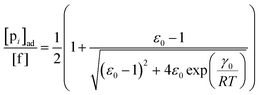 | (4) |
where [f] is the concentration of adsorption sites for the ith (and jth) species, −γ0/2 is the free energy cost of creating one mol of ij neighbouring pairs (such that an exchange in the triad iii → iji (two ij pairs) would entail an energy of −γ0)31 in the absence of cardinal adsorbent C. R is the gas constant, and T is the absolute temperature. ε0 is defined as:| | 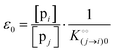 | (5) |
Here, [pi] and [pj] are the concentrations of the free ith and jth solutes, respectively, and 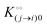 is the intrinsic dissociation constant for a j → i solute exchange in the absence of cardinal adsorbent (contrary to Ling,10,32 we use dissociation constants). Thus, ε0 takes into account the relative concentration of the ith and jth species and the change in free energy,
is the intrinsic dissociation constant for a j → i solute exchange in the absence of cardinal adsorbent (contrary to Ling,10,32 we use dissociation constants). Thus, ε0 takes into account the relative concentration of the ith and jth species and the change in free energy, 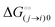 , associated with a j → i exchange of adsorption. The latter is given by:
, associated with a j → i exchange of adsorption. The latter is given by:| | 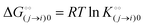 | (6) |
Each fibrillar protein also allows for the adsorption of cardinal adsorbents, C, on cardinal sites, F, and the concentration of adsorbed cardinal adsorbents, [C]ad, can be described analogously to (4) as:| | 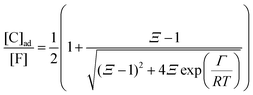 | (7) |
where Ξ is defined as in (5):| | 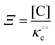 | (8) |
Here, the alternative adsorbent on F is an unspecified adsorbent with a constant concentration (e.g., H2O), included in the apparent dissociation constant 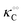 . Now, according to assumption (iii), the adsorption of C to the protein can change
. Now, according to assumption (iii), the adsorption of C to the protein can change 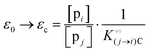 , where
, where 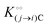 is the dissociation constant for the j to i solute exchange in the presence of C and γ0 → γc, where γc is defined as γ0 but in the presence of cardinal adsorbent. Therefore, the total concentration of the ith adsorbed solute is given by:
is the dissociation constant for the j to i solute exchange in the presence of C and γ0 → γc, where γc is defined as γ0 but in the presence of cardinal adsorbent. Therefore, the total concentration of the ith adsorbed solute is given by:| |  | (9) |
Results
Investigation of hexokinase and pyruvate kinase in crowded environments
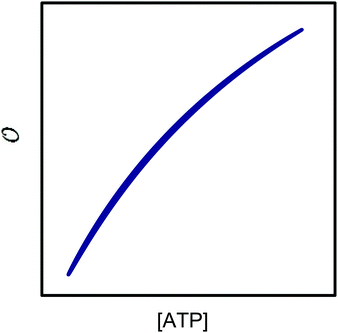
To compare the validity of Michaelis–Menten versus Yang–Ling isotherm kinetics in crowded environments we measured kinetic constants for two enzymes HK and PK in aqueous media with increasing concentrations of PEG as a molecular crowder. These two enzymes catalyze either the consumption (HK) or the production (PK) of ATP. To measure the change in concentration of ATP we used a fluorescence-based ATP nanosensor, that can measure time resolved changes in ATP concentration both in aqueous solutions and in cytoplasma.36 Fig. S3A in the ESI† shows the fluorescence signal from the probe after addition of 1 U mL−1 of yeast HK to a solution containing 2 mM ATP and 10 mM glucose. Fig. S3B (ESI†) shows the corresponding concentration of ATP after applying a calibration curve to the signal in Fig. S3A (ESI†).36 In order to investigate the kinetics of HK we measured both initial rates and transient rates obtained from the computed slope of curves like those in Fig. S3B (ESI†). Calculating the initial slope of the graph in Fig. S3B (ESI†) immediately after addition of HK and of similar graphs corresponding to other initial concentrations of ATP we are able to construct the plot in Fig. S3C (ESI†). This graph can easily be fitted to a rectangular hyperbola as defined by eqn (2) with a Vmax = 8.8 μM s−1 and a KM for ATP of 0.59 mM. Conversely, if we calculate the instantaneous rate v = −d[ATP]/dt from progress curves like that in Fig. S3B (ESI†) and plot them against the corresponding ATP concentration obtained from the ordinate of Fig. S3B (ESI†) we would expect to get a plot like that in Fig. S3C (ESI†). Such a plot is shown in Fig. S3D (ESI†). Clearly this plot deviates strongly from a rectangular hyperbola. The reason is that HK is inhibited by one of its products, ADP.46 The kinetics of HK in dilute aqueous solution has been shown to follow the relation:35| | 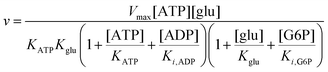 | (10) |
where [glu] indicates the concentration of glucose, KATP and Kglu represent the Michaelis–Menten constants for ATP and glucose, respectively, [G6P] indicates the concentration of glucose 6-phosphate and Ki,ADP and Ki,G6P indicate the inhibition constants of ADP and glucose 6-phosphate, respectively.
Since the initial glucose concentration used in our experiment (10 mM) is much higher than Kglu (∼0.1 mM35,47) and Ki,G6P (of the order of 20–30 mM35,48) is much larger than the concentration of glucose 6-phosphate formed in the experiment (<4 mM) eqn (10) can be reduced to:
| | 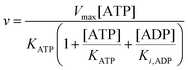 | (11) |
Furthermore, since the sum of concentrations of ADP and ATP is equal to the initial ATP concentration [ATP]
0 we can rewrite
eqn (11) as:
| | 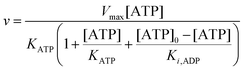 | (12) |
The best fit of eqn (12) to the experimental data (minimizing R2 in eqn (1)) was obtained with Vmax = 8.7 μM s−1, KATP = 0.6 ± 0.2 mM and Ki,ADP = 0.5 ± 0.2 mM. However, we also note from Fig. 1 that the best fit of Ki,ADP shifts to higher values as the ADP concentrations increases (ATP concentration decreases). A similar approach to study to HK kinetics by plotting the transient rate versus substrate concentration as shown in Fig. 1 was made with glucose as the limiting substrate.39 It should be emphasized that the Michaelis–Menten equation and similar equations based on steady state kinetics are not limited to only initial rates versus substrate concentration, but as mentioned in the previous section, it is indeed be possible to obtain the relevant kinetic constants from substrate concentration versus time progress curves38 like those in Fig. S3A and B (ESI†).
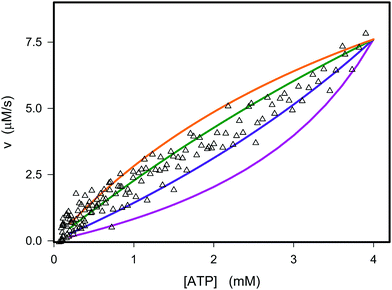 |
| | Fig. 1 Experimental and theoretical data for the dependence of the instantaneous rate v on the ATP concentration. The open triangles represent the experimental data from Fig. S3D (ESI†). The graphs are plots of v against concentration of ATP using eqn (12) with the parameters Vmax = 8.8 μM s−1, KATP = 0.6 mM and values of Ki,ADP of 0.2 mM (purple), 0.4 mM (blue), 0.8 mM (green), and 1.2 mM (orange). | |
If we perform the same experiment as shown in Fig. S3 (ESI†) and Fig. 1 in a solution containing PEG the fit of the experimentally determined rates versus rates predicted from eqn (12) becomes very poor (Fig. 2, red curve).
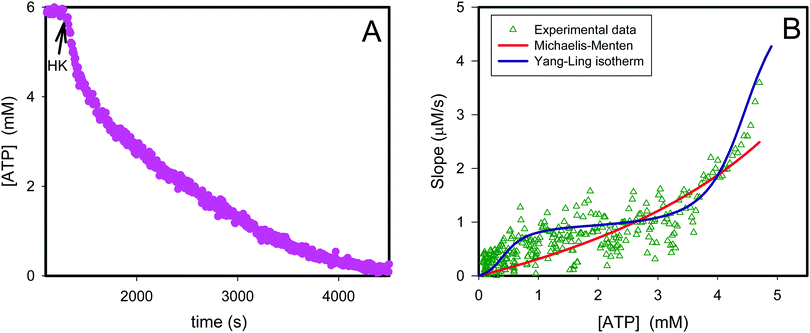 |
| | Fig. 2 Transient kinetics of hexokinase catalyzed phosphorylation of glucose by ATP. In (A) is plotted the ATP concentration before and after addition of 1 U of yeast hexokinase (HK) (arrow) to a 1 mL aqueous solution containing 10% PEG, 6 mM ATP and ATP sensor corresponding to 1 mg mL−1. The graph is calculated from the data in original fluorescence data using a calibration curve.36 The triangles in (B) represent the slope from the graph in (A) plotted against the ATP concentration. The red curve represents the best fit of eqn (12) to the experimental data while the violet curve represents the best fit of eqn (13)–(16). | |
Instead we implement the Yang–Ling isotherm model31,32 (eqn (4)–(9)) for the enzyme HK. We consider ATP to be an adsorbed species (substrate), while ADP is considered to be a cardinal adsorbent.32 Hence, the rate of ATP consumption can be described by the equation:
| | 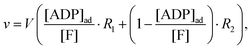 | (13) |
where
V is the maximal activity of HK, and [ADP]
ad is the concentration of adsorbed ADP. The form of
(13) is equivalent to
(9), and the terms
R1 and
R2 are given as:
| | 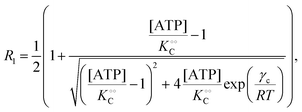 | (14a) |
| | 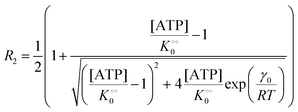 | (14b) |
while [ADP]
ad can be described similar to
(7) as:
| | 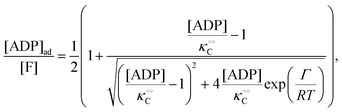 | (15) |
When comparing
eqn (14a) or
(14b) to
eqn (9) and
eqn (15) to
eqn (7) we assume that the binding sites for ATP and ADP both have water as an alternative adsorbent. Again, using that [ADP] = [ATP]
0 − [ATP] we obtain a very good fit to the experimental data in
Fig. 2B using
eqn (13)–(15) and the parameters
V = 5 μM s
−1,
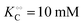
, −
γc/2 = 1 kcal mol
−1,
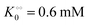
, −
γ0/2 = 0.25 kcal mol
−1,
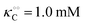
and −
Γ/2 = 0.05 kcal mol
−1 (violet curve in
Fig. 2B).
Thus, it seems that in an artificially crowded environment the Yang–Ling isotherm model describes the experimental data significantly better than classical Michaelis–Menten kinetics. Furthermore, measurements of the kinetic constants also revealed that Vmax decreases while 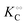 ,
, 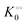 and
and 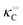 increase with increasing molecular crowding (increasing concentration of PEG, Table 1). Plots of these constants against the ACDAN GP value are shown in Fig. S4 (ESI†). It is worth pointing out here that if we evaluate only the initial rate of ATP consumption from eqn (13)–(15) (corresponding to an ADP concentration of zero) then we obtain a plot of v against [ATP] forming essentially a rectangular hyperbola as that shown in Fig. S3C (ESI†). In fact, the Yang–Ling adsorption isotherm used to model HK activity has several advantages over the more traditional models, such as Michaelis–Menten or MWC. As already noted by Yang and Ling,32 the model is general and has a statistical–mechanical basis. Furthermore, the model can produce both cooperative and non-cooperative enzyme kinetics if we change the value of the nearest neighbour interaction energy (γ0). γ0 ≠ 0 generates cooperative kinetics (γ0 < 0 yields positive cooperativity, γ0 > 0 yields negative cooperativity), while γ0 = 0 generates non-cooperative (hyperbolic) kinetics. This is illustrated in Fig. S5 (ESI†), which shows both sigmoidal and hyperbolic initial rates. It should be noted that since the Yang–Ling isotherm relies solely on the presence of adsorption sites to generate cooperativity, it has no requirements for the presence of specific enzymatic states or number of enzymatic subunits. Thus, unlike MWC and KNF models, the Yang–Ling adsorption isotherm allows for monomeric enzymes to exhibit cooperativity (observed experimentally in, e.g., ref. 49).
increase with increasing molecular crowding (increasing concentration of PEG, Table 1). Plots of these constants against the ACDAN GP value are shown in Fig. S4 (ESI†). It is worth pointing out here that if we evaluate only the initial rate of ATP consumption from eqn (13)–(15) (corresponding to an ADP concentration of zero) then we obtain a plot of v against [ATP] forming essentially a rectangular hyperbola as that shown in Fig. S3C (ESI†). In fact, the Yang–Ling adsorption isotherm used to model HK activity has several advantages over the more traditional models, such as Michaelis–Menten or MWC. As already noted by Yang and Ling,32 the model is general and has a statistical–mechanical basis. Furthermore, the model can produce both cooperative and non-cooperative enzyme kinetics if we change the value of the nearest neighbour interaction energy (γ0). γ0 ≠ 0 generates cooperative kinetics (γ0 < 0 yields positive cooperativity, γ0 > 0 yields negative cooperativity), while γ0 = 0 generates non-cooperative (hyperbolic) kinetics. This is illustrated in Fig. S5 (ESI†), which shows both sigmoidal and hyperbolic initial rates. It should be noted that since the Yang–Ling isotherm relies solely on the presence of adsorption sites to generate cooperativity, it has no requirements for the presence of specific enzymatic states or number of enzymatic subunits. Thus, unlike MWC and KNF models, the Yang–Ling adsorption isotherm allows for monomeric enzymes to exhibit cooperativity (observed experimentally in, e.g., ref. 49).
Table 1 Experimental kinetic constants for the Yang–Ling isotherm model of HK (eqn (13)–(15)) in artificially crowded aqueous solutions
| % PEG w/w |
V (μM s−1) |
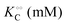
|
−γc/2 (kcal mol−1) |
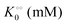
|
−γ0/2 (kcal mol−1) |
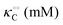
|
−Γ/2 (kcal mol−1) |
| 0 |
8.3 |
8 |
1 |
0.3 |
0.25 |
0.6 |
0.05 |
| 10 |
5 |
10 |
1 |
0.6 |
0.25 |
1.0 |
0.05 |
| 30 |
2.9 |
12 |
1 |
1.0 |
0.25 |
1.6 |
0.05 |
Next we studied the kinetics of the reaction catalyzed by the enzyme pyruvate kinase (PK), Fig. S6A and B (ESI†) show the ATP concentration change after adding 1 U mL−1 of rabbit PK to an aqueous phosphate buffer solution, pH 7.0, containing ATP sensor and 0.5 mM (Fig. S6A, ESI†) or 3 mM ADP (Fig. S6B, ESI†). We note that after addition of PK the ATP concentration increases due to transfer of phosphate from phosphoenolpyruvate (PEP) to ADP. We also note that in the beginning the change in ATP concentration is more linear compared to the ATP concentration change in reactions catalyzed by HK (Fig. S3B, ESI†). Fig. S6C (ESI†) shows a plot of the initial velocity of ATP formation catalyzed by PK against the ADP concentration. The plot was fitted to a rectangular hyperbola and an apparent KM for ADP and Vmax were determined as 0.62 mM and 16 μM s−1, respectively. The inset shows that also for PK does v0 increase linearly with the concentration of PK. The apparent KM for ADP of 0.62 mM is slightly larger than that estimated for rabbit PK previously50 under quite different experimental conditions. Fig. S6D (ESI†) shows a plot similar to that in Fig. 1, where we have taken the slope of the graph of ATP concentration against time (corresponding to Fig. S6A and B (ESI†) but with initial ADP concentration [ADP]0 = 2 mM) and plotted it against ADP concentration (calculated as [ADP]0 − [ATP]). From this plot we estimate an apparent KM for ADP of 0.63 mM and a Vmax = 20 μM s−1, in good agreement with the values estimated from the plot of v0 against [ADP]. This suggests that product inhibition by ATP and pyruvate are not contributing (or contribute only little) to the temporal change in ATP concentration following addition of PK to a solution containing PEP and ADP. A similar fit to the data could be obtained with the Yang–Ling isotherm with ADP as adsorbing species and no cardinal adsorbent, i.e.
| |  | (16) |
(corresponding to
V = 19 μM s
−1,
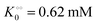
, −
γ0/2 = 0.1 kcal mol
−1). Repeating the experiments in 10% and 30% PEG solution resulted in data that could be fitted to the Yang–Ling isotherm (
eqn (16)) with
Vmax = 12 μM s
−1,
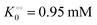
, −
γ0/2 = 0.1 kcal mol
−1 and
Vmax = 8 μM s
−1,
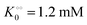
, −
γ0/2 = 0.1 kcal mol
−1, respectively. Thus, for PK molecular crowding also results in a decrease in
Vmax and an increase in
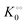
.
To summarize, our studies of two enzymes in artificially crowded environments showed that both enzymes could be modelled by the Yang–Ling isotherm approach and that an increased molecular crowding resulted in a decrease in maximal rates and increases in dissociation constants for the binding of both substrates and cardinal adsorbents. Measurements of the ACDAN GP for the 0, 10 and 30% PEG solutions showed an increase in GP with increasing concentration of PEG,24 (see Fig. S4, ESI† for graphs related to HK) corresponding to a decrease in the extent of water dipolar relaxation. This result can be interpreted as an increase in the order 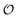 of intracellular water. In the following section we shall use this information to construct a simple model for the coupling of glycolytic oscillations to
of intracellular water. In the following section we shall use this information to construct a simple model for the coupling of glycolytic oscillations to 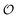 .
.
Simple Yang–Ling model of glycolytic oscillations
An important aim of this study was to construct a mathematical model that can simulate and explain our previous observations of the tight coupling between the dynamics of intracellular water and the intracellular ATP concentration.24,25 This new model should make use of the kinetic information obtained in the previous section and the Yang–Ling isotherm equations. In this endeavour we have been inspired by a simple glycolytic model,51 that involves only ATP and ADP and where phosphofructokinase (PFK) is the central regulatory enzyme. We use that this enzyme shows cooperativity with respect to the binding of ATP and (as opposed to HK discussed above) the activity of PFK is stimulated by ADP. Thus, in our model we assume (as for HK) that ATP is the substrate and ADP is a cardinal adsorbent. However, unlike HK, binding of ADP stimulates the rate of consumption of ATP. Nevertheless the rate expression for PFK is the same as for HK, i.e. vPFK is defined by:| | 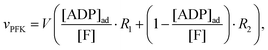 | (17) |
where V is the maximal activity of PFK, and [ADP]ad is the concentration of ADP adsorbed to PFK. The form of (17) is equivalent to (9) and (13), where ADP (as for HK) acts as a cardinal adsorbent and R1, R2 and [ADP]ad are described by eqn (14a), (14b) and (15), respectively.
A change in the nearest neighbour interaction energies γc and γ0 and 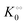 (compared to those estimated for HK) will change the regulatory function of ADP from an inhibitor to an activator. Thus, the binding of ADP as a cardinal adsorbent will increase the activity of PFK by changing the equilibrium of ATP vs. ADP adsorption to PFK via changing the relative weights of R2 and R1 in eqn (17) (see Fig. S7, ESI†).
(compared to those estimated for HK) will change the regulatory function of ADP from an inhibitor to an activator. Thus, the binding of ADP as a cardinal adsorbent will increase the activity of PFK by changing the equilibrium of ATP vs. ADP adsorption to PFK via changing the relative weights of R2 and R1 in eqn (17) (see Fig. S7, ESI†).
The resulting model for glycolytic oscillations is similar to that of Goldbeter and Lefever:51
| | 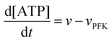 | (18) |
| | 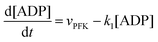 | (19) |
The model assumes that ATP is supplied to the system at a constant rate,
v, and is in turn transformed into ADP in the PFK-catalysed reaction at the rate
vPFK defined by
eqn (17). Finally, ADP is removed at a rate that is proportional to its concentration, with rate constant
k1. In the current form of the model, [ATP], [ADP], and time
t appear as dimensionless variables. The model is simulated using the results obtained from the kinetics studies in the previous section,
i.e. we assume that as for HK V is inversely proportional to
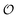
and
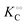
is proportional to
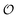
as suggested by Fig. S4 (ESI
†) (note that as discussed in the Introduction
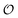
is equivalent to the ACDAN GP). In principle we could also make other constants (
γc,
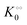
,
γ0,
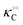
and
Γ) dependent on
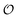
, but numerical simulations showed that this does not change the qualitative behaviour of the model. Plots of the simulated amplitudes and frequencies
versus the value of
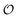
are shown in
Fig. 3. We note that these plots are very similar to those in Fig. S2 (ESI
†) (obtained experimentally
25), except that in the model, the frequency decreases slightly with increasing
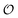
.
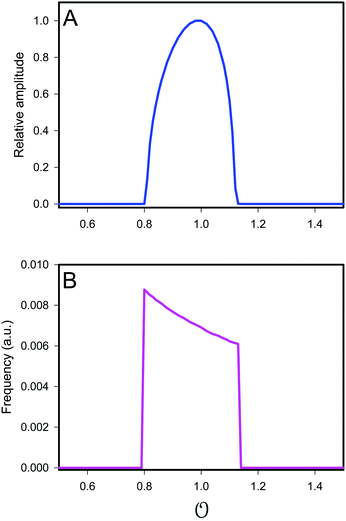 |
| | Fig. 3 Plot of (A) relative amplitude and (B) frequency of ATP oscillations versus the value of 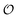 obtained from simulations of eqn (18) and (19). The parameters, most of which are dimensionless, are as follows: v = 0.4; obtained from simulations of eqn (18) and (19). The parameters, most of which are dimensionless, are as follows: v = 0.4; 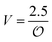 ; ; 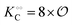 ; ;  ; ; 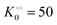 ; ;  ; ; 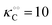 ; ;  ; k1 = 0.07. ; k1 = 0.07. | |
Coupling of the physical state of water to the oscillations of metabolites
In the previous section 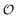 was treated as a parameter. However, as observed in previous work the ACDAN GP, which is the experimental equivalent of
was treated as a parameter. However, as observed in previous work the ACDAN GP, which is the experimental equivalent of 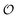 , changes with time and hence in what follows
, changes with time and hence in what follows  will be treated as a variable. According to Ling's AI hypothesis,41 the presence of specific cardinal adsorbents (e.g., ATP) on certain fibrillar proteins (e.g., actin) has the effect of polarizing water to a more structured state with lower mobility and higher local viscosity. In our treatment, this is analogous to creating an increase in
will be treated as a variable. According to Ling's AI hypothesis,41 the presence of specific cardinal adsorbents (e.g., ATP) on certain fibrillar proteins (e.g., actin) has the effect of polarizing water to a more structured state with lower mobility and higher local viscosity. In our treatment, this is analogous to creating an increase in  . This effect has recently been indirectly observed using ACDAN,24,25 where it was shown that glycolytic ATP oscillations in yeast were in phase with the extent of dipolar relaxation of intracellular water (see also Fig. S1, ESI†). The adsorption of ATP to a fibrillar protein is described analogously to (7) as:
. This effect has recently been indirectly observed using ACDAN,24,25 where it was shown that glycolytic ATP oscillations in yeast were in phase with the extent of dipolar relaxation of intracellular water (see also Fig. S1, ESI†). The adsorption of ATP to a fibrillar protein is described analogously to (7) as:| |  | (20) |
Any adequate description of enzymatic action should account for the environmental effects on the enzyme. Hence, in addition to eqn (18) and (19), we will describe the change in the physical state of water, 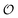 , as:
, as:| | 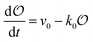 | (21) |
where k0 is a first-order rate constant, and the rate v0 is proportional to the concentration of ATP adsorbed to fibrillar proteins (described by eqn (20)):| | 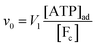 | (22) |
We then couple eqn (21) to eqn (18) and (19), again with the assumption that the maximum activity of PFK and the dissociation constant of ATP binding to PFK are functions of the variable 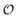 , i.e.,
, i.e., 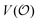 and
and 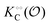 . Simulations of [ATP], [ADP] and
. Simulations of [ATP], [ADP] and 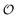 are shown in Fig. S8 in the ESI.† A phase plot of the simulations of the full model (eqn (18), (19) and (21)) are shown in Fig. 4. Previously, oscillations in ACDAN GP, which serves as a measure of
are shown in Fig. S8 in the ESI.† A phase plot of the simulations of the full model (eqn (18), (19) and (21)) are shown in Fig. 4. Previously, oscillations in ACDAN GP, which serves as a measure of 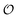 , have been shown to oscillate in phase with [ATP]24,25 (see also Fig. S1, ESI†); to the best of our knowledge, this is the first model that can reproduce and explain this observation. Furthermore, reducing either the maximum velocity V1 from eqn (22) or increasing the rate constant k0 will abolish the oscillations. Changing the rate constant k0 will change the steady-state level of
, have been shown to oscillate in phase with [ATP]24,25 (see also Fig. S1, ESI†); to the best of our knowledge, this is the first model that can reproduce and explain this observation. Furthermore, reducing either the maximum velocity V1 from eqn (22) or increasing the rate constant k0 will abolish the oscillations. Changing the rate constant k0 will change the steady-state level of 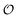 , which again will affect the amplitude and the frequency of the oscillations.
, which again will affect the amplitude and the frequency of the oscillations.
 |
| | Fig. 4 Phase plot of 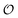 versus ATP concentration obtained from simulations of the model described by eqn (18), (19) and (21). The phase plot is very similar to the experimental phase plot (Fig. S1, ESI†) in that versus ATP concentration obtained from simulations of the model described by eqn (18), (19) and (21). The phase plot is very similar to the experimental phase plot (Fig. S1, ESI†) in that 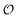 and [ATP] are in complete phase. The parameters are as described in Fig. 3, but with additional V1 = 2.3; and [ATP] are in complete phase. The parameters are as described in Fig. 3, but with additional V1 = 2.3; 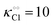 ; ;  ; k0 = 2.3. Initial (dimensionless) values for [ATP], [ADP] and ; k0 = 2.3. Initial (dimensionless) values for [ATP], [ADP] and 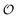 are 10, 4 and 1.13 respectively. are 10, 4 and 1.13 respectively. | |
Discussion
In the current study, we have compared the Yang–Ling isotherm kinetic model with the Michaelis–Menten model in describing the kinetics of two glycolytic enzymes in artificially crowded aqueous solutions. Using polyethylene glycol (PEG) as the crowding agent we found that the Yang–Ling isotherm model describes the kinetics better than the Michaelis–Menten model. A somewhat related approach was made by Olsen et al.39 to study hexokinase kinetics, but with glucose as the limiting substrate. Their experimental conditions differ from those used here in that ATP was present in excess compared to glucose, so the ATP concentration does not change significantly during an experiment and hence substrate inhibition by ADP will be very small (the term 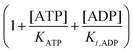 in eqn (10) will be essentially constant). Therefore, their results cannot be directly compared to those presented here. In addition, these authors found limited effect of crowding agents on the enzyme's Vmax and KM for glucose using serum albumin as the crowding agent. This is not surprising within the framework of the Association-Induction hypothesis. Specifically, it has been shown that globular proteins (or proteins denatured by sodium dodecyl sulfate (SDS) and by n-propanol) have much less capacity to polarize water than fully extended proteins (fibrillar proteins such as gelatin, or urea-, guanidine, HCl-, as well as NaOH-denatured proteins). Ling classified these two model systems as introverts and extroverts respectively.52,53 In the case of the introverts the NH and CO groups of the polypeptide chains are internally neutralized and as a result have minimal effects on the solvency of the bulk-phase water. On the other hand, the NH and CO groups of the polypeptide chains of the extrovert proteins are directly exposed to the bulk-phase water, reducing its solvency for Na2SO4, glycine and sucrose.53 This higher ability to polarize water has also been demonstrated for PEG-8000 and other oxygen containing polymers, e.g., polyvinylpyrrolidone (PVP), polyvinyl methyl ether (PVME) where the oxygen atoms of the linear polymers produce a similar effect on water to that of extroverted proteins.52 This behaviour has been confirmed for PEG-8000 from our results using ACDAN, i.e. the extent of dipolar relaxation decreased by increasing the amount of the polymer in the sample (Fig. S4, ESI,† see also ref. 24). The specific effect of PEG on the kinetic parameters of HK compared to that produced by albumin39 shows that the effect of crowding is a necessary but not a sufficient condition to explain the changes observed on the kinetic parameters of the enzyme, i.e. the polarizing effect on water by extroverts (that affects it activity and dynamical properties) seem to be an important phenomenon to explain this discrepancy. This is fully consistent with the Association-Induction hypothesis.
in eqn (10) will be essentially constant). Therefore, their results cannot be directly compared to those presented here. In addition, these authors found limited effect of crowding agents on the enzyme's Vmax and KM for glucose using serum albumin as the crowding agent. This is not surprising within the framework of the Association-Induction hypothesis. Specifically, it has been shown that globular proteins (or proteins denatured by sodium dodecyl sulfate (SDS) and by n-propanol) have much less capacity to polarize water than fully extended proteins (fibrillar proteins such as gelatin, or urea-, guanidine, HCl-, as well as NaOH-denatured proteins). Ling classified these two model systems as introverts and extroverts respectively.52,53 In the case of the introverts the NH and CO groups of the polypeptide chains are internally neutralized and as a result have minimal effects on the solvency of the bulk-phase water. On the other hand, the NH and CO groups of the polypeptide chains of the extrovert proteins are directly exposed to the bulk-phase water, reducing its solvency for Na2SO4, glycine and sucrose.53 This higher ability to polarize water has also been demonstrated for PEG-8000 and other oxygen containing polymers, e.g., polyvinylpyrrolidone (PVP), polyvinyl methyl ether (PVME) where the oxygen atoms of the linear polymers produce a similar effect on water to that of extroverted proteins.52 This behaviour has been confirmed for PEG-8000 from our results using ACDAN, i.e. the extent of dipolar relaxation decreased by increasing the amount of the polymer in the sample (Fig. S4, ESI,† see also ref. 24). The specific effect of PEG on the kinetic parameters of HK compared to that produced by albumin39 shows that the effect of crowding is a necessary but not a sufficient condition to explain the changes observed on the kinetic parameters of the enzyme, i.e. the polarizing effect on water by extroverts (that affects it activity and dynamical properties) seem to be an important phenomenon to explain this discrepancy. This is fully consistent with the Association-Induction hypothesis.
We have then used the results of our kinetic studies to constructed a simple model of oscillating glycolysis in yeast. The model is based on thermodynamic rather than mass-action kinetic considerations, and seems to capture the essential properties of the real system. The model uses our experimental observations that the Yang–Ling isotherm31,32 seems to describe the kinetics of glycolytic enzymes in crowded environments better than classical mass action-based enzyme kinetics, and that the maximum activities of these enzyme decrease while the dissociation constants for binding of substrates and cardinal adsorbents increase with increasing ACDAN GP (corresponding to an increase in the variable 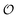 in our model). The increase in dissociation constants may be due to a decrease in the kon constant, while the koff constant remains the same. Such a decrease in kon is consistent with a decrease in the local diffusion rate of substrates and products and is to be expected in a more polarized solvent. Our finding that the maximum rate and the dissociation constants for adsorption of species (substrates) and cardinal adsorbents depend on the polarization of intracellular water are in line with previous observations made on enzymes in viscous solutions. Here it was shown that the maximum activity and dissociation constants of substrates change with crowding.54,55
in our model). The increase in dissociation constants may be due to a decrease in the kon constant, while the koff constant remains the same. Such a decrease in kon is consistent with a decrease in the local diffusion rate of substrates and products and is to be expected in a more polarized solvent. Our finding that the maximum rate and the dissociation constants for adsorption of species (substrates) and cardinal adsorbents depend on the polarization of intracellular water are in line with previous observations made on enzymes in viscous solutions. Here it was shown that the maximum activity and dissociation constants of substrates change with crowding.54,55
The proposed model for the coupling of glycolytic oscillations and water dynamics using the Yang–Ling adsorption isotherm instead of classical enzyme kinetics allows for the type of chemo-electrodynamic coupling of chemical reactions to the physical state of water observed in our previous work.24,25 The model is centered around PFK, which most experimental and theoretical studies point to as the key control point in glycolysis.26,40,56 It reproduces several experimental observations in addition to glycolytic oscillations, namely: (i) oscillations in ACDAN GP, which is taken as a measure of the variable 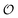 , occur in phase with ATP oscillations, and (ii) ACDAN GP (and by extension
, occur in phase with ATP oscillations, and (ii) ACDAN GP (and by extension 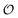 ) decreases when glucose and KCN are added to resting yeast.25 It was previously shown that the intracellular ATP concentration36 experiences a similar decrease, and when glucose is exhausted, both the ATP concentration and ACDAN GP increase again. In the framework of this model this drop is naturally explained as the decrease in ATP concentration is accompanied by a decrease in the amount of adsorbed water molecules, in accordance with the AI hypothesis.10
) decreases when glucose and KCN are added to resting yeast.25 It was previously shown that the intracellular ATP concentration36 experiences a similar decrease, and when glucose is exhausted, both the ATP concentration and ACDAN GP increase again. In the framework of this model this drop is naturally explained as the decrease in ATP concentration is accompanied by a decrease in the amount of adsorbed water molecules, in accordance with the AI hypothesis.10
As for the ability to reproduce oscillations in glycolytic intermediates this new model is comparable to previous models of glycolysis in that PFK and its regulation is central to the occurrence of the oscillations and hence the feed-back regulation by ADP used here is not new. Thus, the success of previous glycolytic models based on classical enzyme kinetics (e.g.ref. 35, 51 and 56–62) should not be underestimated. However, classical enzyme kinetics does not take into account the physical state of the solvent (in this case intracellular water) and hence it cannot be used to describe the experimentally observed coupling24,25 between changes in metabolite concentration and the dynamics of intracellular water (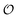 in our model). By contrast, the AI hypothesis is based on a description of the polarization of intracellular water and how it affects cellular processes10,32,41 and hence it may be better suited to model the coupling of metabolic oscillations to oscillations in the polarization of water. Furthermore, our model may be able to account for how areas of high
in our model). By contrast, the AI hypothesis is based on a description of the polarization of intracellular water and how it affects cellular processes10,32,41 and hence it may be better suited to model the coupling of metabolic oscillations to oscillations in the polarization of water. Furthermore, our model may be able to account for how areas of high 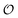 may polarize adjacent areas of low
may polarize adjacent areas of low 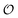 , which would be accompanied by a phase delay. This effect was observed in earlier studies,24,25 where metabolic oscillations in the cytosol of resting yeast were measured using LAURDAN or Nile Red, both hydrophobic probes that partition in intracellular lipid droplets, cellular membranes or both. Oscillations in these probes display the same frequency, as observed for the ACDAN GP or NADH concentration, but with a small phase shift compared to oscillations in ACDAN fluorescence. While earlier models of glycolysis do not even consider how oscillations in glycolytic intermediates can cause oscillations of water polarization in regions where glycolysis is absent, this result may be easily explained by a model coupling glycolysis and water polarization as an effect transmitted through the intracellular water, which is present in the entire cellular volume. Fig. S9 in the ESI† illustrates this nicely: The figure shows a phase plot of oscillations of Nile Red versus oscillations of the three DAN probes ACDAN, PRODAN and LAURDAN. While Nile Red and LAURDAN, both of which are polarity sensitive probes localized in lipid droplets, oscillate in complete phase with each other, PRODAN, which is both water soluble and soluble in hydrophobic solvents, oscillates slightly out of phase with Nile Red and finally ACDAN, which is very water soluble and hence predominantly localized in the cytoplasm24,25 oscillates even more out of phase with Nile Red. This we interpret as the polarization of water is somehow transmitted from the cytoplasm to the lipid droplets. How this transmission occurs is still under investigation.
, which would be accompanied by a phase delay. This effect was observed in earlier studies,24,25 where metabolic oscillations in the cytosol of resting yeast were measured using LAURDAN or Nile Red, both hydrophobic probes that partition in intracellular lipid droplets, cellular membranes or both. Oscillations in these probes display the same frequency, as observed for the ACDAN GP or NADH concentration, but with a small phase shift compared to oscillations in ACDAN fluorescence. While earlier models of glycolysis do not even consider how oscillations in glycolytic intermediates can cause oscillations of water polarization in regions where glycolysis is absent, this result may be easily explained by a model coupling glycolysis and water polarization as an effect transmitted through the intracellular water, which is present in the entire cellular volume. Fig. S9 in the ESI† illustrates this nicely: The figure shows a phase plot of oscillations of Nile Red versus oscillations of the three DAN probes ACDAN, PRODAN and LAURDAN. While Nile Red and LAURDAN, both of which are polarity sensitive probes localized in lipid droplets, oscillate in complete phase with each other, PRODAN, which is both water soluble and soluble in hydrophobic solvents, oscillates slightly out of phase with Nile Red and finally ACDAN, which is very water soluble and hence predominantly localized in the cytoplasm24,25 oscillates even more out of phase with Nile Red. This we interpret as the polarization of water is somehow transmitted from the cytoplasm to the lipid droplets. How this transmission occurs is still under investigation.
The experimental evidence obtained so far from our group24,25 suggest an important paradigm-shift concerning a possible key role of the dynamical state of intracellular water during cellular function. For example, if water is taken into account, not as a passive medium dominated by random thermally driven collisions, but as a reversibly dynamically structured active participant (as proposed in the association-induction hypothesis), then general coupling principles naturally follow. This implies a drastic change in the view of the cellular interior, traditionally seen as an aqueous environment where mass action kinetics and van't Hoff dilute solution theory apply, to a highly dynamic and structured milieu. Additionally, in a recent publication we provided evidence for the existence of an isentropic (adiabatic) process during glycolytic oscillations, suggesting that heat is not dissipated during oscillations but can be stored and moved around in the system to minimize further energy consumption63 challenging the classical view of steady-state energetics. In this respect it is of interest that the Yang–Ling isotherm is based on equilibrium statistical mechanics.
It should be possible to use the Yang–Ling adsorption isotherm to set up more detailed models incorporating all enzymes involved in glycolysis, equivalent to the detailed models based on enzyme kinetic expressions.56,59–61 A more rigorous version of the current model might also include the effects of the environment, specifically 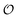 , on creating neighbouring ij pairs (i.e.,
, on creating neighbouring ij pairs (i.e., 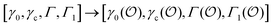 ), but we have refrained from this since making this change will not have a major qualitative effect on the model's behaviour, but may only affect, e.g., the position and the width of the critical region of
), but we have refrained from this since making this change will not have a major qualitative effect on the model's behaviour, but may only affect, e.g., the position and the width of the critical region of 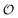 (Fig. 3).
(Fig. 3).
Finally, we conjecture that the state of intracellular water plays an important role in cellular activity in general and that a similar formalism can be used to propose a model for how this information may be rapidly transmitted throughout the cell. This idea has previously been suggested,3 and the general formalism presented here for cardinal adsorbents should apply to any enzyme involved in metabolism and cell signalling, e.g., intracellular Ca2+, which also exhibits oscillations.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
H. S. T. and L. F. O. acknowledge the support from the Danish Council for Independent Research, Natural Sciences (DFF 4002-00465). L. A. B. is a member of the Argentinian Research Council (CONICET) research career.
References
- S. Zimmerman and S. Trach, J. Mol. Biol., 1991, 222, 599–620 CrossRef PubMed.
- R. Ellis, Trends Biochem. Sci., 2001, 26, 597–604 CrossRef PubMed.
- M. Chaplin, Nat. Rev. Mol. Cell Biol., 2006, 7, 861–866 CrossRef PubMed.
- G. N. Ling, Ann. N. Y. Acad. Sci., 1965, 2, 401–417 Search PubMed.
- G. N. Ling and W. Negendank, Physiol. Chem. Phys., 1970, 2, 15–33 Search PubMed.
- J. Clegg, Am. J. Physiol., 1984, 246, R133–R151 Search PubMed.
- K. Luby-Phelps, Int. Rev. Cytol., 2000, 192, 189–221 Search PubMed.
- L. Jaeken, Prog. Biophys. Mol. Biol., 2017, 126, 31–46 CrossRef PubMed.
- H. Knull and A. P. Minton, Cell Biochem. Funct., 1996, 14, 237–248 CrossRef PubMed.
-
G. N. Ling, Life at the cell and below-cell level: The hidden history of a fundamental revolution in biology, Pacific Press New York, NY, 2001 Search PubMed.
- J. Fels, S. N. Orlov and R. Grygorczyk, Biophys. J., 2009, 96, 4276–4285 CrossRef PubMed.
- H. Yoo, E. Nagornyak, R. Das, A. D. Wexler and G. H. Pollack, J. Phys. Chem. Lett., 2014, 5, 947–952 CrossRef PubMed.
- C. Lu, D. Prada-Gracia and F. Rao, J. Chem. Phys., 2014, 141, 045101 CrossRef PubMed.
- H.-X. Zhou, G. Rivas and A. P. Minton, Annu. Rev. Biophys., 2008, 37, 375–397 CrossRef PubMed.
- V. A. Parsegian, R. P. Rand and R. C. Rau, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 3987–3992 CrossRef.
- N. A. Chebotareva, B. I. Kurganov and N. B. Livanova, Biochemistry, 2004, 69, 1239–1251 Search PubMed.
- T. J. Nott, E. Petsalaki, P. Farber, D. Jervis, E. Fussner, A. Plochowietz, T. D. Craggs, D. P. Bazett-Jones, T. Pawson, J. D. Forman-Kay and A. J. Baldwin, Mol. Cell, 2015, 57, 936–947 CrossRef PubMed.
- S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298 CrossRef PubMed.
- I. M. Kuznetsova, B. Y. Zaslavsky, L. Breydo, K. K. Turoverov and V. N. Uversky, Molecules, 2015, 20, 1377–1409 CrossRef PubMed.
- L. Duysens and J. Amesz, Biochim. Biophys. Acta, 1957, 24, 19–26 CrossRef.
- A. Betz and B. Chance, Arch. Biochem. Biophys., 1965, 109, 579–584 CrossRef PubMed.
- P. Richard, B. Teusink, M. B. Hemker, K. van Dam and H. V. Westerhoff, Yeast, 1996, 12, 731–740 CrossRef PubMed.
- L. F. Olsen, A. Z. Andersen, A. Lunding, J. C. Brasen and A. K. Poulsen, Biophys. J., 2009, 96, 3850–3861 CrossRef PubMed.
- H. S. Thoke, A. Tobiesen, J. Brewer, P. L. Hansen, R. P. Stock, L. F. Olsen and L. A. Bagatolli, PLoS One, 2015, 10, e0117308 CrossRef PubMed.
- H. S. Thoke, S. Thorsteinsson, R. P. Stock, L. A. Bagatolli and L. F. Olsen, Sci. Rep., 2017, 7, 16250 CrossRef PubMed.
-
A. Goldbeter, Biochemical Oscillations and Cellular Rhythms: The Molecular Bases of Periodic and Chaotic Behaviour, Cambridge University Press, Cambridge, 1996 Search PubMed.
-
L. A. Bagatolli and R. P. Stock, in Perspectives on Fluorescence: A Tribute to Gregorio Weber, ed. D. M. Jameson, Springer, Heidelberg, 2016, pp. 197–216 Search PubMed.
-
L. A. Bagatolli, in Fluorescent Methods to Study Biological Membranes, ed. Y. Mely and G. Duportail, Springer, Berlin, Heidelberg, 2013, pp. 3–35 Search PubMed.
- T. Parasassi, E. Krasnowska, L. Bagatolli and E. Gratton, J. Fluoresc., 1998, 8, 365–373 CrossRef.
- T. Parasassi, G. De Stasio, R. Rusch and E. Gratton, Biophys. J., 1991, 59, 466–475 CrossRef PubMed.
- G. Karreman, Bull. Math. Biophys., 1965, 27, 91–104 CrossRef.
- G. Ling, Proc. Natl. Acad. Sci. U. S. A., 1970, 67, 296–301 CrossRef.
- T. De Vringer, J. Joosten and H. Junginger, Colloid Polym. Sci., 1986, 264, 623–630 CrossRef.
- A. Rahaman, V. H. Grassian and C. J. Margulis, J. Phys. Chem. C, 2008, 112, 2109–2115 CrossRef.
- B. Teusink, J. Passarge, C. Reijenga, E. Esgalhado, C. van der Weijden, M. Schepper, M. Walsh, B. Bakker, K. van Dam, H. Westerhoff and J. Snoep, Eur. J. Biochem., 2000, 267, 5313–5329 CrossRef PubMed.
- V. C. Özalp, T. R. Pedersen, L. J. Nielsen and L. F. Olsen, J. Biol. Chem., 2010, 285, 37579–37588 CrossRef PubMed.
- T. D. Schrøder, V. C. Özalp, A. Lunding, K. D. Jernshøj and L. F. Olsen, FEBS J., 2013, 280, 6033–6044 CrossRef PubMed.
-
A. Cornish-Bowden, Fundamentals of Enzyme Kinetics, Portland Press, London, 3rd edn, 2004 Search PubMed.
- S. N. Olsen, H. Ramlov and P. Westh, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 2007, 148, 339–345 CrossRef PubMed.
-
E. Klipp, W. Liebermeister, C. Wierling, A. Kowald, H. Lehrach and R. Herwig, Systems Biology, A Textbook, Wiley VCH Verlag, Weinheim, 2009 Search PubMed.
- G. Ling, Tex. Rep. Biol. Med., 1964, 22, 244–265 Search PubMed.
- M. C. Munder, D. Midtvedt, T. Franzmann, E. Nüske, O. Otto, M. Herbig, E. Ulbricht, P. Müller, A. Taubenberger, S. Maharana, L. Malinovska, D. Richter, J. Guck, V. Zaburdaev and S. Alberti, eLife, 2016, 5, e09347 CrossRef PubMed.
- R. P. Joyner, J. H. Tang, J. Helenius, E. Dultz, C. Brune, L. J. Holt, S. Huet, D. J. Müller and K. Weis, eLife, 2016, 5, e09376 CrossRef PubMed.
- R. B. Macgregor and G. Weber, Ann. N. Y. Acad. Sci., 1981, 366, 140–154 CrossRef.
-
R. Macgregor, A Description of the Electrostatic Interactions of Fluorophores with Polar Solvents Based on a Gaussian Distribution of Interaction Energies, University of Illinois, Urbana-Champaign, 1983 Search PubMed.
- G. Hammes and D. Kochavi, J. Am. Chem. Soc., 1962, 84, 2073–2076 CrossRef.
- M. Banuelos and C. Gancedo, Arch. Microbiol., 1978, 117, 197–201 CrossRef PubMed.
- R. Viola, F. Raushel, A. Rendina and W. Cleland, Biochemistry, 1982, 21, 1295–1302 CrossRef PubMed.
- K. Kamata, M. Mitsuya, T. Nishimura, J. Eiki and Y. Nagata, Structure, 2004, 12, 429–438 CrossRef PubMed.
- A. Reynard, P. Boyer, D. Jacobsen and L. Hass, J. Biol. Chem., 1961, 236, 2277–2283 Search PubMed.
- A. Goldbeter and R. Lefever, Biophys. J., 1972, 12, 1302–1315 CrossRef PubMed.
- G. Ling and W. Hu, Physiol. Chem. Phys. Med. NMR, 1988, 20, 293–307 Search PubMed.
- G. N. Ling, Physiol. Chem. Phys. Med. NMR, 2014, 43, 1–73 Search PubMed.
- I. Svensson, E. Wehtje, P. Adlercreutz and B. Mattiasson, Biotechnol. Bioeng., 1994, 44, 549–556 CrossRef PubMed.
- S. B. Zimmerman and A. P. Minton, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27–65 CrossRef PubMed.
- A.-K. Gustavsson, D. D. van Niekerk, C. B. Adiels, B. Kooi, M. Goksor and J. L. Snoep, FEBS J., 2014, 281, 2784–2793 CrossRef PubMed.
- E. Selkov, Eur. J. Biochem., 1968, 4, 79–86 CrossRef.
- J. Wolf and R. Heinrich, Biochem. J., 2000, 345, 321–334 CrossRef PubMed.
- F. Hynne, S. Danø and P. Sørensen, Biophys. Chem., 2001, 94, 121–163 CrossRef PubMed.
- B. O. Hald and P. G. Sørensen, Biophys. J., 2010, 99, 3191–3199 CrossRef PubMed.
- F. B. du Preez, D. D. van Niekerk, B. Kooi, J. M. Rohwer and J. L. Snoep, FEBS J., 2012, 279, 2810–2822 CrossRef PubMed.
- F. B. du Preez, D. D. van Niekerk and J. L. Snoep, FEBS J., 2012, 279, 2823–2836 CrossRef PubMed.
- H. S. Thoke, L. F. Olsen, L. Duelund, R. P. Stock, T. Heimburg and L. A. Bagatolli, J. Biol. Phys., 2018, 44 DOI:10.1007/s10867-018-9499-2.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ib00099a |
| ‡ These authors are part of MEMPHYS – International and Interdisciplinary Research Network. |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Luis A.
Bagatolli‡
b and
Lars F.
Olsen‡
a,
Luis A.
Bagatolli‡
b and
Lars F.
Olsen‡
 *a
*a
 , which refers to the order or polarization of intracellular water. For bulk aqueous water, where the dipole vectors of the water molecules are randomly oriented in space we take
, which refers to the order or polarization of intracellular water. For bulk aqueous water, where the dipole vectors of the water molecules are randomly oriented in space we take 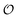 as equal to zero. On the other hand, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction,10,34 and here
as equal to zero. On the other hand, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction,10,34 and here 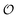 must be greater than 0. Furthermore, following Bagatolli and Stock27 we may assume that the experimentally determined ACDAN GP value is a measure of
must be greater than 0. Furthermore, following Bagatolli and Stock27 we may assume that the experimentally determined ACDAN GP value is a measure of 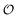 . Finally, inspired by previous work by Teusink et al.,35 who demonstrated that it is possible to construct models of in vivo metabolic process from in vitro kinetic studies, we use our in vitro studies of HK and PK to construct a simple model of glycolysis, based on Yang–Ling isotherms for glycolytic enzymes. We show that this model may exhibit oscillations in intracellular ATP coupled to oscillations in
. Finally, inspired by previous work by Teusink et al.,35 who demonstrated that it is possible to construct models of in vivo metabolic process from in vitro kinetic studies, we use our in vitro studies of HK and PK to construct a simple model of glycolysis, based on Yang–Ling isotherms for glycolytic enzymes. We show that this model may exhibit oscillations in intracellular ATP coupled to oscillations in 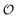 . The model is capable of reproducing all our previously observed observations of the coupling of glycolysis to polarization of water, including the phase relationship between ATP concentration and water dynamics as well as the narrow region of water dynamics flanked by two supercritical Hopf bifurcations giving rise to oscillations in glycolysis. We strongly believe that our model represents a paradigm shift in the perception of intracellular water and its role in cell physiology.
. The model is capable of reproducing all our previously observed observations of the coupling of glycolysis to polarization of water, including the phase relationship between ATP concentration and water dynamics as well as the narrow region of water dynamics flanked by two supercritical Hopf bifurcations giving rise to oscillations in glycolysis. We strongly believe that our model represents a paradigm shift in the perception of intracellular water and its role in cell physiology.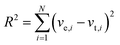
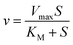
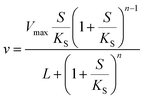
 , which we will refer to as the order of the intracellular water. For bulk aqueous water, where the dipole vector of each water molecule is randomly oriented in space,
, which we will refer to as the order of the intracellular water. For bulk aqueous water, where the dipole vector of each water molecule is randomly oriented in space, 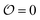 . In contrast, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction10,34 corresponding to
. In contrast, a water molecule adsorbed to an appropriate surface, on average, has a preferred direction10,34 corresponding to 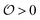 . According to the AI hypothesis4 (and as found in MD simulations13) this water, in addition to a preferred direction, has a reduced rotational velocity. Since dipolar relaxation is affected by the dipolar strength, average dipolar direction and rotational correlation times,44,45 we treat the GP function as a measure of
. According to the AI hypothesis4 (and as found in MD simulations13) this water, in addition to a preferred direction, has a reduced rotational velocity. Since dipolar relaxation is affected by the dipolar strength, average dipolar direction and rotational correlation times,44,45 we treat the GP function as a measure of 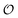 , such that a low GP value (i.e., high extent of dipolar relaxation) corresponds to a small
, such that a low GP value (i.e., high extent of dipolar relaxation) corresponds to a small 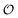 value, and a high GP value (low extent of dipolar relaxation) corresponds to a large
value, and a high GP value (low extent of dipolar relaxation) corresponds to a large 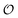 value. As we shall demonstrate below we may assume that the order of intracellular water has a regulatory effect on enzymatic reactions.
value. As we shall demonstrate below we may assume that the order of intracellular water has a regulatory effect on enzymatic reactions.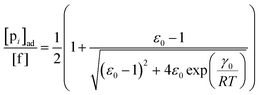
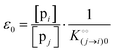
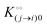 is the intrinsic dissociation constant for a j → i solute exchange in the absence of cardinal adsorbent (contrary to Ling,10,32 we use dissociation constants). Thus, ε0 takes into account the relative concentration of the ith and jth species and the change in free energy,
is the intrinsic dissociation constant for a j → i solute exchange in the absence of cardinal adsorbent (contrary to Ling,10,32 we use dissociation constants). Thus, ε0 takes into account the relative concentration of the ith and jth species and the change in free energy, 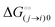 , associated with a j → i exchange of adsorption. The latter is given by:
, associated with a j → i exchange of adsorption. The latter is given by: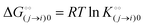
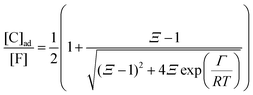
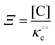
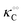 . Now, according to assumption (iii), the adsorption of C to the protein can change
. Now, according to assumption (iii), the adsorption of C to the protein can change 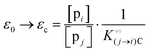 , where
, where 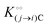 is the dissociation constant for the j to i solute exchange in the presence of C and γ0 → γc, where γc is defined as γ0 but in the presence of cardinal adsorbent. Therefore, the total concentration of the ith adsorbed solute is given by:
is the dissociation constant for the j to i solute exchange in the presence of C and γ0 → γc, where γc is defined as γ0 but in the presence of cardinal adsorbent. Therefore, the total concentration of the ith adsorbed solute is given by:


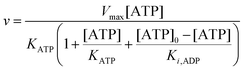


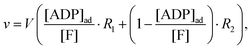



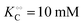 , −γc/2 = 1 kcal mol−1,
, −γc/2 = 1 kcal mol−1, 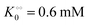 , −γ0/2 = 0.25 kcal mol−1,
, −γ0/2 = 0.25 kcal mol−1, 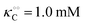 and −Γ/2 = 0.05 kcal mol−1 (violet curve in Fig. 2B).
and −Γ/2 = 0.05 kcal mol−1 (violet curve in Fig. 2B).
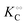 ,
, 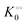 and
and 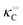 increase with increasing molecular crowding (increasing concentration of PEG, Table 1). Plots of these constants against the ACDAN GP value are shown in Fig. S4 (ESI†). It is worth pointing out here that if we evaluate only the initial rate of ATP consumption from eqn (13)–(15) (corresponding to an ADP concentration of zero) then we obtain a plot of v against [ATP] forming essentially a rectangular hyperbola as that shown in Fig. S3C (ESI†). In fact, the Yang–Ling adsorption isotherm used to model HK activity has several advantages over the more traditional models, such as Michaelis–Menten or MWC. As already noted by Yang and Ling,32 the model is general and has a statistical–mechanical basis. Furthermore, the model can produce both cooperative and non-cooperative enzyme kinetics if we change the value of the nearest neighbour interaction energy (γ0). γ0 ≠ 0 generates cooperative kinetics (γ0 < 0 yields positive cooperativity, γ0 > 0 yields negative cooperativity), while γ0 = 0 generates non-cooperative (hyperbolic) kinetics. This is illustrated in Fig. S5 (ESI†), which shows both sigmoidal and hyperbolic initial rates. It should be noted that since the Yang–Ling isotherm relies solely on the presence of adsorption sites to generate cooperativity, it has no requirements for the presence of specific enzymatic states or number of enzymatic subunits. Thus, unlike MWC and KNF models, the Yang–Ling adsorption isotherm allows for monomeric enzymes to exhibit cooperativity (observed experimentally in, e.g., ref. 49).
increase with increasing molecular crowding (increasing concentration of PEG, Table 1). Plots of these constants against the ACDAN GP value are shown in Fig. S4 (ESI†). It is worth pointing out here that if we evaluate only the initial rate of ATP consumption from eqn (13)–(15) (corresponding to an ADP concentration of zero) then we obtain a plot of v against [ATP] forming essentially a rectangular hyperbola as that shown in Fig. S3C (ESI†). In fact, the Yang–Ling adsorption isotherm used to model HK activity has several advantages over the more traditional models, such as Michaelis–Menten or MWC. As already noted by Yang and Ling,32 the model is general and has a statistical–mechanical basis. Furthermore, the model can produce both cooperative and non-cooperative enzyme kinetics if we change the value of the nearest neighbour interaction energy (γ0). γ0 ≠ 0 generates cooperative kinetics (γ0 < 0 yields positive cooperativity, γ0 > 0 yields negative cooperativity), while γ0 = 0 generates non-cooperative (hyperbolic) kinetics. This is illustrated in Fig. S5 (ESI†), which shows both sigmoidal and hyperbolic initial rates. It should be noted that since the Yang–Ling isotherm relies solely on the presence of adsorption sites to generate cooperativity, it has no requirements for the presence of specific enzymatic states or number of enzymatic subunits. Thus, unlike MWC and KNF models, the Yang–Ling adsorption isotherm allows for monomeric enzymes to exhibit cooperativity (observed experimentally in, e.g., ref. 49).
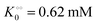 , −γ0/2 = 0.1 kcal mol−1). Repeating the experiments in 10% and 30% PEG solution resulted in data that could be fitted to the Yang–Ling isotherm (eqn (16)) with Vmax = 12 μM s−1,
, −γ0/2 = 0.1 kcal mol−1). Repeating the experiments in 10% and 30% PEG solution resulted in data that could be fitted to the Yang–Ling isotherm (eqn (16)) with Vmax = 12 μM s−1, 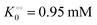 , −γ0/2 = 0.1 kcal mol−1 and Vmax = 8 μM s−1,
, −γ0/2 = 0.1 kcal mol−1 and Vmax = 8 μM s−1, 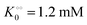 , −γ0/2 = 0.1 kcal mol−1, respectively. Thus, for PK molecular crowding also results in a decrease in Vmax and an increase in
, −γ0/2 = 0.1 kcal mol−1, respectively. Thus, for PK molecular crowding also results in a decrease in Vmax and an increase in 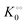 .
.
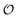 of intracellular water. In the following section we shall use this information to construct a simple model for the coupling of glycolytic oscillations to
of intracellular water. In the following section we shall use this information to construct a simple model for the coupling of glycolytic oscillations to 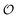 .
.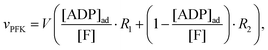
 (compared to those estimated for HK) will change the regulatory function of ADP from an inhibitor to an activator. Thus, the binding of ADP as a cardinal adsorbent will increase the activity of PFK by changing the equilibrium of ATP vs. ADP adsorption to PFK via changing the relative weights of R2 and R1 in eqn (17) (see Fig. S7, ESI†).
(compared to those estimated for HK) will change the regulatory function of ADP from an inhibitor to an activator. Thus, the binding of ADP as a cardinal adsorbent will increase the activity of PFK by changing the equilibrium of ATP vs. ADP adsorption to PFK via changing the relative weights of R2 and R1 in eqn (17) (see Fig. S7, ESI†).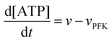
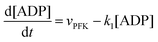
 and
and  is proportional to
is proportional to  as suggested by Fig. S4 (ESI†) (note that as discussed in the Introduction
as suggested by Fig. S4 (ESI†) (note that as discussed in the Introduction 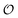 is equivalent to the ACDAN GP). In principle we could also make other constants (γc,
is equivalent to the ACDAN GP). In principle we could also make other constants (γc, 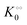 , γ0,
, γ0, 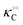 and Γ) dependent on
and Γ) dependent on 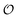 , but numerical simulations showed that this does not change the qualitative behaviour of the model. Plots of the simulated amplitudes and frequencies versus the value of
, but numerical simulations showed that this does not change the qualitative behaviour of the model. Plots of the simulated amplitudes and frequencies versus the value of 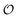 are shown in Fig. 3. We note that these plots are very similar to those in Fig. S2 (ESI†) (obtained experimentally25), except that in the model, the frequency decreases slightly with increasing
are shown in Fig. 3. We note that these plots are very similar to those in Fig. S2 (ESI†) (obtained experimentally25), except that in the model, the frequency decreases slightly with increasing 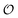 .
.

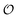 obtained from simulations of eqn (18) and (19). The parameters, most of which are dimensionless, are as follows: v = 0.4;
obtained from simulations of eqn (18) and (19). The parameters, most of which are dimensionless, are as follows: v = 0.4; 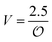 ;
; 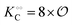 ;
;  ;
; 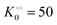 ;
;  ;
; 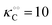 ;
;  ; k1 = 0.07.
; k1 = 0.07.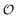 was treated as a parameter. However, as observed in previous work the ACDAN GP, which is the experimental equivalent of
was treated as a parameter. However, as observed in previous work the ACDAN GP, which is the experimental equivalent of  , changes with time and hence in what follows
, changes with time and hence in what follows  will be treated as a variable. According to Ling's AI hypothesis,41 the presence of specific cardinal adsorbents (e.g., ATP) on certain fibrillar proteins (e.g., actin) has the effect of polarizing water to a more structured state with lower mobility and higher local viscosity. In our treatment, this is analogous to creating an increase in
will be treated as a variable. According to Ling's AI hypothesis,41 the presence of specific cardinal adsorbents (e.g., ATP) on certain fibrillar proteins (e.g., actin) has the effect of polarizing water to a more structured state with lower mobility and higher local viscosity. In our treatment, this is analogous to creating an increase in  . This effect has recently been indirectly observed using ACDAN,24,25 where it was shown that glycolytic ATP oscillations in yeast were in phase with the extent of dipolar relaxation of intracellular water (see also Fig. S1, ESI†). The adsorption of ATP to a fibrillar protein is described analogously to (7) as:
. This effect has recently been indirectly observed using ACDAN,24,25 where it was shown that glycolytic ATP oscillations in yeast were in phase with the extent of dipolar relaxation of intracellular water (see also Fig. S1, ESI†). The adsorption of ATP to a fibrillar protein is described analogously to (7) as:
 , as:
, as: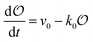
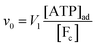
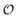 , i.e.,
, i.e., 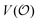 and
and 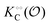 . Simulations of [ATP], [ADP] and
. Simulations of [ATP], [ADP] and  are shown in Fig. S8 in the ESI.† A phase plot of the simulations of the full model (eqn (18), (19) and (21)) are shown in Fig. 4. Previously, oscillations in ACDAN GP, which serves as a measure of
are shown in Fig. S8 in the ESI.† A phase plot of the simulations of the full model (eqn (18), (19) and (21)) are shown in Fig. 4. Previously, oscillations in ACDAN GP, which serves as a measure of  , have been shown to oscillate in phase with [ATP]24,25 (see also Fig. S1, ESI†); to the best of our knowledge, this is the first model that can reproduce and explain this observation. Furthermore, reducing either the maximum velocity V1 from eqn (22) or increasing the rate constant k0 will abolish the oscillations. Changing the rate constant k0 will change the steady-state level of
, have been shown to oscillate in phase with [ATP]24,25 (see also Fig. S1, ESI†); to the best of our knowledge, this is the first model that can reproduce and explain this observation. Furthermore, reducing either the maximum velocity V1 from eqn (22) or increasing the rate constant k0 will abolish the oscillations. Changing the rate constant k0 will change the steady-state level of  , which again will affect the amplitude and the frequency of the oscillations.
, which again will affect the amplitude and the frequency of the oscillations.
 versus ATP concentration obtained from simulations of the model described by eqn (18), (19) and (21). The phase plot is very similar to the experimental phase plot (Fig. S1, ESI†) in that
versus ATP concentration obtained from simulations of the model described by eqn (18), (19) and (21). The phase plot is very similar to the experimental phase plot (Fig. S1, ESI†) in that  and [ATP] are in complete phase. The parameters are as described in Fig. 3, but with additional V1 = 2.3;
and [ATP] are in complete phase. The parameters are as described in Fig. 3, but with additional V1 = 2.3; 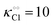 ;
;  ; k0 = 2.3. Initial (dimensionless) values for [ATP], [ADP] and
; k0 = 2.3. Initial (dimensionless) values for [ATP], [ADP] and  are 10, 4 and 1.13 respectively.
are 10, 4 and 1.13 respectively.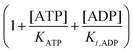 in eqn (10) will be essentially constant). Therefore, their results cannot be directly compared to those presented here. In addition, these authors found limited effect of crowding agents on the enzyme's Vmax and KM for glucose using serum albumin as the crowding agent. This is not surprising within the framework of the Association-Induction hypothesis. Specifically, it has been shown that globular proteins (or proteins denatured by sodium dodecyl sulfate (SDS) and by n-propanol) have much less capacity to polarize water than fully extended proteins (fibrillar proteins such as gelatin, or urea-, guanidine, HCl-, as well as NaOH-denatured proteins). Ling classified these two model systems as introverts and extroverts respectively.52,53 In the case of the introverts the NH and CO groups of the polypeptide chains are internally neutralized and as a result have minimal effects on the solvency of the bulk-phase water. On the other hand, the NH and CO groups of the polypeptide chains of the extrovert proteins are directly exposed to the bulk-phase water, reducing its solvency for Na2SO4, glycine and sucrose.53 This higher ability to polarize water has also been demonstrated for PEG-8000 and other oxygen containing polymers, e.g., polyvinylpyrrolidone (PVP), polyvinyl methyl ether (PVME) where the oxygen atoms of the linear polymers produce a similar effect on water to that of extroverted proteins.52 This behaviour has been confirmed for PEG-8000 from our results using ACDAN, i.e. the extent of dipolar relaxation decreased by increasing the amount of the polymer in the sample (Fig. S4, ESI,† see also ref. 24). The specific effect of PEG on the kinetic parameters of HK compared to that produced by albumin39 shows that the effect of crowding is a necessary but not a sufficient condition to explain the changes observed on the kinetic parameters of the enzyme, i.e. the polarizing effect on water by extroverts (that affects it activity and dynamical properties) seem to be an important phenomenon to explain this discrepancy. This is fully consistent with the Association-Induction hypothesis.
in eqn (10) will be essentially constant). Therefore, their results cannot be directly compared to those presented here. In addition, these authors found limited effect of crowding agents on the enzyme's Vmax and KM for glucose using serum albumin as the crowding agent. This is not surprising within the framework of the Association-Induction hypothesis. Specifically, it has been shown that globular proteins (or proteins denatured by sodium dodecyl sulfate (SDS) and by n-propanol) have much less capacity to polarize water than fully extended proteins (fibrillar proteins such as gelatin, or urea-, guanidine, HCl-, as well as NaOH-denatured proteins). Ling classified these two model systems as introverts and extroverts respectively.52,53 In the case of the introverts the NH and CO groups of the polypeptide chains are internally neutralized and as a result have minimal effects on the solvency of the bulk-phase water. On the other hand, the NH and CO groups of the polypeptide chains of the extrovert proteins are directly exposed to the bulk-phase water, reducing its solvency for Na2SO4, glycine and sucrose.53 This higher ability to polarize water has also been demonstrated for PEG-8000 and other oxygen containing polymers, e.g., polyvinylpyrrolidone (PVP), polyvinyl methyl ether (PVME) where the oxygen atoms of the linear polymers produce a similar effect on water to that of extroverted proteins.52 This behaviour has been confirmed for PEG-8000 from our results using ACDAN, i.e. the extent of dipolar relaxation decreased by increasing the amount of the polymer in the sample (Fig. S4, ESI,† see also ref. 24). The specific effect of PEG on the kinetic parameters of HK compared to that produced by albumin39 shows that the effect of crowding is a necessary but not a sufficient condition to explain the changes observed on the kinetic parameters of the enzyme, i.e. the polarizing effect on water by extroverts (that affects it activity and dynamical properties) seem to be an important phenomenon to explain this discrepancy. This is fully consistent with the Association-Induction hypothesis.
 in our model). The increase in dissociation constants may be due to a decrease in the kon constant, while the koff constant remains the same. Such a decrease in kon is consistent with a decrease in the local diffusion rate of substrates and products and is to be expected in a more polarized solvent. Our finding that the maximum rate and the dissociation constants for adsorption of species (substrates) and cardinal adsorbents depend on the polarization of intracellular water are in line with previous observations made on enzymes in viscous solutions. Here it was shown that the maximum activity and dissociation constants of substrates change with crowding.54,55
in our model). The increase in dissociation constants may be due to a decrease in the kon constant, while the koff constant remains the same. Such a decrease in kon is consistent with a decrease in the local diffusion rate of substrates and products and is to be expected in a more polarized solvent. Our finding that the maximum rate and the dissociation constants for adsorption of species (substrates) and cardinal adsorbents depend on the polarization of intracellular water are in line with previous observations made on enzymes in viscous solutions. Here it was shown that the maximum activity and dissociation constants of substrates change with crowding.54,55 , occur in phase with ATP oscillations, and (ii) ACDAN GP (and by extension
, occur in phase with ATP oscillations, and (ii) ACDAN GP (and by extension  ) decreases when glucose and KCN are added to resting yeast.25 It was previously shown that the intracellular ATP concentration36 experiences a similar decrease, and when glucose is exhausted, both the ATP concentration and ACDAN GP increase again. In the framework of this model this drop is naturally explained as the decrease in ATP concentration is accompanied by a decrease in the amount of adsorbed water molecules, in accordance with the AI hypothesis.10
) decreases when glucose and KCN are added to resting yeast.25 It was previously shown that the intracellular ATP concentration36 experiences a similar decrease, and when glucose is exhausted, both the ATP concentration and ACDAN GP increase again. In the framework of this model this drop is naturally explained as the decrease in ATP concentration is accompanied by a decrease in the amount of adsorbed water molecules, in accordance with the AI hypothesis.10 in our model). By contrast, the AI hypothesis is based on a description of the polarization of intracellular water and how it affects cellular processes10,32,41 and hence it may be better suited to model the coupling of metabolic oscillations to oscillations in the polarization of water. Furthermore, our model may be able to account for how areas of high
in our model). By contrast, the AI hypothesis is based on a description of the polarization of intracellular water and how it affects cellular processes10,32,41 and hence it may be better suited to model the coupling of metabolic oscillations to oscillations in the polarization of water. Furthermore, our model may be able to account for how areas of high  may polarize adjacent areas of low
may polarize adjacent areas of low  , which would be accompanied by a phase delay. This effect was observed in earlier studies,24,25 where metabolic oscillations in the cytosol of resting yeast were measured using LAURDAN or Nile Red, both hydrophobic probes that partition in intracellular lipid droplets, cellular membranes or both. Oscillations in these probes display the same frequency, as observed for the ACDAN GP or NADH concentration, but with a small phase shift compared to oscillations in ACDAN fluorescence. While earlier models of glycolysis do not even consider how oscillations in glycolytic intermediates can cause oscillations of water polarization in regions where glycolysis is absent, this result may be easily explained by a model coupling glycolysis and water polarization as an effect transmitted through the intracellular water, which is present in the entire cellular volume. Fig. S9 in the ESI† illustrates this nicely: The figure shows a phase plot of oscillations of Nile Red versus oscillations of the three DAN probes ACDAN, PRODAN and LAURDAN. While Nile Red and LAURDAN, both of which are polarity sensitive probes localized in lipid droplets, oscillate in complete phase with each other, PRODAN, which is both water soluble and soluble in hydrophobic solvents, oscillates slightly out of phase with Nile Red and finally ACDAN, which is very water soluble and hence predominantly localized in the cytoplasm24,25 oscillates even more out of phase with Nile Red. This we interpret as the polarization of water is somehow transmitted from the cytoplasm to the lipid droplets. How this transmission occurs is still under investigation.
, which would be accompanied by a phase delay. This effect was observed in earlier studies,24,25 where metabolic oscillations in the cytosol of resting yeast were measured using LAURDAN or Nile Red, both hydrophobic probes that partition in intracellular lipid droplets, cellular membranes or both. Oscillations in these probes display the same frequency, as observed for the ACDAN GP or NADH concentration, but with a small phase shift compared to oscillations in ACDAN fluorescence. While earlier models of glycolysis do not even consider how oscillations in glycolytic intermediates can cause oscillations of water polarization in regions where glycolysis is absent, this result may be easily explained by a model coupling glycolysis and water polarization as an effect transmitted through the intracellular water, which is present in the entire cellular volume. Fig. S9 in the ESI† illustrates this nicely: The figure shows a phase plot of oscillations of Nile Red versus oscillations of the three DAN probes ACDAN, PRODAN and LAURDAN. While Nile Red and LAURDAN, both of which are polarity sensitive probes localized in lipid droplets, oscillate in complete phase with each other, PRODAN, which is both water soluble and soluble in hydrophobic solvents, oscillates slightly out of phase with Nile Red and finally ACDAN, which is very water soluble and hence predominantly localized in the cytoplasm24,25 oscillates even more out of phase with Nile Red. This we interpret as the polarization of water is somehow transmitted from the cytoplasm to the lipid droplets. How this transmission occurs is still under investigation. , on creating neighbouring ij pairs (i.e.,
, on creating neighbouring ij pairs (i.e., 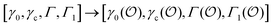 ), but we have refrained from this since making this change will not have a major qualitative effect on the model's behaviour, but may only affect, e.g., the position and the width of the critical region of
), but we have refrained from this since making this change will not have a major qualitative effect on the model's behaviour, but may only affect, e.g., the position and the width of the critical region of  (Fig. 3).
(Fig. 3).