Quantum dynamics of isolated molecules: general discussion
Dmitri
Babikov
 ,
David
Benoit
,
David
Benoit
 ,
Joel
Bowman
,
Timothy
Burd
,
Joel
Bowman
,
Timothy
Burd
 ,
David
Clary
,
Robert
Donovan
,
Ingo
Fischer
,
Francesco
Gianturco
,
Majdi
Hochlaf
,
Susmita
Kar
,
Adam
Kirrander
,
David
Clary
,
Robert
Donovan
,
Ingo
Fischer
,
Francesco
Gianturco
,
Majdi
Hochlaf
,
Susmita
Kar
,
Adam
Kirrander
 ,
Stephen
Leone
,
Thomas
Malcomson
,
Uwe
Manthe
,
Stephen
Leone
,
Thomas
Malcomson
,
Uwe
Manthe
 ,
Anne B.
McCoy
,
Anne B.
McCoy
 ,
Jens
Petersen
,
Jeremy
Richardson
,
Jens
Petersen
,
Jeremy
Richardson
 ,
Petr
Slavíček
,
Petr
Slavíček
 ,
Thierry
Stoecklin
,
Krzysztof
Szalewicz
,
Ad
van der Avoird
,
Roland
Wester
,
Thierry
Stoecklin
,
Krzysztof
Szalewicz
,
Ad
van der Avoird
,
Roland
Wester
 ,
Graham
Worth
,
Graham
Worth
 and
Anne
Zehnacker-Rentien
and
Anne
Zehnacker-Rentien
First published on 4th December 2018
Ingo Fischer opened a general discussion of the paper by Stephen Leone: Your presentation closed with an outlook on future experiments in which specific IR frequencies are eliminated from the laser pulse. Could you provide some more details on how these experiments are conducted and what information you will obtain?Stephen Leone answered: The new direction presented is a new multidimensional attosecond experiment, where four-wave mixing is carried out with one XUV attosecond pulse and two near-infrared pulses, one of which has been phase-shaped to remove a small slice of frequencies or to modify the phase of a small slice. As a result, a second dimension in the near-infrared is achieved, as this small slice is swept in frequency. Thus we have a two-dimensional plot of XUV wavelength versus near-infrared wavelength, and each single feature in the 2D map reveals a specific single state and its time dynamics in the spectrum. The results were carried out on Ar atoms.
Joel Bowman said: This is very exciting work. You show a schematic of a wavepacket localized in one well and then a short time later in a second well. But isn’t it possible that there is amplitude in both wells? Can you determine this in your experiment?
Stephen Leone answered: There is most likely amplitude in both wells, but predominantly in one or the other.
Robert Donovan asked: Can you see individual vibrational levels in the two a′′ wells, and can you see above the top of the barrier? Could there be any tunnelling near the top of the barrier and would you see this? The outer limb of the a′′ state looks very soft. Exciting an electron out of the bonding sigma into the antibonding sigma could produce an ion pair state. How much ionic character do you think the a state has? Once you get over the barrier would you sample the whole ion pair potential? Have you got any evidence to support ion pair behaviour?
Stephen Leone replied: These are two important new types of experiments that are possible. With longer wavelengths it should be possible probe the barrier region in the double-well potential. With core-level spectroscopy of the N atoms in nitrogen, it should be possible in the future to detect the ionic character on the outer turning point. This will require improvements in flux and higher photon energies in the X-ray region of the spectrum, but it is definitely achievable.
David Clary remarked: At the end of your paper (DOI: 10.1039/C8FD00074C), you say that there is potential for using this technique on reactive species. Please could you share your thoughts on that?
Stephen Leone responded: We are already thinking about the next steps to use these four-wave mixing methods for collisional and reactive systems. It would have to be at higher densities and would not embody attosecond time-resolution, because of the time between collisions, but the ability to place a molecule into a specific part of the potential, such as the outer turning point of a double-well potential, is appealing for collisional investigations.
David Clary asked: Do you have a specific system in mind?
Stephen Leone answered: Nitrogen molecules represent a first target system for collisional investigations at higher density, where it might be possible to investigate the inner and outer well regions in collisions.
Graham Worth enquired: The time-resolution of these experiments looks amazing, but you have so far only looked at a diatomic. Will it be straightforward to extend this to polyatomic molecules? Will the requirement of a double-well structure for the dark state restrict the types of molecule that can be examined?
Stephen Leone answered: The methodology is readily extended to polyatomic molecules, and we have considered water molecules and carbon dioxide as good candidates. The double-well structure is just one type of dynamics. We are interested in passage through conical intersections in the future.
Ingo Fischer opened a general discussion of the paper by Adam Kirrander: Ion pair states are common in many molecules, NaI being a particularly prominent example. Is it possible to describe the level structure in molecules like NaI with your approach? Furthermore, does the inverse mass relation, i.e. the negative particle being the significantly more heavy one, influence the description?
Adam Kirrander answered: This is a nice point, especially given the important role that molecules such as NaI have played in the early development of ultrafast spectroscopy. In fact, in early work by Ahmed Zewail, a strong excitation–energy dependence of the predissociative lifetime in excited vibrational wavepackets was noted1,2 and caused some consternation. It was eventually resolved that the source of this effect was that the lifetime of the predissociative resonances, which make up the excited wavepacket, is modulated periodically as a function of energy.3 More recently, elegant work by Hossein Sadeghpour and colleagues demonstrated how this periodic modulation of lifetimes, which can be seen as an interferometric effect, leads to Fano reversals in the lineshapes of these resonances,4,5 and it has been proposed that the great variation of lifetimes, which can be many orders of magnitude, can be exploited in photoassociation experiments by the identification of particularly long-lived resonances.6 The fact that the negative particle is significantly more heavy does not notably affect the computations, which are done in the molecular frame using the reduced molecular mass. However, it might be useful to point out that the density of states does depend strongly on the reduced mass.
1 T. S. Rose, M. J. Rosker and A. H. Zewail, J. Chem. Phys., 1988, 88, 6672–6673
2 T. S. Rose, M. J. Rosker and A. H. Zewail, J. Chem. Phys., 1989, 91, 7415–7436
3 S. Chapman and M. S. Child, J. Phys. Chem., 1991, 95, 578–584.
4 S. T. Cornett, H. R. Sadeghpour and M. J. Cavagnero, Phys. Rev. Lett., 1999, 82, 2488–2491.
5 N. Balakrishnan, B. D. Esry, H. R. Sadeghpour, S. T. Cornett and M. J. Cavagnero, Phys. Rev. A, 1999, 60, 1407–1413.
6 A. Kirrander, S. Rittenhouse, M. Ascoli, E. E. Eyler, P. L. Gould and H. R. Sadeghpour, Phys. Rev. A, 2013, 87, 031402.
Ingo Fischer asked: In H+H−, negative quantum defects appear, which seems to be counterintuitive to me. Can you explain the occurrence of negative quantum defects in a simple picture?
Adam Kirrander responded: First, it should be realized that the quantum defect and the principal quantum number are defined only modulo 1 in the theory. They occur in the Rydberg equation via the effective principal quantum number n* = n – μ, which is the quantity related to the (observable or calculable) energy. Therefore n and μ may be redefined formally by adding or subtracting any arbitrary integer to or from each of them, with the result that n* = n – μ remains the same. The value of the principal quantum number and the associated quantum defect for any given series must therefore be chosen based on some physical argument. Consider for instance the 3s ground state of the sodium atom. The effective principal quantum number of this state is known to be n* = 1.63. Customarily, one calls this state 3s, taking account of the fact that in the Na+ core the 1s and the 2s electrons are present. Note, however, that this type of argument tends to fail in molecules where the orbital ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) quantum number is no longer well-defined for core electrons.1 Hence, adopting this point of view, one finds that the quantum defect for the Na ground state is +1.37, i.e. it is positive, due, as one says, to “penetration effects”. However, Parsons and Weisskopf2 have pointed out that one may just as well denote the ground state of the Na atom as 1s, as this is the first s state outside the closed-shell Na+ core. The quantum defect is then negative and amounts to −0.63. Indeed, by representing the Na+ core by a hard sphere of radius rc = 0.91 bohr and a Coulomb field for r > rc, Parsons and Weisskopf were able to reproduce the whole Rydberg spectrum of the sodium atom quantitatively including its ground state.
quantum number is no longer well-defined for core electrons.1 Hence, adopting this point of view, one finds that the quantum defect for the Na ground state is +1.37, i.e. it is positive, due, as one says, to “penetration effects”. However, Parsons and Weisskopf2 have pointed out that one may just as well denote the ground state of the Na atom as 1s, as this is the first s state outside the closed-shell Na+ core. The quantum defect is then negative and amounts to −0.63. Indeed, by representing the Na+ core by a hard sphere of radius rc = 0.91 bohr and a Coulomb field for r > rc, Parsons and Weisskopf were able to reproduce the whole Rydberg spectrum of the sodium atom quantitatively including its ground state.
The negative quantum defects in H+ + H− can be understood in an analogous fashion as being due to the excluded volume at short range, i.e. the fact that the ion pair electrostatic Coulomb potential deviates more strongly from the ideal 1/R Coulomb potential at short distance compared to an electronic Rydberg state due to the repulsion between the positive nuclei in the two fragments. The energetically low-lying states in the heavy Rydberg series are therefore more displaced compared to a pure Coulomb potential. See also the comment from Robert Donovan on this topic, the figure relating to phase space effects in ref. 3, and our answer to the question from Prof. Ad van der Avoird.
1 C. Jungen, J. Chem. Phys., 1970, 53, 4168–4182.
2 R. G. Parsons and V. F. Weisskopf, Z. Phys., 1967, 202, 492–497.
3 R. J. Donovan, K. P. Lawley and T. Ridley, J. Chem. Phys., 2015, 142, 204306.
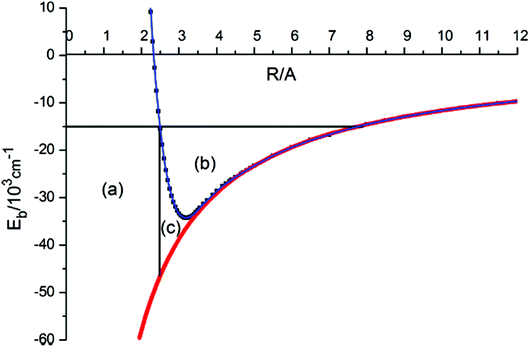
Robert Donovan remarked: I have a nice illustration of the origin of the large negative quantum defects in “heavy Rydberg” states. Theoretical work by Asaro and Dalgarno (1985),1 and by Pan and Mies (1988),2 had shown that such states would be present when atoms are bound by a Coulomb potential. But that work only dealt with the alkali halides. We were observing charge transfer states in the halogens, and I did a quick calculation, some 20 years ago, to see if it worked, but the result looked ridiculous! Everyone knows that for electronic Rydberg states, quantum defects are small positive numbers. Fortunately, Kenneth Lawley persevered and explained what was happening. On the right of Fig. 1 of our paper (DOI: 10.1039/C8FD00096D), you can see the energy levels for a heavy electron – this is for a point charge, not for the heavy Rydberg molecule, H+H−. For a heavy Rydberg molecule, there is repulsive wall which excludes a large amount of phase space (see Fig. 1 below). Thus, the vibrational motion in a heavy Rydberg state is restricted and you have excluded a large volume, the whole of area (a) in the figure. For the halogens, we’re looking at quantum defects of about −300; in hydrogen they are about −40.
1 C. Asaro and A. Dalgarno, Chem. Phys. Lett., 1985, 118, 64.
2 S. Pan and F. H. Meis, J. Chem. Phys., 1988, 89, 3096.
Stephen Leone followed up with another question to Adam Kirrander: How are the heavy Rydberg states affected by blackbody radiation? Normal Rydberg states are easily destroyed by long wavelength radiation. However, momentum conservation considerations and effective potentials might make for different considerations for heavy Rydberg states. Are heavy Rydberg states as susceptible to absorbing blackbody light and being lost?
Adam Kirrander responded: This is an interesting question. Rydberg states have long radiative lifetimes, which for instance underpins the importance of dissociative recombination as a key process for charge neutralisation in interstellar space.1 The heavy Rydberg levels close to dissociation could absorb black-body radiation and photodissociate, although the oscillator strength is probably small. Photodissociation would add to the other decay channels such as radiation, autoionisation and predissociation, all of which reduce the lifetime and make experimental observation of such states difficult. The influence of stray fields will also influence lifetimes and this point is addressed in our other comment. From a practical point of view, we know that the heavy Rydberg experiments performed to date have not required any additional shielding or cooling, even when quite high (>1000) principal quantum number heavy Rydberg states were observed.2 Generally speaking, we expect the spontaneous emission rate to scale as 1/n3 and the total black body decay rate as 1/n2, just like in electronic Rydberg states.3 These relationships would be shifted by the reduced mass scaling of n in heavy Rydberg states but should otherwise follow the same pattern.
1 M. Larsson, Ann. Rev. Phys. Chem., 1997, 48, 179.
2 W. Ubachs, private communication, September 2018.
3 T. F. Gallagher, Rydberg Atoms, Cambridge University Press, 1st edn, 1994.
Stephen Leone said: The question stems from my wondering about the momentum matching conditions for the heavy Rydberg states compared to the light electron in normal Rydberg states, and whether there is anything different about light absorption and release of the two particles.
Adam Kirrander replied: Our current thinking on this topic is that there is no difference in terms of momentum matching conditions between normal (light) and heavy Rydberg states.
Ad van der Avoird remarked: I suppose that among the heavy Rydberg states the H2 molecule must be special, because the H+ ion in the complex with H− is a bare proton, while in other systems both the positive and negative ions in the complex carry electrons. Is that indeed the case? Is the excluded volume therefore smaller than in other heavy Rydberg states?
Adam Kirrander answered: In H2 there is only one ion pair limit, corresponding to the single meta-stable H− (1s2) negative ion and a bare proton. In other molecular systems, one is likely to encounter several different ion pair limits corresponding to different asymptotic combinations of positive and negative ion states. This leads to (potentially many) distinct heavy Rydberg channels that may interact if they are reasonably close in energy, much in analogy to the multichannel situation observed in electronic Rydberg states.1,2 In terms of the excluded volume, the radius of the repulsive wall at close approach between the two fragments indeed relates to the size of the fragments. The net effect is that the quantum defects for the heavy Rydberg states of H2 are generally smaller than those for other molecules at the same position in the Coulomb potential. However, one should keep in mind that the quantum defect is a measure of how much the potentials deviate from the pure 1/R Coulomb potential in the entire interaction region, and will therefore relate to the shape of the potential energy curves at short and intermediate range, as well as the nonadiabatic couplings. Generally speaking, the ion pair and the associated ion pair potential will couple to other electronic states in the interaction region well before the actual repulsive wall between the two collision fragments is encountered. The perceived effect of the interactions in the collision complex on the spectrum will therefore relate not only to the size of the fragments, but also to various aspects of how the ion pair state couples to other electronic states such as valence and electronic Rydberg states. The quantum defect in the ion pair state of HCl is, coincidentally, similar to that in the ![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) H state of H2 (65–70 over ∼15
H state of H2 (65–70 over ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) and almost linear.
000 cm−1) and almost linear.
1 C. H. Greene and C. Jungen, Adv. Atom. Mol. Phys., 1985, 21, 51–121.
2 C. Jungen, Handbook of High-resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, 2010.
Ingo Fischer asked: Is it correct to associate the quantum numbers l and ml of common “light” Rydberg atoms and molecules with the rotational quantum numbers J and MJ in heavy Rydberg states?
Adam Kirrander responded: Absolutely, the analogy is very close, especially for 1S anion/cation pairs. In the external region, i.e. outside the interaction region, this analogy is essentially fully correct. To the best of my knowledge, this relationship was first pointed out by Frederick Mies,1–3 but other authors such as Alex Dalgarno also noted the deep analogy between heavy and ‘light’ Rydberg states4 around the same time.
1 F. H. Mies, J. Chem. Phys., 1984, 80, 2514–2525.
2 F. H. Mies and P. S. Julienne, J. Chem. Phys., 1984, 80, 2526–2536.
3 S.-H. Pan and F. H. Mies, J. Chem. Phys., 1988, 89, 3096–3103.
4 C. Asaro and A. Dalgarno, Chem. Phys. Lett., 1985, 118, 64–66.
David Clary said: It’s fascinating that even in almost the simplest molecule, H2, there’s still new information to be obtained. In going forward beyond H2 to more complex systems, are there any simple models or principles that come out of your calculations that can be used for further applications?
Adam Kirrander responded: The most striking aspect of the calculations in H2, apart from the great complexity contained in even so-called ‘simple’ systems at high energy, is how powerful a divide-and-conquer approach can be. The treatment of electronic and heavy Rydberg systems relies on the realisation that there are distinct regions of the dynamics where different physical pictures are most appropriate. In each region, a different partitioning of the Hamiltonian and a different computational method yield the best results. Such a patchwork of regions provides a globally accurate representation of the dynamics as long as the regions are assembled correctly, which of course is an approach that lies at the heart of scattering theory. In terms of more complex systems, I would be keen to extend our current work in three directions. The first is to combine dissociation and ionisation, including electronic and heavy Rydberg resonances, on an equal footing in the theoretical treatment. The second is to tackle polyatomics, most obviously triatomic molecules. Finally, on a grander scale, I am curious if this type of scattering theory-based approach demonstrated in our paper (DOI: 10.1039/C8FD00096D) could yield helpful results in the description of the type of roaming states first identified by Arthur Suits, Joel Bowman and colleagues1.
1 D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, Science, 2004, 306, 1158–1161.
Jeremy Richardson remarked: You said that in the inner interaction region, the system is very non-adiabatic. This suggests to me that the Born–Oppenheimer expansion may not be the best approach to solving the problem. Seeing as H2 is a very simple molecule, might it be possible to study this more easily from a different viewpoint?
Adam Kirrander responded: The system is indeed highly nonadiabatic in the interaction region, however a Born–Huang expansion over many adiabatic electronic states combined with the nonadiabatic coupling terms remains the most effective description computationally and conceptually. In fact, even for electronic Rydberg states in molecules, an arguably even more nonadiabatic situation, the Born–Oppenheimer separation of the nuclear and electronic degrees of freedom is still the most appropriate separation of the Hamiltonian while the Rydberg electron is inside the interaction region (commonly referred to as the ‘core’). This is exploited in multichannel quantum defect theory1,2 and R-matrix theory3 to make calculations tractable by treating the problem with a Born–Oppenheimer Hamiltonian when the Rydberg electron is inside the core, while adapting a molecular ion plus Rydberg electron Hamiltonian when the Rydberg electron is outside the core.4 Finally, it is worth noting that the continuity of the quantum defect as a function of the binding energy indicates that the Born–Oppenheimer description is the best model.
1 C. H. Greene and C. Jungen, Adv. Atom. Mol. Phys., 1985, 21, 51–121.
2 C. Jungen, Handbook of High-resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, 2010.
3 J. Tennyson, Phys. Rep., 2010, 491, 29–76.
4 C. Jungen and O. Atabek, J. Chem. Phys., 1977, 66, 5584–5609.
Ingo Fischer asked: Rydberg molecules experience l and ml mixing in electric fields, which leads to a lifetime enhancement. This effect was used in pulsed field ionisation/zero kinetic energy photoelectron spectroscopy to record high resolution spectra of molecular ions. The equivalent in heavy Rydberg molecules would be J and MJ mixing. Has such mixing been observed experimentally or computationally and do you have an estimate of the magnitude of the effect?
Adam Kirrander responded: This is correct. Notably, the lifetimes observed in experiments on heavy Rydberg states in H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 demonstrate lifetimes about an order of magnitude longer than theoretical predictions,2 something that has been attributed to J mixing by stray electric fields. We also know that a very similar approach to electronic ZEKE is possible in ion pair (heavy Rydberg) states from the work of Arthur Suits and colleagues.3,4
1 demonstrate lifetimes about an order of magnitude longer than theoretical predictions,2 something that has been attributed to J mixing by stray electric fields. We also know that a very similar approach to electronic ZEKE is possible in ion pair (heavy Rydberg) states from the work of Arthur Suits and colleagues.3,4
1 E. Reinhold and W. Ubachs, Phys. Rev. Lett., 2002, 88, 013001-1–013001-4.
2 A. Kirrander, J. Chem. Phys., 2010, 133, 121103.
3 X. Liu, R. L. Gross and A. G. Suits, Science, 2001, 294, 2527–2529.
4 A. Suits and J. W. Hepburn, Ann. Rev. Phys. Chem., 2006, 57, 431–465.
Francesco Gianturco said: From your accurate treatment of exotic atoms in heavy Rydberg states, which actual details of the involved dynamics you feel would be more profitable for clarifying experimental findings, and for which systems at your current level of accuracy in your calculations? Are there explanations using the familiar language of dynamical observables that you think you can provide to experimentalists?
Adam Kirrander answered: Our calculations directly provide the position and width of resonances, and hence predissociation lifetimes, and also lineshapes if required, allowing for quite detailed comparison with experimental spectra and other measurements. One of the major remaining issues is the actual excitation process taking a molecule into heavy Rydberg states. In a Franck–Condon picture, one would expect the heavy Rydberg states to be dark, yet clearly they have been observed and even appear to be quite common in molecular spectra. Clearly some sort of doorway states play an important role. A more detailed understanding of how this happens would be interesting and useful to experimentalists, but will most likely require that the electronic Rydberg states are accounted for, certainly in H2. An interesting aspect experimentally, and one where there still appears to be some discrepancy between theory and experiment, is the lifetime of heavy Rydberg states. Here, a unified study of ionisation, dissociation, radiative lifetimes, the effect of J-mixing due to stray fields, and, as suggested in the question from Prof. Stephen Leone in this meeting, the effect of blackbody radiation should be investigated.
When it comes to the type of molecular systems that can realistically be treated at the current level of accuracy, this is limited to molecules that can be treated accurately using scattering theory calculations. In practice, this means that the calculations could relatively easily be extended to triatomic molecules such as H2O and with some effort to somewhat larger molecules. An approximate assignment of spectra according to a heavy Rydberg progression is however completely general, and should be applicable as a general tool for classifying ion pair/heavy Rydberg states, many of which have previously been treated as anharmonic progressions involving numerous anharmonic parameters when a simple Rydberg expression would be more physically meaningful.1
1 R. J. Donovan, K. P. Lawley and T. Ridley, J. Chem. Phys., 2015, 142, 204306.
Dmitri Babikov opened a general discussion of the paper by Graham Worth: About 15 years ago, a similar method was proposed by Gert Billing. I always thought that it’s a great approach and wanted to follow it! Can you underline the similarities and differences between your method, and that of Billing?
Graham Worth answered: I think the method you are referring to is the Gauss–Hermite basis set that Gert Billing worked on.1 This was a different approach in that it was aiming to correct semiclassical dynamics rather than approximate the full quantum dynamics. The method built a set of Gauss–Hermite functions on top of a Gaussian function that followed a classical trajectory. This basis set was then used to expand the evolving wavepacket. Building a Gauss–Hermite basis is a nice idea as it gives greater flexibility at little cost. It would be interesting to add this to our multi-configurational approach.
1 G. D. Billing, J. Chem. Phys., 1999, 110, 5526.
Petr Slavíček remarked: The old problem of non-adiabatic simulations is the electronic structure theory. We are often left with the CASSCF method, (i) which is quantitatively inaccurate and (ii) potential energy discontinuities appear as new orbitals may rotate in the active space. The second problem seems to be also observed in the present work. The PES discontinuities are not necessarily disastrous for local methods, requiring only forces. The problem seems more severe in the DD-vMCG approach where the matrix elements involving the PES need to be calculated. How do you cope with this issue?
Graham Worth responded: This is indeed a key problem. The method we have been using to try and control discontinuities when using CASSCF-level potential functions is two-fold. The first is to propagate the CAS space orbitals and store these in the database along with the energies and derivatives. Each CASSCF calculation thus starts with a guess from the nearest set of orbitals and should be a good starting point, allowing the CAS space to smoothly change. The formamide example shows that this is not wholly successful as discontinuities are indeed seen in the N–H dissociation channel where high lying states are clearly crossing into the manifold and changing the CAS space required. The second part of the strategy is by ignoring failed CAS calculations which occur in regions of configuration space where the CAS is so poor that it, for example, does not lead to converged energies. It is assumed that these points are in non-important regions of space and the surfaces here can be provided by extrapolation from the database information.
Petr Slavíček asked: In the conclusions, you mention that “the diabatic surfaces also need to be tested beyond visual inspection for any inconsistencies.” How exactly is this non-visual inspection done?
Graham Worth replied: At the moment, this non-visual inspection is not done! What is meant by this statement is that we should check whether the propagated adiabatic–diabatic transformation (ADT) matrices are path-dependent or not. If they are path-dependent, then an error in the diabatisation is being introduced. For example, we are obtaining the ADT matrices by propagating from the nearest point in the database using the ab initio derivative couplings. An analysis could be done obtaining them from different points to see whether a significant difference is obtained. If not, they could be considered to be path independent.
Jens Petersen said: How computationally expensive is your method compared to classical trajectory-based approaches such as surface hopping, especially given the fact that a certain (not too small) number of Gaussians seems to be necessary in order to properly account for branching of the initial ensemble due to, e.g., isomerisation or fragmentation processes. What is the largest size of a molecule that you can think of simulating to date?
Graham Worth replied: When talking about expense one must also consider desired accuracy. vMCG is much more expensive than trajectory-based methods as the inversion of a matrix with rank f × n is required at each step, where f is the number of degrees of freedom and n is the number of basis functions. Classical methods scale linearly with both f and N (number of trajectories). However, classical trajectory-based methods are very slow to converge, and there is no guarantee that they will converge on the correct answer. In fact, if nuclear coherence or tunnelling is important, they will not. Thus, N ≫ n and if it appears that we are needing a large number of functions, then even more trajectories will be required. At present, molecules of the size of 10–20 atoms are realistic. Improvements are still possible and under investigation at present to improve on this.
Joel Bowman asked: On running direct dynamics vs. using potential energy surfaces, I’m sure you agree that to have the latter is preferable, but not always possible. Could you comment on this in your calculations? Also, the rather prompt dynamics showing more or less exponential decay suggests that classical calculations might capture the dynamics adequately in this case. Would you please comment on this?
Graham Worth answered: For accurate calculations I agree that at present, potential energy surfaces are the preferred method. A good surface can be made to fit globally using different information (including experimental) for different regions of the surface, whereas at present, electronic structure methods struggle to be accurate over a range of configurations. For accurate results, grid-based dynamics are also preferable to trajectory-based methods due to their completeness and simpler numerical behaviour. The big advantage of direct dynamics is the property of just searching the important part of configuration space. A major utility of direct dynamics is thus not only as a simulation method but also as a starting point for providing data for potential surface generation. This is one of the reasons we collect the ab initio data from a DD-vMCG calculation in a database of energies and derivatives.
Prof. Bowman is probably correct in his analysis that in the case of formamide classical trajectories, they would adequately capture the dynamics as the dissociation is pretty direct and non-adiabatic behaviour does not seem to be very important. In this case, particularly for dynamics in the S1 state, the challenge would be the convergence as there are a number of fragmentation channels open and many trajectories would be needed for good statistics, whereas the vMCG method provides a measure of the density going into each channel with a small number of Gaussian basis functions.
Joel Bowman asked: One point about potential energy surfaces vs direct dynamics is that the former can do a good job of smoothly interpolating “bumpy” ab initio energies that are sometimes encountered in direct dynamics.
Graham Worth replied: I agree. It is also difficult in direct dynamics to observe and assess the level of “bumpiness” experienced by the evolving wavepacket.
Anne B. McCoy said: Following up on several of these questions about your potentials – in your paper (DOI: 10.1039/C8FD00090E), you describe using an interpolation scheme for the gradients and Hessians as well as the electronic energies. Can you comment on the sensitivity of your results to the interpolation scheme? How are these sensitivities mitigated or made more severe when you use the interpolated potential for the propagation of a wave packet expressed as an ensemble of Gaussians, rather than strict classical dynamics?
Graham Worth responded: This sensitivity to the interpolation scheme is presently being investigated. We know it can be severe as changing the parameters used in the Shepard interpolation (e.g. the power law used in the weighting) can lead to substantial changes in the dynamics, seen as large fluctuations of the total energy. The difficulty in knowing how to mitigate for this is that we use a local harmonic approximation for the matrix elements of the Hamiltonian in the Gaussian basis. This also introduces an error and compounds any problems with the interpolation as the Hessians often contain errors, especially when calculated using electronic structure theory away from equilibrium points. Classical dynamics is less sensitive as it only requires first derivatives.
Joel Bowman asked: With respect to Shepard interpolation and oscillations in the fit, a known issue, there are now smoother interpolation methods that I can recommend. One is Gaussian process regression and the other is permutationally invariant polynomials. Have you investigated using these methods?
Graham Worth replied: We have not yet investigated these interpolation methods, but I agree they could provide much better and smoother surfaces. Work on this is being done by Scott Habershon who is trying to combine DD-vMCG calculations with automatic generation of surfaces for grid-based dynamics using Gaussian process regression.1 In addition, the Gaussian process regression might provide a suitable way around the restriction of using a local harmonic approximation (LHA) for the Hamiltonian matrix elements in the vMCG Gaussian basis by providing the surfaces also in a Gaussian basis.
1 G. W. Richings and S. Habershon, Chem. Phys. Lett., 2017, 683, 228.
Anne Zehnacker-Rentien said: The DD-vMCG studies you presented only consider the singlet states, as most of the curve-crossing studies do. I find it surprising, especially for large biomolecules with n π* transistions, that the triplet manifold is never considered. Can you comment on this?
Graham Worth responded: There is in principle no problem with adding intersystem crossing to a triplet manifold – one just uses spin–orbit coupling between the singlet and triplet states in addition to any non-adiabatic coupling between states of the same spin. We have implemented the methodology and are presently testing it in benzene, a system we have previously treated using a vibronic coupling model.1 The difficulties are practical rather than theoretical due to the large number of states involved and the need to keep track of couplings as states change order along a propagation.
1 T. J. Penfold et al., J. Chem. Phys., 2012, 137, 204310.
Joel Bowman addressed Graham Worth and Anne Zehnacker-Rentien: Concerning singlet–triplet couplings, these are of course present, and in fact, in formaldehyde photodissociation, in the energy range explored by experiment and theory, the mechanism is S1 to T1 to S0. See ref. 1 for example. However, for spin orbit coupling of the order of 10 cm−1, the timescale for intersystem transfer is relatively slow compared to transfer via a conical intersection, provided of course the intersection can be reached rapidly by the dynamics.
1 B. Fu, B. C. Shepler and J. M. Bowman, J. Am. Chem. Soc., 2011, 133, 7957–7968.
Graham Worth answered: I would like to add to this, and extend my response to Prof. Zehnacker-Rentien, that the often small spin–orbit coupling is a challenge to direct dynamics both due to the requirement of accuracy in the calculated couplings and the long timescales involved.
Dmitri Babikov commented: I am somewhat lost in the numbers. You mentioned that the number of basis functions is on the order of 100. If each of those is propagated for, say, 100 time steps, then we need to compute 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ab initio data points. Isn’t that sufficient to construct the PES? Instead of doing it on the flight?
000 ab initio data points. Isn’t that sufficient to construct the PES? Instead of doing it on the flight?
Graham Worth replied: Because we use a database of calculated points and interpolate when close to previously calculated data, we do not compute an ab initio point at every time step. Exactly how often new points get calculated is highly problem specific – for systems that are harmonic only a few points are needed, whereas if large range motions and dissociation takes place, many more are calculated. In the formamide example in the paper (DOI: 10.1039/C8FD00090E), which includes dissociation, around 6000 points were calculated for a 100 fs propagation, which is about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps (we use a variable step size integrator and steps average around 0.01 fs).
000 steps (we use a variable step size integrator and steps average around 0.01 fs).
Petr Slavíček asked: The vMCG approach with the fully coupled localized basis resembles approaches based on “quantum trajectories”. This refers either to Bohmian dynamics or to phase space analogues such as the “entangled classical trajectories” (see e.g. Donoso and Martens1). In Bohmian dynamics, a quantity called “quantum force” emerges. This quantum force has certain unfortunate properties which makes its use for impractical calculations problematic. Some sort of quantum force should also emerge from the coupled Gaussian approach. Would one get such a force if one subtracts the mass attributed to the basis multiplied by its acceleration and the gradient of the potential?
1 A. Donoso and C. C. Martens, Phys. Rev. Lett., 2001, 87, 22320.
Graham Worth responded: This is an interesting topic that requires more thought. The Gaussian basis functions in vMCG do indeed feel a “quantum” force which is related to the curvature of the potential surfaces under the function. This is seen as coupling between the functions due to terms in the potential higher than linear. It is, however, also basis set-dependent as it relates to the width of the function, and I do not know if it can be related to the Bohmian quantum force.
Francesco Gianturco remarked: You have shown in your presentation that a variety of numerical problems exist when interpolating the existing PESs, when employing the local harmonic approximation or when having to extend the time interval of the reaction progress. Would you be able to comment, at the current level of accuracy of the method you have developed, on how realistic the comparison of its computed observables would be, if any, with existing experimental observables on current systems? What are the quantities which you expect you would be more likely to represent at an acceptable level of accuracy?
Graham Worth responded: At present, results from the direct dynamics calculations are indeed very “noisy”, and it is only possible to extract highly averaged quantities such as state populations and timescales. As shown in the paper (DOI: 10.1039/C8FD00090E), we can also get branching ratios. In principle, the vMCG method is able to reproduce spectra in the same way that grid-based calculations can. This has been demonstrated for model Hamiltonians using polynomials up to fourth order with exact integrals (Richings et al. Int. Rev. Phys. Chem., 2015, 34, 269).1 There is also no problem in including an explicit light field. Thus it is hoped that once we have solved the interpolation and integral problems we will be able to access observables that can be compared directly with experiment. It is unlikely that the method will ever be accurate enough to calculate sensitive properties such as scattering cross-sections.
1 G.W. Richings et al., Int. Rev. Phys. Chem., 2015, 34, 269–308.
Adam Kirrander commented: As a brief remark to Prof. Gianturco’s interesting question, I would like to point out that one of the fascinating developments in ultrafast science is the increasing ability of experiments to probe the evolution of quantum systems, e.g. small molecules, in ever greater detail. This includes, to name but a few, developments in ultrafast spectroscopy,1–3 ultrafast X-ray scattering,4,5 ultrafast electron diffraction,6 other imaging techniques,7 and the potential for direct probes of electronic coherence8,9 or non-linear measurements.10 The collective impact of these increasingly sophisticated measurements will be to challenge computations and simulations by necessitating much more detailed comparisons between theory and experiment than just, say, an overall exponential decay.
1 C. Z. Bisgaard, O. J. Clarkin, G. Wu, A. M. D. Lee, O. Gessner, C. C. Hayden and A. Stolow, Science, 2009, 323, 1464–1468.
2 A. R. Attar, A. Bhattacherjee, C. D. Pemmaraju, K. Schnorr, K. D. Closser, D. Prendergast and S. R. Leone, Science, 2017, 356, 54–59.
3 A. D. Smith, E. M. Warne, D. Bellshaw, D. A. Horke, M. Tudorovskya, E. Springate, A. J. H. Jones, C. Cacho, R. T. Chapman, A. Kirrander and R. S. Minns, Phys. Rev. Lett., 2018, 120, 183003.
4 M. P. Minitti, J. M. Budarz, A. Kirrander, J. S. Robinson, D. Ratner, T. J. Lane, D. Zhu, J. M. Glownia, M. Kozina, H. T. Lemke, M. Sikorski, Y. Feng, S. Nelson, K. Saita, B. Stankus, T. Northey, J. B. Hastings and P. M. Weber, Phys. Rev. Lett., 2015, 114, 255501.
5 J. M. Glownia, A. Natan, J. P. Cryan, R. Hartsock, M. Kozina, M. P. Minitti, S. Nelson, J. Robinson, T. Sato, T. van Driel, G. Welch, C. Weninger, D. Zhu and P. H. Bucksbaum, Phys. Rev. Lett., 2016, 117, 153003.
6 J. Yang, M. Guehr, X. Shen, R. Li, T. Vecchione, R. Coffee, J. Corbett, A. Fry, N. Hartmann, C. Hast, K. Hegazy, K. Jobe, I. Makasyuk, J. Robinson, M. S. Robinson, S. Vetter, S. Weathersby, C. Yoneda, X. Wang and M. Centurion, Phys. Rev. Lett., 2016, 117, 153002.
7 R. Forbes, V. Makhija, K. Veyrinas, A. Stolow, J. W. L. Lee, M. Burt, M. Brouard, C. Vallance, I. Wilkinson, R. Lausten and P. Hockett, J. Chem. Phys., 2017, 147, 013911.
8 M. Vacher, M. J. Bearpark, M. A. Robb and J. P. Malhado, Phys. Rev. Lett., 2017, 118, 083001.
9 A. Kirrander, K. Saita and D. V. Shalashilin, J. Chem. Theory Comput., 2016, 12, 957–967.
10 M. Kowalewski, K. Bennett, K. E. Dorfman and S. Mukamel, Phys. Rev. Lett., 2015, 115, 113001.
Adam Kirrander followed up with a question: An interesting consequence of the variationally derived equations of motion is that the phase space is covered quite efficiently and that convergence, especially in low-dimensionality highly quantum systems, is more efficient than with semiclassical trajectories. On the other hand, the propagation of semiclassical trajectories is more convenient computationally and appears to be numerically more stable. Can one have the best of both worlds via a hybrid method that primarily relies on the variational propagation but is augmented by semiclassical trajectories? Would that be sensible?
Also, would you like to comment on the use of the complex absorption potential in the calculations? Complex absorption potentials are of course well-established, but I would naively have assumed that the trajectories would decouple asymptotically and that they could be propagated almost trivially using analytical extensions of their phase and coordinates thereafter.
Graham Worth answered: Indeed I believe that the variational nature of the basis functions in the vMCG algorithm is key to efficiency through fast convergence, and also to correctly treating nuclear quantum effects such as tunnelling and curve crossing. However, Dr Kirrander is correct in stating that they are less efficient in the sense of computational effort than semiclassical trajectories. It is fortunately easy to have a hybrid quantum/semiclassical method within the framework of vMCG. The equations of motion for the centres of the Gaussian functions can be written as a classical part plus a non-classical part that provides the quantum coupling. One can simply ignore these non-classical terms to obtain “semiclassical” basis functions, and this can be done to a subset of “bath” modes, retaining the full quantum treatment for the important modes. This hybrid method remains fully quantum mechanical through the variational treatment of the expansion coefficients, but with a less than optimal basis. For modes that are classical in nature, this should not be a problem but result in a saving of computer effort. This is implemented in our code, but has not been tested to any great extent.
Complex absorbing potentials were used to prevent the need to integrate the fast phases of dissociating parts of the wavepacket, which leads to small time steps for no gain in information. The use of an analytic extension to propagate basis functions that decouple asymptotically in a dissociation channel is a good idea that would allow the propagation to continue after dissociation takes place without this problem. We will investigate this.
Adam Kirrander addressed Francesco Gianturco and Graham Worth: One final comment on this topic is that the non-adiabatic internal conversion processes is not necessarily much faster than intrasystem crossing driven by spin–orbit coupling if the spin–orbit coupling is reasonably strong, mostly due to the presence of comparatively heavy atoms. Recent examples from our own work include the molecules carbon disulfide1 and diiodobenzene.2
1 A. D. Smith, E. M. Warne, D. Bellshaw, D. A. Horke, M. Tudorovskya, E. Springate, A. J. H. Jones, C. Cacho, R. T. Chapman, A. Kirrander, and R. S. Minns, Phys. Rev. Lett., 2018, 120, 183003.
2 B. Stankus, N. Zotev, D. M. Rogers, Y. Gao, A. Odate, A. Kirrander and P. M. Weber, J. Chem. Phys., 2018, 148, 194306.
Thomas Malcomson commented: Assuming I am understanding your method correctly, it would appear that you are currently limited to quite a small area surrounding the conical intersection itself. With this in mind, and looking towards the study of a full photochemical dynamic reaction coordinate, what do you consider to be the potential for your method to expand to a point where it could replace/enhance study of the entire ‘cone’ of the conical intersection, an area more traditionally covered by the IRD (initial reaction direction) protocol? And what do you consider to be the main difficulties in expanding this method to account for both the area of the PES that would need to be covered, and the accuracy needed to begin to probe and predict these conical intersection-based photochemical reactive processes?
Graham Worth responded: Calculations using the vibronic coupling model Hamiltonian are indeed limited to regions around an intersection (or more usually around the Frank–Condon point). The direct dynamics DD-vMCG calculations are, at least in principle, not limited in any way. The algorithm uses a time-evolving fully quantum mechanical wavefunction, and thus nuclear coherences are retained on passing through an intersection. One limiting factor is the approximate nature of the presently used propagation diabatisation, that may accumulate errors as a propagation progresses. A more major limitation for the scope that can be covered is the quantum chemistry method chosen, e.g. CASSCF calculations may fail moving away from the starting region as the chosen CAS space becomes inappropriate.
Stephen Leone made a general comment to all delegates: I would like to discuss experimental observables of curve crossings and conical intersections and to encourage the discussion group to consider how to bring theoretical calculations along to address new kinds of experimental results. In the famous IBr experiments of Zewail, the wave packet in the excited state of IBr was observed to leak out. We now are starting to see some experiments on electron diffraction and X-ray diffraction, where passing through conical intersections is recorded, as well as X-ray and XUV transient absorption methods, which are core-level specific, so there are new spectroscopic signatures of passage through curve crossings and conical intersections. In a recent example on IBr in an attosecond experiment, we can see the changes in energy of the atomic core-level transitions of both I and Br as the molecule passes through the curve crossing. This result shows new observables and what is going to be required to explain the very short time dynamics of the iodine and bromine spectral features, as they report on the passage through the crossing. The sweeping changes in energy and shifting of intensities of these atomic transitions in the molecule provide a complete record of the dynamical event. New work will be required to visualize the spectral transitions through the curve crossing regions for these new types of ultrafast/attosecond spectroscopic experiments.
Joel Bowman opened a general discussion of the paper by Uwe Manthe: This is a very nice decomposition approach to get these transition state states. In the F + CH3D reaction where there are evidently resonances, according to a recent report from the group of Kopin Liu, I have two questions. First, can you can calculate resonances in principle using your approach, and if so, can you distinguish them from the transition state states?
Uwe Manthe responded: The resonances in the F + CH3D reaction result from long-living quasibound states caused by van der Waals wells in the entrance channel of the reaction. These resonances, which clearly can affect the reactivity and the natural reaction channels, should be distinguished from the vibrational states of the activated complex and the corresponding natural reaction channels discussed in the present work. The natural reaction probabilities or, equivalently, the eigen reaction probabilities introduced in earlier work with W. H. Miller1 represent the transmission mission coefficients corresponding to the natural reaction channels. For barrier reactions, these transmission coefficents show thresholds at energies where the channel opens up. Truhlar, Skodje and coworkers2,3 interpret these thresholds (which are observable in the cumulative reaction probability) as series of resonances, but I do not find this interpretation particularly helpful. I prefer to view the natural reaction channels as true channels, i.e. as one-dimensional pathways over the reaction barrier, and not as sets of discrete resonance states. The eigen reaction probabilities or natural reaction probabilites then are simply the corresponding transmission coefficients and the structures seen in these probabilities can be mostly interpreted as threshold energies and not as resonance energies.
1 U. Manthe and W. H. Miller, J. Chem. Phys., 1993, 99, 3411.
2. D. C. Chatfield, R. S. Friedman, D. W. Schwenke, and D. G. Truhlar, J .Phys. Chem. 1992, 96, 2414.
3. M. Gustafsson, R. T. Skodje, J. Chem. Phys. 2006, 124, 144311.
Roland Wester remarked: In your article, you focus on the initial vibrational states of the reactants. From an experimental point of view, that’s possible to observe but fairly difficult. We recently did some work in this direction.1 In crossed-beam experiments, it is more straightforward to get information on final states. I assume your calculations also produce results for the branching into final vibrational channels? Is this correct, and if yes, what can you learn from this?
1 M. Stei et al., Sci. Adv., 2018, 4, 7.
Uwe Manthe replied: The present paper (DOI: 10.1039/C8FD00081F) focuses on reactant states, since for H + CHD3 we presently have only completed the simulations describing the wave packet motion from the transition state into the entrance channel. We are presently finishing our calculations for the motion into the product region. However, for the H + CH4 reaction, we already presented state-to-state calculations which studied final state distributions. There, it was found that for low to moderate total energies, only the umbrella vibration of the methyl product is excited. Significant amounts of energy are deposited in this mode. However, no other vibrations are excited in the products. Employing a simple sudden model, i.e. considering Franck–Condon factors between the transition state and the products, one can easily rationalize why no excitation in the other methyl modes are found. However, the absence of the H2-stretching excitation is a result which is in disagreement with the predictions of sudden models. Here we found that the large amount of energy required for a single excitation of the H2-stretch, about 4000 cm−1, plays a key role. Exciting this vibration would require a very large fraction of the available total energy and thus is improbable. This finding marks a breakdown of the otherwise successful sudden picture: the sudden decay of the activated complex requires a sizeable amount of energy in the relative translation. I think these findings for the H + CH4 reaction remain valid also for its isotopic analogs as well as for many other reactions of methane.
Jeremy Richardson asked: Is it easy to predict what the reaction channels will be? For instance, do they generally correspond to excitations of normal modes of the transition state?
Uwe Manthe replied: For reactions proceeding via sizeable reaction barriers, yes. Here, the natural reaction channels correspond to vibrational states of the activated complex. The normal mode picture at the transition state typically provides a good approximation for the vibrational states of the activated complex. However, anharmonicity can change the precise energy values of the vibrational states and can result in state mixing between vibrational states which are nearly degenerated in the harmonic approximation.
Francesco Gianturco remarked: Very interesting, very nice work – the method of single decomposition for the scattering matrix is a very interesting idea. If one now focuses on the sum over the index k, you are in the end producing a number of single values that you’re obtaining from the full scattering matrix. My question is, if instead of introducing a full scattering matrix summed over the n indices of all the channels produced by the reactants and products, you were to use a reduced sum over those S-matrix indices, can the sum over the k index also be reduced? What would then be the physical meaning of the reduced sum over the dimension of the single decomposition space?
Uwe Manthe replied: To compute natural reaction channels from the S-matrix, one has to know the full S-matrix including the full set of asymptotic quantum states for the total energies under consideration. It is not possible to compute a partial set of natural reaction channels from partial S-matrix information. However, natural reaction probabilities can be computed directly from reaction rate calculations which simulate the quantum dynamics in the region close to the transition state only. As the natural reaction channels are connected to specific pathways through the reaction barrier, the computation of the number of reaction channel and the associated natural reaction probabilities does not require asymptotic state information. Thus, the natural reaction channel analysis can be performed without knowledge of the full S-matrix.
David Clary asked: There are several reported experimental measurements of H2 rotational product distributions from reactions of polyatomic molecules. Experiments even go beyond methane to more complicated hydrocarbons. Do you think that your findings can be useful when you go to more complicated systems beyond methane, or are they just related to the special symmetry that you have in the system you studied?
Uwe Manthe responded: I think that many of the qualitative results obtained for the H + CH4 reaction are transferable to the reactions of other hydrocarbons. The physical pictures emerging from the analysis of the H + CH4 reaction should remain valid. The additional hydrocarbon group can be expected to largely act as a spectator. However, some difference might be found since the methyl umbrella motion is no longer present in the same form as in the reaction of methane. Considering full-dimensional quantum dynamics calculations, the accurate treatment of larger hydrocarbons will presumably not be possible in the near future. In contrast to the reaction of methane, in reactions of larger hydrocarbons, rotational motions around the C–C bonds would have to be considered. This is a challenging subject for rigorous quantum dynamics simulations.
Susmita Kar commented: Though the reaction channels discussed in the paper (DOI: 10.1039/C8FD00081F) consist of saturated hydrocarbons, is this necessary? Or, can similar types of molecule such as ammonia, in which umbrella-type inversion occurs, also be applicable in this type of reaction channels?
Uwe Manthe replied: The concept of natural reaction channels is applicable to any type of reaction including reactions which show multiple transitions or even reactions proceeding via a potential well. However, the intuitive understanding of the natural channels is most straightforward in the case of reactions proceeding via a potential barrier. Here, the natural reaction channels can be associated with the different (ro)vibrational states of the activated complex. For reactions proceeding via multiple different pathways, one can often simply associate different sets of natural reaction channels with the different pathways available. However, if interference effects between different transition states are relevant, this interference will also show up in the natural reaction channels. Reactions of ammonia might be a case where this interference could be found: here, the inversion of the ammonia fragment might offer a low-energy pathway between transition states with similar energies but different geometries.
Timothy Burd opened a general discussion of the paper by Jeremy Richardson: You state in your paper (DOI: 10.1039/C8FD00085A) that the location of the instanton can depend quite strongly on the quality of the potential energy surface being used. When you are using an interpolated surface, as in this work, can you be sure your instanton will be located accurately?
Jeremy Richardson replied: Because we add more training points along the instanton path, we expect the interpolation to be accurate in this local region. There are a number of approaches we could use to test this more carefully, by comparing the results of new points with what would have been predicted from the interpolated PES or by using GPR to make error predictions.
David Benoit asked: Jeremy, in your paper (DOI: 10.1039/C8FD00085A) you mention results from another group that use neural networks for instanton theory instead of Gaussian processes – can you comment on the advantages of each technique? Our experience is that neural networks are sometimes superior to Gaussian processes when fitting multi-dimentional surfaces.
Jeremy Richardson replied: We found Gaussian process regression to be very stable and were able to reproduce exactly the rates of an on-the-fly calculation. GPR works well here perhaps because we only need to fit the surface in a small local region, whereas it is true that many people have identified problems in using GPR to fit global surfaces. Neural networks may be better at fitting global surfaces, but not necessarily for local surfaces. However, we have not done a direct comparison ourselves.
David Clary asked: You do the calculations of rate constants for different temperatures. Once you have done the computations for one temperature, is there extra computational expense for other temperatures, or do you essentially get them for free?
Jeremy Richardson replied: As the system is cooled down, the instanton will explore new parts of the PES so it is necessary to include further training points in order to retain a high accuracy. Although we did not test this very carefully, one would expect that for intermediate temperatures, enough of the surface would be well-described such that rates could be obtained essentially for free.
Majdi Hochlaf remarked: Do you need to explore the potential energy surface of the system in the vicinity of the transition state using standard methods in order to guide the reaction path you are showing?
Jeremy Richardson replied: We typically start our calculations by optimizing the transition state using standard methods and then place a few training points in the direction of the eigenvector corresponding to the imaginary mode. This is enough to start the instanton optimization and the PES is learned by adding more points iteratively.
Majdi Hochlaf asked: Can you use this approach for weakly bound van der Waals systems?
Jeremy Richardson replied: We can, for instance, describe the tunnelling effect of rearrangements of water clusters1,2 and the same approach would also be applicable to van der Waals complexes. However, if the complex is so weakly bound that the zero-point energy is higher than the rearrangement barrier, it is no longer a tunnelling problem and instanton theory is no longer the right approach.
1 J. O. Richardson, S. C. Althorpe and D. J. Wales., J. Chem. Phys., 2011, 135, 124109.
2 J. O. Richardson, C. Pérez, S. Lobsiger, A. A. Reid, B. Temelso, G. C. Shields, Z. Kisiel, D. J. Wales, B. H. Pate and S. C. Althorpe., Science, 2016, 351, 1310.
David Clary remarked: There are many reactions with more than one transition state, where you might get two or more instantons. Can the theory be extended to something like that in a straightforward way?
Jeremy Richardson responded: If the two instantons are well-separated, it is very easy to simply add the two rates together. However, the method would not be applicable to a liquid where many transition states are strongly coupled to each other. For this problem, one should use the related ring polymer molecular dynamics1,2 instead.
1 I. R. Craig and D. E. Manolopoulos., J. Chem. Phys., 2005, 122, 084106.
2 J. O. Richardson and S. C. Althorpe., J. Chem. Phys., 2009, 131, 214106.
David Clary commented: We know from our own calculations on H + propane1 that the two distinct reaction channels hardly interfere with each other.
1 H. F. von Horsten, S. T. Banks and D. C. Clary, J. Chem. Phys., 2011, 135, 094311.
Anne Zehnacker-Rentien asked: Could you extend your theory to intramolecular proton transfer, in the particular case where the dominant pathway you use in your calculations is strongly coupled to another vibration? I mean, could you reproduce the effect of promoting or inhibiting modes, i.e. calculate the rate constant corresponding to the excitation of one of these peculiar modes?
Jeremy Richardson replied: We also use instanton theory for computing tunnelling splittings due to intramolecular proton transfer, for example in formic acid dimer.1 In order to describe the effects of vibrational excitation, some extension to the theory is required which we are currently working on.
1 J. O. Richardson, Phys. Chem. Chem. Phys., 2017, 19, 966.
Francesco Gianturco remarked: When you have more than one transition state in a polyatomic system, one could work as a filter for the flux density which is coming over into the next one – in other words, you have a flux restriction from the first tunneling when going through the second barrier. You therefore perhaps get a smaller quantity of reactants into the second barrier, which has to be taken into account in the final accounting for the rate. But are the instantons able to differentiate the flux densities? So the final rate should not be exactly the sum of the two probabilities since that sum has to be weighted with the filtering of the population created by each new tunneling process.
Jeremy Richardson replied: In the example you describe, a nonequilibrium distribution would build up in between the two barriers and thus the standard instanton approach would not be applicable. It is for this reason that we are working on the derivation of a microcanonical instanton theory1,2 which would be able to describe such a problem, at least qualitatively.
1 S. Chapman, B. C. Garrett and W. H. Miller, J. Chem. Phys., 1975, 63, 2710–2716.
2 J. O. Richardson, Faraday Discuss., 2016, 195, 49–67.
Krzysztof Szalewicz commented: Are you familiar with the method of interpolating moving least squares? It is a method of fitting potential energy surfaces (PESs) developed in recent years mainly by Richard Dawes and collaborators.1–3 This method allows one to fit a surface locally and then if needed extend the fit to a nearby region of space. This may be a useful approach for the type of work you are doing since you can use small numbers of grid points if the region of interest is of limited range.
1 R. Dawes, D. L. Thompson, Y. Guo, A. F. Wagner and M. Minkoff, J. Chem. Phys., 2007, 126, 184108.
2 R. Dawes, X.-G. Wang and T. Carrington Jr., J. Phys. Chem. A, 2013, 117, 7612.
3 M. Majumder, S. A. Ndengue and R. Dawes, Mol. Phys., 2016, 114, 1–18.
Jeremy Richardson answered: Thank you for the suggestion. We will look into these methods more closely to see if it has advantages over our current approach.
Joel Bowman commented: Concerning fitting with Gaussian process regression, we have recently shown how this approach can be made permutationally invariant1 and this is always a good aspect to include in fits. I appreciate for instanton calculations that this is probably not needed but in general one gets more accurate fits including this fundamental symmetry.
1 Q. Chen et al., J. Chem. Theory Comput., 2018, 14, 3381–3396.
Jeremy Richardson responded: As you say, this is not necessary for our approach as we only consider one reaction at a time. However, it may be useful when we use the approach to study degenerate rearrangements for which it is important to have permutationally invariant surfaces.
Joel Bowman asked: Very nice comparison for the H + ethane reaction with the work from the Clary group. Did you all use the same electronic structure method?
Jeremy Richardson answered: It is similar, although unfortunately not exactly the same so it is difficult to rigorously assign the minor difference in the rate to either the PES or to the theory. We suspect that as this is such a simple reaction, the theories both perform well and the minor differences are due to the PES. The SCTST calculations were performed using CCSD(T)/cc-pVTZ for energies, and MP2/cc-pVTZ for Hessian calculations, whereas we used CCSD(T)-F12/cc-pVTZ-F12 for both energies and Hessians.
David Clary commented: The rate constants in Table 4 of Richardson et al. for H + ethane are very small indeed for the lower temperatures, and would look quite similar on the usual Arrhenius log plot.
Joel Bowman remarked: It would be good to get comments from both of you concerning the pros and cons of SCTST and the instanton theory and a general comparison of these two methods. Please consider accuracy.
Jeremy Richardson responded: SCTST will be more accurate than instanton theory for reactions occurring near the barrier top because it includes higher order derivatives of the PES and does not overestimate the rate at the crossover temperature. However, instanton theory is expected to be more accurate at lower temperatures, especially in cases involving a lot of corner cutting. An on-the-fly ab initio instanton approach would probably be less efficient than SCTST as it requires computing many Hessians along the path. However, our new GPR-aided instanton method is probably now more efficient than SCTST as we have reduced the number of electronic structure calculations required by an order of magnitude.
David Clary replied: We are planning a detailed comparison of the two methods. This will examine both the computational efficiency of the procedures and their accuracy in calculating rate constants at the same level of ab initio theory. The parameters needed for SCTST are easily expressed in terms of the derivatives of the potential at the transition state, and the computation of these parameters from ab initio calculations does not have to be repeated for different temperatures. However, the paper from Richardson and co-workers (DOI: 10.1039/C8FD00085A) demonstrates that significant progress is being made in enabling the instanton rate constants to be produced from a small number of ab initio computations.
David Clary commented: We did apply the Wagner correction1 in our SCTST computations and this ensures the correct exothermicity of the reaction. The differences between the rate constants summarised in Table 4 of the paper by Richardson et al. (DOI: 10.1039/C8FD00085A) for H + ethane are most likely due to the various electronic structure methods used in the different calculations.
1 A. F. Wagner, J. Phys. Chem. A, 2013, 117, 13089–13100.
Timothy Burd asked: For some reactions, for example the reaction of H with ethane, you must be quite careful with the treatment of internal rotational degrees of freedom, which I believe are treated harmonically in this model. Whilst this is accurate at very low temperatures, at higher temperatures their behaviour may be more like that of a free rotor. This is particularly important for reactions where the internal rotation is present in only one of either the reactant or transition state configurations (for example, the reaction of CH4 with CH3). Is there a way to treat these more rigorously within the instanton formalism?
Jeremy Richardson replied: In the paper (DOI: 10.1039/C8FD00085A), we compare a quantum instanton (QI) calculation with our semiclassical instanton result for H + ethane. As QI describes internal rotations accurately, the difference between these approaches will highlight the error we are making and it is seen to be less than 50%. You may be right that CH4 + CH3 will show a larger effect and this would be worth studying in the future. The problem of treating internal rotations is something which also exists for Eyring transition state theory. Many of the techniques developed to improve this description could probably also be used with instanton theory, although further work would be needed to determine the details.
Petr Slavíček asked: Is there a non-adiabatic verson of the instanton rate theory?
Jeremy Richardson replied: We have derived an instanton theory for the nonadiabatic (golden rule) limit1–3 and are working on deriving a more general theory applicable to any regime.
1 J. O. Richardson, R. Bauer and M. Thoss., J. Chem. Phys., 2015, 143, 134115.
2 J. O. Richardson, J. Chem. Phys., 2015, 143, 134116.
3 J. Mattiat and J. O. Richardson, J. Chem. Phys., 2018, 148, 102311.
Uwe Manthe commented: I want to put Jeremy’s work in the historic perspective of calculating rates on locally accurate potential energy surfaces (PES). About 15 years ago, we computed reaction rates for the H + CH4 reaction combining a locally accurate PES constructed using Shepard interpolation and accurate quantum dynamics with the MCTDH approach.1–3 To obtain converged results for the full temperature range considered, about 50 Hessians were required. I want to ask Jeremy to comment on the progress achieved in his recent work. What do you think are the reasons that you can get accurate results with 6 to 8 Hessians instead of 50? Is it the improved interpolation scheme, the backfeeding of information from the instanton to the potential energy surface generation, or the smaller portion of the PES sampled by the instanton?
1 T. Wu and U. Manthe, J. Chem. Phys., 2003, 119, 14.
2 T. Wu, H.-J. Werner, and U. Manthe, Science, 2004, 305, 2227.
3 T. Wu, H.-J. Werner, and U. Manthe, J. Chem. Phys., 2006, 124, 026102.
Jeremy Richardson replied: I suppose that it is a combination of all three points which make our PES so easy to build. In particular, note that the instanton is a line along the PES with zero width and thus it is effectively a one-dimensional interpolation. In contrast, a wavepacket explores a wide region of the PES and will thus surely require much more information to converge. Another point is that GPR is expected to be a better fitting algorithm than Shepard interpolation. Of particular importance to this work is that it gives a smooth differentiable PES, whereas Shepard interpolation may include tiny unphysical bumps which cause semiclassical approaches to fail.
Adam Kirrander said: Jeremy, you mentioned that in some cases the instanton is quite far removed from the transition state. I am curious at what point an algorithm that starts building the potential energy surface at the transition state and then expands outwards begins to become expensive? Is this ever a problem? And as the necessary potential energy surface becomes larger and more expansive, does one potentially face any issues relating to the distance matrix description of the internal coordinates and the redundancy of the distance matrix?
Jeremy Richardson answered: When the temperature drops much lower than the crossover temperature, the instanton may find a path which is far from the transition state. This is particularly clearly seen when using instanton theory to compute tunnelling splittings which is performed in the T→0 limit. In these cases, we would use a different initial guess for the instanton optimization and build the PES iteratively around that. We do not expect to have a problem with trying to describe a larger region of the PES, but it would anyway be unnecessary. As new points are introduced into the GPR, old points can also be taken away if they are deemed to be far from the region of interest.
Roland Wester asked: What can be learned from the instanton model for triatomic systems, for which full quantum calculations are available?
Jeremy Richardson responded: We have carried out a number of comparisons, in particular for the H + H2 reaction on the BKMP2 surface. We generally find that thermal rates are in good agreement with full quantum rates even at very low temperatures with typically only about 20% error. Our results are presented in the following review paper.
1 K. Karandashev, Z.-H. Xu, M. Meuwly, J. Vaníček and J. O. Richardson, Struct. Dyn., 2017, 4, 061501.
Thierry Stoecklin opened a general discussion of the paper by Dmitri Babikov: You distinguish Feshbach and shape resonances by performing two different calculations – one excluding the overlap matrix and the other including it. Could you tell us if the positions of the shape resonances are shifted when you perform the calculations including the overlap matrix and if some of them disappear? I imagine that the energies of some formal shape resonances may be very close to some of the Feshbach resonances. So could you tell us how you make sure that a resonance is a Feshbach resonance and not a shifted shape resonance?
Dmitri Babikov answered: Our calculations indicate that the non-diagonal elements of the overlap matrix, responsible for the coupling of the diabatic vibrational channels (and eventually for the formation of Feshbach resonances), cannot be viewed as a small perturbation to the spectrum of shape resonances (determined by tunneling). The role of coupling appears to be rather significant. When these couplings are included and the formation of the Feshbach resonances is enabled, not only the energies and widths of resonances change significantly, but also the total number of resonances increases, and the rate coefficient of the recombination process grows, roughly by a factor of 20. From this we conclude that in the ozone molecule the majority of scattering resonances are Feshbach-type resonances, with a relatively small number of pure shape resonances (which makes sense intuitively, since the tunneling is weak for heavy atoms, such as oxygen). Comparing the two spectra (shape resonances vs Feshbach) we could not find any clear similarities or draw a definite one-to-one correspondence between the states.
David Clary said: I think for a complete theory for this problem, you have to treat three-body collisions. This treatment has been done, for example, in ref. 1. Have you thought about somehow linking that into your calculations?
1 D. Charlo and D. C. Clary, J. Chem. Phys., 2002, 117, 1660–1672.
Dmitri Babikov replied: Yes, it would be nice to have a truly complete theory, capable of treating the overall O + O2 + M collision process in one step, regardless of the mechanism of the process, but at this time such a brute force approach is computationally unfeasible. Thus, we have to simplify the picture, splitting the overall process onto several components and treating those separately. For example, in principle, there is a possibility of forming a metastable complex between the bath gas atom or molecule (M) and either O or O2, with the subsequent atom exchange: O + M → OM + O2 → O3 + M or O2 + M → O2M + O → O3 + M.
This is known as a “chaperon” mechanism, important at low temperatures, when a weakly bound van der Waals complex is stable. Here, however, for the description of the room temperature kinetics, this mechanism can be safely neglected. Similarly, the direct three-body mechanism, when the reaction proceeds in one step, O + O2 + M → O3 + M, can be important at high pressure (above 1000 bar).
However, for the pressure range below 1 bar (as in the stratosphere) the recombination reaction proceeds in the low-pressure regime, when the three body collisions can be safely ignored. Thus, our focus here is exclusively on the energy transfer mechanism, since it is expected to be dominant: O + O2 → O3* + M → O3 + M. Here, the metastable ozone states O3* are rather stable, since they are formed above a deep well on the PES (∼1.1 eV). Overall, this mechanism is an approximation to the entire process, but for the temperature and pressure ranges of interest, this is expected to be a good approximation.
Francesco Gianturco asked: Could you please explain in more detail how you have used the 3-body potential of your system to generate the resonance positions and which ab initio potential was effectively employed for the short-range region of the interaction?
Dmitri Babikov answered: In our calculations we used a global potential energy surface that covers the entire range of molecular shapes, from the deep ozone well (short-range) to the asymptotic O + O2 channels. This surface was built by Dawes and coworkers1 based on the MRCI-level calculations of the electronic structure.
1 W. Xie, L. Liu, Z. Sun, H. Guo and R. Dawes, J. Chem. Phys., 2015, 142, 064308.
Francesco Gianturco said: How do you proceed in practice to select between a shape resonance and a Feshbach resonance? How do you reduce the coupling strength when going from one sector to the next in your radial propagation?
Dmitri Babikov answered: There are two questions here. I will respond separately. We neither select, nor try to assign individual resonances as “shape” resonances or Feshbach-type resonances. We found that for the recombination process at room temperature a very large number of resonances (thousands) are involved, so analyzing the nature of each individual state, manually, would not be practical. Instead, we have done two sets of calculations. In one set, we disabled the mechanism of formation of Feshbach resonances by neglecting the couplings between the diabatic vibrational states in the system, and performing a large number of uncoupled calculations (e.g. for every individual curve in Fig. 2 of the paper, separately, DOI: 10.1039/C8FD00089A). In this case, resonances can be formed only by trapping behind the centrifugal barrier, and populated exclusively by tunneling. By definition these are shape-resonances, due to the shape of potential. In the other set of calculations we included these couplings to enable interaction between the open and closed channels, which is a mechanism of Feshbach resonance formation. We found that the recombination reaction is dominated by these vibrationally non-adiabatic interaction processes, rather than by tunneling.
Concerning the coupling strength, we do not adjust anything. Please look at the expression for the Hamiltonian matrix Hklnm in section II-B of the paper. It includes the overlap matrix elements Oklnm computed along the hyper-radial direction (the expression is also given in the Section II B of the paper). Overlaps of the locally optimal basis states flm and fkn are different for different sectors. The values of these overlaps determine the strength of coupling.
Conflicts of interest
There are no conflicts to declare.| This journal is © The Royal Society of Chemistry 2018 |