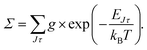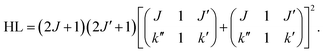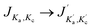Open Access Article
Open Access ArticleCollisional relaxation kinetics for ortho and para NH2− under photodetachment in cold ion traps
Francesco A.
Gianturco
 *a,
Olga Y.
Lakhmanskaya
a,
Mario Hernández
Vera
ac,
Ersin
Yurtsever
*a,
Olga Y.
Lakhmanskaya
a,
Mario Hernández
Vera
ac,
Ersin
Yurtsever
 b and
Roland
Wester
b and
Roland
Wester
 a
a
aInstitut für Ionenphysik und Angewandte Physik Universität Innsbruck, Technikerstraße 25/3, A-6020 Innsbruck, Austria. E-mail: francesco.gianturco@uibk.ac.at
bDepartment of Chemistry, Koç University, TR-34450, Istanbul, Turkey
cDepartment of Chemistry, Ludwig-Maximilians-Universität München, Butenandtstr. 7 (C), D-81377 München, Germany
First published on 24th May 2018
Abstract
The collisional cooling of the internal rotational states of the nonlinear anion NH2− (1A1), occurring at the low temperature of a cold ion trap under helium buffer gas cooling, is examined via quantum dynamics calculations and ion decay rate measurements. The calculations employ a novel ab initio potential energy surface that describes the interaction anisotropy and range of action between the molecular anions and the neutral He atoms. The state changing integral cross sections are employed to obtain the state-to-state rate coefficients, separately for the ortho- and the para-NH2− ions. These rates are in turn used to compute the state population evolution in the trap for both species, once photodetachment by a laser is initiated in the trap. The present work shows results for the combined losses of both species after the photodetachment laser is switched on and analyzes the differences of loss kinetics between the two hyperfine isomers.
1 Introduction
The collisional cooling of internal molecular states, especially for diatomic and simple polyatomic molecules and ions, has become a visible and mature area of experimental and theoretical investigation by many research groups in a broad range of laboratories.1,2 It has come from the development, among other tools, of ion confinement in cold traps followed by additional translational and internal cooling of the trapped ions by buffer gas atoms, usually helium because of its broad versatility. The technique relies on collisions with cold buffer gas atoms to bring neutral molecules3,4 or molecular ions5–8 to lower temperatures. The gas is employed to dissipate translational energy of the target species and, for the molecular partners, their rotational energy as well. Since this dissipation scheme does not depend on the existing level patterns, it is very versatile and used for many molecular species. Generally, the collision-induced internal quenching is far more efficient for rotations than for vibrations, while vibrations are more efficiently quenched by radiative transitions.9–11In the present work we investigate the rotational quenching kinetics for a triatomic molecular ion. Recently we studied the absolute inelastic collision rate coefficient for the diatomic molecular anion OH−.12 Here we focus on the collisional cooling of the ortho and para rotational states of the NH2− anion due to differences in the relative collision and photodetachment rates. The results for our calculations are compared with experimental ion loss rate measurements of trapped NH2− irradiated by a photodetachment laser.
NH2− in the 1A1 electronic ground state is a nonlinear molecular anion that is described as an asymmetric top rotor. Vibrational excitation does not play a role under the conditions of the trap experiments due to radiative and collisional cooling: thus, it is not treated here. In terms of the structural features of the trapped molecular species, the physical and chemical properties of anions are very different from those of neutral molecules or cations, as their residual negative charge causes them to interact with the surrounding species in the trap in a different way: as an example, because of their weakly bound excess electron densities, they have fairly large polarisabilities and thus exhibit stronger van-der-Waals interactions with the other trap partners.13
First we will discuss the features of the potential energy surface (PES) that originates from the anion’s interaction with the neutral He atoms of the buffer gas. This will be done in the following Section 2. In the same section we will briefly review the quantum collision dynamics for the rotational state-changing processes. In the experiments we employ selective photodetachment (PD) from specific rotational states of the anions. The experimental procedures will be reported in Section 5. In order to make contact between the experimental findings and the results from the computational modeling of the cooling kinetics in the trap we have generated the relevant state-changing inelastic rates from the computed inelastic cross section. Such quantities are the necessary starting point for modeling the evolutionary behavior of the rotational states which are populated by the molecular anions in the cold trap. In Section 4 we describe in detail the procedure employed and show how the selective effects from the laser switching step are added by including additional photodetachment rates within the set of coupled equations.
The results of our simulations for the population kinetics in the trap, their dependence on different choices for the trap parameters (e.g. trap temperature, helium gas density, PD cross sections) and their comparison with what has been found in the experiments will be analyzed and discussed in Section 6, while our final conclusions will be presented in Section 7.
2 Interaction forces and dynamics
A detailed presentation of the calculations of the relevant PES for the NH2− + He system from ab initio quantum chemistry methods is given in a separate publication.14 There we focus on the structural aspects and the inelastic quantum dynamics for the collisional part of this investigation. Here we shall therefore provide only an outline of the computational method and a brief review of its outcomes.The interaction between a rigid rotor anion and the He atom is represented by a 3D potential as a function of (R, θ, ϕ) variables, which are here defined according to their representation, given in Fig. 1. The Cartesian coordinates originate from the center of mass (COM) of the molecular anion. Within the body-fixed frame of reference the actual ab initio points of the present PES are given by R, the distance of the He atom from the COM, and the two angles (θ, ϕ), which locate the same atom with respect to the Cartesian frame, containing the molecule. The latter is placed on the (x, z) plane, with the two H atoms located symmetrically with respect to the x-axis and along its negative direction. The grid of ab initio points, due to the symmetry of the overall interaction, considers the region of space with θ: 0° ≤ θ ≤ 90° and with ϕ: 0° ≤ ϕ ≤ 180° and then extends it by duplication.
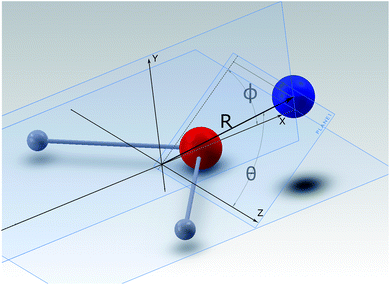 | ||
| Fig. 1 Body-fixed representation of the Cartesian coordinates describing the present PES between partner systems in the trap. The polar coordinates give the PES’s points, labeled as (R, θ, ϕ). | ||
The calculations reported in ref. 14 were carried out with the suite of codes of the MOLPRO package.15 The level of post-Hartree–Fock treatment was at the CCSD(T) with complete-basis-set-extrapolation that started from aug-cc-p-VXZ, where X varied from triple, quadruple and quintuple-Z successively. The molecular geometry was found to change very little in going from NH2 to NH2− (ref. 14) and therefore the calculated electron affinity (EA) was negligibly changed by adding the zero-point-energy (ZPE) correction.
The present molecule has an experimental EA value of 0.71 eV (ref. 16) from a fairly old experiment. Our calculations yielded a value of 0.77 eV. The permanent dipole moment of the anion is also a quantity of interest: we found its calculated value to be 1.4965 D (debye) and its direction within the molecule to coincide with the positive orientation of the ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) -axis in Fig. 1. It is also interesting to compare these findings with values from previous calculations: 1.311(0.01) D,17 1.396 D18.
-axis in Fig. 1. It is also interesting to compare these findings with values from previous calculations: 1.311(0.01) D,17 1.396 D18.
We found that the excess electron bound to the anion physically describes a valence-bound state (VBS) in a doubly occupied π* orbital located on the nitrogen atom and directed along the Ŷ axis of Fig. 1, i.e. perpendicular to the molecular plane. This structural feature of the anion’s electronic density is an important item for better understanding the orientational anisotropy shown by the PES that we have employed in our calculations. It is a well known property of the He atom, in fact, to exhibit largely repulsive interaction with partners that carry an excess negative charge.19 Thus, the presence of a fairly localized region of diffuse negative charge in the NH2− will reflect into an overall interaction with the He partner which markedly depends on the direction of approach to that localized negative charge. We have already discussed this feature previously,14 so we shall only briefly illustrate its consequences on the anisotropy of the PES.
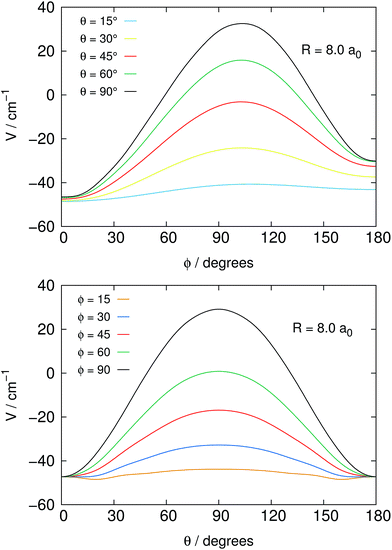
Fig. 2 reports in its two panels two different views of the angular shape of the potential, taken at a fixed distance of the He atom from the center of mass of the NH2− molecule. The data refer to the total electronic energies for the complex system calculated with the BSSE correction at all points and relative to the separate electronic energies of the molecular anion at its equilibrium geometry and of the ground state of the He atom. We can make the following comments, when perusing the present data:
1. The most repulsive approach is shown for θ = 90°, ϕ = 90° in both panels of the figure. It corresponds to the He partner approaching the molecular anion perpendicular to the molecular plane and at the region of the π* extra electron on the nitrogen atom.
2. On the other hand, the strongest attractive interaction approach is seen, when going around the range of the angle ϕ, while θ → 0°, which means that the He atom samples the potential on the same plane as it moves on a whole circle from the N-side to the middle direction between the two H-atoms (negative ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) -axis).
-axis).
3. One should also be aware of the fact that the present system, because of its fairly strong ionic interaction, can support global bound states by forming four-atom bound structures when the relative collision energies in the trap could get dissipated into bound states of that complex. Such path of energy disposal could get to ions’ losses in the trap via what would be a radiative association mechanism. However, given the low photon density in the bath and the relatively small spacings expected between the complex bound levels, one can surmise that, in analogy with previous studies of ours, the associative rates would be fairly negligible under trap conditions and therefore will not be considered in the present study.
On the whole, the present interaction is seen to be strongly anisotropic and to provide through this general feature an effective potential coupling for the rotational state-changing collision process, as discussed in detail in our earlier work.14
Our inelastic scattering calculations employ the above PES by expanding it in terms of the conventional spherical harmonics in 3D space:
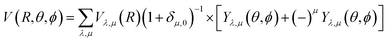 | (1) |
We generated the solution of the Schrödinger equation for the asymmetric-top Hamiltonian by writing down the corresponding wave functions as
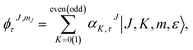 | (2) |
The index τ together with J quantum number labels rotational energy levels. It is defined as τ = Ka − Kc, where the latter labels are the “prolate” and “oblate” limits of the rotor representation, respectively. The index τ runs from −J to a +J in order of ascending energy. The K quantum number defines the projection of the total angular momentum J on the Ẑ-axis of the BF frame, m is the projection of J on the Ẑ-axis of the space-fixed (SF) frame14 and the parity ε = ±1.
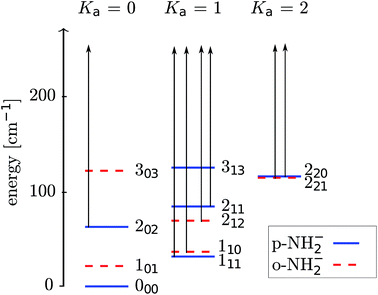
We present in Fig. 3 a picture of the relative positioning of the lower-lying rotational levels for the ortho- and para-isomeric species of the molecular anion. The scattering calculations carried out in the present work dynamically couple together more levels than those shown in the figure, while we report in it only the physical levels which will be significantly populated in the experiment.
We have calculated the relevant state-changing integral cross sections by solving the corresponding coupled-channel (CC) equations of the time-independent quantum dynamics.14 The inelastic integral cross sections between the physical levels of interest were obtained by employing a version of the HIBRIDON code,23 using the following rotational constants for the target molecule (in units of cm−1): A = 23.051, B = 13.067, C = 8.121 as taken from previous experiments.24 The cross sections were generated over a range of energies from 0.2 cm−1 up to 270 cm−1 in steps of 0.2 cm−1, while for energies up to 770 cm−1 the energy step was of 1.0 cm−1. The angular bases functions, which were involved in the CC expansion for the calculations, went up to J = 7, which allowed us to reach convergence within a relative error of less than 5% for all the transitions between the first 6 rotational levels of para-NH2− and ortho-NH2−. The terms of the multipolar expansion included from eqn (1) went up to λmax = 8 and μmax = 4 to reach that level of convergence.14
3 Photodetachment cross sections
The energy levels in Fig. 3 of the anionic and neutral states are coupled by single-photon photodetachment transitions, as shown by the vertical arrows. The relative PD cross sections for the transitions for ortho- and para-NH2− for a given photon energy hv and temperature T are given by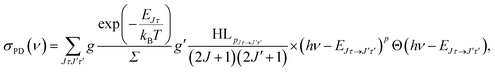 | (3) |
| g = (2J + 1)(2IN + 1)(2IH + 1) |
| g′ = (2J′ + 1)(2S′ + 1)(2IN + 1)(2IH + 1), |
The relative PD cross section for ortho (para) states are summed over the state-to-state cross sections between ortho (para) rotational states of an anion state Jτ and a neutral state J′τ′ that is accessible at a given photon energy. Rotational levels up to Jτ = 32, J′τ′ = 32 were considered.
For the calculation of the Hönl–London factors only “A1”-type PD transitions, i.e. transitions with the detached electron of A1 symmetry, are taken into account. These transitions are governed by μc-type selection rules. The exponent p in eqn (3) is fixed at 0.2 to account for the dipole interaction of the outgoing electron (see ref. 25 for details). The Hönl–London coefficients are obtained using Wolfram Mathematica. For this, we took into account expansion coefficients for asymmetric top functions (see eqn (2)) and an expression for the Hönl–London coefficients for symmetric top wave functions from eqn (6.117) in ref. 26. They take the following form for μc-type transitions:
For the analysis of the time evolution of ortho- and para-NH2−, it is instructive to evaluate the ratio of the PD cross sections σorthoPD(ν)/σparaPD(ν). Its dependence on the PD photon energy hv is shown in Fig. 4. The ratio ranges from about 1 to 1000 and depends strongly on the rotational ion temperature and the photon energy. By changing the photon energy and the exposure time in the experiment, we can thus selectively deplete the abundances of ortho NH2−.
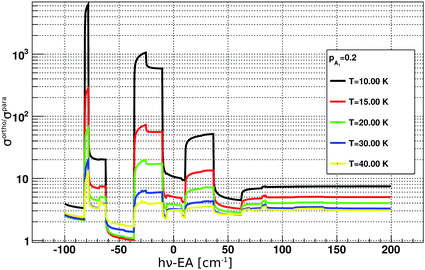 | ||
| Fig. 4 Ratios between ortho and para photodetachment cross sections plotted as a function of PD photon energy. The cross sections were obtained according to eqn (3), more details can be found in the main text. EA corresponds to the electron affinity of NH2.25 | ||
For the rate equation simulations of the time evolution (see next section) we use the PD cross sections σPDi(ν) for a given anionic state i = Jτ, summed over all accessible neutral states:
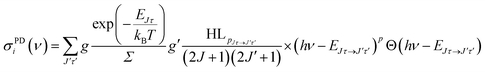 | (4) |
4 Solving the kinetics modeling
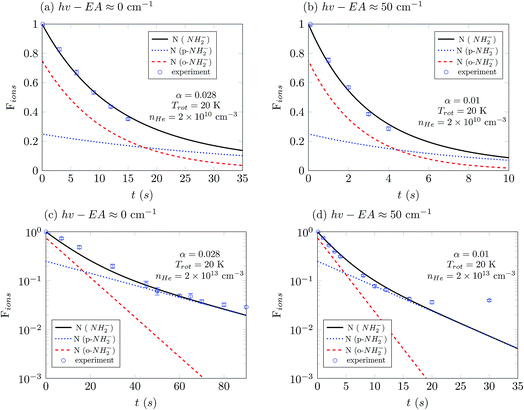
Based on the above calculations, we now present our model of the time-evolution of the populations of the rotational states of ortho-NH2− and para-NH2− under the collisional cooling dynamics with He buffer gas, followed by the “switching on” of the PD process by laser photons. We first need to evaluate the necessary inelastic, state-to-state rate constants from a standard Boltzmann convolution of the computed cross sections.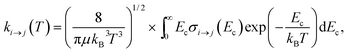 | (5) |
We have used the inelastic cross sections of our previous work14 in order to compute inelastic rates between 5 K and 30 K among the first 6 rotational energy levels of the molecular ions. The convolution was carried out over a fairly broad range of kinetic energies as described earlier.14 In those calculations we discovered marked differences of sizes and behavior between the rates for ortho- and para-systems. In particular, the calculations showed that around 20 K the rate k101→110 of the ortho species can be a factor of 4 larger than the rate k100→111 of the para spin isomer, as can also be appreciated from the results of further calculations that we report in Fig. 5. This particular difference in size could be associated with differences within the coupling strength of different multipolar coefficients of the potential and with the variations in energy gaps between different levels in ortho- and para-NH2−, respectively.14 Such differences will be playing a significant role in selectively driving the kinetics behavior of the target’s rotational states cooling processes.
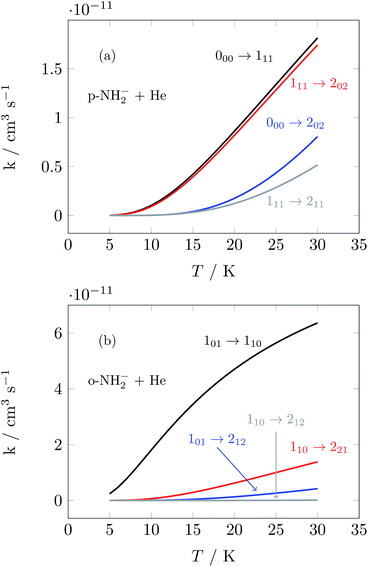 | ||
| Fig. 5 Computed state-to-state inelastic rates over a range of temperatures between 5 and 30 K. The upper panel presents transitions from the ground rotational state of the para-NH2− isomer and involves excitations to three different levels (see Fig. 3). The lower panel reports excitation transitions for the ortho-NH2− isomer, where three different excitation processes are also shown. See the text for further details. | ||
Another interesting piece of information regarding the general features of the present system can be obtained by comparing some of our computed cross sections with those which can be obtained for an isoelectronic system which has been studied many times in the current literature: the OH2 neutral molecule interacting with helium atoms. The data in Table 1 show such a comparison with the most recent calculations which have appeared in the literature on the neutral, isoelectronic system:27
| H2O + He (Sarma et al.27) | NH2− + He (this work) | |
|---|---|---|
| 000 → 111 | 8.9650 | 10.5652 |
| 000 → 202 | 2.2613 | 15.3947 |
| 000 → 211 | 0.0077 | 0.3057 |
| 000 → 313 | 0.8397 | 3.9040 |
| 111 → 202 | 3.2928 | 7.6086 |
| 111 → 211 | 2.6600 | 14.6834 |
| 111 → 220 | 1.0398 | 1.1457 |
| 101 → 110 | 4.7053 | 7.7395 |
| 101 → 212 | 5.1073 | 6.5183 |
| 101 → 221 | 0.5756 | 3.5283 |
| 101 → 303 | 1.0136 | 3.9151 |
| 101 → 312 | 0.1093 | 0.2280 |
| 101 → 321 | 0.4334 | 0.9571 |
An analysis of the relative sizes of the inelastic cross sections shown in the table allows us to make the following comments:
1. All the para-transitions shown in the upper part of the table indicate that the excitation processes in the present system consistently yield much larger cross sections, as should be expected from the longer range of action appearing in its ionic PES in comparison with the neutral PES of the H2O + He system.
2. The same occurs for the excitation cross sections involving the ortho-transitions, also reported in the lower part of the same table. All the excitation probabilities for the present ionic interaction partners are consistently larger than those referring to the neutral system isoelectronic with the present one. The differences in going from H2O to NH2-partners vary from a few percent up to a factor of two in some cases. Such differences also indicate that, additionally to the role played by the increased range of action in the ionic PES, the differences in the energy gaps between the rotational levels (see details in ref. 27) between the two systems also play a significant role.
To further continue now the modeling of the rotational populations during the evolutionary dynamics, we solve the master equations using the collisional thermal rates obtained before at each chosen value of the trap temperature and of the selected He density.28
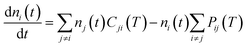 | (6) |
| Pij(T) = nHeki→j(T) | (7) |
| Cji(T) = nHekj→i(T) | (8) |
This describes the collision-only time evolution process of thermalizing the relative population of the rotational levels to the selected buffer gas temperature at a given density nHe in the trap. Once the thermalisation process is reached and the PD laser is turned on, one needs to modify the coefficients in eqn (7) by rewriting the destruction rates as:
| Pij(T) = nHeki→j + KPDi, | (9) |
| KPDi = α(v)σPDi(v), | (10) |
After the selected time duration of the “laser on” step we can further define the ratio, Fions, which can tell us after a time t, during which the laser is applied, what is the fraction of the ions which are lost, after the previous thermalising step, due to the additional laser action on the trap’s components:
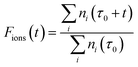 | (11) |
This ratio will therefore be reduced, during the anions’ loss process, from its initial value of unity for both the ortho- and the para-isomers, describing the case where one treats the two isomers as separate depletion processes and with equal initial abundances. Since the experiments are carried out with both nuclear spin isomers in the trap, we refine the above model by explicitly including the initial relative ortho/para ratio (OPR). Hence, expecting ortho-NH2− to be initially three times more abundant in the trap than para-NH2− (see Section 5), we scale the ratio of eqn (11) by treating the two isomers on a different footing:
| Fions(t) = 0.75 × Forthoions(t) + 0.25 × Fparaions(t). | (12) |
The individual quantities on the r.h.s. have been obtained from separate kinetics calculations involving each of the two isomers.
The master equations have been numerically integrated by using a fourth-order Runge–Kutta method. We have also included, in solving the coupled 1st order equations, the anion’s rotational transitions involving the first 6 rotational states of either isomer, although at the temperatures expected in the traps only the first three rotational level populations will effectively drive the solutions, since those higher up in energy will only be negligibly populated. During the “laser on” step we will depopulate 6 rotational levels of each spin-isomer, although at 20 K only 4 levels will be sufficient for our present modeling, since the next level will not be directly coupled by selection rules.
5 Experimental procedure
A detailed description of the photodetachment spectroscopy experiment of NH2− and their relative photodetachment cross section can be found in a different publication.25 In brief, the ions are produced in a plasma discharge of the gas mixture He/NH3 (90%, 10%) and are then loaded into the 22-pole ion trap.5,29Assuming that the anions are predominantly formed through the following dissociative electron attachment (DEA) reaction: NH3 + e− → NH2− + H, we can estimate the ortho to para ratio (OPR) of the anions, which will be loaded into the trap. The nuclear spin selection rules reported in the reactions outlined below can be obtained by using the method presented by Oka30
| o-NH3 + e− → o-NH2− + H (1/1) |
| p-NH3 + e− → o-NH−2 + H (1/2) |
| p-NH3 + e− → p-NH−2 + H (1/2) |
The numbers in brackets give the statistical weights. Since the ortho-to-para-ratio (OPR) of NH3 at 300 K is unity, we obtain the value of OPR = 3 for NH2− upon production in the ion source.
During the experiment the ion trap, together with its shield and He buffer gas with the densities of about 2 × 1013 cm−3, are cooled to 9(±1) K. Another set of measurements was obtained at much lower densities of about 2 × 1010 cm−3. Internal and translational thermalisation of the ions is then achieved by collisions with the He atoms. Previous studies31–35 show that the ion temperatures do not exactly follow the trap temperature, although the reasons for this are not completely understood so far.36 It is therefore safer to assume that the internal ion temperature should be between 10 K and 30 K.
The photodetachment laser beam is aligned with the trap axis. It is admitted to the trap after 0.5 s of trapping time to assure the thermalisation of the ions. The absorption of the infrared photon now induces the ion losses in the trap. After a certain exposure time, the ions are extracted and then detected following a time-of-flight mass separation process. The procedure is repeated for different exposure times to evaluate the photodetachment rate Kpd (loss rate of ions in the trap). The ortho and para NH2− isomers are, in fact, two independent species indistinguishable by their mass. The dynamics of the photodetachment losses are therefore more complex, because they have to be described by a double exponential decay:
| [NH2−] = [NH2−]ortho0 × exp(−Korthopdt) + [NH2−]para0 × exp(−Kparapdt), |
6 Results and discussion
Here we present the numerical results for the time evolution of the ortho and para state populations as a function of storage time and compare it with experimental results for NH2− for different trapping conditions. The model uses the computed collisionally inelastic rates from our ab initio quantum dynamics together with calculated relative PD cross sections. It is based on the solution of master equations with an initial OPR value equal to 3. As we will discuss below, the obtained temporal evolution of Fions depends on the intensity of the radiation, the effective temperature of the trap and additionally on the density of the buffer gas.Fig. 6 shows how sensitive our model turns out to be to each specific parameter. In this figure we plot the time-dependent change of the fraction of ions remaining in the trap, Fions. In the four panels we report simulation results for different values of the parameters nHe, α and Trot. The data of panel (a) are shown as a reference, because, as we shall discuss below, these parameters have been found to be close to the best fit of the experimental results.
Fig. 6(a) and (b) show the changes occurring for the function Fions by increasing the parameter α by a factor of 2. The depopulation rates of the ions are clearly enhanced and as a consequence both spin isomers reach the same abundance faster than in the reference situation illustrated in Fig. 6(a). We can also see that after 30 s most of the ions are para-NH2− and that therefore the signal observed in the experiment should be exclusively produced by those ions.
The comparison between the panels (a) and (c) in Fig. 6 shows the effect of increasing by three orders of magnitude the density of the He gas in the trap. The effect is to increase collision numbers and therefore our computed collision rates, thus making it more difficult for the laser action to depopulate one specific rotational state since the collisional energy transfers become more efficient and less selective. The effect of modifying the nHe in the trap therefore does not seem to impact significantly the time dependence of the Fions depletion. A further increase of nHe above the shown value of 1013 cm−3 does not modify the solution of the master equation, thus indicating that the collisional process has reached saturation.
Finally, the comparison between the data in the panels (a) and (d) of Fig. 6 shows the effect of changing the trap’s temperature. If we decrease the temperature by 5 K, the depopulation of the ions takes more time because most of the molecules spend more time in the rotational ground state and therefore are not affected by the selective wavelength of the laser. At 15 K the master equations are coupling mainly two levels of the ions so that the higher levels are difficult to populate because of the insufficient kinetic energy of He atoms colliding in the trap with the negative ions.
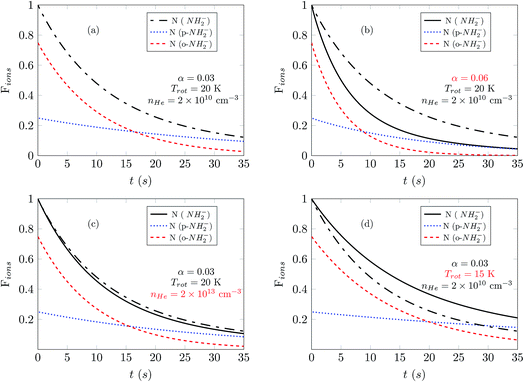
In Fig. 7 we show the comparison between the temporal evolution simulations and the results of the experimental decay curves. We show data for a photon energy near the electron affinity (EA), taken from ref. 25, in the left panels and about 50 cm−1 above the EA in the right panels. We first consider the measured data at higher buffer gas pressure, where laser-induced depletion of the rotational state population is not expected to be occurring since the faster collisional cooling rates rapidly produce a thermal distribution of the molecular ions. Two different sets of measurements were performed at a fixed PD photon energy: at shorter and at longer exposure times. For the latter we increased the gain of the detector to be capable to detect the significantly reduced ion signals. The obtained sets are plotted together by scaling one measurement in respect to another, normalized to the amplitude at the shortest exposure time.
The data for high density are presented in Fig. 7(c) and (d). There we observe a non-exponential decay of the ion signal, associated with slower PD rates for longer exposure times. This is rationalized with the depletion of the ortho-species in the trap. At the longest exposure times one may observe termination of the ion losses. This effect becomes especially prominent at a photon energy 50 cm−1 above the EA. At this photon energy the rotational states including the ground states are involved, the photodetachment cross section ratio between ortho and para species, shown in Fig. 4 is small and indicates a fast decay of both ortho and para species. Therefore, we expect a prominent decay of both ortho- and para-NH2− and associate the observed offset with the presence of another ion. This is assumed to be the parasitic OH ion, which can be formed in the source due to water contamination, so that such ions can be loaded together with the target ions due to their very small mass difference. Their abundance in the trap is expected to be negligibly small and indeed only becomes noticeable when the vast majority of NH2− ions have been rapidly destroyed by the PD lasing action.
The experimental results reported in panels (a) and (c) of Fig. 7 were obtained by employing different He densities while keeping the frequency and intensity of the laser unchanged. As we have shown before (Fig. 6(a) and (c)), changes of the buffer gas density should not affect greatly the exponential decay of the ion populations, and this feature is also observed in these experimental results. The population of the ions is fitted well by employing computed simulations which use the same value of α for the PD laser intensity scaling. The same quality of good agreement between experiments and our present computational simulations is also found by the additional comparison between experimental results and simulations presented in the panels in the right column of Fig. 7, (b) and (d), only by changing the value of the He density in the trap.
The data reported in Fig. 7(a) and (b) show experimental results obtained at the same helium pressure but now employing a different frequency of the laser. As one increases the laser frequency, the PD cross sections become larger and new transitions become energetically available between NH2− and NH2 during the photodetachment process. At the frequency reported in the panel of Fig. 7(b) the laser can also cause photodetachment of the large fraction of ions that remain in the ground rotational states at 20 K. As a consequence, in panel (b) the ion population decreases faster than in panel (a). To improve the fit, we use different values of α in the left and right panels. The increase of α by a factor of three as we change the laser frequency accounts for PD transitions higher above threshold and for the inclusion of further PD transitions.
In panels (a) and (b) the photodetachment rates have the same order of magnitude as the collisional rates and therefore both determine the temporal evolution of the Fions populations. However in panels (c) and (d), where the helium density is three orders of magnitude larger, the collisional rates which control state populations in the trap are dominant. In such a situation, any additional increase of the helium density would not change the results of the simulations.
As already demonstrated by earlier work in our group for OH− colliding with helium,12 it is possible to manipulate the relative populations of the rotational states of a negative ion confined in a cold trap by an intense PD laser if the buffer gas density is low. From the collision-driven data that we have obtained from our computational methods, we can model the experimental procedure of the PD processes once the laser is switched on. At the low temperatures considered here, we then deplete the lowest excited rotational levels 111 and 110 (see Fig. 3).
The loss of molecular anions can then be used to infer inelastic rates as has previously been done for the diatomic anion OH−.12 Specifically, if the rotational temperature of NH2− is reduced to below 15 K and the density of He is kept at 1010 cm−3, it is possible to fairly rapidly reach a trapping regime in which the exponential law of the population decay is completely determined by the inelastic collision rates in the trap. Hence, by using a PD laser frequency near the EA, the laser would rapidly depopulate the first excited rotational level of the ions without affecting the ions that are in the ground rotational state. After a time interval, which would depend on the intensity of the laser, the ortho isomers are fully depopulated on account of the larger PD cross sections related to this isomer, as shown above. Therefore the ion signal will now come nearly exclusively from the para-NH2− ions and depend essentially only on the inelastic excitation rates of the lowest para states. We can therefore approximate the time kinetics via a pseudo-two-level system:
A further increase of the intensity of the laser under the above conditions should not modify the exponential factor which is now driving the time-dependence of the ion populations for times larger than 30 s. Similar ideas could be employed to estimate the OPR in the trap and estimate the collision rates of similar ions analyzed in different experiments. A further numerical set of examples can be gleaned from the results which we report in the following figure.
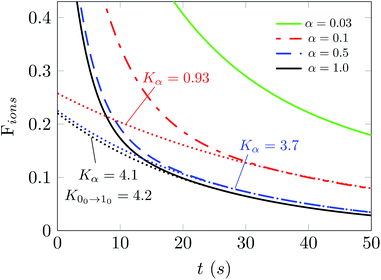
In fact, it is of further interest to try to analyze in more detail the effects produced from a broader range of changes of the parameter α on the behavior of the depopulations of the ions in the trap. The results of such an analysis are reported in Fig. 8. The values of the parameter α now run from 0.03 to 1.0, thereby indicating a very broad change of intensity for the PD laser. Each of the decay curves shown also indicates the behavior of the decay in populations after laser application. The calculations reported in this figure were performed at 15 K and we selected a buffer gas density of 1010 cm−3. The dashed lines are the fit of the ion population after 30 s when the ortho-NH2− molecular anion is almost fully depleted. The Kα values denote the exponential factor of the fits. The unit of the collisional rates (rate coefficient multiplied by the helium density) is 10−2 s−1.
The simulation in Fig. 8 shows that selecting the largest two values for the α parameter produces values of the depletion rates which are very close to our calculated rate value from the first rotational excitation transition in what is now the dominant species in the trap, the para-NH2− molecular anion. This means that selectively depleting one of the isomeric species allows our temporal evolution modeling to give us an estimate of the decay rate that can be directly compared with that given from scaling the experimentally used laser intensity. The procedure that we have introduced for OH− in earlier work12 is thus quite general and could also be used for other similar molecular anions.
7 Present conclusions
In the present paper we have endeavored to analyze in detail the possibility of realistically modeling the experiments we have carried out on the laser photodetachment of electrons in an ion trap containing a mixture of para-NH2− and ortho-NH2− negative ions which are previously collisionally cooled by He atoms as a buffer gas. We have employed an ab initio full Born–Oppenheimer potential energy surface between the molecular anion and the helium atom and we have used it to carry out quantum dynamical calculations for the rotationally inelastic collision cross sections. The latter have been employed to obtain the state-to-state inelastic rates over a broad range of temperatures which span those present in our ion trap experiment. The next step has been that of solving the first order coupled differential equations describing the temporal evolution of the molecular states in the trap and due to both the collisional energy transfer mechanism and the photodetachment, laser-induced rates.The calculations have shown a marked difference of behavior between the temporal evolutions of the ortho and para hyperfine isomers and have also allowed, by a series of parametric scaling of the laser intensities suggested by the experiments, to obtain a direct estimate of the PD rates from the ones obtained in our modeling study and to further estimate with them the decay rates of the residual species obtained from the experiments. Thus, we have shown that it is possible to obtain direct indication on the values of the photodetachment rates for a triatomic molecular anion, by combining experimental results with numerical simulations involving both the collision-driven population evolutions and the laser-driven anion depletion. Since such a procedure is quite general in its implementation, we expect that one can apply the same method to other, similar molecular systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. A. G. and R. W. thank the Austrian Science Fund (FWF) for supporting the present research through Project No. P29558-N36. The support of the Computational Center of the University of Innsbruck is also acknowledged.References
- L. D. Carr, D. DeMille, R. V. Krems and J. Ye, New J. Phys., 2009, 11, 055049 CrossRef.
- R. V. Krems, W. C. Stwalley and B. Friedrich, Cold molecules: theory, experiment, applications, CRC Press, 2009, p. 721 Search PubMed.
- J. Kim, B. Friedrich, D. P. Katz, D. Patterson, J. D. Weinstein, R. DeCarvalho and J. M. Doyle, Phys. Rev. Lett., 1997, 78, 3665–3668 CrossRef.
- D. Egorov, J. D. Weinstein, D. Patterson, B. Friedrich and J. M. Doyle, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 63, 030501 CrossRef.
- D. Gerlich, Inhomogeneous RF-fields – a versatile tool for the study of processes with slow ions, John Wiley & Sons, Inc., 1992, vol. 82, pp. 1–176 Search PubMed.
- S. Schlemmer, T. Kuhn, E. Lescop and D. Gerlich, Int. J. Mass Spectrom., 1999, 185–187, 589 CrossRef.
- R. Otto, J. Mikosch, S. Trippel, M. Weidemüller and R. Wester, Phys. Rev. Lett., 2008, 101, 063201 CrossRef PubMed.
- A. K. Hansen, O. O. Versolato, L. Klosowski, S. B. Kristensen, A. Gingell, M. Schwarz, A. Windberger, J. Ullrich, J. R. C. Lopez-Urrutia and M. Drewsen, Nature, 2014, 508, 76–79 CrossRef PubMed.
- U. Hechtfischer, Z. Amitay, P. Forck, M. Lange, J. Linkemann, M. Schmitt, D. Schwalm, R. Wester, D. Zajfman and A. Wolf, Phys. Rev. Lett., 1998, 80, 2809–2812 CrossRef.
- C. Meyer, A. Becker, K. Blaum, C. Breitenfeldt, S. George, J. Göck, M. Grieser, F. Grussie, E. a. Guerin, R. von Hahn, P. Herwig, C. Krantz, H. Kreckel, J. Lion, S. Lohmann, P. M. Mishra, O. Novotný, A. O’Connor, R. Repnow, S. Saurabh, D. Schwalm, L. Schweikhard, K. Spruck, S. Sunil Kumar, S. Vogel, A. Wolf, A. P. O’Connor, R. Repnow, S. Saurabh, D. Schwalm, L. Schweikhard, K. Spruck, S. Sunil Kumar, S. Vogel and A. Wolf, Phys. Rev. Lett., 2017, 119, 023202 CrossRef PubMed.
- H. T. Schmidt, G. Eklund, K. C. Chartkunchand, E. K. Anderson, M. Kamińska, N. de Ruette, R. D. Thomas, M. K. Kristiansson, M. Gatchell and P. Reinhed, et al. , Phys. Rev. Lett., 2017, 119, 073001 CrossRef PubMed.
- D. Hauser, S. Lee, F. Carelli, S. Spieler, O. Lakhmanskaya, E. S. Endres, S. S. Kumar, F. Gianturco and R. Wester, Nat. Phys., 2015, 11, 467–470 Search PubMed.
- H. Massey, Negative ions, Cambridge University Press, New York, 1976 Search PubMed.
- M. Hernández Vera, E. Yurtsever, R. Wester and F. A. Gianturco, J. Chem. Phys., 2018, 148, 184305 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schuetz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 Search PubMed.
- C. T. Wickham-Jones, K. M. Ervin, G. B. Ellison and W. C. Lineberger, J. Chem. Phys., 1989, 91, 2762–2763 CrossRef.
- P. Botschwina, S. Seeger and J. Flügge, J. Chem. Phys., 1993, 99, 8349 CrossRef.
- D. J. Swanton, G. B. Bacskay and N. S. Hush, Chem. Phys., 1986, 107, 25–31 CrossRef.
- E. Coccia, F. Marinetti, E. Bodo and F. A. Gianturco, J. Chem. Phys., 2008, 128, 134511 CrossRef PubMed.
- B. J. Garrison, W. A. Lester Jr and W. H. Miller, J. Chem. Phys., 1976, 65, 2193–2200 CrossRef.
- P. J. Dagdigian and M. Alexander, Mol. Phys., 2010, 108, 1159–1169 CrossRef.
- A. Palma, S. Green, D. J. DeFrees and A. D. McLean, J. Chem. Phys., 1988, 89, 1401–1407 CrossRef PubMed.
- The Hibridon package was written by M. H. Alexander et al. Copyright for 1987, 1991, 1993, 1996, 2000, 2001, 2003, 2004, 2007, 2008, 2009, 2010, 2011 University of Maryland at College Park. All rights reserved.
- L. M. Tack, N. H. Rosenbaum, J. C. Owrutsky and R. J. Saykally, J. Chem. Phys., 1986, 84, 7056 CrossRef.
- O. Lakhmanskaya, M. Simpson, S. Murauer, V. Kokoouline and R. Wester, J. Chem. Phys., 2018, 149(10), 104302 CrossRef PubMed.
- R. N. Zare, Angular momentum: understanding spatial aspects in chemistry and physics, Wiley, 1988, p. 349 Search PubMed.
- G. Sarma, A. K. Saha, C. K. Bishwakarma, R. Scheidsbach, C.-H. Yang, D. Parker, L. Wiesenfeld, U. Buck, L. Mavridis and S. Marinakis, Phys. Chem. Chem. Phys., 2017, 19, 4678–4687 RSC.
- S. Schiller, I. Kortunov, M. Hernández Vera, F. Gianturco and H. da Silva, Phys. Rev. A, 2017, 95, 043411 CrossRef.
- R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001 CrossRef.
- T. Oka, J. Mol. Spectrosc., 2004, 228, 635–639 CrossRef.
- J. Mikosch, H. Kreckel, R. Wester, R. Plašil, J. Glosík, D. Gerlich, D. Schwalm and A. Wolf, J. Chem. Phys., 2004, 121, 11030–11037 CrossRef PubMed.
- R. Otto, A. von Zastrow, T. Best and R. Wester, Phys. Chem. Chem. Phys., 2013, 15, 612–618 RSC.
- P. Jusko, O. Asvany, A.-C. Wallerstein, S. Brünken and S. Schlemmer, Phys. Rev. Lett., 2014, 112, 253005 CrossRef PubMed.
- O. Asvany, O. Ricken, H. S. P. Müller, M. C. Wiedner, T. F. Giesen and S. Schlemmer, Phys. Rev. Lett., 2008, 100, 233004 CrossRef PubMed.
- H. Kreckel, D. Bing, S. Reinhardt, A. Petrignani, M. Berg and A. Wolf, J. Chem. Phys., 2008, 129(16), 164312 CrossRef PubMed.
- E. S. Endres, G. Egger, S. Lee, O. Lakhmanskaya, M. Simpson and R. Wester, J. Mol. Spectrosc., 2017, 332, 134–138 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |