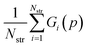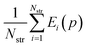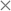Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Repulsion–dispersion parameters for the modelling of organic molecular crystals containing N, O, S and Cl†
Christina A.
Gatsiou
,
Claire S.
Adjiman
 and
Constantinos C.
Pantelides
*
and
Constantinos C.
Pantelides
*
Molecular Systems Engineering Group, Centre for Process Systems Engineering, Department of Chemical Engineering, Imperial College London, London SW7 2AZ, UK. E-mail: c.pantelides@imperial.ac.uk
First published on 12th July 2018
Abstract
In lattice energy models that combine ab initio and empirical components, it is important to ensure consistency between these components so that meaningful quantitative results are obtained. A method for deriving parameters of atom–atom repulsion dispersion potentials for crystals, tailored to different ab initio models, is presented. It is based on minimization of the sum of squared deviations between experimental and calculated structures and energies. The solution algorithm is designed to avoid convergence to local minima in the parameter space by combining a deterministic low-discrepancy sequence for the generation of multiple initial parameter guesses with an efficient local minimization algorithm. The proposed approach is applied to derive transferable exp-6 potential parameters suitable for use in conjunction with a distributed multipole electrostatics model derived from isolated molecule charge densities calculated at the M06/6-31G(d,p) level of theory. Data for hydrocarbons, azahydrocarbons, oxohydrocarbons, organosulphur compounds and chlorohydrocarbons are used for the estimation. A good fit is achieved for the new set of parameters with a mean absolute error in sublimation enthalpies of 4.1 kJ mol−1 and an average rmsd15 of 0.31 Å. The parameters are found to perform well on a separate cross-validation set of 39 compounds.
1 Introduction
Crystal Structure Prediction (CSP) has become a valuable tool for determining and understanding the solid states of an increasingly wide range of compounds and mixtures. As highlighted in the most recent (2016) blind test,1 CSP methods for organic molecules are now applicable to a wide range of real systems, including salts, hydrates and large flexible molecules, with at least one successful prediction being achieved for each target system in the test.Notwithstanding this significant progress, the results of the blind test also demonstrated some outstanding challenges for CSP methods specifically relating to energy ranking. In some cases, experimentally-observed structures for a given organic compound were deemed to have too high a lattice energy to occur in nature, and were consequently discarded from further consideration. Even methods that are generally successful in identifying the experimentally-observed crystal structures often fail to predict the experimentally-observed relative stability order.2 While this may partly be due to the neglect of entropic contributions, the problem primarily arises from the insufficient accuracy of the lattice energy model in evaluating the energy differences between predicted structures, which can be as low as 1 kJ mol−1.3
A variety of models have been developed and used in CSP for the calculation of the lattice energy, ranging from empirical force fields to electronic structure methods. Dispersion-corrected Density Functional Theory (DFT) models4–6 have emerged as accurate methods for calculating energies,1 with benchmark studies suggesting an uncertainty of 3 kJ mol−1 for absolute lattice energies.7,8 However, the computational cost of these models precludes their use for the minimization of large numbers (tens or hundreds of thousands) of structures, a critical step in current CSP methodologies. On the other hand generic force fields such as COMPASS,9 CVFF10 and others are computationally efficient but of limited accuracy.11,12 In view of these factors, the development of force fields that bridge the gap between these extremes has been an important step for all successful CSP methods. In this context, the models used in the sixth blind test included tailor-made potentials fitted to periodic ab initio data,13 potentials derived from symmetry-adapted perturbation theory based on DFT (SAPT(DFT)) calculations,14 and hybrid models combining isolated-molecule electronic structure calculations with empirical repulsion–dispersion potentials.15–17 Further details of the different lattice energy models that have been used in CSP through the years and their performance can be found in the blind test papers18–22 and review papers.11,23
In the CSP approach developed in our group,24 different energy models are used for the global search step in which thousands of possible structures are generated (CrystalPredictor16,17,25,26) and in the refinement step in which the ranking of structures is finalized (CrystalOptimizer27,28). Recent developments in the model for the global search16,17 have led to significant improvements in the accuracy of the force fields for large flexible molecules (such as molecule XXVI in the sixth blind test); in general, all experimentally-relevant structures are typically identified within 20 kJ mol−1 of the global minimum and carried through to the refinement stage.16,17 The latter requires a higher degree of accuracy in the lattice energy. The intramolecular energy is calculated using local approximate models derived from the isolated-molecule ab initio energy27 computed at a chosen level of theory. The intermolecular energy is derived by combining electrostatic interactions represented by distributed multipoles15,29,30 derived from the isolated molecule charge density calculated at the same level of theory, and repulsion–dispersion interactions modelled by an empirical exp-6 potential with parameters taken from the literature such as the FIT potential,31–37 W01 (ref. 38) or other parameterizations.39
The values of the repulsion–dispersion potential parameters used in most current methodologies were originally estimated from experimental crystal data analysed using an atomic charge representation of electrostatics, with charges fitted to the HF/6-31G(d,p) charge density; intramolecular energy contributions were neglected.10,18,39–41 As a result, such parameters are not necessarily consistent with more sophisticated electrostatic models such as those based on multipoles. In addition, only parameters relating to the most common atoms (C, N, O, H, Cl, F) were derived from extensive datasets. For atoms such as sulphur or bromine, parameters from a variety of literature sources are currently being used, a practice that is likely to result in inaccuracies. Furthermore, even within the set of atoms considered in the FIT and W01 parameterizations, some cross interactions (e.g., O–N) were not fitted to experimental data; instead, they were approximated using geometric combining rules that are known to be of limited validity and may lead to inaccurate predictions.42
Overall, as has been stated elsewhere,13 force fields should be carefully parameterized so that the different terms complement each other. In practical terms, repulsion–dispersion potentials need to be reparameterized for the specific electrostatics and intramolecular energy models with which they are intended to be used. There has been a recent effort42 in this direction through the partial reparameterization of the FIT set using the B3LYP/6-31G** and B3LYP/6-311G** levels of theory and multipole expansions for the electrostatics. Focusing on O and N parameters, the work led to encouraging results, with experimental unit cells being reproduced to within 3% and hydrogen bond geometries and sublimation enthalpies between 7.4 and 9.0%.
In this paper, we present a systematic approach for the reparameterization of the repulsion–dispersion term using experimental structural and sublimation enthalpy data. The proposed algorithm can easily be used to derive empirical parameters consistent with different electrostatic models or levels of theory. Here, its applicability is demonstrated by deriving a set of exp-6 repulsion–dispersion potential parameters for C, H, N, O, S and Cl consistent with electrostatic interactions described by distributed multipoles derived from the M06/6-31G(d,p) level of theory. For the first time, this leads to parameters for sulphur that are consistent with the remaining parameter set and this is shown to lead to a significant improvement in performance.
2 The lattice energy model
To relate computational models of crystal structures to experimental data, it is generally assumed that the experimentally-observed crystals correspond to local minima of the Gibbs free energy. Moreover, given the relatively small contribution of entropic effects at low temperatures and the complexity associated with their calculation, the lattice energy is usually employed as an approximation of the free energy. Thus, the objective of CSP is the identification of all low-energy local minima in the lattice energy surface.2.1 Defining the crystal structure
In frequently-used codes in CSP, such as the CrystalOptimizer27,28 code on which we focus, the lattice energy of a crystal is a function of the following independent variables:• The unit cell lengths and angles, collectively denoted by X.
• The positions of the centres of mass and the orientation of chemical entities within the unit cell, collectively denoted by β.
• The molecular conformational degrees of freedom (CDFs), i.e. bond lengths, angles and torsions, collectively denoted by θ.
It is also useful to introduce two dependent quantities, i.e. variables that are functions of the independent variables:
• Q(θ) denotes the set of parameters in the distributed multipoles43 describing the molecule’s electrostatic field for a given molecular conformation θ.
• Y(θ,β) denotes the Cartesian coordinates of all atoms in the unit cell, which depend on the molecular positions and orientations β and the molecular conformations θ.
2.2 Lattice energy model for CSP
The lattice energy of a crystal Ulatt can be expressed as the sum of intramolecular and intermolecular energy contributions:| Ulatt(X,β,θ) = ΔUintra(θ) + Ue(Y,X,Q) + Urd(Y,X) | (1) |
The intramolecular contribution ΔUintra(θ) in the above expression is typically computed via a QM evaluation of the conformational energy at given θ.
The intermolecular electrostatic model is based on a distributed multipole representation of electrostatics, placing an expansion up to the hexadecapole moment at each atomic position (as in DMACRYS15 and hence CrystalOptimizer27). The GDMA program30 is used to derive the parameters Q(θ) from the isolated molecule wavefunction;29 the latter is also determined by the QM calculation used for the computation of ΔUintra(θ) at given θ. The intermolecular electrostatic energy, Ue, is calculated as the sum of interactions between multipoles on atomic sites of different molecules. Such a representation of electrostatics has been shown to be successful in predicting highly-directional (anisotropic) lone-pair interactions, π–π stacking in aromatic rings and hydrogen bond geometries in organic crystals.44–46
The repulsion–dispersion component of the intermolecular energy, Urd, is calculated as the sum of all repulsion–dispersion interactions within a predefined cutoff. Each interaction, Urdij, between two atoms of types i and j occurring in two different molecules and separated by a distance r is described through an isotropic atom–atom Buckingham potential:
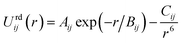 | (2) |
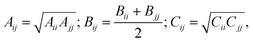 | (3) |
Finally, in calculating Ue and Urd, summations of intermolecular atom–atom interactions between the central unit cell and other cells in the crystal must be computed. This is done via a combination of direct and Ewald summations within a predefined cutoff which is set to 15 Å by default.15
2.3 Lattice energy model for parameterization
While the intramolecular energy plays an important role in CSP for flexible molecules, accounting for conformational changes leads to significant increases in the computational cost of energy evaluations. As a result, in keeping with previous work on the parameterization of force fields for CSP,31–36 we rely on a dataset that contains structures of relatively rigid molecules with no flexible torsions. For such a dataset, intermolecular interactions within the solid will not significantly distort the conformation of the molecule, and the experimental values of the molecular conformation variables, θexp, can be expected to be close to those for the global minimum in the QM energy function for the isolated molecule, θgas. However, due to experimental error and theoretical approximations, there are typically some small differences between θexp and θgas. Thus, for the purpose of the calculations, we fix the CDFs to the values of θgas consistent with the chosen level of the theory. The intramolecular energy, ΔUintra, is then equal to zero and as a result the lattice energy model takes the simplified form:| Ulatt(X,β;θgas) = Ue(Y,X,Q(θgas)) + Urd(Y,X,p) | (4) |
To assess the validity of the lattice energy model, and in particular of the parameter values p, we seek a local energy minimum close to the given experimental structure, (Xexp,βexp). The lattice energy computed for a given p, denoted by 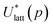 , is given by:
, is given by:
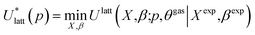 | (5) |
The quantities 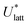 and (X*,β*) form the basis for comparison between predicted and experimental structures, as discussed in the next section.
and (X*,β*) form the basis for comparison between predicted and experimental structures, as discussed in the next section.
3 Parameter estimation
An extensive set of experimental crystal property data is required to determine appropriate values for the repulsion–dispersion parameters. More specifically, the properties that can be most directly related to the lattice energy model are the geometries of experimentally-observed crystal structures determined by diffraction methods, and sublimation enthalpies.3.1 Quantifying deviations in crystal geometry
The structural features predicted by the model can be assessed by comparison to different types of experimental structure data as available in the Cambridge Structural Database (CSD).47 As experimental X-ray diffraction (XRD) data are subject to relatively small uncertainties, they are valuable for parameter estimation. However, there are well-known difficulties in determining hydrogen positions39 and in determining the bond lengths of polar or high-order bonds (such as C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) due to the fact that interatomic nuclei distances in XRD are defined as distances between electron densities.48,49 Thermal effects may be another source of error in structural data: typically, unit cell lengths in organic crystals may increase by around 3% over a temperature range of several hundred degrees.50
C) due to the fact that interatomic nuclei distances in XRD are defined as distances between electron densities.48,49 Thermal effects may be another source of error in structural data: typically, unit cell lengths in organic crystals may increase by around 3% over a temperature range of several hundred degrees.50
In order to minimize the potential effects of experimental errors, our study applied the following criteria in selecting appropriate experimental crystallographic data from the CSD:
1. Relatively rigid molecules should be chosen.
2. Solvate and hydrate crystals are avoided.
3. Structures at high pressures (above ambient pressure) and above room temperature are rejected.
4. Single-crystal diffraction data are preferable over powder diffraction data.
5. Structures resolved via neutron scattering are preferred when available.
6. Structures resolved with XRD with an X-ray discrepancy factor (R) exceeding 5% are normally rejected, unless their sublimation enthalpies are also available or other criteria are met.
Several distance metrics are available for quantifying the deviation between two given crystal structures.51 In our work, the deviation between experimental and predicted structures for a crystal i is described by a metric Gi(p) that consists of two contributions. The first contribution measures the relative deviations between the experimental and predicted unit cell parameter vectors, Xexpi and 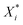 respectively:
respectively:
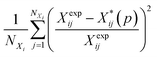 | (6) |
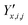 ,
, 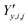 and
and 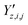 ‡ of an atom j in the asymmetric unit of a crystal i, its relative position vector with respect to a reference atom,§ denoted by the subscript “ref”, is given by:
‡ of an atom j in the asymmetric unit of a crystal i, its relative position vector with respect to a reference atom,§ denoted by the subscript “ref”, is given by: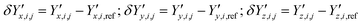 | (7) |
The contribution of atomic positions to the deviation measure Gi(p) between experimental and predicted structures for crystal i is then given by:
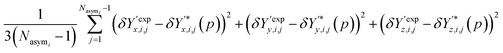 | (8) |
The calculation of the relative position vectors is described in detail in the ESI.† In order to avoid introducing an inherent offset in the deviation metric Gi(p), the fractional atomic coordinates in the experimental crystal are computed based on the predicted (rather than the experimental) molecular conformation. This is appropriate provided that the differences between θgas and θexp are small, a condition that needs to be verified when constructing the experimental dataset.
Overall, the function Gi(p) used as a measure of similarity between experimental and predicted structures is defined as:
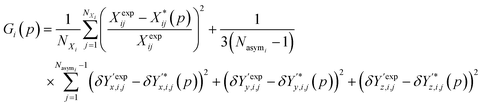 | (9) |
It is worth noting that the above expression aims to balance the contributions of various terms via the application of appropriate scaling factors. Thus, relative (rather than absolute) deviations are used for the unit cell parameters. No such scaling is needed for the position vectors as they are already normalized. Moreover, since the two summations may comprise very different numbers of terms, the first one is divided by the number of unit cell parameters not constrained by symmetry, NXi, and the second one by the number of fractional coordinates describing the asymmetric unit, 3(Nasymi−1).
The quantity Gi(p) is directly incorporated in the objective function of the parameter estimation problem. In analysing the quality of the results of the parameter estimation, the root mean squared deviation of the 15 molecule coordination sphere, rmsd15,52 is used as an additional measure of similarity between predicted and experimental crystals.
3.2 Quantifying deviations in sublimation enthalpy
The accuracy of the computed lattice energies can be assessed from sublimation enthalpies reported in thermophysical properties databases such as NIST53 and DETHERM.54 Uncertainties in measured sublimation enthalpies can be very large due to several factors such as polymorphism, a lack of standards for compounds with low vapour pressures, chirality, systematic errors associated with the measurement techniques and further errors that can be introduced in measurements by adjustment to a reference temperature (which is necessary when comparing different measurements).55 Based on 451 measurements of 80 compounds, Chickos et al.55 estimated the average uncertainty of sublimation enthalpies to be 4.9 kJ mol−1. Consequently, our study does not make use of any sublimation enthalpy measurement with a reported error exceeding 4.9 kJ mol−1.A calculated enthalpy of sublimation at temperature T and pressure P, 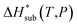 , can be obtained from the predicted lattice energy
, can be obtained from the predicted lattice energy 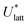 by the following commonly-used approximation:56–58
by the following commonly-used approximation:56–58
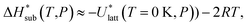 | (10) |
In previous studies by Arnautova et al.59 and Gavezzotti,60 computed lattice energies were directly compared to experimental sublimation enthalpies without any correction, an approach justified by the authors on the basis of uncertainty in the sublimation enthalpy data. We prefer to apply the correction shown in eqn (10) in order to reduce any systematic error in the comparison between predicted and experimental values. Thus, we employ the following deviation function as a measure of the difference between the experimental and predicted sublimation enthalpies for a given crystal i:
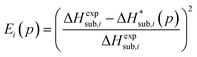 | (11) |
3.3 Obtaining globally optimal parameter estimates
Parameter estimation aims to determine the values of parameters p for which the calculated quantities best match the experimentally-observed quantities. This can be expressed mathematically as the minimization of a combined deviation metric R(p):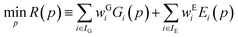 | (12) |
In general, we seek to establish the values of p that lie within given lower and upper bounds, pl and pu respectively, and lead to a globally minimal value of R(p). To compute R(p) at a given set of parameter values p, we need to perform the lattice energy minimization (5) for each crystal structure i ∈ IG starting from the corresponding experimental structure. Once the optimal solution is obtained, we can compute the geometry deviation Gi(p) and, if i ∈ IE, the sublimation enthalpy deviation Ei(p). The quantities Gi(p) and Ei(p) can then be used to compute R(p) viaeqn (12). Overall, this is a relatively expensive computation as it involves a large number of crystal structure minimizations, but these can be carried out in parallel.
A more serious challenge for the reliable solution of problem (12) is that the objective function R(p) may have multiple local minima, in which case the solution obtained via the application of standard local minimization algorithms may depend on the starting points (i.e. the initial guesses) for the parameters p. In order to increase the likelihood of identifying the globally optimal parameter vector, we adopt a step-wise approach involving the generation of many starting points in the space of parameters p, followed by a gradient-based local minimization from selected starting points:
1. Compute the reference quantity R(pFIT) where pFIT are the values of the parameters in the existing FIT parameterization.
2. Generate N points pk, k = 1, …, N, in the parameter space by means of a Sobol’ sequence61,62 within the defined bounds [pl,pu]. The advantages of low-discrepancy (such as Sobol’) sequences over other methods (e.g. Monte Carlo sampling or uniform grids) for efficiently searching multivariable domains are well established.63
3. For each point pk, evaluate the corresponding R(pk) as described above; discard all points for which R(pk) exceeds the reference value R(pFIT) by more than a specified factor α (e.g. 5) as these are unlikely to yield parameter estimates that are better than the FIT one.
4. Starting from pk as the initial guess, perform the local minimization (eqn (12)) to obtain a (locally) optimal parameter estimate p*,k with a corresponding objective function value R(p*,k). As described in the ESI,† a sequential quadratic programming (SQP) algorithm with a Broyden–Fletcher–Goldfarb–Shanno (BFGS)64 update of the Hessian matrix is used for this purpose.
5. Choose the solution p*,k with the lowest corresponding value R(p*,k) as the best parameter estimate p*.
A flowchart of the overall parameter estimation methodology is shown in Fig. 1.
3.4 Cross-validation of optimal parameter estimates
To further assess the quality of the optimal parameter estimates p* obtained by the procedure described in the previous section, we examine its ability to reproduce experimental geometry and sublimation enthalpy data both for the structures used for the estimation, and for a separate set of structures reserved for cross-validation purposes.The quality of geometry reproduction is assessed based on the usual rmsd15,i measure between an experimental and predicted crystal i calculated using the COMPACK52 code. We also consider the rmsd15 averaged over a set of crystal structures.
For assessing the quality of sublimation enthalpy prediction for each individual crystal i, we use the Absolute Deviation (ADi) defined as:
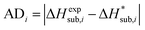 | (13) |
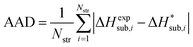 | (14) |
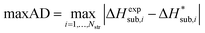 | (15) |
We generally aim to derive parameter estimates for which the average values AAD and rmsd15 do not exceed 5 kJ mol−1 and 1 Å respectively.22
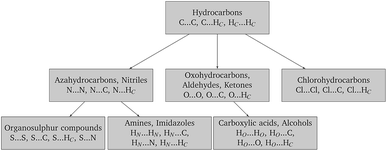
4 Parameterization strategy
For a parameter estimation study involving NA distinct types of atoms, there are NA(NA + 1)/2 possible interaction pairs that need to be considered, and consequently 3NA(NA + 1)/2 repulsion–dispersion parameters that need to be estimated from experimental data. Overall, even for relatively small NA, this is a difficult and computationally expensive problem to solve.An approach commonly used for reducing the parameter space is to use combining rules for the parameters describing interactions between atoms of different types. The use of such combining rules for the dispersion coefficient does have some physical justification at the level of the Unsöld approximation to the rij−6 dispersion. However, other rules are known to be limited in their accuracy,65 and their use may lead to lower quality of predictions in crystal structure calculations.32,42,66 Therefore, in this study we prefer not to use combining rules, relying instead on the estimation of the cross-interaction parameters directly from experimental data.
On the other hand, and in common with the approach adopted by Pyzer-Knapp et al.,42 we do hold the exponential Bij parameters fixed at the FIT values: the shape of the potential is very sensitive to even small changes in these parameters, which renders their numerical handling as part of the parameter estimation procedure problematic.
Finally, in order to make the problem computationally manageable and ensure compatibility and transferability of the different sets of parameters, the parameter estimation is carried out in a sequential manner as shown schematically in Fig. 2. Similarly to the work of Sun,67 optimal parameters for carbon and hydrogen (Hc) are determined first based on experimental data for hydrocarbons. These are then fixed for the subsequent steps, and interaction parameters for other atom pairs are estimated from data on appropriate compounds.
5 Illustration of methodology
The methodology proposed in this paper is illustrated for the estimation of parameters for the C⋯C, C⋯HC and HC⋯HC interactions using experimental data for hydrocarbon crystals (cf. the top box in Fig. 2). As indicated in the flowchart in Fig. 1, we start by collecting relevant experimental data based on the general criteria described in Section 3.1. The experimental crystallographic data and energetic data collected for hydrocarbons are listed in Table S1 of the ESI.† This consists of 19 compounds and exhibits a diversity of hybridizations not present in the training sets for the FIT parameterization.We then perform an isolated-molecule gas-phase QM calculation for each molecule using Gaussian09 (ref. 68) with the M06 (ref. 69) functional and a 6-31G(d,p) basis set. The resulting wavefunctions are used to generate multipole moments via the distributed multipole analysis method43 as implemented in the GDMA 2.2 program.43
We now fix the three Bij parameters to their FIT values, and aim to determine optimal estimates for the 6 Aij and Cij parameters; the latter constitute our parameter vector p. For the purposes of this estimation, we will allow p to vary within ±40% of the FIT values. As explained in Section 3.3, in order to increase the probability of obtaining globally optimal parameter estimates, we use a Sobol’ sequence to generate 1000 starting points pk, k = 1, …, 1000.
Before proceeding with actually performing local minimizations of function R(p) (cf.eqn (12)) starting from some of the above points, it is instructive to gain some insight as to the appropriate choices of the weighting factors wGi and wEi. For simplicity, we use the same weight values (wG or wE) for all 19 structures i. We consider 15 distinct combinations of these weights as shown in Table 1, and evaluate the objective function R(pk) for each such combination. The 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 local lattice energy minimizations required for evaluating R(pk), k = 1, …, 1000 are performed with DMACRYS at 0 Pa pressure.
000 local lattice energy minimizations required for evaluating R(pk), k = 1, …, 1000 are performed with DMACRYS at 0 Pa pressure.
| w G | w E |
|---|---|
| 100 | 1 |
| 50 | 1 |
| 20 | 1 |
| 15 | 1 |
| 10 | 1 |
| 5 | 1 |
| 2 | 1 |
| 1 | 1 |
| 1 | 2 |
| 1 | 5 |
| 1 | 10 |
| 1 | 15 |
| 1 | 20 |
| 1 | 50 |
| 1 | 100 |
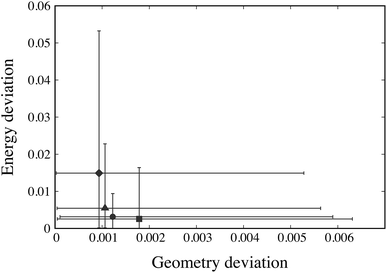
For each weight combination, having evaluated the objective function R(pk) at the 1000 Sobol’ points pk, we select the Sobol’ point with the lowest value of the objective function. This serves as an approximation to the optimal parameter estimate p* that might be obtained using that particular combination of weights. The solutions arising from different weight combinations are compared in Fig. 3 based on the geometry and sublimation deviation functions, G(p*) and E(p*), averaged over the 19 crystal structures under consideration.
The maximum and minimum values of Gi(p*) across all 19 crystal structures i are also depicted on the horizontal axis of Fig. 3 while the maximum and minimum Ei(p*) are shown against the vertical axis. We note that several weight ratios lead to the same solution; in fact, only 4 distinct solutions are obtained, as depicted by the solid symbols in Fig. 3. Based on these results, the weights wG = 1 and wE = 1 appear to offer both the best trade-off between geometry and energy errors, and the smallest variation of these errors across the different structures being considered. Accordingly, these values are chosen to be used throughout our parameter estimation methodology in this paper.
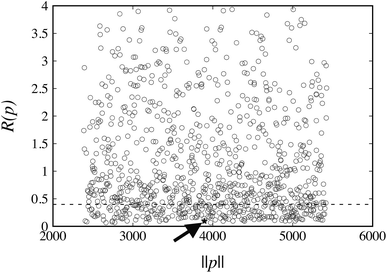
The values of R(pk) for the weights wG = wE = 1 at the 1000 points pk are plotted in Fig. 4. The corresponding reference value R(pFIT) for the FIT parameter values pFIT is also shown. We note that the FIT parameter point, pFIT, lies among the lowest points in this figure, which suggests that the FIT parameter values are already good estimates, a result that was expected given the similarity between the training set used in this work for hydrocarbons and that used by Williams et al.31
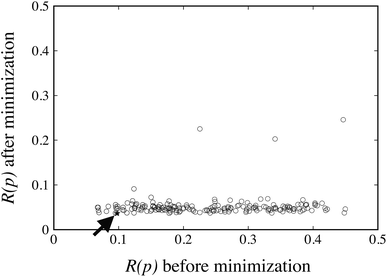
The FIT reference value R(pFIT) allows us to prune out any Sobol’ points that are unlikely to result in an improved fit of the experimental data over the already available FIT parameters (cf. step 5 of the algorithm in Fig. 1). Here we apply a cutoff ratio α of approximately 5, which excludes all but 250 of the original Sobol’ points from further consideration. We then solve the optimization problem expressed by eqn (12) starting from each of the remaining 250 points. The initial objective function values R(pk) and the final objective function values after local minimization, R(p*,k), are shown in Fig. 5. It can be seen that the minimization does result in a significant reduction of the objective function R(p). The results suggest a “flat” objective function with many broad and shallow minima; however, it is also possible that some of the points are not true local minima, but simply arise due to premature termination of the challenging local minimization.
The parameter values p* resulting in the lowest objective function value are given in Table 2 where they are also compared with the original FIT parameters. A comparison of the corresponding objective function values is presented in Table 3. The objective function value for p* is 63% lower than the corresponding value for the FIT parameters. The new parameters also achieve 23% and 72% reductions in the geometry and energy deviation functions respectively. Overall, the new parameters yield a significantly better reproduction of both the geometries and energies of the crystals in the training set even in the case of such a relatively simple and well-studied parameter set. Further details of the quality of fit for each individual structure are presented in Table S4 of the ESI.†
6 Results and discussion
In this section, the stagewise procedure depicted in Fig. 2 is applied to derive optimal estimates of the repulsion–dispersion interaction parameters for a range of atoms. The parameters obtained are consistent with a distributed multipole electrostatic model derived from charge densities calculated at the M06/6-31G(d,p) level of theory.6.1 Choice of training set and cross-validation set
The crystal structures of 106 organic molecular crystals including hydrocarbons, azahydrocarbons, oxohydrocarbons, organosulphur compounds, chlorohydrocarbons, amines, imidazoles, carboxylic acids and alcohols were collected from the CSD47 for the purpose of the parameter estimation reported in this work. The training set was selected to contain molecules with each element in different bonding situations. For example, the training set of hydrocarbons contains alkanes and cycloalkanes with sp3 hybridized carbons that form single bonds, aromatics with sp2 hybridized carbons forming sigma bonds and the delocalization of electrons between the ring carbons and hydrocarbons with an alkynyl group of sp hybridized carbons that form a triple bond. Similar considerations underpinned the selection of molecules containing N, O and S, as summarized in Table 4. The molecular diagrams, CSD refcodes, numbers of molecules in the unit cell Z, space groups, R-factors and experimental temperatures are summarized in Table S1 of the ESI.†Gas-phase molecular conformations are computed at the M06/6-31G(d,p) level of theory. The rigidity of the molecules is ascertained through rmsd1 comparisons between computed and experimental conformations with COMPACK, giving an average rmsd1 of only 0.05 Å. In a previous study by Arnautova et al.,59 the C–H bond lengths of the experimental conformations were adjusted to the average experimental value from neutron diffraction data to overcome issues of unreliable hydrogen positions determined by X-ray diffraction. We found the C–H bond lengths in the gas-phase conformations to be approximately 1.087 Å, which is very close to the average experimental value of 1.089 Å derived from neutron data given in the CSD. Therefore, no modification was applied to the C–H bond lengths.
Experimentally determined enthalpies of sublimation were identified for 53 of the 106 molecules, which is significantly more than the number used in the parameterization of FIT. The sublimation enthalpies used in this work are given in Table S1 of the ESI.†
6.2 Optimized parameters
The optimal parameter estimates for the 24 atom–atom interactions occurring in the datasets are listed in Table 5, where they are also compared with the corresponding FIT parameters. The optimized parameters for sulphur interactions are further compared with two additional sets of parameters, namely those by No et al.70 (denoted as S-No) and by Abraha et al.71 (denoted as S-Ab). These alternative parameter sets are presented in Table 6.| Atom type | FITa | This work | |||||
|---|---|---|---|---|---|---|---|
| i | j | A ij /eV | B ij /Å | C ij /eV Å6 | A ij /eV | B ij /Å | C ij /eV Å6 |
| a Parameters from (ref. 37). | |||||||
| C | C | 3832.147 | 0.278 | 25.287 | 2299.288 | 0.278 | 18.020 |
| C | HC | 689.537 | 0.272 | 5.979 | 449.3172 | 0.272 | 6.265 |
| HC | HC | 124.072 | 0.267 | 1.414 | 173.559 | 0.267 | 1.957 |
| C | N | 3179.515 | 0.271 | 19.007 | 3355.322 | 0.271 | 24.171 |
| N | N | 2638.029 | 0.265 | 14.286 | 3687.092 | 0.265 | 17.577 |
| HC | N | 572.105 | 0.266 | 4.494 | 516.587 | 0.266 | 2.696 |
| C | O | 3022.85 | 0.265 | 17.16 | 1352.853 | 0.265 | 10.164 |
| HC | O | 543.916 | 0.260 | 4.057 | 304.084 | 0.260 | 2.481 |
| O | O | 2384.466 | 0.253 | 11.645 | 963.846 | 0.253 | 18.632 |
| C | S | 3990.989 | 0.290 | 38.957 | 2819.374 | 0.290 | 46.499 |
| N | S | 3311.305 | 0.282 | 29.281 | 3760.816 | 0.282 | 31.148 |
| HC | S | 718.118 | 0.284 | 9.211 | 802.131 | 0.284 | 9.891 |
| S | S | 4156.415 | 0.303 | 60.016 | 3401.359 | 0.303 | 95.872 |
| C | HN | 446.952 | 0.242 | 2.374 | 478.038 | 0.242 | 3.561 |
| HC | HN | 80.422 | 0.238 | 0.561 | 40.211 | 0.238 | 0.842 |
| N | HN | 370.834 | 0.237 | 1.784 | 297.752 | 0.237 | 0.892 |
| HN | HN | 52.129 | 0.215 | 0.223 | 78.194 | 0.215 | 0.111 |
| HO | C | 446.952 | 0.242 | 2.374 | 519.271 | 0.242 | 2.488 |
| HO | HC | 80.422 | 0.238 | 0.561 | 128.676 | 0.238 | 0.224 |
| HO | O | 352.562 | 0.232 | 1.611 | 231.169 | 0.232 | 0.644 |
| HO | HO | 52.129 | 0.215 | 0.223 | 61.708 | 0.215 | 0.089 |
| C | Cl | 6060.173 | 0.281 | 45.040 | 2627.877 | 0.290 | 39.868 |
| HC | Cl | 1090.436 | 0.276 | 10.650 | 1371.320 | 0.276 | 17.708 |
| Cl | Cl | 9583.584 | 0.285 | 80.224 | 7940.587 | 0.285 | 67.687 |
| Atom type | S-Ab | S-No | |||||
|---|---|---|---|---|---|---|---|
| i | j | A ij /eV | B ij /Å | C ij /eV Å6 | A ij /eV | B ij /Å | C ij /eV Å6 |
| C | S | 2623.650 | 0.308 | 55.295 | 3064.776 | 0.308 | 46.911 |
| N | S | 2176.830 | 0.299 | 41.562 | 2542.830 | 0.299 | 35.260 |
| HC | S | 472.092 | 0.301 | 13.074 | 551.467 | 0.301 | 11.092 |
| S | S | 1796.306 | 0.345 | 120.918 | 2451.128 | 0.345 | 87.029 |
The optimized parameters differ significantly from the original set. However, because of the high degree of correlation between the Aij and Cij parameters, large changes in their individual values do not necessarily result in a large change in the potential. Fig. 6 shows the differences in equilibrium distances and well depths of the potentials. For most pairwise interactions, these differences are relatively small. A striking exception is the O⋯O interaction for which we observe a significant change in the potential well depth and location of the minimum (cf.Fig. 7a), with the new parameters indicating stronger and shorter-range interactions. On the other hand, the differences between our potentials for the interactions of oxygen with other atoms and the corresponding FIT potentials are not very pronounced. This is an indication of the inaccuracies that may be introduced by relying on combining rules for estimating cross-interaction parameters.
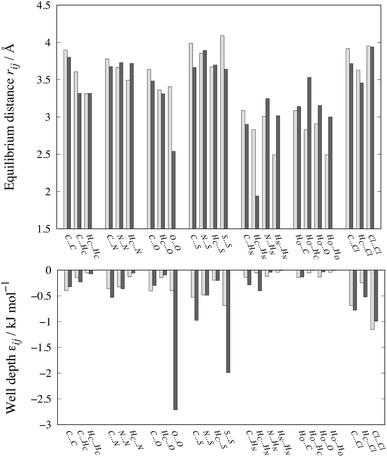 | ||
| Fig. 6 Comparison of equilibrium distances and well depths for 24 interactions as calculated with FIT (light grey bars) and our new parameter set (dark grey bars). The data along with the results for the S-Ab and S-No parameter sets are given in Table S3 of the ESI.† | ||
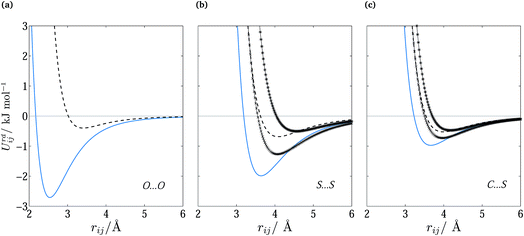 | ||
Fig. 7 Repulsion–dispersion potential curves for (a) O⋯O, (b) S⋯S and (c) C⋯S interactions. The optimized potential curves (continuous curves) are compared with the FIT potential curves (dashed curves) and with S-No70 ( ) and S-Ab71 ( ) and S-Ab71 ( ). ). | ||
Shorter equilibrium distances and deeper wells are also observed for all S interactions apart from the HC⋯S one (cf.Fig. 6 and 7b and c). We note that significant differences also exist among the FIT, S-Ab and S-No parameter sets as shown in Fig. S3 of the ESI.†
Both oxygen interactions and sulphur interactions were fitted to a number of sublimation enthalpy data. We note that no such data were used in the derivation of the FIT set. The resulting improvement in sublimation enthalpy prediction demonstrates the impact of using energetic data to fit the potentials.
6.3 Performance of new parameters: sublimation enthalpy
Overall, the new parameter values result in a good fit for the experimental structures in the training set. As shown in Table 7, the sublimation enthalpy AAD is 4.1 kJ mol−1, which is 53% smaller than the corresponding FIT value while the average rmsd15 of 0.31 Å is practically identical to that achieved by FIT. In fact, for hydrocarbons and azahydrocarbons, the achieved sublimation enthalpy AADs of less than 2 kJ mol−1 are similar to the errors observed with some dispersion-corrected DFT methods.7 There is also a decrease in the spread of the sublimation enthalpy errors, with a maxAD value of 16.7 kJ mol−1 compared to 38.7 kJ mol−1 with FIT.| Training set | Absolute sublimation enthalpy error (kJ mol−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| FIT | This work | S-Ab | S-No | |||||
| AAD | maxAD | AAD | maxAD | AAD | maxAD | AAD | maxAD | |
| Hydrocarbons | 2.66 | 4.83 | 1.47 | 4.08 | ||||
| Azahydrocarbons | 3.43 | 6.80 | 1.28 | 3.56 | ||||
| Oxohydrocarbons | 9.46 | 18.22 | 6.88 | 16.66 | ||||
| Organosulphur compounds | 20.97 | 38.71 | 5.29 | 10.44 | 7.94 | 16.74 | 25.73 | 46.85 |
| Amines, imidazoles | 11.00 | 19.40 | 9.17 | 13.67 | ||||
| Carboxylic acids, alcohols | 13.98 | 24.93 | 5.94 | 10.50 | ||||
| Chlorohydrocarbons | 7.30 | 8.90 | 0.15 | 0.46 | ||||
| Overall | 8.78 | 38.71 | 4.11 | 16.66 | ||||
| Absolute rmsd15 error (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|
| FIT | This work | S-Ab | S-No | |||||
| Average | Max | Average | Max | Average | Max | Average | Max | |
| Hydrocarbons | 0.349 | 0.922 | 0.285 | 0.985 | ||||
| Azahydrocarbons | 0.223 | 0.747 | 0.231 | 0.631 | ||||
| Oxohydrocarbons | 0.342 | 0.728 | 0.306 | 0.808 | ||||
| Organosulphur compounds | 0.321 | 1.047 | 0.326 | 1.047 | 0.298 | 0.996 | 0.430 | 1.195 |
| Amines, imidazoles | 0.289 | 0.581 | 0.291 | 0.640 | ||||
| Carboxylic acids, alcohols | 0.336 | 0.868 | 0.434 | 0.875 | ||||
| Chlorohydrocarbons | 0.246 | 0.529 | 0.263 | 0.735 | ||||
| Overall | 0.305 | 1.047 | 0.309 | 1.047 | ||||
In addition to the training set, we employ a cross-validation set consisting of 39 crystal structures for representative molecules for all the classes of compounds considered here (see Table S2 in the ESI†). For six of these structures, the sublimation enthalpy is also available. The criteria for the choice of the cross-validation set were similar to those for the training set (cf. Section 3.1) although, due to the limited availability of such data for rigid molecules, the requirements regarding experimental error were less stringent in some cases. The sublimation enthalpy results reported in Table 8 indicate similar improvements to those for the training set (cf.Table 7). However, the sublimation enthalpy AAD of 7.87 kJ mol−1 is larger than the corresponding value for the training set. This may be due to the relative sparsity of energetic data, which leads to reduced statistical significance for the parameters. We also note that some of the experimental sublimation enthalpy values in the cross-validation set are less reliable than the enthalpies reported for the compounds in the training set.
| Training set | Absolute sublimation enthalpy error (kJ mol−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| FIT | This work | S-Ab | S-No | |||||
| AAD | maxAD | AAD | maxAD | AAD | maxAD | AAD | maxAD | |
| Hydrocarbons | 8.65 | 13.49 | 8.31 | 16.82 | ||||
| Azahydrocarbons | 9.51 | 9.51 | 7.49 | 7.49 | ||||
| Amines, imidazoles | 11.45 | 11.45 | 4.91 | 4.91 | ||||
| Carboxylic acids, alcohols | 23.26 | 23.26 | 9.87 | 9.87 | ||||
| Overall | 11.69 | 23.26 | 7.87 | 16.82 | ||||
| Absolute rmsd15 error (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|
| FIT | This work | S-Ab | S-No | |||||
| Average | Max | Average | Max | Average | Max | Average | Max | |
| Hydrocarbons | 0.201 | 0.286 | 0.169 | 0.285 | ||||
| Azahydrocarbons | 0.402 | 0.747 | 0.317 | 0.433 | ||||
| Oxohydrocarbons | 0.147 | 0.188 | 0.197 | 0.289 | ||||
| Organosulphur compounds | 0.239 | 0.340 | 0.275 | 0.499 | 0.221 | 0.390 | 0.276 | 0.450 |
| Amines, imidazoles | 0.327 | 0.574 | 0.275 | 0.377 | ||||
| Carboxylic acids, alcohols | 0.526 | 1.828 | 0.579 | 1.537 | ||||
| Chlorohydrocarbons | 0.246 | 0.316 | 0.235 | 0.311 | ||||
| Overall | 0.294 | 1.828 | 0.282 | 1.537 | ||||
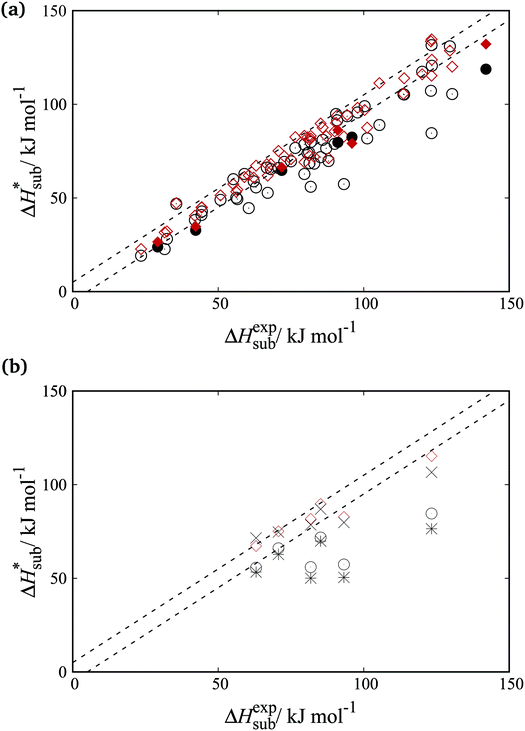
Fig. 8a shows parity plots between experimental and computed sublimation enthalpies for both the training and cross-validation sets. A significant improvement over the FIT set is evident across both sets. Fig. 8b focuses on the organosulphur compounds. It is clear that the accuracy of sublimation enthalpy predictions varies substantially across the previously derived parameter sets (FIT, S-No, and S-Ab). The improved predictive accuracy of the new parameters is important as the study of molecular crystals containing sulphur has so far been hampered by the limited availability of reliable transferable parameters.
6.4 Performance of new parameters: rmsd15
As mentioned in previous sections, the rmsd15 between the optimized unit cells and the experimentally observed ones is also used to assess the ability of our optimal parameter estimates to accurately predict unit cell geometries. An rmsd15 below 0.5 Å is generally considered to indicate a good degree of agreement between two structures. In our case, the average rmsd15 over the entire training set was 0.31 Å. The rmsd15 averages for each separate set, shown in Table 7, are below 0.5 Å. Overall, we can conclude that there is a good agreement with the experimental structures for each class although a few individual structures show rmsd15 values nearer 1.As indicated by the entries in the last rows of Tables 7 and 8, our new parameter set does not have a clear overall advantage over FIT in terms of rmsd15. This is partly explained by the fact that we used a different metric for geometry in our objective function. In our methodology, improved geometry reproduction could be achieved by setting wG ≫ wE), thereby placing greater importance on the geometry terms than the energy terms. However, the results presented here demonstrate that using equal weights leads to a significant increase in the accuracy of the computed sublimation enthalpies while maintaining good accuracy in geometry reproduction. In particular, as shown in Fig. 9, the new parameters lead to fewer points showing large errors in the sublimation enthalpy (>5 kJ mol−1) or/and in the rmsd15 (>0.5 Å).
7 Concluding remarks
The fundamental premise of the work reported in this paper is that the values of the repulsion–dispersion parameters estimated from experimental data depend on the model of electrostatic interactions¶ used in this estimation. Accordingly, this electrostatic model needs to be the same as that used in the subsequent CSP calculations. The approach proposed here allows the systematic reparameterization of the repulsion–dispersion model to derive transferable parameters that are consistent with the rest of the lattice energy model. This is particularly important in the context of current CSP methodologies which are relying on increasingly sophisticated representations of electrostatic and intramolecular contributions based on ab initio quantum mechanical calculations.The estimation of the repulsion–dispersion parameters in the lattice energy model has been formulated mathematically as a weighted least-squares minimization of the deviation between the computed and experimentally measured crystal geometries and sublimation enthalpies. Important aspects of our formulation are the weighting and scaling schemes used for balancing the contributions of different elements of the experimental dataset. The proposed solution algorithm aims to mitigate the large computational cost associated with this problem and to reduce the risk of the minimization being trapped in local minima.
The feasibility and effectiveness of the proposed approach were demonstrated by the estimation of a set of atom–atom interaction parameters for the isotropic Buckingham potential, consistent with distributed multipole electrostatics derived from charge densities computed via isolated-molecule quantum mechanical calculations at the M06/6-31G(d,p) level of theory.|| Interaction parameters between unlike atom types were also included directly in the estimation instead of being approximated via combining rules. The study reported here focused on organic molecular crystals with N, O, S and Cl atoms, and made use of a training dataset containing 106 crystal geometries and the sublimation enthalpies for 53 of these structures. A separate set of 39 structures (including 6 sublimation enthalpy values) was used for cross-validation of the derived parameter estimates. Overall, compared to the commonly used FIT parameter set, the new parameter values were found to result in significantly improved sublimation enthalpy predictions while maintaining a comparable quality of geometry reproduction.
In the work reported here, the Bij parameters of the Buckingham potential were kept fixed at the corresponding FIT values. This was mainly done in order to avoid the numerical problems caused by the unphysical predictions of this potential at low interatomic separation distances. Including these parameters in the estimation set could result in improved predictive accuracy. However, with the availability of systematic ways of estimating reliable and consistent parameter values for any form of repulsion–dispersion potential, it may be worth considering alternative potential forms that do not exhibit such unphysical behavior in the first place.
Data statement
All underlying data supporting this article are available in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from the Engineering and Physical Sciences Research Council (EPSRC) grants EP/J014958/1 and EP/J003840/1 and access to computational resources and support from the High Performance Computing Cluster at Imperial College London. We are grateful to Professor S. L. Price for supplying the DMACRYS code.Notes and references
- A. M. Reilly, A. M. Cooper, C. S. Adjiman, S. Bhattacharya, D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Gadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. Distasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C. A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Luzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H. Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, Á. Vásquez-Mayagoittia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CrossRef PubMed.
- M. Vasileiadis, A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 677–685 CrossRef PubMed.
- A. T. Hulme and S. L. Price, J. Chem. Theory Comput., 2007, 3, 1597–1608 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. A. Neumann and M. A. Perrin, J. Phys. Chem. B, 2005, 109, 15531–15541 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. Otero-De-La-Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103 CrossRef PubMed.
- J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621 CrossRef.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef.
- P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Proteins: Struct., Funct., Bioinf., 1988, 4, 31–47 CrossRef PubMed.
- G. M. Day, Crystallogr. Rev., 2011, 17, 3–52 CrossRef.
- G. M. Day, W. D. S. Motherwell and W. Jones, Phys. Chem. Chem. Phys., 2007, 9, 1693–1704 RSC.
- M. A. Neumann, J. Phys. Chem. B, 2008, 112, 9810–9829 CrossRef PubMed.
- M. Jeziorska, W. Cencek, K. Patkowski, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2007, 127, 124303 CrossRef PubMed.
- S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490 RSC.
- M. Habgood, I. J. Sugden, A. V. Kazantsev, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2015, 11, 1957–1969 CrossRef PubMed.
- I. Sugden, C. S. Adjiman and C. C. Pantelides, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 864–874 CrossRef PubMed.
- J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, W. T. M. Mooij, S. L. Price, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 697–714 CrossRef.
- W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko, P. Erk, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, J. P. M. Lommerse, W. T. M. Mooij, S. L. Price, H. Scheraga, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 647–661 CrossRef.
- G. M. Day, W. D. S. Motherwell, H. L. Ammon, S. X. M. Boerrigter, R. G. Della Valle, E. Venuti, A. Dzyabchenko, J. D. Dunitz, B. Schweizer, B. P. van Eijck, P. Erk, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, F. J. J. Leusen, C. Liang, C. C. Pantelides, P. G. Karamertzanis, S. L. Price, T. C. Lewis, H. Nowell, A. Torrisi, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt and P. Verwer, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 511–527 CrossRef PubMed.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125 CrossRef PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551 CrossRef PubMed.
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef PubMed.
- C. C. Pantelides, C. S. Adjiman and A. V. Kazantsev, in General Computational Algorithms for Ab Initio Crystal Structure Prediction for Organic Molecules, ed. S. Atahan-Evrenk and A. Aspuru-Guzik, Springer International Publishing, Cham, 2014, pp. 25–58 Search PubMed.
- P. G. Karamertzanis and C. C. Pantelides, J. Comput. Chem., 2005, 26, 304–324 CrossRef PubMed.
- P. G. Karamertzanis and C. C. Pantelides, Mol. Phys., 2007, 105, 273–291 CrossRef.
- A. V. Kazantsev, P. G. Karamertzanis, C. C. Pantelides and C. S. Adjiman, in Process Systems Engineering, Wiley-VCH Verlag GmbH and Co. KGaA, 2014, vol. 6, pp. 1–42 Search PubMed.
- A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2011, 7, 1998–2016 CrossRef PubMed.
- A. J. Stone and M. Alderton, Mol. Phys., 1985, 56, 1047–1064 CrossRef.
- A. J. Stone, J. Chem. Theory Comput., 2005, 1, 1128–1132 CrossRef PubMed.
- D. E. Williams and S. R. Cox, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 404–417 CrossRef.
- D. S. Coombes, S. L. Price, D. J. Willock and M. Leslie, J. Phys. Chem., 1996, 100, 7352–7360 CrossRef.
- T. Beyer and S. L. Price, J. Phys. Chem. B, 2000, 104, 2647–2655 CrossRef.
- S. R. Cox, L.-Y. Hsu and D. E. Williams, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1981, 37, 293–301 CrossRef.
- D. E. Williams and D. J. Houpt, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 286–295 CrossRef.
- L.-Y. Hsu and D. E. Williams, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1980, 36, 277–281 CrossRef.
- CPOSS Website, The FIT and WILL01 empirical “repulsion–dispersion” potentials, 2014, http://www.chem.ucl.ac.uk/cposs/dmacrys/fit_and_will01_empirical_potentials.htm, last accessed, 04 March 2018.
- D. E. Williams, J. Comput. Chem., 2001, 22, 1154–1166 CrossRef.
- Y. A. Arnautova, A. Jagielska, J. Pillardy and H. A. Scheraga, J. Phys. Chem. B, 2003, 107, 7143–7154 CrossRef.
- A. T. Hagler, E. Huler and S. Lifson, J. Am. Chem. Soc., 1974, 96, 5319–5327 CrossRef PubMed.
- A. T. Hagler and S. Lifson, J. Am. Chem. Soc., 1974, 96, 5327–5335 CrossRef PubMed.
- E. O. Pyzer-Knapp, H. P. G. Thompson and G. M. Day, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 477–487 CrossRef PubMed.
- A. J. Stone, J. Chem. Theory Comput., 2005, 1, 1128–1132 CrossRef PubMed.
- S. Brodersen, S. Wilke, F. J. J. Leusen and G. Engel, Phys. Chem. Chem. Phys., 2003, 5, 4923–4931 RSC.
- G. M. Day, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 1023–1033 CrossRef.
- W. T. M. Mooij and F. J. J. Leusen, Phys. Chem. Chem. Phys., 2001, 3, 5063–5066 RSC.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef.
- R. G. Little, D. Pautler and P. Coppens, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 1493–1499 CrossRef.
- P. Coppens, T. M. Sabine, G. Delaplane and J. A. Ibers, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 2451–2458 CrossRef.
- D. E. Williams, J. Comput. Chem., 2001, 22, 1–20 CrossRef.
- R. Hundt, J. C. Schön and M. Jansen, J. Appl. Crystallogr., 2006, 39, 6–16 CrossRef.
- J. A. Chisholm and S. Motherwell, J. Appl. Crystallogr., 2005, 38, 228–231 CrossRef.
- P. J. Linstrom and W. G. Mallard, J. Chem. Eng. Data, 2001, 46, 1059–1063 CrossRef.
- U. Westhaus, T. Dröge and R. Sass, Fluid Phase Equilib., 1999, 158, 429–435 CrossRef.
- J. S. Chickos, Netsu Sokutei, 2003, 30, 116–124 Search PubMed.
- L. Lorenzo Maschio, B. Civalleri, P. Ugliengo and A. Gavezzotti, J. Phys. Chem. A, 2011, 115, 11179–11186 CrossRef PubMed.
- A. Otero-de-la Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103 CrossRef PubMed.
- A. M. Reilly and A. Tkatchenko, J. Chem. Phys., 2013, 139, 024705 CrossRef PubMed.
- Y. A. Arnautova, J. Pillardy, C. Czaplewski and H. A. Scheraga, J. Phys. Chem. B, 2003, 107, 712–723 CrossRef.
- A. Gavezzotti, Theoretical Aspects and Computer Modeling of the Molecular Solid State, John Wiley & Sons, 1997, p. 97 Search PubMed.
- I. M. Sobol, USSR Computational Mathematics and Mathematical Physics, 1967, vol. 7, pp. 86–112 Search PubMed.
- P. Bratley and B. L. Fox, ACM Trans. Math Software, 1988, 14, 88–100 CrossRef.
- P. G. Karamertzanis, PhD thesis, Imperial College London, 2004.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef.
- A. J. Stone and C.-S. Tong, J. Comput. Chem., 1994, 15, 1377–1392 CrossRef.
- H. H. Y. Tsui and S. L. Price, CrystEngComm, 1999, 1, 24–32 RSC.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- K. T. No, O. Y. Kwon, S. Y. Kim, K. H. Cho, C. N. Yoon, Y. K. Kang, K. D. Gibson, M. S. Jhon and H. A. Scheraga, J. Phys. Chem., 1995, 99, 13019–13027 CrossRef.
- A. Abraha and D. E. Williams, Inorg. Chem., 1999, 38, 4224–4228 CrossRef.
- C.-A. Gatsiou, PhD thesis, Imperial College London, 2016.
Footnotes |
| † Electronic supplementary information (ESI) available: Further information on calculation methods, training and cross-validation data sets, detailed description of the new potentials and results of crystal packing calculations with all parameter sets. See DOI: 10.1039/c8fd00064f |
| ‡ Fractional coordinates can be computed directly from the Cartesian coordinates Y and the unit cell parameters X, i.e. Y′ = Y′(X,Y). |
| § The first heavy atom listed in the SHELX file. |
| ¶ And, in the case of flexible molecules, the model used for intramolecular energy contributions. |
| || Parameter values consistent with QM calculations at the HF/6-31G(d,p) and MP2/6-31G(d,p) levels of theory are reported elsewhere.72 |
| This journal is © The Royal Society of Chemistry 2018 |