Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stability and mobility of supported Nin (n = 1–10) clusters on ZrO2(111) and YSZ(111) surfaces: a density functional theory study†
Abdelaziz
Cadi-Essadek
 ,
Alberto
Roldan
,
Alberto
Roldan
 and
Nora H.
de Leeuw
and
Nora H.
de Leeuw
 *
*
School of Chemistry, Cardiff University, Main Building, Park Place, CF10 3AT, Cardiff, UK. E-mail: DeLeeuwN@cardiff.ac.uk; Tel: +44 (0)2920870658
First published on 20th February 2018
Abstract
The performance of supported metal catalysts, such as nickel nanoparticles decorating yttria-stabilized zirconia (YSZ), depends on their microstructure and the metal–support interface. Here, we have used spin polarized density functional theory (DFT) to evaluate different Ni cluster geometries and determined the electronic structure of the most stable configurations. We have described the interaction of Nin (n = 1–10) clusters supported on the cubic ZrO2(111) and YSZ(111) surfaces, which show a preference for pyramidal shapes rather than flat structures wetting the surface. The interfacial interaction is characterized by charge transfer from the cluster to the surface. We also show how yttrium, present in YSZ, affects the Ni–Ni interaction. Through analysing the difference between the cohesive energy and the clustering energy, we show the preference of Ni–Ni bond formation over Ni-surface interaction; this energy difference decreases with the increase of the Nin cluster size. From the evaluation of the Ni atomic hopping rates on YSZ, we have demonstrated that under different temperature conditions, Ni atoms aggregate with other atoms and clusters, which affects the cluster size stability.
1. Introduction
There is a growing interest in the stabilities and properties of supported clusters and metal-oxide interfaces, since many industrial processes use oxide-supported metal particles as catalysts, i.e. in the water gas shift reaction,1 steam reforming processes,2,3 microelectronics, sensors and solid oxide fuel cells (SOFC).4–6 These processes depend, among other things, on the particle sizes and the particle–support interactions.7–9 For instance, the performance of the electrode in SOFCs – electrochemical devices that convert chemical energy into electrical energy – depends on the microstructure and the size distribution of the metal particles and the oxide phase in the cermet10 (ceramic matrix containing metal nanoparticles). A common electrode in SOFCs is metallic nickel, used as an electron conductor, supported on an oxygen conductor, usually an oxide. For instance, Ni supported on zirconia (ZrO2) doped with yttria (Y2O3) (Ni/YSZ), is a suitable material for SOFCs as it has a high mixed electronic-ionic conductivity and high mechanical strength.11 The key reactions in these devices occur at the triple phase boundary (TPB) where the gas phase, Ni particles and the YSZ surface meet. Therefore, tuning and stabilizing the Ni microstructure will affect the SOFC performance and electrode lifetime.12 For example, the performance decay of the SOFC is associated with the sintering of Ni particles through atomic or cluster diffusion across the oxide support.13While atomic-level information on the metal-oxide interface is difficult to obtain experimentally, computational tools facilitate the evaluation of individual factors and thereby can provide crucial insight.14,15 For example, previous density functional theory (DFT) calculations have been used to study the interaction of certain metals on γ-Al2O3;16–19 Rajesh et al. studied the adsorption of Aun (n = 2–10) on α-Al2O3 (0001), showing favourable metal clustering rather than wetting i.e. spreading across the surface.20 Di Valentin et al. investigated the stability and growth of Ni clusters on the MgO surface,21 where small Nin (n ≤ 9) clusters adsorb weakly on the surface and their diffusion can be stopped by surface defects such as oxygen vacancies. Molina et al.22 have shown that an Au20 cluster keeps its tetrahedral geometry upon adsorption on the MgO(100) surface. Here, we have systematically analysed the interaction of Nin (n = 2–10) clusters on cubic zirconia (c-ZrO2)(111) and YSZ(111) surfaces in order to characterize the electronic structure of the interface and the cluster geometry as a function of their size, and to evaluate the stability and sintering rate of Ni clusters on both c-ZrO2(111) and YSZ(111) surfaces.
2. Models and computational methods
We have employed calculations based on density functional theory (DFT)23 as implemented in the Vienna Ab initio Simulation Package (VASP),24–27 where the generalized gradient approximation (GGA)28 with the Perdew–Burke–Ernzerhof (PBE) density functional was used to approximate the exchange–correlation functional. Long-range dispersion interactions were described by using the semi-empirical method of Grimme29 and we have employed the projected augmented wave method (PAW)30 to describe the interaction between the valence and the core electrons, where O (2s, 2p), Ni (3d, 4s), Zr (4d, 5s) and Y (4s, 4p, 4d, 5s) atomic orbitals have been treated as valence electrons. All the calculations were spin polarized. The unit cell of c-ZrO2 has the fluorite structure with space group Fm3m. We have converged the bulk energy for different k-points (from 7 × 7 × 7 to 11 × 11 × 11) and cutoff energies (from 350 eV to 550 eV) with a convergence criterion of 0.001 eV per atom. The bulk convergence was reached for a kinetic energy cutoff of 500 eV and a Monkhorst–Pack grid of 9 × 9 × 9 mesh of k-points. For the 1 × 1 slab calculations, we have tried four sets of k-points (from 6 × 6 × 1 to 9 × 9 × 1) with the same convergence criterion and convergence was reached for a 7 × 7 × 1 mesh of k-points. For the 2 × 2 slab calculations, three sets of k-points were tried (3 × 3 × 1, 4 × 4 × 1, and 5 × 5 × 1) with convergence reached for the 3 × 3 × 1 mesh. The tetrahedron method with Blöchl corrections was used to define the Brillouin zone.The ZrO2(111) surface was obtained with the METADISE code,31 which takes into account the atomic charges and the periodicity of the plane leading to a stacking of atomic layers with zero dipole moment perpendicular to the surface plane.
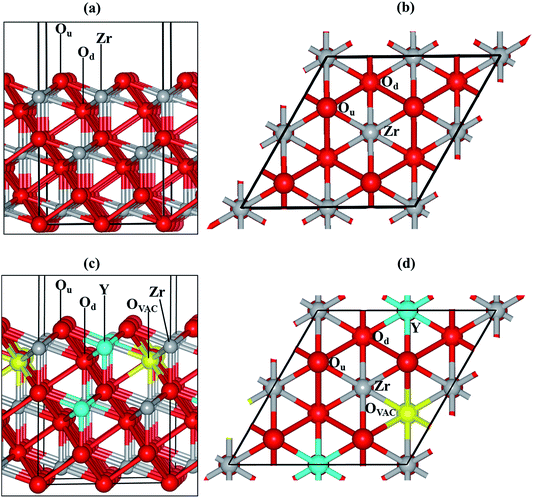
We have modelled the most stable zirconia surface, ZrO2(111)32–35 (Fig. 1(a) and (b)), considering a slab with nine periodic atomic layers (three O–Zr–O trilayers). The five top atomic layers were relaxed during the optimization, while the four bottom layers were kept fixed at their bulk equilibrium position to represent the rest of the crystal. The vacuum size between slabs was set to 15 Å in order to minimise interactions with the perpendicular images.
In our previous investigation,35 we determined the band gap to be 3.14 for the ZrO2(111) surface. Although the calculated band gap is in agreement with previous computational studies,36,37 it is lower than the experimentally measured bulk values (5–6 eV),38,39 as DFT calculations tend to underestimate the band gap.
We substituted two Zr with two Y atoms and removed one oxygen atom in order to obtain the yttria-stabilized zirconia (YSZ) surface with a dopant concentration of 9.09%, which is in the range of an optimized oxygen transport YSZ electrode (8–10%). We have previously evaluated the energy of different non-equivalent configurations of the YSZ(111) surface and found that the most stable structure had the two yttrium atoms located in the top and sub O–Zr–O trilayers.35 The oxygen vacancy is positioned in the lower oxygen layer of the top O–Zr–O trilayer and at the next nearest neighbour site (NNN) to the two Y atoms (Fig. 1(c) and (d)).
There are many possible shapes and adsorption sites for Nin clusters. We have chosen the Nin geometries based on the stability of fcc Ni surfaces40–43 and small particles44 to form triangular based structures in agreement with previous studies. We have therefore grown clusters exposing the Ni(111)-facet45,46 on the ZrO2(111) and YSZ(111) surfaces, where the initial atomic spacing between the Ni atoms is 2.2 Å, similar to the interatomic distance in the Ni(111) surface. We have based the initial positions of our clusters on our previous findings.35 On the ZrO2(111) surface, the clusters interact with the oxygen atoms located in the top oxygen layer, Ou (Fig. 1(a) and (b)), which act as a trap for the Ni. On the YSZ(111) surface, Ni atoms adsorb preferentially on top of the oxygen vacancy, away from the Y atoms,35 and hence, we have grown the Nin (n = 2–10) clusters away from the Y atoms.
We have evaluated the stability of the growing Ni cluster by using the clustering energy per atom (Eclus), eqn (1):
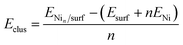 | (1) |
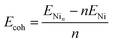 | (2) |
 | (3) |
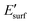 is the energy of the geometry of the clean oxide surface taken from the optimized Nin/surf structure and nC is the number of Ni atoms in contact with the surface. The charge transfer between the surface and the molecules was analysed using Bader analysis as implemented in the Henkelman algorithm.47
is the energy of the geometry of the clean oxide surface taken from the optimized Nin/surf structure and nC is the number of Ni atoms in contact with the surface. The charge transfer between the surface and the molecules was analysed using Bader analysis as implemented in the Henkelman algorithm.47
We also implemented the DFT results in kinetic Monte Carlo simulations to study the coalescence of Ni atoms and clusters on YSZ(111), thus providing information regarding coverage and time at specific temperatures.
3. Results and discussion
3.1. Structural analysis
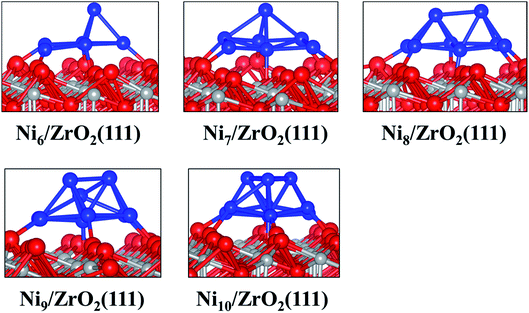 | ||
| Fig. 2 Side views of the most stable configurations of Nin/ZrO2(111) systems. Colour key: red, grey and blue spheres correspond to oxygen, Zr and Ni atoms, respectively. | ||
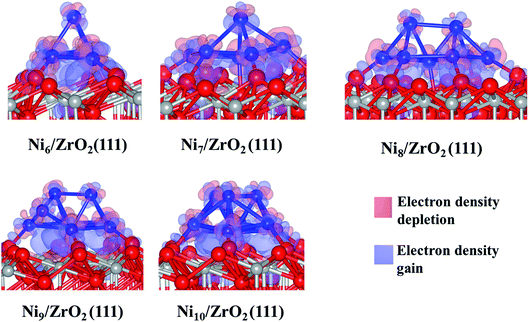
The analysis of the interfacial distances in the Ni6/ZrO2(111) system shows that each Ni atom is at ∼1.9 Å from its nearest Ou neighbour. In addition, we note that these Ou atoms are shifted from their initial position: the Ou–Ou distance is 3.6 Å in the clean ZrO2(111) surface, whereas it is approximately 4.1 Å upon Ni6 adsorption. The Ou atoms are pushed apart in order to accommodate the cluster and minimise the forces on it. The adsorption of this cluster also affects the electronic structure of ZrO2. We have evaluated the atomic charges (Table 1) and observed a total charge transfer of 0.5 e from the metal cluster to the surface. The charge transfer is slightly higher for the Ni9 and Ni10 clusters: +0.6 and +0.7 e, respectively.
| Nin | E clus | E coh | E int | Total Nin charge | ||||
|---|---|---|---|---|---|---|---|---|
| ZrO2(111) | YSZ(111) | ZrO2(111) | YSZ(111) | ZrO2(111) | YSZ(111) | ZrO2(111) | YSZ(111) | |
| Ni2 | 2.16 | 2.39 | 3.83 | 3.85 | −2.38 | −1.64 | +0.2 | +0.1 |
| Ni3 | 1.77 | 2.02 | 3.38 | 3.38 | −2.16 | −1.53 | +0.3 | +0.2 |
| Ni4 | 1.57 | 1.80 | 3.11 | 3.06 | −2.04 | −1.82 | +0.4 | +0.1 |
| Ni5 | 1.53 | 1.79 | 2.88 | 2.89 | −2.05 | −1.60 | +0.4 | +0.2 |
| Ni6 | 1.51 | 1.76 | 2.77 | 2.67 | −1.94 | −1.51 | +0.5 | +0.2 |
| Ni7 | 1.47 | 1.67 | 2.67 | 2.54 | −1.95 | −1.42 | +0.5 | +0.2 |
| Pyr-Ni8 | 1.42 | 1.68 | 2.51 | 2.51 | −1.95 | −1.50 | +0.5 | +0.2 |
| Flat-Ni8 | — | 1.67 | — | 2.66 | — | −1.66 | — | +0.3 |
| Ni9 | 1.39 | 1.57 | 2.40 | 2.32 | −2.01 | −1.31 | +0.6 | +0.3 |
| Ni10 | 1.31 | 1.58 | 2.30 | 2.22 | −1.87 | −1.26 | +0.7 | +0.2 |
This charge transfer causes an electronic rearrangement of the surface atoms interacting with the cluster: the negative charge of the Ou atoms decreases from −1.2 to −1.1 e, while the charge of the Zr atoms (near the cluster) decreases from 2.3 to 2.1 e. We have also noted that only the five Ni atoms directly bonded to the surface transfer charge to ZrO2(111), since each of those Ni atoms are +0.1 e while the Ni atom at the top of the cluster remains uncharged. Generally, Ni atoms at the vertex are either negatively charged (−0.1 e) or neutral, which indicates that the atoms at the base of the cluster transfer charge to the surface, while the low coordinated metal atoms, i.e. vertex and corners, accumulate electron density.44 Thus, the Ni located at the vertex of the cluster could be a source of electrons for an eventual reaction with electron receptor molecules approaching the cluster from the gas phase.50 Analysing the electron density difference between the cluster and the surface (Fig. 3), we have confirmed a charge accumulation between the Ni atoms directly bonded to the surface and the surface atoms; there is no charge relocation between the top Ni atom which remains fully metallic. We also note the well-localised accumulation of electron density between the Ou and the Ni atoms, indicating the formation of a Ni–O bond. A previous report has also shown this electron rearrangement between Pt clusters and the zirconia surface.51
Next, we have analysed the interaction of Ni7, Ni8, Ni9 and Ni10 with the ZrO2(111) surface where we have tried, respectively, five, six, three and four non-equivalent initial configurations (Fig. S2 to S5 in the ESI†). The most stable shapes are shown in Fig. 2 and the calculated clustering energies are 1.47, 1.42, 1.39 and 1.31 eV, respectively (Table 1). The four configurations have a similar pyramid shape and the only difference is the number of the Ni atoms in the top Ni layer of each cluster (Fig. 2).
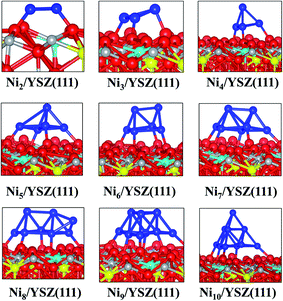
We have optimised several initial configurations for the flat Ni2/YSZ(111) and Ni3/YSZ(111) clusters (Fig. S6 and S7 in the ESI†) and the most stable ones are shown in Fig. 4, with an average clustering energy of 2.21 eV (Table 1).
For Nin (n = 4–7), the average Eclus is 1.76 eV and the clusters adopt a Ni(111) facet shape, in agreement with a previous study by Li et al.14 who showed that the Ni4 cluster prefers to adopt a similar pyramid shape on top of γ-Al2O3. Similarly, Carrasco et al.52 have also found that the pyramid Ni4 geometry is preferred over the planar one, when the cluster is adsorbed on the isostructural CeO2(111) surface.
In the Nin/YSZ(111) (n = 2–7) configurations, the Ni-surface atomic spacing is 2.3 Å, i.e. slightly larger than in the pure ZrO2(111) systems. In addition, each Ou is pushed towards the neighbouring vacancy, since we observe an average decrease of 0.1 Å of the Ou-vacancy distance. This movement explains the preference of the Ni clusters to adsorb on this site: it is easier to drive the Ou towards a vacancy where it tends to fill this defect. Moreover, the most stable adsorption site is the one involving two Ou atoms with one neighbouring oxygen vacancy.
Charge analysis (Table 1) shows a slight charge transfer from the cluster to the surface of ∼+0.2 e. As was observed for the Nin/ZrO2(111) systems, this charge transfer affects the electronic structure of the surface: the charges of Zr and Y atoms (near the metal cluster) decrease from 2.2 to 2.1 e and the negative charge of Ou decreases from −1.2 to −1.1 e. We also observe charge accumulation on the Ni atom at the vertex of the pyramid of the Nin/YSZ(111) (n = 4–7) configurations, since this latter atom has a −0.1 e charge. The electron density difference plot (Fig. 5) shows this charge accumulation between the cluster and the surface and shows the localized orbitals of Ou and Y atoms interacting with the cluster.
The flat shapes of the Nin/YSZ(111) (n = 2–7) structures, shown in the ESI,† are less stable by ∼0.11 eV (which corresponds to a thermal energy of 638 K), i.e. the Ni atoms prefer to aggregate rather than spread over the surface, as was also observed for the Nin/ZrO2(111) systems.
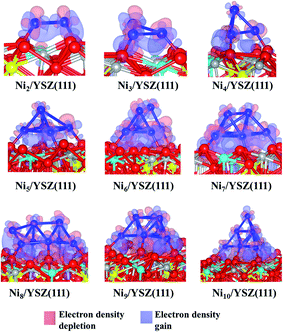
It is worth noting that for the Ni8/YSZ(111) cluster, the flat and pyramid shapes are in equilibrium since their clustering energies differ by only 0.01 eV (58 K) (Table 1). These two configurations are also the lowest energy ones from the six configurations considered (Fig. S16 and S17 in the ESI†). In the flat configuration (Fig. S16 in the ESI†) the Ni8 cluster interacts with six Ou atoms at an average Ni–Ou distance of 2.0 Å. In addition, the oxygen vacancy is filled by one displaced Ou which contributes to the stability of the system. Indeed, the movement of Ou towards the vacancy allows the cluster to optimise its interaction with the other six Ou surface atoms. This could be a drawback, for example in SOFCs, since the role of the oxygen vacancies is to enhance the oxygen transport. As for the three-dimensional shape (Fig. 4), the cluster interacts with five Ou atoms but none of the oxygen vacancies are filled by an Ou atom. This shape is similar to the one found for Ni7/YSZ(111), although the next Ni atom avoids interaction with Y from the surface and forms a (111)-facetted shape with the rest of the cluster. Bader charge analysis (Table 1) shows that the charge transfer from the cluster to the surface is slightly higher in the flat configuration (+0.3 e) than in the pyramid shape (+0.2 e) owing to the former’s interaction with an extra Ou atom. This comparison shows the importance of the two parameters responsible for the stability of the cluster on top of the surface: the number of Ou atoms interacting with the cluster and the shape of the cluster.
The last cluster studied in this work is Ni10/YSZ(111), where three configurations have been considered (Fig. S20 and S21 in the ESI†), and the most stable shape found is the pyramid one (Fig. 5). The calculated clustering energy is 1.58 eV (Table 1) which is similar to the value found for Ni9/YSZ(111). This is predictable since both Ni9/YSZ(111) and Ni10/YSZ(111) have exactly the same shape and the only difference is the tenth Ni atom located at the apex of the pyramid in Ni10/YSZ(111). Therefore, the modification of the surface geometry upon adsorption and the number of Ou atoms involved in the interaction are similar to Ni9/YSZ(111). As to the Bader charge (Table 1), the cluster is +0.3 e charged and we note that the Ni atom located at the apex of the cluster is −0.2 e charged, while all the other Ni atoms are positively charged (average of +0.1 e). We also note the same variation of the charge of the surface atoms interacting with Ni10 as was observed for Ni9/YSZ(111). Thus, the Ni atoms close to the surface transfer charge to the surface atoms and to the Ni atom located at the top of the cluster, which can be seen from the electron density difference plot (Fig. 5), where we have a gain of charge between the cluster and the surface.
In general, in Nin/YSZ(111) (n = 2–10), the Nin clusters interact with Ou atoms with an average distance of 1.9 Å. The metal clusters transfer charge to the surface, depending on the size, ranging from +0.1 to +0.3 e. The three-dimensional cluster shape is more favourable due to the repulsive interaction between Y and Ni.
3.2. Ni sintering on top of ZrO2(111) and YSZ(111)
We have shown that Nin clusters on both ZrO2(111) and YSZ(111) surfaces prefer to adopt a three-dimensional structure rather than flat shapes for clusters containing at least 4 atoms. The same conclusion was drawn for a similar system, CeO2-supported Au nanoparticles,53 where it was shown that planar Au13 on top of the CeO2 surface is unstable compared to three-dimensional Au13. Pan et al.54 have also shown that a Ni4 cluster prefers to adopt a 3-D pyramid shape on top of the γ-Al2O3(110) surface, with a large clustering energy. Giordano et al.55 have also demonstrated that the Ni4 cluster prefers to adopt a tetrahedron shape on top of the MgO(001) surface.The total energies of four individual Ni atoms (4Ni) compared to the Ni4 cluster adsorbed on the surface are 3.38 eV and 2.20 eV less stable on the ZrO2(111) and YSZ(111) surfaces, respectively, thus showing that aggregation of the Ni atoms is clearly preferred energetically over dispersion. We have also compared the total energy of two Ni4 clusters, separated by approximately 6.0 Å, with the Ni8/surface system and here we also found that (Ni4 + Ni4) is less stable than Ni8, now by 1.67 eV and 1.11 eV on ZrO2(111) and YSZ(111), respectively.
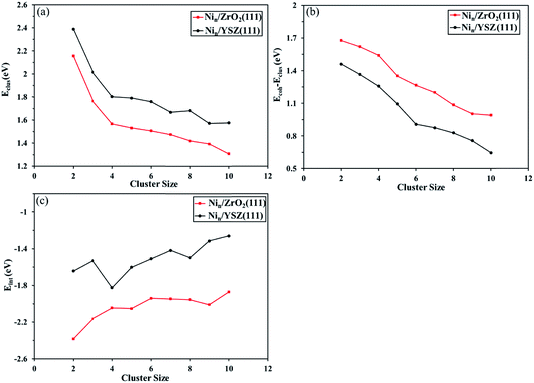
Furthermore, in Fig. 6(a) we have plotted the clustering energy (Eclus) as a function of the cluster size, for both ZrO2(111) and YSZ(111) surfaces. This graph shows a probable aggregation of Ni on both surfaces owing to a thermodynamic driving force as the cluster size increases. The trend in the clustering energy shows that for the same cluster size, the clustering energy is lower on ZrO2(111), in agreement with the two aggregation examples calculated for Ni4 and Ni8 clusters. The Y atoms affect the geometry of the surface and anion rearrangement, making the interaction between the clusters and the Ou surface atoms less favourable, thus enhancing the preference for the formation of Ni clusters.
We have also evaluated the difference between the cohesive energy (Ecoh) and the clustering energy (Eclus) as a function of the cluster size. The difference between those energies expresses the trend to form a Ni–Ni bond instead of a Ni-surface bond. Fig. 6(b) shows that for both surfaces, this energy difference decreases with increasing cluster size due to the preference of the Ni–Ni interaction over Ni-surface interactions. The Ecoh − Eclus graph also shows that for the same cluster size, the energy difference is lower for YSZ(111) than for ZrO2(111), indicating that the degree of interaction between Ni atoms is greater for Nin clusters on top of YSZ(111).
The interaction energy (Eint) calculated as a function of the cluster size (Fig. 6(c)) confirms the affinity of the Nin clusters for the ZrO2(111) surface over YSZ(111). Note that the Ni cluster interaction energy is more favourable for zirconia than yttria-stabilized zirconia, whose preference is even more striking for larger clusters. This demonstrates that cluster aggregation is more favourable on the YSZ(111) surface than on ZrO2(111), in good agreement with, for instance, the difference in energy between two Ni4 clusters and a Ni8 cluster, which is larger on ZrO2(111) than YSZ(111).
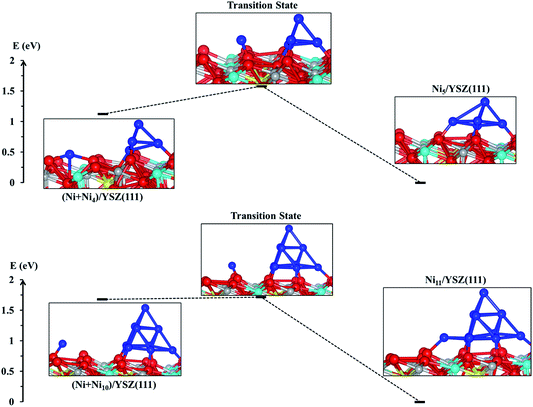
From the energy profiles in Fig. 7, we note that the Ni5/YSZ(111) configuration is more stable than (Ni + Ni4)/YSZ(111), indicating that Ni atoms prefer to aggregate to form larger clusters rather than wetting the surface. This is in good agreement with the graph in Fig. 6, where we have shown a decrease of the Ecoh − Eclus difference, indicating the energetic favourability of aggregation of Ni atoms over their dispersion on both surfaces. From Fig. 7, we also observe that the activation energy, i.e. the energy difference between the (Ni + Ni4)/YSZ(111) structure and the transition state, is ΔENi5/YSZ = 0.46 eV, which is lower than the same Ni collection adsorbed on ZrO2(111) (ΔENi5/ZrO2 = 0.72 eV).48 This difference in activation energies for the addition of a Ni atom to a larger cluster implies that single Ni atoms can more easily join a bigger cluster when those metal atoms are adsorbed on the YSZ(111) surface rather than ZrO2(111). It indicates that the aggregation of Ni atoms to form larger clusters is facilitated when the zirconia surface is doped with yttria, which is in good agreement with our Eclus and Ecoh − Eclus plots in Fig. 6.
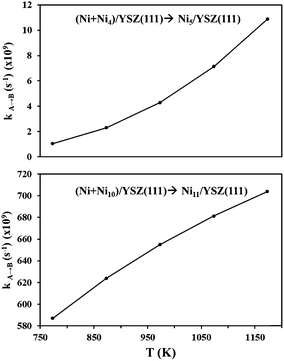
From the calculated activation energies, we have evaluated the hopping rate of one Ni atom from state (Ni + Nin)/YSZ(111) to state Ni(n+1)/YSZ(111): k![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0041_20d1.gif) B = ν
B = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔE/kBT) where A is either state (Ni + Ni4)/YSZ(111) or (Ni + Ni10)/YSZ(111) and B is either state Ni5/YSZ(111) or Ni11/YSZ(111) (Fig. 8). The Boltzmann constant is kB = 8.6 × 10−5 eV K−1 and the vibrational frequency, ν, is accepted as 1012 s−1. We have therefore calculated kA→B for a range of temperatures corresponding to the working temperature of a SOFC (T = 500–900 °C). Fig. 8 shows the variation of kA→B (for five Ni atoms on the surface) from 1.05 × 108 to 1.09 × 1010 s−1, which is higher than the values found for ZrO2(111) in our previous investigations (kA→B varies from 1.87 × 107 to 7.66 × 108 s−1),48 indicating that the diffusion of a Ni atom towards a cluster is more favourable on the YSZ(111) surface. This hopping rate is even higher when the cluster diffuses towards a larger cluster, since for eleven Ni atoms kA→B varies from 586.99 × 107 to 703.93 × 108 s−1 (Fig. 8). Thus, this evaluation of the hopping rate further strengthens the conclusions drawn from Fig. 6: the aggregation of Ni atoms is preferred over dispersion on the surface and this aggregation is more favourable on the YSZ(111) surface.
exp(−ΔE/kBT) where A is either state (Ni + Ni4)/YSZ(111) or (Ni + Ni10)/YSZ(111) and B is either state Ni5/YSZ(111) or Ni11/YSZ(111) (Fig. 8). The Boltzmann constant is kB = 8.6 × 10−5 eV K−1 and the vibrational frequency, ν, is accepted as 1012 s−1. We have therefore calculated kA→B for a range of temperatures corresponding to the working temperature of a SOFC (T = 500–900 °C). Fig. 8 shows the variation of kA→B (for five Ni atoms on the surface) from 1.05 × 108 to 1.09 × 1010 s−1, which is higher than the values found for ZrO2(111) in our previous investigations (kA→B varies from 1.87 × 107 to 7.66 × 108 s−1),48 indicating that the diffusion of a Ni atom towards a cluster is more favourable on the YSZ(111) surface. This hopping rate is even higher when the cluster diffuses towards a larger cluster, since for eleven Ni atoms kA→B varies from 586.99 × 107 to 703.93 × 108 s−1 (Fig. 8). Thus, this evaluation of the hopping rate further strengthens the conclusions drawn from Fig. 6: the aggregation of Ni atoms is preferred over dispersion on the surface and this aggregation is more favourable on the YSZ(111) surface.
3.3. Microkinetics for Nin/YSZ(111)
We have used kinetic Monte Carlo simulations in order to understand how time (t) and Ni coverage (θ) influence the coalescence of Ni clusters on top of the YSZ(111) surface. To achieve our kinetic Monte Carlo study, we have used the same equations as the ones described in the ESI of the investigation by Tafreshi et al.56 Additionally, quantum-mechanical tunnelling57 has been taken into account. Coverage has been defined in eqn (4):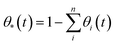 | (4) |
The first system considered is a YSZ(111) surface with a coverage of 50% of Ni1 (θNi1 = 50%) as a starting point. In Fig. 9 we show a schematic representation of the initial conditions where one Ni atom covers 50% of the system, i.e., at t = 0.0 seconds, half of the system is considered as a clean 2 × 2 YSZ(111) surface and the other half is Ni1 supported on YSZ(111).
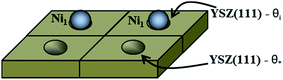 | ||
| Fig. 9 Schematic representation of the coverage of the free sites (θ*) and occupied sites (θi) by Ni atoms on the YSZ(111) surface. Here, θi = θ* = 50%. | ||
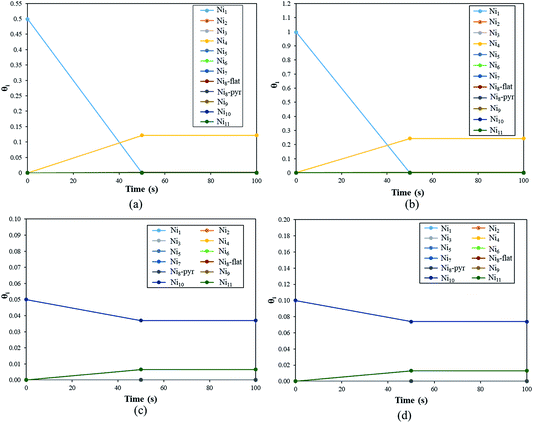
The coverage (θi(t)) of the Nin clusters as a function of time for a fixed temperature of 500 K is represented in Fig. 10(a).
During the first 50 seconds the concentration of Ni1 drops to 0.0%. In the meantime, θNi4 increases to reach a plateau of 12%. Thus, at T = 500 K, if 50% of the YSZ(111) surface is covered by single Ni atoms, the metal atoms will aggregate spontaneously to generate Ni4 clusters. This quick coalescence process is in good agreement with the previous section: for high temperatures, the Ni atoms tend to form clusters on top of YSZ(111) rather than wet the surface.
In Fig. 10(b) we plot the coverage as a function of time, for T = 500 K with an initial θNi1 of 100%. The result is similar to the previous initial condition (θNi1 = 50%): after 50 seconds, all of the single Ni atoms aggregate to form Ni4 pyramids. Indeed, from t = 50 s, θNi4 = 24% and θ* = 76%. Furthermore, whatever the initial coverage of single Ni atoms is, the aggregation speed is the same as for both initial coverages (θNi1 = 50% and θNi1 = 100%), within 50 seconds Ni4 pyramid clusters are generated. We have also calculated the reaction rates and noted that the one corresponding to Ni4 + Ni → Ni5 has the lowest value. Thus, Ni atoms will aggregate quickly to generate Ni4 but the formation of larger clusters is negligible.
In Fig. 10(c) we describe the evolution of a Ni10 cluster on YSZ(111) with a starting coverage of 5%. Within 50 seconds Ni10 coverage decreases (3.7%) in order to generate Ni9 (0.65%) and Ni11 (0.65%). The formation of the Ni9 clusters is the consequence of the generation of Ni11: one Ni atom, belonging to Ni10, detaches to aggregate with a neighbouring Ni10 cluster giving Ni9 and Ni11.
In Fig. 10(d), we show θNi10 with an initial coverage of 10%, and the evolution of the cluster size is similar to an initial θNi10 of 5% because the interaction between metal moieties is neglected in the model.
Finally, this kinetic Monte Carlo study shows that Nin always tend to form larger clusters; single Ni atoms and Ni10 clusters generate Ni4 and Ni11, respectively. However, under experimental conditions no specific cluster size will be dominant, as we saw, for instance, that Ni10 can generate Ni9 and Ni11.
4. Conclusions
We have used spin polarized DFT and kinetic Monte Carlo calculations to study the interaction of Nin (n = 1–10) clusters with both ZrO2(111) and YSZ(111) surfaces. The general trend observed for Nin clusters (n = 2–10) adsorbed on the ZrO2(111) and YSZ(111) surfaces shows the importance of the interaction of Ni with the Ou atoms, as well as the shapes of the adsorbed Nin clusters. We have seen that the Ou atoms facilitate the adsorption of the clusters and that these atoms are shifted from their initial position upon adsorption. In Nin/YSZ(111) systems, the clusters pushed the Ou atoms towards filling neighbouring vacancies which could be a drawback in, for instance, SOFCs since these vacancies play an important role in oxygen transport. Bader charge analysis of the clusters revealed that there is charge transfer from the cluster to the surface, in particular from the metal atoms at the interface. The distribution of the charge within the cluster is similar for all clusters with a pyramid shape (Nin, n = 4–10): the Ni atoms bound to the surface are positively charged and those at the top of the pyramid are either charge-neutral or even some negative charge is accumulated at the apex. In some instances, the Ni atoms located at the top of the clusters have a non-negligible amount of charge, which could play a role in the adsorption of molecules: for example, an electrophilic molecule would adsorb on top of the Ni cluster, rather than at the meeting point between the cluster and the surface. Finally, from calculation of the clustering and cohesive energies and evaluation of the diffusion barriers and hopping rates, we conclude that, on both ZrO2(111) and YSZ(111) surfaces, the aggregation of the Ni atoms takes place spontaneously, especially on the YSZ(111) surface. Kinetic Monte Carlo simulations showed that Ni atoms aggregate on the YSZ(111) surface once they are exposed to medium temperature: single Ni atoms tend to form Ni4 clusters, while Ni10 clusters generate Ni9 and Ni11 clusters. We also noted that the sintering speed does not depend on the initial coverage.Acknowledgements
We acknowledge the Engineering and Physical Sciences Research Council (Grant no. EP/K001329 and EP/K016288) for funding. Via our membership of the UK’s HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of ARCHER, the UK’s national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC’s High End Computing Programme. The authors also acknowledge the use of the UCL@Legion High Performance Computing Facility, and associated support services, in the completion of this work. Finally, the authors acknowledge the use of the IRIDIS High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work. Information about the data underpinning the results presented here, including how to access them, can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2018.0050609499.References
- C. Rhodes, G. J. Hutchings and A. M. Ward, Water-Gas Shift Reaction: Finding the Mecanistic Boundary, Catal. Today, 1995, 23, 43–58 CrossRef.
- A. Haryanto, S. Fernando, N. Murali and S. Adhikari, Current Status of Hydrogen Production Techniques by Steam Reforming of Ethanol: A Review, Energy Fuels, 2005, 19, 2098–2106 CrossRef.
- D. J. Moon, Hydrogen Production by Catalytic Reforming of Gaseous Hydrocarbons (Methane & LPG), Catal. Surv. Asia, 2008, 12, 188–202 CrossRef.
- R. Grau-crespo, N. C. Hernandez, J. F. Sanz and N. H. de Leeuw, Theoretical Investigation of the Deposition of Cu, Ag, and Au Atoms on the ZrO2(111) Surface, J. Phys. Chem. C, 2007, 2, 10448–10454 Search PubMed.
- C. R. A. Catlow, S. A. French, A. A. Sokol, M. Alfredsson and S. T. Bromley, Understanding the Interface between Oxides and Metals, Faraday Discuss., 2003, 124, 185 RSC.
- W. Wang, Z. Liang, X. Han, J. Chen, C. Xue and H. Zhao, Mechanical and Thermodynamic Properties of ZrO2 under High-Pressure Phase Transition: A First-Principles Study, J. Alloys Compd., 2015, 622, 504–512 CrossRef.
- C. R. Henry, Surface Studies of Supported Model Catalysts, Surf. Sci. Rep., 1998, 31, 231–233 CrossRef.
- D. W. Goodman, Model Studies in Catalysis Using Surface Science Probes, Chem. Rev., 1995, 95, 523–536 CrossRef.
- J. Y. Park, L. R. Baker and G. A. Somorjai, Role of Hot Electrons and Metal-Oxide Interfaces in Surface Chemistry and Catalytic Reactions, Chem. Rev., 2015, 115, 2781–2817 CrossRef PubMed.
- S. Kim, H. Moon, S. Hyun, J. Moon, J. Kim and H. Lee, Performance and Durability of Ni-Coated YSZ Anodes for Intermediate Temperature Solid Oxide Fuel Cells, Solid State Ionics, 2006, 177, 931–938 CrossRef.
- E. Drożdż, J. Wyrwa and M. Rękas, Influence of Sintering Temperature and Aging on Properties of Cermet Ni/8YSZ Materials Obtained by Citric Method, Ionics, 2013, 19, 1733–1743 CrossRef.
- Y. Chen, S. Chen, G. Hackett, H. Finklea, X. Song and K. Gerdes, Microstructural and Chemical Evolution near Anode Triple Phase Boundary in Ni/YSZ Solid Oxide Fuel Cells, Solid State Ionics, 2011, 204–205, 87–90 CrossRef.
- S. Gao, J. Li and Z. Lin, Theoretical Model for Surface Diffusion Driven Ni-Particle Agglomeration in Anode of Solid Oxide Fuel Cell., J. Power Sources, 2014, 255, 144–150 CrossRef.
- J. Li, E. Croiset and L. Ricardez-sandoval, Effect of Metal–Support Interface During CH4 and H2 Dissociation on Ni/γ-Al2O3: A Density Functional Theory Study, J. Phys. Chem. C, 2013, 117, 16907–16920 Search PubMed.
- T. Ogura, K. Nakao, T. Ishimoto and M. Koyama, Computational Study on Impurities Poisoning and Degradation of an SOFC Anode Based on Density Functional Theory, ECS Trans., 2011, 35, 853–858 Search PubMed.
- D. Cao, Y. Li, J. Wang and H. Jiao, Mechanism of γ-Al2O3 Support in CO2 Reforming of CH4-A Density Functional Theory Study, J. Phys. Chem. C, 2011, 115, 225–233 Search PubMed.
- L. G. V. Briquet, C. R. A. Catlow and S. A. French, Platinum Group Metal Adsorption on Clean and Hydroxylated Corundum Surfaces, J. Phys. Chem. C, 2009, 113, 16747–16756 Search PubMed.
- D. Mei, J. H. Kwak, J. Szanyi, Q. Ge and C. H. F. Peden, Catalyst Size and Morphological Effects on the Interaction of NO2 with BaO/γ-Al2O3 Materials, Catal. Today, 2010, 151, 304–313 CrossRef.
- Z. Liu, L. Ma and A. S. M. Junaid, NO and NO2 Adsorption on Al2O3 and Ga Modified Al2O3 Surfaces: A Density Functional Theory Study, J. Phys. Chem. C, 2010, 114, 4445–4450 Search PubMed.
- C. Rajesh, S. Nigam and C. Majumder, The Structural and Electronic Properties of Aun Clusters on the α-Al2O3(0001) Surface: A First Principles Study, Phys. Chem. Chem. Phys., 2014, 16, 26561–26569 RSC.
- C. Di Valentin, L. Giordano, G. Pacchioni and N. Rösch, Nucleation and Growth of Ni Clusters on Regular Sites and F Centers on the MgO(001) Surface, Surf. Sci., 2003, 522, 175–184 CrossRef.
- L. Molina and B. Hammer, The Activity of the Tetrahedral Au20 Cluster: Charging and Impurity Effects, J. Catal., 2005, 233, 399–404 CrossRef.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Open-Shell Transition Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef.
- G. Kresse and J. Hafner, Norm-Conserving and Ultrasoft Pseudopotentials for First-Row and Transition Elements, J. Phys.: Condens. Matter, 1994, 6, 8245–8257 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef PubMed.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- G. W. Watson, E. T. Kelsey, N. H. de Leeuw, D. J. Harris and S. C. Parker, Atomistic Simulation of Dislocations, Surfaces and Interfaces in MgO, J. Chem. Soc., Faraday Trans., 1996, 92, 433 RSC.
- A. Christensen and E. Carter, First-Principles Study of the Surfaces of Zirconia, Phys. Rev. B, 1998, 58, 8050–8064 CrossRef.
- S. Gennard, F. Cora and C. R. A. Catlow, Comparison of the Bulk and Surface Properties of Ceria and Zirconia by Ab Initio Investigations, J. Phys. Chem. B, 1999, 103, 10158–10170 CrossRef.
- X. Xia, R. Oldman and R. Catlow, Computational Modeling Study of Bulk and Surface of Yttria-Stabilized Cubic Zirconia, Chem. Mater., 2009, 21, 3576–3585 CrossRef.
- A. Cadi-Essadek, A. Roldan and N. H. de Leeuw, Ni Deposition on Yttria-Stabilized ZrO2(111) Surfaces: A Density Functional Theory Study, J. Phys. Chem. C, 2015, 119, 6581–6591 Search PubMed.
- M. Shishkin and T. Ziegler, The Oxidation of H2 and CH4 on an Oxygen-Enriched Yttria-Stabilized Zirconia Surface: A Theoretical Study Based on Density Functional Theory, J. Phys. Chem. C, 2008, 112, 19662–19669 Search PubMed.
- M. Alfredsson and C. R. A. Catlow, Modelling of Pd and Pt Supported on the {111} and {011} Surfaces of Cubic-ZrO2, Phys. Chem. Chem. Phys., 2001, 3, 4129–4140 RSC.
- R. H. French, S. J. Glass, F. S. Ohuchi, Y.-N. Xu and W. Y. Ching, Experimental and Theoretical Determination of the Electronic Structure and Optical Properties of Three Phases of ZrO2, Phys. Rev. B, 1994, 49, 5133–5142 CrossRef.
- S. Sayan, R. A. Bartynski, X. Zhao, E. P. Gusev, D. Vanderbilt, M. Croft, M. Banaszak Holl and E. Garfunkel, Valence and Conduction Band Offsets of a ZrO2/SiOxNy/n-Si CMOS Gate Stack: A Combined Photoemission and Inverse Photoemission Study, Phys. Status Solidi, 2004, 241, 2246–2252 CrossRef.
- Y. Liu, Y. Wang and G. Chen, Nucleation and Mobility Model of Agn Clusters Adsorbed on Perfect and Oxygen Vacancy MgO Surfaces, J. Mol. Model., 2011, 17, 1061–1068 CrossRef PubMed.
- C. Jung, H. Tsuboi, M. Koyama, M. Kubo, E. Broclawik and A. Miyamoto, Different Support Effect of M/ZrO2 and M/CeO2 (M = Pd and Pt) Catalysts on CO Adsorption: A Periodic Density Functional Study, Catal. Today, 2006, 111, 322–327 CrossRef.
- Z. Li, C. V. Ciobanu, J. Hu, J.-P. Palomares-Báez, J.-L. Rodríguez-López and R. Richards, Experimental and DFT Studies of Gold Nanoparticles Supported on MgO(111) Nano-Sheets and Their Catalytic Activity, Phys. Chem. Chem. Phys., 2011, 13, 2582–2589 RSC.
- X. Ma, Y. Dai, M. Guo, Y. Zhu and B. Huang, Insights into the Adsorption and Energy Transfer of Ag Clusters on the AgCl(100) Surface, Phys. Chem. Chem. Phys., 2013, 15, 8722–8731 RSC.
- A. Roldan, J. J. M. Ricart and F. Illas, Growth and Properties of Au Nanowires, Mol. Simul., 2009, 35, 1051–1056 CrossRef.
- J. Li, E. Croiset and L. Ricardez-Sandoval, Carbon Clusters on the Ni(111) Surface: A Density Functional Theory Study, Phys. Chem. Chem. Phys., 2014, 16, 2954–2961 RSC.
- S. Hong, Y.-H. Shin and J. Ihm, Crystal Shape of a Nickel Particle Related to Carbon Nanotube Growth, Jpn. J. Appl. Phys., 2002, 41, 6142–6144 CrossRef.
- R. F. W. A. Bader, Quantum Theory of Molecular Structure and Its Applications, Chem. Rev., 1991, 91, 893–928 CrossRef.
- A. Cadi-Essadek, A. Roldan and N. H. de Leeuw, Density Functional Theory Study of Ni Clusters Supported on the ZrO2(111) Surface, Fuel Cells, 2017, 17, 125–131 CrossRef.
- S. Zhang, C. Li, H. Yan, M. Wei, D. G. Evans and X. Duan, Density Functional Theory Study on the Metal–Support Interaction between Ru Cluster and Anatase TiO2(101) Surface, J. Phys. Chem. C, 2014, 118, 3514–3522 Search PubMed.
- S. S. Tafreshi, A. Roldan and N. H. de Leeuw, Density Functional Theory Calculations of the Hydrazine Decomposition Mechanism on the Planar and Stepped Cu(111) Surfaces, Phys. Chem. Chem. Phys., 2015, 17, 21533–21546 RSC.
- A. Eichler, Chemical Characterization of a Zirconia-Supported Pt Cluster, Phys. Rev. B, 2005, 71, 125418-1 CrossRef.
- J. Carrasco, L. Barrio, P. Liu, J. A. Rodriguez and M. Vero, Theoretical Studies of the Adsorption of CO and C on Ni(111) and Ni/CeO2(111): Evidence of a Strong Metal–Support Interaction, J. Phys. Chem. C, 2013, 2, 8241–8250 Search PubMed.
- H. Y. Kim, H. M. Lee and G. Henkelman, CO Oxidation Mechanism on CeO2-Supported Au Nanoparticles, J. Am. Chem. Soc., 2012, 134, 1560–1570 CrossRef PubMed.
- Y. Pan, C. Liu and Q. Ge, Effect of Surface Hydroxyls on Selective CO2 Hydrogenation over Ni4/γ-Al2O3: A Density Functional Theory Study, J. Catal., 2010, 272, 227–234 CrossRef.
- L. Giordano, G. Pacchioni, A. M. Ferrari, F. Illas and N. Rosch, Electronic Structure and Magnetic Moments of Co4 and Ni4 Clusters Supported on the MgO(001) Surface, Surf. Sci., 2001, 473, 213–226 CrossRef.
- S. S. Tafreshi, A. Roldan and N. H. de Leeuw, Micro-Kinetic Simulations of the Catalytic Decomposition of Hydrazine on the Cu(111) Surface, Faraday Discuss., 2017, 197, 41–57 RSC.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Theoretical Calculations of CH4 and H2 Associative Desorption from Ni(111): Could Subsurface Hydrogen Play an Important Role?, J. Chem. Phys., 2006, 124, 1–9 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Less stable configurations and their respective binding energies of Ni clusters on ZrO2(111) (Fig. S1 to S5) and YSZ(111) (Fig. S6 to S21) surfaces. See DOI: 10.1039/c7fd00217c |
| This journal is © The Royal Society of Chemistry 2018 |