Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Aggregation and sedimentation of shattered graphene oxide nanoparticles in dynamic environments: a solid-body rotational approach†
Peyman
Babakhani
 *ab,
Jonathan
Bridge
*ab,
Jonathan
Bridge
 c,
Tanapon
Phenrat
c,
Tanapon
Phenrat
 de,
Ruey-an
Doong
de,
Ruey-an
Doong
 *bf and
Karl R.
Whittle
*bf and
Karl R.
Whittle
 a
a
aSchool of Engineering, University of Liverpool, Liverpool, Merseyside L69 7GH, UK. E-mail: p.babakhani@liverpool.ac.uk; Tel: +44 (0)7913000434
bDepartment of Biomedical Engineering and Environmental Sciences, National Tsing Hua University, No. 101, Section 2, Kuang Fu Road, Hsinchu, 30013, Taiwan. E-mail: radoong@mx.nthu.edu.tw; Fax: +886 3 5725958; Tel: +886 3 726785
cDepartment of the Natural and Built Environment, Sheffield Hallam University, Sheffield, UK S1 1WB
dResearch Unit for Integrated Natural Resources Remediation and Reclamation (IN3R), Department of Civil Engineering, Faculty of Engineering, Naresuan University, Phitsanulok, 65000, Thailand
eCenter of Excellence for Sustainability of Health, Environment and Industry (SHE&I), Faculty of Engineering, Naresuan University, Phitsanulok, 65000, Thailand
fInstitute of Environmental Engineering, National Chiao Tung University, No. 1001, University Road, Hsinchu, 30010, Taiwan
First published on 16th July 2018
Abstract
Nanoparticle (NP) aggregation is typically investigated in either quiescent or turbulent mixing conditions; neither is fully representative of dynamic natural environments. In groundwater, complex interacting influences of advective–diffusive transport, pore tortuosity, and the arrival of aggregates from up-gradient pores impacts the aggregation behaviour of NPs, whereas in surface waters, continuous mixing of fresh particle and aged aggregate populations amends aggregation rates. To mimic such conditions, a cylinder reactor containing shattered graphene oxide NP (<100 nm) suspension was set to rotate with a Reynolds number (Re) close to one and with zero shear. Two main aggregation phases were then observed. Up to 250–350 min, NP remained near the rotational axis longer than in static conditions, giving rise to higher aggregation rates interpreted as an enhanced perikinetic aggregation and differential sedimentation due to mixing with resuspending aggregates. In this phase, a population-balance model estimated an attachment efficiency >5 times in the rotating system than in the static system. Later (5–13 h) aggregates collided with extensively each other, broke, and reformed on the rotating cylinder wall giving rise to larger, denser aggregates (>1 cm). These results thus shed new light on the differences in aggregation behaviour between porous media and other natural environmental systems compared to quiescent batch experiments.
Environmental significanceAs production and application of graphene-based nanomaterials increase and taking into consideration their potential for environmental clean-up, concerns about their transport and fate in the environment are growing. A better understanding under realistic environmental conditions is required, in about process of aggregation which plays a fundamental role in long-term fate of nanomaterials, to help developing predictive models for managing the release of these nanomaterials. To investigate the impact of environmental dynamics on the aggregation processes of shattered graphene oxide nanoparticles, this study uses a solid-body rotational approach to mimic dynamics of interacting populations of nanoaggregate with different sizes and structures. This sheds light on the greater aggregation rates observed in the aquatic environments such as groundwater and surface water systems compared to those observed in simplifying laboratory batch experiments. |
Introduction
With the increasing global proliferation of commercial applications for nanomaterials, they are becoming increasingly released into the natural environment either accidentally in waste streams or deliberately within environmental clean-up, agronomy, and petroleum reservoir recovery applications.1 Among various nanomaterials, the use of graphene nanomaterials is rapidly growing due to their broad constructional, industrial, environmental, and medical applications and arising from their use with other nanomaterials as nanohybrids.2–7 Graphene nanosheets may end up in the environment in various forms of particulate matter such as crumpled graphene,8–10 multilayer graphene,4,5,11 shattered nanosheets,12 and fractal aggregates/hetero-aggregates.13,14 Once they have entered aquatic environments, aggregation of such particles can significantly affect their functionality and transport behaviour, particularly in aqueous and porous media.4,5,15 Despite the existence of many studies on homo- and hetero-aggregation of various nanoparticles (NP),14,16–21 and abundant reports on the impacts of various factors on the aggregation behaviour of these NP,22–26 it still remains a problem of how system dynamics modify aggregation. It is particularly of paramount importance in groundwater (GW) transport to understand how complex multi-cascade processes of advective and diffusive transport,27–30 tortuosity in porous media,31 and the arrival of aggregates from up-gradient pores32,33 impact the aggregation behaviour of NP. Additionally, it is critical to investigate how resuspension phenomenon occurring within surface water (SW) bodies, such as lakes, river, and sea at various scales, influences the aggregation of NP in these environments.34–37Typically, current experimental techniques investigating NP aggregation dynamics are limited to simple quiescent or turbulent mixing batch experiments which may not adequately capture aggregation conditions in real systems.38,39 Whilst research into incorporating aggregation models within porous media transport models continues,38,40,41 steps must be taken to validate the individual aspects of aggregation models in dynamic media. One of these impacts can be the heterogeneous or anisotropic mixing in the population of nanoaggregates induced by the environmental dynamics such as cascading/cycling conditions within GW and SW systems27–30,32,33,36,37,42–44 that can modify the particle size distribution (PSD) evolution trends under aggregation/sedimentation conditions. To investigate such systems, we used a slow rotating cylinder in which these impacts are simulated by slow continuous revolutions of the cylinder. This simple apparatus allows monitoring the particle size dynamics during aggregation which is cumbersome or impossible in other experimental approaches used for studying the NP fate, such as packed column experiments45 or mesocosm tests.46
Rolling cylinders have been used extensively in marine science to mimic the natural condition of marine snow aggregate formation.47 This system consists of a cylinder which is saturated with water and is placed horizontally to rotate around its axis slowly so that no significant shear is induced in the fluid inside. Since the initial condition is static, i.e., the cylinder is initially at rest at zero time, the initial rotations can cause shear in the fluid. Once this has passed, the system rotates as a solid body.48,49 This technique,50,51 has been also utilized to study the interactions of bacteria,52 organic carbon accumulation in marine sediments,53 aggregation of diatom,54 and their interactions with resuspended sediments,55 larvae interactions with anisotropic fluid motions,56 and interactions of microplastic with phytoplankton aggregates.57 However, to the best of our knowledge there has not been any systematic application of rolling cylinders to determine the aggregation of engineered NP in aqueous environmental systems to date. To mimic the condition of porous media, the system was designed with a Reynolds number (Re) below one. The main objective of using such a system was to investigate how NP aggregation behaviour changes over time when the local mass concentration is kept constant, a phenomenon that can occur in pores of subsurface porous media and in resuspending surface waters. Using such a rotating cylinder, the angle between NP displacement directions and the gravity or removal direction is continuously changing without significant mechanical shear, thus preventing particle removal via settling within the axial area of the cylinder. This allows aggregates to develop to very large dimensions until gravity forces impacting on large grown aggregates which are probably more compact than initial aggregates overcome rotational displacements, and the system enters an unstable situation where aggregates tend to settle. The primary aim therefore is to shed light on unexpected higher aggregation rates of NP in GW systems when compared with many standard experimental and modelling results, and on how NP aggregation can be influenced by resuspension and population mixing in SW systems.34,38,58,59 This may underpin development of new mathematical descriptions of aggregation mechanisms for a more accurate consideration of these mechanisms in models of NP fate and transport in the environment which take other complex concurrent transport/transformation phenomena into account.38,41,60
Since the largest use of graphene nanomaterials may result from their high strength and flexibility (∼100 stronger than steel),4 it is possible that they release into the environment as shattered graphene because they may undergo extreme physical or chemical stresses during the usage or upon entering waste streams. Therefore, in this study we use shattered graphene oxide (SGO) particles with a primary hydrodynamic size (DH) of 90 nm. In the scope of this study, which lumps the impact of particle surface characteristics and interactions in one free parameter, i.e., attachment efficiency, within the fitting process, SGO may also act as a representative for other NP types due to their small hydrodynamic size (DH < 100 nm) and since in terms of general aggregation behaviour, e.g., hydrodynamic size and mass concentration trends over time, they exhibit similar patterns to other NP, such as hydroxyapatite (HAp) NP.40 It should be mentioned that the pristine GO sheets may not represent NP due to their large aspect ratio and being considered as a 2-D material.
Materials and methods
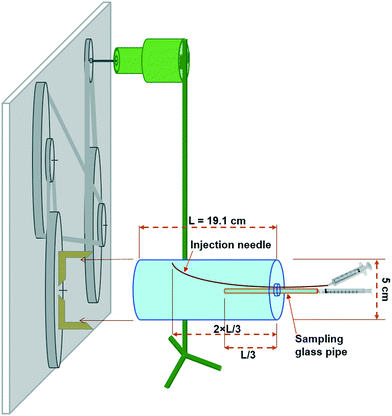
Rotating cylinder setup
Acrylic cylinders were manufactured with inner diameters of 5 cm and length of 19.1 cm to rotate at 4.71 rotations per hour (rph) corresponding to a Reynolds number of 0.91. Methylene blue was used to investigate both the dispersion of matter inside the cylinder and the flow regime as a solid-body rotation. In this case the dye was injected through a needle as an instant point source into the cylinder to see how its diffusion/dispersion is affected by the rotations. A belt-pulley was set to reduce, by >200 times, the rotational velocity of a laboratory stirrer (Eyela NZ, Japan) with an adjustable revolution rate as illustrated in Fig. 1 and S1.† The connection of cylinder to the rotational apparatus was filled with soft plastic, preventing any transfer of shaking from the apparatus to the cylinder. The prepared NP dispersions were poured into the cylinder in the beginning of each experiment to set up each case with an initially homogeneous dispersion. Sampling for particle size measurement was challenging due to the possibility of aggregate breakage resulting from any shear force. To alleviate this, we selected all the channels through which the samples had to pass including syringe tips and a glass pipe inside the cylinder, with an inner diameter larger than ∼2 mm. Sampling was performed by syringe removal (without needle) with a minor flow rate to minimize the impact of shear force on aggregates. With great care they were then directly transferred to the dynamic light scattering (DLS) cuvette for size measurement. Samples were taken using a straight glass pipe centred on one side of the cylinder up to approximately one-third of the length (Fig. 1). In order to keep the reactor saturated at all times during the experiment and to prevent bubble formation, a syringe with a long needle was used to inject the stock dispersion into the cylinder simultaneous with sampling, with the needle leaned towards the wall of the cylinder and entered up to approximately two-third of the length of the cylinder, to be far enough from the sampling point in the middle (see Fig. 1). The volume of each sample was <1.5 mL and an average of 16 samples were taken in each experimental setup. Therefore, the total volume of reactor exchanged with the initially provided stock dispersion was around 24 mL which is less than 10% when compared with the total volume of the cylinder (∼375 mL). After obtaining, the samples were immediately analysed for size and PSD using DLS (Malvern Zetasizer, Nano ZS model, UK) selecting the number of runs to 5 each with a duration of 10 sec and adjusting the beam attenuator to 11 and the position of measurement at 6.5 mm. The refractive index of graphene oxide (GO) used in the calculation of volume-based PSD was assumed as 1.333 and the absorption as 0.01. It should be noted that the sensitivity of volume-based PSD to these factors was minor despite their being expected to be influential. Based on preliminary batch experiment, ionic strength (IS) was selected at 0.5 and 0.75 mM CaCl2 with a pH of 6. These IS values are less than or close to the critical coagulation concentration (CCC) (results not shown).The derived count rate (DCR) of DLS output has been used as a measure of mass concentration.61–63 However, since DCR significance under the reaction limited aggregation (RLA) remains unvalidated, we also determined the mass concentration in each sample using UV-vis spectroscopy (Hitachi, U-4100 model, Japan) at a wavelength of 230 nm, with a calibrated absorption curve. With such a curve (intercept = 0) we used measured absorbance normalized by the initial absorbance in each experiment as representative of normalized mass concentrations.
SGO synthesis
Graphene oxide was synthesized by the thermal exfoliation of natural graphite flakes using a modified Hummers method.64 This was conducted through constant stirring of graphite (2.0 g) in a solution of 225 mL sulfuric acid and 50 mL phosphoric acid, followed by gradual addition of 5 g potassium permanganate at a constant temperature of 35 °C and continuous stirring, which was maintained for 10 h. The mixture was then diluted with 225 mL of deionized (DI) water and kept in an ice bath, subsequently, 3 mL of H2O2 was added for permanganate residual removal, with the mixture centrifuged and washed with 1 M hydrochloric acid. This was followed by washing with phosphate buffer (pH 11). Finally, the synthesized GO was washed with DI water repeatedly to reach the neutral pH. Shattered GO was prepared via intensive ultra-sonication of a GO dispersion (2 g L−1) to achieve initial uniform hydrodynamic size below 100 nm. This was conducted using a probe sonication at a power of 40 W for 2 h with 30 sec stops following 30 sec sonication intervals. This dispersion was then centrifuged for 30 min at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ± 500 rpm to remove the larger fraction of particles. Finally, the dispersion was passed through a 0.45 μm syringe filter, and the filtrate kept in the dark at 4 °C as the stock dispersion. Sodium azide was added (10 mM) to each experimental dispersion to prevent the growth of bacteria during analysis and due to its buffering ability in maintaining a constant pH during the course of experiments.40
500 ± 500 rpm to remove the larger fraction of particles. Finally, the dispersion was passed through a 0.45 μm syringe filter, and the filtrate kept in the dark at 4 °C as the stock dispersion. Sodium azide was added (10 mM) to each experimental dispersion to prevent the growth of bacteria during analysis and due to its buffering ability in maintaining a constant pH during the course of experiments.40
Experimental procedure
The cylinder tests were performed as follows: (1) prepare particle dispersions in DI water with a final SGO concentration 50 mg L−1, and sodium azide concentration 10 mM; (2) adjust pH at 6 ± 0.05 with NaOH/HCl (100 mM) while stirring with a magnet stirrer; (3) ultrasonicate for 5 min in sonication bath, add electrolyte, (CaCl2) to reach final concentrations 0.5 and 0.75 mM, stop stirring 5 sec after adding the electrolyte, and take the first sample; (4) fill the cylinder with the prepared dispersion, emplace the syringe and the sampling pipe, seal, and leave at rest for static cases or on the rotating mode for dynamic cases (in total taking ∼10–15 min from the time of stopping the stirrer until the complete setup of the cylinder); and (5) take samples (<1.5 mL) at certain times to be analysed immediately by DLS. After obtaining each sample the glass pipe was evacuated using a syringe to prevent interference of the solution inside the pipe with the next sampling. After analysis by DLS, the same samples were carefully preserved at 4 °C for analysis using UV-vis, which were carried out following dilution by 7.5 times and sonication for 5 min to obtain a uniform dispersion. Selected experiments which could have been prone to uncertainties (e.g., due to higher IS) were carried out in duplicate. Control experiments were undertaken in a similar condition to cylinder experiment but inside 3 mL DLS cuvettes with time resolved online measurement. In these experiments after ultrasonication of the suspension for 5 min, the electrolyte was added, and the sample was immediately vortexed for 5 sec. Then it was transferred to a disposable cuvette, after which time-resolved DLS measurement was started immediately. The whole process duration, from ultrasonication until the start of the first measurement, was 70 ± 20 sec. The sample volume of 3 mL corresponds to a measurement depth of ∼23.3 mm which is close to the radius of the cylinder. In control experiments, time-resolved DCR data normalized to the initially observed DCR was used as an indicator of mass concentration.40,61–63Theory and modelling
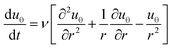 | (1) |
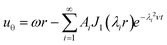 | (2) |
ux = −uθ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (3) |
uy = uθ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − Uk θ − Uk | (4) |
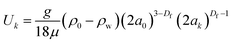 | (5) |
Once the system reaches the equilibrium conditions, i.e. solid-body rotation, particle trajectories can be calculated as:48
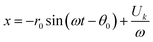 | (6) |
y = r0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt − θ0) sin(ωt − θ0) | (7) |
The shear rate, γ, resulted from the gradient of velocity across the cylinder radius is given as:48
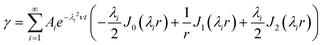 | (8) |
Particle aggregation
A flexible population-balance model known as fixed pivot (FP),70 capable of considering initial PSD and consequent evolution of PSD in early and late stages of aggregation is used to model the dynamic behaviour of hydrodynamic diameter, overall mass concentration, and PSD for SGO aggregation experiments. Conserving two properties of mass and number, the model equation for aggregation combined with sedimentation term is as follows:70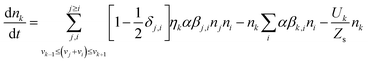 | (9) |
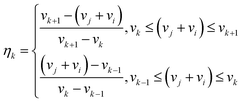 | (10) |
An explicit forward Euler scheme was used for the time discretization of eqn (9) with an adjustable time-step, as this can be more efficient than higher-order schemes for solving “stiff” problems such as population balance models.71,72 Since the Brinkman permeability-based model73–75 performs best for modelling collision frequencies, this approach was used in the present study. All collision kernels were expressed based on aggregate volume so that the impact of aggregate shapes which are unknown will interfere less in the model results. The measured initial PSD was directly used as the initial condition. A new optimization algorithm code40 was also used here to estimate the parameter values (α and Df) by matching the modelled with experimental data for mean hydrodynamic diameter (DH) and normalized concentration data (C/C0). In these fittings, the contribution weight of the DH was assumed to be twice C/C0. Aggregation modelling was performed only at a single spatial point, i.e., the centre of the cylinder cross-section, corresponding to the point of measurement and considering the sedimentation depth in eqn (9), Zs, as the radius of the cylinder. Full model equations together with details of extensive model testing and the MATLAB codes and optimization algorithm are available in the ESI† and in Babakhani et al.40 A summary of the model parameters and experimental characteristics are provided in Table 1.
| Parameter | Symbol | Value |
|---|---|---|
| Shear rate (s−1) | G | 0 |
| Dynamic viscosity of fluid (water) (Pa s) | μ | 0.00089 |
| Temperature (K) | T | 298 |
| Density of primary particle (kg m−3) | ρ 0 | 1800 |
| Density of the medium (water) (kg m−3) | ρ w | 1000 |
| Initial NP concentration (mg L−1) | C 0 | 50 |
| Cylinder radius (cm) | a cyl | 2.5 |
| Cylinder length (cm) | L cyl | 19.1 |
| Sedimentation depth (cm) | Z s | 2.33, 2.5 |
| Angular velocity (rph) | ω | 4.71 |
| Reynolds number | Re | 0.91 |
| Radius of the primary particles (nm), variable depending on the first non-zero bin of initial PSD | a 0 | 6.75–45 |
| Ionic strength (mM CaCl2) | 0.5, 0.75 | |
| pH | 6.0 | |
| Number of size classes, variable depending on broadness of the initial PSD | 63–86 | |
| Attachment efficiency | α | Fitting parameter |
| Fractal dimension | D f | Fitting parameter |
Results
Flow regime and particle trajectory analysis
The experimental results of the cylinder with a drop of dye injected in the beginning of the experiment (Fig. S2†) shows that generally within the first ∼10–20 min a thin layer of dye forms at the rotating wall. After ∼60 min, however, this thin layer is still noticeable, but begins to slowly diffuse into the bulk solution and after ∼90–100 min it is barely visible. These results suggest that the rotational regime can be considered as solid-body and the diffusion of dye is the only mechanism of mixing in the cylinder after ∼10–20 min. Consistent with these outcomes, the calculations of rotation velocity and shear rate for the cylinder, shown in Fig. S3,† demonstrate that within 10 min rotational velocity reaches a steady-state (solid-body rotation) and the shear stress produced in cylinder fluid totally disappears (blue lines). This duration is negligible compared to the total course of experiment >5 h and is not captured in the sampling intervals when NP dispersions are used in the cylinder. Both experimental and modelling results confirm the validity of assuming steady-state and zero-shear conditions in the system.Fig. 2 shows results of particle trajectory analysis modelled using eqn (1)–(8) with varying fractal dimension and particle radius for two scenarios: (1) particle is initially placed in the middle of the cylinder radius and (2) particle is initially placed near the wall of the cylinder. Based on this analysis, the movement of NP and their aggregates ranging in radius from 20 nm to 100 μm depends significantly on the fractal dimension. For aggregates up to a radius of ∼1 μm and for fractal dimension up to 2.5, their trajectories follow the “fixed” solid-body rotation regime as illustrated by Tagawa et al.76 However, for aggregate radii in range of 10–100 μm with Df ≥ 2.5, trajectories start to deviate from this regime and show a tendency towards the so-called “cascading” or “suspending” regimes.76 Sedimentation velocity is so rapid for aggregates of radius >100 μm and Df = 2.9 that they interact with the cylinder wall instead of rotating with the solid body. In agreement with these results, Fig. S4† shows that velocity vectors exhibit a nonuniform distribution for aggregates with 10 μm radius and Df = 2.9, highlighting the importance of aggregate fractal dimensionality and size in controlling particle trajectories.
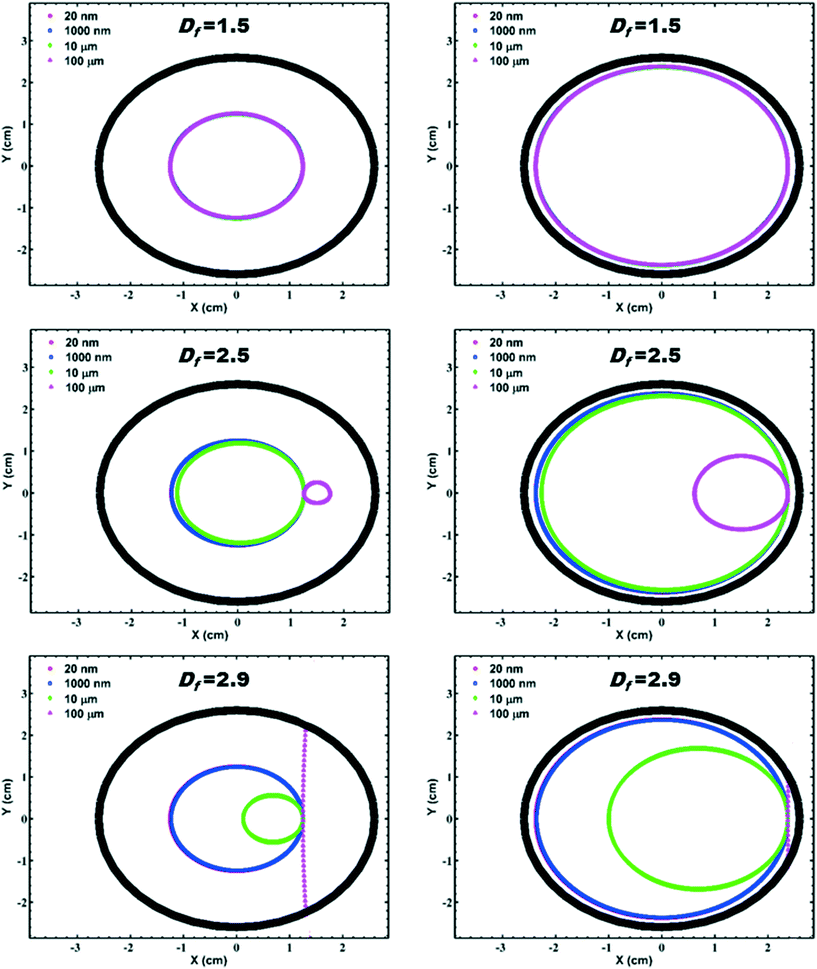 | ||
| Fig. 2 Particle trajectories resulted from eqn (1)–(8) with virtually varying Df and particle radii considering two scenarios: (1) for particle initially placed in the middle of the cylinder radius (left-hand side panels) and (2) particle initially placed near the wall of the cylinder (right-hand side panels). The rotational direction is counter clockwise. | ||
Aggregation experiment results
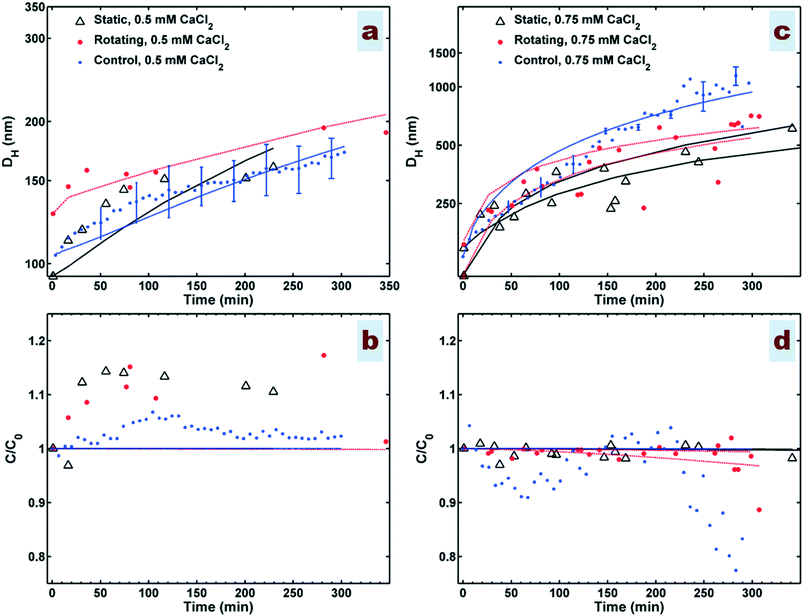
Experiments were undertaken in the cylinder under both rotating and static (non-rotating) conditions, and as a control within a cuvette under static conditions with continuous monitoring using dynamic light scattering (DLS). Fig. 3a shows that the averaged hydrodynamic diameter (DH) follows a log-linear trend with time at 0.5 mM CaCl2 in all experiments. However, at 0.75 mM CaCl2 (Fig. 3c) the gradient decreases over time after a rapid initial rise, which we interpret as a transition from early (fresh, monodisperse particle population) to late (aged, polydisperse particle population) stage conditions within a coupled aggregation/sedimentation system.Under the solutions present and within the selected periods for size measurement (up to 300–350 min), the sedimentation is not generally significant (Fig. 3b and d). The trend of DH measurement at 0.5 mM CaCl2 within the static cylinder closely matches that in the control, demonstrating the validity of the design of sampling in the cylinder experiments. This was also the case at 0.75 mM CaCl2 but only in the early stages <120 min, as shown in Fig. 3c after this time DH in the control continues to rise, whereas DH in the static cylinder tends towards an asymptote over time. The reason for this behaviour is not clear, it could be due to minor differences in the conditions between the two experiments, such as variation in temperature or dimensionality between the cylinder and the cuvette. One might attribute this behaviour to the breakage of aggregates larger than ∼500 nm during sampling from the cylinder experiments. However, this is less likely to be a reason for the observed lower growth of aggregates in the static cylinder compared to the control system, because the control experiment shows a level of sedimentation which is not observed for the static case (Fig. 3d) whereas sedimentation measurement, is not expected to be affected by the breakage. This suggests that in this case there might be a level of uncertainty for the control test rather than the occurrence of breakage in the cylinder samples as also indicated by the larger standard deviations in the control after ∼230 min.
Generally, the experimental observations using the rotating cylinder initially show higher aggregation rates than that of the static cylinder (Fig. 3a and c). In the case of 0.5 mM CaCl2, normalized mass concentration curves show increases in concentration to above the initial uniform concentration at the point of measurement (Fig. 3b). Interestingly, these results are consistent for both measurement techniques, i.e., UV-vis used for the cylinder samples and DLS derived count rate used for the control data, and are also in agreement with previous measurements of DCR for HAp NP aggregation at IS below CCC.40 Babakhani et al.40 used the FP model already to validate the use of DCR data as representative of mass concentration during NP aggregation at IS above CCC leading to a decline in mass over time. The present study's results tend to agree with the use of DCR data as representative of mass concentration at IS below CCC as well.
The experimental photos of the rotating cylinder at 0.75 mM CaCl2 at different times are shown in Fig. S5† and the magnified images of aggregates formed at each time are shown in Fig. 4. It appears that visible aggregates form on the wall after ∼290 min, corresponding to the start of removal in the sedimentation curve after 250–300 min (Fig. 3d). Large networks of gel-like aggregates form at the bottom after ∼315 min which as a result of extensive sliding on the wall and consequent collisions, breakage, and reforming, become denser over time until finally they form larger (>1 cm) granular dense aggregates as indicated by their darker colour compared to those formed at earlier times (Fig. 4 and S5†).77,78 When finally, the sizes of aggregates grow larger and their structure become more compact to induce their higher settling velocity due to their higher bulk density, the settling velocity overcomes the resuspension due to the cylinder rotation. This results in millimetre-sized aggregates appear immediately on the cylinder wall sliding and colliding consequently producing compact centimetre-sized SGO granules appear on the wall of the rotating cylinder in longer time (5–13 h), and the suspension becomes clear of the SGO NP.
 | ||
| Fig. 4 Experimental photos of SGO aggregates formed over longer times for the case of rotating cylinder filled with SGO NP in 0.75 mM CaCl2 solution and pH 6. The full photographs of cylinder corresponding to each time is available in Fig. S5, ESI.† The snapshots in this figure were obtained at the same scale from the bottom of the cylinder. | ||
Aggregation modelling results
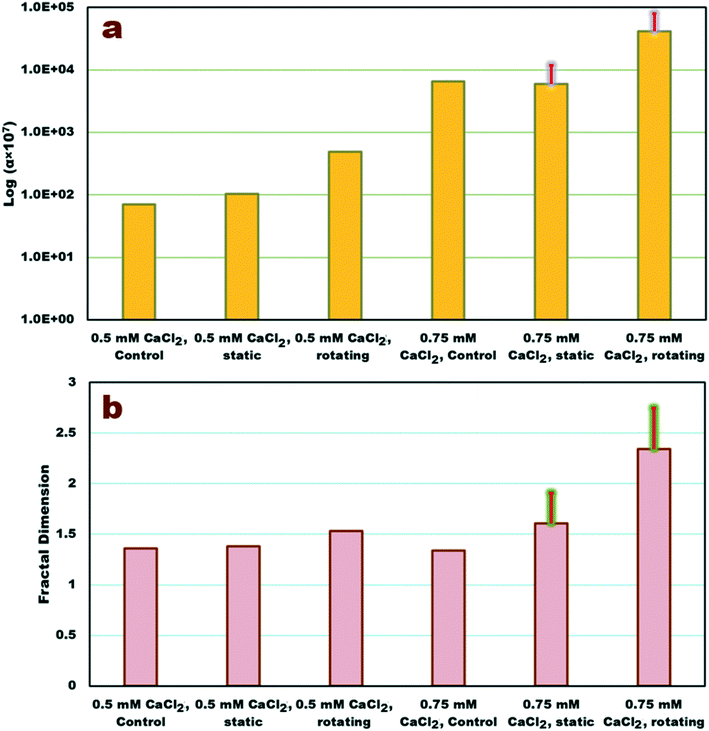
Data from the first 250–350 min of experiments (before the evolution of larger, settling macro-aggregates) were used to fit models of the aggregation in the suspended phase. The estimated parameter values are shown in Fig. 5 and are also available in Table S1† along with Nash–Sutcliffe15 goodness-of-fit criterion, R2NS, values. The model set used in this study (FP population-balance technique with the power-law model for settling velocity and the Brinkman permeability model for collision frequencies) can fit both DH and normalized concentration (C/C0) well with an average R2NS 0.758 ± 0.18 for DH data. Parameter values estimated for the model matched to the control data agree well with those of static cylinder measurements at electrolyte concentrations of 0.5 mM CaCl2 and 0.75 mM CaCl2 (<29% difference). The rolling cylinder experiment shows 5 and 7 times greater attachment efficiency (Fig. 5a) than that of the static system at 0.5 and 0.75 mM CaCl2, respectively. Likewise, Df estimated in the rolling cylinder experiment is on average 10% and 31% larger than that of the static cylinder at 0.5 and 0.75 mM CaCl2, respectively (Fig. 5b).The results clearly indicate that conditions within the rotating cylinder enhance aggregation rate and leads to aggregates with more compact structures (via increasing Df). For higher IS than those of present study's experimental conditions and longer times than those of aggregation simulations, the impact of system dynamics may well be higher (Fig. 4 and S5†). Although the process of the aggregation at longer times (sliding on the wall) is different from that at early stages (aggregation of suspended particles/aggregates), occurrence of both phases is relevant to the natural environment. In GW system, large aggregates attached to porous medium solid surfaces can be translated, rolled over and collide with each other, thereby aggregating in the retained phase.32,38 They can also be detached and transported to a new pore where they can interact with new NP or aggregates,32,38 whether in the suspended phase or in the retained phase. Likewise, in a SW system the aggregates which have already settled onto deeper depths, can be transported with sediments or be resuspended where they could encounter new particles. It should be noted that in both modes, aggregates become more compact, shown either by enhanced Df resulted from the model or by change in colour of aggregates to a darker colour observed in the cylinder.77,78 The current cylinder condition ignores many aspects of convoluted groundwater pores, such the constricted geometry of pores, shear effect, nonuniform flow regime, and dynamic interactions between suspended particles and solid surfaces.79–82 Nevertheless, ignoring such aspects may allow a better understanding of the dynamic impacts on the individual aggregation/sedimentation mechanisms. For instance, including shear stress in the system39,82,83 can overshadow the impact of system dynamics due to addition of other complexities such as break-up of aggregates.84 This cylinder can be further modified in future studies, e.g., by modifying the wall surface roughness or adding short edges/partitions on the inner wall in order to consider more complexities of natural conditions.
The system developed different stages in respect to the interplay between aggregation and sedimentation mechanisms within the rotating cylinder. Up to 250–350 min, where the sliding of aggregates on the wall is still not significant, the maximum Df obtained in the present study is 2.34 (at 0.75 mM CaCl2 within the rotational cylinder) and the maximum aggregate DH is below 1 μm (Fig. 3a and c). According to the particle tracking analysis results (Fig. 2 and S4†), for these values of Df and DH, the effect of gravity on aggregates may not be strong enough to deviate aggregate trajectories from a uniform solid-body regime. In agreement with this, the results from sedimentation over time (Fig. 3b) show minor or no removal of NP over the periods up to 250 or 350 min. Hence, within these periods the only difference between the static and rotating systems is seemingly that particle orientations with respect to the gravitational force vector are continuously changing for aggregates in the rotational system while they remain constant within the static system. This might maintain the local particle concentration within the axial area high at initial stages and therefore enhance the number of collisions resulting from Brownian motion, thereby increasing the overall rate of aggregation. At 0.75 mM CaCl2, at times <150 min normalized mass concentration data shows a slight decrease in the suspended mass in both the control and static cylinder experiments which is not noticeable in the case of rotational cylinder (Fig. 3d). However, after 250–300 min mass removal in the rotating cylinder becomes increasingly significant as the aggregates become large and dense enough for the gravity force on them to overcome the rotational force leading to their settlement on the cylinder wall. Enhanced aggregation and removal within the rotating cylinder compared to the static cylinder emanates also from differential sedimentation mechanism85 of aggregation. In fact, attachment efficiency is generally expected to be a function of NP surface characteristics.86 However, the present study indicates that system dynamics increase the effective attachment efficiency, even though chemical conditions controlling surface properties were consistent between rotating, static and control experiments. To investigate this behaviour, we calculated the collision frequencies between particles with radii of 50, 500, and 5000 nm and particles with all other size classes up to a radius of 15 μm and for various Df (1.5–2.9) as illustrated in Fig. S6.† Based on collision frequency formulations used in the present study, representing the state-of-art equations for environmentally-relevant NP,40,72,87 the impact of differential sedimentation mechanism of aggregation, which is notably affected by the structure of aggregates (Df), is around 3–5 orders-of-magnitude lower than that of perikinetic aggregation, which is impacted less by the structure of aggregates (Df), for the range of aggregate sizes observed in this study in early stages of aggregation. Experimental photos (at 0.75 mM CaCl2, Fig. 4 and S5†) suggest that at 290 min aggregates are sufficiently large (>10 μm, based on Fig. 2) and/or compact enough (Df > 2.5, based on Fig. 2) for the trajectories to deviate from solid body rotation and to settle on the wall, suggesting that in this condition sedimentation and therefore differential settling mechanism of aggregation is significant. However, the current collision frequency formulation may not be able to take this effect into account because for a similar range of aggregate size/fractal dimension they predict negligible contribution for differential sedimentation. This deviation may also arise from restructuring or change in the fractal dimension over the course of the experiment increases its significance in the later stages of aggregation.40,68,88 Taking such a transient change in the fractal dimension, which causes a variation in the particle volume discretization, into account needs special computational consideration. Modelling the whole rotating cylinder domain for aggregation may shed light on the complex interactions of resuspending aggregates and the reasons for the observed differences in the attachment efficiency between the two systems of dynamic and static. Furthermore, additional experimental analysis on the structure of aggregates is needed to verify the estimated fractal dimension values, e.g., using static light scattering (SLS)88 to monitor the dynamics of the aggregate structure online during the test. The impact of system dynamics can be even more crucial where the existence of natural colloids induces hetero-aggregation with NP.16 In such systems, the initial diversities in density, size, and interactions of particles may affect both the initial availability of surfaces for Brownian-driven aggregation and differential settling aggregation. These are beyond the scope of current study and may be subject of future studies.
Conclusions
In the early stage of experiments reported here, whilst the majority of particles remain suspended, maintenance of mass concentration in the axial area of the rotating cylinder increased the number of collisions induced by Brownian motion and arising from differential sedimentation collisions with resuspending larger aggregates. This enhanced the aggregation rate which emerged relating to the attachment efficiency estimated based on model fit to experimental data. As the system evolves and aggregates grow sufficiently to show significant sedimentation, resuspension of settling aggregates in the rotating cylinder increased differential sedimentation, further enhancing the aggregation rate. This consequently leads to an immediate formation of aggregates on the cylinder wall that afterwards start rolling and sliding on the wall. These processes give rise to the formation of more compact aggregates, leading to an increase in fractal dimension in all stages as revealed by greater fractal dimension in the rotating system compared to that of static system and control and indicated by dark colour of aggregate formed on the cylinder wall at the end of experiments.Numerous studies have reported higher aggregation rates in groundwater, surface-water and other natural environmental systems when compared to quiescent batch experiments.34,38,58,59 The results from this study demonstrate that this effect can be understood in terms of systems where, even in the absence of hydrodynamic shear, particle suspensions are to some extent prevented from sedimentation. Such effects are simulated here by continuous rotation in a slow-moving cylinder, which models slow flow through tortuous pore networks in natural systems which are characteristic of changing flow directions and mixing of old and new particle populations. It should be noted that considering the importance of hetero-aggregation (aggregation of NP with natural colloids) in the fate of NP in natural waters,16,89–91 the present study serves as a first stage to investigate hetero-aggregation in more realistic conditions. The system used in this study has also important applications for water treatment, e.g., as a settling unit that can be optimized through adjustment of the fractal dimension and aggregation rate where the adsorption of contaminants to NP is maximised whilst the NP removal due to settling is minimised. Further studies are required to consider a variable fractal dimension in the model for taking reorganization of aggregates into account and to investigate the spatial variations of aggregate sizes in both phases of suspended and settled particles. It also remains for future studies to experimentally verify the model estimated fractal dimension values through direct, online measurements.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support from the University of Liverpool and National Tsing Hua University through a Dual-PhD program to PB is gratefully acknowledged. JB was supported by Sheffield Hallam University through an allocation of research time. This work was also funded by the Taiwan's Ministry of Science and Technology (MOST) under the grant No. 104-2221-E-009-020-MY3. We gratefully acknowledge Chien-Hou Wu and Chung-Yi Wu for providing full-time access to the DLS instrument, and Rama Shanker Sahu for help in synthesis of GO. MATLAB codes for aggregation model solution, parameter estimation, and trajectory analysis have been provided as ESI.†References
- S. S. Patil, U. U. Shedbalkar, A. Truskewycz, B. A. Chopade and A. S. Ball, Nanoparticles for environmental clean-up: a review of potential risks and emerging solutions, Environ. Technol. Innovation, 2016, 5, 10–21 CrossRef.
- D. Wang, Y. Jin, C. M. Park, J. Heo, X. Bai, N. Aich and C. Su, Investigating and Modeling the Transport of the ‘New-Horizon’Reduced Graphene Oxide—Metal Oxide Nanohybrids in Water-Saturated Porous Media, Environ. Sci. Technol., 2018, 52, 4610–4622 CrossRef PubMed.
- W. Ren and H.-M. Cheng, The global growth of graphene, Nat. Nanotechnol., 2014, 9, 726 CrossRef PubMed.
- M. V. D. Z. Park, E. A. J. Bleeker, W. Brand, F. R. Cassee, M. van Elk, I. Gosens, W. H. De Jong, J. A. J. Meesters, W. J. G. M. Peijnenburg and J. T. K. Quik, Considerations for safe innovation: the case of Graphene, ACS Nano, 2017, 11, 9574–9593 CrossRef PubMed.
- J. Zhao, Z. Wang, J. C. White and B. Xing, Graphene in the aquatic environment: adsorption, dispersion, toxicity and transformation, Environ. Sci. Technol., 2014, 48, 9995–10009 CrossRef PubMed.
- A. Y. Romanchuk, A. S. Slesarev, S. N. Kalmykov, D. V. Kosynkin and J. M. Tour, Graphene oxide for effective radionuclide removal, Phys. Chem. Chem. Phys., 2013, 15, 2321–2327 RSC.
- S. Yu, X. Wang, X. Tan and X. Wang, Sorption of radionuclides from aqueous systems onto graphene oxide-based materials: a review, Inorg. Chem. Front., 2015, 2, 593–612 RSC.
- X. Ma, M. R. Zachariah and C. D. Zangmeister, Crumpled nanopaper from graphene oxide, Nano Lett., 2011, 12, 486–489 CrossRef PubMed.
- M. M. Gudarzi, Colloidal stability of graphene oxide: aggregation in two dimensions, Langmuir, 2016, 32, 5058–5068 CrossRef PubMed.
- M. S. Spector, E. Naranjo, S. Chiruvolu and J. A. Zasadzinski, Conformations of a tethered membrane: Crumpling in graphitic oxide?, Phys. Rev. Lett., 1994, 73, 2867 CrossRef PubMed.
- S. Kamrani, M. Rezaei, M. Kord and M. Baalousha, Transport and retention of carbon dots (CDs) in saturated and unsaturated porous media: Role of ionic strength, pH, and collector grain size, Water Res., 2018, 133, 338–347 CrossRef PubMed.
- H. W. Yang, M. Y. Hua, T. L. Hwang, K. J. Lin, C. Y. Huang, R. Y. Tsai, C. C. M. Ma, P. H. Hsu, S. P. Wey and P. W. Hsu, Non-Invasive Synergistic Treatment of Brain Tumors by Targeted Chemotherapeutic Delivery and Amplified Focused Ultrasound-Hyperthermia Using Magnetic Nanographene Oxide, Adv. Mater., 2013, 25, 3605–3611 CrossRef PubMed.
- Z. Hua, Z. Tang, X. Bai, J. Zhang, L. Yu and H. Cheng, Aggregation and resuspension of graphene oxide in simulated natural surface aquatic environments, Environ. Pollut., 2015, 205, 161–169 CrossRef PubMed.
- H. Wang, Y.-N. Dong, M. Zhu, X. Li, A. A. Keller, T. Wang and F. Li, Heteroaggregation of engineered nanoparticles and kaolin clays in aqueous environments, Water Res., 2015, 80, 130–138 CrossRef PubMed.
- P. Babakhani, J. Bridge, R.-a. Doong and T. Phenrat, Parameterization and prediction of nanoparticle transport in porous media: A reanalysis using artificial neural network, Water Resour. Res., 2017, 53, 4564–4585 CrossRef.
- E. M. Hotze, T. Phenrat and G. V. Lowry, Nanoparticle Aggregation: Challenges to Understanding Transport and Reactivity in the Environment, J. Environ. Qual., 2010, 39, 1909–1924 CrossRef PubMed.
- T. Phenrat, N. Saleh, K. Sirk, R. D. Tilton and G. V. Lowry, Aggregation and sedimentation of aqueous nanoscale zerovalent iron dispersions, Environ. Sci. Technol., 2007, 41, 284–290 CrossRef PubMed.
- N. P. Sotirelis and C. V. Chrysikopoulos, Heteroaggregation of graphene oxide nanoparticles and kaolinite colloids, Sci. Total Environ., 2017, 579, 736–744 CrossRef PubMed.
- H.-J. Kim, T. Phenrat, R. D. Tilton and G. V. Lowry, Effect of kaolinite, silica fines and pH on transport of polymer-modified zero valent iron nano-particles in heterogeneous porous media, J. Colloid Interface Sci., 2012, 370, 1–10 CrossRef PubMed.
- M. Therezien, A. Thill and M. R. Wiesner, Importance of heterogeneous aggregation for NP fate in natural and engineered systems, Sci. Total Environ., 2014, 485, 309–318 CrossRef PubMed.
- J. Zhao, F. Liu, Z. Wang, X. Cao and B. Xing, Heteroaggregation of graphene oxide with minerals in aqueous phase, Environ. Sci. Technol., 2015, 49, 2849–2857 CrossRef PubMed.
- K. Afshinnia, I. Gibson, R. Merrifield and M. Baalousha, The concentration-dependent aggregation of Ag NPs induced by cystine, Sci. Total Environ., 2016, 557, 395–403 CrossRef PubMed.
- K. Afshinnia, M. Sikder, B. Cai and M. Baalousha, Effect of nanomaterial and media physicochemical properties on Ag NM aggregation kinetics, J. Colloid Interface Sci., 2017, 487, 192–200 CrossRef PubMed.
- M. Baalousha, Aggregation and disaggregation of iron oxide nanoparticles: Influence of particle concentration, pH and natural organic matter, Sci. Total Environ., 2009, 407, 2093–2101 CrossRef PubMed.
- M. Baalousha, Effect of nanomaterial and media physicochemical properties on nanomaterial aggregation kinetics, NanoImpact, 2017, 6, 55–68 CrossRef.
- M. Baalousha, Y. Nur, I. Römer, M. Tejamaya and J. R. Lead, Effect of monovalent and divalent cations, anions and fulvic acid on aggregation of citrate-coated silver nanoparticles, Sci. Total Environ., 2013, 454, 119–131 CrossRef PubMed.
- A. A. Shapiro and P. G. Bedrikovetsky, A stochastic theory for deep bed filtration accounting for dispersion and size distributions, Phys. A, 2010, 389, 2473–2494 CrossRef.
- C. V. Chrysikopoulos and V. E. Katzourakis, Colloid particle size-dependent dispersivity, Water Resour. Res., 2015, 51, 4668–4683 CrossRef.
- M. R. Soltanian, R. W. Ritzi, C. C. Huang and Z. Dai, Relating reactive solute transport to hierarchical and multiscale sedimentary architecture in a Lagrangian-based transport model: 2. Particle displacement variance, Water Resour. Res., 2015, 51, 1601–1618 CrossRef.
- M. R. Soltanian, R. Ritzi, C. C. Huang, Z. Dai and H. Deng, A note on upscaling retardation factor in hierarchical porous media with multimodal reactive mineral facies, Transp. Porous Media, 2014, 108, 355–366 CrossRef.
- T. H. Illangasekare, C. C. Frippiat and R. Fučík, Dispersion and Mass Transfer Coefficients in Groundwater of Near-Surface Geologic Formations, CRC Press/Taylor and Francis Group, 2010 Search PubMed.
- S. A. Bradford, J. Simunek and S. L. Walker, Transport and straining of E. coli O157: H7 in saturated porous media, Water Resour. Res., 2006, 42, 1–12 Search PubMed.
- W. P. Johnson, X. Li and S. Assemi, Deposition and re-entrainment dynamics of microbes and non-biological colloids during non-perturbed transport in porous media in the presence of an energy barrier to deposition, Adv. Water Resour., 2007, 30, 1432–1454 CrossRef.
- I. Velzeboer, J. T. K. Quik, D. van de Meent and A. A. Koelmans, Rapid settling of nanoparticles due to heteroaggregation with suspended sediment, Environ. Toxicol. Chem., 2014, 33, 1766–1773 CrossRef PubMed.
- A. A. Markus, J. R. Parsons, E. W. M. Roex, P. de Voogt and R. Laane, Modeling aggregation and sedimentation of nanoparticles in the aquatic environment, Sci. Total Environ., 2015, 506, 323–329 CrossRef PubMed.
- Y. P. Wang, G. Voulgaris, Y. Li, Y. Yang, J. Gao, J. Chen and S. Gao, Sediment resuspension, flocculation, and settling in a macrotidal estuary, J. Geophys. Res.: Oceans, 2013, 118, 5591–5608 Search PubMed.
- A.-R. Diercks, C. Dike, V. L. Asper, S. F. DiMarco, J. P. Chanton and U. Passow, Scales of seafloor sediment resuspension in the northern Gulf of Mexico, Elementa, 2018, 6, 1–28 Search PubMed.
- P. Babakhani, J. Bridge, R.-a. Doong and T. Phenrat, Continuum-based models and concepts for the transport of nanoparticles in saturated porous media: A state-of-the-science review, Adv. Colloid Interface Sci., 2017, 246, 75–104 CrossRef PubMed.
- J. C. Zahnow, R. D. Vilela, U. Feudel and T. Tél, Coagulation and fragmentation dynamics of inertial particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 026311 CrossRef PubMed.
- P. Babakhani, R.-a. Doong and J. Bridge, The significance of early and late stages of coupled aggregation and sedimentation in the fate of nanoparticles: measurement and modelling, Environ. Sci. Technol., 2018 DOI:10.1021/acs.est.7b05236.
- P. Babakhani, F. Fagerlund, A. Shamsai, G. V. Lowry and T. Phenrat, Modified MODFLOW-based model for simulating the agglomeration and transport of polymer-modified Fe nanoparticles in saturated porous media, Environ. Sci. Pollut. Res., 2015, 1–20, DOI:10.1007/s11356-015-5193-0.
- S. A. Bradford, S. Torkzaban and J. Simunek, Modeling colloid transport and retention in saturated porous media under unfavorable attachment conditions, Water Resour. Res., 2011, 47, 1–12 CrossRef.
- T. Phenrat, A. Cihan, H.-J. Kim, M. Mital, T. Illangasekare and G. V. Lowry, Transport and deposition of polymer-modified Fe0 nanoparticles in 2-D heterogeneous porous media: Effects of particle concentration, Fe0 content, and coatings, Environ. Sci. Technol., 2010, 44, 9086–9093 CrossRef PubMed.
- S. Torkzaban, S. A. Bradford and S. L. Walker, Resolving the Coupled Effects of Hydrodynamics and DLVO Forces on Colloid Attachment in Porous Media, Langmuir, 2007, 23, 9652–9660 CrossRef PubMed.
- E. J. Roth, B. Gilbert and D. C. Mays, Colloid deposit morphology and clogging in porous media: Fundamental insights through investigation of deposit fractal dimension, Environ. Sci. Technol., 2015, 49, 12263–12270 CrossRef PubMed.
- G. V. Lowry, B. P. Espinasse, A. R. Badireddy, C. J. Richardson, B. C. Reinsch, L. D. Bryant, A. J. Bone, A. Deonarine, S. Chae and M. Therezien, Long-term transformation and fate of manufactured Ag nanoparticles in a simulated large scale freshwater emergent wetland, Environ. Sci. Technol., 2012, 46, 7027–7036 CrossRef PubMed.
- B. E. Logan and J. R. Kilps, Fractal dimensions of aggregates formed in different fluid mechanical environments, Water Res., 1995, 29, 443–453 CrossRef.
- G. A. Jackson, Particle trajectories in a rotating cylinder: implications for aggregation incubations, Deep Sea Res., Part I, 1994, 41, 429–437 CrossRef.
- G. A. Jackson, Coagulation in a rotating cylinder, Limnol. Oceanogr.: Methods, 2015, 13, 194–201 Search PubMed.
- H. P. Grossart, M. Simon and B. E. Logan, Formation of macroscopic organic aggregates (lake snow) in a large lake: The significance of transparent exopolymer particles, plankton, and zooplankton, Limnol. Oceanogr., 1997, 42, 1651–1659 CrossRef.
- J. C. Prairie, K. Ziervogel, C. Arnosti, R. Camassa, C. Falcon, S. Khatri, R. M. McLaughlin, B. L. White and S. Yu, Delayed settling of marine snow at sharp density transitions driven by fluid entrainment and diffusion-limited retention, Mar. Ecol.: Prog. Ser., 2013, 487, 185–200 CrossRef.
- D. Ionescu, M. Bizic-Ionescu, A. Khalili, R. Malekmohammadi, M. R. Morad, D. De Beer and H.-P. Grossart, A new tool for long-term studies of POM-bacteria interactions: overcoming the century-old Bottle Effect, Sci. Rep., 2015, 5, 1–12 Search PubMed.
- U. Passow and C. L. De La Rocha, Accumulation of mineral ballast on organic aggregates, Global Biogeochem. Cycles, 2006, 20, 1–7 CrossRef.
- K. M. Crocker and U. Passow, Differential aggregation of diatoms, Mar. Ecol.: Prog. Ser., 1995, 117, 249–257 CrossRef.
- K. Ziervogel and S. Forster, Aggregation and sinking behaviour of resuspended fluffy layer material, Cont. Shelf Res., 2005, 25, 1853–1863 CrossRef.
- H. L. Fuchs, A. J. Christman, G. P. Gerbi, E. J. Hunter and F. J. Diez, Directional flow sensing by passively stable larvae, J. Exp. Biol., 2015, 218, 2782–2792 CrossRef PubMed.
- M. Long, B. Moriceau, M. Gallinari, C. Lambert, A. Huvet, J. Raffray and P. Soudant, Interactions between microplastics and phytoplankton aggregates: Impact on their respective fates, Mar. Chem., 2015, 175, 39–46 CrossRef.
- S. E. Jones, C. F. Jago, A. J. Bale, D. Chapman, R. J. M. Howland and J. Jackson, Aggregation and resuspension of suspended particulate matter at a seasonally stratified site in the southern North Sea: physical and biological controls, Cont. Shelf Res., 1998, 18, 1283–1309 CrossRef.
- J. Cross, W. A. M. Nimmo-Smith, R. Torres and P. J. Hosegood, Biological controls on resuspension and the relationship between particle size and the Kolmogorov length scale in a shallow coastal sea, Mar. Geol., 2013, 343, 29–38 CrossRef.
- J. J. M. de Klein, J. T. K. Quik, P. S. Bäuerlein and A. A. Koelmans, Towards validation of the NanoDUFLOW nanoparticle fate model for the river Dommel, The Netherlands, Environ. Sci.: Nano, 2016, 3, 434–441 RSC.
- S. J. Wallace, J. Li, R. L. Nation and B. J. Boyd, Drug release from nanomedicines: selection of appropriate encapsulation and release methodology, Drug Delivery Transl. Res., 2012, 2, 284–292 CrossRef PubMed.
- T. Missana, U. Alonso, N. Albarran, M. García-Gutiérrez and J.-L. Cormenzana, Analysis of colloids erosion from the bentonite barrier of a high level radioactive waste repository and implications in safety assessment, Physics and Chemistry of the Earth Parts A/B/C, 2011, 36, 1607–1615 CrossRef.
- M. Holmboe, S. Wold, M. Jonsson and S. Garcia-Garcia, Effects of γ-irradiation on the stability of colloidal Na+-Montmorillonite dispersions, Appl. Clay Sci., 2009, 43, 86–90 CrossRef.
- R. S. Sahu, K. Bindumadhavan and R.-a. Doong, Boron-doped reduced graphene oxide-based bimetallic Ni/Fe nanohybrids for the rapid dechlorination of trichloroethylene, Environ. Sci.: Nano, 2017, 4, 565–576 RSC.
- M. Blyth, Fluid Mechanics, Personal Comunication, 2015, https://archive.uea.ac.uk/~h007/notes/index.html Search PubMed.
- D. H. Li and J. Ganczarczyk, Fractal geometry of particle aggregates generated in water and wastewater treatment processes, Environ. Sci. Technol., 1989, 23, 1385–1389 CrossRef.
- B. M. Dolgonosov, Kinetics of sedimentation of a coagulating suspension, Theor. Found. Chem. Eng., 2005, 39, 635–642 CrossRef.
- C. Allain, M. Cloitre and F. Parisse, Settling by cluster deposition in aggregating colloidal suspensions, J. Colloid Interface Sci., 1996, 178, 411–416 CrossRef.
- M. C. Sterling, J. S. Bonner, A. N. S. Ernest, C. A. Page and R. L. Autenrieth, Application of fractal flocculation and vertical transport model to aquatic sol–sediment systems, Water Res., 2005, 39, 1818–1830 CrossRef PubMed.
- S. Kumar and D. Ramkrishna, On the solution of population balance equations by discretization—I. A fixed pivot technique, Chem. Eng. Sci., 1996, 51, 1311–1332 CrossRef.
- I. Nopens, D. Beheydt and P. A. Vanrolleghem, Comparison and pitfalls of different discretised solution methods for population balance models: a simulation study, Comput. Chem. Eng., 2005, 29, 367–377 CrossRef.
- A. L. Dale, G. V. Lowry and E. A. Casman, Accurate and fast numerical algorithms for tracking particle size distributions during nanoparticle aggregation and dissolution, Environ. Sci.: Nano, 2017, 4, 89–104 RSC.
- A. Thill, S. Moustier, J. Aziz, M. R. Wiesner and J. Y. Bottero, Flocs restructuring during aggregation: experimental evidence and numerical simulation, J. Colloid Interface Sci., 2001, 243, 171–182 CrossRef.
- S. Veerapaneni and M. R. Wiesner, Hydrodynamics of fractal aggregates with radially varying permeability, J. Colloid Interface Sci., 1996, 177, 45–57 CrossRef PubMed.
- X.-Y. Li and B. E. Logan, Permeability of fractal aggregates, Water Res., 2001, 35, 3373–3380 CrossRef PubMed.
- Y. Tagawa, J. van der Molen, L. van Wijngaarden and C. Sun, Wall forces on a sphere in a rotating liquid-filled cylinder, Phys. Fluids, 2013, 25, 063302 CrossRef.
- R. K. Chakraborti, K. H. Gardner, J. F. Atkinson and J. E. Van Benschoten, Changes in fractal dimension during aggregation, Water Res., 2003, 37, 873–883 CrossRef PubMed.
- G. C. Bushell, Y. D. Yan, D. Woodfield, J. Raper and R. Amal, On techniques for the measurement of the mass fractal dimension of aggregates, Adv. Colloid Interface Sci., 2002, 95, 1–50 CrossRef PubMed.
- A. Abdel-Salam and C. V. Chrysikopoulos, Modeling of colloid and colloid-facilitated contaminant transport in a two-dimensional fracture with spatially variable aperture, Transp. Porous Media, 1995, 20, 197–221 CrossRef.
- S. C. James and C. V. Chrysikopoulos, Effective velocity and effective dispersion coefficient for finite-sized particles flowing in a uniform fracture, J. Colloid Interface Sci., 2003, 263, 288–295 CrossRef PubMed.
- N. H. Pham and D. V. Papavassiliou, Hydrodynamic effects on the aggregation of nanoparticles in porous media, Int. J. Heat Mass Transfer, 2018, 121, 477–487 CrossRef.
- T. Phenrat, H. J. Kim, F. Fagerlund, T. Illangasekare, R. D. Tilton and G. V. Lowry, Particle size distribution, concentration, and magnetic attraction affect transport of polymer-modified Fe0 nanoparticles in sand columns, Environ. Sci. Technol., 2009, 43, 5079–5085 CrossRef PubMed.
- M. Elimelech, J. Gregory and X. Jia, Particle deposition and aggregation: measurement, modelling and simulation, Butterworth-Heinemann, 1998 Search PubMed.
- K. Higashitani, K. Iimura and H. Sanda, Simulation of deformation and breakup of large aggregates in flows of viscous fluids, Chem. Eng. Sci., 2001, 56, 2927–2938 CrossRef.
- D. Risovic and M. Martinis, The role of coagulation and sedimentation mechanisms in the two-component model of sea-particle size distribution, Fizika, 1994, 3, 103–118 Search PubMed.
- T. Phenrat, H.-J. Kim, F. Fagerlund, T. Illangasekare and G. V. Lowry, Empirical correlations to estimate agglomerate size and deposition during injection of a polyelectrolyte-modified Fe0 nanoparticle at high particle concentration in saturated sand, J. Contam. Hydrol., 2010, 118, 152–164 CrossRef PubMed.
- R. I. Jeldres, F. Concha and P. G. Toledo, Population balance modelling of particle flocculation with attention to aggregate restructuring and permeability, Adv. Colloid Interface Sci., 2015, 224, 62–71 CrossRef PubMed.
- Z. Meng, S. M. Hashmi and M. Elimelech, Aggregation rate and fractal dimension of fullerene nanoparticles via simultaneous multiangle static and dynamic light scattering measurement, J. Colloid Interface Sci., 2013, 392, 27–33 CrossRef PubMed.
- A. Praetorius, J. Labille, M. Scheringer, A. Thill, K. Hungerbühler and J.-Y. Bottero, Heteroaggregation of titanium dioxide nanoparticles with model natural colloids under environmentally relevant conditions, Environ. Sci. Technol., 2014, 48, 10690–10698 CrossRef PubMed.
- J. T. K. Quik, I. Velzeboer, M. Wouterse, A. A. Koelmans and D. Van de Meent, Heteroaggregation and sedimentation rates for nanomaterials in natural waters, Water Res., 2014, 48, 269–279 CrossRef PubMed.
- A. Praetorius, R. Arvidsson, S. Molander and M. Scheringer, Facing complexity through informed simplifications: a research agenda for aquatic exposure assessment of nanoparticles, Environ. Sci.: Processes Impacts, 2013, 15, 161–168 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8en00443a |
| This journal is © The Royal Society of Chemistry 2018 |