Effects of calcium on the kinetics of a model disjunctive ligand exchange reaction: implications for dynamic trace metal ion speciation†
Received
6th July 2018
, Accepted 23rd October 2018
First published on 24th October 2018
Abstract
Trace metal ion speciation in natural waters is often under kinetic control due to slow exchange reactions involving multidentate ligands (both natural and anthropogenic) and constituent ions (e.g. calcium). Incomplete understanding of the kinetic behavior (rates, rate laws, and mechanisms) of multidentate ligand exchange reactions hinders prediction of metal ion bioavailability and mobility in these systems. Here, we aim to improve understanding (1) by examining the mechanism by which calcium suppresses ligand exchange rates and (2) by developing conceptual tools for predicting the kinetic behavior in environmental systems. Using capillary electrophoresis, we examined the effect of calcium concentration on the kinetics of a model disjunctive multidentate ligand exchange reaction between nickel(II)-nitrilotriacetate (NiNTA) and trans-1,2-cyclohexylenedinitrilotetraacetate (CDTA) at constant temperature (25 °C) and ionic strength (10 mM). Initial NiCDTA formation rates under varying reactant and calcium concentrations were fit with a single disjunctive ligand exchange kinetic model. While the overall reaction pathway is disjunctive under all conditions studied, the presence of calcium causes a non-linear decrease in reaction rates and alters the overall reaction order with respect to free multidentate ligand concentration. The overall rate law is affected by the relative calcium affinity of exchanging ligands, which controls the balance of product formation and reactant reformation rates from the free metal ion intermediate. The log ratio of these rates is proposed as a metric for determining the appropriate simplified form of the rate law for disjunctive ligand exchange reactions. The implications for in situ ligand lability assays and metal ion bioavailability are discussed.
Environmental significance
Trace metal speciation controls bioavailability and mobility. In natural waters containing multidentate ligands (metallophores, natural organic matter, and synthetic chelating agents) and constituent ions such as calcium, metal speciation can be far from equilibrium. Predicting metal bioavailability and mobility in these systems requires greater understanding of the kinetic behavior (rates, rate laws, and mechanisms) of multidentate ligand exchange reactions. Here, we carefully examine the kinetic behavior of a model disjunctive multidentate ligand exchange reaction in the presence of calcium. Calcium reduces overall rates non-linearly and the relative calcium affinity of exchanging ligands controls the overall reaction order. We discuss implications for designing assays of in situ metal–ligand complex lability and predicting metal ion bioavailability.
|
Introduction
Environmental models that assume equilibrium (e.g. Free Ion Activity Model, Biological Ligand Model) do not accurately predict metal ion mobility and bioavailability when metal ion speciation is controlled by exchange kinetics.1–5 In systems where multidentate ligands (e.g. metallophores, natural organic matter (NOM), ethylenediaminetetraacetate (EDTA)) are present, kinetically controlled speciation is likely even for metal ions that exhibit moderate rates of water exchange (e.g. Ni(II), Co(II), Cu(II)).6–12 Both natural and anthropogenic multidentate ligands are commonly found in natural waters13–16 and form metal complexes that dissociate slowly, contributing to persistent disequilibrium.6,12,17 For example, Xue et al. (2001) found that more than 99.9% of total dissolved nickel was bound by strong ligands in the River Glatt, Switzerland and that nickel speciation responded slowly to inputs from sewage treatment plant effluent and agricultural runoff because of slow exchange kinetics.12 Furthermore, natural waters (seawater, soil porewater and many freshwaters) also frequently contain high concentrations of labile metal ions such as calcium or magnesium. Multidentate ligands rapidly bind the labile metal ions to form complexes that then slowly exchange with more inert metal ions to form thermodynamically favored complexes.17–19 Hering and Morel (1989) observed that when Cu(II) is introduced to a model system containing two ligands (one strong and one weak) pre-equilibrated with calcium, slow displacement of calcium from strong ligand complexes results in formation of Cu(II)-weak ligand complexes that then slowly undergo double (metal- and ligand-) exchange to reach equilibrium.7 Despite documented examples of kinetically-controlled metal ion speciation, there remains a dearth of knowledge about the complete kinetic behavior (rates, rate laws, and mechanisms) of exchange reactions involving multidentate ligands.20
While the kinetics of monodentate ligand exchange are well-understood through the dissociative-interchange-associative (IAD) paradigm (which describes the mechanisms of elementary ligand exchange steps),21 it is much harder to predict the kinetics of multidentate ligand exchange reactions. Multidentate ligand exchange reactions,
where one multidentate ligand, Y, replaces another multidentate ligand, L, proceed through a reaction pathway of many elementary ligand exchange steps. (Note that bound water molecules, ligand protonation and charges are omitted from reaction
(1) for clarity.) Monodentate ligand exchange reactions with metal ions that undergo dissociative or interchange exchange (
e.g. Ni(
II)), follow the Eigen–Wilkins–Tamm mechanism, and rates are proportional to the rates of water exchange of the particular metal ion.
22–24 Rate constants for these reactions can be predicted from the product of the metal ion-specific water exchange rate constant,
kH2O, and estimated equilibrium constants for the outersphere encounter complex between the metal ion and incoming ligand,
KOS.
25–27 Rate constants for complex formation between bidentate ligands and hexaaquanickel(
II) can also be predicted, but, if the ligand is an aminocarboxylate, prediction may require knowledge of the rate constants for chelate ring closing/opening.
24,27 Multidentate ligand exchange reactions, however, are characterized by interactions between the two multidentate ligands that affect the overall order of exchange steps, the reaction pathway.
27,28 Therefore, multidentate ligand exchange for a given metal ion with different multidentate ligands exhibit rates that vary by many orders of magnitude.
27
Multidentate ligand exchange reaction pathways fall on a continuum.28,29 On one end of the continuum, “adjunctive” ligand exchange reactions proceed via direct attack by Y to form a ternary complex, MLY' (the apostrophe (') indicates a partially coordinated multidentate ligand):
| | 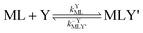 | (2) |
| |  | (3) |
where
kYML is the second-order rate constant for formation of the ternary complex MLY',
k−YMLY' is the first-order rate constant for dissociation of Y from MLY', and
k−LMLY' is the first order rate constant for dissociation of L from MLY' to form MY. If, however, the presence of L in the inner coordination sphere of the metal ion impedes attack by Y, then partial dissociation of the initial complex, ML, is a necessary first step in a “semijunctive” ligand exchange pathway.
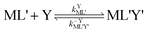
28| | 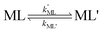 | (4) |
| |  | (5) |
| |  | (6) |
where
k′ML is the first-order rate constant for partial dissociation of ML,
kML' is the first order-rate constant for reformation of ML from ML',
kYML' is the second-order rate constant for formation of the ternary complex ML'Y',
k−YML'Y' is the first-order rate constant for dissociation of Y from ML'Y', and
k−LML'Y' is the first-order rate constant for dissociation of L from ML'Y' to form MY. On the other end of the continuum, “disjunctive” ligand exchange pathways only proceed following complete dissociation of ML because the presence of L in the inner coordination sphere of the metal ion prevents coordination by Y.
| | 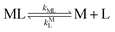 | (7) |
| | 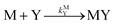 | (8) |
where
kML is the first-order rate constant for dissociation of ML,
kML is the second-order rate constant for formation of ML from free M and free L, and
kMY is the second-order rate constant for formation of MY from free M and free Y. Assuming that reaction intermediates reach steady state rapidly, we can write a generic rate law for the formation of product, MY, for each of the three reaction pathways (see Rate Law Derivations in ESI
†):
Adjunctive rate law
| | 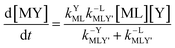 | (9) |
Semijunctive rate law
| | 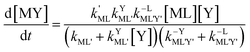 | (10) |
Disjunctive rate law
| | 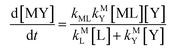 | (11) |
In principle, each reaction pathway can be distinguished experimentally by differences in reaction order with respect to free L and Y.28,29 Here, we focus our attention on the kinetic behavior of disjunctive ligand exchange pathways in the presence of calcium. Numerous environmentally-relevant multidentate ligand exchange reactions have been identified explicitly or implicitly as disjunctive pathways.3,30–35 The early work by Hering and Morel (1989), revealed that calcium significantly lowers multidentate ligand exchange rates. However, they did not explicitly identify the ligand exchange pathway or the effect of calcium concentrations on overall reaction rate laws.7 Indeed, there remain several unanswered questions: Does calcium reduce ligand exchange rates through competitive complexation or by altering the overall reaction pathway? Is the effect of calcium on ligand exchange reaction rates linear? If not, what is the simplest model that can accurately predict ligand exchange rates in the presence of calcium?
Here we aim to (1) improve understanding of multidentate ligand exchange kinetics by examining the mechanism of the effect of calcium on disjunctive ligand exchange kinetics, and (2) develop conceptual tools for predicting the kinetic behavior in environmental systems. To this end, we examine how calcium concentrations affect the kinetic behavior of a model disjunctive ligand exchange reaction between nickel(II)-nitrilotriacetate (NiNTA) and trans-1,2-cyclohexylenedinitrilotetraacetate (CDTA) (multidentate ligand structures are shown in Fig. 1). Ligand exchange reactions were initiated in solutions at fixed temperature (25 °C) and ionic strength (10 mM) over a wide range of pH and reactant concentrations. Reaction kinetics were monitored using capillary electrophoresis with UV visible detection and initial rate data was used to develop a single kinetic model to describe disjunctive ligand exchange in the presence or absence of calcium. We note that the relative calcium affinity of NTA and CDTA controls the form of the overall rate law and propose that this observation is generalizable to any system containing multidentate ligands and constituent ions. Finally, we discuss the implications of our kinetic model on disjunctive ligand exchange rate predictions in environmental systems.
 |
| | Fig. 1 Structures of nitrilotriacetate (NTA) and trans-1,2-cyclohexylenedinitrilotetraacetate (CDTA). | |
Materials and methods
Nomenclature
NiT, NTAT, CDTAT, and CaT represent the total dissolved concentrations of nickel(II) (from now on the oxidation state will be omitted), the initial multidentate ligand NTA, the incoming multidentate ligand CDTA, and calcium, respectively. “Free” multidentate ligand refers to the total concentration of multidentate ligand that is not bound to a metal ion (nickel or calcium) and “free” metal ion refers to the total concentration of metal ion that is not bound by multidentate ligand. The quantity of free multidentate ligand or free metal ion is denoted by a subscript (e.g. NTAfree or Nifree). Note that free multidentate ligand includes all protonated and unprotonated forms of the ligand. Nomenclature for multidentate ligands and their metal complexes follow IUPAC recommendations.36 When referring specifically to the negative log activity of protons, “paH” is used, otherwise “pH” is used to refer to the negative log concentration of protons.
Reagents
All chemicals were reagent grade or higher purity. Nickel(II) chloride hexahydrate, hydrochloric acid (36%), 1,4-diethylpiperazine (DEPP), nitrilotriacetic acid trisodium salt monohydrate (NTA), and trans-1,2-diaminocyclohexane-N,N,N′,N′-tetraacetic acid monohydrate (CDTA) were purchased from Alfa Aesar (Ward Hill, MA, USA). 3-(N-Morpholino)-propane sulfonic acid (MOPS) and 2-(N-morpholino)-ethane sulfonic acid monohydrate (MES) were purchased from Avantor Performance Materials (Center Valley, PA, USA). Sodium acid pyrophosphate was purchased from Spectrum Chemicals (Gardena, CA, USA). Tetradecyl trimethyl ammonium bromide (TTAB) was purchased from Amresco (Solon, OH, USA). Sodium hydroxide was purchased from EMD Millipore (Billerica, MA, USA, USA).
Glassware and polypropylene bottles were pre-soaked in 5 M nitric acid (Fisher Scientific; Hampton, NH, USA) and rinsed with ultra-pure water (18 MΩ cm resistivity) from a Milli-Q water purification system (Millipore, Milford, MA, USA). Stock solutions were prepared from the appropriate mass of reagent, brought to volume with ultrapure water in class A borosilicate glass volumetric flasks, and then stored in polypropylene bottles at 4 °C. Nickel chloride stock solutions were prepared with one equivalent of hydrochloric acid to minimize nickel adsorption to container walls and formation of hydroxo species. Total dissolved nickel concentration in stock solutions was confirmed using flame atomic absorption spectroscopy.
Kinetic analyses by capillary electrophoresis
Ligand exchange reactions were initiated by rapidly mixing two solutions that were each pre-equilibrated for at least 24 hours: solution A containing 100 μM nickel chloride and 105 to 500 μM NTA and solution B containing 105 to 1000 μM CDTA. Both solutions were prepared with identical concentrations of calcium chloride (varied from 0 to 2 mM) and pH buffer (5 mM), and sufficient NaCl to raise the ionic strength to 10 (±1) mM. A series of non-complexing pH buffers were used: DEPP (4.2 < paH < 5.2 and 8.3 < paH < 9.3), MES (5.7 < paH < 6.7), and MOPS (6.6 < paH < 7.6).37 Stock buffer paH was measured using a glass combination microelectrode (Thermo Scientific, Chelmsford, MA, USA) and adjusted with HCl or NaOH to the desired paH. After preparation, each solution was re-measured to confirm paH.
Reaction progress was monitored by periodically analyzing aliquots of the mixed reaction solution using a temperature-controlled P/ACE MDQ (Beckman-Coulter; Brea, CA, USA) capillary electrophoresis instrument with a photodiode array UV detector. The details of the instrumental method used were described previously28 (see Initial Rate Experiments in ESI†). Electrophoretic separations were performed with a background electrolyte (BGE) solution containing 20 mM pyrophosphate (pH 7.1) and 0.4 mM TTAB, an electroosmotic flow modifier. An example absorbance vs. electromigration time plot (electropherogram) is shown in Fig. 2. Consistently, electropherograms at 214 nm yielded both detection and complete separation of NiCDTA from free multidentate ligand and Ca-multidentate ligand complexes. Two pairs of species (Ca(cdta)2− and CDTAfree, Ni(nta)− and Ca(nta)−) co-electromigrate and could not be quantified. Integrated NiCDTA peak areas were normalized by dividing by electromigration times to correct for run-to-run differences in electroosmotic flow rates. NiCDTA peak areas were calibrated with a series of six standard solutions containing fixed CDTAT, CaT, pH buffer and varying NiT. Calibration standards were run every three hours of reaction time to correct for drift in instrument response. Reaction progress was monitored by observing NiCDTA formation over time and initial rates were obtained by applying a linear least squares fit to a minimum of three data points within the first 20% of the reaction (Fig. 3). Only the first 20% of reaction was utilized because longer reaction times result in a greater probability of artifacts due to sample evaporation and day-to-day differences in BGE composition.28 Linear fits to the first 20% of reaction typically had R2 values greater than 0.95. If R2 was less than 0.95, residuals plots were evaluated for evidence of curvature. If curvature was noted, later data points were removed from fit. Standard error in the slope of the fitted line is reported as the uncertainty in initial rate values. Replicate experiments are reported as separate values.
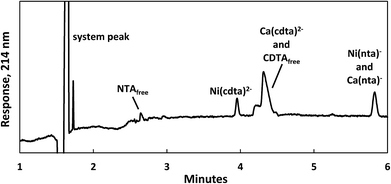 |
| | Fig. 2 Electropherogram illustrating the separation of nickel, calcium and multidentate ligand species 1 day after 200 μM CDTAT was added to a pre-equilibrated solution of 75 μM NTAT and 50 μM NiT. Reaction conditions: 500 μM CaT, 5.0 mM MES (pH 5.5), and sufficient NaCl to fix the ionic strength at 10 mM. Separation conditions – capillary: underivatived fused silica with 75 μm inner diameter, injection: 15 seconds at 0.5 psi, separation voltage: −28 kV, background electrolyte: 20 mM pyrophosphate (pH 7.1) and 0.4 mM TTAB. | |
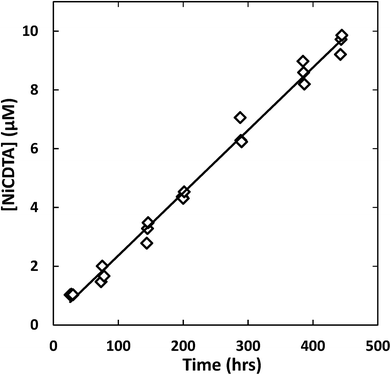 |
| | Fig. 3 Example kinetic data with linear least squares fit (line) to determine the initial rate of reaction. Reaction conditions: 200 μM CDTAT, 50 μM NiT, 250 μM NTAT, 0.5 mM CaT, 5 mM MOPS (pH 7.01), I = 10 mM, 25 °C. Linear fit R2 = 0.979. | |
Equilibrium and rate modeling
The computer program HYDRAQL38 was used to calculate equilibrium concentrations of nickel, calcium, and multidentate ligand species initially present in solutions A, B and in the mixed reaction solution before and after equilibrium is attained. The critically reviewed equilibrium constants39 shown in Table 1 are adjusted for the ionic strength conditions of our experiments (10 mM) using the Davies equation. For input into HYDRAQL, equilibrium constants were adjusted for 0.0 M ionic strength (see Equilibrium Calculations in ESI†). The Davies equation was also used to interconvert between experimentally determined paH values and pH values used as inputs in equilibrium and rate models.
Table 1 Relevant equilibrium constants39 at an ionic strength of 0.01 Ma and 25 °C
| Equation |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
Equation |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
Where necessary, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values were corrected to I = 0.01 M with activity coefficients calculated using the Davies equation, K values were corrected to I = 0.01 M with activity coefficients calculated using the Davies equation, 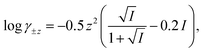 unless otherwise noted.
At I = 1.0 M. Due to the limitations of the Davies equation this value was not converted to I = 0.01 M. unless otherwise noted.
At I = 1.0 M. Due to the limitations of the Davies equation this value was not converted to I = 0.01 M.
|
| H4(nta)+ = H3(nta)0 + H+ |
−0.9 |
Ni2+ + nta3− = Ni(nta)− |
12.30 |
| H3(nta)0 = H2(nta)− + H+ |
−1.9 |
Ni2+ + 2nta3− = Ni(nta)24− |
16.71 |
| H2(nta)− = H(nta)2− + H+ |
−2.78 |
Ni(OH)(nta)2− + H+ = Ni(nta)− |
11.12 |
| H(nta)2− = nta3− + H+ |
−10.05 |
Ca2+ + nta3− = Ca(nta)− |
7.1 |
|
|
|
Ca2+ + 2nta3− = Ca(nta)24− |
9.20 |
| H5(cdta)+ = H4(cdta)0 + H+ |
−1.6b |
|
|
| H4(cdta)0 = H3(cdta)− + H+ |
−2.61 |
Ni2+ + cdta4− = Ni(cdta)2− |
21.3 |
| H3(cdta)− = H2(cdta)2− + H+ |
−3.8 |
Ni(cdta)2− + H+ = NiH(cdta)− |
2.74b |
| H2(cdta)2− = H(cdta)3− + H+ |
−6.46 |
Ca2+ + cdta4− = Ca(cdta)2− |
14.2 |
| H(cdta)3− = cdta4− + H+ |
−12.8 |
|
|
|
|
|
Ni(OH)2(s,am) + 2H+ = Ni2+ + 2H2O |
12.8 |
| Ca(OH)2(s,am) + 2 H+ = Ca2+ + 2H2O |
6.5 |
Ni2+ + H2O = NiOH+ + H+ |
−10.0 |
| Ca2+ + H2O = CaOH+ + H+ |
−12.8 |
Ni2+ + 2H2O = Ni(OH)2 + 2H+ |
−19 |
|
|
|
Ni2+ + 3H2O = Ni(OH)3− + 3H+ |
−30 |
|
|
|
4 Ni2+ + 4H2O = Ni4(OH)44+ + 4H+ |
−27.5 |
Initial reaction rates were modeled using the appropriate rate law equation (see Results and discussion below) with calculated initial reactant concentrations and previously reported rate constants (Table 2) as inputs. Values for the remaining rate constants, were obtained by minimizing squared differences between log initial rates from kinetic experiments and calculated log initial rates. The standard errors in fitted rate constants were obtained using SolverAid, a macro for determining non-linear least squares statistics published with the Macrobundle for Excel software package.40 Initial reactant concentrations in reaction mixtures were calculated assuming rapid dilution upon mixing equal volumes of solutions A and B. Due to slow exchange rates of nickel species, initial reaction concentrations of Ni-NTA species were calculated as half the initial concentrations in solution A. Given fast calcium exchange and protonation/deprotonation kinetics, concentrations of calcium, NTAfree, and CDTAfree in the reaction mixture were calculated assuming that pre-equilibrium is attained before significant NiCDTA formation. The pH range (4 < pH < 8.5) of our experiments was selected so that initial concentrations of Nifree were small and final concentrations of Ni(cdta)2− were nearly 100% of NiT.
Table 2 Rate constants for reactions in the kinetic model
| Reaction |
Rate constant |
Value |
Source (conditions) |
|
No uncertainty reported.
Fitted value is not statistically significant in our model (uncertainty is greater than value).
Estimated from an analogous reaction with edta, an analog of cdta.
|
| Ni(nta)− → Ni2+ + nta3− |
k
NiL
|
7.0 (±0.4) × 10−6 s−1 |
28(I = 0.01 M) |
| Ni2+ + nta3− → Ni(nta)− |
k
NiL
|
3.5 (±0.2) × 106 M−1 s−1, 4.8 × 105 M−1 s−1 |
This work (I = 0.01 M)44(I = 1.25 M)a |
| H+ + Ni(nta)− → Ni2+ + H(nta)2− |
k
HNiL
|
1.93 (±0.08) M−1 s−1 |
28(I = 0.01 M) |
| Ni2+ + H(nta)2− → H+ + Ni(nta)− |
k
NiHL
|
9 M−1 s−1 |
This work (I = 0.01 M)b |
|
|
|
7.5 M−1 s−1 |
44(I = 1.25 M)a |
| Ni2+ + cdta4− → Ni(cdta)2− |
k
NiY
|
6 × 106 M−1 s−1 |
42(I = 0.01 M)a,c |
| Ni2+ + H(cdta)3− → Ni(cdta)2− + H+ |
k
NiHY
|
3.6 (±0.3) × 105 M−1 s−1 |
43(I = 0.1 M) |
Results and discussion
In order to determine the effect of calcium on the kinetics of our model disjunctive reaction between NiNTA and CDTA, we systematically examined the influence of reactant concentrations (CDTAT 52.5 to 500 μM, NTAT 52.5 to 250 μM, CaT 0 to 2 mM) and reaction pH (4 to 8.5) on initial rates of NiCDTA formation (see Initial Rate Experiments in ESI†). First, equilibrium speciation calculations were used to predict the initial and final speciation of our reaction solutions under each set of conditions. Then, the kinetic model derived from our proposed reaction mechanism, with calculated initial reactant concentrations and available rate constants as inputs, was fit to initial rates from kinetic experiments.
Calculated initial and final speciation of reaction solutions
For each set of reaction conditions, initial and final speciation of the reaction solution were calculated in order to determine the extent of reaction. Example calculations of initial and final speciation for a representative reaction solution containing 50 μM NiT, 52.5 μM NTAT, and 200 μM CDTAT are shown as a function of pH in the top and bottom left panels of Fig. 4, respectively. In the initial state, reaction solution at pH 4 contains 47 μM Ni(nta)− (94% of NiT) (Fig. 4, top left panel). The amount of NiT present as Ni(nta)− increases to nearly 50 μM (>99% of NiT) between pH 5 and 8.5. Also in the initial state, the major free CDTA species 4.0 < pH < 6.5 is H2(cdta)2− and H(cdta)3− is the major species 6.5 < pH < 8.5. Concentrations of cdta4− are below 10 nanomolar across the pH range studied. In final equilibrium state, Ni(cdta)2− reaches more than 95% of NiT from pH 4 to 8.5 (Fig. 4, bottom left panel) and free NTA is present almost entirely in the singly protonated form, H(nta)2−.
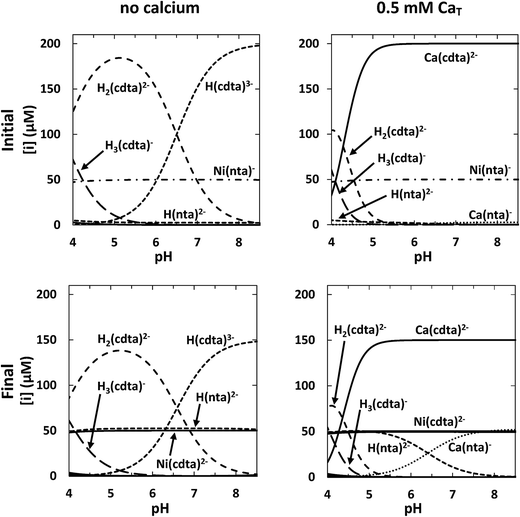 |
| | Fig. 4 Calculated initial (top row) and final (bottom row) concentrations in a representative reaction solution as a function of pH without calcium (left column) and with 0.5 mM CaT (right column). Conditions: 50 μM NiT, 52.5 μM NTAT, 200 μM CDTAT, 10 mM ionic strength, 25 °C. | |
Initial and final speciation calculations for the same conditions as the representative reaction solution above but containing 0.5 mM CaT are shown in the top and bottom right panels of Fig. 4, respectively. Nickel speciation is effectively unchanged by the presence of calcium in both the initial and final equilibrium states of the reaction solution. However, calcium greatly affects free multidentate ligand speciation. Initial speciation calculations indicate that CDTAfree is much lower in the presence of calcium (Fig. 4, top right panel). Approximately 173 μM of CDTA is free (87% of CDTAT) at pH 4. As CDTA binds calcium at higher pHs, CDTAfree decreases to submicromolar concentrations above pH 5.5 and Ca(cdta)2− reaches more than 99.9% of CDTAT. NTAfree is also decreased in the presence of calcium, but not to the same extent as CDTAfree. Excess NTA binds calcium, yielding micromolar concentrations of Ca(nta)− above pH 6. CDTA that is not bound to nickel (Ca(cdta)2− and free CDTA) is distributed similarly in the initial and final equilibrium states (Fig. 4, top and bottom right panels). NTA released in the reaction is present primarily as either H(nta)2− (below pH ∼ 6.5) or bound to calcium as Ca(nta)− (above pH ∼ 6.5).
Effect of pH, CDTAT, NTAT, and CaT on disjunctive ligand exchange kinetics
In the absence of calcium, initial rates of Ni(cdta)2− formation via ligand exchange between NiNTA and CDTA were measured previously.28 These data are included as filled symbols in Fig. 5. Rates are highest at low pH. As pH is increased, rates drop and become constant from pH ∼6 to 8.5 (solid symbols in Fig. 5A). Rates in the absence of calcium are independent of CDTAT and NTAT (solid symbols in Fig. 5B and C).
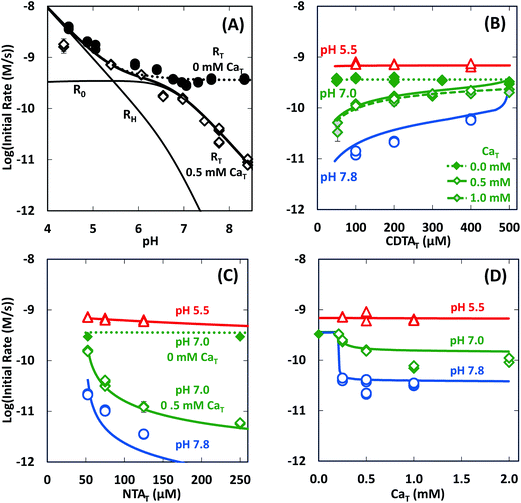 |
| | Fig. 5 Initial rates of ligand exchange as a function of reaction conditions: (A) pH, (B) CDTAT, (C) NTAT, (D) CaT. Reaction conditions: 50 μM NiT, 5.0 mM pH buffer, and sufficient NaCl to fix the ionic strength at 10 mM; in (A): 200 μM CDTAT, 52.5 μM NTAT, 0.0 mM CaT (solid symbols)28 or 0.5 mM CaT (open symbols); in (B): 52.5 μM NTAT, and 0.0 mM CaT (solid symbols),28 0.5 mM CaT (open symbols) or 1.0 mM CaT (shaded symbols); in (C): 200 μM CDTAT, and 0.0 mM CaT (solid symbols)28 or 0.5 mM CaT (open symbols); and in (D): 200 μM CDTAT, 52.5 μM NTAT. Lines indicate modeled rates. | |
In presence of calcium, initial rate dependence is considerably more complicated. Initial rates are again high at low pH, but in contrast to rates in the absence of calcium, rates in the presence of calcium continue to decrease as pH increases (Fig. 5A). At pH 8.3 and in the presence of 0.5 mM CaT, rates are nearly 3 orders of magnitude lower than rates in the absence of calcium. Initial rate dependence on CDTAT (Fig. 5B), NTAT (Fig. 5C), and CaT (Fig. 5D) were evaluated at pH 5.5, 7.0 and 7.8. At pH 5.5, initial rates are nearly independent of CDTAT, NTAT, and CaT. However, in the presence of calcium, initial rates become increasingly sensitive to CDTAT and NTAT at higher pH. At pH 7.0 and 7.8, increasing NTAT decreases initial rates (Fig. 5C). Varying CDTAT or CaT affects initial rates the most when the values of CDTAT and CaT are within 10% of each other (Fig. 5B and D). At pH 7.0 and 7.8, increasing CDTAT increases initial rates sharply as CDTAT approaches CaT (Fig. 5B). At pH 7, rate dependence on CDTAT was evaluated at different CaT (Fig. 5B). As CaT is increased, initial rates have greater sensitivity to changes in CDTAT. Rate dependence on CaT was evaluated with pH (Fig. 5D). At pH 7.0 and 7.8, initial rates are similar when CaT is less than CDTAT (200 μM), but when CaT is in excess of CDTAT, initial rates are lower.
Rate law for ligand exchange in the absence and presence of calcium
It was previously proposed that, in the absence of calcium, ligand exchange between NiNTA and CDTA proceeds via a disjunctive pathway.28,41 The first step of the reaction is complete dissociation of the initial Ni(nta)− complex:| |  | (12) |
where kNiL is the first-order rate constant for dissociation of Ni(nta)−, and kNiL is the second-order rate constant for formation of Ni(nta)− from free Ni2+ and fully deprotonated NTA, nta3−. NiNTA can also dissociate via a acid-catalyzed pathway:| |  | (13) |
where kHNiL is the second-order acid-catalyzed dissociation of Ni(nta)−, and kNiHL is the second-order rate constant for formation of Ni(nta)− from free Ni2+ and singly protonated NTA, H(nta)2−. In the second step of the reaction, free nickel is complexed rapidly and irreversibly by free CDTA:| |  | (14) |
| |  | (15) |
where kNiY and kNiHY are the second-order rate constants for formation of Ni(cdta)2− from free Ni2+ reacting with fully deprotonated and singly protonated CDTA, cdta4− and H(cdta)3−, respectively. Here, we ignore reaction with either H2(cdta)2− or H3(cdta)− because, when both amine Lewis base groups of CDTA are protonated, reaction with Ni2+ is much slower,27 and because reaction pH in our experiments was always greater than pH 4 so that significant concentrations of the more reactive H(cdta)3− and cdta4− species are present.
When calcium is present, there are additional reactions between calcium and free multidentate ligand that must be considered:
| | 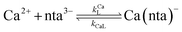 | (16) |
| |  | (17) |
| |  | (18) |
| |  | (19) |
where the rate constants are given above and below the reversible reaction arrows for the corresponding reactions. Calcium complex formation and dissociation rate constants are much greater than those for nickel complexes (see Including Calcium in Rate Calculations in ESI
†).
27 In our reactions, calcium is in large excess of free nickel, therefore, we can assume rapid pre-equilibrium is established between Ca
2+, free NTA, free CDTA, Ca(nta)
−, and Ca(cdta)
2−. The net effect of calcium on the rate of disjunctive ligand exchange between NiNTA and CDTA is to decrease the net initial NTA
free and CDTA
free. By including calcium in equilibrium calculations of initial concentrations of free NTA and free CDTA species, the effect of calcium on overall disjunctive ligand exchange rates can be determined.
Taking together the reactions (12) through (15) and applying a steady-state approximation to [Ni2+] yields rate laws for two parallel pathways leading to Ni(cdta)2− formation (see Derivation of Overall Rate Law for Ni(cdta)2− Formation in ESI†): an uncatalyzed reaction rate, R0, (eqn (20)) and an acid catalyzed reaction rate, RH, (eqn (21)). The overall rate of Ni(cdta)2− formation, RT, (eqn (22)) is the sum of the uncatalyzed and acid catalyzed reaction rates.
| | 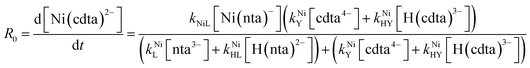 | (20) |
| | 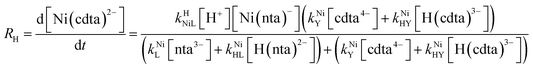 | (21) |
| | 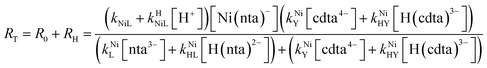 | (22) |
The relative magnitude of the two parenthetical terms in the denominator of the full rate law (eqn (22)) determines the overall rate dependence on free multidentate ligand concentrations. The first term multiplied by the steady state concentration of free nickel, [Ni2+]ss, is equal to the rate of re-formation of the initial NiNTA complex (RML) via the reverse of reactions (12) and (13). Therefore, we can write that RML is proportional to the first term:
| | | RML ∝ kNiL[nta3−] + kNiHL[H(nta)2−] | (23) |
Similarly, we can write that rate of formation of the final NiCDTA complex (RMY) via reactions (14) and (15) is proportional to the second term:
| | | RMY ∝ kNiY[cdta4−] + kNiHY[H(cdta)3−] | (24) |
If RMY is much greater than RML, then the rate law can be simplified considerably to:
| | 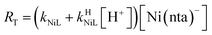 | (25) |
In this limiting case, the overall reaction rate is only limited by the dissociation of the initial complex and is independent of concentrations of either free multidentate ligand. However, if instead RML is much greater than RMY, then the rate law becomes:
| |  | (26) |
where first term in
eqn (26) represents the concentration of free Ni
2+ established by a pre-equilibrium between dissociation of NiNTA and re-association of Ni and free NTA. In this limiting case, overall reaction rates are dependent on concentrations of both free multidentate ligands: free NTA affects the pre-equilibrium concentration of free Ni
2+ and free CDTA affects the rate of NiCDTA formation.
Modeling initial rate data
Boland and Stone (2017) observed that initial rates are independent of CDTAT and NTAT in the absence of calcium and used the simplified rate law in eqn (25) in their kinetic model.28 Given the observed initial rate behavior, it follows that, in the absence of calcium, RMY must be much greater than RML. Here, in the presence of calcium, we observed that initial rates are dependent on CDTAT and NTAT as a function of both pH and CaT. Neither simplified rate law (eqn (25) nor (26)) accurately describes observed initial rate behavior across all conditions. Instead, it is apparent that under some conditions RMY is much greater than RML, but under other conditions the opposite is true.
Assuming that the overall ligand exchange pathway remains disjunctive whether or not calcium is present, the full rate law in eqn (22) was used to model the entire collection of observed initial rates, both in the presence and absence calcium (Fig. 5A–D). Calculated initial concentrations of chemical species (as described above) and previously reported values of kNiL, kHNiL, kNiY, and kNiHY (Table 2) were used as model inputs. Values for the remaining rate constants, kNiL and kNiHL, were obtained by minimizing squared differences between log initial rates from kinetic experiments and those calculated by eqn (22).
Rate constants used as model inputs were obtained as follows. Values for kNiL and kHNiL (NiL dissociation rate constants) were previously determined in reactions with no calcium.28 The value of kNiY was approximated by a previously reported rate constant for the analogous reaction between Ni2+ and EDTA, an analog of CDTA, during metal exchange with Ag(I).42 We deemed that this approximation of kNiY is adequate given that the model was not sufficiently sensitive to the value of kNiY to determine its value through the least squares optimization. We used a value for kNiHY that was reported for the corresponding reaction occurring during metal exchange between Ni(II) and Cu(II) at 0.1 M ionic strength.43
The least squares method yielded fitted values for kNiL and kNiHL of 3.5(±0.2) × 106 M−1 s−1 and 9 M−1 s−1, respectively (Table 2). The value of kNiHL is considered provisional because the uncertainty exceeds its value. However, fitted values of both kNiL and kNiHL are within an order of magnitude of previously reported values for the corresponding reaction during metal exchange between Ni(nta)− and Cu2+ occurring in much higher ionic strength conditions (1.25 M) (Table 2).44
Assuming microscopic reversibility, the ratios of complex formation and dissociation rate constants are equal to the corresponding equilibrium constants for complex formation. The ratio kNiL/kNiL equals 1011.70, which is close to the corresponding equilibrium constant for Ni(nta)− formation (by the reverse of reaction (12)), KML = 1012.30 (Table 1). kNiHL/kHNiL equals 100.68, which is a bit low compared to the expected equilibrium constant for Ni(nta)1− formation (the reverse of reaction (13)), KHML = 102.25, calculated from values in Table 1. However, this difference is unsurprising given the uncertainty in our fitted kNiHL value and the use of the semi-empirical Davies equation to correct equilibrium constants that were obtained at higher ionic strength. Indeed, the literature value of KHML at 0.1 M ionic strength is 100.65,39 which is very close to the value we obtained from the ratio of kNiHL/kHNiL above.
Our attempts to constrain the ratio of formation and dissociation rate constants by corrected equilibrium constants yielded problematic model fits (see Alternative Kinetic Model Fitting in ESI†). By placing this constraint on the model fit, one is weighting the accuracy of corrected equilibrium constants over those of available rate constants. This may be appropriate in other systems. Here, however, we have greater confidence in kNiL and kHNiL, which were measured at the same ionic strength and under similar conditions, than the ionic-strength-corrected equilibrium constants, KML and KHML.
Rate constant values in our model are consistent with expected values for the proposed disjunctive ligand exchange pathway. As noted above, the fitted values of kNiL and kNiHL are close to previously reported values (Table 2). The ratio of kNiL and kNiHL is quite large (∼105) indicating that NiL formation from Ni2+ and H(nta)2− is impeded by protonation of the NTA amine. The large ratio cannot be explained by differences in electrostatic attraction between Ni2+ and NTA species nor the relative abundance of NTA species, which is already accounted for in the rate law. Rather, it suggests that H(nta)2− must undergo an unfavorable and rate-limiting proton transfer from the amine to a carboxylate group before chelating Ni2+.27 Additionally, we confirm that at the pH conditions of our experiments (pH 4–8.5), the most reactive free CDTA species is H(cdta)3−. Although kNiY is large, low concentrations of cdta4− results in minimal contribution (less than 0.1%) to the overall rate except under conditions of very low CaT, where the contribution to total rate is still less than 10%.
Given the uncertainties involved in fitting experimental data using rate and equilibrium constants from multiple sources under various conditions, it is notable how closely our kinetic model agrees with observed rates at all conditions examined, including previously reported initial rates in the absence of calcium28 (Fig. 5A–D). The model deviates somewhat from observed rates at pH 7.8 (Fig. 5), where rates are particularly sensitive to small differences in reaction pH. The model agreement is strong evidence that ligand exchange between NiNTA and CDTA occurs via a disjunctive pathway whether calcium is present or not and that rates can be best approximated by the full rate law, eqn (22). In disjunctive ligand exchange reactions, complete dissociation of the initial complex is the rate-determining step. Adding calcium to our system did not affect this step but had a large influence on overall reaction rates. This is because a reversible process forms Ni2+, the key reaction intermediate. Competition between free NTA and CDTA for Ni2+ results in differing magnitudes of RML and RMY and determines the form of overall rate law. Adding calcium introduces another dimension of competition between NTA and CDTA as calcium decreases free multidentate ligand concentrations. The reaction scheme is summarized in Fig. 6.
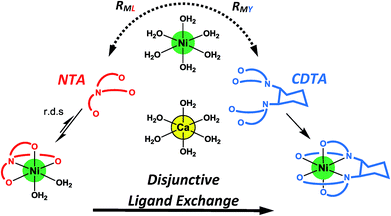 |
| | Fig. 6 Reaction scheme for disjunctive ligand exchange between NiNTA and CDTA in the presence of calcium. | |
Predicting kinetic behavior of disjunctive ligand exchange reactions
Recall that one of our objectives is to develop conceptual tools to predict the kinetic behavior of ligand exchange reactions. Our results highlight that for disjunctive ligand exchange reactions differences in reaction order with respect to free L and Y are due to the relative magnitude of rates of MY formation (RMY) and ML re-formation (RML). One can generalize eqn (23) and (24), respectively,| | 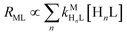 | (27) |
| | 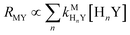 | (28) |
where HnL is the n protonation level of free L, HnY is the n protonation level of free Y, and 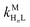 and
and 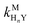 are the second-order complex formation rate constants from reaction between free metal ion and the corresponding free multidentate ligand species. The ratio of RMY and RML can be used to elucidate the cause of differences in reaction order. Specifically, the logarithm of RMY/RML serves as a convenient metric:
are the second-order complex formation rate constants from reaction between free metal ion and the corresponding free multidentate ligand species. The ratio of RMY and RML can be used to elucidate the cause of differences in reaction order. Specifically, the logarithm of RMY/RML serves as a convenient metric:| | 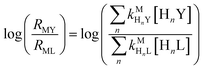 | (29) |
or written in terms of total free multidentate ligand concentrations (Yfree and Lfree):| | 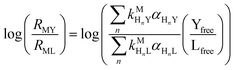 | (30) |
where αHnY and αHnL are the fraction of each protonated multidentate ligand species. A log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML value greater than 1 indicates that MY formation is much faster than ML re-formation. Rates are independent of free multidentate ligand concentrations and controlled solely by the rate of ML dissociation (i.e. rate law has the simplified form of eqn (25)). A log
RMY/RML value greater than 1 indicates that MY formation is much faster than ML re-formation. Rates are independent of free multidentate ligand concentrations and controlled solely by the rate of ML dissociation (i.e. rate law has the simplified form of eqn (25)). A log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML value less than −1 indicates that ML re-formation is much faster than MY formation. In this case, rates are controlled by reaction between pre-equilibrium concentrations of free nickel and free Y, and, therefore, are dependent on both free multidentate ligand concentrations (i.e. rate law has the simplified form of eqn (26)). log
RMY/RML value less than −1 indicates that ML re-formation is much faster than MY formation. In this case, rates are controlled by reaction between pre-equilibrium concentrations of free nickel and free Y, and, therefore, are dependent on both free multidentate ligand concentrations (i.e. rate law has the simplified form of eqn (26)). log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML values between 1 and −1 indicate that MY formation and ML re-formation occur at comparable rates and the overall reaction order with respect to L and Y is mixed (i.e. the full rate law, eqn (22), must be used).
RMY/RML values between 1 and −1 indicate that MY formation and ML re-formation occur at comparable rates and the overall reaction order with respect to L and Y is mixed (i.e. the full rate law, eqn (22), must be used).
We determined log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML values at the same conditions of our experiments using rate constants from Table 2 and calculated free multidentate ligand concentrations (Fig. 7). Three kinetic trends are revealed. First, adding calcium suppresses RMY more than RML, especially at higher pH (Fig. 7A). As discussed in calculated initial and final speciation of reaction solutions above, equilibrium calculations (Fig. 4) indicate that calcium lowers CDTAfree more than NTAfree. Because CDTA has a higher calcium affinity than NTA, adding calcium causes rates of NiNTA re-formation to become competitive with rates of NiCDTA formation. At pH greater than 7.8, adding calcium decreases log
RMY/RML values at the same conditions of our experiments using rate constants from Table 2 and calculated free multidentate ligand concentrations (Fig. 7). Three kinetic trends are revealed. First, adding calcium suppresses RMY more than RML, especially at higher pH (Fig. 7A). As discussed in calculated initial and final speciation of reaction solutions above, equilibrium calculations (Fig. 4) indicate that calcium lowers CDTAfree more than NTAfree. Because CDTA has a higher calcium affinity than NTA, adding calcium causes rates of NiNTA re-formation to become competitive with rates of NiCDTA formation. At pH greater than 7.8, adding calcium decreases log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML below −1 (Fig. 7A), and overall rates are dependent on free multidentate ligand concentrations (Fig. 5B and C). At low pH, however, log
RMY/RML below −1 (Fig. 7A), and overall rates are dependent on free multidentate ligand concentrations (Fig. 5B and C). At low pH, however, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML is greater than 1 even when calcium is added (Fig. 7A and D) because protonation of CDTA competes with calcium complexation (Fig. 4). Second, in the presence of calcium, decreasing CDTAT or increasing NTAT lowers log
RMY/RML is greater than 1 even when calcium is added (Fig. 7A and D) because protonation of CDTA competes with calcium complexation (Fig. 4). Second, in the presence of calcium, decreasing CDTAT or increasing NTAT lowers log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML (Fig. 7B and C). As log
RMY/RML (Fig. 7B and C). As log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML decreases, overall reaction rates decrease and become more sensitive to total multidentate ligand concentrations. However, because the relationship between total multidentate ligand and free multidentate ligand concentrations is non-linear in the presence of calcium, the relationship between total multidentate ligand concentrations and RMY/RML is not proportional. Third, when CaT exceeds CDTAT, RMY decreases precipitously as does log
RMY/RML decreases, overall reaction rates decrease and become more sensitive to total multidentate ligand concentrations. However, because the relationship between total multidentate ligand and free multidentate ligand concentrations is non-linear in the presence of calcium, the relationship between total multidentate ligand concentrations and RMY/RML is not proportional. Third, when CaT exceeds CDTAT, RMY decreases precipitously as does log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML (Fig. 7D). This corresponds to greater rate dependence on free multidentate ligand concentrations (Fig. 5B) and a sharp decrease in overall rates (Fig. 5D). Note that the corollary is also true: when CDTAT exceeds CaT, log
RMY/RML (Fig. 7D). This corresponds to greater rate dependence on free multidentate ligand concentrations (Fig. 5B) and a sharp decrease in overall rates (Fig. 5D). Note that the corollary is also true: when CDTAT exceeds CaT, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML increases sharply (Fig. 7B).
RMY/RML increases sharply (Fig. 7B).
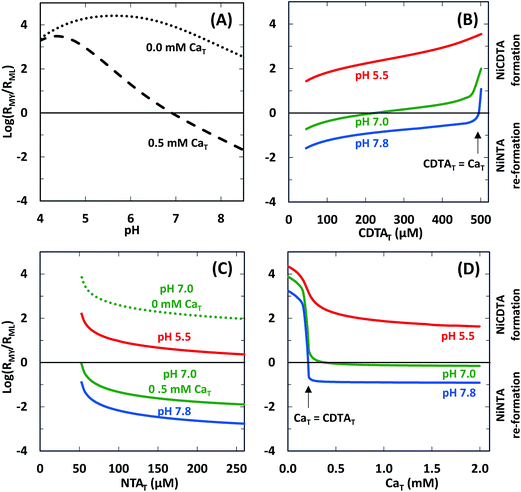 |
| | Fig. 7 Log ratio of the rate of NiCDTA formation (RMY) to the rate of NiNTA re-formation (RML) as a function of reaction conditions: (A) pH, (B) CDTAT, (C) NTAT, (D) CaT. Unless otherwise indicated, reaction conditions are 200 μM CDTAT, 50 μM NiT, 52.5 μM NTAT, 0.5 mM CaT, 5.0 mM pH buffer, and sufficient NaCl to fix the ionic strength at 10 mM. | |
As demonstrated above, trends in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML can be useful for predicting kinetic behavior of disjunctive ligand exchange reactions and determining which simplified form of the rate law applies. We note that RMY/RML depends on three factors: (1) the ratio of free multidentate ligand concentrations, (2) the protonation of free multidentate ligand, and (3) rate constants for complex formation. As we consider the application of this metric to disjunctive ligand exchange reactions more broadly, let us discuss each of these three factors in detail.
RMY/RML can be useful for predicting kinetic behavior of disjunctive ligand exchange reactions and determining which simplified form of the rate law applies. We note that RMY/RML depends on three factors: (1) the ratio of free multidentate ligand concentrations, (2) the protonation of free multidentate ligand, and (3) rate constants for complex formation. As we consider the application of this metric to disjunctive ligand exchange reactions more broadly, let us discuss each of these three factors in detail.
(1) The ratio of free multidentate ligand concentrations.
In most kinetic studies of disjunctive ligand exchange reactions, total concentration of one multidentate ligand is set in excess of the other and it is assumed that one of the limiting rate laws (eqn (25) or (26)) applies.12,29,45–47 This is equivalent to assuming that log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML is much greater than 1 or much less than −1. However, setting total multidentate ligand concentration in excess does not necessarily ensure that the free multidentate ligand concentration is in excess, especially if calcium or other competing metal ions are present. In most of our experiments, we set CDTAT in excess of NTAT, but, because CDTA has a higher calcium affinity than NTA, NTAfree is often greater than CDTAfree. The disparity between total and free multidentate ligand concentrations is likely to hold for most natural waters. Where calcium is abundant, differences in calcium affinity will greatly affect ratios of free multidentate ligand concentrations. In contrast to our model reaction system, one can imagine a pair of multidentate ligands where the initial multidentate ligand L has a much greater affinity for calcium than the incoming multidentate ligand Y. In such a scenario, increasing LT would not decrease log
RMY/RML is much greater than 1 or much less than −1. However, setting total multidentate ligand concentration in excess does not necessarily ensure that the free multidentate ligand concentration is in excess, especially if calcium or other competing metal ions are present. In most of our experiments, we set CDTAT in excess of NTAT, but, because CDTA has a higher calcium affinity than NTA, NTAfree is often greater than CDTAfree. The disparity between total and free multidentate ligand concentrations is likely to hold for most natural waters. Where calcium is abundant, differences in calcium affinity will greatly affect ratios of free multidentate ligand concentrations. In contrast to our model reaction system, one can imagine a pair of multidentate ligands where the initial multidentate ligand L has a much greater affinity for calcium than the incoming multidentate ligand Y. In such a scenario, increasing LT would not decrease log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML significantly until LT and not YT is in excess of CaT. Therefore, when calcium is present, one must evaluate the relative calcium affinity of every multidentate ligand pair undergoing disjunctive ligand exchange before simplifying the rate law. Furthermore, because of the interdependence of proton and calcium equilibria, evaluating relative calcium affinity is not as simple as comparing equilibrium constants for formation of CaL and CaY. In systems where direct measurement of free multidentate ligand concentrations is not possible, one will have to rely on equilibrium calculations based on estimates of free multidentate ligand species and their labile complexes initially present in the system.
RMY/RML significantly until LT and not YT is in excess of CaT. Therefore, when calcium is present, one must evaluate the relative calcium affinity of every multidentate ligand pair undergoing disjunctive ligand exchange before simplifying the rate law. Furthermore, because of the interdependence of proton and calcium equilibria, evaluating relative calcium affinity is not as simple as comparing equilibrium constants for formation of CaL and CaY. In systems where direct measurement of free multidentate ligand concentrations is not possible, one will have to rely on equilibrium calculations based on estimates of free multidentate ligand species and their labile complexes initially present in the system.
(2) Protonation of free multidentate ligand.
Multidentate ligand protonation level affects (a) the fraction of free multidentate ligand that is available to participate in ligand exchange and (b) the magnitude of the corresponding complex formation rate constants. In general, the higher the protonation level, the lower the rate constant. In our experiments, NTA and CDTA have similar Lewis base groups (amines and carboxylic acids), albeit in different abundance. At a given pH, it is likely that the similar Lewis base groups will be protonated or deprotonated. In a case where L and Y have vastly different Lewis base groups, the interplay between the distribution of reactive free multidentate ligand species and total free multidentate ligand concentrations could result in more changes in reaction order with respect to L and Y as a function of pH.
(3) Rate constants for complex formation.
Monodentate complex formation rate constants, where water is the leaving ligand, can be estimated with reasonable accuracy according to the Eigen–Wilkins–Tamm mechanism as described in the Introduction. Consistent with these estimates, monodentate complex formation rate constants for nickel are essentially independent of the incoming ligand identity (apart from its charge).27 The ratio of two monodentate ligand complex formation constants is mostly determined by the difference in ligand charge and its effect on outersphere complex formation. Multidentate complex formation rate constants, however, can be affected by additional phenomena including slow chelation, slow proton transfer, and steric effects.27 As a result, for a given metal ion, complex formation rate constants with two similarly charged multidentate ligands may differ by several orders of magnitude and in ways that cannot yet be readily predicted.20,27 The estimated complex formation rate constant between Ni2+ and an incoming ligand with a −2 charge is 6.5 × 105 M−1 s−1 at 0.01 M ionic strength (using a kH2O for hexaaquo nickel(II) of 3.0 × 104 s−1 and estimates of KOS48 assuming an outersphere encounter distance of 8.5 Å (ref. 49)). However, the experimentally determined rate constant for complex formation between Ni2+ and iminodiacetate (ida2−) is 8.8 × 104 M−1 s−1 (at ionic strength 0.3 M)49 and between Ni2+ and H(nta)2− is 9 M−1 s−1 (0.01 M ionic strength, Table 2), differing from the estimate by a factor of 7 and >105, respectively. The large discrepancy between estimated and actual formation rate constants is certainly due to differences in the location of rate determining step that are not considered in a simplistic approach to the Eigen–Wilkins–Tamm mechanism and precludes a priori estimates for multidentate ligand complexes. Particularly relevant here is that ratios of multidentate ligand complex formation rate constants could differ from estimates even more, posing a barrier to adequate prediction of multidentate ligand exchange kinetics. Identifying structure–reactivity relationships for multidentate ligand complex formation rate constants, therefore, is necessary to close this knowledge gap.
Calcium affinity and analyses of in situ metal–ligand complex lability
Differences in calcium affinity of natural and synthetic multidentate ligands may have implications for the choice of ligand probes for analyses of in situ metal–ligand complex lability. On one hand, the selectivity of many natural siderophores for Fe(III) in the calcium-rich environments is enhanced by their relatively low affinity for calcium.50 Hydroxamate siderophores like desferrioxamine B have relatively low calcium affinity,51 as do the mugineic acid family of phytosiderophores.52–54 On the other hand, some siderophores have high calcium affinity. For example, rhizoferrin, a hydroxycarboxylate type siderophore excreted by the fungus Rhizopus arrhizus, has a relatively high affinity for calcium,55,56 which is why it is suspected that calcium may impede rates of iron acquisition by rhizoferrin.54 The biological receptor responsible for trace metal ion uptake is often assumed to be the same one that is responsible for calcium uptake and has a large effective calcium affinity.57,58 It is well known that synthetic aminocarboxylate multidentate ligands (e.g. EDTA, CDTA, many chelating resins), have particularly high calcium affinity.50,59 Depending on the application, kinetic studies that employ aminocarboxylates as surrogate siderophores may give rates that are unrealistically sensitive to calcium.45 Both diffusive gradients in thin films (DGT) analysis and competitive ligand exchange (CLE or CLEM) analyses typically employ synthetic aminocarboxylates in the role of incoming multidentate ligand Y (chelating resin and probe ligands, respectively). The competitive effects of constituent ions on these methods has been acknowledged.18,60,61 However, interpretations of DGT and CLE results often assume that metal ion capture occurs by disjunctive exchange with in situ complexes (ML) and that because YT is set much greater than LT, rates are independent of resin/probe ligand identity and loading.10,62,63 First, it is likely that metal ion capture by these techniques is not exclusively disjunctive and the ligand exchange pathway depends on the identity of both the in situ ligand (L) and the resin/probe ligand (Y).12,28,29 Second, even if metal ion capture occurs via a disjunctive pathway, the high calcium affinity of aminocarboxylates may be problematic. Even if one sets YT ≫ LT, Yfree may be suppressed by calcium binding so that RML ≫ RMY and ligand exchange rates depend on Y loading/concentration (eqn (26)). Indeed, if this is the case, rates of metal ion capture may be highly dependent on the incoming ligand (Y) identity.28 Further work is needed to evaluate the constituent-ion sensitivity of assays that employ synthetic aminocarboxylates to measure in situ metal–ligand complex lability.
Conclusions
Natural waters are multicomponent systems, frequently containing multidentate ligands and constituent ions like calcium that can contribute to kinetically controlled trace metal speciation. As we develop a systematic understanding of how multidentate ligand exchange kinetics affects dynamic metal ion speciation, it is important to identify conditions where simplifying assumptions may not be appropriate. Here, we provide a clear and unambiguous example of disjunctive ligand exchange and examine the effect of calcium on kinetic behavior. Our results highlight several lessons about kinetic processes that are relevant: (1) because of the complexity of reaction pathways, Eigen–Wilkins–Tamm mechanism is not suited for describing overall multidentate ligand exchange reaction rates. (2) One cannot assume that ratio of free multidentate ligand concentrations scales linearly with ratio of total ligand concentrations because of differences in protonation and competition from constituent ions. (3) For reactions with reversible steps, the slow rate-determining step is not necessarily the only step that controls overall kinetic behavior.
In natural waters, competition by calcium in exchange reactions cannot be ignored. For disjunctive ligand exchange involving relatively inert metals like nickel, formation of calcium–ligand complexes is comparatively fast and can be assumed to be in a pre-equilibrium state. Our results indicate that the effect of calcium on disjunctive ligand exchange rates is non-linear and a function of the relative calcium affinity of exchanging ligands. Competition by calcium for available free multidentate ligand precludes rate law assumptions until free multidentate ligand concentrations have been measured or calculated.
Disjunctive ligand exchange reactions are particularly relevant in systems where free metal ion activities are low and metal ion uptake is limited by dissociation of strong ligand complexes. For disjunctive ligand exchange pathways, the free metal ion is the key reaction intermediate and processes affecting its steady-state concentration significantly affect overall kinetic behavior. This both affirms and complicates models that assume that free metal ion activity mediates bioavailability. The significance of free metal ion is affirmed because any process that influences free metal ion concentration affects overall rates of metal uptake. However, because free metal ion concentrations are at steady state, metal uptake is determined by the competitive rates of all metal–ligand complex dissociation/formation processes. The likelihood of competition undermines the frequent assumption (often made with an appeal to the Eigen–Wilkins–Tamm mechanism) that kinetically-controlled uptake rates are limited only by rates of dissociation of in situ strong complexes. Rather, the rate of re-formation of these complexes may be competitive with complex formation with the biological ligand (RML ≈ RMY), yielding metal uptake rates that exhibit complicated dependence on both free multidentate ligand concentrations. Competition by constituent ions like calcium are particularly relevant to predictions in natural waters. It is for this reason that more mechanistic studies of multidentate ligand exchange reactions are needed. Developing conceptual tools specifically informed by multidentate ligand exchange kinetics will improve predictions of dynamic metal ion speciation.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was possible due to generous support from Whitman College and Lewis B. Perry Summer Research Awards for Laura T. Rea and Yi Xu.
References
- R. Terzano, S. Cesco and T. Mimmo, Dynamics, thermodynamics and kinetics of exudates: crucial issues in understanding rhizosphere processes, Plant Soil, 2014, 386, 399–406 CrossRef
 .
.
- S. Jansen, R. Blust and H. P. van Leeuwen, Metal speciation dynamics and bioavailability: Zn(II) and Cd(II) uptake by mussel (Mytilus edulis) and carp (Cyprinus carpio), Environ. Sci. Technol., 2002, 36, 2164–2170 CrossRef CAS
 .
.
- C. Zhao, P. G. C. Campbell and K. J. Wilkinson, When are metal complexes bioavailable?, Environ. Chem., 2016, 13, 425–433 CrossRef CAS
 .
.
- R. J. M. Hudson, Which aqueous species control the rates of trace metal uptake by aquatic biota? Observations and predictions of non-equilibrium effects, Sci. Total Environ., 1998, 219, 95–115 CrossRef CAS
 .
.
- V. I. Slaveykova and K. J. Wilkinson, Predicting the Bioavailability of Metals and Metal Complexes: Critical Review of the Biotic Ligand Model, Environ. Chem., 2005, 2, 9–24 CrossRef CAS
 .
.
- B. Raspor, H. W. Nürnberg, P. Valenta and M. Branica, Kinetics and mechanism of trace metal chelation in sea water, J. Electroanal. Chem. Interfacial Electrochem., 1980, 115, 293–308 CrossRef CAS
 .
.
- J. G. Hering and F. M. M. Morel, Slow coordination reactions in seawater, Geochim. Cosmochim. Acta, 1989, 53, 611–618 CrossRef CAS
 .
.
- H. Xue, L. Sigg and F. G. Kari, Speciation of EDTA in natural waters: exchange kinetics of Fe-EDTA in river water, Environ. Sci. Technol., 1995, 29, 59–68 CrossRef CAS PubMed
 .
.
- D. L. Sedlak, J. T. Phinney and W. W. Bedsworth, Strongly complexed Cu and Ni in wastewater effluents and surface runoff, Environ. Sci. Technol., 1997, 31, 3010–3016 CrossRef CAS
 .
.
- R. Mandal, A. L. R. Sekaly, J. Murimboh, N. M. Hassan, C. L. Chakrabarti, M. H. Back, D. C. Grégoire and W. H. Schroeder, Effect of the competition of copper and cobalt on the lability of Ni(II)-organic ligand complexes. Part I. In model solutions containing Ni(II) and a well-characterized fulvic acid, Anal. Chim. Acta, 1999, 395, 309–322 CrossRef CAS
 .
.
- M. Shenker, Y. Hadar and Y. Chen, Kinetics of Iron Complexing and Metal Exchange in Solutions by Rhizoferrin, A Fungal Siderophore, Soil Sci. Soc. Am. J., 1999, 63, 1681–1687 CrossRef CAS
 .
.
- H. Xue, S. Jansen, A. Prasch and L. Sigg, Nickel speciation and complexation kinetics in freshwater by ligand exchange and DPCSV, Environ. Sci. Technol., 2001, 35, 539–546 CrossRef CAS
 .
.
- M. Bucheli-Witschel and T. Egli, Environmental fate and microbial degradation of aminopolycarboxylic acids, FEMS Microbiol. Rev., 2001, 25, 69–106 CrossRef CAS PubMed
 .
.
-
B. Nowack and J. M. VanBriesen, in Biogeochemistry of Chelating Agents, ed. B. Nowack and J. VanBriesen, ACS Publications, 2005, vol. 910, pp. 1–18 Search PubMed
 .
.
- K. Turpin-Nagel and T. M. Vadas, Controls on metal exposure to aquatic organisms in urban streams, Environmental Science: Processes & Environ. Sci.: Processes Impacts, 2016, 18, 956–967 Search PubMed
 .
.
- R. M. Boiteau, J. B. Shaw, L. Pasa-Tolic, D. W. Koppenaal and J. K. Jansson, Micronutrient metal speciation is controlled by competitive organic chelation in grassland soils, Soil Biol. Biochem., 2018, 120, 283–291 CrossRef CAS
 .
.
- Y. Louis, C. Garnier, V. Lenoble, S. Mounier, N. Cukrov, D. Omanović and I. Pižeta, Kinetic and equilibrium studies of copper-dissolved organic matter complexation in water column of the stratified Krka River estuary (Croatia), Mar. Chem., 2009, 114, 110–119 CrossRef CAS
 .
.
- M. Fujii, A. L. Rose, T. D. Waite and T. Omura, Effect of divalent cations on the kinetics of Fe(III) complexation by organic ligands in natural waters, Geochim. Cosmochim. Acta, 2008, 72, 1335–1349 CrossRef CAS
 .
.
- J. G. Hering and F. M. M. Morel, Kinetics of trace metal complexation: role of alkaline-earth metals, Environ. Sci. Technol., 1988, 22, 1469–1478 CrossRef CAS PubMed
 .
.
- W. H. Casey, Ligand- and oxygen-isotope-exchange pathways of geochemical interest, Environ. Chem., 2015, 12, 1–19 CrossRef CAS
 .
.
-
C. H. Langford and H. B. Gray, Ligand Substitution Processes, W. A. Benjamin, Inc., New York, NY, 1966 Search PubMed
 .
.
- M. Eigen and K. Tamm, Schallabsorption in Elektrolytösungen als Folge chemischer Relaxation. I. Relaxationstheorie der mehrstufigen Dissoziation, Zeitschrift für Elektrochemie, 1962, 66, 93–121 CAS
 .
.
-
M. Eigen and R. G. Wilkins, in Mechanisms of Inorganic Reactions, ed. J. Kleinberg, R. K. Murmann, R. T. M. Fraser and J. Bauman, American Chemical Society, Washington, DC, 1965, vol. 49, pp. 55–80 Search PubMed
 .
.
- R. G. Wilkins, Mechanisms of ligand replacement in octahedral nickel(II) complexes, Acc. Chem. Res., 1970, 3, 408–416 CrossRef CAS
 .
.
- R. M. Fuoss, Ionic Association. III. The Equilibrium between Ion Pairs and Free Ions, J. Am. Chem. Soc., 1958, 80, 5059–5061 CrossRef CAS
 .
.
-
R. G. Wilkins, Kinetics and mechanism of reactions of transition metal complexes, VCH, New York, NY, 2nd edn, 1991 Search PubMed
 .
.
-
D. W. Margerum, G. R. Cayley, D. C. Weatherburn and G. K. Pagenkopf, in Coordination Chemistry, ed. A. E. Martell, American Chemical Society, Washington, DC, 1978, vol. 2, pp. 1–220 Search PubMed
 .
.
- N. E. Boland and A. T. Stone, Rates of nickel(II) capture from complexes with NTA, EDDA, and related tetradentate chelating agents by the hexadentate chelating agents EDTA and CDTA: evidence of a ‘semijunctive' ligand exchange pathway, Geochim. Cosmochim. Acta, 2017, 212, 176–195 CrossRef CAS
 .
.
- J. G. Hering and F. M. M. Morel, Kinetics of trace metal complexation: ligand-exchange reactions, Environ. Sci. Technol., 1990, 24, 242–252 CrossRef CAS
 .
.
- M. Shuman, Dissociation Pathways and Species Distribution of Aluminum Bound to an Aquatic Fulvic Acid, Environ. Sci. Technol., 1992, 26, 593–598 CrossRef CAS
 .
.
- H. P. Van Leeuwen, Metal speciation dynamics and bioavailability: Inert and labile complexes, Environ. Sci. Technol., 1999, 33, 3743–3748 CrossRef CAS
 .
.
- A. L. R. Sekaly, J. Murimboh, N. M. Hassan, R. Mandal, M. E. B. Younes, C. L. Chakrabarti, M. H. Back and D. C. Grégoire, Kinetic speciation of Co(II), Ni(II), Cu(II), and Zn(II) in model solutions and freshwaters: lability and the d electron configuration, Environ. Sci. Technol., 2003, 37, 68–74 CrossRef CAS
 .
.
- M.-L. Pesch, M. Hoffmann, I. Christl, S. M. Kraemer and R. Kretzschmar, Competitive ligand exchange between Cu-humic acid complexes and methanobactin, Geobiology, 2013, 11, 44–54 CrossRef CAS
 .
.
- Z. Shi, P. Wang, L. Peng, Z. Lin and Z. Dang, Kinetics of Heavy Metal Dissociation from Natural Organic Matter: Roles of the Carboxylic and Phenolic Sites, Environ. Sci. Technol., 2016, 50, 10476–10484 CrossRef CAS
 .
.
- K. W. Warnken, W. Davison, H. Zhang, J. Galceran and J. Puy, In situ measurements of metal complex exchange kinetics in freshwater, Environ. Sci. Technol., 2007, 41, 3179–3185 CrossRef CAS
 .
.
-
Nomenclature of Inorganic Chemistry. IUPAC Recommendations 2005, ed., N. G. Connelly, T. Damhus, R. M. Hartshorn and A. T. Hutton, The Royal Society of Chemistry, Cambridge, UK, 2005 Search PubMed
 .
.
- Q. Yu, A. Kandegedara, Y. Xu and D. B. Rorabacher, Avoiding interferences from Good's buffers: a contiguous series of noncomplexing tertiary amine buffers covering the entire range of pH 3–11, Anal. Biochem., 1997, 253, 50–56 CrossRef CAS PubMed
 .
.
-
C. Papelis, K. F. Hayes and J. O. Leckie, HYDRAQL. Technical Report 306, Stanford, CA, 1988 Search PubMed
 .
.
-
A. E. Martell, R. M. Smith and R. J. Motekaitis, NIST Critically Selected Stability Constants of Metal Complexes Database, version 8.0, National Institute of Science and Technology, Gaithersburg, MD, USA, 2004 Search PubMed
 .
.
-
R. de Levie, MacroBundle for Excel, version 12, Brunswick, ME, USA, 2012 Search PubMed
 .
.
- M. Kimura, The kinetics of the ligand-substitution reactions of nitrilotriacetatoniccolate(II) complexes with trans-1,2-cyclohexanediaminetetraacetate ions, Bull. Chem. Soc. Jpn., 1969, 42, 2841–2843 CrossRef CAS
 .
.
- G. A. Rechnitz and Z. Lin, Reaction rate measurements with
cation-sensitive glass electrodes. Kinetic study of the exchange reaction between silver(I)-EDTA and nickel(II), Anal. Chem., 1967, 39, 1406–1411 CrossRef CAS
 .
.
- D. W. Margerum, P. J. Menardi and D. L. Janes, Multidentate ligand kinetics. X. Exchange reactions of metal(II)-cyclohexylenediaminetetraacetate complexes, Inorg. Chem., 1967, 6, 283–289 CrossRef CAS
 .
.
- T. J. Bydalek and M. L. Blomster, Kinetics of the substitution reaction between copper(II) and nitrilotracetatonickelate(II), Inorg. Chem., 1964, 3, 667–671 CrossRef CAS
 .
.
-
J. G. Hering and F. M. M. Morel, in Aquatic Chemical Kinetics, ed. W. Stumm, John Wiley & Sons, Inc., New York, NY, 1990, pp. 145–171 Search PubMed
 .
.
- M. J. Pullin and S. E. Cabaniss, The effects of pH, ionic strength, and iron-fulvic acid interactions on the kinetics of non-photochemical iron transformations. II. The kinetics of thermal reduction, Geochim. Cosmochim. Acta, 2003, 67, 4079–4089 CrossRef CAS
 .
.
- D. W. Gutzman and C. H. Langford, Kinetic study of the speciation of copper(II) bound to a hydrous ferric oxide, Environ. Sci. Technol., 1993, 27, 1388–1393 CrossRef CAS
 .
.
- C.-T. Lin and D. B. Rorabacher, Electrostatic effects in coordination kinetics. Reaction of nickel(II) ion with a cationic unidentate ligand as a function of solvent dielectric, Inorg. Chem., 1973, 12, 2402–2410 CrossRef CAS
 .
.
- J. C. Cassatt and R. G. Wilkins, Kinetics of reaction of nickel(II) ion with a variety of amino acids and pyridinecarboxylates, J. Am. Chem. Soc., 1968, 90, 6045–6050 CrossRef CAS
 .
.
- K. N. Raymond, G. Müller and B. Matzanke, Complexation of iron by siderophores a review of their solution and structural chemistry and biological function, Struct. Chem., 1984, 49–102 CAS
 .
.
- E. Farkas, É. A. Enyedy and H. Csóka, A comparison between the chelating properties of some dihydroxamic acids, desferrioxamine B and acetohydroxamic acid, Polyhedron, 1999, 18, 2391–2398 CrossRef CAS
 .
.
- T. Murakami, K. Ise, M. Hayakawa, S. Kamei and S. Takagi, Stabilities of metal complexes of mugineic acids and their specific affinities for iron (III), Chem. Lett., 1989, 12, 2137–2140 CrossRef
 .
.
- M. Walter, S. M. Kraemer and W. D. C. Schenkeveld, The effect of pH, electrolytes and temperature on the rhizosphere geochemistry of phytosiderophores, Plant Soil, 2017, 1–19 Search PubMed
 .
.
- S. M. Kraemer, D. E. Crowley and R. Kretzschmar, Geochemical aspects of phytosiderophore-promoted iron acquisition by plants, Adv. Agron., 2006, 91, 1–45 CAS
 .
.
- H. Drechsel, J. Metzger, S. Freund, G. Jung, J. R. Boelaert and G. Winkelmann, Rhizoferrin – a novel siderophore from the fungus Rhizopus microsporus var.rhizopodiformis, Biol. Met., 1991, 4, 238–243 CrossRef CAS
 .
.
- M. Shenker, Y. Chen and Y. Hadar, Stability Constants of the Fungal Siderophore Rhizoferrin with Various Microelements and Calcium, Soil Sci. Soc. Am. J., 1996, 60, 1140–1144 CrossRef CAS
 .
.
- M. Kamo and T. Nagai, An application of the biotic ligand model to predict the toxic effects of metal mixtures, Environ. Toxicol. Chem., 2008, 27, 1479–1487 CrossRef CAS
 .
.
- D. de Paiva Magalhães, M. R. da Costa Marques, D. F. Baptista and D. F. Buss, Metal bioavailability and toxicity in freshwaters, Environ. Chem. Lett., 2015, 13, 69–87 CrossRef
 .
.
- Y. Xu, D. Shi, L. Aristilde and F. Morel, The effect of pH on the uptake of zinc and cadmium in marine phytoplankton: possible role of weak complexes, Limnol. Oceanogr., 2012, 57, 293–304 CrossRef CAS
 .
.
- M. Jiménez-Piedrahita, A. Altier, J. Cecilia, J. Puy, J. Galceran, C. Rey-Castro, H. Zhang and W. Davison, Extending the Use of Diffusive Gradients in Thin Films (DGT) to Solutions Where Competition, Saturation, and Kinetic Effects Are Not Negligible, Anal. Chem., 2017, 89, 6567–6574 CrossRef PubMed
 .
.
- A. H. Shiva, W. W. Bennett, D. T. Welsh and P. R. Teasdale, In situ evaluation of DGT techniques for measurement of trace metals in estuarine waters: a comparison of four binding layers with open and restricted diffusive layers, Environmental Science: Processes & Environ. Sci.: Processes Impacts, 2016, 18, 51–63 Search PubMed
 .
.
- C. H. Langford and R. L. Cook, Kinetic versus equilibrium studies for the speciation of metal complexes with ligands from soil and water, Analyst, 1995, 120, 591–596 RSC
 .
.
- A. L. R. Sekaly, J. Murimboh, N. M. Hassan, R. Mandal, M. E. Ben Younes, C. L. Chakrabarti, M. H. Back and D. C. Grégoire, Kinetic speciation of Co(II), Ni(II), Cu(II), and Zn(II) in model solutions and freshwaters: lability and the d electron configuration, Environ. Sci. Technol., 2003, 37, 68–74 CrossRef CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8em00301g |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  ,
Yi
Xu
,
Yi
Xu
 and
Nathan E.
Boland
and
Nathan E.
Boland
 *
*





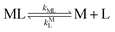

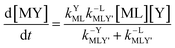
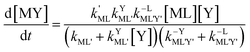
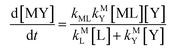

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K
K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K
K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values were corrected to I = 0.01 M with activity coefficients calculated using the Davies equation,
K values were corrected to I = 0.01 M with activity coefficients calculated using the Davies equation, 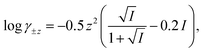 unless otherwise noted.
b At I = 1.0 M. Due to the limitations of the Davies equation this value was not converted to I = 0.01 M.
unless otherwise noted.
b At I = 1.0 M. Due to the limitations of the Davies equation this value was not converted to I = 0.01 M.





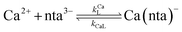



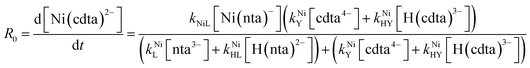
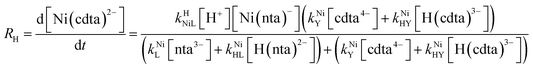
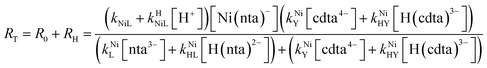
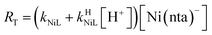


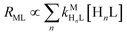
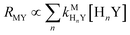
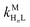 and
and 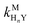 are the second-order complex formation rate constants from reaction between free metal ion and the corresponding free multidentate ligand species. The ratio of RMY and RML can be used to elucidate the cause of differences in reaction order. Specifically, the logarithm of RMY/RML serves as a convenient metric:
are the second-order complex formation rate constants from reaction between free metal ion and the corresponding free multidentate ligand species. The ratio of RMY and RML can be used to elucidate the cause of differences in reaction order. Specifically, the logarithm of RMY/RML serves as a convenient metric: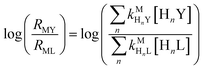
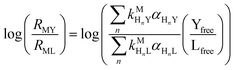
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML value greater than 1 indicates that MY formation is much faster than ML re-formation. Rates are independent of free multidentate ligand concentrations and controlled solely by the rate of ML dissociation (i.e. rate law has the simplified form of eqn (25)). A log
RMY/RML value greater than 1 indicates that MY formation is much faster than ML re-formation. Rates are independent of free multidentate ligand concentrations and controlled solely by the rate of ML dissociation (i.e. rate law has the simplified form of eqn (25)). A log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML value less than −1 indicates that ML re-formation is much faster than MY formation. In this case, rates are controlled by reaction between pre-equilibrium concentrations of free nickel and free Y, and, therefore, are dependent on both free multidentate ligand concentrations (i.e. rate law has the simplified form of eqn (26)). log
RMY/RML value less than −1 indicates that ML re-formation is much faster than MY formation. In this case, rates are controlled by reaction between pre-equilibrium concentrations of free nickel and free Y, and, therefore, are dependent on both free multidentate ligand concentrations (i.e. rate law has the simplified form of eqn (26)). log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML values between 1 and −1 indicate that MY formation and ML re-formation occur at comparable rates and the overall reaction order with respect to L and Y is mixed (i.e. the full rate law, eqn (22), must be used).
RMY/RML values between 1 and −1 indicate that MY formation and ML re-formation occur at comparable rates and the overall reaction order with respect to L and Y is mixed (i.e. the full rate law, eqn (22), must be used).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML values at the same conditions of our experiments using rate constants from Table 2 and calculated free multidentate ligand concentrations (Fig. 7). Three kinetic trends are revealed. First, adding calcium suppresses RMY more than RML, especially at higher pH (Fig. 7A). As discussed in calculated initial and final speciation of reaction solutions above, equilibrium calculations (Fig. 4) indicate that calcium lowers CDTAfree more than NTAfree. Because CDTA has a higher calcium affinity than NTA, adding calcium causes rates of NiNTA re-formation to become competitive with rates of NiCDTA formation. At pH greater than 7.8, adding calcium decreases log
RMY/RML values at the same conditions of our experiments using rate constants from Table 2 and calculated free multidentate ligand concentrations (Fig. 7). Three kinetic trends are revealed. First, adding calcium suppresses RMY more than RML, especially at higher pH (Fig. 7A). As discussed in calculated initial and final speciation of reaction solutions above, equilibrium calculations (Fig. 4) indicate that calcium lowers CDTAfree more than NTAfree. Because CDTA has a higher calcium affinity than NTA, adding calcium causes rates of NiNTA re-formation to become competitive with rates of NiCDTA formation. At pH greater than 7.8, adding calcium decreases log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML below −1 (Fig. 7A), and overall rates are dependent on free multidentate ligand concentrations (Fig. 5B and C). At low pH, however, log
RMY/RML below −1 (Fig. 7A), and overall rates are dependent on free multidentate ligand concentrations (Fig. 5B and C). At low pH, however, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML is greater than 1 even when calcium is added (Fig. 7A and D) because protonation of CDTA competes with calcium complexation (Fig. 4). Second, in the presence of calcium, decreasing CDTAT or increasing NTAT lowers log
RMY/RML is greater than 1 even when calcium is added (Fig. 7A and D) because protonation of CDTA competes with calcium complexation (Fig. 4). Second, in the presence of calcium, decreasing CDTAT or increasing NTAT lowers log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML (Fig. 7B and C). As log
RMY/RML (Fig. 7B and C). As log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML decreases, overall reaction rates decrease and become more sensitive to total multidentate ligand concentrations. However, because the relationship between total multidentate ligand and free multidentate ligand concentrations is non-linear in the presence of calcium, the relationship between total multidentate ligand concentrations and RMY/RML is not proportional. Third, when CaT exceeds CDTAT, RMY decreases precipitously as does log
RMY/RML decreases, overall reaction rates decrease and become more sensitive to total multidentate ligand concentrations. However, because the relationship between total multidentate ligand and free multidentate ligand concentrations is non-linear in the presence of calcium, the relationship between total multidentate ligand concentrations and RMY/RML is not proportional. Third, when CaT exceeds CDTAT, RMY decreases precipitously as does log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML (Fig. 7D). This corresponds to greater rate dependence on free multidentate ligand concentrations (Fig. 5B) and a sharp decrease in overall rates (Fig. 5D). Note that the corollary is also true: when CDTAT exceeds CaT, log
RMY/RML (Fig. 7D). This corresponds to greater rate dependence on free multidentate ligand concentrations (Fig. 5B) and a sharp decrease in overall rates (Fig. 5D). Note that the corollary is also true: when CDTAT exceeds CaT, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML increases sharply (Fig. 7B).
RMY/RML increases sharply (Fig. 7B).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML can be useful for predicting kinetic behavior of disjunctive ligand exchange reactions and determining which simplified form of the rate law applies. We note that RMY/RML depends on three factors: (1) the ratio of free multidentate ligand concentrations, (2) the protonation of free multidentate ligand, and (3) rate constants for complex formation. As we consider the application of this metric to disjunctive ligand exchange reactions more broadly, let us discuss each of these three factors in detail.
RMY/RML can be useful for predicting kinetic behavior of disjunctive ligand exchange reactions and determining which simplified form of the rate law applies. We note that RMY/RML depends on three factors: (1) the ratio of free multidentate ligand concentrations, (2) the protonation of free multidentate ligand, and (3) rate constants for complex formation. As we consider the application of this metric to disjunctive ligand exchange reactions more broadly, let us discuss each of these three factors in detail.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML is much greater than 1 or much less than −1. However, setting total multidentate ligand concentration in excess does not necessarily ensure that the free multidentate ligand concentration is in excess, especially if calcium or other competing metal ions are present. In most of our experiments, we set CDTAT in excess of NTAT, but, because CDTA has a higher calcium affinity than NTA, NTAfree is often greater than CDTAfree. The disparity between total and free multidentate ligand concentrations is likely to hold for most natural waters. Where calcium is abundant, differences in calcium affinity will greatly affect ratios of free multidentate ligand concentrations. In contrast to our model reaction system, one can imagine a pair of multidentate ligands where the initial multidentate ligand L has a much greater affinity for calcium than the incoming multidentate ligand Y. In such a scenario, increasing LT would not decrease log
RMY/RML is much greater than 1 or much less than −1. However, setting total multidentate ligand concentration in excess does not necessarily ensure that the free multidentate ligand concentration is in excess, especially if calcium or other competing metal ions are present. In most of our experiments, we set CDTAT in excess of NTAT, but, because CDTA has a higher calcium affinity than NTA, NTAfree is often greater than CDTAfree. The disparity between total and free multidentate ligand concentrations is likely to hold for most natural waters. Where calcium is abundant, differences in calcium affinity will greatly affect ratios of free multidentate ligand concentrations. In contrast to our model reaction system, one can imagine a pair of multidentate ligands where the initial multidentate ligand L has a much greater affinity for calcium than the incoming multidentate ligand Y. In such a scenario, increasing LT would not decrease log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RMY/RML significantly until LT and not YT is in excess of CaT. Therefore, when calcium is present, one must evaluate the relative calcium affinity of every multidentate ligand pair undergoing disjunctive ligand exchange before simplifying the rate law. Furthermore, because of the interdependence of proton and calcium equilibria, evaluating relative calcium affinity is not as simple as comparing equilibrium constants for formation of CaL and CaY. In systems where direct measurement of free multidentate ligand concentrations is not possible, one will have to rely on equilibrium calculations based on estimates of free multidentate ligand species and their labile complexes initially present in the system.
RMY/RML significantly until LT and not YT is in excess of CaT. Therefore, when calcium is present, one must evaluate the relative calcium affinity of every multidentate ligand pair undergoing disjunctive ligand exchange before simplifying the rate law. Furthermore, because of the interdependence of proton and calcium equilibria, evaluating relative calcium affinity is not as simple as comparing equilibrium constants for formation of CaL and CaY. In systems where direct measurement of free multidentate ligand concentrations is not possible, one will have to rely on equilibrium calculations based on estimates of free multidentate ligand species and their labile complexes initially present in the system.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.




