Modelling oral up-take of hydrophobic and super-hydrophobic chemicals in fish†
Wolfgang
Larisch
 *a and
Kai-Uwe
Goss
*a and
Kai-Uwe
Goss
 *ab
*ab
aDepartment of Analytical Environmental Chemistry, Centre for Environmental Research UFZ, Leipzig-Halle, Permoserstraße 15, Leipzig, D-04318, Germany. E-mail: wolfgang.larisch@ufz.de; kai-uwe.goss@ufz.de
bInstitute of Chemistry, University of Halle-Wittenberg, Kurt-Mothes-Straße 2, Halle, D-06120, Germany
First published on 6th December 2017
Abstract
We have extended a recently published toxicokinetic model for fish (TK-fish) towards the oral up-take of contaminants. Validation with hydrophobic chemicals revealed that diffusive transport through aqueous boundary layers in the gastro-intestinal tract and in the blood is the limiting process. This process can only be modelled correctly if facilitated transport by albumin or bile micelles through these boundary layers is accounted for. In a case study we have investigated the up-take of a super hydrophobic chemical, Dechlorane Plus. Our results suggest that there is no indication of a hydrophobicity or size cut-off in the bioconcentration of this chemical. Based on an extremely high, but mechanistically sound facilitation factor we received model results in good agreement with experimental values from the literature. The results also indicate that established experimental procedures for BCF determination cannot cover the very slow up-take and clearance kinetics that are to be expected for such a chemical.
Environmental SignificanceFish feeding tests are part of the OECD test guideline 305 for aqueous bioconcentration. A sound mechanistic understanding of the involved up-take and distribution processes is desirable for the interpretation of these tests. Our mechanistically based model provides such an understanding based on the physico-chemical properties of the chemical and the physiological properties of the fish. In a case study we apply the validated model to the up-take of a super-hydrophobic chemical. While even regulative documents suggest that super-hydrophobic chemicals are not taken up by fish, our model results in combination with some experimental literature data indicate that up-take and clearance of those chemicals is slow but does occur. |
Introduction
In a recent paper we have presented a physiologically based toxicokinetic (PbTK) model for fish (called TK-fish).1 This model is completely physiologically based (similar to the model from Ng and Hungerbühler 2013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and has some distinct differences to many other fish models. All relevant ADME processes are represented by mechanistic process description based on the respective physiological data of the organism and the physico-chemical data of the chemical. The membrane permeation processes involved in the uptake and distribution of a chemical can serve as an example: rather than defining an empirically determined or fitted up-take efficiency or permeability we model all these processes as a diffusive transport through the respective layers of endothelial cells with explicitly accounting for the different contributions that come from aqueous boundary layers, cytosols and the phospholipid membranes based on the respective diffusion path length, diffusion coefficient and partition coefficient. Thus, the model does not require any calibration and any comparison between model results and experimental data allows for direct mechanistic conclusions in contrast to more empirical PbTK models where calibrated parameters may contain information or corrections for processes that they are not meant to represent.
2) and has some distinct differences to many other fish models. All relevant ADME processes are represented by mechanistic process description based on the respective physiological data of the organism and the physico-chemical data of the chemical. The membrane permeation processes involved in the uptake and distribution of a chemical can serve as an example: rather than defining an empirically determined or fitted up-take efficiency or permeability we model all these processes as a diffusive transport through the respective layers of endothelial cells with explicitly accounting for the different contributions that come from aqueous boundary layers, cytosols and the phospholipid membranes based on the respective diffusion path length, diffusion coefficient and partition coefficient. Thus, the model does not require any calibration and any comparison between model results and experimental data allows for direct mechanistic conclusions in contrast to more empirical PbTK models where calibrated parameters may contain information or corrections for processes that they are not meant to represent.
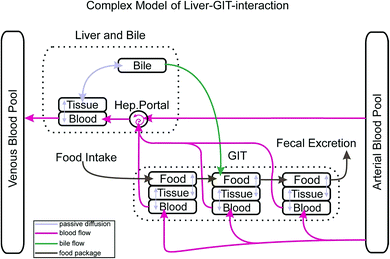
Other features that distinguish our model from many others are: the separate consideration of 6 different sorbing matrices in blood and each organ (structural protein, albumin, collagen, storage lipids, phospholipids and water) and the use of corresponding equilibrium partition constants that are derived from the ppLFER approach. There also is the possibility to account for active transport across membranes and to include sorption kinetics into the calculation. In our first paper we had validated the model for uptake of various non-metabolising chemicals via gills.1 Here we extend the model and its validation towards up-take via food. To this end we introduce an improved gastro-intestinal tract (GIT) in our model including a new bile flow process from the liver to the GIT and discuss the possibility of up-take of super hydrophobic chemicals.
Model concept
Fig. 1 depicts how the GIT is represented in our actual model. The GIT consists of three consecutive compartments, all of them well mixed. Each food package that is taken up will stay in the first GIT compartment for a defined time before it proceeds as a package to the second and then to the third GIT compartment. Within the residence time in each GIT compartment proteins and lipids of the food package are reduced to a degree that is defined by the user. Due to the lack of better knowledge we assume that the reduction of the food follows a linear time trend. The reduction of the food volume (which eventually turns into feces) lowers its sorption capacity and thus increases the fugacity gradient of contaminants from the GIT into the circulatory system. In each time step this gradient is recalculated based on the actual composition of the food. While food passes consecutively from the first to the last GIT compartment blood flows through all GIT compartments in parallel in our model. Permeation of the contaminant from the food into the GIT tissue depends on the gradient in the freely dissolved concentrations in both compartments, the surface area through which passive permeation takes place and the permeability. As mentioned above, permeability is calculated according to a mechanistic concept that we have described in detail in Larisch et al.1 For the surface area of the GIT we found a relationship with body weight from Buddington and Diamond3 (0.23 cm2 g−1) which, however, does not account for the effect of villi in the gut surface. Based on information from the literature (see ESI – Part I† for details) we concluded that villi increase the effective surface area of the gut by about a factor of 7.5 as compared to the value from Buddington and Diamond.Obviously our process description for the GIT is still far from reality because food is moving continuously through the GIT instead of being entered in 3 separate well mixed compartments for a defined time. In the model output this results in rather abrupt concentration changes in the GIT which are certainly not realistic. However, we expect that this temporal and spatial discretization will be sufficient if exposure scenarios are modelled that last longer than one day. One must also note that the availability of important physiological information such as the digestive efficiency as a function of time does usually not allow for any finer discretization.
Chemicals in the liver can either be passively exchanged in both directions with the circulatory system or they can be excreted via bile. We have therefore included the option for diffusive exchange between the liver and bile as well as the possibility for active excretion into the bile in combination with an advective transport of this bile into the second GIT compartment where it is mixed into the rest of the compartment. This advective bile flow is only switched on when there is food in the second GIT compartment. Parametrization of the transport via bile was difficult. For the volumetric flow rate of bile from the liver to the GIT we used the average of two values reported in Nichols (0.87 μl min−1 kg−1 for rainbow trout4) which we assumed to scale linearly with body mass. Due to a lack of detailed information on the sorption capacity of bile we had to revert to a simple Kow relationship based on experimental PAH data from Zhang et al.5 (see ESI – Part II† for details) which certainly falls back behind the mechanistic standard that we have in all other partition processes in our model.
Facilitated transport
When we applied our model to the oral up-take of hydrophobic chemicals it quickly became clear that the predicted internal concentrations were much lower than the experimental data (see below). Analysis of our results showed that this had kinetic reasons. The modelled up-take efficiency was much too small. The dominating limitation for the up-take of hydrophobic chemicals from food into the circulatory system but also for the distribution between blood and the organs lay in the diffusion through the aqueous boundary layers in the GIT tract, the blood capillaries and the cytosols of the endothelial cells (this could be deduced from the calculated fugacity gradients in the various compartments). For highly hydrophobic chemicals the freely dissolved fraction is always extremely small in all parts of the body. And only this small fraction is directly available for diffusion through aqueous boundary layers. However, reality is more complex: hydrophobic chemicals in blood are mostly sorbed to transport proteins and lipids. These can also diffuse through aqueous boundary layers and thus act as a transport shuttle.6 This so-called “facilitated transport” mechanism has already been discussed in various studies for the up-take in the GIT where bile forms micelles that act as transporters.5,7–10 We have therefore included a facilitation-factor into our model which is multiplied with the internally calculated permeability of the freely dissolved chemicals to yield a corrected permeability. In our model the facilitation factor can be set by the user for each permeation process separately, i.e. permeation from GIT content to the GIT tissue, from GIT tissue to blood and from blood to the single organs. In order to quantify the facilitation effect in a mechanistically proper way we used information from Westergaard and Dietschy10 for the effect of bile micelles in the GIT and from Mayer et al.7 for the effect of albumin on permeation into and out of the blood system. The facilitation effect can be covered mechanistically by a term that contains the diffusion coefficient of the carrier (e.g. albumin) the partition coefficient of the chemicals between the freely dissolved state and the sorbed state and the concentration of the carrier. Details are described in ESI (see ESI – Part III†). All these permeation processes also involve diffusion through the cytosol of some endothelial cell layers. It is plausible that transport facilitation with macromolecules or micelles also occurs there but we could not find any information on that. Our internally calculated permeabilities encompass these diffusive resistances and by applying the facilitation factors to these permeabilities they were implicitly also applied to the diffusion through these cytosols. This can be revised when better information becomes available.Validation
Our first validation for oral uptake was done with data from Nichols 2004![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 where a single dose of PCB52 contaminated fathead minnows had been fed to rainbow trout (100 g) which were then analysed after 6 h, 12 h, 24 h, 48 h and 96 h for concentrations in liver, muscle blood and fat. This paper also reports the residence time of the food in three different parts of the GIT and the assimilation efficiency of the food lipids (91%) which is supported by Vandenberg et al.12 As mentioned above our first model calculation for this experiment was done without any facilitated transport and resulted in concentrations far below the measured ones (see Fig. 2). Only 2.6% of the ingested PCB52 had been taken up after 4 days in our model, compared to about 55% in the experiment.
11 where a single dose of PCB52 contaminated fathead minnows had been fed to rainbow trout (100 g) which were then analysed after 6 h, 12 h, 24 h, 48 h and 96 h for concentrations in liver, muscle blood and fat. This paper also reports the residence time of the food in three different parts of the GIT and the assimilation efficiency of the food lipids (91%) which is supported by Vandenberg et al.12 As mentioned above our first model calculation for this experiment was done without any facilitated transport and resulted in concentrations far below the measured ones (see Fig. 2). Only 2.6% of the ingested PCB52 had been taken up after 4 days in our model, compared to about 55% in the experiment.
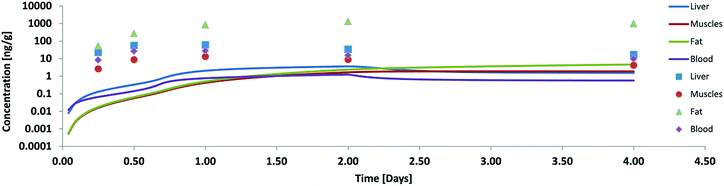 | ||
| Fig. 2 Concentration of PCB52 in various tissues of rainbow trout (on a logarithmic scale) in a fish feeding study: experimental data (symbols) from Nichols 2004 (ref. 11) and model results without facilitated transport. | ||
According to Nichols 2004 we had assumed that PCB52 is not biotransformed and from our model data we could also see that excretion via the gills was negligible. Blood flow limitation as another possible reason for too low internal concentrations could be ruled out because the major fugacity gradient occurred between the food and the tissue of the GIT and not between the GIT and the blood or the blood and the organs. Hence, limited absorption from food into the GIT tissue must have been the main cause for the observed discrepancies. The absorption efficiency is a function of the residence time in the GIT (which was quite well documented for this experiment), the GIT surface area (which – in our case already included the correction for enlargement by the villi) and permeability. Thus we had to conclude that our calculated permeabilities were not yet correct and extended the model to include facilitated transport as described in the theory section. As described in ESI – Part III† the estimated facilitation factor for the permeation of PCB52 from food into the GIT was 30 and the calculated albumin facilitation was 30 as well. Of course, one cannot expect these values to be the same for every scenario because they are based on different carriers. The model results including these facilitation effects are shown in Fig. 3.
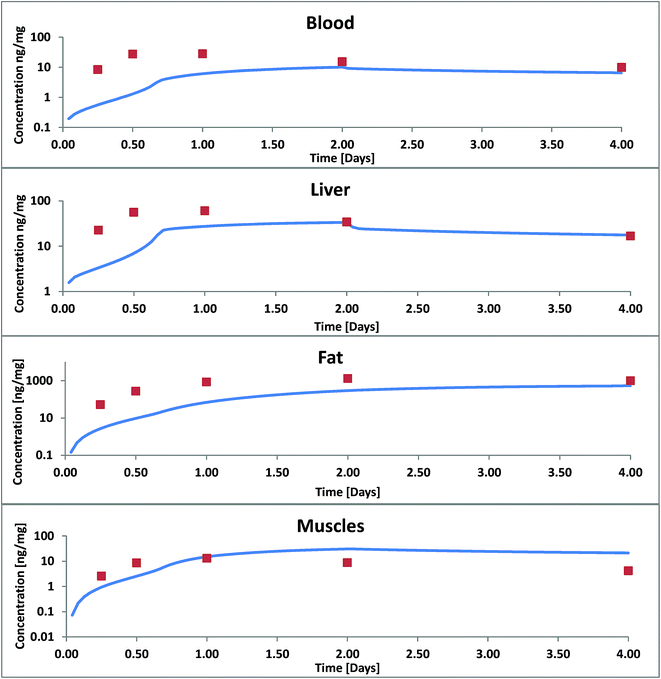 | ||
| Fig. 3 Concentration of PCB52 in various tissues of rainbow trout in a fish feeding study: experimental data (symbols) from Nichols 2004 (ref. 11) and model results with facilitated transport. | ||
For blood, liver and lipids we still underestimate the concentrations increase within the first two days. After two days, concentrations in liver and blood and after 4 days the concentrations in fat are in good agreement. In our model the major up-take and distribution resistance in these four days remain to be in the aqueous boundary layers between food and GIT and between blood and fat. In blood we have so far only considered albumin as a transport vehicle. We assume that blood lipids whose sorption capacity cannot be neglected are part of the large blood cells and can therefore not contribute to the facilitation effect through the ABL. Bile flow had almost no influence on our calculated results: it increased the overall fecal excretion of PCB52 by only 0.43%. This is because the mass flux via bile is small compared to other mass fluxes and because PCB52 excreted into the GIT is partly reabsorbed. Excretion via bile is likely more significant for polar metabolization products that are actively excreted from the hepatocytes into the bile and hardly reabsorbed from the GIT content.
We note that Xiao et al.13 have concluded in a recent work that micelle-mediated diffusion does not improve model predictions for oral up-take. However, the oral up-take efficiency in their model had been calibrated with the PCB52 data from Nichols et al. for which we have shown here that they are likely affected by micelle mediation already. Hence, further calculations with that model would necessarily also have implicit contributions from micelle-mediated transport.
For a second validation we selected data from three different labs that took part in an OECD ring test in 2011 where trout (1.5 g) were fed with food pellets contaminated with hexachlorobenzene (HCB) once a day (3% of their body weight) for 13 days and uncontaminated food pellets thereafter for total duration of 41 days.14 The composition of the food in terms of proteins and lipids differed between different laboratories. This was accounted for in our model input. The reported data show that also the lipid content of the fish varied within a factor 2 with time. This was not accounted for in our model. We used an averaged lipid content over the whole duration of the experiment. For validation we used the results from those 3 labs that differed the most in their experimental set-up (see ESI – Part IV† for details). Again the modelled concentrations were much too low when the facilitation effect was not considered. According to the methods described in ESI† we estimated a facilitation factor of 15 in the GIT and 6.4 in blood for HCB. Fig. 4 shows model results (facilitation included) and experimental data for all three labs. Agreement between model and experiment is good if we consider that the variance between fish individuals in the same test system already amounts to a factor 2 (see individual symbols in Fig. 4).
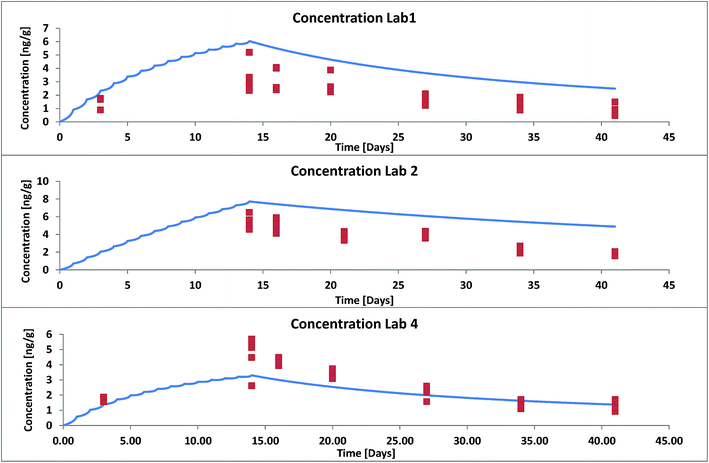 | ||
| Fig. 4 Whole body concentration of HCB in rainbow trout in a fish feeding study: experimental data (symbols) from OECD Ring Test no. 175 (ref. 14) and model results with facilitated transport. | ||
Case study: super hydrophobic chemicals
It is a widespread opinion that chemicals with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow > 8 (or sometimes 10 is given as the threshold) cannot bioaccumulate because they are not taken up in relevant quantities.15,16 Often this believed effect is explained as a lack of membrane permeability due to the size of these chemicals.15–17 However, from the pharmaceutical literature we have ample evidence that molecules with molecular weight > 800 (vinblastine, vincristine and paclitaxel) and even cyclosporine A (MW 1200) are not principally hindered in their membrane permeability although their diffusivity is lower than that of smaller molecules.18,19 Earlier publications in pharmaceutical research reported an increase of membrane permeability up to about log
Kow > 8 (or sometimes 10 is given as the threshold) cannot bioaccumulate because they are not taken up in relevant quantities.15,16 Often this believed effect is explained as a lack of membrane permeability due to the size of these chemicals.15–17 However, from the pharmaceutical literature we have ample evidence that molecules with molecular weight > 800 (vinblastine, vincristine and paclitaxel) and even cyclosporine A (MW 1200) are not principally hindered in their membrane permeability although their diffusivity is lower than that of smaller molecules.18,19 Earlier publications in pharmaceutical research reported an increase of membrane permeability up to about log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow = 2 or 3 and a decrease above this threshold.20–22 However, this is an artifact that comes from measurements that are done in a fixed time frame (often 60 or 90 minutes) and without any mass balance control. For hydrophobic chemicals steady-state flux through cellular monolayers is not yet reached after 60 or 90 minutes because the cells themselves are still sorbing the chemical and hence a flux measurement without sorption correction is flawed. Indeed, almost unhindered absorption in humans has been reported for chemicals with a log
Kow = 2 or 3 and a decrease above this threshold.20–22 However, this is an artifact that comes from measurements that are done in a fixed time frame (often 60 or 90 minutes) and without any mass balance control. For hydrophobic chemicals steady-state flux through cellular monolayers is not yet reached after 60 or 90 minutes because the cells themselves are still sorbing the chemical and hence a flux measurement without sorption correction is flawed. Indeed, almost unhindered absorption in humans has been reported for chemicals with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow up to 6.22 Others again have suggested a hydrophobicity cut-off for the sorption of highly hydrophobic chemicals in biological tissues (see discussion in ref. 23). However, these findings are likely also due to experimental artifacts because it is extremely challenging to work with chemicals whose log
Kow up to 6.22 Others again have suggested a hydrophobicity cut-off for the sorption of highly hydrophobic chemicals in biological tissues (see discussion in ref. 23). However, these findings are likely also due to experimental artifacts because it is extremely challenging to work with chemicals whose log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow is larger than 6.23–25 Thus it seems likely that up-take and therefore also bioaccumulation of super hydrophobic chemicals is principally possible although it can be expected to be kinetically slow. Various studies17,26,27 investigated up-take of polybrominated diphenyl flame retardants in fish and reported very low up take efficiency for the largest one, BDE209, which has been attributed to its size.17 However, Stapleton et al.28 and Munschy et al.29 have shown that BDE209 is debrominated in fish so that this conclusion is not compelling. Another flame retardant, Dechlorane Plus (estimated log
Kow is larger than 6.23–25 Thus it seems likely that up-take and therefore also bioaccumulation of super hydrophobic chemicals is principally possible although it can be expected to be kinetically slow. Various studies17,26,27 investigated up-take of polybrominated diphenyl flame retardants in fish and reported very low up take efficiency for the largest one, BDE209, which has been attributed to its size.17 However, Stapleton et al.28 and Munschy et al.29 have shown that BDE209 is debrominated in fish so that this conclusion is not compelling. Another flame retardant, Dechlorane Plus (estimated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow = 11.2
Kow = 11.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30) may be more indicative of whether bioaccumulation of such chemicals is possible or not. We therefore did a model calculation for the oral up-take of Dechlorane Plus in order to investigate whether we could identify any mechanism that would prevent bioaccumulation of such a super-hydrophobic chemical. A feeding study in which rainbow trout (50 g) were exposed to food fortified with anti-Dechlorane Plus for 49 days served for the validation of our model results. For the modelling we had the problem that the empirical approach for estimating facilitated transport in the GIT does not provide any data for compounds as hydrophobic as Dechlorane. The highest facilitation factor reported in that empirical approach is 145 for cholesterol.10 The albumin based facilitation factor that we calculated for Dechlorane Plus in blood was 450
30) may be more indicative of whether bioaccumulation of such chemicals is possible or not. We therefore did a model calculation for the oral up-take of Dechlorane Plus in order to investigate whether we could identify any mechanism that would prevent bioaccumulation of such a super-hydrophobic chemical. A feeding study in which rainbow trout (50 g) were exposed to food fortified with anti-Dechlorane Plus for 49 days served for the validation of our model results. For the modelling we had the problem that the empirical approach for estimating facilitated transport in the GIT does not provide any data for compounds as hydrophobic as Dechlorane. The highest facilitation factor reported in that empirical approach is 145 for cholesterol.10 The albumin based facilitation factor that we calculated for Dechlorane Plus in blood was 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221, which is much higher. We therefore decided to calculate two scenarios: (a) with a facilitation factor of 15 in GIT and blood as the lowest limit that might possibly be conceivable and (b) with a facilitation factor of 450
221, which is much higher. We therefore decided to calculate two scenarios: (a) with a facilitation factor of 15 in GIT and blood as the lowest limit that might possibly be conceivable and (b) with a facilitation factor of 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221 in GIT and blood which is orders of magnitude higher but which is consistent with our conceptual and mechanistic understanding. In order to avoid any misunderstanding we stress here that this high facilitation factor only indicates the relative importance of molecular and carrier mediated diffusion it does not mean that facilitated transport as such was larger for Dechlorane than for any other strongly sorbing compound.
221 in GIT and blood which is orders of magnitude higher but which is consistent with our conceptual and mechanistic understanding. In order to avoid any misunderstanding we stress here that this high facilitation factor only indicates the relative importance of molecular and carrier mediated diffusion it does not mean that facilitated transport as such was larger for Dechlorane than for any other strongly sorbing compound.
From the results it appears that our model with the high facilitation factor of 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221 is very close to experimental reality (see Fig. 5). The agreement between model and experiment indicates that up-take of super hydrophobic chemicals from food does take place without any anomalies. It is slow but it will eventually result in a huge bioconcentration of these compounds when they are not metabolized. It may take one or two years until an orally contaminated fish reaches steady-state for such compounds. This is beyond the life span of some species but may be very relevant for other species. The estimated depuration half-life via water and feces that we calculated is only in the order of twenty years. Obviously this is too slow to be measured experimentally. Tomy et al.30 report depuration half-lives in the order of 1–2 months based on their experimental data but the respective graphs seem to suggest that elimination is a biphasic process that cannot be evaluated correctly by first order kinetics. An experimental determination of bioconcentration does therefore not seem feasible for such chemicals neither as a kinetic nor as a steady-state BCF. However, a priori we see no reason why super-hydrophobic chemicals would not bioaccumulate. We therefore suggest that such super-hydrophobic chemicals are generally considered as bioaccumulative unless in vitro metabolism studies reveal biotransformation rate constants sufficiently high to prevent this accumulation.
221 is very close to experimental reality (see Fig. 5). The agreement between model and experiment indicates that up-take of super hydrophobic chemicals from food does take place without any anomalies. It is slow but it will eventually result in a huge bioconcentration of these compounds when they are not metabolized. It may take one or two years until an orally contaminated fish reaches steady-state for such compounds. This is beyond the life span of some species but may be very relevant for other species. The estimated depuration half-life via water and feces that we calculated is only in the order of twenty years. Obviously this is too slow to be measured experimentally. Tomy et al.30 report depuration half-lives in the order of 1–2 months based on their experimental data but the respective graphs seem to suggest that elimination is a biphasic process that cannot be evaluated correctly by first order kinetics. An experimental determination of bioconcentration does therefore not seem feasible for such chemicals neither as a kinetic nor as a steady-state BCF. However, a priori we see no reason why super-hydrophobic chemicals would not bioaccumulate. We therefore suggest that such super-hydrophobic chemicals are generally considered as bioaccumulative unless in vitro metabolism studies reveal biotransformation rate constants sufficiently high to prevent this accumulation.
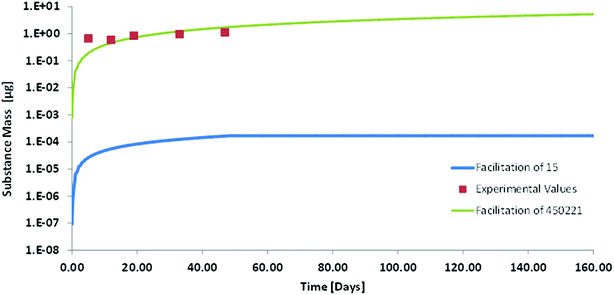 | ||
| Fig. 5 Whole body concentration (on a logarithmic scale) of Dechlorane Plus in rainbow trout in a fish feeding study: experimental values (symbols) from Tomy et al.30 and modelling with two different facilitation factors. | ||
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by Bayer Crop Science.References
- W. Larisch, T. N. Brown and K.-U. Goss, Environ. Toxicol. Chem., 2017, 36, 1538–1546 CrossRef CAS PubMed.
- C. a. Ng and K. Hungerbühler, Environ. Sci. Technol., 2013, 47, 7214–7223 CrossRef CAS PubMed.
- R. K. Buddington and J. M. Diamond, Am. J. Physiol., 1987, 252, G65–G76 CAS.
- J. W. Nichols, P. N. Fitzsimmons and L. P. Burkhard, Environ. Toxicol. Chem., 2007, 26, 1304–1319 CrossRef CAS PubMed.
- Y. Zhang, J. J. Pignatello, S. Tao and B. Xing, Environ. Sci. Technol., 2015, 49, 14641–14648 CrossRef CAS PubMed.
- N. I. Kramer, J. C. H. Van Eijkeren and J. L. M. Hermens, Anal. Chem., 2007, 79, 6941–6948 CrossRef CAS PubMed.
- P. Mayer, M. M. Fernqvist, P. S. Christensen, U. Karlson and S. Trapp, Environ. Sci. Technol., 2007, 41, 6148–6155 CrossRef CAS PubMed.
- B. C. Kelly, F. a. P. C. Gobas and M. S. McLachlan, Environ. Toxicol. Chem., 2004, 23, 2324–2336 CrossRef CAS PubMed.
- K. G. Drouillard, G. Paterson, J. Liu and G. D. Haffner, Environ. Sci. Technol., 2012, 46, 10279–10286 CAS.
- H. Westergaard and J. M. Dietschy, J. Clin. Invest., 1976, 58, 97–108 CrossRef CAS PubMed.
- J. W. Nichols, P. N. Fitzsimmons, F. W. Whiteman and T. D. Dawson, Toxicol. Sci., 2004, 77, 206–218 CrossRef CAS PubMed.
- G. W. Vandenberg and J. De La Noüe, Aquacult. Nutr., 2001, 7, 237–245 CrossRef CAS.
- R. Xiao, J. a. Arnot and M. MacLeod, Chemosphere, 2015, 138, 89–95 CrossRef CAS PubMed.
- Organisation for Economic Co-operation and Development (OECD), Validation report of a ring test for the OECD 305 dietary exposure bioaccumulation fish test, 2012, vol. 175, http://www.oecd.org/chemicalsafety/testing/seriesontestingandassessmenttestingforenvironmentalfate.htm Search PubMed.
- S. D. Dyer, M. J. Bernhard, C. Cowan-Ellsberry, E. Perdu-Durand, S. Demmerle and J.-P. Cravedi, Chemosphere, 2008, 72, 850–862 CrossRef CAS PubMed.
- Y. Sakuratani, Y. Noguchi, K. Kobayashi, J. Yamada and T. Nishihara, J. Environ. Biol., 2008, 29, 89–92 Search PubMed.
- A. Kierkegaard, L. Balk, U. Tjärnlund, C. A. De Wit and B. Jansson, Environ. Sci. Technol., 1999, 33, 1612–1617 CrossRef CAS.
- F. Broccatelli, J. Chem. Inf. Model., 2012, 52, 2462–2470 CrossRef CAS PubMed.
- J. W. Polli, S. A. Wring, J. E. Humphreys, L. Huang, J. B. Morgan, L. O. Webster and C. S. Serabjit-Singh, J. Pharmacol. Exp. Ther., 2001, 299, 620–628 CAS.
- P. Wils, A. Warnery, V. Phung-Ba, S. Legrain and D. Scherman, J. Pharmacol. Exp. Ther., 1994, 269, 654–658 CAS.
- M. Kansy, H. Fischer, K. Kratzat, F. Senner, B. Wagner and I. Parrilla, in Pharmacokinetic Optimization in Drug Research, Verlag Helvetica Chimica Acta, Zürich, 2007, pp. 447–464 Search PubMed.
- S. D. Krämer, Pharm. Sci. Technol. Today, 1999, 2, 373–380 CrossRef.
- M. T. O. Jonker and S. A. Van Der Heijden, Environ. Sci. Technol., 2007, 41, 7363–7369 CrossRef CAS PubMed.
- L. Böhm, C. Schlechtriem and R. A. Düring, Environ. Sci. Technol., 2016, 50, 8316–8323 CrossRef PubMed.
- C. Schlechtriem, L. Böhm, R. Bebon, H. J. Bruckert and R. A. Düring, Environ. Toxicol. Chem., 2017, 36, 906–916 CrossRef CAS PubMed.
- G. T. Tomy, V. P. Palace, T. Halldorson, E. Braekevelt, R. Danell, K. Wautier, B. Evans, L. Brinkworth and A. T. Fisk, Environ. Sci. Technol., 2004, 38, 1496–1504 CrossRef CAS PubMed.
- J. R. Nyholm, A. Norman, L. Norrgren, P. Haglund and P. L. Andersson, Environ. Toxicol. Chem., 2009, 28, 1035–1042 CrossRef CAS PubMed.
- H. M. Stapleton, M. Alaee, R. J. Letcher and J. E. Baker, Environ. Sci. Technol., 2004, 38, 112–119 CrossRef CAS PubMed.
- C. Munschy, K. Héas-Moisan, C. Tixier, N. Olivier, O. Gastineau, N. Le Bayon and V. Buchet, Environ. Pollut., 2011, 159, 229–237 CrossRef CAS PubMed.
- G. T. Tomy, C. R. Thomas, T. M. Zidane, K. E. Murison, K. Pleskach, J. Hare, G. Arsenault, C. H. Marvin and E. D. Sverko, Environ. Sci. Technol., 2008, 42, 5562–5567 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7em00495h |
| This journal is © The Royal Society of Chemistry 2018 |