High-throughput computational prediction of the cost of carbon capture using mixed matrix membranes†
Abstract
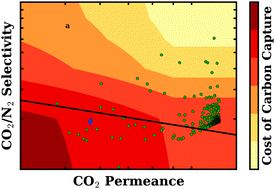
Polymeric membranes are being studied for their potential use in post-combustion carbon capture on the premise that they could dramatically lower costs relative to mature technologies available today. Mixed matrix membranes (MMMs) are advanced materials formed by combining polymers with inorganic particles. Using metal–organic frameworks (MOFs) as the inorganic particles has been shown to improve selectivity and permeability over pure polymers. We have carried out high-throughput atomistic simulations on 112 888 real and hypothetical metal–organic framework structures in order to calculate their CO2 permeabilities and CO2/N2 selectivities. The CO2/H2O sorption selectivity of 2 017 real MOFs was evaluated using the H2O sorption data of Li et al. (S. Li, Y. G. Chung and R. Q. Snurr, Langmuir, 2016, 32, 10368–10376). Using experimentally measured polymer properties and the Maxwell model, we predicted the properties of all of the hypothetical mixed matrix membranes that could be made by combining the metal–organic frameworks with each of nine polymers, resulting in over one million possible MMMs. The predicted gas permeation of MMMs was compared to published gas permeation data in order to validate the methodology. We then carried out twelve individually optimized techno-economic evaluations of a three-stage membrane-based capture process. For each evaluation, capture process variables such as flow rate, capture fraction, pressure and temperature conditions were optimized and the resultant cost data were interpolated in order to assign cost based on membrane selectivity and permeability. This work makes a connection from atomistic simulation all the way to techno-economic evaluation for a membrane-based carbon capture process. We find that a large number of possible mixed matrix membranes are predicted to yield a cost of carbon capture less than $50 per tonne CO2 removed, and a significant number of MOFs so identified have favorable CO2/H2O sorption selectivity.


 Please wait while we load your content...
Please wait while we load your content...