Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Storing electricity as chemical energy: beyond traditional electrochemistry and double-layer compression
Markus
Antonietti
 *a,
Xiaodong
Chen
*a,
Xiaodong
Chen
 b,
Runyu
Yan
a and
Martin
Oschatz
b,
Runyu
Yan
a and
Martin
Oschatz
 a
a
aMax Planck Institute of Colloids and Interfaces, Colloid Chemistry, Research Campus Golm, Am Mühlenberg 1, Potsdam 14476, Germany. E-mail: office.cc@mpikg.mpg.de
bInnovative Center for Flexible Devices, School of Materials Science and Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore
First published on 7th September 2018
Abstract
Extending the range of analysis of previous measurements on energy storage in ionic liquid (IL)-based supercapacitors with very well defined carbon materials indicates that there are two distinct processes at play: the one at lower voltages is (classically) related to the micropore inclusion of single ions, while a previously unknown high voltage transition can be ascribed to a change in the structure and coordination number of the ionic liquid. This opinion article discusses a proof of circumstantial evidence for this so far weakly understood and often overlooked mode of energy storage, which in principle could take supercapacitors to a new level of energy storage.
Broader contextSupercapacitors are storage devices for electric energy, which by principle are cheaper and more sustainable than current battery solutions in that they are not based on rare metals or lithium, but instead on carbon and other organic components. Using ionic liquids (ILs) as a working fluid in supercapacitors not only increases the working voltage and thereby the energy content, it also potentially allows access to new modes of energy storage related to the coordination number and electrostatic order of few nm sized mesopores in the electrodes. This allows such supercapacitors to now surpass the performance of some battery types and also opens up a new challenge for materials chemists to create even better energy storage, namely focusing on the design of mesopores (instead of micropores) and the development of new ILs with multiple liquid structures. |
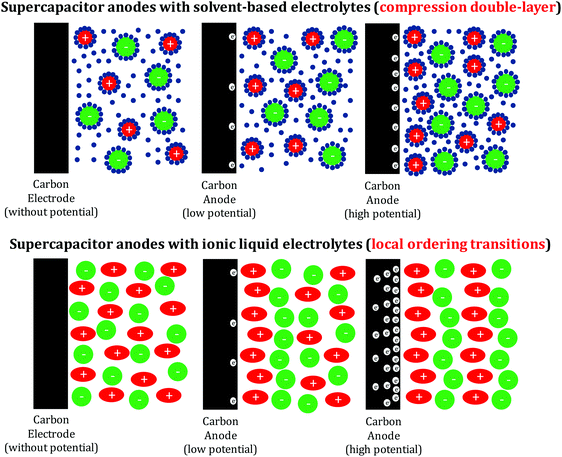
In times where mobile devices are omnipresent on the personal scale, but “excess green energy” only temporally occurs on the grid scale, energy storage has turned into a major issue. It is well known that energy storage in batteries is based on Faradaic reactions, where the voltage corresponds to the electrochemical potential of the redox couple. Another well-established option is electric double-layer capacitors (EDLCs), where the energy is stored via the compression of ions along an electrode, with opposite charges stored in the conductive plates of two electrodes. Both types of energy storage have been heavily reviewed, and their advantages and disadvantages in terms of power density, energy density, safety, and cycle lifetimes are well documented in the literature.1–16 In many cases, double-layer compression occurs alongside Faradaic reactions, resulting in so-called “pseudocapacitance”,17,18 with different techniques available to separate the two contributions.19 The energy and power gaps between faradic and capacitive energy storage principles are known as the “Ragone conflict”.20 It is our belief that the community can close this energy gap between batteries and supercapacitors by the exploration of energy terms that are neither double-layer compression nor faradic. Recent anomalies and observations in supercapacitor testing point to the involvement of further energy terms in electrochemical energy storage, alongside pure ion compression.21–23 It is the focus of this opinion article to discuss these effects and their potentialities.
In principle, any form of chemical energy can be directly translated into a voltage signal, if that the event occurring in the material is coupled to a charge flow in the collector electrodes. In double-layer compression, this energy is related to ion–ion repulsion and therefore does not saturate out within the typically possible potential windows of solvent-based (i.e. “aqueous” or “organic”) electrolytes. However, for all distinct chemical reactions, and also in principle for all other chemical events (Table 1), a voltage can be calculated using the Nernst equation, as long as the chemical effect creates a charge flow in the electrochemical device. The “Rosetta Stone” of interdisciplinary communications translates roughly to a voltage change of 1 V to a chemical energy of ∼100 kJ mol−1. As an illustrative example, the oxidation of lithium metal to lithium cations corresponds to an enthalpy of −299 kJ mol−1, while the standard electrode potential of this redox process is −3.1 V versus SHE.
| Chemical event | Typical enthalpy value (kJ mol−1) |
|---|---|
| Reduction of lithium ions (Li+ + e− → Li) | 299 |
| Hydration of lithium ions (Li+ + 4H2O → Li+·4H2O) | −508 |
| Hydration of ammonium ions | −293 |
| Hydration of magnesium ions | −1908 |
| Solvation of lithium ions with propylene carbonate | −50 |
| Hydrogen bridges | 12–50 |
| van der Waals forces | <25 |
| C–C bond | 350 |
| C–N bond | 295 |
To the surprise of most chemists, hydration and solvation enthalpies are rather high, and, in most cases, fully reversible. The hydration of lithium ions with 4 water molecules for instance in fact produces more energy than the oxidation of bare Li atoms, that is, one could hypothetically build a lithium “dehydration” device, with a voltage higher than that of a lithium battery. The numbers are of course smaller for coordination with organic solvents and also decrease upon an increase in the size of the ions, but in principle still lie in a range that is relevant for energy storage, and the scientific literature has already identified it as being relevant. For example, it has been observed that there is an anomalous increase in the energy storage capacity of electric double-layer capacitors if the size of the pores of the carbon (the material that is usually used as an electrode material) approaches the size of the electrolyte ions, thus resulting in desolvation. It is not surprising that the energy stored at each electrode (measured independently from one another) is about 150 kJ mol−1, which is close to the solvation energy of the applied electrolyte (in this case tetraethylammonium tetrafluoroborate in acetonitrile). The energy stored by the cations is interestingly slightly lower.22 The latter can be assigned to their lower solvation enthalpy caused by a larger diameter. Secondary bonding schemes, such as hydrogen bridges, are in the order of 10–50 kJ mol−1 each (and thus correspond to 0.1–0.5 V on the voltage scale) but can also contribute in a cooperative fashion to energy storage. The problem with all of these storage mechanisms is that the possible voltage to utilize them should be within the electrochemical stability range of the solvent applied, and this range is especially small for water.
Given the square dependence of the energy density on the applied voltage windows for EDLCs, the energy storage capacity can be enhanced by implementing electrolytes with higher electrochemical windows and stabilities. Ionic liquids (ILs), also known as low temperature molten salts (with melting points below 100 °C), are composed solely of ions and thus are promising alternatives to established solvent-based systems due to their wide operation voltage (as high as 4 V), negligible volatility, non-flammability, as well as a wide potential operating temperature range.24–26 In terms of the structures of ILs, the ion coordination numbers have been modelled, and indeed, as exemplified for ethylammonium nitrate, a variety of coordination structures with varying coordination numbers of 2–5 can be imagined and are in an accessible energy range.27,28 This means that the ion coordination structure can indeed play a role in charge storage, with uncompensated partial charges near the electrodes being taken up by electrons and holes with the appropriate voltage related to the energy of the structure change.
Pioneering experimental and theoretical studies have been devoted to exploring the underlying physics for IL charge storage under equilibrium conditions in carbon nanopores, and molecular dynamics simulations29 and nuclear magnetic resonance (NMR) spectroscopic measurements30 have provided information on the charge storage at the molecular level. The dependence of the capacitance on the pore size for IL electrolytes has been investigated in detail, especially the anomalous increase in the capacitance when the pore size decreases to the ion size.24,31,32 Obviously, single cations or anions can penetrate ion-sized micropores, while the countercharge in the electrode and wall–ion interactions replace the interactions of the ions in the IL bulk. Pulling an entity from its own bulk environment into an otherwise foreign matrix is always accompanied with a loss of energy, and this energy corresponds to the voltage needed to drive this process. Using molecular dynamics simulations, the capacitance was also found to depend on the applied voltage, where the capacitance reaches a maximum when all of the co-ions are expelled from the pores.29 Very recently, scattering experiments have been used to resolve the structure of IL molecules confined into nanoporous carbons.33 The results indeed showed that the Coulombic ordering reduced when the pores could accommodate only a single layer of ions. This non-Coulombic ordering was even further enhanced in the presence of an external electric potential and surely represents the first example of a non-traditional energy term that contributes to charge storage in IL-based supercapacitors.
Up to now, the mechanisms for charge storage revealed in these studies have been based on processes occurring in the narrowest, “single ion” carbon micropores and have neglected possible conformation variations and phase changes in the bulk of the rather large IL ions during charging/discharging. The simulation studies have only employed coarse-grained, rigid models of IL ions, and the experimental studies have not taken into account the influence of structural changes, although they are very likely to occur as a function of the electric potential. Some simulation studies have revealed that ion-wall interactions can significantly affect the molecular conformation of IL ions.34 Such structural (ordering) transitions are known to be potential-driven and are not limited to very narrow micropores.35 In mesopores, the contribution of such transitions to the energy storage is significantly higher due to the greater number of involved solvent molecules and the related changes in the conformation and coordination energy.36
In a recent paper, we analyzed the capacitive charge storage in a variety of porous carbon nanomaterials and their hybrids using 1-ethyl-3-methylimidazolium tetrafluoroborate (EMImBF4) as a model ionic liquid between 0 and 3.5 V.21Fig. 1 presents a selected case involving a nanoporous carbon where the micropore size matches the size of the IL ions (denoted as STC-16). Galvanostatic charging/discharging curves with potential limitation are close to the symmetric triangle at a low specific current of 0.5 A g−1, typically characteristic of double-layer capacitor behavior (Fig. 1a and b). However, all of the cyclic voltammetry (CV) curves exhibited small peaks at a cell voltage of ∼0.6 V, which in addition are fully reversible. An even more pronounced peak starts to emerge at higher cell voltages (Fig. 1c). The interesting dimension of these experiments is that we also CO2-etched this specific carbon sample (denoted as Ac-STC-16) to create a similar structure, but with an even greater specific surface area (2833 m2 g−1 instead of 2324 m2 g−1) and enlarged micropores. Obviously, both the specific storage peak at 0.6 V and some of the charge storage capacity (178 F g−1 resp. 7.5 μF cm−2 for STC and 154 F g−1 resp. 5.4 μF cm−2 for the etched sample) vanish, that is, increasing the surface area while otherwise preserving most other structural parameters counter-intuitively reduces the energy storage performance. This was a model experiment to show that double-layer compression only partially describes the energy storage, and that the energy lost is one of the special ion conformations in the appropriately sized pores.
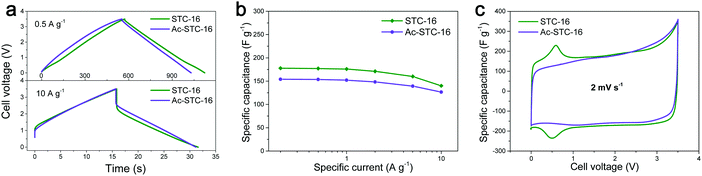 | ||
| Fig. 1 EDLC performance comparison of STC-16 and Ac-STC-16 tested in EMImBF4 ionic liquid using a two-electrode configuration: (a) the galvanostatic charge/discharge profiles at different specific currents, (b) the capacitance retention with specific current increase, and (c) the cyclic voltammograms at scan rates of 2 mV s−1. The difference is due to appropriately sized nanopores which, when enlarged by etching, lose their ability to tightly insert ions. Figures reproduced with permission from ref. 21. | ||
The origin of the peaks in the CVs of the STCs at a cell voltage of ∼0.6 V is in a strict sense still unproven, but from the rate dependence measurements, we would like to rule out a Faradic origin. In addition, we only see such peaks at this potential in materials where the micropore sizes are close to the size of BF4− ions. On an enthalpy scale, 0.6 V translates into 60 kJ mol−1, which is in the range of strong inter-molecular forces and Coulomb isolation. In our opinion, the origin of the peak is likely due to the insertion of single ions into the micropores and the reversible formation and release of inter-molecular forces. For example, the entry of single cations into the wall has been predicted by numerical simulations. Here, a single ion loses all its neighbouring Coulombs, while some of the energy is returned through van der Waals interactions with the carbon and of course localized electrons in the wall to compensate for the ion charge.
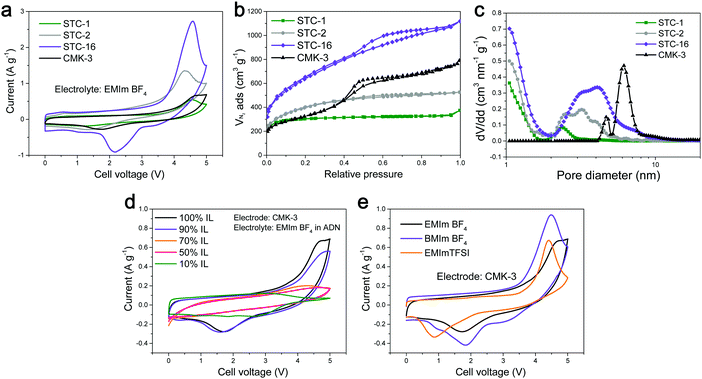
In addition, a rise at a very high voltage was observed in all of the CVs of the mesopore-containing carbons, and, according to our experiments, this is not related to material degradation. For the purposes of this present discussion paper, we ran additional CVs well into the region of metastability, and the energy uptake was found to peak significantly and even turned out to be partially reversible (Fig. 2a). This peak was observed for carbon materials with different pore sizes as well as for different ILs (Fig. 2b). The peak-like CV shape was found to be present only if the ethyl group in the cation of the EMImBF4 was changed to a butyl group and also if the anion was changed from BF4− to TFSI−. After the addition of adiponitrile solvent to the IL electrolyte, the peak disappeared, and the CV exhibited a rather typical EDLC-like appearance (Fig. 2c).
This voltage peak translates to a much higher transition enthalpy of above 350–450 kJ mol−1, which is higher than that of covalent bonds, but in the range of the melting of salts and other collective properties and structural transitions involving serious changes in the ion coordination numbers (Fig. 3).
Due to the onset of material decomposition, electrochemical measurements can only be ran at 5 V for analytical purposes with the present IL. Indeed, below the peak at high voltage, the constant increase in the current may indicate that irreversible electrolysis processes occur in parallel to the ordering transitions, and the peak intensity weakened upon measuring a greater number of cycles. However, in the standard, stable range we were able to tap into the footing of this process, i.e. we observed higher capacities due to this process and expected to observe even further significant increases in the storage capacities, for appropriate solvents systems and optimized solvent–wall interactions.
The amount of specific energy stored in the present systems was found to be one order of magnitude higher than that of commercial EDLCs, without any loss in the excellent power capability.21
The sole contribution of double-layer formation and compression can – by the sheer amount of stored energy – be safely excluded. In our previous paper,21 we translated the stored charge per surface area into the pro forma area per molecule at the electrochemical interface, and up to 2 ions (and the same number of electrons in the carbon phase) per nm2 were calculated, which can be approximated to a dense layer of cations on the carbon surface. In contrast to the aqueous and organic electrolytes, the overall density of cations and anions in ionic liquids is expected to remain close to the bulk value and the energy cannot be stored in ion compression by removal of non-charged solvent. On the contrary, ion rearrangement towards lower coordination numbers is an effect that can progress for nanometers into the bulk phase of the ionic liquid and is therefore not controlled by the specific surface area but rather by pore volume, in agreement with the experimental findings (Fig. 3).
This indeed opens up new possibilities for energy storage, as here the majority of energy is not stored in micropores (and cannot be optimized by the high specific surface area), but rather in appropriately designed mesopores, which support high energy Coulombic rearrangements of the IL in the bulk.
The involved processes are fully reversible, as indicated by the high stability of the devices and the nearly perfect symmetrical charge–discharge curves at low charge densities (Fig. 4), but are still limited by the electrochemical stability window of the IL electrolyte. Structural changes in liquids are in addition comparably fast (much faster than ion insertions or other battery processes), as they are not determined by transport and viscosity, but instead rely on local anion–cation exchange processes on the Angstrom scale. This causes capacitor-like rate performances, thus resulting in favorable power densities. This is mentioned in spite of the very high viscosities of ionic liquids, which are more restrictive for diffusion processes than for local structural rearrangements. Using these “new” effects, supercapacitors with all their strengths (cost, sustainability, rate, stability), even with their main weakness, the specific energy density, move into the range of batteries. The future is notoriously hard to predict, but we assume that going to smaller, higher coordinating ionic liquids, as well as optimizing wall–liquid interactions to promote the smoothness of structural changes, will allow the gap to be closed in current Li-ion battery technology.
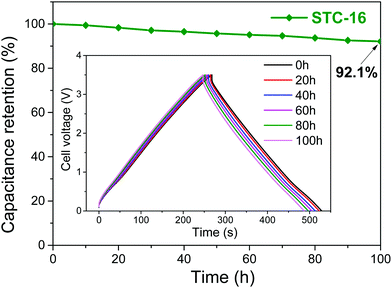 | ||
| Fig. 4 Floating stability of STC-16 at a specific current of 1 A g−1 for 100 h of floating at 3.5 V. The inset shows the charge/discharge profiles every 20 h. Figures reproduced with permission from ref. 21. | ||
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully thank Konstantin Schutjajew for experimental assistance and helpful discussions. Open Access funding provided by the Max Planck Society.References
- M. Armand and J. M. Tarascon, Building better batteries, Nature, 2008, 451, 652–657, DOI:10.1038/451652a.
- L. Borchardt, M. Oschatz and S. Kaskel, Carbon Materials for Lithium Sulfur Batteries-Ten Critical Questions, Chem. – Eur. J., 2016, 22(22), 7324–7351, DOI:10.1002/chem.201600040.
- N. S. Choi, Z. Chen, S. A. Freunberger, X. Ji, Y. K. Sun, K. Amine, G. Yushin, L. F. Nazar, J. Cho and P. G. Bruce, Challenges facing lithium batteries and electrical double-layer capacitors, Angew. Chem., Int. Ed., 2012, 51(40), 9994–10024, DOI:10.1002/anie.201201429.
- J. B. Goodenough and Y. Kim, Challenges for Rechargeable Li Batteries, Chem. Mater., 2010, 22(3), 587–603, DOI:10.1021/cm901452z.
- D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, The emerging chemistry of sodium ion batteries for electrochemical energy storage, Angew. Chem., Int. Ed., 2015, 54(11), 3431–3448, DOI:10.1002/anie.201410376.
- D. Larcher and J. M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7, 19–29, DOI:10.1038/NCHEM.2085.
- J. M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414, 359–367, DOI:10.1038/35104644.
- J. Vetter, P. Novák, M. R. Wagner, C. Veit, K. C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, Ageing mechanisms in lithium-ion batteries, J. Power Sources, 2005, 147, 269–281, DOI:10.1016/j.jpowsour.2005.01.006.
- F. Beguin, V. Presser, A. Balducci and E. Frackowiak, Carbons and electrolytes for advanced supercapacitors, Adv. Mater., 2014, 26, 2219–2251, DOI:10.1002/adma.201304137.
- L. Borchardt, M. Oschatz and S. Kaskel, Tailoring porosity in carbon materials for supercapacitor applications, Mater. Horiz., 2014, 1, 157–168, 10.1039/c3mh00112a.
- P. Simon and Y. Gogotsi, Materials for electrochemical capacitors, Nat. Mater., 2008, 7, 845–854, DOI:10.1038/nmat2297.
- P. Simon and Y. Gogotsi, Capacitive Energy Storage in Nanostructured Carbon-Electrolyte Systems, Acc. Chem. Res., 2013, 46, 1094–1103, DOI:10.1021/ar200306b.
- G. Wang, L. Zhang and J. Zhang, A review of electrode materials for electrochemical supercapacitors, Chem. Soc. Rev., 2012, 41, 797–828, 10.1039/c1cs15060j.
- Z. Yu, L. Tetard, L. Zhai and J. Thomas, Supercapacitor electrode materials: nanostructures from 0 to 3 dimensions, Energy Environ. Sci., 2015, 8, 702–730, 10.1039/c4ee03229b.
- Y. Zhai, Y. Dou, D. Zhao, P. F. Fulvio, R. T. Mayes and S. Dai, Carbon materials for chemical capacitive energy storage, Adv. Mater., 2011, 23, 4828–4850, DOI:10.1002/adma.201100984.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P. L. Taberna, C. P. Grey, B. Dunn and P. Simon, Efficient storage mechanisms for building better supercapacitors, Nat. Energy, 2016, 1, 16070, DOI:10.1038/nenergy.2016.70.
- V. Augustyn, P. Simon and B. Dunn, Pseudocapacitive oxide materials for high-rate electrochemical energy storage, Energy Environ. Sci., 2014, 7, 1597–1614, 10.1039/c3ee44164d.
- T. Brousse, D. Belanger and J. W. Long, To Be or Not To Be Pseudocapacitive?, J. Electrochem. Soc., 2015, 162, A5185–A5189, DOI:10.1149/2.0201505jes.
- P. Simon, Y. Gogotsi and B. Dunn, Where Do Batteries End and Supercapacitors Begin?, Science, 2014, 343, 1210–1211, DOI:10.1126/science.1249625.
- C.-C. Chen and J. Maier, Decoupling electron and ion storage and the path from interfacial storage to artificial electrodes, Nat. Energy, 2018, 3, 102–108, DOI:10.1038/s41560-017-0084-x.
- R. Yan, M. Antonietti and M. Oschatz, Toward the Experimental Understanding of the Energy Storage Mechanism and Ion Dynamics in Ionic Liquid Based Supercapacitors, Adv. Energy Mater., 2018, 1800026, DOI:10.1002/aenm.201800026.
- J. Chmiola, C. Largeot, P. L. Taberna, P. Simon and Y. Gogotsi, Desolvation of ions in subnanometer pores and its effect on capacitance and double-layer theory, Angew. Chem., Int. Ed., 2008, 47, 3392–3395, DOI:10.1002/anie.200704894.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer, Science, 2006, 313, 1760–1763, DOI:10.1126/science.1132195.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, Relation between the Ion Size and Pore Size for an Electric Double-Layer Capacitor, J. Am. Chem. Soc., 2008, 130, 2730–2731, DOI:10.1021/ja7106178.
- M. Salanne, Ionic Liquids for Supercapacitor Applications, Top. Curr. Chem., 2017, 375, 63, DOI:10.1007/s41061-017-0150-7.
- A. Balducci, U. Bardi, S. Caporali, M. Mastragostino and F. Soavi, Ionic liquids for hybrid supercapacitors, Electrochem. Commun., 2004, 6, 566–570, DOI:10.1016/j.elecom.2004.04.005.
- A. Kachmar, M. Carignano, T. Laino, M. Iannuzzi and J. Hutter, Mapping the Free Energy of Lithium Solvation in the Protic Ionic Liquid Ethylammonuim Nitrate: A Metadynamics Study, ChemSusChem, 2017, 10, 3083–3090, DOI:10.1002/cssc.201700510.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Amphiphilicity determines nanostructure in protic ionic liquids, Phys. Chem. Chem. Phys., 2011, 13(8), 3237–3247, 10.1039/c0cp01137a.
- P. Wu, J. Huang, V. Meunier, B. G. Sumpter and R. Qiao, Voltage Dependent Charge Storage Modes and Capacity in Subnanometer Pores, J. Phys. Chem. Lett., 2012, 3, 1732–1737, DOI:10.1021/jz300506j.
- A. C. Forse, J. M. Griffin, C. Merlet, P. M. Bayley, H. Wang, P. Simon and C. P. Grey, NMR Study of Ion Dynamics and Charge Storage in Ionic Liquid Supercapacitors, J. Am. Chem. Soc., 2015, 137, 7231–7242, DOI:10.1021/jacs.5b03958.
- Y. Shim and H. J. Kim, Nanoporous Carbon Supercapacitors in an Ionic Liquid: A Computer Simulation Study, ACS Nano, 2010, 4, 2345–2355, DOI:10.1021/nn901916m.
- C. Merlet, B. Rotenberg, P. A. Madden, P. L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, On the molecular origin of supercapacitance in nanoporous carbon electrodes, Nat. Mater., 2012, 11, 306–310, DOI:10.1038/nmat3260.
- R. Futamura, T. Iiyama, Y. Takasaki, Y. Gogotsi, M. J. Biggs, M. Salanne, J. Segalini, P. Simon and K. Kaneko, Partial breaking of the Coulombic ordering of ionic liquids confined in carbon nanopores, Nat. Mater., 2017, 16, 1225–1232, DOI:10.1038/nmat4974.
- R. Singh, N. N. Rajput, X. He, J. Monk and F. R. Hung, Molecular dynamics simulations of the ionic liquid [EMIM+][TFMSI−] confined inside rutile (110) slit nanopores, Phys. Chem. Chem. Phys., 2013, 15, 16090–16103, 10.1039/c3cp51266e.
- B. Rotenberg and M. Salanne, Structural Transitions at Ionic Liquid Interfaces, J. Phys. Chem. Lett., 2015, 6, 4978–4985, DOI:10.1021/acs.jpclett.5b01889.
- R. Yan, T. Heil, V. Presser, R. Walczak, M. Antonietti and M. Oschatz, Ordered Mesoporous Carbons with High Micropore Content and Tunable Structure Prepared by Combined Hard and Salt Templating as Electrode Materials in Electric Double-Layer Capacitors, Adv. Sustainable Syst., 2018, 2, 1700128, DOI:10.1002/adsu.201700128.
| This journal is © The Royal Society of Chemistry 2018 |