Open Access Article
Open Access ArticleAn assessment of strategies for the development of solid-state adsorbents for vehicular hydrogen storage
Mark D.
Allendorf
 *a,
Zeric
Hulvey
*bc,
Thomas
Gennett
de,
Alauddin
Ahmed
*a,
Zeric
Hulvey
*bc,
Thomas
Gennett
de,
Alauddin
Ahmed
 f,
Tom
Autrey
g,
Jeffrey
Camp
h,
Eun
Seon Cho
p,
Hiroyasu
Furukawa
f,
Tom
Autrey
g,
Jeffrey
Camp
h,
Eun
Seon Cho
p,
Hiroyasu
Furukawa
 ij,
Maciej
Haranczyk
h,
Martin
Head-Gordon
ij,
Maciej
Haranczyk
h,
Martin
Head-Gordon
 ik,
Sohee
Jeong
jo,
Abhi
Karkamkar
g,
Di-Jia
Liu
ik,
Sohee
Jeong
jo,
Abhi
Karkamkar
g,
Di-Jia
Liu
 l,
Jeffrey R.
Long
l,
Jeffrey R.
Long
 ijm,
Katie R.
Meihaus
i,
Iffat H.
Nayyar
ijm,
Katie R.
Meihaus
i,
Iffat H.
Nayyar
 g,
Roman
Nazarov
n,
Donald J.
Siegel
g,
Roman
Nazarov
n,
Donald J.
Siegel
 f,
Vitalie
Stavila
f,
Vitalie
Stavila
 a,
Jeffrey J.
Urban
a,
Jeffrey J.
Urban
 o,
Srimukh Prasad
Veccham
o,
Srimukh Prasad
Veccham
 i and
Brandon C.
Wood
i and
Brandon C.
Wood
 n
n
aEnergy & Transport Technology Center, Sandia National Laboratories, Livermore, CA 94551, USA. E-mail: mdallen@sandia.gov
bFuel Cell Technologies Office, U.S. Department of Energy Office of Energy Efficiency and Renewable Energy, Washington, DC 20585, USA. E-mail: Zeric.Hulvey@hq.doe.gov
cOak Ridge Institute for Science and Education, Washington, DC 20585, USA
dDepartment of Chemistry, Colorado School of Mines, Golden, CO 80401, USA
eNational Renewable Energy Laboratory, Golden, CO 80401, USA
fMechanical Engineering Department, University of Michigan, Ann Arbor, Michigan 48109, USA
gPacific Northwest National Laboratory, Richland, WA 99354, USA
hComputational Research Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
iDepartment of Chemistry, University of California, Berkeley, CA 94720, USA
jMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
kChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
lChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL 60439, USA
mDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, CA 94720, USA
nLawrence Livermore National Laboratory, Livermore, CA 94550, USA
oMolecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
pDepartment of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), Korea
First published on 13th August 2018
Abstract
Nanoporous adsorbents are a diverse category of solid-state materials that hold considerable promise for vehicular hydrogen storage. Although impressive storage capacities have been demonstrated for several materials, particularly at cryogenic temperatures, materials meeting all of the targets established by the U.S. Department of Energy have yet to be identified. In this Perspective, we provide an overview of the major known and proposed strategies for hydrogen adsorbents, with the aim of guiding ongoing research as well as future new storage concepts. The discussion of each strategy includes current relevant literature, strengths and weaknesses, and outstanding challenges that preclude implementation. We consider in particular metal–organic frameworks (MOFs), including surface area/volume tailoring, open metal sites, and the binding of multiple H2 molecules to a single metal site. Two related classes of porous framework materials, covalent organic frameworks (COFs) and porous aromatic frameworks (PAFs), are also discussed, as are graphene and graphene oxide and doped porous carbons. We additionally introduce criteria for evaluating the merits of a particular materials design strategy. Computation has become an important tool in the discovery of new storage materials, and a brief introduction to the benefits and limitations of computational predictions of H2 physisorption is therefore presented. Finally, considerations for the synthesis and characterization of hydrogen storage adsorbents are discussed.
Broader contextThe widespread use of hydrogen as a clean, sustainable energy carrier has the potential to provide several significant benefits, including a reduction in oil dependency and emissions, improved energy security and grid resiliency, and substantial economic opportunities across many sectors. Hydrogen-fueled vehicles are already appearing internationally, and one of the critical enabling technologies for increasing their availability is on-board hydrogen storage. Stakeholders in developing a hydrogen infrastructure (e.g., state governments, automotive manufacturers, station providers, and industrial gas suppliers) are currently focused on high-pressure storage of H2 at 350 and 700 bar, in part because no viable hydrogen storage material has emerged. Novel adsorbents are an important category of storage materials that have attracted considerable interest because of their potential to meet all DOE targets and deliver hydrogen at lower pressures and higher on-board densities. Nevertheless, the most promising materials synthesized to date require cryogenic temperatures to maximize their capacity, and storage under such conditions is undesirable because it adds complexity and cost to the fuel delivery system. Consequently, a successful solid-state materials solution would significantly reduce costs and ensure the economic viability of a U.S. hydrogen infrastructure. |
Introduction
Storage of hydrogen with sufficient gravimetric and volumetric capacity for vehicular use remains a significant obstacle to the widespread adoption of hydrogen fuel cell electric vehicles (FCEVs). Several FCEV models are now commercially available in limited locations around the world, and in these vehicles hydrogen is stored as a gas at room temperature with a fill pressure of 700 bar. The carbon fiber-reinforced H2 tanks used in these vehicles are expensive, and the compression and pre-cooling requirements that are necessary to deliver 700 bar of H2 at the station add significant penalties with regard to cost, reliability, and energy consumption.1 The U.S. Department of Energy (DOE), in conjunction with U.S. DRIVE (Driving Research and Innovation for Vehicle Efficiency and Energy), a public–private partnership between DOE and automotive, energy, and utility companies, has developed a comprehensive set of hydrogen storage system targets for light-duty vehicles to enable widespread commercialization of FCEVs.2 A few of the most relevant targets are listed in Table 1 along with the current performance of 700 bar systems. These values pertain to the entire storage system, which includes the mass and volume of hydrogen in addition to the tank and associated balance-of-plant (BOP) components. Notably, it is physically impossible to meet the 2025 and ultimate volumetric capacity target with pressurized gas, as the density of H2 gas at 700 bar and room temperature is just 40 g L−1 without accounting for the BOP.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 units per year
000 units per year
The search for solid-state H2 storage materials that can supplant compressed gas systems has been ongoing for at least two decades. The development of a viable storage material would enable increased system-level capacities, thereby resulting in a reduction of the mass, volume, and cost requirements of the storage system. Furthermore, materials-based storage would enable lower operating pressures and potentially reduce other requirements such as pre-cooling at the fueling station, providing additional cost and energy savings to the driver. Among the various types of storage materials, porous adsorbents have the potential to offer rapid filling times and delivery response, long cycle life, and easily-controlled delivery pressures. However, several challenges remain in the development and implementation of such materials: both volumetric and gravimetric capacities for the best performing adsorbents are still well below the DOE targets (Table 1) and usable, system-level capacities can be significantly less than total uptake for a given material. Furthermore, it is difficult to extrapolate system-level performance from the typical laboratory measurements carried out to investigate adsorption properties for a given material. Several material design strategies have been proposed to address these challenges, and in 2010 the DOE-funded Hydrogen Sorption Center of Excellence (HSCoE) produced a report with recommendations for continuing material development efforts (see discussion below).4 Since then, the science of hydrogen storage has advanced considerably and some of these earlier recommendations are no longer valid while others have been amplified by subsequent discoveries. Moreover, new strategies have been proposed in recent years, some of which have received only cursory attention.
The objective of this Perspective is to evaluate the various current known and proposed strategies for improving the performance of hydrogen adsorbents, with an eye toward guiding current and ongoing research, as well as proposals to develop new storage concepts. This work also includes essential updates to the conclusions of the 2010 HSCoE report. In our analysis, the primary focus is on optimizing properties that currently represent major impediments to successful materials implementation, namely low isosteric heats of adsorption (Qst) and sub-par usable volumetric and gravimetric capacities. Clearly, there are other material properties that could significantly impact performance, such as material stability, durability, cyclability, adsorption kinetics, packing density, and system engineering effects; however, to include all of these criteria here is impractical. Consequently, we provide a short discussion of the most pertinent practical metrics for evaluating material utility and the various caveats associated with their optimization.
Theory and modeling are now valuable tools for guiding the design of new materials and for characterizing their performance, and hydrogen adsorbents are no exception. Advances in theory and computing power have greatly improved upon earlier models and in some cases have revised the conclusions of previous results. We deemed it important to also provide an abbreviated overview of theoretical methods and predictions and how they compare with current experiment-based understanding. Recommended methods and levels of theory considered to be the best for modeling specific aspects of adsorbent behavior are discussed. In particular, we address the demanding problem of accurately modeling the interaction energy of H2 with strongly binding sites in metal–organic frameworks (MOFs) and the accuracy of force fields used in atomistic modeling to predict H2 adsorption isotherms.
Finally, we provide guidance concerning the feasibility of synthesizing novel adsorbents, and the potential drawbacks associated with characterization tools used to evaluate them. As in the sections on theory and materials properties, this synthesis section is a concise summary rather than a comprehensive review. Our intention is ultimately to raise awareness of potential key issues so that they can be avoided in future research efforts and when reporting results.
Materials evaluation criteria
Usable gravimetric and volumetric capacities
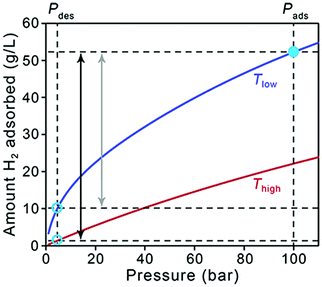
As a starting point, it is useful to briefly address how the target quantities in Table 1 relate to material performance. As stated earlier, these targets are based on the entire storage system, and do not correspond to material-specific properties. Moreover, there can be a significant difference between usable capacity, i.e., H2 that is actually accessible to power the vehicle, and total or excess capacity, which is more typically measured and reported for adsorbents.5 The difference between these two capacities is illustrated in Fig. 1, in which total volumetric H2 uptake versus pressure data is plotted for a hypothetical storage material. The dashed lines correspond to pressures of 5 and 100 bar, which are the pressure bounds typically used for estimating usable capacity in adsorbents. The lower value of 5 bar is a DOE target for the minimum pressure required to deliver H2 to the fuel cell system (the “discharged state”), and the pressure at which the system is fully charged in this case is 100 bar (the “charged state”, or refueling pressure). A refueling pressure of 100 bar is often used to determine usable capacity because it represents the pressure below which an all-metal Type I pressure vessel can be used, imparting significant cost savings over other types of carbon-fiber overwrapped vessels necessary for higher pressure operation.6,7 At the lower pressure end of the isotherm, it is evident that some of the stored H2 is not available for use because the tank pressure is below the lower operating limit of 5 bar. The magnitude of this unused H2 can be substantial for materials with high adsorption energies, i.e., those for which the slope of the isotherm (the Henry's constant in the linear region) is steep at pressures below 5 bar.Storage temperature is another complicating factor, and Fig. 1 also illustrates how the usable capacity of H2 in a given material can change with operating temperature (red and blue curves). As the DOE targets only address hydrogen delivery temperature (−40 to 85 °C, to meet fuel cell system operation specifications) and not the storage system operating temperature, a range of possible system designs can be considered. Materials-based systems designed to operate at lower temperatures may require more complex and costly BOP components (e.g., thermal insulation, heat exchangers) and will therefore likely impart more penalties on the system-level capacity compared to systems designed to operate at ambient temperatures.8 Adsorbent systems could also incorporate a temperature swing step, for example from 77 to 160 K, which increases usable capacities by increasing the quantity of H2 desorbed upon cycling. Systems operating at lower temperatures will also likely require materials with significantly higher capacities compared to ambient temperature systems to compensate for insulation and additional system complexity; unfortunately, there is no simple factor that can be applied to quantify this requirement. Tank design aspects constitute more of an engineering challenge than a materials challenge, and we will not address them in detail here. While it is important to keep operating temperature in mind when comparing the behavior of different adsorbents, it is not necessary to discount a specific class of materials specifically because of operating temperature—the focus herein is on material strategies to increase capacities for any adsorbent.
Historically, much of the early focus on materials development was toward maximizing adsorbent surface area to achieve the necessary gravimetric capacities, and the discovery of ultrahigh surface area materials such as the MOF NU-100 (reported Brunauer–Emmett–Teller [BET] surface area of 6143 m2 g−1) generated excitement that the DOE targets could soon be met.9 This optimism was supported by empirical observations that maximum excess gravimetric capacity increased approximately linearly with increasing surface area, at the rate of ∼1 wt% per 500 m2 g−1 for adsorption at 77 K and moderate pressures of ∼35 bar, commonly referred to as Chahine's rule.10,11 There are some exceptions to this rule, for example in selected carbons an increase in pore size can result in a net decrease in gravimetric H2 uptake, even though the surface area increases.12 Adsorbents that demonstrate very strong binding of H2 can also exhibit gravimetric capacities that exceed those predicted by this relationship.
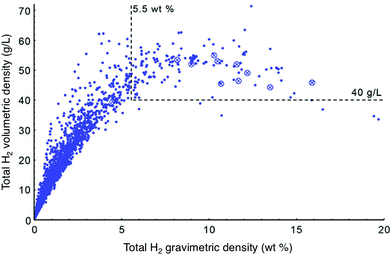
As more high surface area materials were synthesized, it became apparent that exceptional gravimetric capacity often comes at the expense of volumetric capacity. This relationship was reported by Siegel and coworkers, who analyzed the trend between total volumetric and gravimetric capacity calculated for ∼4000 porous materials extracted from the Cambridge Structural Database (Fig. 2). Notably, the authors found that total volumetric capacity is at a maximum for materials with surface areas ranging from 3100–4800 m2 g−1.13 It is unclear whether the trade-off between gravimetric and volumetric capacities represents a peculiarity specific to materials that have been synthesized to date, or instead reflects a universal feature of H2 uptake in adsorbents. Subsequent reports have highlighted the effect of hydrogen storage densities on driving range; these analyses argue that FCEV driving range is more strongly tied to volumetric capacity than gravimetric capacity.6,14,15 Adsorbents with exceptional gravimetric capacities may therefore not be very attractive from a systems-level standpoint, and it is essential that both gravimetric and volumetric capacity be considered simultaneously when analyzing the viability of a specific adsorbent.
Fig. 3 takes these analyses a step further by illustrating the dependence of H2 uptake on adsorbent structural features; here, the simulated total volumetric and gravimetric capacities of a database of MOFs13,14,16 are plotted with respect to five crystallographic properties: density, pore volume, pore diameter (defined as the largest diameter of any internal cavity), gravimetric surface area, and volumetric surface area. The total capacities approximate the usable capacities that could be achieved using a combined temperature–pressure swing process, from T = 77 K and P = 100 bar to T = 160 K and P = 5 bar. Thus, as mentioned above, these total capacities correspond to an upper limit for the amount of H2 that could be delivered by the given material storage system. The ranges of these crystallographic properties that optimize gravimetric and volumetric performance are summarized in Table 2.
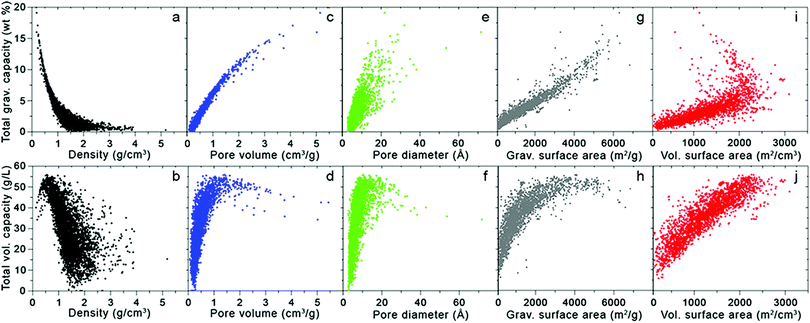 | ||
| Fig. 3 Total gravimetric (top) and volumetric (bottom) capacities as a function of various crystallographic properties for 5309 MOFs extracted from the UM and CoRE databases.13,16 Capacities were calculated at 77 K and 100 bar using Grand Canonical Monte Carlo (GCMC) simulations with the pseudo-Feynman–Hibbs interatomic potential.17–19 | ||
| Crystallographic metric | Range |
|---|---|
| Density (g cm−3) | 0.4–0.5 |
| Pore volume (cm3 g−1) | 1–2 |
| Pore diameter (Å) | 10–20 |
| Gravimetric surface area (m2 g−1) | 4500–5500 |
| Volumetric surface area (m2 cm−3) | 1500–2250 |
Turning first to the dependence of total capacity on MOF density, Fig. 3a shows that gravimetric capacity monotonically decreases with increasing density. In contrast, total volumetric capacity (Fig. 3b) first increases as density increases from zero to ∼0.5 g cm−3, but then drops off for higher densities. These data suggest that maximizing gravimetric and volumetric performance simultaneously can be achieved with densities between 0.4 and 0.5 g cm−3.
With both increasing pore volume and diameter, the gravimetric capacity increases monotonically (Fig. 3c and e, respectively), although the trend is more pronounced in the case of pore volume (Fig. 3c), as might be expected given Chahine's rule (albeit at a higher pressure of 100 bar). The total volumetric capacity displays a non-monotonic dependence on both pore volume and diameter (Fig. 3d and f, respectively), initially increasing with increasing volume and diameter to reach a maximum value for volumes between 1 and 2 cm3 g−1 and diameters between 10 and 20 Å, before decreasing for larger values.
The influence of gravimetric and volumetric surface area on H2 capacity is illustrated in Fig. 3g–j. As expected from Chahine's rule, gravimetric capacity correlates roughly linearly with gravimetric surface area (Fig. 3g). In contrast, the relationship between total volumetric capacity and gravimetric surface area (Fig. 3h) is reminiscent of that observed in Fig. 2: MOFs with very high surface areas (coinciding with large gravimetric capacities) tend to exhibit poor volumetric performance.13 From this data, it is clear that MOFs with gravimetric surface areas ranging from 4500 to 5500 m2 g−1 present a reasonable compromise in balancing gravimetric and volumetric performance. Unsurprisingly, volumetric capacity increases with volumetric surface area in a linear fashion (Fig. 3j), with the highest capacities exhibited by MOFs with surface areas >2000 m2 cm−3. The relationship between gravimetric capacity and volumetric surface area is more complex: although the capacity of most MOFs increases linearly with increasing surface area, the highest capacities are exhibited by several materials with volumetric surface areas in the range of 1000–2000 m2 g−1. Thus, volumetric surface areas between 1500 and 2250 m2 g−1 serve to maximize both gravimetric and volumetric performance.
Additional studies have examined this interplay between gravimetric and volumetric capacities and suggested ranges similar to those given in Table 2 for structural properties that optimize adsorptive H2 storage at cryogenic conditions.20–23 For example, Thornton and coworkers trained a neural network to predict hydrogen uptake across a diverse collection of adsorbents, including MOFs, covalent organic frameworks (COFs), zeolites, zeolitic imidizolate frameworks (ZIFs), and porous polymer networks.20,24 Their model identified several MOFs as amongst the highest capacity materials, with predicted optimal ranges for pore diameter and surface area that closely match those from the MOF-only dataset represented by Fig. 3 and Table 2. This result suggests that these ranges may serve as a reasonable approximation for target structural features in other non-MOF classes of adsorbents, at least under cryogenic conditions.
Can additional optimization of the intrinsic framework structural features increase capacity even more? Metal–organic frameworks already excel on a gravimetric basis, as seen in Fig. 3, with some compounds predicted to exhibit capacities exceeding 15 wt%. On the other hand, under the cryogenic conditions utilized in this study, no known MOFs exhibit total volumetric capacities exceeding 60 g L−1. Given that some MOFs exhibit adsorbed H2 densities comparable to that of liquid or solid H2 (70–76 g L−1), a lofty goal would be to achieve these densities on a total capacity basis, i.e., factoring in both adsorbed and gas-phase H2. Thus, developing new MOFs that improve volumetric performance, without sacrificing high gravimetric density, presents one path forward.
The importance of binding strength
While structural features clearly influence the packing of H2 within an adsorbent, of equal importance are the specific binding locations within the pores and the relative binding strength at these sites. The interaction of H2 with the adsorbent surface is commonly quantified by the enthalpy of adsorption (ΔH) or the isosteric heat of adsorption (Qst), and these values should typically follow the relationship ΔH = −Qst. We note that no strict convention is used when reporting the isosteric heat of adsorption, and it can be given either as −Qst (values >0) or simply Qst (values <0), and in subsequent discussion we report the values as originally reported in the respective publications. These parameters differ slightly in the manner in which they are derived from experimental data and are used somewhat interchangeably by those in the field, although the differential enthalpy of adsorption at zero coverage is most commonly reported, where the gas concentration varies linearly with pressure.11 Since the adsorption enthalpy typically varies as a function of H2 uptake, for practical applications the average ΔH is more important than the low coverage Henry's law enthalpy value, and for most adsorbents the enthalpy of adsorption is expected to decay monotonically with increasing H2 coverage.25At temperatures and pressures above its boiling point, the first monolayer of H2 adsorbed at a solid surface typically exhibits adsorption enthalpies in the range of ∼1–10 kJ mol−1.26 While adsorption enthalpies are reported on a rather limited basis due to measurement challenges, available literature data indicate that enthalpies larger than 10 kJ mol−1 are relatively rare and are mainly found in doped carbons,27 functionalized zeolites,28 and MOFs29 with structural features that impart strong metal–hydrogen interactions (Fig. 4). Examples of some of these materials will be described in detail later in this Perspective. The available literature adsorption enthalpies can be investigated as a function of gravimetric capacity as shown in Fig. 4, and this data reveals that maximum gravimetric uptake at cryogenic temperatures tends to correlate with H2 adsorption enthalpies near 5 kJ mol−1.26,30–33 Qualitatively, a similar trend is observed for volumetric capacities as a function of adsorption enthalpy, although this comparison is difficult as volumetric capacities can be determined in different ways (e.g., utilizing the bulk vs. packing density of a material), resulting in substantially different values.
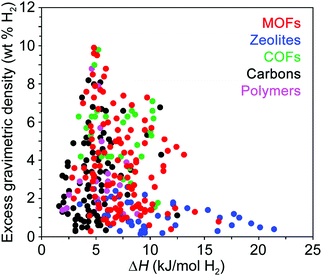 | ||
| Fig. 4 Excess gravimetric H2 uptake versus enthalpy of H2 adsorption for various classes of hydrogen storage materials. The adsorption enthalpy values were taken from ref. 26 and 30–33 and are reported at cryogenic conditions, typically between 77 and 87 K. | ||
A few studies have noted that adsorption enthalpies in the range of 15–25 kJ mol−1 H2—corresponding to H2-framework interactions intermediate between strong physisorption and weak chemisorption—are optimal targets for reversible hydrogen storage.25,34,35 It is important to highlight that these analyses assume a system operating at near-ambient conditions, and adsorption enthalpies are intimately tied to system storage temperatures. Generally speaking, materials with higher heats of adsorption are more likely to exhibit impressive room temperature hydrogen storage behavior. However, because these materials can exhibit steep capacity increases at low pressures, very high heats of adsorption can actually lower usable capacity at a given temperature due to a large amount of inaccessible H2 that remains adsorbed below 5 bar. As the isotherm slope increases, usable capacity will eventually begin to decrease, therefore requiring an upper limit on targeted heat of adsorption values. This balance between high heat of adsorption and optimal usable H2 capacity must be considered when comparing classes of storage materials.
Camp and Haranczyk recently investigated the impact of temperature and binding energy on adsorbent usable capacity, and the results of this study are reported here for the first time. The analysis focused on a model material with the same structure as M2(dobdc) (M-MOF-74 or CPO-27-M; M = Mg, Mn, Fe, Co, Ni, Cu, or Zn; dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate), which contains the highest density of open metal sites of any known framework. The adsorption energy of H2 in M2(dobdc) was modeled by mixing Lennard-Jones parameters for each atom in the structure with Lennard-Jones parameters for hydrogen atoms. For example, the adsorption energy between a framework Mg2+ site and an adsorbed H2 molecule was calculated by using values of σH2 = 2.958 Å and εH2 = 36.7 K36 and σMg = 2.961 Å and εMg = 55.895 K37 in the Lorentz–Berthelot mixing rule38 and applying the 12-6 Lennard-Jones equation:
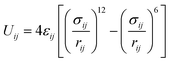 | (1) |
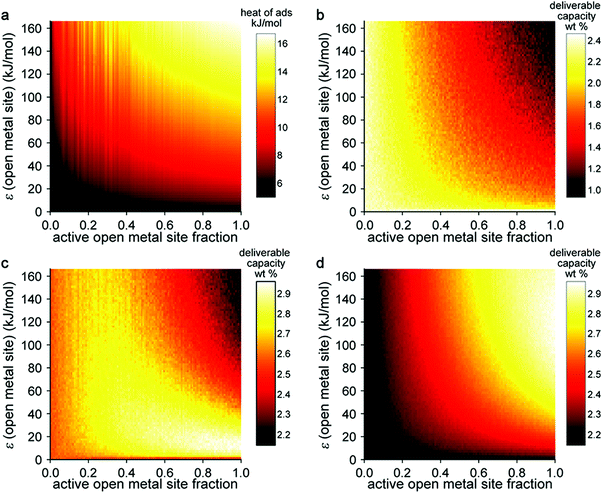
In this model system, the H2-open metal site interaction energy was artificially altered by varying the ε parameter for each metal from 0 to 2 × 104 K, yielding interaction energies of 0–163 kJ mol−1. This variation allowed for the simulation of hypothetical binding interactions with H2 heats of adsorption (at low coverage) as high as 16 kJ mol−1. As a means of probing the effect of strong binding site density, an additional variable corresponding to the fraction of active open metal sites was introduced. This approach was realized by assigning a portion of the total metal sites a dummy value of ε = 0 K, effectively making them inactive for H2 binding. Each pixel on the heat map plots in Fig. 5 corresponds to the output of an independent Grand Canonical Monte Carlo (GCMC) simulation at a given active open metal site concentration (x-axis) and open metal site interaction strength (y-axis).
These simulations showed that at cryogenic temperatures (77 K, Fig. 5b), open metal sites with high interaction energies are not needed to maximize H2 usable capacity, because the enhancement these sites provide results in a large percentage of the adsorbed H2 binding at very low pressures. Thus, a considerable portion of the H2 remains bound to the material in the discharged state at 5 bar and therefore cannot be utilized as fuel. At near-ambient temperatures (243 K, Fig. 5d), stronger and more open metal sites are desired to increase usable capacity, because isotherms are much flatter in the low-pressure region and less H2 is bound to the material in the discharged state. At intermediate temperatures (180 K, Fig. 5c), there is an interesting interplay between these effects—materials that have fewer open metal sites display fairly constant usable capacities regardless of the binding strength at those sites, and materials with more open metal sites display higher usable capacities as the binding strength at those sites decreases.
This work demonstrates that estimating system-level performance is more complicated than simply targeting materials with binding strengths within a specific range, highlighting that the proposed 15–25 kJ mol−1 target enthalpy range for adsorbent materials is only applicable to a certain set of storage conditions at ambient temperatures. We note that this study was carried out for gravimetric capacity only and that as a similar study on volumetric capacity would be valuable. An ideal study would combine, in some form, the two types of sensitivity analyses described in this section, investigating the effect of optimizing both pore structure and strong binding sites. We expect that further development of high throughput simulation approaches and material databases (including both real and hypothetical structures) will enable such analyses. Machine learning techniques will likely play a role in simplifying resulting data into practical materials design rules.
Finally, we note that the entropy change upon H2 adsorption can also influence the overall adsorption thermodynamics, and the magnitude of this value is dominated by the loss of the hydrogen gas entropy in the form of translational, vibrational, and rotational degrees of freedom.35,39,40 However, it is believed that ΔH has a greater effect on the overall thermodynamics of hydrogen adsorption in adsorbents. As a general rule, increasing the strength of the interaction between the H2 molecule and the storage material—except for a few special cases and conditions, such as when this increase results in decreased deliverable capacities—appears to enhance overall material performance, and a major thrust of current materials development efforts are focused on strategies to optimize this interaction.
Theoretical calculations of H2 physisorption
Theory has proven to be an invaluable tool for predicting promising new target storage materials, their properties (e.g., adsorption isotherms), and for interpreting experimental data. In this section, we provide an overview of key computational methods and a qualitative sense of their strengths and weaknesses. Understanding the limitations and relative accuracy of various theoretical methods is important for experimentalists assessing the likelihood that a materials strategy predicted theoretically will be successful. Some of the most common theoretical methods used to compute H2 interactions with adsorbent materials are presented in Table 3, along with the relative strengths and limitations of each method. The methods are divided into three categories, each of which is summarized below.| Method | Key properties determined | Typical accessible scales | Benefits | Limitations and challenges | Sample references | |
|---|---|---|---|---|---|---|
| Static first principles | Ab initio wavefunction methods (quantum chemistry) | Binding energies, vibrational frequencies within static approximation | 50–100 atoms, depending on method | High accuracy (especially CCSD(T)), including explicit evaluation of correlation | Very high computational expense; limited to finite cluster models; no dynamical information; limited scalability on modern architectures | 41–43 and 59–61 |
| Quantum Monte Carlo (QMC) | Binding energies | ∼100 atoms | High accuracy, including explicit evaluation of correlation; provides systematic statistical measure of convergence; can be applied to clusters or extended systems; highly scalable on modern architectures | Very high computational expense; no dynamical information, explicit forces, or structural optimization; requires geometry inputs from DFT or experiments | 44–46 and 62–67 | |
| Static density functional theory (DFT) with van der Waals corrections | Binding energies, vibrational frequencies within static approximation | ∼1000 atoms | Generally offers best overall tradeoff between accuracy and computational expense; can be applied to clusters or extended systems | Intermediate computational expense; accuracy is dependent on choice of XC functional, which is not always straightforward | 47–50 and 68–70 | |
| Dynamical | Ab initio molecular dynamics (AIMD) | Dynamic vibrational frequencies; entropy; enthalpy contributions from gas–gas interactions | Hundreds of atoms (<100 ps) | Based on DFT, so it accounts for polarization, hybridization, charge transfer, etc. within dynamics; explicitly captures anharmonic contributions to entropy; can include relaxation of sorbent geometry | Intermediate to high computational expense; short time scales complicate convergence of statistical quantities; difficult to simulate large frameworks or amorphous systems; no quantum nuclear effects; usually requires fixing total H2 molecules; inherits same limitations as DFT | 51–53 |
| Classical molecular dynamics and empirical force-field methods | Adsorption enthalpy; entropy; enthalpy contributions from gas–gas interactions | Millions of atoms (depends on complexity of force field; ∼1 ns) | Can access much longer scales than first-principles methods; low computational expense for robust convergence of thermodynamic quantities; can include quantum nuclear effects approximately; can include relaxation of sorbent geometry (with properly parameterized potentials) | Parameterization and accuracy validation are difficult; poor transferability; can fail to capture physics of stronger-binding interactions and anharmonicity; usually requires fixing total H2 molecules | 57 and 71–74 | |
| Statistical mechanical | Grand Canonical Monte Carlo (GCMC) | Full pressure–temperature–composition equilibria; adsorption isotherms | Determined by method for energy computation (usually similar to classical MD) | Robust statistical–mechanical method allows for calculation of composition-dependent equilibria; allows for variation of total H2 molecules; typically uses empirical force fields for accessing long scales | Accuracy and limitations depend on method for computing interaction energy (usually empirical force fields); no dynamical information; vibrational/rotational/translational entropy must be computed separately; most implementations assume fixed sorbent geometry | 56–58, 75 and 76 |
Introduction to theoretical methods
The first category in Table 3 includes various static total-energy methods based on first principles that are generally used to evaluate accurate H2 binding energies, as well as certain enthalpy and entropy contributions. These simulations are run at 0 K, and their primary advantages are relative accuracy and transferability (i.e., general applicability), because they rely on quantum mechanics and can therefore capture a variety of physical contributions in an unbiased way, including dispersion, hybridization, and charge transfer. Typically, these methods are used to compute specific interactions between H2 molecules and individual sites, which makes them suitable for computing quantities such as ΔH in the low-pressure regime, where interactions between H2 molecules can often be ignored. Examples of such approaches include ab initio wavefunction methods commonly associated with quantum chemistry,41–43 Quantum Monte Carlo (QMC),44–46 and density functional theory (DFT).47–50 Each method offers different strengths in computational accuracy, expense, and model complexity.The second category consists of dynamical methods, which have the advantage of providing explicit properties at finite temperatures, including enthalpy contributions from gas–gas interactions, as well as vibrational, rotational, and translational entropy contributions. This treatment provides specific advantages for accurately computing the entropy of systems with intermediate-strength binding, for which the available degrees of freedom cannot otherwise be readily approximated. Approaches include ab initio molecular dynamics based on DFT51–53 and classical molecular dynamics based on empirical force fields.54
The third category of computational approaches includes statistical–mechanical methods for computing equilibrium thermodynamics—most notably, GCMC simulations.54–58 These simulations use a stochastic Monte Carlo approach that varies the number of H2 molecules as well as their positions. This strategy permits evaluation of thermodynamic equilibrium properties at any constant H2 pressure. The advantages of GCMC make it the most widely used technique for evaluating full H2 adsorption isotherms, the results of which can be directly compared with experimental data. Because GCMC simulations generate many individual configurations, the corresponding energies are usually evaluated with empirical force fields for computational efficiency.
In the following sections, we explore some of the challenges in accurately predicting H2 physisorption using several of the abovementioned techniques, including key sources of error. We also provide an overview of current trends in the development of improved methods and offer recommendations for best practices, including acceptable concessions when choosing between computational efficiency and accuracy.
Binding energy predictions
| Rank | Functional | RMS error (kJ mol−1) |
|---|---|---|
| 1 | ωB97M-V | 0.75 |
| 2 | B97M-rV | 0.91 |
| 3 | ωB97X-V | 0.99 |
| 4 | B97M-V | 0.99 |
| 5 | B3LYP-D3(CSO) | 1.27 |
| 13 | BLYP-D3(BJ) | 1.42 |
| 25 | TPSS-D3(CSO) | 1.53 |
| 62 | PBE-D3(CSO) | 1.89 |
| 115 | PBE-D2 | 2.69 |
| 159 | PBE | 8.19 |
Nevertheless, although improving quantitative accuracy remains the goal of DFT XC functional development, it is worth emphasizing that qualitative trends in binding energy are often reproduced even with comparatively simple functionals, including generalized gradient approximations (GGAs) with standard −D corrections. Indeed, most modern dispersion-corrected DFT methods (such as those in Table 4) tend to give consistent trends for binding that are derived almost exclusively from dispersion forces. For adsorbent materials that feature significant H2 interactions beyond dispersion, as is generally the case for the most promising hydrogen storage materials, the results can be more varied. While permanent electrostatic effects are typically adequately described even by the simplest DFT XC functionals, treatment of more complex contributions such as Lewis acid–base interactions and backbonding, which involve charge transfer, induction, and orbital hybridization,59,60 can differ broadly across functionals (see Fig. 6 for an example). In these latter cases, predicted trends should be treated with a degree of caution unless the most sophisticated XC functionals are employed, since individual physical contributions may be treated at different levels of accuracy. As a general rule, the safest approach when evaluating the reliability of a predicted binding trend is to limit comparisons to systems for which the primary underlying physical interaction is very similar. This allows one to take advantage of intrinsic error cancellation. Notably, there have also been recent efforts to introduce error estimation directly into the formulation of the XC functional.85
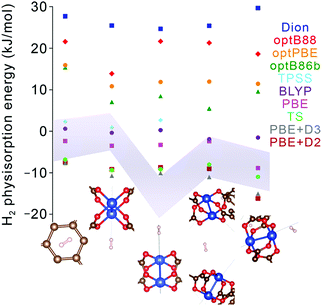 | ||
| Fig. 6 Hydrogen physisorption energies (colored data points) at different binding sites in Cu2(bptc) (MOF-505) predicted using lower-level GGA DFT functionals (PBE, BLYP) and several different formulations of van der Waals-corrected and meta-GGA DFT functionals (Dion, optB88, optBPE, optB86b, TPSS, TS, PBE+D2, PBE+D3).68,79,88–91 Results are compared with the one-σ (68%) confidence interval obtained from QMC runs (grey shaded region). Geometries for each of the sites (bottom) were fixed to those obtained from PBE+D3 and exhibit little variation with the chosen method, unlike the binding energies. The systematic statistical nature of QMC allows for downselecting appropriate DFT functionals for different types of binding sites, with confidence levels based on the degree of QMC convergence. | ||
Quantum Monte Carlo (QMC) is an alternative benchmark method for modeling noncovalent interactions that affords similar accuracy to CCSD(T) and yet can be applied equally to molecular clusters or to extended periodic systems.44–46 To date, most QMC calculations of H2 physisorption have focused on molecular clusters, including Ca2+ complexes,62,63 certain metal–organic complexes,64,67 and aromatic carbon complexes.65,66 The results of these calculations can vary significantly from DFT with simple XC functionals; for instance, in the case of Ca2+, QMC predicted that the binding of four H2 molecules is energetically unstable or hardly stable (and then only at 0 K),62,63 in contrast with earlier DFT and MP2 calculations that predicted stable binding of up to eight H2 molecules.86,87 Likewise, Fig. 6 shows substantial discrepancies between QMC binding energies of H2 on Cu2(bptc) (MOF-505; bptc4− = 3,3′,5,5′-biphenyltetracarboxylate) and a number of DFT-based results; such analyses can aid selection of the best DFT XC functionals. An important qualification for QMC is that input geometries must be precisely known (e.g., from neutron diffraction) or obtained using DFT or another lower level of theory.
These shortcomings suggest the use of a hybrid approach, in which first-principles-derived binding energies are used to parameterize force fields for the stronger-binding interaction sites (often aided by energy decomposition analysis to isolate individual physical contributions95–97), with reliance on more standard force-field formulations for H2 intermolecular interactions and weaker-binding sites. The development and assessment of system-specific force fields for H2 binding and release in adsorbents is a topic for a review in itself.58,98–100 Note that most of the articles referenced here are not specific to H2, but the successful approaches are generic to the binding of any small, non-polar, closed-shell molecule in a nanoporous framework.
Thermodynamic factors beyond binding energy
As a result of significant improvements in first-principles approaches and increased computing power that can facilitate larger benchmark calculations, the evaluation of electronic binding energies is no longer necessarily the accuracy-limiting step in computational studies of the binding free energy of H2. In this subsection, we briefly review other key thermodynamic factors.Alternatively, entropic contributions can be computed directly from finite-temperature molecular dynamics (either ab initio or classical methods). One promising approach for using dynamics trajectories to interpolate and extrapolate entropy over a broad range of temperatures is the two-phase thermodynamic method of Lin et al.106 This method has been used to evaluate the entropy of pure CO2, as well as adsorbates confined within zeolites, suggesting a similar approach may be adopted to obtain accurate entropies of bound H2.107,108
The most widely used approach for incorporating nuclear quantum effects is to modify GCMC and classical molecular dynamics via a so-called Feynman–Hibbs potential.113 Reasonably good agreement with experimental results has been obtained for H2 adsorption in a range of MOF systems using this approach.14 Another recent example is H2 adsorption in Zr6O4(OH)4(bdc)6 and Zr6O4(OH)4(bpdc)6 (known as UiO-66 and UiO-67, respectively; bdc2− = 1,4-benzenedicarboxylate, bpdc2− = biphenyl-4,4′-dicarboxylate).75 Full path-integral formulations of GCMC have also been recently explored.76
Adsorbent models
The previous sections focus primarily on efforts to improve the accuracy of predicted H2 binding thermodynamics. However, another potential source of error arises from the adsorbent models themselves, which are often simplified to render them computationally accessible. Here, we briefly explore some of the primary issues associated with reducing model complexity for both framework materials with long-range order (e.g., MOFs) and high surface-area amorphous materials such as porous carbons.The main alternative to cluster models is the use of periodic boundary conditions (PBCs), which is a natural approach in conjunction with periodic plane-wave basis functions that are commonly used for solid-state DFT calculations.115 However, these models can be more limited in their accuracy; for instance, while dispersion-corrected GGAs are widely used for PBC-DFT calculations, higher-accuracy functionals are less common due to their high computational cost. It is possible to employ cluster-based corrections to PBC-DFT calculations to achieve greater accuracy in modeling local interactions; examples of their application include H2 binding in MOF-5 (Zn4O(bdc)3) and recent work on CO and N2 binding in Mg-MOF-74.116,117
In practice, the presence of disorder and heterogeneity can make it impossible to derive an exact model for many adsorbents, particularly within the size constraints of simulation supercells that are accessible to first-principles methods. Instead, a broader picture of the interaction of a material with hydrogen must be derived from simpler representative fragment models. This strategy is best justified if the dominant physical interaction is relatively short-range; examples include interactions with specific functional groups or substitutional defects that introduce polarization and/or partial charge transfer.120 The actual material may incorporate many different types of functional groups or defects, which can be investigated within the fragment models. However, because this approach does not generate an integrated material model, one cannot utilize GCMC simulations to simulate isotherms over the full pressure range. An alternative is to generate a single representative model based on fragments, provided the computational expense of the larger model can be handled. This hybrid approach has been demonstrated by Singh et al., wherein carbon foam models were constructed by fusing carbon nanotube fragments.112 These integrated models were then varied systematically and used to examine H2 adsorption via GCMC simulations.
Considerations for adsorbent synthesis and characterization
A lack of reproducibility in the available data on hydrogen adsorption in adsorbent materials has historically proven to be a significant impediment to the field, so much so that the topic was the subject of recent reviews.5,121,122 Similar concerns have been raised in the context of other adsorbed gases, including CO2, with new metrics proposed to assess isotherm reproducibility in these systems.123 Irreproducible and erroneous data span various synthetic, material handling, and characterization methods. With regard to synthetic techniques, the majority of porous frameworks are synthesized solvothermally using common organic solvents, although a diverse set of synthetic strategies is available. These methodologies have been reviewed elsewhere, and the specifics of adsorbent synthesis are not the focus of this section.124–129 Instead, we present some suggestions for best practices concerning activation and handling of adsorbents as well as characterization methods employed to confirm products and properties, and we also highlight common areas where incorrect approaches lead to inaccuracy in the assessment of candidate adsorbents for H2 storage.Adsorbents are not porous until solvent or other pore-templating molecules are removed from the as-synthesized material. This activation process is most simply carried out by heating the material under vacuum, but if this approach is not sufficient, or results in some amount of structural degradation, then more complex solvent exchange methods may be necessary.130 Materials that contain very large pores, high surface areas, or solvent molecules bound to metal sites in the framework are typically more challenging to activate. Following synthesis, some strongly metal-bound solvent molecules (e.g., N,N-dimethylformamide [DMF]) can be removed by first performing a solvent exchange, wherein the as-synthesized material is soaked in a lower-boiling or more weakly coordinating solvent (e.g., chloroform or methanol). Over the course of a few days—during which time the soaking solvent is replenished several times—the strongly-bound solvent is gradually displaced and washed from the framework in favor of the soaking solvent. The latter can then be removed from the material by mild heating under vacuum.29 Drying with supercritical CO2 drying has become a widespread approach over the last decade, as it has been demonstrated that the negligible surface tension of the carbon dioxide allows for the activation of more delicate structures that otherwise might collapse upon heating. This method is now used commonly by MOF researchers to achieve high surface areas.131–133
Regardless of the activation method used, it is of utmost importance to ensure that the extent of activation and chemical composition of the material is known. Activation protocols should be accompanied by combined thermogravimetric analysis and mass spectrometry (TGA-MS) experiments, and routine analysis such as IR spectroscopy can be used to identify stretches arising from solvent molecules, decomposition products, or other impurities. For crystalline materials, powder X-ray diffraction patterns collected before and after activation should be measured to confirm that minimal degradation has occurred. Surface area and pore volume measurements should also be carried out and compared to predictions from crystal structures when possible, to ensure optimum material porosity. Even in rare cases where complete activation of the material is not necessarily desired, a quantitative knowledge of the material composition is still essential to understand adsorption data or cycling ability. Following activation, materials should be handled under inert conditions, regardless of how air- or water-sensitive the samples are, in order to ensure the activated material remains pristine. We note that confirmation that an adsorbent is fully activated is becoming even more critical as synthetic complexity increases, for example for materials targeted to bind more than one H2 molecule at an individual open metal site.134 Activation processes for these materials may likely be considerably more difficult than those known to date, and side products or species remaining from metalation reactions or post-synthetic modification will need to be accounted for and completely removed.
Investigation of the adsorption properties of a given material should commence only once diligent activation and characterization procedures have been used to establish that a material is permanently stable, porous, and of known stoichiometry. There are many reviews and documents available to provide guidance on best practices pertaining to hydrogen isotherm collection and data analysis, and the potential errors and difficulties associated with these measurements.5,135,136 Although improper technique in the measurement of adsorption data can result in inaccurate data, even a properly measured isotherm can be corrupted by a sample that has not been properly activated or handled; unfortunately, in such cases the resulting data do not always appear incorrect or anomalous. Consequently, it is advisable that samples prepared for gas adsorption measurements undergo a degassing step prior to isotherm collection, ideally monitored by mass spectrometry. Desorption and cycling measurements are highly recommended, as these can provide both isotherm quality control and verification of reversibility. A desorption isotherm for a physisorptive material that does not exhibit a large degree of flexibility or a pore-opening mechanism should closely mirror the adsorption isotherm; if it does not, then either an instrumental error, sample degradation, or a side reaction with hydrogen may have occurred.137 Side reactions can occur in materials with residual reactive groups or surface oxides, resulting in the formation of water or other bound molecules and erroneously high adsorption capacities. However, simple characterization methods can be used post-isotherm collection to check for these reactions.
It is also important to consider sample size when carrying out capacity and other measurements. In general, larger sample size improves the accuracy of isotherm measurements for reasons that are described in detail in the previously referenced best practices document.135 Often novel adsorbents are prepared using synthetic procedures that yield only small sample sizes, but the suite of high-quality characterization methods described above will typically require gram-scale amounts of adsorbent material to produce the most reliable data. Although increasing material yields beyond a few grams is often secondary to initial exploratory synthesis efforts, it is important to keep in mind that a material that requires difficult or expensive preparation may have diminished utility as a viable storage material. A techno-economic analysis was recently published for three MOFs in the M2(dobdc) series (M = Ni, Mg, Zn) and provides some valuable insight concerning the aspects of synthetic procedures contributing most to material cost.138
Investigations into the nature of hydrogen adsorption beyond storage capacity require additional characterization tools; for example, variable-temperature capacity measurements are commonly used to calculate Qst. Temperature-programmed desorption measurements can also provide information regarding the magnitude of H2 binding at strong adsorption sites. In addition, in situ variable-temperature diffuse reflectance infrared spectroscopy measurements are used to determine the enthalpy of adsorption at a particular binding site.29,139 For crystalline adsorbents, neutron powder diffraction on deuterium-loaded samples is an extremely powerful technique to elucidate crystallographic binding sites for H2 molecules.29,134,140 This method has been extensively used to investigate H2 bound at open metal sites in MOFs and other strong binding sites, as well as to explain adsorption behavior and direct subsequent synthetic efforts. Inelastic and quasi-elastic neutron scattering techniques can provide further site-specific binding details and insights into H2 diffusion behavior.141,142 Finally, although here we are focused on materials challenges, is important to note that it is now possible to predict systems-level performance on the basis of material property data alone, using recently developed models that are continually being updated and are publicly available online for use by researchers.143
Revisiting the results of the 2010 HSCoE final report
In 2010, the DOE-funded Hydrogen Sorption Center of Excellence (HSCoE) published a final report recommending that development efforts for specific material classes be continued where viable synthetic routes exist for adsorbents that can potentially meet the DOE onboard storage targets.4 The four recommended focus areas are summarized below and re-reviewed in light of the previous eight years of advances in the field.Recommendation 1: develop materials for hydrogen storage by weak-chemisorption via a spillover-type mechanism
In so-called spillover materials, H2 molecules are dissociated at a catalytic site and H atoms are subsequently transferred to high surface-area receptor materials. At the time of the HSCoE study, spillover materials were attractive due to reports that they could exhibit binding energies as high as 10–30 kJ mol−1, and initial analyses suggested that excess gravimetric capacities exceeding 7 wt% should also be possible with such materials.144–147 Moreover, the center determined that because spillover should be applicable to materials with >1 g mL−1 bulk density, storage systems exceeding gravimetric and volumetric capacities of 5.5 wt% and 50 g L−1, respectively, should be achievable at ambient temperature and ∼100 bar.Since then, it has been confirmed theoretically and experimentally that the gravimetric storage limits of materials demonstrating the spillover mechanism are sufficiently low to prevent them from being viable for onboard storage.148 Investigators have also discovered that effects such as metal oxide reduction of catalyst particles and irreversible hydrogenation reactions plague many spillover materials.137,149 Many of the previous reports of high capacities in spillover materials ultimately could not be reproduced, leading to an extended debate in the literature concerning several of the assumptions that drove research on these materials around the time of the HSCoE report.121,150–156 Consequently, spillover materials are no longer a significant focus of hydrogen storage materials research.
Recommendation 2: develop materials for multiple-dihydrogen storage on designated sites
Research aimed at demonstrating binding of multiple H2 molecules at a single site continues to be a major focus within the hydrogen storage community. As will be described in subsequent sections, this recommendation presents a daunting synthetic challenge, and only recently has the binding of more than one H2 molecule at a metal site been experimentally demonstrated.134 The associated synthetic efforts are being accompanied by development of advanced computational approaches as outlined earlier, which predict that materials of this type have the potential to meet DOE targets.59Recommendation 3: develop substituted/heterogeneous materials with demonstrated hydrogen binding energies in the range of 10–25 kJ mol−1
This recommendation concerns materials such as doped carbons or framework materials with sites that can achieve H2 binding enthalpies >10 kJ mol−1, with the intention of enabling storage at near-ambient conditions. Efforts to strengthen H2 binding continue to be important, and broadly speaking, this strategy is probably receiving the greatest attention in the field today; several types of materials currently under investigation in this category are discussed below.Recommendation 4: limit development of materials in which the storage mechanism is physisorption to only those with optimized structures
This recommendation refers to weakly binding adsorbents, i.e., non-functionalized carbons or MOFs without open metal sites, in which H2 binds to pore surfaces solely by van der Waals interactions and without enhanced polarization through chemically-functionalized moieties. The report recommends that only materials with surface areas >3000 m2 g−1 and optimized pore sizes in the range of 0.7–1.5 nm should be considered, as these properties are likely necessary to achieve uptakes approaching the DOE targets. Research aimed at synthesizing structures with optimized or well-controlled features is ongoing and benefits from modeling and structural database screening (described above, with data shown in Table 2 and Fig. 3) that correlates uptake with specific crystallographic features.13,14 Of course, these materials may require cryogenic or low-temperature operation and will therefore need to exhibit extremely high volumetric capacities to be viable for application.Perspectives on current material strategies
In the sections below, we briefly review recent work on several classes of adsorbents that have either been extensively evaluated for H2 storage or are currently under evaluation. Their strengths and weaknesses are discussed alongside existing challenges impeding progress. The literature review is not intended to be comprehensive, but rather illustrative of our assessment of progress and potential for the material strategies embodied in each of these classes.MOFs containing metals with unsaturated coordination spheres
In stable inorganic molecular complexes, the coordination sphere of a metal ion is typically fully occupied with organic ligands and/or anions, and the removal of even weakly-bound coordinated species may lead to collapse of the structure or generation of a reactive species prone to decomposition. The metal sites of as-synthesized MOFs are also typically coordinated with organic linkers, solvents such as DMF and ethanol, and/or counter anions such as OH− and F−; however, the rigidity of these frameworks often renders it possible to remove such molecules (via heating or exposure to vacuum, or some combination) without loss of structural integrity. Importantly, the resulting exposed framework metal coordination sites can exhibit strong Lewis acidity, making the material advantageous for gas capture applications.157,158 The accessibility of open metal sites within a MOF was first shown for Cu2(ATC) (also known as MOF-11; ATC4− = adamantane-1,3,5,7-tetracarboxylate), wherein removal of coordinated water molecules from the Cu2+ sites could be accomplished without loss of framework crystallinity or surface area.159 The absence of water within the structure was confirmed by single crystal X-ray diffraction studies. Shortly after the first study of H2 adsorption in MOF-5, the framework MOF-505, which also exhibits open Cu2+ coordination sites, was investigated for H2 adsorption.160,161 Upon removal of coordinated water and/or acetone molecules, the fully desolvated material exhibited an increased H2 uptake (2.41 wt% versus 1.39 wt%) at 77 K and 1 bar.As mentioned previously, detailed characterization of H2 adsorption at framework open metal sites can in some cases be afforded by techniques such as in situ neutron diffraction and diffuse reflectance infrared spectroscopy. In 2006, low temperature neutron diffraction studies of Mn-BTT revealed that H2 adsorption primarily occurs at the exposed Mn2+ sites of the square planar Mn4Cl units (Fig. 7).140 The distance between Mn and D2 determined from these measurements (2.27 Å) was much shorter than observed previously between D2 and the saturated Zn4O(CO2)6 cluster of MOF-5 (∼3.1 Å).162 Strong binding due to polarization of the H2 molecule was supported by a distinctive downshift of the adsorbed H2 stretching band (4038 cm−1) compared to that in MOF-5 (4128 cm−1), observed by in situ IR spectroscopy.114,163 The IR absorption band at 4038 cm−1 evolved gradually as the temperature was lowered from 150 to 14 K, with two peaks arising at 4126 and 4133 cm−1 (below 100 K) and a third absorption band appearing at 4140 cm−1 (below 40 K). Here, the band at 4038 cm−1 corresponds to the adsorption of H2 at the Mn2+ sites and, importantly, the temperature dependence of this peak can provide a means of determining the thermodynamic parameters for adsorption at these specific sites.29,114 From the van’t Hoff plot, the magnitude of the ΔH value for the primary binding sites in Mn-BTT was estimated to be −11.9 ± 0.6 kJ mol−1, which is slightly greater than the Qst for Mn-BTT (−10.1 kJ mol−1), extracted from low-pressure H2 adsorption measurements.114,140 Note that such differences are typical since the Qst values are averaged over all adsorbed H2 species.
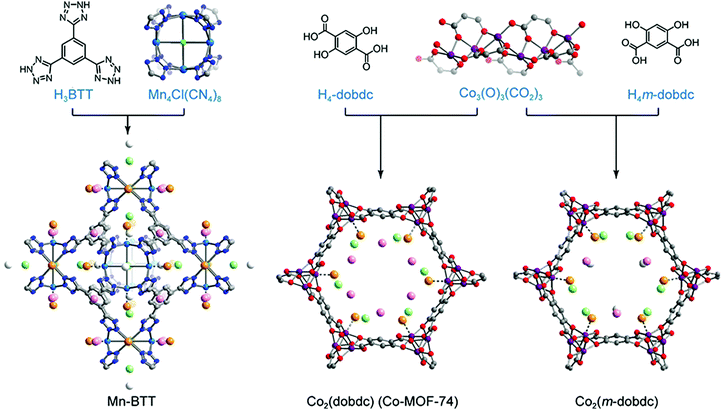 | ||
| Fig. 7 (top) Molecular structures of organic linkers and inorganic building units comprising the Mn-BTT, Co2(dobdc), and Co2(m-dobdc) MOFs. (bottom) Crystal structures of each framework loaded with D2 (16 molecules per Mn4Cl unit in Mn-BTT and 2.25 D2 per Co2+ for Co2(dobdc) and Co2(m-dobdc)). Gray, red, dark blue, blue, and purple spheres represent C, O, N, Mn, and Co atoms, respectively. Deuterium molecules adsorbed at primary, secondary, ternary, and quaternary sites are shown in large orange, light green, pink, and white spheres, respectively. D2-framework interactions for the primary binding site are drawn as dotted lines. Hydrogen atoms of organic linkers are omitted to clarify.29,140 | ||
Owing to their high concentration of coordinatively-unsaturated metal sites, the M2(dobdc) family of frameworks (M = Mg, Co, Ni, Mn, Fe, and Zn) have also been heavily explored for H2 storage (Fig. 7). In this structure type, M2+ ions are connected through 2,5-dioxido-1,4-benzene-dicarboxylate linkers to form one-dimensional hexagonal channels that extend along the c-axis of the crystal, and the octahedral coordination environment of each metal in the as-synthesized material is completed by a solvent molecule. This solvent is readily removed with heating under vacuum to yield one-dimensional channels replete with open metal sites. Hydrogen adsorption has been extensively investigated in this series29,164–166 and it has been shown that at low pressures the strength of the metal–H2 interaction is highly dependent on the identity of the framework metal ion. From H2 isotherm measurements, the Qst value for Ni2(dobdc) was estimated to be −11.9 kJ mol−1,29 and across the entire series the −Qst values follow the trend Zn2+ < Mn2+ < Fe2+ < Mg2+ < Co2+ < Ni2+. This trend in the metal–H2 interaction strength generally follows the Irving–Williams series for high spin octahedral transition metal complexes, such that the −Qst values increase as metal ion radius decreases.167
More recently, the structural isomer of M2(dobdc), M2(m-dobdc) (m-dobdc4− = 4,6-dioxido-1,3-benzenedicarboxylate, M = Mg, Mn, Fe, Co, Ni) (Fig. 7), was identified as a promising alternative material for H2 adsorption, due to the greater charge density of its open metal sites and the lower cost of the organic linker.29 Interestingly, although the porosity of the M2(m-dobdc) series is similar to that of M2(dobdc), the former materials exhibit higher H2 uptake at 77 K and 1 bar, associated with −Qst values that are larger by 0.4–1.5 kJ mol−1 when comparing metal congeners. For example, the Qst value for Ni2(m-dobdc) was estimated from low-pressure H2 isotherms to be as large as −12.3 kJ mol−1, compared to a slightly smaller magnitude of −11.9 kJ mol−1 for Ni2(dobdc). While the significance of this difference could be debatable in the absence of error, values of ΔH for the Ni–H2 interaction in Ni2(m-dobdc) and Ni2(dobdc) were estimated from in situ IR spectroscopy to be −13.7 and −12.3 kJ mol−1, respectively, supporting a much stronger H2 interaction in the former material. Rigorous comparison of M2(m-dobdc) and M2(dobdc) materials via neutron diffraction, IR spectroscopy, and electronic structure calculations revealed that a subtle difference in the local metal environment leads to an increased positive charge density at the open metal sites of the M2(m-dobdc) compounds, promoting greater charge transfer from H2 to the metal center and leading to an enhanced metal–H2 interaction energy.29 Neutron diffraction characterization of Ni2(m-dobdc) also revealed tight packing of adsorbed D2 and a short D2⋯D2 contact of 2.82 Å between molecules adsorbed at primary and secondary sites (Fig. 7). This distance is even smaller than the distance of 3.23 Å observed between molecules in solid H2 at 5 K and highlights the potential for strong primary binding sites to promote a significant increase in the density of adsorbed H2 within the entire pore structure.168 These favorable H2–Ni2+ interactions and resulting efficient confinement of H2/D2 within the pores of Ni2(m-dobdc) result in this framework exhibiting the highest storage capacity to date for an adsorbent operating at 298 K and pressures up to 100 bar. Notably, when used in a process with temperature swings between −75 and 25 °C, this material achieves a usable volumetric capacity of 23.0 g L−1 in the pressure range of 5–100 bar.169
Metal cation exchange reactions have also been explored with MOFs as a means of tuning their gas adsorption properties, including the enhancement of the magnitude of Qst.170 These exchange reactions can also be a useful way to prepare new framework structures, especially if direct synthesis and activation of a particular materials proves challenging.171,172 In relation to H2 storage, a simple strategy was proposed and demonstrated in 2007 to improve the H2 adsorption properties of the framework Mn-BTT.173 In this work, metal cation exchange of the Mn-BTT structure resulted in successful isolation of the frameworks M3[(Mn4Cl)3(BTT)8]2 (M = Li+, Cu+, Fe2+, Co2+, Ni2+, Cu2+, Zn2+). The surface area of the series of metal-exchanged materials was slightly lower than the parent Mn-BTT structure, although a slightly larger Qst value was observed for Co3[(Mn4Cl)3(BTT)8]2 compared to Mn3[(Mn4Cl)3(BTT)8]2 (−10.5 versus −10.1 kJ mol−1, respectively). Based on the computational study of the aluminosilicate zeolite ZSM-5, it has also been proposed that Cu+-exchanged materials can exhibit strong H2 binding, although it was not possible to prepare a Cu+-rich M-BTT material.173,174 In 2014, Cu+ sites were introduced into the MFU-4l-type material Zn5Cl4(BTDD)3 (H2BTDD = bis(1H-1,2,3-triazolo[4,5-b],[4′,5′-i])dibenzo[1,4]dioxin) by a three-step, post-synthetic reaction, and the structure of the resulting material, Cu(I)-MFU-4l, was determined by X-ray diffraction.175 In this procedure, two Cu2+ ions in the metalated Cu(II)2Zn3Cl4 cluster were treated with lithium formate to yield Cu(II)-MFU-4l-formate [Cu(II)2Zn3Cl2(BTDD)3(formate)2], which was heated under vacuum to yield exposed Cu(I) sites. Hydrogen isotherm measurements revealed a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding of H2 to the Cu(I) sites (corresponding to an uptake of 0.34 wt%) over the temperature range of 163–193 K, and 80% of the metal sites were found to be occupied by H2, even at 273 K and 1 bar. From H2 adsorption measurements, the Qst value for Cu(I)-MFU-4l was estimated to be −32.3 kJ mol−1, which, to our knowledge, is the highest value reported to date for any MOF. We note that the strength of this interaction in this framework may in part arise due to back-donation of electrons from the Cu metal center to H2, as has been observed in Kubas-type complexes (see below). Although this binding strength falls beyond the target range of −15 to −25 kJ mol−1 considered to be optimal for ambient-temperature H2 storage with a maximum pressure of 100 bar,25,35 targeting materials that possess metal ions capable of such back-donation and simultaneously exhibit strong physisorption may be a promising strategy to enhance storage capacity.
1 binding of H2 to the Cu(I) sites (corresponding to an uptake of 0.34 wt%) over the temperature range of 163–193 K, and 80% of the metal sites were found to be occupied by H2, even at 273 K and 1 bar. From H2 adsorption measurements, the Qst value for Cu(I)-MFU-4l was estimated to be −32.3 kJ mol−1, which, to our knowledge, is the highest value reported to date for any MOF. We note that the strength of this interaction in this framework may in part arise due to back-donation of electrons from the Cu metal center to H2, as has been observed in Kubas-type complexes (see below). Although this binding strength falls beyond the target range of −15 to −25 kJ mol−1 considered to be optimal for ambient-temperature H2 storage with a maximum pressure of 100 bar,25,35 targeting materials that possess metal ions capable of such back-donation and simultaneously exhibit strong physisorption may be a promising strategy to enhance storage capacity.
As materials are further developed to meet the current DOE onboard hydrogen storage targets (Table 1), one challenge that remains is to increase the density of strong binding sites, such as open metal sites, within a given volume of framework space. It is possible that strategies such as engineering frameworks with shorter organic linkers and optimizing pore topology will promote progress toward this goal, but most likely new material concepts and synthetic chemistry will be necessary to meet the targets.176 For example, prior to being synthesized in the lab, promising novel or already known materials for post-synthetic metalation reactions could first be identified using computational screening tools as outlined in the section on usable gravimetric and volumetric capacities. This type of targeted synthesis could result in materials with strong binding sites within pore structures that also demonstrate efficient H2 packing.
Binding of multiple H2 molecules to an open metal site in a MOF or other material
The hydrogen storage capacity of a MOF is to some extent dictated by the H2 binding enthalpy, but a high initial −Qst value does not necessarily guarantee a high storage capacity, because in most frameworks each metal site is capable of binding only a single H2 molecule.29 For example, in a framework such as Ni2(m-dobdc) that exhibits an open metal site density of ∼6 mmol g−1, binding of one H2 per metal site would achieve a storage density that is only one quarter of the 2020 DOE target of 23.5 mmol g−1 (= 4.5 wt% H2). Considering that metal centers are not the exclusive adsorption sites for gas molecules within a framework, the design of materials exhibiting a high affinity for H2 and metal centers capable of binding more than one H2 molecule may drastically improve storage capacity.29,166 In this section we introduce two representative classes of materials that may be promising in this regard, namely molecular metal complexes and extended frameworks capable of reversibly binding multiple H2 molecules per metal center. We also briefly discuss possible future research directions in this area.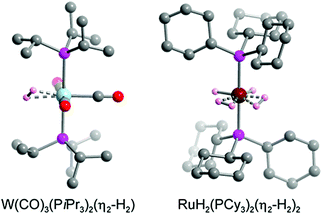 | ||
| Fig. 8 Crystal structure of W(CO)3(PiPr3)2(η2-H2) (left) and RuH2(PCy3)2(η2-H2)2 (right).179,182 Gray, red, pink, blue, dark red, and light pink spheres represent C, O, P, W, Ru, and coordinated H atoms, respectively. Hydrogen atoms of the triphosphine ligands are omitted for clarity. | ||
While the first Kubas complexes exhibited only a single side-on bound H2 ligand, later metal complexes were identified that could reversibly bind two H2 molecules without cleaving the H–H bond.182–185 One representative example is the complex RuH2(PCy3)2(η2-H2)2, the structure of which was elucidated by single-crystal X-ray diffraction (Fig. 8).182,183 In this complex the two bulky phosphine ligands are located trans to each other, similar to the Kubas complexes, although an equatorial coordination pocket results that is capable of binding two H2 molecules and two hydrides. The H–H bond distance of each η2-bound H2 was estimated to be 0.85 Å, a value that is again indicative of a strong interaction when compared to materials exhibiting more conventional H2 physisorption. As expected given this strong interaction, the Ru–H2(centroid) distance of ∼1.50–1.55 Å is significantly shorter than the metal–D2 distance of >2.2 Å determined for Ni2(m-dobdc) from neutron diffraction measurements.29
Despite binding two H2 molecules per metal, RuH2(PCy3)2(η2-H2)2 only coordinates 0.6 wt% H2. Alternatively, the incorporation of a dense array of Kubas-type metal centers within a MOF—e.g., low-spin, first-row transition metals such as Cr or Mn186,187 coordinated by phosphine-based linkers—might be a promising strategy for achieving high H2 uptake; such a pursuit would no doubt be aided by computational screening of candidate framework structures. While the strength of the M–H2 bond dissociation energy in such compounds could reduce material usable capacity and cyclability, it is possible that designing Kubas-type sites within a flexible frameworks could offset this effect.
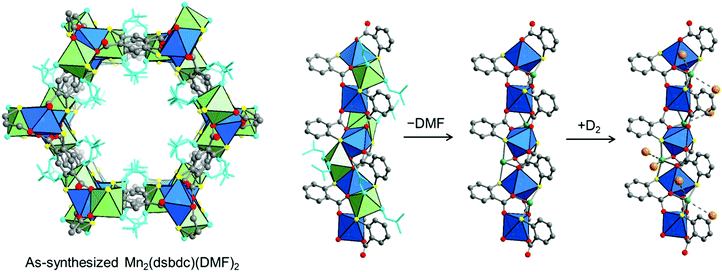 | ||
| Fig. 9 (left) Crystal structure of Mn2(dsbdc)(DMF)2.189 (right) Coordinated DMF molecules (light blue) are removed to create exposed Mn2+ centers (green spheres), which adsorb two D2 molecules at a loading of 0.7 D2 per four-coordinate Mn2+ (at 10 K). Gray, red, yellow spheres represent C, O, and S atoms, respectively; H atoms are omitted for clarity. The coordination spheres of each Mn center are shown as blue and green polyhedra and D2 molecules are represented by orange spheres.134 | ||
The framework Zn2(dobdc) (UTSA-74a) is another material exhibiting two accessible binding sites that was recently studied for C2H2/CO2 separations.190 The as-synthesized, solvated framework exhibits a binuclear secondary building unit consisting of tetrahedral and octahedral Zn2+ ions. The coordination sphere of the octahedral Zn2+ is completed by two trans water molecules, which can be removed to yield a slightly distorted ZnO4 unit as observed by single crystal X-ray diffraction analysis. In the same study, DFT calculations predicted that the ZnO4 unit can accommodate two C2H2 adsorption sites at high loadings, a result that may have wider implications for the binding of other gases, including H2.
These recent reports afford valuable insight for continued optimization of framework design, although precise control over the inorganic unit remains a challenge. One alternative strategy for accessing open metal sites is to design ligands exhibiting secondary coordination sites that can be selectively metalated following framework synthesis.191 When compared with the direct synthesis of frameworks using pre-metalated linkers (e.g., metalated porphyrin or salen linkers),192–194 post-synthetic metalation is also potentially advantageous for accessing a wide variety of chelating moieties and metal ion combinations, although it is important to note that in some cases the protection of chelating sites is required during initial framework synthesis. One of the earliest examples of a framework prepared via post-synthetic metalation was reported in 2005, wherein the 1,1′-bi-2-naphthol moiety of the framework CdCl2(DCDPBN) (DCDPBN = 6,6′-dichloro-4,4′-di(pyridin-4-yl)-[1,1′-binaphthalene]-2,2′-diol) was metalated with titanium isopropoxide.195 Following this report, additional frameworks exhibiting 2,2′-bipyridine and salicylate sites were successfully metalated, and some of the resulting materials exhibited enhanced gas adsorption properties compared with the bare parent frameworks.196,197 However, metalation of neutral chelating groups resulted in pore-confinement of the counter anions and consequently diminished porosity and reduced accessibility of H2 to the metal center.
Another approach is to utilize organic linkers with catecholate sites, which can offer charge-balance for post-synthetically chelated divalent metal ions and obviate the need for countercations that would diminish porosity and capacity. The successful synthesis and subsequent metalation of a framework with catechol groups was first reported in 2010 by Tanabe et al.198 In this work, the authors prepared the framework Zn4O((OBnNO2)2-BDC)(BTB)4/3 (or nitrobenzyl-protected UMCM-1, (OBnNO2)2-BDC2− = 2,3-bis((2-nitrobenzyl)oxy)-1,4-benzenedicarboxylate, BTB3− = 4,4′,4′′-benzene-1,3,5-triyl-tribenzoate),199 which exhibits nitrobenzyl-protected BDC linkers. The nitrobenzyl groups could be removed by irradiation with 365 nm light, and the resulting catechol-functionalized UMCM-1 was then reacted with an iron(III) acetylacetonate solution to impregnate the framework with Fe3+ metal ions. Similar reactions have been carried out using Cr3+ and V4+ salts, which demonstrate the wide applicably of post-synthetic metalation reactions.200,201 These latter metalated frameworks were studied only for their utility in oxidative catalysis, however, and thus further efforts are necessary to examine the H2 affinity of metal-catecholate sites.
The interaction of H2 with some metal-catecholate clusters has been predicted computationally, and it was found that the H2 adsorption enthalpy exceeds that of metal-biphenol or metal–bipyridine complexes.59,60 For example, it was calculated that Mg2+ and Ca2+ catecholate complexes would exhibit H2 adsorption energies of 23.0 and 15.1 kJ mol−1, respectively, compared to the differential adsorption energies ΔE = 4.7 and 5.5 kJ mol−1 for biphenyl-(TiO4)-Me2 and bipyridine-CuCl2.60 The significant enhancement of the adsorption enthalpy can be attributed to the strong dipole moment created by the negatively charged oxygen atoms and positively charged metal ion—in other words, a local polarization interaction is critical to increase the binding energy of H2. It should be noted that the predicted M–H2 interaction energies for the Mg2+ and Ca2+ catecholate complexes are much lower than the H2 binding enthalpies determined for Kubas complexes (∼80 kJ mol−1) because of the absence of back-bonding from the alkaline-earth metal ions to H2, and these values are within a more optimal range for ambient temperature H2 storage. Importantly, within a UiO-66-type structure, it was predicted that Ca2+–catecholates are able to bind up to four H2 molecules per metal site without significant differences between the successive adsorption energies, resulting in a high calculated H2 volumetric usable capacity of 30 g L−1 at 298 K (pressures ranging from 5.8–100 bar).59 Therefore, the development of successful experimental protocols for the metalation of catechol-based frameworks (including the successful desolvation of any coordinated solvents) should be a key target for synthetic chemists.
Porous organic frameworks
In principle, the gravimetric storage capacity of H2 within a given framework could also be improved if the transition metal nodes were replaced with lighter atoms, such as carbon and nitrogen, without sacrificing the robustness of the framework. To synthesize such organic polymers, multitopic organic molecular building blocks are assembled into multidimensional structures via a metal-catalyzed (e.g., Pd or Ni) coupling reaction.202,203 Due to their strong covalent linkages, the resulting polymer frameworks generally exhibit high stability and, importantly, can exhibit permanent porosity in the absence of crystallinity, in contrast to MOFs. Porous organic polymers can be divided into several subclasses, based on the linkage and aromaticity of the organic framework, although we will not consider these differences here.203A major advance in the chemistry of porous organic polymers came in 2009 with the discovery of high hydrothermal stability and exceptional surface area in the material PAF-1 (PAF = porous aromatic framework), a robust framework synthesized via a homo-coupling reaction with the tetrahedral building block tetrakis(4-bromophenyl)methane (Fig. 10).204 This material exhibits a high BET surface area of 5600 m2 g−1 (Langmuir surface area = 7100 m2 g−1) and excess gravimetric H2 uptake of 7.0 wt% at 77 K and 48 bar. Shortly after this report, several isoreticular organic frameworks were synthesized using larger tetrahedral building blocks.205,206 Among these materials, the framework known as PPN-4 (assembled using the tetrakis(4-bromophenyl)silane building unit) was found to possess a remarkably high BET surface area of 6461 m2 g−1 (Langmuir surface area = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 m2 g−1) and excess H2 adsorption as high as 8.3 wt% at 77 K and 55 bar.206 Porous organic frameworks can also be accessed using tritopic and tetratopic building blocks, as was demonstrated with the isolation of the framework JUC-Z7, assembled from tetrakis(4-bromophenyl)methane and tris(4-bromophenyl)amine. This material also exhibits high porosity, with a BET surface area of 4889 m2 g−1 and excess gravimetric H2 uptake of 6.4 wt% at 77 K and 48 bar (−Qst = 5.6 kJ mol−1).207 It should be noted that, similar to other high surface area materials mentioned previously, these materials do not exhibit high volumetric storage capacities due to their very large pores.
063 m2 g−1) and excess H2 adsorption as high as 8.3 wt% at 77 K and 55 bar.206 Porous organic frameworks can also be accessed using tritopic and tetratopic building blocks, as was demonstrated with the isolation of the framework JUC-Z7, assembled from tetrakis(4-bromophenyl)methane and tris(4-bromophenyl)amine. This material also exhibits high porosity, with a BET surface area of 4889 m2 g−1 and excess gravimetric H2 uptake of 6.4 wt% at 77 K and 48 bar (−Qst = 5.6 kJ mol−1).207 It should be noted that, similar to other high surface area materials mentioned previously, these materials do not exhibit high volumetric storage capacities due to their very large pores.
 | ||
| Fig. 10 Schematic representation of the synthesis of PAF-1 (top) and COF-102 (bottom).204,208 Gray, red, and orange spheres represent C, O, and B atoms, respectively; quaternary carbon atoms are shown as grey tetrahedra and H atoms of the triphosphine ligands are omitted for clarity. | ||
At least two challenges must be addressed to improve the H2 storage capacity in porous organic frameworks. The first challenge is the generally low experimental surface areas (typically <1500 m2 g−1) exhibited by porous organic frameworks, relative to expected values, especially for those materials exhibiting additional functionality. The formation of an interpenetrated structure is one likely source of low porosity, which can result from π–π interactions between neighboring frameworks and/or monomeric building blocks.209,210 Recent theoretical studies suggest these π–π interactions can be mitigated by replacing monomer phenyl and alkyne groups with rigid alkyl groups, while introducing bulky side chains into the framework structures may additionally increase the probability of forming dense frameworks.211 In the same work it was also proposed that interpenetrating structures could be avoided by the use of bulky coupling catalysts with dimensions similar to the target framework pore diameter.
A second challenge inherent in using porous organic frameworks for H2 storage is that these materials are only weakly polarizing and thus do not strongly bind H2. As discussed above in the context of MOFs, post-synthetic metalation of porous organic frameworks is one possible strategy for improving H2 binding energy. Successful pre- and post-synthetic metalation reactions have been demonstrated for a limited numbers of porous organic polymers exhibiting bipyridine, salen, porphyrin, and catechol chelating moieties.212–215 For instance, Weston et al. prepared catechol-functionalized porous polymers that could be cleanly metalated with MgMe2, Cu(CH3CO2)2, or Mn(CH3CO2)2, as demonstrated using IR spectroscopy.215 Metalation with Mn2+ afforded a material that exhibited an increase in Qst relative to the parent framework (−9.6 and −8.1 kJ mol−1, respectively), although it was not clear if this enhancement was directly related to the metalation. Fischer et al. have alternatively demonstrated that an anionic framework can be utilized to immobilize metal cations, through successful synthesis of a Li+-decorated borate-based porous polymer via coupling of lithium tetrakis(tetrafluorophenyl)borate and triethynylbenzene.216 The resulting material was found to exhibit moderate porosity, with a surface area of 890 m2 g−1 that was retained upon exchange of Li+ with Na+ or Mn2+ cations (surface areas of 731 and 499 m2 g−1, respectively). Future work would benefit from the investigation of the relationship between metal ion coordination environment and H2 adsorption in such materials.
Covalent organic frameworks
It is possible to achieve crystallinity in porous organic frameworks through the reversible reaction of monomeric organic building blocks via condensation reactions of 1,4-benzenediboronic acid and hexahydroxytriphenylene.217 This class of crystalline materials, known as covalent organic frameworks (COFs), now encompasses two-dimensional layered structures and three-dimensional frameworks with various linkages such as B–O, C–N, B–N, and B–O–Si.217–221 Two-dimensional layered COFs are primarily composed of either hexagonal or square layers, which are stacked in an eclipsed fashion and can be tuned by changing the dimensions of the organic monomers to yield varying pore diameters.222 Three-dimensional COFs are often synthesized by linking tetratopic (tetrahedral and square) building units with linear or triangular organic units, although the first such material was prepared by the self-condensation reaction of tetra(4-dihydroxyborylphenyl)methane (Fig. 10).208 Because the topology of these materials is dependent on the directionality of the organic building blocks, the range of reported structures is limited relative to MOFs. Typical three-dimensional topologies (or nets) are diamond, carbon nitride, boracite, and platinum sulfide, and similar to their amorphous analogues, these materials are also prone to form interpenetrated structures.208,219,223Covalent organic frameworks are generally thermally and structurally robust, and activated samples can therefore be prepared without loss of crystallinity. The surface areas of activated COFs have been evaluated by both N2 and Ar adsorption analysis, and the reported values vary widely depending on the framework structure. For example, the two-dimensional materials COF-6 (prepared from the condensation reaction of hexahydroxytriphenylene and 1,3,5-benzenetriboronic acid) and CTF-1 (prepared from the condensation reaction of 1,4-dicyanobenzene) were found to exhibit BET surface areas of 750 and 791 m2 g−1, respectively, whereas the BET surface areas for three-dimensional frameworks COF-102 and COF-103 (prepared from the self-condensation reactions of tetra(4-(dihydroxy)borylphenyl)methane and tetra(4-(dihydroxy)borylphenyl)silane, respectively), were calculated to be 3620 and 3530 m2 g−1.208,220,224,225 As expected, COF-102 and COF-103 exhibit high excess gravimetric H2 uptakes (6.8 and 6.6 wt%, respectively) at ∼35 bar and 77 K, although their initial Qst values are only −3.9 and −4.4 kJ mol−1, respectively, due to a lack of strong H2 binding sites.225 Two-dimensional COFs such as COF-10 (prepared from the condensation reaction of hexahydroxytriphenylene and 1,4-benzenediboronic acid) and BLP-2(H) (obtained from the thermal decomposition of 1,3,5-(p-aminophenyl)benzene-borane) have been found to exhibit rather moderate saturation excess uptakes of 3.8 and 2.5 wt% at 77 K, relative to three-dimensional variants and the porous polymers described above.221,225 Importantly, the Qst values for two-dimensional COFs with similar pore diameter do not appear to be drastically influenced by the identity of linking moieties. For instance, changing from boronate (COF-6) to borazine (BLP-2(H)) to azine (ACOF-1; prepared by a condensation reaction of hydrazine hydrate and 1,3,5-triformylbenzene) resulted in frameworks with Qst values of −7.0 kJ mol−1, −6.8 kJ mol−1, and −6.0 kJ mol−1, respectively.221,225,226 The similarity of these values may be due in part to the fact that only the edge of each two-dimensional layer is exposed for interactions with H2 molecules, and suggests that such COFs are not ideal materials for practical H2 storage.
Although the impregnation of covalent organic frameworks with metal ions or metal particles could in principle lead to enhanced H2 storage capacities, this area of synthetic research has not been widely explored. To date, frameworks have been constructed with metalloporphyrin linkers or doped with Pd(CH3CO2)2, molybdenyl acetylacetonate, or various metallocenes.227–231 In one of the latter examples, COF-102 was impregnated with Pd(η3-C3H5)(η5-C5H5) and then photo-decomposed to yield Pd nanoparticles in the pores. The H2 uptake of the resulting material Pd@COF-102 was found to be slightly lower than that of pristine COF-102 at 77 K; at 298 K and 20 bar, however, the H2 uptake was 2.6 times greater than the pristine sample (0.42 compared to 0.16 wt%, respectively) due to the additional chemisorption of H2 on Pd.231 While frameworks doped with Pd(CH3CO2)2 and molybdenyl acetylacetonate were investigated for applications in catalysis, H2 adsorption characterization was not reported for any frameworks other than Pd@COF-102. We note that the presence of electron-deficient metal sites in these materials, arising from the electron withdrawing nature of the coordinated groups, could be of relevance for future study in pursuit of materials for H2 storage.
Graphene and graphene oxide materials
Since its discovery, graphene has been explored as a next-generation material for H2 storage with the view that its single-carbon atomic sheet could offer an ideal lightweight adsorbent with a vast, open structure. However, due to the weak enthalpic interaction between graphene and H2 molecules, use of graphene as an adsorbent requires cryogenic temperatures that, as discussed above, increase the cost and complexity of the fueling system.232 Over the last few decades, synthetic research has led to development of new graphene-inspired building blocks and several new carbon-based H2 adsorbents designed to enhance binding enthalpies, such as graphene oxide, graphene origami, and others.233–235 For example, various oxygenated functional moieties, including carboxyl and hydroxyl groups, can be introduced to graphene to form graphene oxide (Fig. 11); subsequent crosslinking of this scaffold with organic ligands can be carried out to prepare three-dimensional H2 adsorbents. Burress et al. reported the preparation of a layered graphene oxide structure of this type by reacting varying amounts of benzene-1,4-diboronic acid with graphene oxide sheets.235 GCMC simulations predicted an optimum interlayer separations of 1.1 nm and an ideal carbon atom-to-boronic acid ratio of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for balancing structural stability with layer accessibility and H2 adsorption capacity. They successfully synthesized a material with roughly these properties which displayed an uptake of 1 wt% at 77 K and 1 bar with a Qst value of 9 kJ mol−1, comparable to some MOFs.
1 for balancing structural stability with layer accessibility and H2 adsorption capacity. They successfully synthesized a material with roughly these properties which displayed an uptake of 1 wt% at 77 K and 1 bar with a Qst value of 9 kJ mol−1, comparable to some MOFs.
More recently, Klechikov et al. evaluated the H2 adsorption properties of various graphene and graphene oxide materials prepared via rapid thermal exfoliation and post-exfoliation activation treatments, which enabled them to systematically study the dependence of H2 uptake versus surface area.236 The authors found that H2 uptake by graphene materials does not exceed 1 wt% at 120 bar H2 at ambient temperatures; however, uptake at 77 K increases linearly as a function of material surface area, and a maximal H2 uptake of ∼5 wt% was observed for a graphene with a surface area of 2300 m2 g−1 (roughly following Chahine's rule behavior).10 The authors concluded that bulk graphene samples follow the standard H2 uptake trends of other nanostructured carbons and do not demonstrate intrinsically superior capacities; thus, unmodified graphene-based materials are essentially weakly-binding adsorbents.
Recently, Kim et al. studied the H2 adsorption properties of aggregated mesoporous graphene oxide intercalated with potassium ions, with the goal of demonstrating experimentally—in two dimensions—the thermodynamic principle that the density of H2 in a potential well increases exponentially relative to the ambient gas by the corresponding Boltzmann factor.234 The authors reported a gravimetric H2 storage density of 4.65 wt% at 40 bar and room temperature for this material, although in the absence of potassium ions they found the material exhibits a storage density of 0.21 wt% at ∼5 bar. The exceptional H2 uptake was rationalized as arising from the attractive potential of the mesopores and the intercalated potassium ions and, if accurate, would be the highest value reported for any adsorbent at ambient temperature; however validation of this result is needed by means of more comprehensive isotherm measurements on bulk samples beyond the quartz-crystal microbalance method used in the study. Further characterization of these materials should also be carried out to rule out the type of undesired side reactions that result in erroneously high capacities described above for materials containing surface oxides or reactive groups.
The malleable nature of graphene offers another potentially valuable route for the preparation of high-capacity H2 adsorbents, for example, Zhu and Li have proposed a hydrogenation-assisted graphene origami for hydrogen storage.233 Using MD simulations, the authors showed that a origami nanocage—which can be converted between open or closed configurations via an external electric field—could obtain a gravimetric capacity up to 9.7 wt%. Such a concept, although interesting, has yet to be experimentally verified.
A few experimental and theoretical studies have recently reported that enhanced H2 uptake can be achieved by metal atom doping of graphene surfaces. For example, Beheshti et al. predicted that double-sided Ca-decorated graphene doped with 12 atomic% of individual boron atoms can theoretically achieve a gravimetric H2 capacity of 8.38 wt% with an average binding energy of ∼38.6 kJ mol−1.237 Lee et al. similarly reported a first-principles study on hydrogen adsorption over Ca-decorated zigzag graphene nanoribbons (ZGNR), which predicted that each Ca atom is capable of binding up to six H2 molecules at a binding energy of ∼19.3 kJ mol−1 of H2, leading to a H2 gravimetric capacity of ∼5 wt%.87 However, both studies employed a relatively low level of DFT, which, as discussed above, is not always consistent with higher levels of theory (e.g., QMC calculations), and so these values should perhaps be interpreted with caution. Moreover, the synthesis of such adsorbents with low-coordinate dopant metal atoms that can accommodate several H2 molecules is likely to be extremely difficult, and has yet to be demonstrated. Nevertheless, some metal-doped carbons have been shown experimentally to exhibit improved storage properties; for example, Chen et al. synthesized a Pd-doped two-dimensional graphene sheet mixed with an activated carbon receptor and experimentally found a 49% enhancement in H2 gravimetric capacity and a higher Qst compared to the undoped mixtures at ambient temperature.238 In contrast to metal-site H2 adsorption predicted by the above theoretical studies, these enhancements were attributed to spillover effects. Zhou et al. have also reported a Ni–graphene composite containing nanocrystalline nickel particles uniformly dispersed over a graphene substrate, which exhibited room temperature gravimetric H2 capacities of 0.14 wt% at 1 bar and 1.18 wt% at 60 bar, respectively.239
Other graphene derivatives of interest involve new topologies such as carbon nanotubes and porous aromatic sp2 frameworks. Since the work by Dillon et al., which reported excellent H2 uptake by carbon nanotubes, extensive research has been conducted on hydrogen storage applications using carbon materials such as nanotubes and graphene derivatives.240 Despite initial enthusiasm, however, the reported performance by carbon nanotubes has been challenging to reproduce and architectures composed of undoped nanotubes are not a promising class of materials for practical storage applications.241 On the other hand, with the emerging aforementioned porous materials, other types of three-dimensional graphene architectures have been developed for H2 storage. Although various approaches to meeting the large storage capacity demands under ambient conditions have been proposed, the weak interactions between graphene materials and H2 molecules remain a daunting hurdle. Synthetic challenges surrounding metal doping of these structures still exist, including imparting precise control over the species present upon metal insertion, the degree of metal doping, and reversibility of H2 adsorption at these sites. Regardless, these materials display some potential towards ultimately meeting DOE targets if such challenges can be overcome.
Boron- and other heteroatom-doped carbons
In addition to the graphene and metal-doped graphene materials, there has been considerable effort focused on doping carbon structures with various heteroatoms to increase the H2 binding enthalpy. A computational study suggested that doping C36 fullerenes with boron could lead to an H2 binding enthalpy of ∼20 kJ mol−1, as a result of partial charge transfer from the H2 σ bond to the localized empty pz orbital of boron.65 This level of theory predicted a B–H2 distance of ∼1.4 Å—23% longer than the sum of the covalent radii of B and H (1.14 Å)—and an elongated H–H bond of 0.85 Å that is ∼10% longer than the typical molecular distance of 0.77 Å. Fig. 12a illustrates the side-on interaction of H2 with the sp2 boron bound in fullerene. It was noted by the authors that the predicted H2 bond elongation and B–H2 distance is comparable to the H2 interaction with metal centers in Kubas complexes (vide supra).184,242 Stable gas phase fullerene compounds containing as many as 12 boron atoms were predicted to be accessible with additional doping. | ||
| Fig. 12 Structural model illustrating inclusion of one (a) or six (b) boron atoms in a fullerene and their interaction with molecular H2; green, blue, and white spheres represent C, B, and H atoms, respectively. Reprinted Fig. 1 and 4 (adapted) with permission from Y.-H. Kim, Y. Zhao, A. Williamson, M. J. Heben and S. B. Zhang, Phys. Rev. Lett., 2006, 96, 016102. Copyright 2016 by the American Physical Society. | ||
As a consequence of these promising theoretical studies, a number of experimental approaches have been explored to synthesize boron doped carbon materials with high surface areas and tunable porosity. In one of the first studies, B- and N-doped microporous carbons were synthesized via substitution reactions.243 The resulting doped graphite sheets were found to exhibit much higher surface areas and 53% higher H2 storage capacity than the pure carbon materials at room temperature. However, subsequent investigations of similar materials found little enhancement of H2 binding energy or storage capacity. This discrepancy between the computational predictions and the experimental observations is likely due to the difficulty of achieving experimentally the same boron environment that is modeled in the calculations; for example, the boron atom in the above fullerene calculations has a unique BC3 (sp2) non-planar, trigonal geometry, it is difficult to realize the same geometry by doping boron into planar graphitic structures. Other early experimental studies attempted to dope carbon with boron using anhydrous boric acid, but this approach provided little control over the doping site or the final functionality. In an attempt to address this synthetic challenge, Chung et al. used a specific class of boron-containing polymeric precursors with known connectivity to achieve a controlled approach to incorporating boron.27 Pyrolysis of the precursors resulted in relatively high surface area carbon materials (780 m2 g−1) with high boron content (7.2 wt%) and an H2 binding energy of 11 kJ mol−1. The substitutional p-type boron dopant was proposed to polarize the carbon surface, resulting in a binding energy higher than that achieved with neat carbon but lower than predicted for boron-doped fullerene structures.
The authors further used 11B magic angle spinning (MAS) NMR to gain insight into the boron environment in the carbon framework (Fig. 13).27 Deconvolution of the spectra of several B-doped carbon materials obtained at different pyrolysis temperatures revealed two components (best illustrated in the pale blue curve in Fig. 13b): one downfield arising from boron sites of trigonal planar symmetry, and one upfield corresponding to boron sites in a puckered configuration (Fig. 13c).
Chung and Jeong subsequently developed an alternative approach to prepare a range of porous boron-doped carbon materials, via pyrolysis of polymeric boron precursors in the presence of pore-templating LiCl or NaCl.244 Annealing at temperatures ranging from 600–1800 °C resulted in a range of structures, from those exhibiting minimal π conjugation and a boron-puckered configuration (600–800 °C) to more ordered structures with extensive π conjugation and a planar configuration (1500 °C). The planar graphitic layers were reported to accommodate <3 mol% B, while the amorphous materials exhibited much higher surface areas (500–800 m2 g−1) and 12 mol% B. The report claimed experimentally derived binding enthalpies of 12.5 and 20 kJ mol−1 for two structures, albeit with low capacities due to the small surface areas of the materials.
Tour and coworkers have alternatively used a bottom-up, solvothermal synthesis approach to prepare boron-, nitrogen-, and phosphorus-doped carbon scaffolds with surface areas as high as 900 m2 g−1, via the reaction of chlorine-containing organic molecules with metallic sodium at reflux in high boiling solvents, followed by the addition of heterotopic electrophiles for dopant incorporation.245 Hydrogen adsorption data for each material exhibited the expected type I isotherm behavior (Fig. 14), and heats of adsorption extrapolated to zero-coverage afforded Qst values of 8.6 and 8.3 kJ mol−1 for boron- and phosphorus-doped carbons, respectively. These values are notably higher than typical binding energies of 4–6 kJ mol−1 for undoped carbons, although the nitrogen-doped material was found to have a binding energy of 5.6 kJ mol−1, within this range.
Further experimental and computational work is underway to more precisely quantify the increased enthalpy of adsorption exhibited by these materials as well as to understand how boron modifies the graphitic carbon surface. Trigonal boron is more stable in a planar rather than puckered geometry, as the former enables more efficient electron donation to the electron-deficient boron atom. As such, a defect is generated when boron is substituted into a non-planar carbon matrix, and the nature of this defect may lead to an enhanced H2 binding energy to the carbon matrix. However, the lack of a reproducible value for the H2 binding energy in such materials presents a roadblock to their serious inquiry for H2 storage, and whether the variability in reported values is a reflection of synthetic difficulties or measurement complications remains unclear. Ultimately, any binding energy advantages achieved from boron (or other heteroatom) doping must also be accompanied by the ability to incorporate such sites into carbons with sufficient surface areas and porosities that can accommodate high H2 capacities.
Conclusions
The recent commercial availability of hydrogen fuel cell electric vehicles represents a major advance for this technology, but the use of compressed gas storage is disadvantageous from a number of perspectives, including insufficient volumetric capacity and the higher costs associated with fueling and infrastructure. Consequently, new solid-state hydrogen storage materials that can meet all of the DOE targets are still a pressing need. Adsorbents are one of two major classes of storage materials currently under consideration for H2 storage (the other being metal hydrides), and while some of these materials meet many of the DOE targets, one common deficiency is generally low volumetric capacity. Many material strategies have been proposed to address this problem, and some of the most prominent include targeting materials with open metal sites, those that are capable of binding multiple H2 molecules at a given binding site, and heteroatom-doped carbons. Our intention in this Perspective has been to provide an objective assessment of the strengths, weaknesses, and outstanding challenges for these strategies, both to motivate intensified research and stimulate new efforts in underexplored or completely new areas. Not all strategies discussed here have received in-depth experimental consideration thus far, and some are motivated primarily by predictions from theory. In our estimation, the chosen emphases in this Perspective concerning theoretical methods, synthesis and characterization challenges, metrics of usable gravimetric and volumetric capacities, and trends in binding energies, represent key areas of inquiry in the continued evaluation of materials for ambient temperature H2 storage. It is our hope that the foregoing discussion will afford interested readers with the requisite background information needed to understand the relevant limitations when evaluating the merits of a particular strategy (new or existing) toward the development and characterization of H2 adsorbents. For example, theoretical methods used to predict hydrogen uptake vary widely in their accuracy and readers should take this into account in assessing the corresponding predictions. Similarly, synthetic approaches for preparing new storage materials each have their own limitations, and realistic consideration should be given to the difficulties involved prior to embarking on an extensive synthesis campaign. Nevertheless, numerous discoveries and developments in the past decade have created new opportunities to address the challenges facing onboard materials-based storage applications. We are optimistic that successful materials can be found that will meet the requirements for this important transportation technology.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Jesse Adams for helpful discussions. Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy's National Nuclear Security Administration (NNSA) under contract DE-NA-0003525. The authors gratefully acknowledge support from the Hydrogen Materials—Advanced Research Consortium (HyMARC), established as part of the Energy Materials Network under the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office, under Contract Number DE-AC04-94AL85000 with Sandia National Laboratories, Contract Number DE-AC36-08-GO28308 with the National Renewable Energy Laboratory, Contract Number DE-AC02-05CH11231 with Lawrence Berkeley National Laboratory, and Contract Number DE-AC52-07NA27344 with Lawrence Livermore National Laboratory. J. U. is supported by the Molecular Foundry at Lawrence Berkeley National Laboratory, which is supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract Number DE-AC02-05CH11231. Pacific Northwest National Laboratory is a multi-program national laboratory operated by Battelle for the U.S. Department of Energy under Contract Number DE-AC05-76RL01830. Argonne National Laboratory is supported by Office of Science of U. S. Department of Energy under the Contract Number DE-AC02-06CH11357. D. J. S. and A. A. acknowledge financial support provided by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, under Contract Numbers DE-EE0007046 and DE-EE0008093. Partial computing resources were provided by the U.S. National Science Foundation via grant 1531752 MRI: Acquisition of Conflux, A Novel Platform for Data-Driven Computational Physics (Tech. Monitor: Ed Walker). Z. H. is supported through the Oak Ridge Institute for Science and Education (ORISE). ORISE is managed by Oak Ridge Associated Universities (ORAU) under DOE Contract Number DE-AC05-06OR23100. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, nor usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights.References
- D. J. Durbin and C. Malardier-Jugroot, Int. J. Hydrogen Energy, 2013, 38, 14595 CrossRef.
- Target Explanation Document: Onboard Hydrogen Storage for Light-Duty Fuel Cell Vehicles, U.S. Department of Energy, https://energy.gov/sites/prod/files/2017/05/f34/fcto_targets_onboard_hydro_storage_explanation.pdf, accessed Mar 2018.
- DOE Hydrogen and Fuel Cells Program Record, U.S. Department of Energy, https://www.hydrogen.energy.gov/pdfs/15013_onboard_storage_performance_cost.pdf, accessed Mar 2018.
- L. Simpson, “HSCoE Final Report,” U.S. Department of Energy Fuel Cell Technologies Office, https://www.energy.gov/sites/prod/files/2014/03/f12/hydrogen_sorption_coe_final_report.pdf, accessed Mar 2018.
- P. A. Parilla, K. Gross, K. Hurst and T. Gennett, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 201 CrossRef.
- M. Veenstra, J. Yang, C. Xu, M. Gaab, L. Arnold, U. Muller, D. J. Siegel and Y. Ming, U.S. Department of Energy, Hydrogen and Fuel Cells Program 2014 Annual Merit Review Proceedings: Project ST010, https://www.hydrogen.energy.gov/pdfs/review14/st010_veenstra_2014_o.pdf, accessed Mar 2018.
- D. L. Anton and T. Motyka, U.S. Department of Energy, U.S. Department of Energy, Hydrogen and Fuel Cells Program 2015 Annual Merit Review Proceedings: Project ST004, https://www.hydrogen.energy.gov/pdfs/review15/st004_anton_2015_o.pdf, accessed Mar 2018.
- D. P. Broom, C. J. Webb, K. E. Hurst, P. A. Parilla, T. Gennett, C. M. Brown, R. Zacharia, E. Tylianakis, E. Klontzas, G. E. Froudakis, Th. A. Steriotis, P. N. Trikalitis, D. L. Anton, B. Hardy, D. Tamburello, C. Corgnale, B. A. van Hassel, D. Cossement, R. Chahine and M. Hirscher, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 151 CrossRef.
- O. K. Farha, A. O. Yazaydin, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944 CrossRef PubMed.
- B. Panella, M. Hirscher and S. Roth, Carbon, 2005, 43, 2209 CrossRef.
- R. Chahine and P. Bénard, Adsorption Storage of Gaseous Hydrogen at Cryogenic Temperatures, in Advances in Cryogenic Engineering, ed. P. Kittel, Plenum Press, New York, 1998, vol. 43, pp. 1257–1264 Search PubMed.
- E. Masika and R. Mokaya, J. Phys. Chem. C, 2012, 116, 25734 CrossRef.
- J. Goldsmith, A. G. Wong-Foy, M. J. Cafarella and D. J. Siegel, Chem. Mater., 2013, 25, 3373 CrossRef.
- A. Ahmed, Y. Liu, J. Purewal, L. D. Tran, A. G. Wong-Foy, M. Veenstra, A. J. Matzger and D. J. Siegel, Energy Environ. Sci., 2017, 10, 2459 RSC.
- J. A. Mason, M. Veenstra and J. R. Long, Chem. Sci., 2014, 5, 32 RSC.
- Y. G. Chung, J. Camp, M. Haranczyk, B. J. Sikora, W. Bury, V. Krungleviciute, T. Yildirim, O. K. Farha, D. S. Sholl and R. Q. Snurr, Chem. Mater., 2014, 26, 6185 CrossRef.
- R. J. Sadus, Molecular simulation of fluids: theory, algorithms, and object-orientation, Elsevier, Amsterdam, 1999 Search PubMed.
- T. L. Hill, An introduction to statistical thermodynamics, Dover Publications, 1986 Search PubMed.
- M. Fischer, F. Hoffmann and M. Fröba, ChemPhysChem, 2009, 10, 2647 CrossRef PubMed.
- A. W. Thornton, C. M. Simon, J. Kim, O. Kwon, K. S. Deeg, K. Konstas, S. J. Pas, M. R. Hill, D. A. Winkler, M. Haranczyk and B. Smit, Chem. Mater., 2017, 29, 2844 CrossRef PubMed.
- D. A. Gómez-Gualdrón, Y. J. Colón, X. Zhang, T. C. Wang, Y.-S. Chen, J. T. Hupp, T. Yildirim, O. K. Farha, J. Zhang and R. Q. Snurr, Energy Environ. Sci., 2016, 9, 3279 RSC.
- N. S. Bobbitt, J. Chen and R. Q. Snurr, J. Phys. Chem. C, 2016, 120, 27328 CrossRef.
- D. Gómez-Gualdrón, T. C. Wang, P. García-Holley, R. M. Sawelewa, E. Argueta, R. Q. Snurr, J. T. Hupp, T. Yildirim and O. K. Farha, ACS Appl. Mater. Interfaces, 2017, 9, 33419 CrossRef PubMed.
- Nanoporous Materials Genome Center, http://www1.chem.umn.edu/nmgc/, accessed Mar 2018.
- S. K. Bhatia and A. L. Myers, Langmuir, 2006, 22, 1688 CrossRef PubMed.
- K. M. Thomas, Hydrogen Adsorption and Storage in Porous Materials, in Handbook of Hydrogen Energy, ed. S. A. Sherif, D. Y. Goswami, E. K. Stefanakos and A. Steinfield, CRC Press, 2015 Search PubMed.
- T. C. M. Chung, Y. Jeong, Q. Chen, A. Kleinhammes and Y. Wu, J. Am. Chem. Soc., 2008, 130, 6668 CrossRef PubMed.
- G. T. Palomino, M. R. L. Carayol and C. O. Arean, Catal. Today, 2008, 138, 249 CrossRef.
- M. T. Kapelewski, S. J. Geier, M. R. Hudson, D. Stück, J. A. Mason, J. N. Nelson, D. J. Xiao, Z. Hulvey, E. Gilmour, S. A. FitzGerald, M. Head-Gordon, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 12119 CrossRef PubMed.
- Hydrogen Storage Materials Database, http://hydrogenmaterialssearch.govtools.us, accessed Mar 2018.
- S. Tedds, A. Walton, D. P. Broom and D. Book, Faraday Discuss., 2011, 151, 75 RSC.
- M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782 CrossRef PubMed.
- Y. Xia, Z. Yang and Y. Zhu, J. Mater. Chem. A, 2013, 1, 9365 RSC.
- Y.-S. Bae and R. Q. Snurr, Microporous Mesoporous Mater., 2010, 132, 300 CrossRef.
- E. Garrone, B. Bonelli and C. O. Areán, Chem. Phys. Lett., 2008, 456, 68 CrossRef.
- V. Buch, J. Chem. Phys., 1994, 100, 7610 CrossRef.
- A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024 CrossRef.
- H. A. Lorentz, Ann. Phys., 1881, 248, 127 CrossRef.
- G. T. Palomino, C. P. Cabello and C. O. Areán, Eur. J. Inorg. Chem., 2011, 1703 CrossRef.
- S. M. Chavan, O. Zavorotynska, C. Lamberti and S. Bordiga, Dalton Trans., 2013, 42, 12586 RSC.
- E. G. Hohenstein and C. D. Sherrill, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 304 Search PubMed.
- K. E. Riley, M. Pitoňák, P. Jurečka and P. Hobza, Chem. Rev., 2010, 110, 5023 CrossRef PubMed.
- J. Řezáč and P. Hobza, Chem. Rev., 2016, 116, 5038 CrossRef PubMed.
- M. s. Dubecký, P. Jurečka, R. Derian, P. Hobza, M. Otyepka and L. Mitas, J. Chem. Theory Comput., 2013, 9, 4287 CrossRef PubMed.
- M. Dubecký, L. Mitas and P. Jurečka, Chem. Rev., 2016, 116, 5188 CrossRef PubMed.
- L. K. Wagner, Int. J. Quantum Chem., 2014, 114, 94 CrossRef.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974 CrossRef.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315 CrossRef.
- K. Capelle, Braz. J. Phys., 2006, 36, 1318 CrossRef.
- S. Kummel and L. Kronik, Rev. Mod. Phys., 2008, 80, 3 CrossRef.
- D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, Cambridge University Press, 2009 Search PubMed.
- T. Mueller and G. Ceder, J. Phys. Chem. B, 2005, 109, 17974 CrossRef PubMed.
- P. Srepusharawoot, R. H. Scheicher, C. Moysés Araújo, A. Blomqvist, U. Pinsook and R. Ahuja, J. Phys. Chem. C, 2009, 113, 8498 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017 Search PubMed.
- D. J. Adams, Mol. Phys., 1975, 29, 307 CrossRef.
- S. S. Han, J. L. Mendoza-Cortes and W. A. Goddard III, Chem. Soc. Rev., 2009, 38, 1460 RSC.
- R. B. Getman, Y.-S. Bae, C. E. Wilmer and R. Q. Snurr, Chem. Rev., 2012, 112, 703 CrossRef PubMed.
- S. Keskin, J. Liu, R. B. Rankin, J. K. Johnson and D. S. Sholl, Ind. Eng. Chem. Res., 2009, 48, 2355 CrossRef.
- E. Tsivion, S. P. Veccham and M. Head-Gordon, ChemPhysChem, 2017, 18, 184 CrossRef PubMed.
- E. Tsivion, J. Long and M. Head-Gordon, J. Am. Chem. Soc., 2014, 136, 17827 CrossRef PubMed.
- A. Cohen, P. Mori-Sanchez and W. Yang, Chem. Rev., 2012, 112, 289 CrossRef PubMed.
- M. Bajdich, F. A. Reboredo and P. R. C. Kent, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081405 CrossRef.
- W. Purwanto, H. Krakauer, Y. Virgus and S. Zhang, J. Chem. Phys., 2011, 135, 164105 CrossRef PubMed.
- X. Jiang, X. Cheng, G. Chen and H. Zhang, Int. J. Quantum Chem., 2012, 112, 2627 CrossRef.
- Y.-H. Kim, Y. Zhao, A. Williamson, M. J. Heben and S. B. Zhang, Phys. Rev. Lett., 2006, 96, 016102 CrossRef PubMed.
- J. Ma, A. Michaelides and D. Alfè, J. Chem. Phys., 2011, 134, 134701 CrossRef PubMed.
- B. Vlaisavljevich, J. Huck, Z. Hulvey, K. Lee, J. A. Mason, J. B. Neaton, J. R. Long, C. M. Brown, D. Alfè, A. Michaelides and B. Smit, J. Phys. Chem. A, 2017, 121, 4139 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef PubMed.
- J. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- J. Klimes and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- S. Dodziuk and G. Dolgonos, Chem. Phys. Lett., 2002, 356, 79 CrossRef.
- H. Cheng, A. C. Cooper, G. P. Pez, M. K. Kostov, P. Piotrowski and S. J. Stuart, J. Phys. Chem. B, 2005, 109, 3780 CrossRef PubMed.
- Q. Yang and C. Zhong, J. Phys. Chem. B, 2005, 109, 11862 CrossRef PubMed.
- A. Skoulidas and D. S. Sholl, J. Phys. Chem. B, 2005, 109, 15760 CrossRef PubMed.
- S. Andersson and P. E. Larsson, Microporous Mesoporous Mater., 2016, 224, 349 CrossRef.
- D. Durette, P. Benard, R. Zacharia and R. Chahine, Sci. Bull., 2016, 61, 594 CrossRef.
- S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031 RSC.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, J. Antony, T. Schwabe and C. Muck-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741 RSC.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287 RSC.
- S. Kristyan and P. Pulay, Chem. Phys. Lett., 1994, 229, 175 CrossRef.
- J. Witte, N. Mardirossian, J. B. Neaton and M. Head-Gordon, J. Chem. Theory Comput., 2017, 13, 2043 CrossRef PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- Y.-H. Kim, Y. Y. Sun and S. B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115424 CrossRef.
- H. Lee, J. Ihm, M. L. Cohen and S. G. Louie, Nano Lett., 2010, 10, 793 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- J. Sun, M. Marsman, G. I. Csonka, A. Ruzsinszky, P. Hao, Y.-S. Kim, G. Kresse and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035117 CrossRef.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897 CrossRef.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef.
- T. Pham, K. A. Forrest, J. Eckert and B. Space, Cryst. Growth Des., 2016, 16, 867 CrossRef.
- P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067 RSC.
- Y. Mo, P. Bao and J. Gao, Phys. Chem. Chem. Phys., 2011, 13, 6760 RSC.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887 CrossRef.
- H. J. Fang, H. Demir, P. Kamakoti and D. S. Sholl, J. Mater. Chem. A, 2014, 2, 274 RSC.
- J. G. McDaniel and J. R. Schmidt, in Annual Review of Physical Chemistry, ed. M. A. Johnson and T. J. Martinez, 2016, vol. 67, pp. 467–488 Search PubMed.
- J. R. Schmidt, K. Yu and J. G. McDaniel, Acc. Chem. Res., 2015, 48, 548 CrossRef PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955 CrossRef PubMed.
- Y. P. Li, J. Gomes, S. M. Sharada, A. T. Bell and M. Head-Gordon, J. Phys. Chem. C, 2015, 119, 1840 CrossRef.
- I. Savchenko, B. Gu, T. Heine, J. Jakowski and S. Garashchuk, Chem. Phys. Lett., 2017, 670, 64 CrossRef.
- G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479 CrossRef PubMed.
- Y. P. Li, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 2861 CrossRef PubMed.
- S.-T. Lin, P. K. Maiti and W. A. Goddard III, J. Phys. Chem. B, 2010, 114, 8191 CrossRef PubMed.
- S.-N. Huang, T. A. Pascal, W. A. Goddard III, P. K. Maiti and S.-T. Lin, J. Chem. Theory Comput., 2011, 7, 1893 CrossRef PubMed.
- B. J. Borah, P. K. Maiti, C. Chakravarty and S. Yashonath, J. Chem. Phys., 2012, 136, 174510 CrossRef PubMed.
- I. Matanović, J. L. Belof, B. Space, K. Sillar, J. Sauer, J. Eckert and Z. Bacic, J. Chem. Phys., 2012, 137, 014701 CrossRef PubMed.
- T. Pham, K. A. Forrest, M. Mostrom, J. R. Hunt, H. Furukawa, J. Eckert and B. Space, Phys. Chem. Chem. Phys., 2017, 19, 13075 RSC.
- L. P. Lindoy, S. J. Kolmann, J. H. D’Arcy, D. L. Crittenden and M. J. T. Jordan, J. Chem. Phys., 2015, 143, 194302 CrossRef PubMed.
- A. K. Singh, J. Lu, R. S. Aga and B. I. Yakobson, J. Phys. Chem. C, 2011, 115, 2476 CrossRef.
- R. P. Feynman, A. R. Hibbs and D. F. Styer, Quantum mechanics and path integrals, Courier Corporation, 2010 Search PubMed.
- K. Sumida, D. Stück, L. Mino, J. Chai, E. Bloch, O. Zavorotynska, L. Murray, M. Dincă, S. Chavan, S. Bordiga, M. Head-Gordon and J. Long, J. Am. Chem. Soc., 2013, 135, 1083 CrossRef PubMed.
- P. J. Hasnip, K. Refson, M. I. J. Probert, J. R. Yates, S. J. Clark and C. J. Pickard, Philos. Trans. R. Soc., A, 2014, 372, 20130270 CrossRef PubMed.
- K. Sillar, A. Hofmann and J. Sauer, J. Am. Chem. Soc., 2009, 131, 4143 CrossRef PubMed.
- A. Kundu, G. Piccini, K. Sillar and J. Sauer, J. Am. Chem. Soc., 2016, 138, 14047 CrossRef PubMed.
- D. Dutta, B. C. Wood, S. Y. Bhide, K. G. Ayappa and S. Narasimhan, J. Phys. Chem. C, 2014, 118, 7741 CrossRef.
- D. Henwood and J. D. Carey, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245413 CrossRef.
- K. Ulman, D. Bhaumik, B. C. Wood and S. Narashimhan, J. Chem. Phys., 2014, 140, 174708 CrossRef PubMed.
- D. P. Broom and M. Hirscher, Energy Environ. Sci., 2016, 9, 3368 RSC.
- K. E. Hurst, P. A. Parilla, K. J. O’Neill and T. Gennett, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 42 CrossRef.
- J. Park, J. D. Howe and D. S. Sholl, Chem. Mater., 2017, 29, 10487 CrossRef.
- S. T. Meek, J. A. Greathouse and M. D. Allendorf, Adv. Mater., 2011, 23, 249 CrossRef PubMed.
- Y. Sun and H.-C. Zhou, Sci. Technol. Adv. Mater., 2015, 16, 054202 CrossRef PubMed.
- J. Jiang, Y. Zhao and O. M. Yaghi, J. Am. Chem. Soc., 2016, 138, 3255 CrossRef PubMed.
- A. J. Howarth, A. W. Peters, N. A. Vermeulen, T. C. Wang, J. T. Hupp and O. K. Farha, Chem. Mater., 2017, 29, 26 CrossRef.
- X. Yu, Z. Tang, D. Sun, L. Ouyang and M. Zhu, Prog. Mater. Sci., 2017, 88, 1 CrossRef.
- P. A. Julien, C. Mottillo and T. Friščić, Green Chem., 2017, 19, 2729 RSC.
- J. E. Mondloch, O. Karagiaridi, O. K. Farha and J. T. Hupp, CrystEngComm, 2013, 15, 9258 RSC.
- A. P. Nelson, O. K. Farha, K. L. Mulfort and J. T. Hupp, J. Am. Chem. Soc., 2009, 131, 458 CrossRef PubMed.
- Y.-P. He, Y.-X. Tan and J. Zhang, Inorg. Chem., 2012, 51, 11232 CrossRef PubMed.
- B. Liu, A. G. Wong-Foy and A. J. Matzger, Chem. Commun., 2013, 49, 1419 RSC.
- T. Runčevski, M. T. Kapelewski, R. M. Torres-Gavosto, J. D. Tarver, C. M. Brown and J. R. Long, Chem. Commun., 2016, 52, 8251 RSC.
- K. J. Gross, K. R. Carrington, S. Barcelo, A. Karkamkar, J. Purewal, S. Ma, H.-C. Zhou, P. Dantzer, K. Ott, T. Burrell, T. Semelsberger, Y. Pivak, B. Dam, D. Chandra and P. Parilla, Recommended Best Practices for the Characterization of Storage Properties of Hydrogen Storage Materials, U.S. Department of Energy, 2012, https://energy.gov/sites/prod/files/2014/03/f12/best_practices_hydrogen_storage.pdf, accessed Mar 2018.
- D. P. Broom and C. J. Webb, Int. J. Hydrogen Energy, 2017, 42, 29320 CrossRef.
- H. Oh, T. Gennett, P. Atanassov, M. Kurttepeli, S. Bals, K. E. Hurst and M. Hirscher, Microporous Mesoporous Mater., 2013, 177, 66 CrossRef.
- D. DeSantis, J. A. Mason, B. D. James, C. Houchins, J. R. Long and M. Veenstra, Energy Fuels, 2017, 31, 2024 CrossRef.
- C. O. Areán, S. Chavan, C. P. Cabello, E. Garrone and G. T. Palomino, ChemPhysChem, 2010, 11, 3237 CrossRef PubMed.
- M. Dincă, A. Dailly, Y. Liu, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128, 16876 CrossRef PubMed.
- Y. Liu, C. M. Brown, D. A. Neumann, V. K. Peterson and C. J. Kepert, J. Alloys Compd., 2007, 446-447, 385 CrossRef.
- J. Purewal, J. B. Keith, C. C. Ahn, C. M. Brown, M. Tyagi and B. Fultz, J. Chem. Phys., 2012, 137, 224704 CrossRef PubMed.
- Hydrogen Storage Engineering Center of Excellence Models, http://www.hsecoe.org/models.php, accessed March 2018.
- A. J. Lachawiec, Jr. and R. T. Yang, Langmuir, 2008, 24, 6159 CrossRef PubMed.
- Y. Li and R. T. Yang, J. Am. Chem. Soc., 2006, 128, 8136 CrossRef PubMed.
- R. T. Yang and Y. Wang, J. Am. Chem. Soc., 2009, 131, 4224 CrossRef PubMed.
- M. Suri, M. Dornfeld and E. Ganz, J. Chem. Phys., 2009, 131, 174703 CrossRef PubMed.
- Y. Zhao and T. Gennett, Phys. Rev. Lett., 2014, 112, 076101 CrossRef PubMed.
- C. M. Ghimbeau, C. Zlotea, R. Gadiou, F. Cuevas, E. Leroy, M. Latroche and C. Vix-Guterl, J. Mater. Chem., 2011, 21, 17765 RSC.
- N. P. Stadie, J. J. Purewal, C. C. Ahn and B. Fultz, Langmuir, 2010, 26, 15481 CrossRef PubMed.
- A. Ansón, E. Lafuente, E. Urriolabeitia, R. Navarro, A. M. Benito, W. K. Maser and M. T. Martínez, J. Phys. Chem. B, 2006, 110, 6643 CrossRef PubMed.
- R. Campesi, F. Cuevas, M. Latroche and M. Hirscher, Phys. Chem. Chem. Phys., 2010, 12, 10457 RSC.
- S. M. Luzan and A. V. Talyzin, Microporous Mesoporous Mater., 2010, 135, 201 CrossRef.
- Y. Li, L. Wang and R. T. Yang, Microporous Mesoporous Mater., 2010, 135, 206 CrossRef.
- M. Hirscher, Microporous Mesoporous Mater., 2010, 135, 209 CrossRef.
- S. M. Luzan and A. V. Talyzin, Microporous Mesoporous Mater., 2011, 139, 216 CrossRef.
- M. Dincă and J. R. Long, Angew. Chem., Int. Ed., 2008, 47, 6766 CrossRef PubMed.
- H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- B. Chen, M. Eddaoudi, T. M. Reineke, J. W. Kampf, M. O’Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2000, 122, 11559 CrossRef.
- N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O’Keeffe and O. M. Yaghi, Science, 2003, 300, 1127 CrossRef PubMed.
- B. Chen, N. W. Ockwig, A. R. Millward, D. S. Contreras and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4745 CrossRef PubMed.
- T. Yildirim and M. R. Hartman, Phys. Rev. Lett., 2005, 95, 215504 CrossRef PubMed.
- J. G. Vitillo, L. Regli, S. Chavan, G. Ricchiardi, G. Spoto, P. D. C. Dietzel, S. Bordiga and A. Zecchina, J. Am. Chem. Soc., 2008, 130, 8386 CrossRef PubMed.
- W. Zhou, H. Wu and T. Yildirim, J. Am. Chem. Soc., 2008, 130, 15268 CrossRef PubMed.
- K. Sumida, C. M. Brown, Z. R. Herm, S. Chavan, S. Bordiga and J. R. Long, Chem. Commun., 2011, 47, 1157 RSC.
- W. L. Queen, E. D. Bloch, C. M. Brown, M. R. Hudson, J. A. Mason, L. J. Murray, A. J. Ramirez-Cuesta, V. K. Peterson and J. R. Long, Dalton Trans., 2012, 41, 4180 RSC.
- H. Irving and R. J. P. Williams, J. Chem. Soc., 1953, 3192 RSC.
- A. E. Curzon and A. J. Mascall, Br. J. Appl. Phys., 1965, 16, 1301 CrossRef.
- M. T. Kapelewski, T. Runčevski, J. D. Tarver, H. Z. H. Jiang, K. E. Hurst, A. Ayala, T. Gennett, S. A. FitzGerald, C. M. Brown and J. R. Long, submitted.
- M. Lalonde, W. Bury, O. Karagiaridi, Z. Brown, J. T. Hupp and O. K. Farha, J. Mater. Chem. A, 2013, 1, 5453 RSC.
- S. Das, H. Kim and K. Kim, J. Am. Chem. Soc., 2009, 131, 3814 CrossRef PubMed.
- X. Song, T. K. Kim, H. Kim, D. Kim, S. Jeong, H. R. Moon and M. S. Lah, Chem. Mater., 2012, 24, 3065 CrossRef.
- M. Dincă, W. S. Han, Y. Liu, A. Dailly, C. M. Brown and J. R. Long, Angew. Chem., Int. Ed., 2007, 46, 1419 CrossRef PubMed.
- X. Solans-Monfort, V. Branchadell, M. Sodupe, C. M. Zicovich-Wilson, E. Gribov, G. Spoto, C. Busco and P. Ugliengo, J. Phys. Chem. B, 2004, 108, 8278 CrossRef.
- D. Denysenko, M. Grzywa, J. Jelic, K. Reuter and D. Volkmer, Angew. Chem., Int. Ed., 2014, 53, 5832 CrossRef PubMed.
- M. Witman, S. Ling, A. Gladysiak, K. C. Stylianou, B. Smit, B. Slater and M. Haranczyk, J. Phys. Chem. C, 2017, 121, 1171 CrossRef PubMed.
- T. Arliguie, B. Chaudret, R. H. Morris and A. Sella, Inorg. Chem., 1988, 27, 598 CrossRef.
- G. J. Kubas, Chem. Rev., 2007, 107, 4152 CrossRef PubMed.
- G. J. Kubas, R. R. Ryan, B. I. Swanson, P. J. Vergamini and H. J. Wasserman, J. Am. Chem. Soc., 1984, 106, 451 CrossRef.
- G. J. Kubas, Acc. Chem. Res., 1988, 21, 120 CrossRef.
- G. J. Kubas, C. J. Burns, G. R. K. Khalsa, L. S. Van Der Sluys, G. Kiss and C. D. Hoff, Organometallics, 1992, 11, 3390 CrossRef.
- A. F. Borowski, B. Donnadieu, J.-C. Daran, S. Sabo-Etienne and B. Chaudret, Chem. Commun., 2000, 543 RSC.
- M. L. Christ, S. Sabo-Etienne, G. Chung and B. Chaudret, Inorg. Chem., 1994, 33, 5316 CrossRef.
- M. Grellier, L. Vendier, B. Chaudret, A. Albinati, S. Rizzato, S. Mason and S. Sabo-Etienne, J. Am. Chem. Soc., 2005, 127, 17592 CrossRef PubMed.
- M. Grellier, L. Vendier and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2007, 46, 2613 CrossRef PubMed.
- G. J. Kubas, J. E. Nelson, J. C. Bryan, J. Eckert, L. Wisniewski and K. Zilm, Inorg. Chem., 1994, 33, 2954 CrossRef.
- A. Toupadakis, G. J. Kubas, W. A. King, B. L. Scott and J. Huhmann-Vincent, Organometallics, 1998, 17, 5315 CrossRef.
- M. Dincă and J. R. Long, J. Am. Chem. Soc., 2005, 127, 9376 CrossRef PubMed.
- L. Sun, T. Miyakai, S. Seki and M. Dincă, J. Am. Chem. Soc., 2013, 135, 8185 CrossRef PubMed.
- F. Luo, C. Yan, L. Dang, R. Krishna, W. Zhou, H. Wu, X. Dong, Y. Han, T.-L. Hu, M. O’Keeffe, L. Wang, M. Luo, R.-B. Lin and B. Chen, J. Am. Chem. Soc., 2016, 138, 5678 CrossRef PubMed.
- S. M. Cohen, Chem. Rev., 2012, 112, 970 CrossRef PubMed.
- D. W. Smithenry, S. R. Wilson and K. S. Suslick, Inorg. Chem., 2003, 42, 7719 CrossRef PubMed.
- W. Morris, B. Volosskiy, S. Demir, F. Gándara, P. L. McGrier, H. Furukawa, D. Cascio, J. F. Stoddart and O. M. Yaghi, Inorg. Chem., 2012, 51, 6443 CrossRef PubMed.
- B. Chen, X. Zhao, A. Putkham, K. Hong, E. B. Lobkovsky, E. J. Hurtado, A. J. Fletcher and K. M. Thomas, J. Am. Chem. Soc., 2008, 130, 6411 CrossRef PubMed.
- C.-D. Wu, A. Hu, L. Zhang and W. Lin, J. Am. Chem. Soc., 2005, 127, 8940 CrossRef PubMed.
- E. D. Bloch, D. Britt, C. Lee, C. J. Doonan, F. J. Uribe-Romo, H. Furukawa, J. R. Long and O. M. Yaghi, J. Am. Chem. Soc., 2010, 132, 14382 CrossRef PubMed.
- C. J. Doonan, W. Morris, H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 9492 CrossRef PubMed.
- K. K. Tanabe, C. A. Allen and S. M. Cohen, Angew. Chem., Int. Ed., 2010, 49, 9730 CrossRef PubMed.
- K. Koh, A. G. Wong-Foy and A. J. Matzger, Angew. Chem., Int. Ed., 2008, 47, 677 CrossRef PubMed.
- H. Fei, J.-W. Shin, Y. S. Meng, M. Adelhardt, J. Sutter, K. Meyer and S. M. Cohen, J. Am. Chem. Soc., 2014, 136, 4965 CrossRef PubMed.
- H. G. T. Nguyen, M. H. Weston, A. A. Sarjeant, D. M. Gardner, Z. An, R. Carmieli, M. R. Wasielewski, O. K. Farha, J. T. Hupp and S.-B. T. Nguyen, Cryst. Growth Des., 2013, 13, 3528 CrossRef.
- U. H. F. Bunz, K. Seehafer, F. L. Geyer, M. Bender, I. Braun, E. Smarsly and J. Freudenberg, Macromol. Rapid Commun., 2014, 35, 1466 CrossRef PubMed.
- S. Das, P. Heasman, T. Ben and S. Qiu, Chem. Rev., 2017, 117, 1515 CrossRef PubMed.
- T. Ben, H. Ren, S. Ma, D. Cao, J. Lan, X. Jing, W. Wang, J. Xu, F. Deng, J. M. Simmons, S. Qiu and G. Zhu, Angew. Chem., Int. Ed., 2009, 48, 9457 CrossRef PubMed.
- W. Lu, D. Yuan, D. Zhao, C. I. Schilling, O. Plietzsch, T. Muller, S. Bräse, J. Guenther, J. Blümel, R. Krishna, Z. Li and H.-C. Zhou, Chem. Mater., 2010, 22, 5964 CrossRef.
- D. Yuan, W. Lu, D. Zhao and H.-C. Zhou, Adv. Mater., 2011, 23, 3723 CrossRef PubMed.
- C. Pei, T. Ben, Y. Li and S. Qiu, Chem. Commun., 2014, 50, 6134 RSC.
- H. M. El-Kaderi, J. R. Hunt, J. L. Mendoza-Cortés, A. P. Côté, R. E. Taylor, M. O’Keeffe and O. M. Yaghi, Science, 2007, 316, 268 CrossRef PubMed.
- J. M. H. Thomas and A. Trewin, J. Phys. Chem. C, 2014, 118, 19712 CrossRef.
- P. Fayon and A. Trewin, Phys. Chem. Chem. Phys., 2016, 18, 16840 RSC.
- A. Tarzia, A. W. Thornton, C. J. Doonan and D. M. Huang, J. Phys. Chem. C, 2017, 121, 16381 CrossRef.
- J.-X. Jiang, C. Wang, A. Laybourn, T. Hasell, R. Clowes, Y. Z. Khimyak, J. Xiao, S. J. Higgins, D. J. Adams and A. I. Cooper, Angew. Chem., Int. Ed., 2011, 50, 1072 CrossRef PubMed.
- Y. Xie, T.-T. Wang, X.-H. Liu, K. Zou and W.-Q. Deng, Nat. Commun., 2013, 4, 1960 CrossRef PubMed.
- N. B. McKeown, S. Hanif, K. Msayib, C. E. Tattershall and P. M. Budd, Chem. Commun., 2002, 2782 RSC.
- M. H. Weston, O. K. Farha, B. G. Hauser, J. T. Hupp and S.-B. T. Nguyen, Chem. Mater., 2012, 24, 1292 CrossRef.
- S. Fischer, J. Schmidt, P. Strauch and A. Thomas, Angew. Chem., Int. Ed., 2013, 52, 12174 CrossRef PubMed.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O’Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166 CrossRef PubMed.
- J. R. Hunt, C. J. Doonan, J. D. LeVangie, A. P. Côté and O. M. Yaghi, J. Am. Chem. Soc., 2008, 130, 11872 CrossRef PubMed.
- F. J. Uribe-Romo, J. R. Hunt, H. Furukawa, C. Klöck, M. O’Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 4570 CrossRef PubMed.
- P. Kuhn, M. Antonietti and A. Thomas, Angew. Chem., Int. Ed., 2008, 47, 3450 CrossRef PubMed.
- K. T. Jackson, T. E. Reich and H. M. El-Kaderi, Chem. Commun., 2012, 48, 8823 RSC.
- J. W. Colson and W. R. Dichtel, Nat. Chem., 2013, 5, 453 CrossRef PubMed.
- G. Lin, H. Ding, D. Yuan, B. Wang and C. Wang, J. Am. Chem. Soc., 2016, 138, 3302 CrossRef PubMed.
- A. P. Côté, H. M. El-Kaderi, H. Furukawa, J. R. Hunt and O. M. Yaghi, J. Am. Chem. Soc., 2007, 129, 12914 CrossRef PubMed.
- H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 8875 CrossRef PubMed.
- Z. Li, X. Feng, Y. Zou, Y. Zhang, H. Xi, X. Liu and Y. Mu, Chem. Commun., 2014, 50, 13825 RSC.
- X. Feng, L. Liu, Y. Honsho, A. Saeki, S. Seki, S. Irle, Y. Dong, A. Nagai and D. Jiang, Angew. Chem., Int. Ed., 2012, 51, 2618 CrossRef PubMed.
- S.-Y. Ding, J. Gao, Q. Wang, Y. Zhang, W.-G. Song, C.-Y. Su and W. Wang, J. Am. Chem. Soc., 2011, 133, 19816 CrossRef PubMed.
- W. Zhang, P. Jiang, Y. Wang, J. Zhang, Y. Gao and P. Zhang, RSC Adv., 2014, 4, 51544 RSC.
- S. B. Kalidindi, K. Yusenko and R. A. Fischer, Chem. Commun., 2011, 47, 8506 RSC.
- S. B. Kalidindi, H. Oh, M. Hirscher, D. Esken, C. Wiktor, S. Turner, G. Van Tendeloo and R. A. Fischer, Chem. – Eur. J., 2012, 18, 10848 CrossRef PubMed.
- B. Szczęśniak, J. Choma and M. Jaroniec, Adv. Colloid Interface Sci., 2017, 243, 46 CrossRef PubMed.
- S. Zhu and T. Li, ACS Nano, 2014, 8, 2864 CrossRef PubMed.
- T. H. Kim, J. Bae, T. H. Lee, J. Hwang, J. H. Jung, D. K. Kim, J. S. Lee, D. O. Kim, Y. H. Lee and J. Ihm, Nano Energy, 2016, 27, 402 CrossRef.
- J. W. Burress, S. Gadipelli, J. Ford, J. M. Simmons, W. Zhou and T. Yildirim, Angew. Chem., Int. Ed., 2010, 49, 8902 CrossRef PubMed.
- A. G. Klechikov, G. Mercier, P. Merino, S. Blanco, C. Merino and A. V. Talyzin, Microporous Mesoporous Mater., 2015, 210, 46 CrossRef.
- E. Beheshti, A. Nojeh and P. Servati, Carbon, 2011, 49, 1561 CrossRef.
- C.-H. Chen, T.-Y. Chung, C.-C. Shen, M.-S. Yu, C.-S. Tsao, G.-N. Shi, C.-C. Huang, M.-D. Ger and W.-L. Lee, Int. J. Hydrogen Energy, 2013, 38, 3681 CrossRef.
- C. Zhou, J. A. Szpunar and X. Cui, ACS Appl. Mater. Interfaces, 2016, 8, 15232 CrossRef PubMed.
- A. C. Dillon, K. M. Jones, T. A. Bekkedahl, C. H. Kiang, D. S. Bethune and M. J. Heben, Nature, 1997, 386, 377 CrossRef.
- C. Liu, Y. Chen, C.-Z. Wu, S.-T. Xu and H.-M. Cheng, Carbon, 2010, 48, 452 CrossRef.
- H. J. Wasserman, G. J. Kubas and R. R. Ryan, J. Am. Chem. Soc., 1986, 108, 2294 CrossRef PubMed.
- L. F. Wang, F. H. Yang and R. T. Yang, AIChE J., 2009, 55, 1823 CrossRef.
- Y. Jeong and T. C. M. Chung, Carbon, 2010, 48, 2526 CrossRef.
- Z. Jin, Z. Z. Sun, L. J. Simpson, K. J. O’Neill, P. A. Parilla, Y. Li, N. P. Stadie, C. C. Ahn, C. Kittrell and J. M. Tour, J. Am. Chem. Soc., 2010, 132, 15246 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |