 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New horizons for inorganic solid state ion conductors
Zhizhen
Zhang
ab,
Yuanjun
Shao
a,
Bettina
Lotsch
 c,
Yong-Sheng
Hu
c,
Yong-Sheng
Hu
 a,
Hong
Li
a,
Jürgen
Janek
a,
Hong
Li
a,
Jürgen
Janek
 *d,
Linda F.
Nazar
*d,
Linda F.
Nazar
 *b,
Ce-Wen
Nan
*e,
Joachim
Maier
*b,
Ce-Wen
Nan
*e,
Joachim
Maier
 *c,
Michel
Armand
*f and
Liquan
Chen
*c,
Michel
Armand
*f and
Liquan
Chen
 *a
*a
aKey Laboratory for Renewable Energy, Beijing Key Laboratory for New Energy Materials and Devices, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100190, China. E-mail: lqchen@aphy.iphy.ac.cn
bDepartment of Chemistry, Waterloo Institute of Nanotechnology, University of Waterloo, 200 University Avenue West, Waterloo, Ontario N2L 3G1, Canada. E-mail: lfnazar@uwaterloo.ca
cMax Planck Institute for Solid State Research, Stuttgart 70569, Germany. E-mail: s.weiglein@fkf.mpg.de
dInstitute of Physical Chemistry & Center for Materials Research, Justus-Liebig-University Giessen, Heinrich-Buff-Ring 17, 35392 Giessen, Germany. E-mail: Juergen.Janek@phys.Chemie.uni-giessen.de
eSchool of Materials Science and Engineering, Tsinghua University, Beijing 100084, China. E-mail: cwnan@mail.tsinghua.edu.cn
fCIC Energigune, Alava Technology Park, Albert Einstein, 4801510 MIÑANO Álava, Spain. E-mail: marmand@cicenergigune.com
First published on 11th June 2018
Abstract
Among the contenders in the new generation energy storage arena, all-solid-state batteries (ASSBs) have emerged as particularly promising, owing to their potential to exhibit high safety, high energy density and long cycle life. The relatively low conductivity of most solid electrolytes and the often sluggish charge transfer kinetics at the interface between solid electrolyte and electrode layers are considered to be amongst the major challenges facing ASSBs. This review presents an overview of the state of the art in solid lithium and sodium ion conductors, with an emphasis on inorganic materials. The correlations between the composition, structure and conductivity of these solid electrolytes are illustrated and strategies to boost ion conductivity are proposed. In particular, the high grain boundary resistance of solid oxide electrolytes is identified as a challenge. Critical issues of solid electrolytes beyond ion conductivity are also discussed with respect to their potential problems for practical applications. The chemical and electrochemical stabilities of solid electrolytes are discussed, as are chemo-mechanical effects which have been overlooked to some extent. Furthermore, strategies to improve the practical performance of ASSBs, including optimizing the interface between solid electrolytes and electrode materials to improve stability and lower charge transfer resistance are also suggested.
Broader contextDriven by the necessity to reduce greenhouse effects caused by the emission of CO2, the development of new electrochemical energy conversion and storage devices is of prime significance. Lithium ion batteries have revolutionized the portable electronics industry but may not be able to satisfy future customers’ demands in the field of large-scale energy storage systems such as electrical vehicles and power grids. In particular, safety concerns have been a long-standing issue hindering the development of commercial liquid batteries with liquid organic electrolytes. In this context, all solid-state batteries (ASSBs) based on solid electrolytes (SEs) can not only address safety concerns, but may also enable the use of high voltage cathode materials and Li/Na metal anodes to enable long life and high energy density batteries. As the most important component in ASSBs, the SE determines the power density, long cycle stability and the safety of batteries. In this review a state of art and comprehensive description of the recent developments in SEs will be given, and general descriptors to guide the design of SEs are proposed. Critical issues of SEs with respect to their potential problems for practical applications (e.g., the chemical and electrochemical stability of SE, chemo-mechanical effects, large charge transfer resistance at the interface) are discussed, and strategies to overcome these obstacles are also proposed. |
1. Introduction
The development of electrochemical energy conversion and storage devices is one of the most important challenges to alleviate the greenhouse effects caused by emission of CO2.1,2 Owing to their high specific energy, large-scale rechargeable batteries have recently become highly sought after for applications in power grids and electric vehicles.2,3 However, the flammable, reactive organic electrolytes used in conventional batteries incur severe safety issues.4 In addition, although Li metal has an extremely high theoretical specific capacity (3860 mA h g−1), low mass and the lowest negative electrochemical potential (−3.04 V vs. SHE), rechargeable batteries using Li metal have not been commercialized because of lithium metal's low cycling efficiency and tendency to form dendrites during repeated charge/discharge.5,6 The only exceptions are the Blue Solutions™ batteries for EVs and buses that use a polymer electrolyte that operates at about 70 °C instead of a liquid electrolyte.In this context, all solid-state batteries (ASSBs) based on solid electrolytes (SEs) can not only address safety concerns, but may also enable the use of high voltage cathode materials and Li/Na metal anodes to allow for long-term stable and high energy density batteries. An increase of more than 20% in energy density (depending on additional cathode capacity at high voltage) can be achieved by increasing the cell voltage from 4.2 V to 5 V.7 Oxide-based inorganic solid electrolytes can endure such high voltages whereas liquid electrolytes are not stable at such very oxidizing potentials.7 ASSBs exhibit additional advantages including low self-discharge, versatile geometries, high thermal stability, and thus wide operating temperature,2 and as well as resistance to shocks and vibrations.8 Moreover, the solidification of the electrolyte allows for the design of high-voltage bipolar stacked batteries and effectively decreases the dead space between single cells with thinner current collectors.
The SE is the most vital component in solid-state batteries – together with the electrode materials – as it determines the power density, long-term stability and the safety of the batteries. To realize ASSBs that can operate at ambient and moderate temperatures, SEs with high ion conductivity (>10−4 S cm−1, better >10−3 S cm−1 in case of thick composite electrodes),9 negligible electronic conductivity (<10−12 S cm−1),9 and a wide electrochemical window10,11 are necessary. The greatest obstacles to the integration of SEs into batteries are the inherently poor ion conductivity of most SEs and the large resistance at the interface between the SE and active material, but also chemo-mechanical issues related to volume changes of active materials. Favorable interfacial contact and chemical stability between the SE and the electrode materials are both critical to achieve good electrochemical performance. The electrode–electrolyte interface particularly becomes an issue if nanostructured electrodes are to be considered and/or if large volume variations arise during cycling.12–14 The chemical stability of SEs is not necessarily better than that of liquid electrolytes and, in the majority of cases, relies on kinetic, not thermodynamic factors (as in liquid systems).
Inorganic conductors and organic polymers are the most commonly used solid electrolyte materials in ASSBs. The former are characterized by high ion conductivity (>10−4 S cm−1) in many cases and high thermal stability. Furthermore, typical inorganic SEs are single ion conductors that preclude concentration polarization effects. However, ASSBs using inorganic ceramics often exhibit lower-than-expected electrochemical performance due to their poor interfacial contact with the electrode material.4,15 Inorganic ceramics and organic polymers differ greatly in their mechanical properties and are thus suitable for different battery designs. The high elastic moduli of ceramics lead to poor processability because of their brittleness and hardness. Nevertheless, they are appropriate for rigid battery designs, such as thin-film batteries. In contrast, polymer electrolytes are well suited for flexible battery designs owing to their low elastic moduli. However, they suffer from other drawbacks, such as low ion conductivity (<10−5 S cm−1 at ambient temperature), low cation transference number (t+ ≈ 0.2–0.5) unless the anion itself is tethered to a polymer and poor oxidation resistance.16 Ceramic/polymer composite electrolytes may combine the high conductivity of ceramics and excellent flexibility of polymers and hence have recently attracted much attention.17
Full reviews of inorganic Li-ion conductors were published by Knauth in 2009,18 Shao-Horn's group in 2015,19 and Chen et al. in 2016,20 in addition to many other shorter articles which focus on specific classes of SEs, including perovskites21 and garnets.22 Brief accounts of the pros and cons of solid electrolytes in battery systems have been recently provided.7,23 Following the fast progress in the search for new and optimized SEs, our current review gives an up-to-date, yet comprehensive description of the recent exciting developments in inorganic solid electrolytes, including Na-ion conductors and covering both oxide and sulfide-based materials. Based on a survey of the previous studies, the major factors that influence the ion conductivity are summarized and general descriptors that govern conductivity are also proposed. Even though low-conductivity phases (e.g. LiF) may act as relevant electrolytes for very thin film systems, we concentrate here on bulk phases with high conductivities above 10−4 S cm−1. Finally, the chemical and electrochemical stabilities of SEs against Li/Na metal and electrode materials are evaluated, a topic that has been somewhat overlooked except in a few recent reports.14,23–25 Moreover, strategies to enhance the stability of SEs and to modify the interface between the SEs and electrode layers are proposed.
2. Lithium ion conductors
Crystalline ion conductors exhibit better thermal stability than polymeric materials. However, several difficulties arise for crystalline electrolytes that are associated with their grain boundaries and their fabrication into thin sheets or layers. Grain boundaries in polycrystalline conductors can lead to a locally perturbed structure – often in conjunction with high defect concentrations9 – which may cause a large resistive barrier and hinder ion migration across the interface in materials with otherwise high bulk conductivity. The transport of mobile ions across grain boundaries thus becomes the rate-determining step. The opposite effect can also occur: in solid electrolytes with low bulk conductivity, a high fraction of grain boundaries (i.e., in nanostructured materials) may improve the total conductivity by providing better transport paths. The beneficial effect of interfaces on ion transport is highlighted in Section 4.2.Compared to crystalline ceramic materials, glasses are superior in terms of isotropic conductivity and lack of grain boundaries. From the technological point of view, glasses are often easy to process into thin films. The use of thin film separators can significantly reduce the internal resistance of batteries. For practical applications, the minimum conductivity required depends on the thickness of the separator layer. A total Li ion conductivity greater than 10−6 S cm−1 is required in order to avoid having to use a separator thickness well below one micron to minimize the IR drop across the film. Lithium phosphorous oxide nitride (LiPON) is one of the successful examples that has been employed in thin-film solid-state batteries. LiPON is an amorphous phase deposited by magnetron sputtering of Li3PO4 in a N2 atmosphere.26 The conductivity is a function of the N/O ratio and deposition conditions, with the maximum reported conductivity being ca. 2 × 10−6 S cm−1 to 3.3 × 10−6 S cm−1.27–31 Aside from their moderate ion conductivity, LiPON films exhibit very low electronic conductivities (8 × 10−14 S cm−1), making them appropriate for practical applications.32,33 LiPON can also be used as a protective layer in conventional lithium ion batteries. Thin-film solid-state batteries containing LiPON film as the electrolyte, Li or V2O5 as the anode, and LiMn2O4 or LiCoO2 as the cathode display excellent cycling performance.32,33 Another important family of glasses is based on mixtures of Li2S and P2S5, where conductivity on the order of 10−3 S cm−1 has been reported with the addition of lithium halides.34–36 Interest in glasses has reignited recently due to observations of dendrite growth through grain boundaries in polycrystalline ion conductors such as LLZO.37–39 A particularly important advance was reported by Hayashi in 2014, where an extremely high conductivity of 1.7 × 10−2 S cm−1 was reported for a Li2S–P2S5 glass-ceramic phase.40 By employing glasses, unavoidable local mechanical pressure during cycling in ASSBs may be better compensated, while protective interphases are necessary in order to stabilize anode and/or cathode contacts. Although this review focusses on crystalline oxide and sulfide conductors owing to several major breakthroughs in crystalline conductors, some discussion on glasses and glass-ceramics is also covered here.
2.1 Crystalline conductors
A wide variety of lithium metal oxides, sulfides, phosphates, nitrides, and halides have been shown to exhibit high ion conductivities, as summarized in Fig. 1.41–52 LiI,53 Li3N,54 Li–β′′-Al2O3,55,56 and LiSICON51 were the first studied. Although single crystals of Li3N possess a high ion conductivity (10−3 S cm−1 at room temperature),57 the low decomposition voltage of Li3N57 (0.44 V based on thermodynamic considerations) and its extreme sensitivity toward moisture have limited its practical use. Nonetheless, thin films of Li3N formed in situ by reaction of Li with N2 gas can be used to protect other SEs from direct contact with Li.58 Sputtering of Cu3N followed by evaporation of Li metal results in a Cu0/Li3N composite that has been used to protect another solid electrolyte.59 Single crystals of Li–β′′-Al2O3 also show excellent conductivity (3 × 10−3 S cm−1) at room temperature.55,56 However, this phase is unlikely to be used in practical applications, since it is extremely hygroscopic and difficult to prepare dry.55,56 Following this early work on Li solid electrolytes, several classes of materials were developed. In the following we will discuss the most important inorganic crystalline Li ion conductors. These can be classified as Li3xLa2/3−x□1/3−2xTiO3 (LLTO, perovskite),50 Li3OCl (anti-perovskite),60 Li14ZnGe4O16 (LiSICON),51 Li1.3Ti1.7Al0.3(PO4)3 (NaSICON type),52 Li7La3Zr2O12 (garnet),22 Thio-LiSICON,61 Li6PS5X (X = Cl, Br, I), argyrodites,62 and Li10MP2S12, (M = Ge, Sn).45,63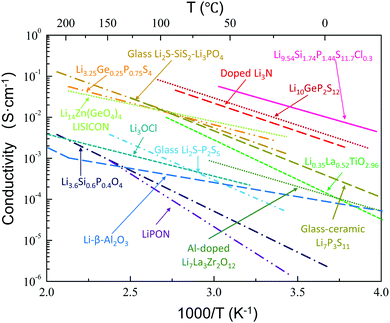 | ||
| Fig. 1 Ion conductivity of several well-known solid lithium ion conductors, including glass and crystalline conductors. The data are taken from ref. 41–52. Reproduced with permission from ref. 41, 44, 51. Copyright (1978, 1993, 2017), Elsevier. Reproduced with permission from ref. 42. Copyright (2001), The Electrochemical Society. Reproduced with permission from ref. 43, 48. Copyright (2005, 2011), Wiley. Reproduced with permission from ref. 45, 46. Copyright (2011, 2016), Springer Nature. Reproduced with permission from ref. 47, 49, 50, 52. Copyright (2002, 2012, 2016), American Chemical Society. | ||
2.1.1.1 Perovskite type conductors. Li3xLa2/3−x□1/3−2xTiO3 (LLTO, 0.04 < x < 0.17) and its variants have attracted much interest because of their high bulk ion conductivities (∼10−3 S cm−1),50 negligible electronic conductivities under normal conditions,64 and wide electrochemical windows (reported to be greater than 8 V). LLTO has a perovskite (ABO3) structure, with the A-sites partially occupied by Li or La. The A-site cations are not randomly distributed, but are ordered to form alternately stacked La-rich (La1) and La-poor (La2) layers along the c axis.65–70 Previous studies have shown that the Li-ion conducting behavior in the grain interior is highly dependent on the crystal structure, composition (e.g., A-site vacancy concentration, the degree of A site cation ordering, and dopants) and structural distortions.65–70 Li-ion jump events occur only when adjacent vacant A-site cavities are available.21 The Li-poor (0.03 ≤ x < 0.1) compositions are reported to show orthorhombic symmetry (Fig. 2a), with high La occupancy in the La-rich layer (Fig. 2d) and anti-phase tilted TiO6 octahedra along the b axis;65–70 while in Li-rich (0.1 ≤ x < 0.167) compositions, the symmetry becomes tetragonal70 (Fig. 2a) and the degree of La ordering decreases as the Li+ content increases (Fig. 2e). The dimension of the Li+ trajectory is determined by the Li+ ion concentration and the A-site vacancy. In the Li-poor LLTO, the La-rich layer acts as a barrier to Li+ diffusion in the [001] direction because of the high La occupancy (∼0.95) and low vacancy concentration (∼0.05). The 2D Li ion pathways are thus predominantly confined within the La-poor layer.67 On the other hand, Li-rich LLTO has relatively low La occupation (0.65)71 and a higher concentration of vacancies and Li ions in the La-rich layer. In the latter, the Li migration between alternating La1 and La2 layers becomes possible, resulting in 3D conduction, at least within certain regions.
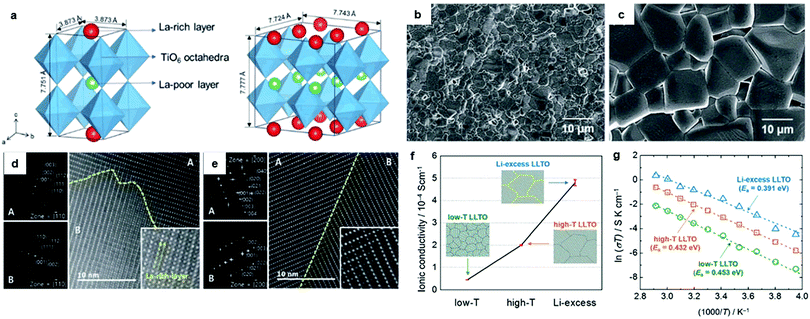 | ||
| Fig. 2 (a) A schematic of the crystal structures of LLTOs: a tetragonal structure (left) and orthorhombic structure (right). FESEM micrographs of LLTOs sintered at different temperatures; (b) low-T LLTO (1200 °C) and (c) high-T LLTO (1400 °C). HRTEM images combined with SAEDs of (d) low-T LLTO and (e) high-T LLTO (magnified images are given in the inset): (f) a comparison of Li+ conductivities along with schematics of the domain microstructures of the LLTO electrolytes: low-T LLTO, high-T LLTO and Li-excess LLTO. (g) Arrhenius plots of the boundary conductivities for low-T LLTO, high-T LLTO and Li-excess LLTO measured over a temperature range of 20 °C to 70 °C. The activation energy (Ea) values calculated are indicated.90 Reproduced with permission from ref. 90. Copyright (2017), the Royal Society of Chemistry. | ||
To further improve the conductivity, efforts have been made to substitute the A-site La3+ (ref. 72 and 73) and/or B-site Ti4+.74–77 However, only the substitution of Sr2+,72 Ba2+,78 and Nd3+ (ref. 79) for La3+ and the partial substitution of Al3+ (ref. 74–76) or Ge4+ (ref. 77) for Ti4+ offer improvement in the bulk conductivity, which is nonetheless marginal.
Earlier studies also found the total conductivity of LLTOs is governed by ion transfer across the grain boundary (GB). The latter conductivities are reported to be in the order of 10−4–10−5 S cm−1, which is about 1–2 orders of magnitudes lower than that of the bulk. Scrutiny through high-resolution transmission electron microscopy (HRTEM) reveals LLTOs have complex microstructures: domains with different crystal orientations and periodicities are observed. The relationship between conductivity and microstructures (e.g., density, domain size, atomistic structure, and composition of the domain boundaries)70,80–89 were recently examined. The heat-treatment temperature affects the domain size, with a higher sintering temperature leading to a larger domain size and higher domain boundary conductivity (see Fig. 2b–f).90 Scanning transmission electron microscopy (STEM) verified the existence of a large fraction of 90° domain boundaries, which was proven by DFT calculations to be detrimental to ion transfer.89 Their elimination is predicted to increase the conductivity by about three orders of magnitude.89 As shown in Fig. 2f and g, higher conductivity is also achieved when the Li concentration at the boundaries increases.
The origin of the poor grain boundary conductivity in LLTO was explored by Nan's group.88 STEM/EELS analysis (Fig. 3a–g) revealed that dramatic structural deviations and chemical variations from the bulk framework can be observed at most grain boundaries. The grain boundary resembled more of a Ti–O binary phase, devoid of La3+ and more importantly, of the charge carrier Li+; Fig. 3h schematically depicts the atomic configuration of the grain boundary and the Li site distribution. This mechanism explains previous observations that the introduction of Li ion conducting intergranular phases (Li2O, LiF, Li3BO3, Li4SiO4, LLZO) may increase the grain boundary conductivity, if the new interface between the perovskite grains and the second phase does not act as a new barrier for Li migration.84,91 Adding inert oxides, e.g. SiO2 and Al2O3 as flux agents can also improve the conductivity of LLTO.92–94 In the LLTO/SiO2 composite, SiO2 accommodates Li from LLTO grains to form an amorphous lithium silicate which greatly enhances the grain boundary conductivity.92 Similarly, the addition of Al2O3 formed LiAl5O8 leads to a boost in both the bulk and grain boundary conductivity.93
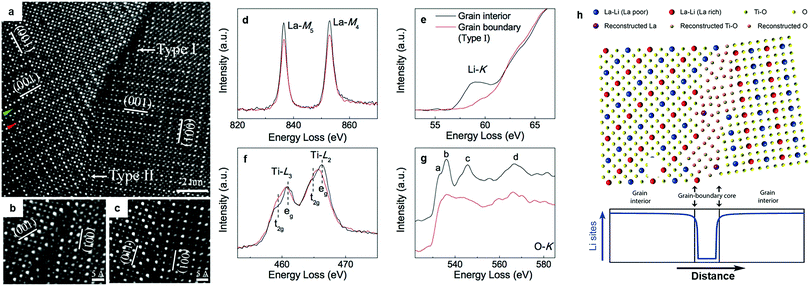 | ||
| Fig. 3 (a) HAADF-STEM image of a GB exhibiting both dark- and normal-contrast regions, labelled as Type I and Type II, respectively. Within the grains, a row of atomic columns for a La-poor layer and one for a La-rich layer were indicated by green and red arrows on the left-hand side of the image, respectively. The (001) planes of the alternating La-rich/La-poor layers (arbitrarily designated as (001) planes in image) of different regions in the grain were marked to highlight the existence of nanodomains; (b) further magnified Type I GB feature; (c) further magnified Type II GB feature; (d) schematic of the atomic configuration of the Type I GB based on the HAADF-STEM images and EELS analysis, along with an illustration of the Li site distribution across the Type I GB. EELS data of (e) La-M4,5, (f) Li-K, (g) Ti-L2,3, and (h) O-K edges for the Type I GB and the bulk. The spectra were normalized to the integrated intensity of the Ti-L2,3 edge. The normalized O-K edge of the bulk was shifted vertically for clarification.88 Reproduced with permission from ref. 88. Copyright (2014), the Royal Society of Chemistry. | ||
2.1.1.2 Anti-perovskite type conductors. Inspired by high temperature ion-conducting perovskites such as (Na, K)MgF3,95,96 KZnF3,95,96 and CsPbF3,97 a new and promising family of “structurally-inverted” anti-perovskites, Li3OX (X = Cl−, Br−, I−, or a mixture of halides), was reported.47,60,98 The anti-perovskite compounds have the same space group and similar structure as conventional perovskites (cubic, Pm
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) but with inverted cation and anion sublattices and, hence, charges. In one representation of the Li3OX anti-perovskites, X− ions occupy the corner sites of the cube, O2− ions occupy the body-centered site, and Li-ions form octahedra around the oxygen (Fig. 4a).60 As noted by Ceder's group, this arrangement of Li ions in a bcc sublattice is optimal for fast ion conduction.99 A conductivity of 8.5 × 10−5 S cm−1 (ref. 47) is exhibited by Li3OCl at room temperature.
m) but with inverted cation and anion sublattices and, hence, charges. In one representation of the Li3OX anti-perovskites, X− ions occupy the corner sites of the cube, O2− ions occupy the body-centered site, and Li-ions form octahedra around the oxygen (Fig. 4a).60 As noted by Ceder's group, this arrangement of Li ions in a bcc sublattice is optimal for fast ion conduction.99 A conductivity of 8.5 × 10−5 S cm−1 (ref. 47) is exhibited by Li3OCl at room temperature.
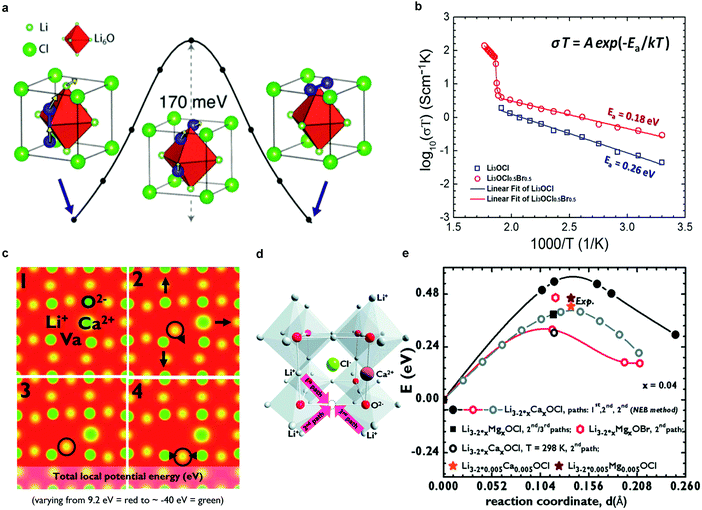 | ||
| Fig. 4 (a) Low-barrier migration pathway for a neutral Li split interstitial in Li3OCl. The barriers range from 145 to 175 meV depending on the charge state of the interstitial (neutral or +1) and host material (Li3OBr or Li3OCl);47 (b) Arrhenius plots of log(σT) versus 1/T for Li3OCl and Li3OCl0.5Br0.5 anti-perovskites, including Ea;47 Reproduced with permission from ref. 47. Copyright (2012) American Chemical Society. (c) Li+ diffusion and corresponding lattice dynamics, showing how the lattice adjusts during diffusion from 1 → 4; (d) alternative representation of the crystal structure of Li3OCl highlighting the formation of a vacancy and three different paths for Li+ diffusion upon Ca2+-doping; (e) activation energies for different paths in (d), dopants and temperatures calculated by DFT-GGA and the Nudged Elastic Band (NEB) method compared with the experimental values obtained in the solid-like (Arrhenius) regime for Li3−2x0.005M0.005OCl (M = Ca, Mg, Ba).60 Elastic Band (NEB) method compared with the experimental values obtained in the solid-like (Arrhenius) regime for Li3−2x0.005M0.005OCl (M = Ca, Mg, Ba).60 Reproduced with permission from ref. 60. Copyright (2014), The Royal Society of Chemistry. | ||
The anti-perovskites can be structurally tailored through chemical substitution, either by replacing Cl− with larger Br− or I− anions or by substituting divalent cations for Li, to give rise to an ion conductivity above 10−3 S cm−1.60,98,100 For example, the mixed halide compound Li3OCl0.5Br0.5 presents an improved conductivity of 1.94 × 10−3 S cm−1, (Fig. 4b).47 Cation-substituted Li3−2xMxOX glassy electrolytes (M = Ca, Mg, or Ba) were prepared by Braga et al.,60 and an unusually high ion conductivity of 2.5 × 10−2 S cm−1 at 25 °C was reported for Li3−2xBaxClO (x = 0.005). We note, however, that these results have not yet been reproduced to our knowledge, due to incomplete information on the synthesis. It has also been reported that these materials exhibit low electronic conductivity (10−9–10−7 S cm−1),60 an apparently wide electrochemical window (>5 V,60,98,100i.e., beyond the oxidation of Cl−), good thermal stabilities up to ca. 550 K,47,60 and more importantly, stability against Li metal,60 but they are highly sensitive to moisture.
The Li+ ion transport mechanism in the anti-perovskites is also under intensive debate. Based on DFT calculations, Zhang et al.98 and Emly et al.100 found that anti-perovskites such as Li3OCl, Li3OBr, and their mixed compounds are thermodynamically metastable. A transition at ∼150 °C was predicted, which was later deduced to be the glass transition. MD simulations98 showed that anti-perovskites with perfect crystal structures are poor Li-ion conductors whereas Li vacancies and structural disorder promote Li-ion diffusion by reducing activation energy barriers. Emly et al.100 proposed a collective hop-migration mechanism involving Li interstitial dumbbells with a barrier of only 0.17 eV (Fig. 4a), which was approximately 50% lower than that of vacancy driven migration. However, the high ion conductivity of lithium anti-perovskites could not be explained by this mechanism, because of the high formation energy of Li interstitial defects.100 Later, Mouta et al.101 employed classical atomistic simulation computations to calculate the concentration of Li vacancies and interstitials in Li3OCl. Vacancies created by Schottky defects were predicted to be the charge carriers in Li3OCl, since the concentration of interstitials (i.e., Frenkel defects) was 6 orders of magnitude lower due to the very high energy required for their formation. Although the vacancy migration energy (0.30 eV, above room temperature) is larger than that driven by interstitial migration (0.133 eV), the former mechanism likely dominates ion conduction because of the significantly higher concentration of vacancies. However, in LiCl-deficient materials, the opposite was proposed to be likely true due to charge compensating mechanisms. DFT calculations were also performed to understand the role of aliovalent cation doping. Four snapshots of the Ca-doped structure during Li hopping suggest that the lattice dynamics cause further disorder (Fig. 4c). Doping with higher valent cations, i.e., Ca2+, Mg2+, Ba2+, creates Li vacancies in the cation sublattice and lowers the activation energy for Li ion conduction (Fig. 4d and e).60 The deleterious role of resistive grain boundaries on the ion conductivity of polycrystalline Li3OCl is suggested in a recent theoretical study (namely, the grain boundaries exhibit about one order of magnitude lower conductivity than the bulk).102
Recently, Li et al.103 suggested that the as-prepared “Li3OX” might be Li2OHX rather Li3OX. They reported that replacing some of the OH− by F− was possible. The obtained Li2(OH)0.9F0.1Cl was claimed to be stable on contact with Li metal with an apparent electrochemical window extending to 9 V versus Li+/Li.103 In addition, Braga et al.104,105 reported that the existence of H+ was beneficial for the formation of an amorphous glassy phase, and a very high ion conductivity of more than 10−2 S cm−1 was reported – again the synthesis was not well described, and reproduction of the results is required.
2.1.1.3 NaSICON-type conductors. NaSICON (Na Super Ion CONductors) type electrolytes with the general formula Na1+xZr2Si2−xPxO12 (0 ≤ x ≤ 3) were first reported in 1976 by Goodenough and Hong.106,107 They are derived from NaZr2(PO4)3 by partial substitution of Si for P with excess Na to balance the negative charge. Their Li analogues, LiM2(PO4)3 (M = Zr, Ti, Hf, Ge, or Sn),108–117 are effectively isostructural.
The NaSICON framework is constituted by a rigid M2(PO4)3− skeleton, which is linked by MO6 octahedra and PO4 tetrahedra sharing O atoms (Fig. 5a).118 For the LiM2(PO4)3 (M = Ti, Ge) series, rhombohedral symmetry (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) was confirmed using X-ray and neutron diffraction,112,113 while for compositions with larger tetravalent cations such as LiM2(PO4)3 (M = Zr, Hf, or Sn), a triclinic phase (C
c) was confirmed using X-ray and neutron diffraction,112,113 while for compositions with larger tetravalent cations such as LiM2(PO4)3 (M = Zr, Hf, or Sn), a triclinic phase (C![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) of lower symmetry – induced by the displacement of Li ions – was also reported at low temperature.114–116 In the rhombohedral phase, two crystallographic sites are possible for Li ions: M1 (6b) sites, surrounded by six oxygens, and M2 (18e) sites, which are located between two M1 positions with 10-fold oxygen coordination. In triclinic phases, the structural distortion drives Li cations to the more stable intermediate M12 sites, which are located midway between M1 and M2 sites in 4-fold-oxygen coordination.115,116
) of lower symmetry – induced by the displacement of Li ions – was also reported at low temperature.114–116 In the rhombohedral phase, two crystallographic sites are possible for Li ions: M1 (6b) sites, surrounded by six oxygens, and M2 (18e) sites, which are located between two M1 positions with 10-fold oxygen coordination. In triclinic phases, the structural distortion drives Li cations to the more stable intermediate M12 sites, which are located midway between M1 and M2 sites in 4-fold-oxygen coordination.115,116
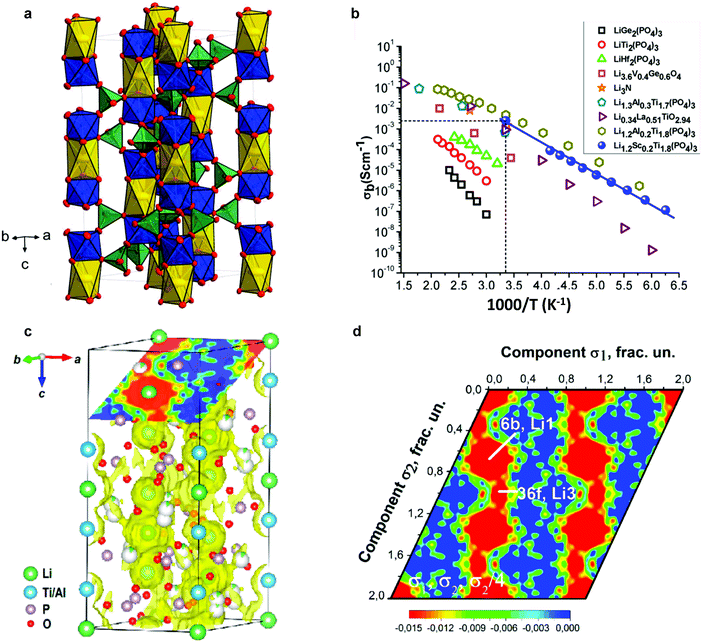 | ||
Fig. 5 (a) Unit cell (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) of LiTi2(PO4)3. Yellow elongated octahedra (M1/6b) are occupied by Li+; blue octahedra (12c) are occupied by Ti4+; and green tetrahedra are occupied by P5+ (18e); O2− is located at the corners of the polyhedra (small red circles, two Wyckoff positions 36f).118 (b) Ion conductivity of NaSICON structured Li ion solid electrolytes.134 (c) MEM-reconstructed negative nuclear density maps.52 (d) Sections of bond-valence mismatch and negative nuclear densities Li1.3Al0.3Ti1.7(PO4)3.52 Reproduced with permission from ref. 52, 118, 134. Copyright (2016, 2017) American Chemical Society. c) of LiTi2(PO4)3. Yellow elongated octahedra (M1/6b) are occupied by Li+; blue octahedra (12c) are occupied by Ti4+; and green tetrahedra are occupied by P5+ (18e); O2− is located at the corners of the polyhedra (small red circles, two Wyckoff positions 36f).118 (b) Ion conductivity of NaSICON structured Li ion solid electrolytes.134 (c) MEM-reconstructed negative nuclear density maps.52 (d) Sections of bond-valence mismatch and negative nuclear densities Li1.3Al0.3Ti1.7(PO4)3.52 Reproduced with permission from ref. 52, 118, 134. Copyright (2016, 2017) American Chemical Society. | ||
Among the widely studied LiM2(PO4)3 (M = Zr, Ge, Ti, or Hf) materials, LiTi2(PO4)3 offers the most suitable lattice size for Li ion conduction.119 However, LiTi2(PO4)3 pellets obtained by a conventional sintering process showed very high porosity (34%).120 Even the relative densities of hot-pressed ceramics were only ∼95%, resulting in a low room temperature conductivity of 2 × 10−7 S cm−1.121 The partial substitution of Ti4+ by trivalent cations, such as Al3+, Sc3+, Ga3+, Fe3+, In3+, and Cr3+ in Li1+xRxTi2−x(PO4)3 materials, improves ion conductivity.122–131 In particular, a high lithium conductivity at room temperature, 7 × 10−4 S cm−1 was reported in the case of Li1.3R0.3Til.7(PO4)3 (R = Al3+), abbreviated as LATP.123 Similar effects caused by trivalent cation doping at M sites are also observed in the LiGe2(PO4)3 phase and an ion conductivity of 2.4 × 10−4 S cm−1 can be achieved in well-known Li1+xAlxGe2−x(PO4)3, abbreviated as LAGP.132 The incorporation of trivalent cations influences the conductivity by increasing the concentration of mobile ions in the framework, as well as by invoking additional interstitial migration with lower activation energy.133
Besides the bulk conductivity, the grain boundary conductivity was also augmented by the greater densification of the pellet allowed by R3+ substitution. The conductivities of these compositions are shown in Fig. 5b.134
In LiTi2(PO4)3, Li ions tend to preferentially occupy the M1 sites (0, 0, 0) in the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c,113,114 as recently confirmed by single crystal X-ray diffraction analysis.118 A combination of NPD and synchrotron-based high-resolution powder diffraction revealed that the partial replacement of Ti4+ by Al3+ in LATP causes Li ions to occupy an additional interstitial position, a Li3 site (36f), that is located between two adjacent Li1 sites. Li diffusion preferentially occurs between two adjacent Li positions through this Li3 site, forming a Li1–Li3–Li3–Li1 zigzag chains in three dimensions (Fig. 5c and d).52
c,113,114 as recently confirmed by single crystal X-ray diffraction analysis.118 A combination of NPD and synchrotron-based high-resolution powder diffraction revealed that the partial replacement of Ti4+ by Al3+ in LATP causes Li ions to occupy an additional interstitial position, a Li3 site (36f), that is located between two adjacent Li1 sites. Li diffusion preferentially occurs between two adjacent Li positions through this Li3 site, forming a Li1–Li3–Li3–Li1 zigzag chains in three dimensions (Fig. 5c and d).52
Another effective strategy to improve the conductivity of LiM2(PO4)3 is by addition of a second lithium compound such as Li2O,119,135 LiNO3,136 Li3PO4,137 Li4P2O7,135 Li3BO3137 or LiF,138 which acts as a flux at grain boundaries, generating higher density ceramics with improved conductivities. For example, when 20% Li2O is incorporated in LiTi2(PO4)3, the conductivity can be improved to 5 × 10−4 S cm−1.119,135
Superionic conducting glass-ceramics (lithium–aluminum–titanium–phosphate (LATP) and lithium–aluminum–germanium–phosphate (LAGP)) were first reported by the Ohara company139,140 and subsequently by other researchers.141–146 An extremely high conductivity of 5.08 × 10−3 S cm−1 at 27 °C, much higher than that of the crystalline analogue, can be obtained by optimizing the heat-treatment conditions.144 The presence of dielectric phases (Li2O and AlPO4) – unavoidable by-products that form during the sintering process of these glass-ceramics which mainly segregate at the grain boundary – have been detected and identified.141–144,146 AlPO4 could either block or increase the conductivity, depending on its concentration and crystallite size.145
2.1.1.4 Garnet type conductors. Ideal garnets have the general formula A3B2M3O12 (A = Ca2+, Mg2+, or Fe2+; B = Al3+, Cr3+, Fe3+, or Ga3+; M = Si4+ or Ge4+) and crystallize in the space group Ia
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d, in which A, B, and M are filled with eight-, six-, and four-coordinated cation sites in a 3
d, in which A, B, and M are filled with eight-, six-, and four-coordinated cation sites in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio, respectively. Li garnets of the general formula Li3Ln3Te2O12 (Ln = Y3+, Pr3+, Nd3+, or Sm3+–Lu3+) follow this stoichiometry, with Ln and Te occupying the eight- and six-coordinated sites, respectively, and Li fully occupying tetrahedral sites (24d). Li-ion conducting garnets attracted significant interest after the first report of Li5La3M2O12 (M = Nb or Ta) by Thangadurai et al.,147 in which an ion conductivity of ∼10−6 S cm−1 was achieved at 25 °C. The Ta members were reported to be surprisingly chemically stable to reaction with molten Li or moisture, and a wide electrochemical window was reported.147 Subsequently, the conductivity of Li5La3Nb2O12 was optimized by partial substitution of La3+ by K+ (ref. 148) and partial substitution of Nb5+ with either In3+ (ref. 148) or Y3+.149 As the tetrahedral M site can not accommodate all five Li cations, excess Li cations occupy the six-coordinate sites (the octahedral or trigonal prismatic sites), which are empty in the original garnet structure. Garnets containing five to seven Li atoms per formula unit are referred to as Li-stuffed, or Li-rich garnets.
3 ratio, respectively. Li garnets of the general formula Li3Ln3Te2O12 (Ln = Y3+, Pr3+, Nd3+, or Sm3+–Lu3+) follow this stoichiometry, with Ln and Te occupying the eight- and six-coordinated sites, respectively, and Li fully occupying tetrahedral sites (24d). Li-ion conducting garnets attracted significant interest after the first report of Li5La3M2O12 (M = Nb or Ta) by Thangadurai et al.,147 in which an ion conductivity of ∼10−6 S cm−1 was achieved at 25 °C. The Ta members were reported to be surprisingly chemically stable to reaction with molten Li or moisture, and a wide electrochemical window was reported.147 Subsequently, the conductivity of Li5La3Nb2O12 was optimized by partial substitution of La3+ by K+ (ref. 148) and partial substitution of Nb5+ with either In3+ (ref. 148) or Y3+.149 As the tetrahedral M site can not accommodate all five Li cations, excess Li cations occupy the six-coordinate sites (the octahedral or trigonal prismatic sites), which are empty in the original garnet structure. Garnets containing five to seven Li atoms per formula unit are referred to as Li-stuffed, or Li-rich garnets.
Thangadurai et al. demonstrated that partial substitution at the La site by divalent alkaline earth ions generates a new class of garnet-like structures, Li6ALa2M2O12 (A = Ca2+, Sr2+, or Ba2+; M = Nb5+ or Ta5+),150,151 among which Li6BaLa2Ta2O12 exhibited the highest conductivity of 4 × 10−5 S cm−1 at 22 °C and the lowest activation energy of 0.4 eV.151 Aside from the niobate/tantalate garnets mentioned above, antimony-containing garnets Li5Ln3Sb2O12 (Ln = La, Pr, Nd, or Sm). were also investigated.152,153 Moreover, M can be replaced by tetravalent cations to generate Li-rich garnets such as Li7La3M2O12 (M = Zr, Sn, or Hf).154–157
Within the garnet family, cubic Li7La3Zr2O12 (LLZO), first reported by Murugan et al.,154 is considered the most attractive candidate for solid electrolytes owing to its high room temperature conductivity (>10−4 S cm−1), high chemical stability against Li, and a wide electrochemical potential window. It is moisture-sensitive, however. In cubic LLZO (space group: Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d), Li ions are disordered over the tetrahedral 24d Li(1), octahedral 48g and 96h Li(2) sites (Fig. 6a).158 LLZO also exists in a more thermodynamically stable tetragonal phase (I41/acd). It exhibits a conductivity that is one to two orders of magnitude lower than that of the cubic phase because of the fully ordered arrangement of Li ions at the tetrahedral 8a sites and octahedral 16f and 32g sites.159 Therefore, major efforts have been focused on using substitution strategies to stabilize the highly conductive cubic phase through a reduction in Li content and/or an increase in the Li vacancy concentration. The substituent Al3+ – either intentionally added or unintentionally introduced from alumina crucibles – was first found to be effective.49,160–163 Stabilization originates from the increased Li sublattice disorder owing to Li vacancies created via aliovalent substitution of Li+ by Al3+.164 However, the site preference (the 24d tetrahedral or 48g/96h octahedral Li sites) for Al3+ ions in the framework remains ambiguous.49,160–163,165,166 Düvel et al.49 found that with an increase in Al content (above 0.2–0.24 moles per LLZO formula unit), Al3+ ions occupy non-Li cation sites. The addition of Al3+ or Si4+ aids the sintering process, leading to a densification of the obtained ceramics and an improvement in the Li ion conductivity (6.8 × 10−4 S cm−1).167,168 This was attributed to an effective reduction of grain boundary resistance through the formation of nano-crystalline LiAlSiO4 in the grain boundaries.168
d), Li ions are disordered over the tetrahedral 24d Li(1), octahedral 48g and 96h Li(2) sites (Fig. 6a).158 LLZO also exists in a more thermodynamically stable tetragonal phase (I41/acd). It exhibits a conductivity that is one to two orders of magnitude lower than that of the cubic phase because of the fully ordered arrangement of Li ions at the tetrahedral 8a sites and octahedral 16f and 32g sites.159 Therefore, major efforts have been focused on using substitution strategies to stabilize the highly conductive cubic phase through a reduction in Li content and/or an increase in the Li vacancy concentration. The substituent Al3+ – either intentionally added or unintentionally introduced from alumina crucibles – was first found to be effective.49,160–163 Stabilization originates from the increased Li sublattice disorder owing to Li vacancies created via aliovalent substitution of Li+ by Al3+.164 However, the site preference (the 24d tetrahedral or 48g/96h octahedral Li sites) for Al3+ ions in the framework remains ambiguous.49,160–163,165,166 Düvel et al.49 found that with an increase in Al content (above 0.2–0.24 moles per LLZO formula unit), Al3+ ions occupy non-Li cation sites. The addition of Al3+ or Si4+ aids the sintering process, leading to a densification of the obtained ceramics and an improvement in the Li ion conductivity (6.8 × 10−4 S cm−1).167,168 This was attributed to an effective reduction of grain boundary resistance through the formation of nano-crystalline LiAlSiO4 in the grain boundaries.168
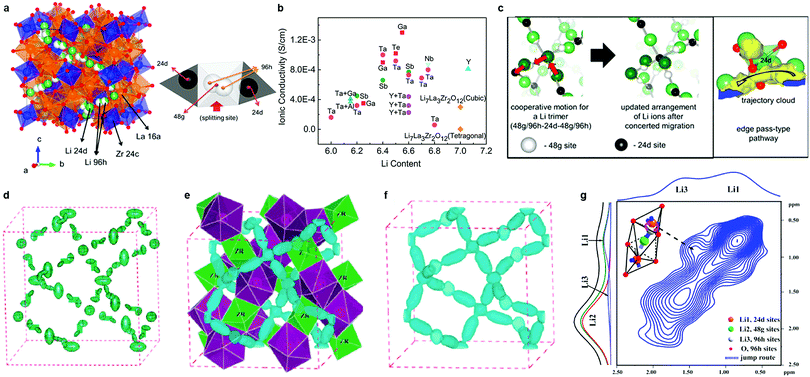 | ||
Fig. 6 (a) Crystal structure of cubic-type LLZO (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d), and Li environment. The center of the tetrahedral Li1 sites are the 24d sites, and the center of the octahedral Li2 sites are the 48g sites. Meanwhile, positions slightly displaced from the 48g sites and near the face (but still inside the Li2 octahedron) are the 96h sites.158 (b) Conductivities of doped LLZO.147–151,154,156,157,168,169,171,175–178,181,183–186 (c) Snapshots of Li ions’ mobility from the MD simulation and enlarged view of the selected Li atoms showing the tetrahedral edge pass according to the trajectory cloud.158 (d) Anisotropic harmonic lithium vibrations in c-7Li7La3Zr2O12 shown as green thermal ellipsoids obtained from Rietveld analysis of room-temperature neutron diffraction data.197 (e) Nuclear distribution of lithium calculated by MEM from neutron powder diffraction data obtained at 600 °C; three-dimensional 7Li nuclear-density data shown as blue contours (equivalue 0.15 fm Å−3 of the negative portion of the coherent nuclear scattering density distribution). The green octahedra represent ZrO6 and the purple dodecahedra represent LaO8 units.197 Reproduced with permission from ref. 197. Copyright (2012), The Royal Society of Chemistry. (f) The distribution of lithium calculated by MEM from neutron powder diffraction data obtained at 400 and 600 °C, respectively, and three-dimensional Li nuclear-density data shown as blue contours (equivalue 0.15 fm Å−3 of the negative portion of the coherent nuclear scattering density distribution).197 (g) 6Li–6Li exchange spectra of Li7−2x−3yAlyLa3Zr2−xWxO12 (x = 0.5) sintered at 1150 °C for 12 h.179 Reproduced with permission from ref. 158, 179. Copyright (2013, 2015) American Chemical Society. d), and Li environment. The center of the tetrahedral Li1 sites are the 24d sites, and the center of the octahedral Li2 sites are the 48g sites. Meanwhile, positions slightly displaced from the 48g sites and near the face (but still inside the Li2 octahedron) are the 96h sites.158 (b) Conductivities of doped LLZO.147–151,154,156,157,168,169,171,175–178,181,183–186 (c) Snapshots of Li ions’ mobility from the MD simulation and enlarged view of the selected Li atoms showing the tetrahedral edge pass according to the trajectory cloud.158 (d) Anisotropic harmonic lithium vibrations in c-7Li7La3Zr2O12 shown as green thermal ellipsoids obtained from Rietveld analysis of room-temperature neutron diffraction data.197 (e) Nuclear distribution of lithium calculated by MEM from neutron powder diffraction data obtained at 600 °C; three-dimensional 7Li nuclear-density data shown as blue contours (equivalue 0.15 fm Å−3 of the negative portion of the coherent nuclear scattering density distribution). The green octahedra represent ZrO6 and the purple dodecahedra represent LaO8 units.197 Reproduced with permission from ref. 197. Copyright (2012), The Royal Society of Chemistry. (f) The distribution of lithium calculated by MEM from neutron powder diffraction data obtained at 400 and 600 °C, respectively, and three-dimensional Li nuclear-density data shown as blue contours (equivalue 0.15 fm Å−3 of the negative portion of the coherent nuclear scattering density distribution).197 (g) 6Li–6Li exchange spectra of Li7−2x−3yAlyLa3Zr2−xWxO12 (x = 0.5) sintered at 1150 °C for 12 h.179 Reproduced with permission from ref. 158, 179. Copyright (2013, 2015) American Chemical Society. | ||
The aliovalent substitution of Li+ by Ga3+ (ref. 169–172) has the same stabilizing effect. By sintering the ceramic in a dry O2 atmosphere, an optimum conductivity of 1.3 × 10−3 S cm−1 (ref. 171) at 24 °C was achieved, although the Ga3+ distribution in the LLZO lattice was difficult to determine.171,173,174 Other supervalent dopants for Zr4+ sites (Sb5+, Nb5+, Ta5+, Te6+, and W6+ (ref. 175–179)) have also been employed, resulting in some remarkable improvements in conductivity. The highest conductivities of ca. 1.0 × 10−3 S cm−1 at room temperature were achieved for Ta-doping,177 and Te-doping.178 Lower conductivity was reported for simultaneous substitution of Al at Li+ site, Y3+, Ba2+ at La3+ site, and/or Ta5+, Sb5+, Te6+ at Zr4+ sites, however.180–182 The conductivities of these compounds and other garnet oxides are listed in Table 1 and Fig. 6b.147–151,154,156,157,168,169,171,175–178,181,183–186 While it was believed that “accidental” Al3+ substitution on the Li+ site from crucible contamination was actually responsible for stabilizing the cubic phase in many cases,163,187 recently it was confirmed that Ta-substituted cubic LLZO exhibits high ion conductivity in the absence of any Al3+.188,189 Approximately 0.4–0.5 Li vacancies per formula unit are required to stabilize the cubic polymorph of LLZO.188,189
| Composition | Conductivity (S cm−1) | Temperature (°C) | E a (eV) | Ref. |
|---|---|---|---|---|
| Li3Nd3Te2O12 (850 °C) | 1 × 10−5 | 600 | 1.22 | 186 |
| Li5La3Nb2O12 (950 °C) | 1 × 10−5 | 22 | 0.43 | 147 |
| Li5La3Ta2O12 (950 °C) | 1.2 × 10−6 | 25 | 0.56 | 147 |
| Li5.5La2.75K0.25Nb2O12 (950 °C) | 6.0 × 10−5 | 50 | 0.49 | 148 |
| Li5.5La3Nb1.75In0.25O12 (950 °C) | 1.8 × 10−4 | 50 | 0.51 | 148 |
| Li6.5La3Nb1.25Y0.75O12 (1000 °C) | 10−4 | 24 | — | 149 |
| Li6La3Nb1.5Y0.5O12 (1000 °C) | 10−4 | 24 | — | 149 |
| Li6CaLa2Nb2O12 (900 °C) | 1.6 × 10−6 | 22 | 0.55 | 150 |
| Li6SrLa2Nb2O12 (900 °C) | 4.2 × 10−6 | 22 | 0.5 | 150 |
| Li6BaLa2Nb2O12 (900 °C) | 6.0 × 10−6 | 22 | 0.44 | 150 |
| Li6SrLa2Ta2O12 (900 °C) | 7.0 × 10−6 | 22 | 0.5 | 151 |
| Li6BaLa2Ta2O12 (900 °C) | 4 × 10−5 | 22 | 0.40 | 151 |
| Li7La3Zr2O12 (1230 °C, cubic) | 3.0 × 10−4 | 25 | 0.31 | 154 |
| Li7La3Zr2O12 (980 °C, tetragonal) | 1.63 × 10−6 | 27 | 0.54 | 159 |
| Li7La3Sn2O12 (900 °C, tetragonal) | 2.6 × 10−8 | 85 | 0.79 | 156 |
| Li7La3Hf2O12 (1000 °C, tetragonal) | 3.17 × 10−7 | 27 | 0.53 | 157 |
| Li7La3Zr2O12 (1.7 wt% Al, 0.1 wt% Si, 1125 °C) | 6.8 × 10−4 | 25 | — | 168 |
| Li7La3Zr1.89Al0.15O12 (1150 °C) | 3.4 × 10−4 | 25 | 0.33 | 183 |
| Li7.06La3Y0.06Zr1.94O12 (1200 °C) | 8.1 × 10−4 | 25 | 0.26 | 184 |
| Li6.25La3Zr2Ga0.25O12 | 3.5 × 10−4 | RT | — | 169 |
| Li6.55La3Zr2Ga0.15O12 (1085 °C, O2) | 1.3 × 10−3 | 24 | 0.30 | 171 |
| Li6.4La3Zr2Ga0.2O12 (1085 °C) | 9.0 × 10−4 | 24 | — | 171 |
| Li6.8La3Zr1.8Sb0.2O12 (1100 °C) | 5.9 × 10−5 | 30 | 0.39 | 175 |
| Li6.6La3Zr1.6Sb0.4O12 (1100 °C) | 7.7 × 10−4 | 30 | 0.34 | 175 |
| Li6.4La3Zr1.4Sb0.6O12 (1100 °C) | 6.6 × 10−4 | 30 | 0.36 | 175 |
| Li6.2La3Zr1.2Sb0.8O12 (1100 °C) | 4.5 × 10−4 | 30 | 0.37 | 175 |
| Li6La3ZrSbO12 (1100 °C) | 2.6 × 10−4 | 30 | 0.38 | 175 |
| Li6.75La3Zr1.75Nb0.25O12 (1200 °C) | 8.0 × 10−4 | 25 | 0.31 | 176 |
| Li6.8La3Zr1.8Ta0.2O12 (1230 °C) | 2.8 × 10−4 | 25 | — | 177 |
| Li6.6La3Zr1.6Ta0.4O12 (1230 °C) | 7.3 × 10−4 | 25 | — | 177 |
| Li6.5La3Zr1.5Ta0.5O12 (1230 °C) | 9.2 × 10−4 | 25 | — | 177 |
| Li6.4La3Zr1.4Ta0.6O12 (1230 °C) | 1.0 × 10−3 | 25 | 0.35 | 177 |
| Li6.2La3Zr1.2Ta0.8O12 (1230 °C) | 3.2 × 10−4 | 25 | — | 177 |
| Li6La3ZrTaO12 (1230 °C) | 1.6 × 10−4 | 25 | — | 177 |
| Li6.7La3Zr1.7Ta0.3O12 (900 °C) | 6.9 × 10−4 | 25 | 0.36 | 177 |
| Li6.75La3Zr1.75Ta0.25O12 (1000 °C) | 8.7 × 10−4 | 25 | 0.22 | 185 |
| Li6.5La3Zr1.75Te0.25O12 (1100 °C) | 1.02 × 10−3 | 30 | 0.39 | 178 |
| Li6.15La3Zr1.75Ta0.25Al0.2O12 (1000 °C) | 3.7 × 10−4 | 25 | 0.30 | 185 |
| Li6.15La3Zr1.75Ta0.25Ga0.2O12 (1000 °C) | 4.1 × 10−4 | 25 | 0.27 | 185 |
| Li6.6La2.875Y0.125Zr1.6Ta0.4O12 (1200 °C) | 3.17 × 10−4 | 27 | 0.35 | 181 |
| Li6.6La2.75Y0.25Zr1.6Ta0.4O12 (1200 °C) | 4.36 × 10−4 | 27 | 0.34 | 181 |
| Li6.6La2.5Y0.5Zr1.6Ta0.4O12 (1200 °C) | 2.26 × 10−4 | 27 | 0.39 | 181 |
Many X-ray and neutron diffraction studies have been geared towards determining the crystal structure and the Li environment in garnet type electrolytes. However, the phase stability and the ion transport mechanism are still controversial,190–192 due to the limitations of these techniques in determining the exact Li occupancy on the tetrahedral and octahedral sites. Using neutron diffraction, Cussen et al.193 confirmed that Li5La3M2O12 (M = Nb or Ta) crystallized in the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d space group with Li distributed over the tetrahedral and distorted octahedral sites. They also investigated the relationship between ion conductivity and Li site occupation in Li3Ln3Te2O12 (Ln = Y, Pr, Nd, or Sm–Lu).186 Li ions were found to exclusively occupy the tetrahedral (24d) sites. Given that Li3Nd3Te2O12 exhibits a extremely low conductivity (∼10−5 S cm−1 at 600 °C) and very high activation energy (1.22 eV), it was deduced that the Li ions at the tetrahedral sites play no direct role in facile ion mobility. Later, the exact location and dynamics of Li ions in Li5La3Nb2O12 were investigated using solid-state nuclear magnetic resonance (NMR).194 Indeed, the octahedrally coordinated Li cations were revealed to be the only mobile species. Neutron diffraction studies were also performed on Li5+xBaxLa3−xTa2O12 (0 < x < 1.6) by Cussen et al.195 They found that as the Li content increases, the tetrahedral site occupancy is reduced whereas the fraction of Li in octahedral site increases. This results in a shift in the Li environment from primarily tetrahedral (at x = 0) to octahedral (at x = 1.6). Since the tetrahedra and octahedra are connected by a shared face, simultaneous occupation of adjacent polyhedral sites inevitably leads to reduced Li–Li distances and displacement of Li away from the shared faces. The electrostatic repulsion associated with this arrangement leads to the high mobility of Li+ in these materials.
d space group with Li distributed over the tetrahedral and distorted octahedral sites. They also investigated the relationship between ion conductivity and Li site occupation in Li3Ln3Te2O12 (Ln = Y, Pr, Nd, or Sm–Lu).186 Li ions were found to exclusively occupy the tetrahedral (24d) sites. Given that Li3Nd3Te2O12 exhibits a extremely low conductivity (∼10−5 S cm−1 at 600 °C) and very high activation energy (1.22 eV), it was deduced that the Li ions at the tetrahedral sites play no direct role in facile ion mobility. Later, the exact location and dynamics of Li ions in Li5La3Nb2O12 were investigated using solid-state nuclear magnetic resonance (NMR).194 Indeed, the octahedrally coordinated Li cations were revealed to be the only mobile species. Neutron diffraction studies were also performed on Li5+xBaxLa3−xTa2O12 (0 < x < 1.6) by Cussen et al.195 They found that as the Li content increases, the tetrahedral site occupancy is reduced whereas the fraction of Li in octahedral site increases. This results in a shift in the Li environment from primarily tetrahedral (at x = 0) to octahedral (at x = 1.6). Since the tetrahedra and octahedra are connected by a shared face, simultaneous occupation of adjacent polyhedral sites inevitably leads to reduced Li–Li distances and displacement of Li away from the shared faces. The electrostatic repulsion associated with this arrangement leads to the high mobility of Li+ in these materials.
Several simulations combined with experiments have been performed to explore the Li ion diffusion mechanism. Using the nudged elastic band (NEB) method, Xu et al. found that in the Li-stuffed garnet, Li+ ions can migrate between tetrahedral and octahedral sites,196 although only limited insights can be gained from NEB since it reflects the local migration behavior. On the other hand, MD simulations evaluate the Li ion hopping events, and quantitatively assess the collective migration behavior. As shown in Fig. 6b, MD simulations indicate a concerted migration mechanism in cubic LLZO, indicative of a complex cooperative mechanism.158 The Li diffusion pathways in LLZO and the evolution of Li motion with temperature were also investigated by high-temperature neutron diffraction techniques combined with the maximum-entropy method (MEM).197 Temperature-driven dynamic Li-ion displacements exhibited a 3D diffusion pathway constituted by an interlocking network of 24d–96h–48g–96h–24d site segments (Fig. 6d–f), indicating that Li ions diffuse through the tetrahedral 24d sites, consistent with the results of Xu et al.196 NMR results179 also show evidence of ion exchange between the 24d and 96h sites (Fig. 6g) and the bulk conductivity is found to be limited by the Li mobility at the 24d sites.
2.1.2.1 Thio-LiSICONs. Thio-LiSICONs were first developed by Kanno et al.42,61 by replacing oxide ions in LiSICON with larger and more polarizable S2− anions. The high polarizability of S2− weakens interactions of Li+ with the anionic sub-lattice, leading to higher Li-ion conductivity in sulfides than in their oxide analogues. Sulfide electrolytes are also highly ductile and exhibit a lower grain boundary resistance than oxides. As a consequence, excellent contact with electrode materials can be realized by simple cold-pressing, making the fabrication of bulk solid-state batteries more convenient.198,199
The thio-LiSICON family contains a very wide range of solid solutions with the general formula LixM1−yM′yS4 (M = Si or Ge; M′ = P, Al, Zn, Ga, or Sb), that exhibit ion conductivities ranging from 10−7–10−3 S cm−1,61,200,201 amongst which Li4−xGe1−xPxS4 exhibits the highest conductivity (2.2 × 10−3 S cm−1).42 The conductivities of thio-LiSICON electrolytes and other typical crystalline sulfides such as Li3PS4, Li4SiS4, Li4SnS4, Li2SiS3, Li4P2S6 as well as meta-stable Li7P3S11 are listed in Table 2.46,201–209 The role of the different structural building units (P2S74− or PS43−) in the conductivity of glass and crystalline lithium thiophosphates (LPS) phases has recently been clarified by monitoring in situ crystallization and phase evolution in this class of material.210,211 Glasses with only ortho-thiophosphate units show the highest lithium ion conductivity, the lowest activation energy and favorable thermal resistance towards decomposition, while glasses in which the major PS43− building units are linked by P–S–P bonds cleave at elevated temperatures to form sulfur and Li4P2S6, thereby losing their contribution to lithium ion conduction.
| Composition | Conductivity (S cm−1) | Temperature (°C) | Ref. |
|---|---|---|---|
| Li4GeS4 | 2.0 × 10−7 | 25 | 61 |
| Li3.9Zn0.05GeS4 | 3.0 × 10−7 | 25 | 61 |
| Li4.275Ge0.61Ga0.25S4 | 6.5 × 10−5 | 25 | 61 |
| Li3.25Ge0.25P0.75S4 | 2.2 × 10−3 | 25 | 42 |
| Li3.4Si0.4P0.6S4 | 6.4 × 10−4 | 25 | 200 |
| Li4.8Si0.2Al0.8S4 | 2.3 × 10−7 | 25 | 200 |
| Li2.2Zn0.1Zr0.9S3 | 1.2 × 10−4 | 30 | 202 |
| γ-Li3PS4 (crystal) | 3.0 × 10−7 | 25 | 203 |
| β-Li3PS4 (nanoporous) | 1.6 × 10−4 | 25 | 201 |
| Li2SiS3 | 2.0 × 10−6 | 25 | 204 |
| Li4SiS4 | 5.0 × 10−8 | 25 | 204 |
| Li6P2S4 | 1.6 × 10−10 | 25 | 207 |
| Li7P3S11 | 3.2 × 10−3 | 25 | 205 |
| Li4SnS4 | 7.0 × 10−5 | 20 | 206 |
| Li10GeP2S12 | 1.2 × 10−2 | 27 | 45 |
| Li10SnP2S12 | 4.0 × 10−3 | 27 | 63 |
| Li10SiP2S12 | 2.3 × 10−3 | 27 | 208 |
| Li10Ge0.95Si0.05P2S12 | 8.6 × 10−3 | 25 | 209 |
| Li9.54Si1.74P1.44S11.7Cl0.3 | 2.5 × 10−2 | 25 | 46 |
2.1.2.2 The LGPS family. In 2011, Kanno's group discovered a new sulfide – Li10GeP2S12 (LGPS) – that exhibits an extremely high conductivity of 1.2 × 10−2 S cm−1,45 which is comparable to or higher than that of liquid organic electrolytes currently used in commercially available Li-ion batteries. Unfortunately, Li10GeP2S12 shows a limited electrochemical window,212 and poor interfacial stability against Li metal.213 In addition, the low abundance and high cost of Ge restricts its application in batteries. Substitutions of Ge4+ with Si4+ or Sn4+ (ref. 63, 208, 209, 214 and 215) generate Li10MP2S12 (M = Si4+, Sn4+) (either experimentally (Sn4+) or theoretically (Si)) and Li10+δM1+δP2−δS12 (M = Si4+, Sn4+)216 with high ion conductivity, which varied as a function of M, with the Si and Sn systems showing lower conductivity than Ge. While the substitution with smaller Si4+ leads to a lower conductivity due to narrower diffusion pathways, the structural reasons behind the reduction in conductivity upon moving from Ge4+ to larger Sn4+ were not well understood. The structure–property relationships governing this behavior was employed by Zeier's group217 employing a combination of speed of sound measurements and electrochemical impedance spectroscopy (EIS). It was shown that increasing the Sn4+ fraction in Li10Ge1−xSnxP2S12 leads to a more tight structural bottleneck along the diffusion channels in the z-direction, and concurrent increase in the lattice softness, which causes stronger local ionic bonding interactions between Li+ and S2−, and therefore an increased activation barrier.217 A different composition, Li11Si2PS12, shows a conductivity of 2 × 10−2 S cm−1 at room temperature as inferred from NMR diffusivity data. This represents a very high value for solid Li ion conductors; however the phase can only be accessed under pressure.215
The tetragonal structure of LGPS (space group P42/nmc (137)) in Kanno's report45 was determined from powder diffraction and Rietveld refinement. The reported framework is composed of GeS4/PS4 tetrahedra, LiS4 tetrahedra and LiS6 octahedra. The tetrahedrally coordinated Li1 (16h) and Li3 (8f) sites form a 1D tetrahedral chain along the c-axis while the octahedrally coordinated Li2 position between these chains was assumed to be inactive for ion conduction.45 MD simulation performed by Mo et al.11 supported this highly anisotropic diffusivity in the LGPS structure. Careful examination of the isosurface from long MD simulation by Adams et al.218 suggested the existence of an additional site at (0, 0, 0.22) (marked as Li4, Fig. 7a and b). Single crystal structure analysis identified a similar Li4 site at (0, 0, 0.251(2)) with an occupancy of 0.81(7) and rather large anisotropic displacement parameters similar to the Li1 and Li3 positions.219 The thermal ellipsoid of the Li4 site is aligned perpendicular to the c-axis, and provides an extra diffusion pathway connecting the channels along the c-axis formed by Li1 and Li3.219 A recent neutron diffraction study combined with nuclear density maps verified the quasi-isotropic lithium diffusion in LGPS and three most prominent pathways for lithium transport, namely, along the 〈001〉 direction (Li3–[Li1–Li1]–Li3) and along 〈110〉 (i.e., at z = 0, 1/4, 1/2, 3/4; Li4–[Li1–Li1]–Li4 and Li3–[Li2–Li2]–Li3, Fig. 7c and d) are identified.220 This reconciles the theoretical findings by Adams et al., namely the hops between the Li3 and Li2 pathways along the 〈110〉 direction significantly contribute to the overall conductivity (Fig. 7f), along with the previously identified lithium migration channels along the 〈001〉 direction (Fig. 7e).218 Their calculations also suggested increasing occupancy in the Li4 site with increasing temperature (Fig. 7g) and its role in connecting Li4–Li1 thus enabling a 3D network for Li ion migration.218
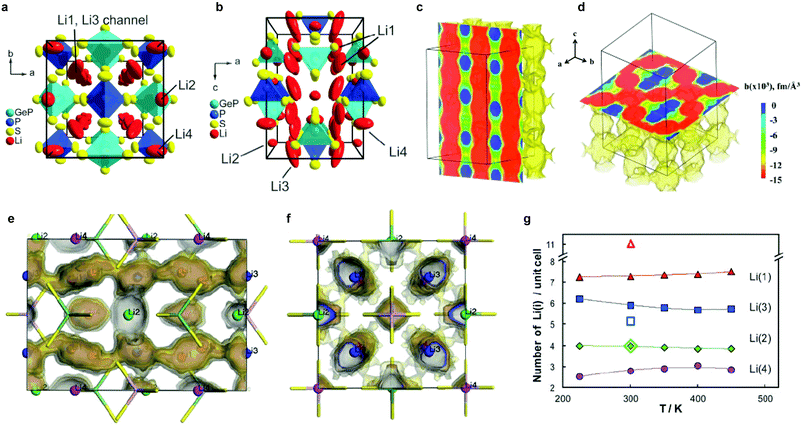 | ||
| Fig. 7 (a and b) Unit cell of tetragonal Li10GeP2S12 with thermal ellipsoids (p = 0.8);219 Reproduced with permission from ref. 219. Copyright (2013) the Royal Society of Chemistry. (c) MEM reconstructed negative nuclear density maps in Li10GeP2S12 (surface threshold −0.015 fm Å−3, cell grid 256 × 256 × 512) and slices in (c) (011) and (d) (001) planes, respectively; (d) shows the diffusion tunnels within Li10GeP2S12 along the 〈001〉 direction, whereas the Li distribution along 〈110〉 can be seen in (d);220 Reproduced with permission from ref. 220. Copyright (2016) American Chemical Society. (e and f) Li distribution from a 10 ns NVT MD simulation of a 3 × 3 × 2 supercell at T = 300 K projected into a single unit cell (shown (e) along [100] and (f) along [001]). Regions of highest Li density (darkest isosurface) coincide with the 4 Li sites, the easiest path for transport (lighter isosurface) corresponds to the Li(3)–Li(1) channels along [001]. The lightest isosurface reveals a significant probability for hops Li(3)–Li(2) establishing a 3D network of pathways. With a lower probability, Li(4) sites are attached to this pathway network (not shown);218 (g) temperature dependence of Li distribution on the four Li sites identified by MD simulations (filled symbols). The corresponding open symbols refer to the neutron refinements by Kanno's group,45 who distributed the 20 Li per unit cell onto Li(1), Li(2) and Li(3) sites only.218 Reproduced with permission from ref. 218. Copyright (2012) the Royal Society of Chemistry. | ||
Very recently, a remarkably high conductivity (2.5 × 10−2 S cm−1 at 25 °C) was reported again by Kanno's group46 for a new sulfide material, Li9.54Si1.74P1.44S11.7Cl0.3 (Fig. 8a and b) whose structure is related to LGPS. This is the highest value reported to date for Li ion conductors. The anisotropic thermal displacement and nuclear density distribution of Li suggest a three-dimensional (3D) migration pathway (Fig. 8c), in agreement with previous studies.220 Another LGPS-related composition, Li9.6P3S12,46 exhibits a lower conductivity (1.2 × 10−3 S cm−1 at 25 °C), but was claimed to be stable in a window of 0–5 V. Both new compositions were not prepared in a phase-pure state, however, and contain significant fractions of other ion-conductive phases. Nonetheless, all-solid-state batteries using these new materials set a record in demonstrating high specific power and long cycle life.46
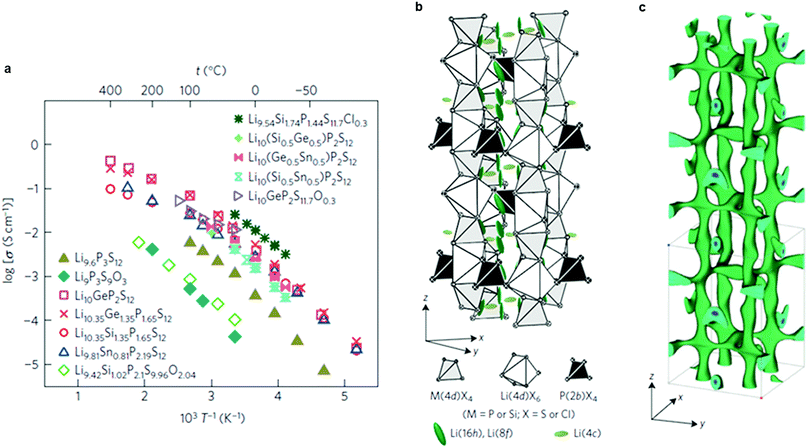 | ||
| Fig. 8 (a) Arrhenius conductivity plots for the LGPS family, Li9.6P3S12 and Li9.54Si1.74P1.44S11.7Cl0.3. (b) Crystal structure of Li9.54Si1.74P1.44S11.7Cl0.3. The thermal ellipsoids are drawn with a 50% probability. The framework structure consists of 1D polyhedral chains (edge-sharing M(4d)X4 and Li(4d)X6) connected by P(2b)X4 tetrahedra. Lithium is located on the 16h, 8f and 4c sites. (c) Nuclear distribution of Li atoms in Li9.54Si1.74P1.44S11.7Cl0.3 at 25 °C, calculated using the maximum entropy method at the iso-surface level of −0.06 fm Å−3.46 Reproduced with permission from ref. 46. Copyright (2016), Springer Nature. | ||
2.1.2.3 Argyrodite type. The addition of halides to thiophosphates can increase the conductivity of quasi-binary or quasi-ternary systems. Outstanding examples are the halogen-substituted argyrodites Li6PS5X (X = Cl, Br, I).62 The “parent” argyrodite of Li7PS6 crystallizes both in a cubic high temperature (HT) phase and an orthorhombic low temperature phase. The partial substitution of sulfur by halogen anions can stabilize the cubic HT phase at room temperature221,222 and results in a good conductivity of ∼10−3 S cm−1.223
Fig. 9a shows the unit cell of Li6PS5X. The framework of the lattice is built-up by PS43− anions that are centered at the 4b sites, with the remaining sulfur occupying the 4a and 4c sites.224 Upon substitution of sulfur with halogens, sulfur constituting the PS4 groups are not replaced but instead, halogens occupy the 4a or 4c sites. The Li+ ions are located at the 48h and 24g Wyckoff sites, with the 24g sites acting as the transition state between hops from 48h to 48h. Twelve 48h sites surround each 4c site, and form a cagelike structure depicted in Fig. 9b.224 Li diffusion occurs through three different jump processes: the 48h–24g–48h, which is termed a doublet jump; and the 48h–48h jumps within the cage, and between cages, which are deemed the intracage and intercage jump, respectively.222,224 MD simulations show that the low jump rate of intracage jumps limit the macroscopic diffusion, as shown in the trajectory and jump events in Fig. 9c and d.222 With the replacement of sulfur by a halogen, Li vacancies are introduced via charge compensation. The halogen distribution determines the distribution of Li vacancies and thus the local Li ion diffusivity. I− ions only occupy the 4a site, whereas Cl− (or Br−) show disorder over the 4a sites (inside the cage) and 4c sites (outside the cage). The disorder of halogen ions over the 4a and 4c site was confirmed responsible for the high conductivity in Li6PS5Cl and Li6PS5Br; in contrast the I− derivative lacks disorder and hence the conductivity is orders of magnitude lower.222 The effect of an increase of Li+ concentration and the lattice parameters on the ion conductivity was demonstrated by substitution of P5+ with Si4+, showing that the conductivity can be improved to 2 × 10−3 S cm−1.225
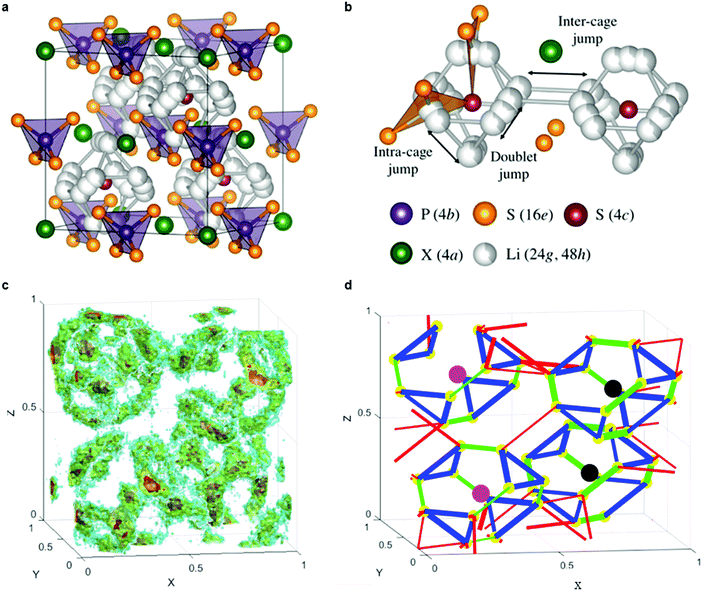 | ||
| Fig. 9 (a) Crystal structures of Li6PS5X with X = Cl, Br, I. In the ordered structure, X-anions form a cubic close-packed lattice with PS43− tetrahedra in the octahedral sites and the free S2− (Wyckoff 4c) in half of the tetrahedral holes.224 (b) The free S2− anions and the corner of the PS43− tetrahedra form Frank–Kasper polyhedra, which enclose two different Li positions. The Li positions form localized cages in which multiple jump processes are possible. Jumps between the lithium positions (48h–24g–48h, doublet jump), intracage jumps (48h–48h), and intercage jumps can occur.224 (c) Li-ion density in Li6PS5Cl unit cell during MD simulations at 450 K.222 (d) Jump statistics from the MD simulations of Li6PS5Cl at 450 K. The lines represent three types of Li-ion jumps; green for doublet, blue for intracage, and red for intercage;222 thicker lines represent larger jump rates. The colored spheres indicate S at 4c (black), Cl at site 4c (pink) and Li-ion sites (48h) (yellow).222 Reproduced with permission from ref. 222, 224. Copyright (2016, 2017) American Chemical Society. | ||
2.1.2.4 Other new thiophosphates. A few new Li-ion thiophosphate conductors have been recently reported that are not strictly related to the above. One is the very simple compound Li4PS4I, discovered utilizing a solvent-based synthesis approach. It exhibits a new structure and a room temperature ion conductivity of about 10−4 S cm−1.226 Previously identified as Li7P2S8I, the structure is distantly related to the argryodites, and comprises Li ions and isolated PS43− tetrahedra arranged in layers perpendicular to the c-axis that are held apart by I− ions. Recent calculations give hope that an even higher conductivity >10−2 S cm−1 may be achieved.227 The first experimental elucidation of fast lithium ion conductors in the Li1+2xZn1−xPS4 (LZPS; x < 0.5) solid solution whose existence (and conductivity) had only been predicted by theory228 has also been recently reported.229 The presence of excess interstitial Li ions in the structure – resulting from the partial substitution of Zn in the parent phase, LiZnPS4 – was identified by combined neutron and synchrotron X-ray powder diffraction studies and correlated with ion conductivity upon increasing the Li/Zn ratio. While the ion conductivity of the parent phase was found to be higher than predicted by theory, conductivities of the solid solution series as high as 1.3 × 10−4 S cm−1, were still two orders of magnitude lower than computation suggested. This was ascribed to the fact that although substoichiometric phases close to those targeted were successfully synthesized, all “defect compositions” were in fact highly metastable. As a result, amorphous and potentially less conductive materials formed as side-products in the grain boundaries may have precluded realization of the true crystalline conductivity.
2.1.2.5 Layered sulfides. A series of fast-conducting sulfide solid electrolytes have recently been identified in the solid solution system Li3x[LixSn1−xS2]. The Li-rich prototype with x = 0.33, Li2SnS3, crystallizes in the layered Na2IrO3 structure type (space group C2/c), where Li is distributed both in and between Li/Sn-ordered honeycomb sulfide layers according to Li[Li0.33Sn0.67S2].230 Brant et al. reported Li2SnS3 to be a fast Li ion conductor with a room temperature conductivity of 1.5 × 10−5 S cm−1 and a conductivity of 1.6 × 10−3 S cm−1 at 100 °C.231 In the Li-depleted version, Li2Sn2S5 – with a Li distribution corresponding to Li0.6[Li0.2Sn0.8S2] (x = 0.2) – only 60% of the interlayer gallery Li sites are occupied, thus giving rise to more facile Li diffusion in the ab-plane as compared to Li2SnS3.232 In addition, the Li diffusion pathway in Li2Sn2S5 involves hops between face-sharing octahedral (O) and tetrahedral (T) Li sites (O–T–O), rather than pure O–O trajectories as in Li2SnS3. This pathway is expected to reduce the activation energy for Li diffusion (0.17 eV for Li2Sn2S5 as measured by 7Li T1 relaxation time measurements vs. 0.59 eV for Li2SnS3, determined from impedance spectroscopy). Indeed, Li+ diffusivities on the order of 10−7 cm2 s−1 were obtained for Li2Sn2S5 by pulsed field gradient (PFG) NMR, corresponding to a bulk conductivity of σNMR = 9.3 × 10−3 S cm−1. Polarization measurements and impedance spectroscopy reveal a grain boundary limited conductivity of 1.2 × 10−4 S cm−1 and a bulk conductivity that was extrapolated to be two orders of magnitude larger (1.5 × 10−2 S cm−1), in agreement with the PFG NMR measurements.
3. Sodium ion conductors
Sodium-ion batteries (NIBs) have been extensively studied in recent years as candidates for large-scale energy storage, because of the high abundance and low cost of sodium.233–235 Similar to LIBs, NIBs also face safety concerns associated with the liquid organic electrolytes contained in the batteries. The pursuit of higher safety, lower cost and longer cycle life batteries renders the development of all-solid-state sodium batteries and sodium ion solid electrolytes highly desirable. In this section, different types of inorganic solid sodium ion conductors are described to give a global view of the solid-state sodium ion conductors available to date.3.1 Na–β′′-Al2O3
Na-β′′-Al2O3 ceramics are well-known fast Na+ ion conductors and are widely used as solid electrolytes for Na–S and Na–metal chloride batteries.236 Owing to its high ion conductivity (0.2–0.4 S cm−1 at 300 °C), Na-β′′-Al2O3 is considered as one of the best solid electrolytes for solid-state sodium batteries.236 However, its extremely high sintering temperature (1200–1500 °C) limits its application. The development, applications as well as the challenges of Na-β′′-Al2O3 in high temperature Na batteries have been reviewed by Rojo's group.2363.2 NaSICON-type sodium ion conductors
NaSICON-type Li conductors were introduced in Section 2.1.5; in this part, NaSICON-type Na-ion conductors will be reviewed. NaSICONs derive from NaZr2(PO4)3 by partial substitution of Si for P, yielding the general formula Na1+xZr2SixP3−xO12 (0 ≤ x ≤ 3). The optimum total ion conductivity is obtained when x ≈ 2, i.e. Na3Zr2Si2PO12 (6.7 × 10−4 S cm−1 at 25 °C and 0.2 S cm−1 at 300 °C).107,237 The prominent ion conductivity of this system is due to the high mobility of Na ions throughout the open three-dimensional (3-D) framework, which is created by corner-sharing SiO4/PO4 tetrahedra and ZrO6 octahedra via common oxygen atoms. Apart from its excellent ion conductivity, NaSICON ceramics are reported to show low thermal expansion, and are thus suitable for use at medium or high temperature. The open framework of NaSICON allows a wide range of chemical substitutions, for example, the Zr4+ site can be occupied by a variety of di, tri, tetravalent and pentavalent cations, and the Si/P site can be substituted by Ge4+ or As4+.238,239The efforts at chemical substitution have shown some success in improving the conductivity. For example, Hf-substituted NaSICON – Na3.2Hf2(SiO4)2.2(PO4)0.8 – exhibits a much higher ion conductivity than its Zr analogue (2.3 × 10−3 S cm−1 at room temperature).240 Unfortunately, Hf is a rare metal and in limited supply. Takahashi et al. investigated the effects of divalent (Mg2+, Zn2+), trivalent (Y3+), tetravalent (Ti4+, Sn4+), and pentavalent dopants (V5+, Nb5+, Ta5+) on the electrical conductivity and density of NaSICON.241 All of these result in well-sintered, dense ceramics and enhanced electrical conductivity at high temperature, but the conductivity at low temperature was not reported. However, these doped systems are mixed conductors and only for Mg-doped and Nb-doped systems can the electronic conductivity be neglected. NaSICON ceramics are often not monophasic but are accompanied by a glassy phase.242 The glassy phase generally comprises sodium, phosphate or silicate and the doping element,241–243 as demonstrated in the Mg2+,241 Co2+,241 Ce4+,243 Yb3+ (ref. 243) and Gd3+ doped243 NaSICON systems. In addition, monoclinic zirconia is easily formed from the liquid phase during the sintering.243–247 Some studies found that the doping and sintering conditions also affect the microstructure and the nature of grain boundaries, and hence influence the conductivity.248
Recently, a high ion conductivity of 4.0 × 10−3 S cm−1 at room temperature was reported for Sc-doped NaSICON, which is the highest value amongst the reported NaSICON-type conductors.249 Based on a range of ion conductivity and structural data of NaSICON-type materials, Guin et al.250 concluded that the highest ion conductivity was obtained when the Na content approximates 3.3 mol of Na per formula unit and the mean size of the M cations is close to 0.72 Å. In addition, the monoclinic-to-rhombohedral phase transition temperature was found to be influenced by doping. Jolley et al.251 found that aliovalent substitution of Zr4+ stabilized the higher symmetry rhombohedral phase of NaSICON, among which Y3+ substitution resulted in the lowest phase transition temperature and the smallest lattice distortion.
Zhang et al. proposed a self-forming strategy to develop composite solid electrolytes with high ion conductivity, which was demonstrated by modifying NaSICON with La3+.252 For example, in the case of La3+, its very limited solubility in the NaSICON framework ultimately results in separation of Na3La(PO4)2 as a second phase, which mediates both the composition of the bulk and the grain boundary, leading to improved conductivity (3.4 × 10−3 S cm−1 at 25 °C). This strategy can be extended to design other fast ion conductors. Extensive studies of the stability of NaSICON with respect to metallic Na have been conducted.253,254 Unfortunately, especially when phosphorus is present, NaSICONs are not stable at 300 °C in contact with molten sodium, but at lower temperatures (100 °C) no reaction is seen.253,254
3.3 Sulfide based sodium ion conductors
As in the case of Li, sodium thiophosphate materials have attracted much attention in recent years because of their relatively high ion conductivity, negligible grain boundary resistance and good ductility.45,255 Nonetheless, there are much fewer Na superionic conductors compared to Li sulfides, and their room temperature ion conductivities remain low. Exploration of highly conductive sulfide-based sodium ion conductors is eagerly underway.An exciting milestone in the development of Na ion conductors was the stabilization of the high-temperature cubic phase of Na3PS4 (c-Na3PS4, space group: I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) by crystallization from the glassy state, which exhibited high Na+-ion conductivity (2 × 10−4 S cm−1).198 The conductivity was subsequently improved to 4.6 × 10−4 S cm−1 by using high purity (>99%) Na2S as a precursor. This achievement for c-Na3PS4 ignited a resurgence of interest in sodium thiophosphates, given that the tetragonal phase of Na3PS4 (t-Na3PS4, space group: P
3m) by crystallization from the glassy state, which exhibited high Na+-ion conductivity (2 × 10−4 S cm−1).198 The conductivity was subsequently improved to 4.6 × 10−4 S cm−1 by using high purity (>99%) Na2S as a precursor. This achievement for c-Na3PS4 ignited a resurgence of interest in sodium thiophosphates, given that the tetragonal phase of Na3PS4 (t-Na3PS4, space group: P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c) exhibits a conductivity one order of magnitude lower.256 The substantial difference in the ion conduction properties was initially assumed to imply that fast ion conduction is causally related to the symmetry of Na3PS4. Fig. 10a shows the average cubic and tetragonal Na3PS4 crystal structures along the b-axis.257 Only small structural differences exist between the two polymorphs of Na3PS4, mostly in the Na cation distribution, the orientation of the PS43− tetrahedral, and the lattice dimensions.
21c) exhibits a conductivity one order of magnitude lower.256 The substantial difference in the ion conduction properties was initially assumed to imply that fast ion conduction is causally related to the symmetry of Na3PS4. Fig. 10a shows the average cubic and tetragonal Na3PS4 crystal structures along the b-axis.257 Only small structural differences exist between the two polymorphs of Na3PS4, mostly in the Na cation distribution, the orientation of the PS43− tetrahedral, and the lattice dimensions.
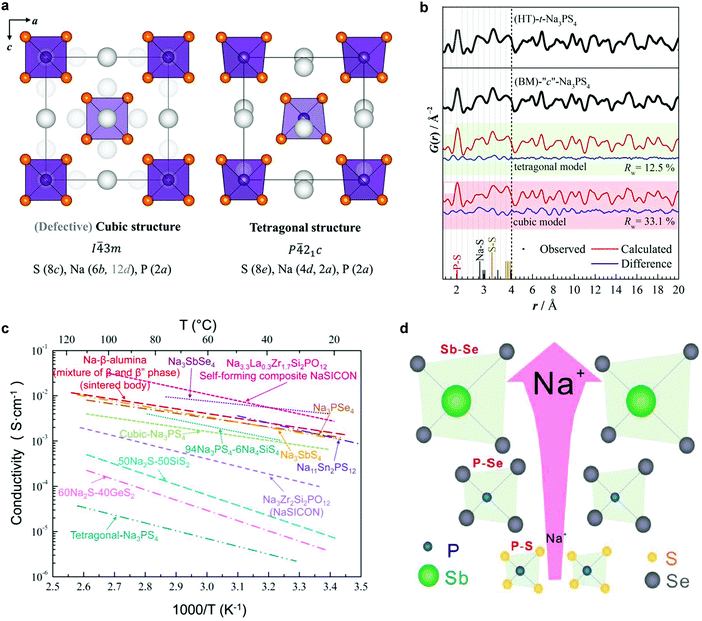 | ||
| Fig. 10 (a) Crystal structure of cubic and tetragonal Na3PS4 projected in the (010) plane. The perfectly cubic phase (i.e., no occupancy of the 12d positions) shows PS43− tetrahedra in a body centered lattice. In the tetragonal modification, a minor rotation of the tetrahedra leads to a splitting of the Na positions and an elongation of the c-lattice parameter;257 (b) experimentally obtained G(r) data for (a) HT-t-Na3PS4 and BM-“c”-Na3PS4 showing that there is no significant difference in the local structure. BM-“c”-Na3PS4 was fitted using a tetragonal model, shaded in green and a cubic model shaded in red. Experimental data are shown as black points. The red line denotes the calculated pattern, and the difference profile is shown in blue.257 Reproduced with permission from ref. 257. Copyright (2018) American Chemical Society. (c) Temperature-dependent ionic conductivities of various Na+ ion solid electrolytes, including both oxides and sulfides.198,252,256,261,262,265–270 Reproduced with permission from ref. 198, 265. Copyright (2012, 2017), Springer Nature. Reproduced with permission from ref. 252, 261, 262. Copyright (2015, 2016), Wiley. Reproduced with permission from ref. 256, 268, 269, 270. Copyright (1980, 1981, 1992, 2012), Elsevier. Reproduced with permission from ref. 266, 267. Copyright (2014, 2018), Royal Society of Chemistry. (d) Schematic diagram of Na ion diffusion in Na3PS4 and related phases.265 | ||
Nevertheless, despite the experimental discrepancy between the cubic and tetragonal phases, theoretical calculations indicated, in fact, that both pristine c-Na3PS4 and t-Na3PS4 structures exhibit extremely poor and similar ion conductivity.258 Systematic investigations of the synthesis parameters for Na3PS4 under different conditions (e.g., temperature, nature of the reaction vessel, mass of the precursors) revealed that reaction of the precursors with the reaction vessels produced different polymorphs.259 These results suggest that the stabilization of metastable c-Na3PS4 can not be explained only by an entropy contribution, but is more likely induced by the precursors reacting with the silica reaction tubes. Elements from the tubes may be incorporated into the structure of Na3PS4 or alternatively, off-stoichiometry may be induced in the structure by consumption of some precursors via the reaction with the tubes. The latter is more likely,259 considering that aliovalent doping (e.g., the replacement of P5+ with Si4+) appears to be not energetically favorable.258
New efforts have been made to uncover the origin of the enhanced ion conductivity in cubic Na3PS4, and to determine if the difference in the transport behaviour between the cubic and tetragonal phases arises from structural differences, microstructural variations, or disparities in the defect concentration. Rietveld and pair distribution function (PDF) analyses were performed to probe the average and local structures of Na3PS4 prepared through two different synthetic routes (ball-milling and high temperature synthesis).257 While Rietveld analysis indeed points to the average structure of Na3PS4 prepared through ball-milling and high temperature routes being cubic and tetragonal, respectively, PDF analyses showed that both Na3PS4 compounds exhibit the same tetragonal structural motif on the local scale (Fig. 10b). EIS suggests that the high ionic conductivity of “c”-Na3PS4 is not related to the crystal structure, but rather the defects induced by the harsh ball-milling conditions.257
Although stoichiometric Na3PX4 (X = S, Se) compounds were determined to be poor Na ion conductors, theoretical work also suggested that reasonably high conductivity can be realized with the introduction of Na+ interstitials or Na vacancies that induce disorder.258,260 A computational study on the effect of aliovalent doping of M4+ (M = Si, Ge, Sn) for P5+ in c-Na3PS4 predicted a conductivity of 1.66 × 10−3 S cm−1 for 6.25% Si-doped Na3PS4, in very good agreement with the reported experimental value of 7.4 × 10−4 S cm−1. Remarkably, Sn4+ doping at the same concentration contributed to a much higher predicted conductivity of 1.07 × 10−2 S cm−1 even though the dopant formation energy is higher than the Si4+ dopant.258 These studies prove that the presence of defects are essential to enable fast Na-ion diffusion in Na3PX4.
Anion substitution with Se2− – larger than S2− – is another strategy to improve conductivity. Due to its higher polarizability, the replacement of Se2− for S2− expands the lattice and weakens the binding energy between the mobile cations and anion framework. Cubic Na3PSe4 with a conductivity of 1.16 × 10−3 S cm−1 and a low activation energy of 0.21 eV was first reported by Zhang et al.261 They also reported vacancy-containing tetragonal Na3SbS4 with a very high conductivity of 3 × 10−3 S cm−1 formed by substituting Sb5+ for P5+ in Na3PS4.262–264 Na3SbS4 was reported to be stable in dry air,262 as rationalized by hard and soft acid and base (HSAB) theory. Very surprisingly (and questionably), Na3SbS4 is reported to show good compatibility with metallic Na, and to be electrochemically inert up to 5 V based on cyclic voltammetry (CV) measurements. Nonetheless, although CV is a valuable technique, it is not sufficient to assess stability of an SE since it is too fast to detect slow decomposition reactions in ASSBs. Recently, Zhang's group successfully synthesized Sb- and Se-substituted Na3SbSe4 with a high conductivity of 3.7 × 10−3 S cm−1 and low activation energy of 0.19 eV.265 The conductivity of these compositions and the schematic illustration of anion and cation size on Na ion transport are shown in Fig. 10c and d, respectively.198,252,256,261,262,265–270
The Na version of LGPS represents another class of sulfide conductors. Na10GeP2S12 (NGPS) was computationally predicted to have a conductivity of 4.7 × 10−3 S cm−1 by Kandagal et al.271 Richards et al.272 subsequently predicted an increase in the Na+ diffusivity and a decrease in activation energy in the series Sn < Ge < Si for Na10MP2S12 (M = Si, Ge, Sn). They reported the composition Na10SnP2S12 with an experimental conductivity of 4 × 10−4 S cm−1,272 but the structure was not disclosed. MD simulations suggested it is a 1D ion conductor, with chains of NaS4 tetrahedra linked along the c-axis providing facile diffusion. Later, Hayashi's group reported a glass-ceramic with a nominal composition of “Na10GeP2S12” that showed a conductivity of 2.4 × 10−5 S cm−1 and a XRD pattern similar to the simulated “Na10SnP2S12”. However, the structure was again not resolved.272 Very recently, the targeted synthesis of stoichiometric Na11Sn2PS12 as a polycrystalline powder provided a pure phase material that exhibits a very high conductivity of 1.4 × 10−3 S × cm−1 and low activation energy of 0.24 eV.267 The structure of the new phase, Na11Sn2PS12 was solved from single crystal X-ray diffraction (Fig. 11a and b). In contrast to the LGPS (or NGPS) structure type, the Na+ ions occupy only octahedral sites and the Na ion conductivity is completely three dimensional as demonstrated by AIMD simulations (Fig. 11c–e).267 Vital to ion conduction in this 3D percolating network is the disorder of the Na+ ions over the almost-fully occupied and partially occupied sites that alternate in all crystallographic directions. Low energy Na+-ion hopping is favored by the equi-energetic octahedral sites, and spacious iso-energetic pathways for transport. Experimental measurement of ion conductivity and activation barrier for Na-ion mobility closely matched that from AIMD simulation (0.20 eV), with the Ea being the lowest reported for a sodium thiophosphate in the literature to date. Following this publication, the same phase was also reported elsewhere, with a higher conductivity (3.7 × 10−3 S cm−1) but also with an unusually higher activation energy (0.39 eV).273
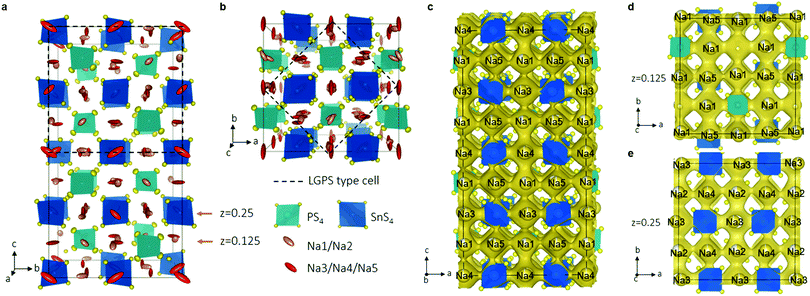 | ||
| Fig. 11 Structure of Na11Sn2PS12 from single crystal data. (a) The framework showing ordering of the SnS4 (dark blue) and PS4 (light blue) tetrahedra; yellow spheres are S; and rose/red ellipsoids are sodium ions. The Na(1)/Na(2) ions (sites with fractional occupancy) are represented by pink ellipsoids and the Na(3)/Na(4)/Na(5) ions (almost fully occupied sites) are shown as red ellipsoids; (b) the small tetragonal cell (a′ × a′ × c′) equivalent to Li10GeP2S12 is related to the actual tetragonal cell (a × a × c) of Na11Sn2PS12 as follows: a = a′√2; c = 2c′; Na-ion probability density isosurface (yellow) obtained from ab initio molecular dynamics (AIMD) studies at 1050 K for 40 ps, showing the nature of the 3D Na+ ion conduction paths: (c) sodium diffusion along the c axis involves a pathway along –Na(4)–Na(1)–Na(3)–Na(1)– chains; the Na-ion probability density obtained from the AIMD Na-ion trajectories in the ab plane shows the pathways at (d) z = 0.125 and (e) z = 0.25.267 Reproduced with permission from ref. 267. Copyright (2018), Royal Society of Chemistry. | ||
4. Ion conduction mechanism and principles to design fast ion conductors
4.1 Mechanism of ion conduction
Understanding the ion transport mechanism is critical to guide the design of fast ion conductors. The conventional knowledge of ion transport in solid materials is based on the classic diffusion model which depicts ion diffusion as the hopping of an individual ion from one lattice site to its adjacent vacant site, which is termed “direct-hopping” (Fig. 12a). | ||
| Fig. 12 (a) Schematic illustration of the direct hop mechanism and knock-off mechanism; (b) schematic drawing of pore diffusion in the porous organic layer of SEI and knock-off diffusion in the dense inorganic layer of SEI (Li2CO3).275 The open circles represent the Li+ already in the SEI. In the porous organic layer, the blue solid lines denote channels through which Li+ in the electrolyte (green filled circles) transports with anions (yellow filled circles) via pore diffusion. The red arrows denote that only Li+ can diffuse in the dense inorganic layer via the knock-off mechanism;275 Reproduced with permission from ref. 275. Copyright (2012) American Chemical Society. (c) Schematic illustration of single-ion migration versus multi-ion concerted migration. For single-ion migration (upper insets), the migration energy barrier is the same as the barrier of the energy landscape. In contrast, the concerted migration of multiple ions (lower insets) has a lower energy barrier as a result of strong ion–ion interactions and unique mobile ion configuration in super-ion conductors.274 Reproduced with permission from ref. 274. Copyright (2017), Springer Nature. | ||
The ion conductivity of solid materials is closely related to crystal structure and is governed by the ion concentration (n), activation energy (Ea), and the mobility of mobile ion carrier (μ):
| σ = nqμ and μ ∝ exp(−Ea/kBT) |
A low activation energy and high concentration of mobile ion carrier species (vacancies or interstitials) are necessary to obtain high conductivity. The underlying crystal framework determines the energy landscape of ion migration, while the energy barrier depends on the highest energy of the energy landscape along the decisive migration pathway (saddle-point). For the same crystal framework, similar migration barriers were predicted according to the classic diffusion model, which failed to explain the significantly lower activation energy barriers and abrupt increase in ion conductivity observed at certain doped composition (e.g., doped LLZO and NaSICON).274
Besides the classical “direct hopping” mechanism, another conduction mechanism was also proposed. Using DFT calculations, Shi et al.275 predicted that the dominant intrinsic defect in Li2CO3, Lii+, prefers to diffuse through a correlated migration mechanism (Fig. 12b and c), as opposed to the direct hop mechanism. Later, they also found that in β-Li3PS4, the correlated migration of Lii+ along [010] has the lowest migration barrier.276 The correlated mechanism is in fact the same as the later proposed “concerted mechanism” or “collective mechanism”. The lower migration barrier of the concerted mechanism compared to the conventional direct hop mechanism was also reported in Li3OX (X = Cl, Br),100 doped Li3PO4,277 and LLZO.158 Recently, Mo's group274 surveyed ion diffusion in a series of fast ion conductors, including Li7P3S11, β-Li3PS4, LiSICON, LLTO, revealing that the mobile ions occupying the high-energy sites can activate concerted migration with a reduced diffusion barrier. Strong ion–ion Coulomb interactions in the unique mobile-ion configuration with high-energy site occupancy are key for achieving low-barrier concerted migration in these solid ion conductors. During the concerted migration of multiple ions, the ions located at the high energy sites migrate downhill, and cancel out a fraction of the energy barrier caused by the uphill-climbing ions. This explains why the super-ionic conduction in doped LLZO and NaSICON is activated at certain compositions with increased alkali ion concentration, and provides a simple strategy to design fast ion conductors: inserting mobile ions into high energy sites to trigger concerted migration with a lower energy barrier.
4.2 Principles to design fast ion conductors
In general, certain structural prerequisites should be satisfied in order to ensure fast ion conduction in solid materials: (1) as ion transport proceeds locally by thermally activated jumps between adjacent sites (local energy minima), jumps need to be connected in “conduction channels” that allow long range transport. These conduction channels should have a suitable geometry that enables direct passage of the mobile ions but obviates energetically high transition states. While narrow bottlenecks obviously restrict mobility, passages that are too wide also impair motion. For example, the β′′-Al2O3 and NaSICON structures are more suitable for Na ions, and exhibit higher conduction for Na than Li ions. This may seem counter-intuitive, but results from the interplay between polarizing effect and polarizability. (2) Materials with face-sharing polyhedra, as opposed to edge-sharing, have favorable ion mobility since the bottleneck in the face-shared case is larger. Thus, ion channels with high mobility are easily formed when face-sharing polyhedra are connected throughout the structure of the SE.99 (3) Different alkali ion sites along the transport path should ideally have similar potential energies with low migration barriers for ion transport between adjacent sites.278 (4) Structural disorder and hence “partial” vacancies or interstitials in the mobile ion sub-lattice are necessary.279 Compounds that exhibit only small concentrations of well defined vacancies or interstitials, formed by either Frenkel or Schottky-type defect formation reactions, are usually poor room temperature electrolytes, as the defect formation enthalpy is then included in the activation energy of ion conductivity. (5) The anion sub-lattice arrangement is also paramount for the diffusion of ions as recently highlighted.99 (6) High polarizability of the anion sub-lattice is advantageous for good cation mobility. Numerous sulfide, thiophosphate, and iodide materials show higher conductivity than oxides for this reason. The important role of the polarizability of the anion sublattice has recently been highlighted using lithium superionic argyrodites Li6PS5X (X = Cl, Br, I) and sodium superionic Na3PS4−xSex as examples: softer bonds lower the activation barrier but simultaneously decrease the prefactor of the moving ions.224,280 In fact, the softer lattice is associated with smaller attempt frequencies, and thus, a smaller pre-factor.279 This explains some old empirical rules connecting prefactors and activation energies, and suggest that design rules for SEs need to consider both the energy landscape (activation barriers) and the phonon spectrum (attempt frequencies).224,279,280 (7) General thermodynamic arguments have led to – at least in simple structures – a powerful search strategy that is based on the correlation between charge carrier concentrations and melting points (also Tammann's rule281) that has been elucidated by Maier's group.282Ceder's group proposed (geometric) design principles for superionic conductors and suggested that a body-centered cubic-like (bcc) anion framework allows the Li+ ions to migrate within a network of interconnected tetrahedral sites with a lower activation barrier than other close-packed frameworks and is most desirable for achieving high ionic conductivity.99 This feature was verified in recently discovered highly conducting materials such as Li10GeP2S12220 and Li7P3S11,210 whose sulfide sub-lattices match a bcc lattice very closely (note α-AgI is a prototype bcc structure and an excellent SE283). Poorer conductors such as Li2S have a fcc sulfide sublattice, while Li4GeS4, Li3PS4 and thio-LiSICON have a hcp sulfide sublattice. This can be readily explained by considering that for all the sulfide sublattices, tetrahedral sites are energetically most stable for Li+ ions. In the bcc sulfide sublattice, the Li+ ion migrates with an extremely low barrier of 0.15 eV along the path connecting two face-sharing tetrahedral sites (Fig. 13a). In the fcc lattice, Li+ ions migrating between two tetrahedral sites have to pass through an intermediate octahedral site, which makes the energy barrier much higher (Fig. 13b). The same situation exists in the a–b plane of the hcp lattice (Fig. 13c). The frameworks of some structures cannot be closely matched to either a bcc, fcc or hcp sublattice, but accommodate a network composed entirely of tetrahedral sites for the mobile cations, in which cation migration through the percolating face-shared tetrahedral sites also shows low activation energy. Such frameworks can be found in argyrodite-type Li6PS5Cl224 and cubic-Na3PS4.198 Li4PS4I is another example, where PS43− and I− ions together form a bbc anion sublattice.226
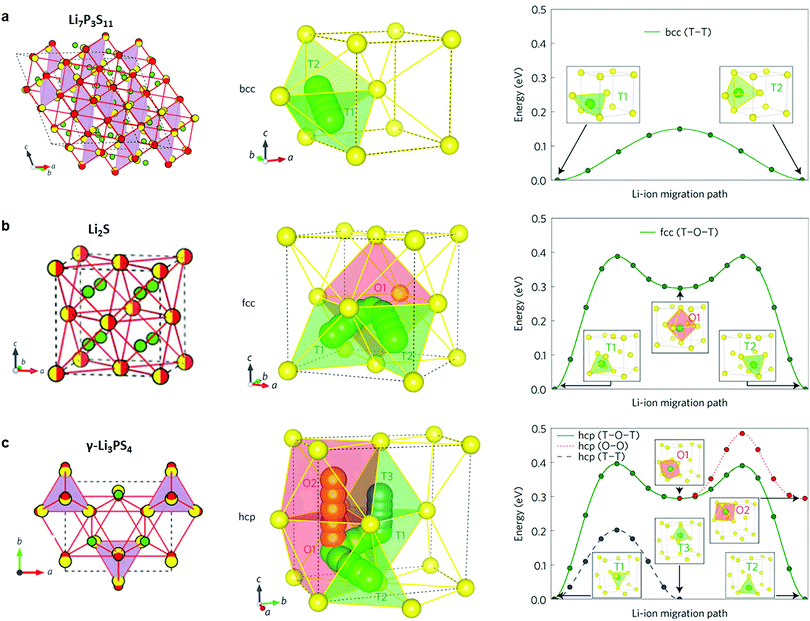 | ||
| Fig. 13 (a–e) Crystal structure of the Li-ion conductors: (a) Li7P3S11, (b) Li2S; (c) γ-Li3PS4. The Li ions, partially occupied Li+ sites, S2− anion, PS4 tetrahedra and GeS4 tetrahedra (partially occupied in Li10GeP2S12) are coloured green, green-white, yellow, purple and blue, respectively. In both Li10GeP2S12 and Li7P3S11, the sulfur anion sublattice can be closely mapped to a bcc framework (red circles connected by red lines). In Li2S, the anion sublattice is an exact fcc matrix (yellow-red circles). The anion sublattices in γ-Li3PS4 and Li4GeS4 are closely matched to a hcp framework.99 Reproduced with permission from ref. 99. Copyright (2015), Springer Nature. | ||
Additionally, it is worth noting that more efforts are needed to reduce the grain boundary resistance for crystalline materials, especially oxides. In heterogeneous systems, the contribution of interfaces determines the overall conducting property. The research on synergistic ion conduction effects in heterogeneous systems originated from the discovery of solid–solid composite electrolytes (typically formed by uniformly admixing fine oxide particles in an ion conducting matrix, e.g., LiI:Al2O3 or CaF2:SiO2) which show an anomalously high conductivity in comparison with pure phases284 due to increased carrier contributions.285 The space charge concept was introduced to interpret the adsorption effect of one type of ion on an insulating surface along with the significance of boundary layers with regard to ionic conduction. There is the possibility of excess storage in nano-composite materials due to the space charge effects.
This composite concept proved powerful for increasing carrier concentrations but not mobilities. In Section 2.1.1.1 we briefly mentioned LLT composites in which the admixture of SiO2 or Al2O3 decreased the grain boundary resistance by affecting the grain boundary structure directly. The conductivity of glass-ceramic electrolytes is influenced by the interface between them.286 The existence of a fast ion conduction interfacial regime between the glassy and crystalline phases was verified by Schirmeisen et al.287 A general explanation for these anomalies relies on space charge models that consider the depletion or accumulation of lithium vacancy point defects as a consequence of the defects at the interface.
Solid–liquid composite systems such as soggy-sand electrolytes288,289 or ion-exchange polymers290,291 deserve a brief mention in this context as they can offer excellent compromises between electrical properties (high conductivities and high Li-transference numbers) and mechanical properties (malleability, flexibility and good contact to electrode particles) that are difficult to achieve with pure solid phases. Similarly, enhanced conductivity with a percolation behavior has also been observed in these heterogeneous systems.288
Another very interesting synergistic coupling between Li6.75La3Zr1.75Ta0.25O12 (LLZTO) ceramics and poly(vinylidene fluoride) (PVDF) polymer electrolyte was reported by Nan's group.292 A combination of experiments and DFT calculations imply that the La atom of LLZTO could complex with the N atom and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group of solvent molecules such as N,N-dimethylformamide, along with electrons enriched at the N atom, which behaves like a Lewis base and induces the chemical dehydrofluorination of the PVDF skeleton. Partially modified PVDF chains activate the interactions between the PVDF matrix, lithium salt, and LLZTO fillers, hence leading to significantly improved conductivity.293
O group of solvent molecules such as N,N-dimethylformamide, along with electrons enriched at the N atom, which behaves like a Lewis base and induces the chemical dehydrofluorination of the PVDF skeleton. Partially modified PVDF chains activate the interactions between the PVDF matrix, lithium salt, and LLZTO fillers, hence leading to significantly improved conductivity.293
5. Evaluation of the electrochemical stability of SEs
Although significant progress has been made in the search for solid electrolytes with high ion conductivity, there are still many fundamental challenges impeding the commercialization of solid-state batteries.7,294 Most notably, these include chemical/electrochemical stability and resistance at the interface between the solid electrolytes and electrode materials. The properties of the SE/electrode interface – at both the positive and negative sides – are of vital importance to the function of the ASSBs.Although some fast-ion conducting solid electrolytes (mainly sulfides, thiophosphates and their derivatives, e.g., Li10GeP2S12, Li7P3S11, Li6PS5Cl) show promising conductivity comparable to – or even higher than – liquid electrolytes, the ASSBs assembled with these SEs typically exhibit inferior electrochemical performance than their liquid-cell counterparts. The sluggish charge-transfer across the SE/electrode interface caused by high interfacial resistance is usually the limiting factor for the poor cell kinetics.7 The origins of the interfacial resistance are nested in one or more factors: poor physical interfacial contact;295 mechanical failure of the contact with volume variation;296 formation of lithium/sodium-depleted space-charge layers due to the large chemical potential difference between SE and electrode materials;297 and degradation at the interface that is caused by mutual diffusion of elements and/or reactivity that results in formation of an interphase.298 Interphase formation may be ascribed299 to several different sources. One is the reduction (at the negative electrode) or oxidation of SEs (at the positive electrode) due to the intrinsic thermodynamic instability of the SEs. SEs are often claimed to exhibit excellent stability based on wide electrochemical windows of 0–5 V or even higher that are typically derived from relatively fast CV measurements on the Li/SE/inert blocking electrode. These experiments do not reflect the practical battery situation as they are too fast to detect slow decomposition reactions at the interfaces. A second source is reactions between the SE and the electrode materials caused by the chemical instability between these two layers. Finally, interphases can be formed in situ by electrochemical reactions of the SE/electrode interface during charge/discharge processes. These three reaction types are different at the positive and negative electrodes, and are explained in more detail below.
At the negative electrode, three different types of interfaces can be distinguished in the Li metal/SE contact, as schematically presented in Fig. 14a: (1) a thermodynamically stable interface; (2) a mixed conducting (growing) interphase (MCI); (3) and a metastable (non-growing) interphase (SEI).299 The properties of these three interfaces influence the charge transfer kinetics differently. In the first case, Li metal and the SE in contact are a priori in thermodynamic equilibrium and metal ion transfer and associated relaxation steps will be rate-limiting. In the second and third cases, Li metal and the SE are thermodynamically unstable when in contact, and the reaction products control the transport properties of the interphase. As shown in Fig. 14b, a mixed conducting interphase forms and grows “into” the bulk of the SE material, if the formed products possess sufficient partial electronic and ion conductivity, resulting in the destruction of the electrolyte and eventual self-discharge of the battery. On the other hand, a stable interphase may form if the reaction products are ion-conducting but electronically insulating or if the electronic conductivity is fairly low (Fig. 14c). The decomposition products inhibit continuous decomposition, acting as SEIs. While such interphases are inevitably formed, they are extremely difficult to monitor because of their thickness and the sparse techniques that are available to explore their buried nature. High resolution transmission electron microscopy studies – an obvious first choice – can in fact result in extensive beam damage, occluding the subject of investigation. Both surface science and theory have proven more insightful in predicting and identifying the interphase. In particular, in situ XPS (Fig. 14d), in combination with EIS has been shown to be a powerful tool to investigate the compatibility of SEs with lithium metal.213,299,300
 | ||
| Fig. 14 Types of interfaces between lithium metal and a solid lithium ion conductor. (a) Non-reactive and thermodynamically stable interface. (b) reactive and mixed conducting interphase (MCI). (c) Reactive and metastable solid–electrolyte interphase (SEI).299 Reproduced with permission from ref. 299. Copyright (2015), Elsevier. (d) In situ lithiation of solid electrolytes during XPS surface analysis. The argon ion gun is used to sputter from a lithium metal foil placed in the vicinity of the sample of interest. (e) XPS detail spectra of an LATP and LAGP sample before (bottom, black line) and after lithiation (middle, red line). (f) SEM cross-section image of a LATGP sample after approximately 12 h contact with lithium metal. The white arrow indicates the chemical diffusion of lithium into the material.300 Reproduced with permission from ref. 300. Copyright (2013), American Chemical Society. | ||
DFT calculations suggest that most Li–SEs are thermodynamically unstable against lithium metal as expected.10,301 Sulfides show a significantly narrower thermodynamic stability window than oxide-based SEs.301 The reduction products of thiophosphates at the Li interface are predicted to include Li3P and Li2S, and for those SE materials containing Ge, Cl, and I, a Li–Ge alloy, LiCl and LiI are formed, respectively. Theory11 and XPS results302 both show that LGPS is reduced at 0–1.7 V and oxidized at 2–2.5 V. The final decomposition products in equilibrium with Li metal are Li15Ge4, Li3P and Li2S. These data are in contrast to the originally reported 0–5 V electrochemical window from CV measurement.45 The electrochemical stability window of SEs is overestimated by CV method because of the slow kinetics of the decomposition reactions due to the limited contact area between the SE and the inert blocking electrode.303 However, in practical bulk ASSBs, the reduction/oxidation kinetics of SE in the composite electrode is greatly accelerated, owing to the much larger contact area between the SE and electronic conductive additives that are poised at the electrode potential. Along the same lines, even though LiPON is reduced at 0.69 V according to theory, it was thought to be stable in contact with lithium metal; however, in situ XPS reveals that it actually reacts with lithium metal to form Li3PO4, Li3P, Li3N and Li2O.304 Similarly, Ge-containing oxide materials Li1.5Al0.5Ge1.5(PO4)3 (LAGP) and Li3.5Zn0.25GeO4 (LiSICON), are reduced at 2.7 V and 1.4 V, respectively, in agreement with in situ XPS experimental studies18,305,306 (see Fig. 14e and f). In their calculations, Mo et al. found that in Ti containing oxide-based SE materials (i.e., LLTO and LATP), Ti4+ is reduced to Ti(3−x)+ at low potentials, again consistent with the results of in situ XPS (see Fig. 14e and f).299,300 We note that a new method using a Li/SE/SE-carbon cell has been proposed to identify the intrinsic electrochemical stability window of SE materials. The viability of this method was confirmed by the examination of the reduction and oxidation of LGPS and LLZO by a combination of in situ XPS and DFT calculations.303 Among all the oxides investigated, garnet type SEs, in particular, LLZO, exhibit the best resistance to Li reduction.
However, LiPON, as well as sulfides such as Li3PS4, and Li7P2S8I (which appears to be better described as Li4PS4I),226 are practically found to be compatible with Li metal. This is due to kinetic factors: the interphase that is formed passivates the SE and mitigates continued reaction. For example, the decomposition products of LiPON, Li3PS4, and Li7P2S8I are Li2O, Li2S, Li3P, Li3N, and LiI, which are all electronically insulating, and thermodynamically stable against Li reduction. The electrochemical potential of Li+ is constant across the interface. However, due to the poor electronic conductivity of the interphase, the electrochemical potential of the electronic carrier decreases abruptly from the anode to the SE. Therefore, the Li chemical potential (the sum of ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Li+ and
Li+ and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e−) decreases in the interphase layer from the anode to the SE and is within the electrochemical window of the SE. As a result, the decomposition of the SE has no thermodynamic driving force to continue into the bulk and the SE materials are stabilized by the reduction interphase layer. This is the case illustrated by Fig. 14c, above. In contrast, passivation is not possible when the interphase layer is electronically and ionically conductive. The decomposition interphases of Ge-containing LAGP and LiSICON with Li metal, or Ti-containing LLTO and LATP are mixed electronic and ion conductors (see above), which leads to continuous decomposition of the SEs. Thus, the reduction reaction advances into the bulk of the SE (Fig. 14b and g). In the case of sodium SEs much less work has been reported, but in principle sodium SEs exhibit the same thermodynamic instability against Na metal. Janek's group has recently proven the stability of Na-β′′-Al2O3 against Na metal and the instability of Na3PS4 in a combined XPS and impedance study.307
e−) decreases in the interphase layer from the anode to the SE and is within the electrochemical window of the SE. As a result, the decomposition of the SE has no thermodynamic driving force to continue into the bulk and the SE materials are stabilized by the reduction interphase layer. This is the case illustrated by Fig. 14c, above. In contrast, passivation is not possible when the interphase layer is electronically and ionically conductive. The decomposition interphases of Ge-containing LAGP and LiSICON with Li metal, or Ti-containing LLTO and LATP are mixed electronic and ion conductors (see above), which leads to continuous decomposition of the SEs. Thus, the reduction reaction advances into the bulk of the SE (Fig. 14b and g). In the case of sodium SEs much less work has been reported, but in principle sodium SEs exhibit the same thermodynamic instability against Na metal. Janek's group has recently proven the stability of Na-β′′-Al2O3 against Na metal and the instability of Na3PS4 in a combined XPS and impedance study.307
The electrochemical stability of many Li-ion solid electrolytes against oxidation with respect to cathode materials has also been investigated by DFT calculations,10,301 showing that many Li–SEs are thermodynamically unstable at high voltages (Fig. 15a).10,301 While some oxide-based SEs show a higher reduction potential than sulfides, they also exhibit a much higher oxidation potential, up to 4 V and higher; particularly, NaSICON type materials (i.e., LATP and LAGP) are thermodynamically stable up to 4.2 V. In reality, an even higher nominal oxidation threshold of >5 V is exhibited due to the sluggish kinetics of oxidation and the electronically insulating properties of the decomposition products, which give rise to a significant overpotential. In the case of sulfides, a lower oxidation potential is predicted by calculations, namely, the oxidation of Li6PS5Cl and LGPS starts at 2.0 V and 2.15 V, respectively, and Li3PS4 exhibits a similar oxidation potential of 2.31 V. Both calculations308 and experiments309 show thermodynamically unstability of the interface between sulfide SEs and LCO. The formation of electronically conductive cobalt sulfides are detrimental to the stability of the interface. With the carbon additive in sulfide-based SSBs, the electrochemical decomposition reactions of sulfide SEs at the cathode/SE interface is facilitated by transferring the low chemical potential of lithium in the charged state deeper into the SE and extending the decomposition region.310 The accumulation of highly oxidized sulfur species at the interface causes a large charge transfer resistance and thereby capacity fading (Fig. 15b).310 Furthermore, considerable redox activity of sulfide SEs in contact with cathode active materials presents more critical issues at the interface.311 This sulfide SEs oxidation is verified to occur predominantly in close proximity to the current collector. The thickness of the formed degradation layer is determined by the cut-off voltage and the associated potential drop at the interface between the current collector and the SE.311
 | ||
| Fig. 15 (a) Electrochemical window (solid color bar) of solid electrolyte and other materials. The oxidation potential to fully delithiate the material is marked by the dashed line.301 (b) Direct comparison of the first charge curves of carbon-free (blue) and carbon-containing (red) SSBs and a schematic representation of situations that occur on the cathode/SE interface of the SSB during charge processes (insertion). The presence of carbon leads to an additional slope during the first charge. Compared to the case without carbon, a growing overpotential directly results in capacity loss. The presence of carbon facilitates oxidation processes by providing sufficient electronic percolation paths toward the current collector.310 (c) Electrochemical window of the proposed and previously demonstrated coating layer materials applied between SEs and cathode materials. The dashed line marks the equilibrium voltage to fully delithiate the materials.308 Reproduced with permission from ref. 308. Copyright (2016), the Royal Society of Chemistry. (d) Schematic diagram illustrating the electrochemical window (color bars) and the Li chemical potential profile (black line) in the solid-state Li-ion battery. The profile of the chemical potential is schematic in this plot and may not be linear. The high μLi in the anode (silver) and low μLi in the cathode (blue) are beyond the stability window of the solid electrolyte (green). The observed nominal electrochemical window is extended by the overpotential (dashed line) and by the interphases (orange and yellow), which account for the gap of μLi between the solid electrolyte and electrodes across the interfaces.301 Reproduced with permission from ref. 301, 310. Copyright (2015, 2017), American Chemical Society. | ||
Fortunately, the better oxidation stability of oxides has enabled engineering of the interface between fast-ion conducting thiophosphate-based solid electrolytes, and positive electrode materials such as lithium transition metal oxides. The reaction between the SE and cathode is hence ameliorated by surface coatings that protect the SE material. Calculations demonstrate that commonly used coating layer materials, including Li4Ti5O12,312,313 LiTaO3,314 LiNbO3,315,316 Li2SiO3,317 Li3PO4,318 are stable between 2 and 4 V and show low electronic conductivity in this voltage domain (Fig. 15c).308 These coating materials for cathode materials can act as artificial SEIs to passivate the their surface and extend the electrochemical window, as illustrated in Fig. 15d. The large interfacial resistance that would otherwise arise from solid–solid contact is thus mitigated, contributing to excellent performance of ASSBs.46
6. Conclusions and future prospects for solid electrolytes and solid state batteries
To realize high performance solid-state batteries, solid electrolytes with high Li/Na ion conductivity, good chemical and electrochemical stability against cathode materials are required. If Li metal anodes need to be employed, SEs need also to be stable against reduction or have to be protected by a suitable protecting film. The total conductivity of oxide-based ceramics is highly dependent on the sintering conditions, the dopants, the density of the samples, and the nature of the grain boundaries. Alkali thiophosphate-based conductors show high conductivities ranging from 10−3 to 10−2 S cm−1 even for cold-pressed pellets. However, they must be handled under an ultra-dry atmosphere since most of them are prone to hydrolysis because of their hygroscopic nature. Oxides are typically unstable in contact with Li metal and exhibit slightly lower ion conductivities than sulfides, but are more stable in air and easier to handle. A severe disadvantage of oxide crystalline conductors is their large grain boundary resistance, which is often several orders of magnitude higher than bulk values. Further efforts are needed to decrease this contribution. It should be noted that oxide or phosphate conductors should not contain elements that are easily reduced when in contact with a Li metal anode, such as Ti or Ge. Garnet conductors exhibit both excellent conductivities and high chemical stability, and thus they are thought to be one of the most promising oxide crystalline Li ion conductors. Nevertheless, the preparation of thin-films is necessary to reduce the total ohmic resistance of these oxide electrolytes, and ceramic processing of garnets requires high temperatures.Although the search for solid electrolytes has experienced a recent upsurge, the development of ASSBs is still in its infancy. Compared with conventional liquid batteries, ASSBs can be stacked within a single package by alternating SE and bipolar electrodes (Fig. 16a),319 thus reducing the weight and volume of the package and increasing the energy density. However, some challenges still remain in the development of ASSBs: the instability of most SE in contact with Li/Na metal; the large interfacial resistance between SE and electrode materials mostly because of the limited contact area (Fig. 16b and c); and the incompatibility between SE and electrodes. The challenges and requirements for the large-scale production of all-solid-state lithium ion and lithium metal batteries are evaluated in a recent review.320
 | ||
| Fig. 16 Configurations of solid-state batteries and fabrication processes for performance improvement. (a) In a bipolar configuration, the electrode materials are coated on the two sides of the current collector, reducing the weight and volume of the battery package. (b) A typical solid-state battery consists of a cathode, an anode and a solid electrolyte. (c) A zoomed-in image of the contact between the electrolyte (yellow spheres) and the electrode (red spheres), which is limited in a typical solid-state battery. The black spheres represent carbon black and the black arrows indicate the Li+ migration pathway. (d) By putting a mixed conducting network coating (green) on the surface of electrode materials, the electrolyte–electrode contact is enhanced. (e) A powder pressing process for fabricating solid-state batteries. (f) A pasting route analogous to that used in solid oxide fuel cell fabrication. (g) A wet coating process for fabricating solid-state batteries. The electrode slurry is fed into a coating machine and spread on a current collector followed by a drying process and another electrolyte coating process. The obtained electrodes are cut and laminated together to make the solid-state batteries.319 Reproduced with permission from ref. 319. Copyright (2016), Springer Nature. | ||
To effectively utilize active materials and achieve good rate performance, appropriate techniques are needed to increase the electrode–electrolyte contact area and reduce the interfacial resistance between the electrodes and electrolyte, and allow for sufficient mechanical flexibility during charge/discharge. The mechanochemical preparation of nanocomposite electrodes and the surface modification of active material particles using electrolyte thin-films are effective strategies for achieving a favorable contact between the electrodes and electrolytes and enhancing the energy density of bulk solid-state batteries.319 One other possible strategy is to form a mixed conducting network into the active material, so as to achieve fast electron conduction and create Li+ ion transport channels. This conducting network could be an amorphous material or a wetting agent such as a non-flammable ionic liquid (indicated in green in Fig. 16d). As demonstrated in a recent paper, improved interface kinetics can be realized by adding a very small amount of ionic liquid (PP13FSI) at the cathode side of the solid-state battery.252 These solid-state batteries exhibit excellent cycling performance (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles at room temperature without capacity decay) and rate capability. Another possible solution is to develop hybrid electrolytes that combine inorganic electrolyte and polymer electrolytes to assemble a flexible all-solid-state battery, as demonstrated by Nan's group.292,321–323 Obvious solutions that are not fully explored are solid–liquid composites.288,289
000 cycles at room temperature without capacity decay) and rate capability. Another possible solution is to develop hybrid electrolytes that combine inorganic electrolyte and polymer electrolytes to assemble a flexible all-solid-state battery, as demonstrated by Nan's group.292,321–323 Obvious solutions that are not fully explored are solid–liquid composites.288,289
Another challenge associated with ASSBs is the thickness of the SE layer and the electrode layer, which is determined by the fabrication technology. Well-known cold pressing methods (Fig. 16e), largely used for sulfide based ASSBs, will limit energy density and are difficult to scale up for practical applications. One strategy to reduce the electrode thickness is to spray cathode and anode materials on both sides of the electrolyte (Fig. 16f) by adding small amount of a wetting agent. Another approach is to employ a wet coating process that is widely used in commercial production of conventional batteries (Fig. 16g). This approach has the advantages of controllability of the layer thickness and the scalability, and has been employed to fabricate solid polymer batteries.324
Future research should focus on the understanding of interfacial reactions and developing strategies to solve the incompatibility and instability of SE and electrode materials, as well as developing approaches to protect the electrodes and reduce the large resistance of the interface. It is also especially necessary to develop highly scalable methods for SE synthesis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Technologies R&D Program, China (2016YFB0901500), the National Natural Science Foundation of China (51788104, 51725206 and 51421002). J. J. acknowledges financial support by BMBF within the project “BenchBatt”. L. F. N. thanks BASF and NSERC for financial support. B. V. L. acknowledges financial support by the BMBF (project “StickLis”), the Nanosystems Initiative Munich (NIM) and the Max Planck Society. M. A. is indebted to CIC Energigune, Spain, for support. Open Access funding provided by the Max Planck Society.References
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef PubMed.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2009, 22, 587–603 CrossRef.
- J. B. Goodenough, J. Solid State Electrochem., 2012, 16, 2019–2029 CrossRef.
- S. Chandrashekar, N. M. Trease, H. J. Chang, L.-S. Du, C. P. Grey and A. Jerschow, Nat. Mater., 2012, 11, 311–315 CrossRef PubMed.
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. Zhang, Energy Environ. Sci., 2014, 7, 513–537 RSC.
- J. Janek and W. G. Zeier, Nat. Mater., 2016, 1, 16141 Search PubMed.
- J. Vetter, P. Novák, M. Wagner, C. Veit, K.-C. Möller, J. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269–281 CrossRef.
- N. J. Dudney, Lithium batteries, 2003, ch. 20, pp. 624–642 Search PubMed.
- J. Zhu, X. Hea and Y. Mo, J. Mater. Chem. A, 2016, 4, 3253–3266 RSC.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2011, 24, 15–17 CrossRef.
- W. Zhang, D. Schröder, T. Arlt, I. Manke, R. Koerver, R. Pinedo, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, J. Mater. Chem. A, 2017, 5, 9929–9936 RSC.
- W. Zhang, D. A. Weber, H. Weigand, T. Arlt, I. Manke, D. Schröder, R. Koerver, T. Leichtweiß, P. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2017, 9, 17835–17845 CrossRef PubMed.
- R. Koerver, I. Aygun, T. Leichtweiß, C. Dietrich, W. Zhang, J. Binder, P. Hartmann, W. G. Zeier and J. Janek, Chem. Mater., 2017, 29, 5574–5582 CrossRef.
- J. F. Oudenhoven, L. Baggetto and P. H. Notten, Adv. Energy Mater., 2011, 1, 10–33 CrossRef.
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef PubMed.
- H. Zhai, P. Xu, M. Ning, Q. Cheng, J. Mandal and Y. Yang, Nano Lett., 2017, 17, 3182–3187 CrossRef PubMed.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2015, 116, 140–162 CrossRef PubMed.
- R. Chen, W. Qu, X. Guo, L. Li and F. Wu, Mater. Horiz., 2016, 3, 487–516 RSC.
- S. Stramare, V. Thangadurai and W. Weppner, Chem. Mater., 2003, 15, 3974–3990 CrossRef.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- B. V. Lotsch and J. Maier, J. Electroceram., 2017, 38, 128–141 CrossRef.
- Z. Wang, J. Z. Lee, H. L. Xin, L. Han, N. Grillon, D. Guy-Bouyssou, E. Bouyssou, M. Proust and Y. S. Meng, J. Power Sources, 2016, 324, 342–348 CrossRef.
- Y. Tian, T. Shi, W. D. Richards, J. Li, J. C. Kim, S.-H. Bo and G. Ceder, Energy Environ. Sci., 2017, 10, 1150–1166 RSC.
- J. Bates, N. Dudney, G. Gruzalski, R. Zuhr, A. Choudhury, C. Luck and J. Robertson, Solid State Ionics, 1992, 53, 647–654 CrossRef.
- Y. Hamon, A. Douard, F. Sabary, C. Marcel, P. Vinatier, B. Pecquenard and A. Levasseur, Solid State Ionics, 2006, 177, 257–261 CrossRef.
- S. Jacke, J. Song, L. Dimesso, J. Brötz, D. Becker and W. Jaegermann, J. Power Sources, 2011, 196, 6911–6914 CrossRef.
- J. Bates, N. Dudney, G. Gruzalski, R. Zuhr, A. Choudhury, C. Luck and J. Robertson, J. Power Sources, 1993, 43, 103–110 CrossRef.
- B. Fleutot, B. Pecquenard, H. Martinez, M. Letellier and A. Levasseur, Solid State Ionics, 2011, 186, 29–36 CrossRef.
- N. Suzuki, S. Shirai, N. Takahashi, T. Inaba and T. Shiga, Solid State Ionics, 2011, 191, 49–54 CrossRef.
- M. Baba, N. Kumagai, N. Fujita, K. Ohta, K. Nishidate, S. Komaba, H. Groult, D. Devilliers and B. Kaplan, J. Power Sources, 2001, 97, 798–800 CrossRef.
- B. Wang, J. Bates, F. Hart, B. Sales, R. Zuhr and J. Robertson, J. Electrochem. Soc., 1996, 143, 3203–3213 CrossRef.
- M. Menetrier, C. Estournes, A. Levasseur and K. Rao, Solid State Ionics, 1992, 53, 1208–1213 CrossRef.
- R. Mercier, J.-P. Malugani, B. Fahys and G. Robert, Solid State Ionics, 1981, 5, 663–666 CrossRef.
- H. Wada, M. Menetrier, A. Levasseur and P. Hagenmuller, Mater. Res. Bull., 1983, 18, 189–193 CrossRef.
- Y. Ren, Y. Shen, Y. Lin and C.-W. Nan, Electrochem. Commun., 2015, 57, 27–30 CrossRef.
- F. Aguesse, W. Manalastas, L. Buannic, J. M. Lopez del Amo, G. Singh, A. Llordés and J. Kilner, ACS Appl. Mater. Interfaces, 2017, 9, 3808–3816 CrossRef PubMed.
- X. Xie, J. Xing, D. Hu, H. Gu, C. Chen and X. Guo, ACS Appl. Mater. Interfaces, 2018, 10, 5978–5983 CrossRef PubMed.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627–631 RSC.
- Y. Inaguma, C. Liquan, M. Itoh, T. Nakamura, T. Uchida, H. Ikuta and M. Wakihara, Solid State Commun., 1993, 86, 689–693 CrossRef.
- R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148, A742–A746 CrossRef.
- F. Mizuno, A. Hayashi, K. Tadanaga and M. Tatsumisago, Adv. Mater., 2005, 17, 918–921 CrossRef.
- K. Takada, N. Aotani and S. Kondo, J. Power Sources, 1993, 43, 135–141 CrossRef.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama and K. Kawamoto, Nat. Mater., 2011, 10, 682–686 CrossRef PubMed.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef.
- Y. Zhao and L. L. Daemen, J. Am. Chem. Soc., 2012, 134, 15042–15047 CrossRef PubMed.
- K. Minami, A. Hayashi and M. Tatsumisago, J. Am. Ceram. Soc., 2011, 94, 1779–1783 CrossRef.
- A. Düvel, A. Kuhn, L. Robben, M. Wilkening and P. Heitjans, J. Phys. Chem. C, 2012, 116, 15192–15202 CrossRef.
- G. Adachi, N. Imanaka and S. Tamura, Chem. Rev., 2002, 102, 2405–2430 CrossRef PubMed.
- H.-P. Hong, Mater. Res. Bull., 1978, 13, 117–124 CrossRef.
- M. Monchak, T. Hupfer, A. Senyshyn, H. Boysen, D. Chernyshov, T. Hansen, K. G. Schell, E. C. Bucharsky, M. J. Hoffmann and H. Ehrenberg, Inorg. Chem., 2016, 55, 2941–2945 CrossRef PubMed.
- C. R. Schlaikjer and C. C. Liang, J. Electrochem. Soc., 1971, 118, 1447–1450 CrossRef.
- S. Shi, L. Xu, C. Ouyang, Z. Wang and L. Chen, Ionics, 2006, 12, 343–347 CrossRef.
- G. Adachi, N. Imanaka and H. Aono, Adv. Mater., 1996, 8, 127–135 CrossRef.
- A. Robertson, A. West and A. Ritchie, Solid State Ionics, 1997, 104, 1–11 CrossRef.
- A. G. Belous, G. N. Novitskaya, S. V. Polyanetskaya and Y. I. Gornikov, Russ. J. Inorg. Chem., 1987, 32, 156–157 Search PubMed.
- M. Wu, Z. Wen, Y. Liu, X. Wang and L. Huang, J. Power Sources, 2011, 196, 8091–8097 CrossRef.
- S. J. Visco, Y. S. Nimon and B. D. Katz, US8778522 B2, 2014.
- M. Braga, J. A. Ferreira, V. Stockhausen, J. Oliveira and A. El-Azab, J. Mater. Chem. A, 2014, 2, 5470–5480 RSC.
- R. Kanno, T. Hata, Y. Kawamoto and M. Irie, Solid State Ionics, 2000, 130, 97–104 CrossRef.
- H. J. Deiseroth, S. T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiss and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755–758 CrossRef PubMed.
- P. Bron, S. Johansson, K. Zick, J. r. Schmedt auf der Günne, S. Dehnen and B. Roling, J. Am. Chem. Soc., 2013, 135, 15694–15697 CrossRef PubMed.
- O. Bohnke, C. Bohnke and J. Fourquet, Solid State Ionics, 1996, 91, 21–31 CrossRef.
- M. Abe and K. Uchino, Mater. Res. Bull., 1974, 9, 147–155 CrossRef.
- Y. Inaguma, T. Katsumata, M. Itoh and Y. Morii, J. Solid State Chem., 2002, 166, 67–72 CrossRef.
- M. Yashima, M. Itoh, Y. Inaguma and Y. Morii, J. Am. Chem. Soc., 2005, 127, 3491–3495 CrossRef PubMed.
- J. Ibarra, A. Varez, C. León, J. Santamarıa, L. Torres-Martınez and J. Sanz, Solid State Ionics, 2000, 134, 219–228 CrossRef.
- Y. Zou and N. Inoue, Ionics, 2005, 11, 333–342 CrossRef.
- J. Fourquet, H. Duroy and M. Crosnier-Lopez, J. Solid State Chem., 1996, 127, 283–294 CrossRef.
- Y. Inaguma, T. Katsumata, M. Itoh, Y. Morii and T. Tsurui, Solid State Ionics, 2006, 177, 3037–3044 CrossRef.
- A. Morata-Orrantia, S. García-Martín and M. Á. Alario-Franco, Chem. Mater., 2003, 15, 363–367 CrossRef.
- O. Bohnke, C. Bohnke, J. Ould Sid'Ahmed, M. Crosnier-Lopez, H. Duroy, F. Le Berre and J. Fourquet, Chem. Mater., 2001, 13, 1593–1599 CrossRef.
- L. He and H. Yoo, Electrochim. Acta, 2003, 48, 1357–1366 CrossRef.
- V. Thangadurai and W. Weppner, Ionics, 2000, 6, 70–77 CrossRef.
- A. Morata-Orrantia, S. García-Martín, E. Morán and M. Á. Alario-Franco, Chem. Mater., 2002, 14, 2871–2875 CrossRef.
- H.-T. Chung, J.-G. Kim and H.-G. Kim, Solid State Ionics, 1998, 107, 153–160 CrossRef.
- A. Kishimoto, Solid State Ionics, 1998, 107, 153–160 CrossRef.
- T. Teranishi, M. Yamamoto, H. Hayashi and A. Kishimoto, Solid State Ionics, 2013, 243, 18–21 CrossRef.
- H. Kawai and J. Kuwano, J. Electrochem. Soc., 1994, 141, L78–L79 CrossRef.
- Y. Harada, T. Ishigaki, H. Kawai and J. Kuwano, Solid State Ionics, 1998, 108, 407–413 CrossRef.
- M. Nakayama, T. Usui, Y. Uchimoto, M. Wakihara and M. Yamamoto, J. Phys. Chem. B, 2005, 109, 4135–4143 CrossRef PubMed.
- K.-Y. Yang, J.-W. Wang and K.-Z. Fung, J. Alloys Compd., 2008, 458, 415–424 CrossRef.
- A. Mei, X.-L. Wang, J.-L. Lan, Y.-C. Feng, H.-X. Geng, Y.-H. Lin and C.-W. Nan, Electrochim. Acta, 2010, 55, 2958–2963 CrossRef.
- H. Geng, J. Lan, A. Mei, Y. Lin and C. Nan, Electrochim. Acta, 2011, 56, 3406–3414 CrossRef.
- X. Gao, C. A. Fisher, T. Kimura, Y. H. Ikuhara, H. Moriwake, A. Kuwabara, H. Oki, T. Tojigamori, R. Huang and Y. Ikuhara, Chem. Mater., 2013, 25, 1607–1614 CrossRef.
- X. Gao, C. A. Fisher, T. Kimura, Y. H. Ikuhara, A. Kuwabara, H. Moriwake, H. Oki, T. Tojigamori, K. Kohama and Y. Ikuhara, J. Mater. Chem. A, 2014, 2, 843–852 RSC.
- C. Ma, K. Chen, C. Liang, C.-W. Nan, R. Ishikawa, K. More and M. Chi, Energy Environ. Sci., 2014, 7, 1638–1642 RSC.
- H. Moriwake, X. Gao, A. Kuwabara, C. A. Fisher, T. Kimura, Y. H. Ikuhara, K. Kohama, T. Tojigamori and Y. Ikuhara, J. Power Sources, 2015, 276, 203–207 CrossRef.
- W. J. Kwon, H. Kim, K.-N. Jung, W. Cho, S. H. Kim, J.-W. Lee and M.-S. Park, J. Mater. Chem. A, 2017, 5, 6257–6262 RSC.
- K. Chen, M. Huang, Y. Shen, Y. Lin and C. Nan, Solid State Ionics, 2013, 235, 8–13 CrossRef.
- A. Mei, X.-L. Wang, Y.-C. Feng, S.-J. Zhao, G.-J. Li, H.-X. Geng, Y.-H. Lin and C.-W. Nan, Solid State Ionics, 2008, 179, 2255–2259 CrossRef.
- H. Zhang, X. Liu, Y. Qi and V. Liu, J. Alloys Compd., 2013, 577, 57–63 CrossRef.
- Y. Deng, S.-J. Shang, A. Mei, Y.-H. Lin, L.-Y. Liu and C.-W. Nan, J. Alloys Compd., 2009, 472, 456–460 CrossRef.
- A. Yoshiasa, D. Sakamoto, H. Okudera, M. Sugahara, K. i. Ota and A. Nakatsuka, Z. Anorg. Allg. Chem., 2005, 631, 502–506 CrossRef.
- C. D. Martin, S. Chaudhur, C. P. Grey and J. B. Parise, Am. Mineral., 2005, 90, 1522–1533 CrossRef.
- V. Bouznik, Y. N. Moskvich and V. N. Voronov, Chem. Phys. Lett., 1976, 37, 464–467 CrossRef.
- Y. Zhang, Y. Zhao and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134303 CrossRef.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef PubMed.
- A. Emly, E. Kioupakis and A. Van der Ven, Chem. Mater., 2013, 25, 4663–4670 CrossRef.
- R. Mouta, M. A. B. Melo, E. M. Diniz and C. W. A. Paschoal, Chem. Mater., 2014, 26, 7137–7144 CrossRef.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2017, 140, 362–368 CrossRef PubMed.
- Y. Li, W. Zhou, S. Xin, S. Li, J. Zhu, X. Lu, Z. Cui, Q. Jia, J. Zhou, Y. Zhao and J. B. Goodenough, Angew. Chem., Int. Ed., 2016, 55, 9965–9968 CrossRef PubMed.
- M. H. Braga, N. S. Grundish, A. J. Murchison and J. B. Goodenough, Energy Environ. Sci., 2017, 10, 331–336 RSC.
- M. H. Braga, A. J. Murchison, J. A. Ferreira, P. Singh and J. B. Goodenough, Energy Environ. Sci., 2016, 9, 948–954 RSC.
- J. Goodenough, H.-P. Hong and J. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef.
- H.-P. Hong, Mater. Res. Bull., 1976, 11, 173–182 CrossRef.
- K. Arbi, M. París and J. Sanz, Dalton Trans., 2011, 40, 10195–10202 RSC.
- M. A. París and J. Sanz, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 14270 CrossRef.
- E. Morin, T. Le Mercier, M. Quarton, E. Losilla, M. Aranda and S. Bruque, Powder Diffr., 1999, 14, 53–60 CrossRef.
- M. Weiss, D. A. Weber, A. Senyshyn, J. Janek and W. G. Zeier, ACS Appl. Mater. Interfaces, 2018, 10, 10935–10944 CrossRef PubMed.
- M. Alami, R. Brochu, J. Soubeyroux, P. Gravereau, G. Le Flem and P. Hagenmuller, J. Solid State Chem., 1991, 90, 185–193 CrossRef.
- M. A. París, A. Martínez-Juárez, J. M. Rojo and J. Sanz, J. Phys.: Condens. Matter, 1996, 8, 5355–5366 CrossRef.
- E. R. Losilla, M. A. Aranda, M. Martínez-Lara and S. Bruque, Chem. Mater., 1997, 9, 1678–1685 CrossRef.
- K. Arbi, S. Mandal, J. M. Rojo and J. Sanz, Chem. Mater., 2002, 14, 1091–1097 CrossRef.
- M. Catti, S. Stramare and R. Ibberson, Solid State Ionics, 1999, 123, 173–180 CrossRef.
- Y. Zhang, K. Chen, Y. Shen, Y. Lin and C.-W. Nan, Ceram. Int., 2017, 43, S598–S602 CrossRef.
- M. Giarola, A. Sanson, F. Tietz, S. Pristat, E. Dashjav, D. Rettenwander, G. n. J. Redhammer and G. Mariotto, J. Phys. Chem. C, 2017, 121, 3697–3706 CrossRef.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, J. Electrochem. Soc., 1993, 140, 1827–1833 CrossRef.
- K. Thomas, G. Subba Rao, K. Radhakrishnan and B. Chowdari, Mater. Res. Bull., 1989, 24, 221–229 CrossRef.
- R. Shannon, B. Taylor, A. English and T. Berzins, Electrochim. Acta, 1977, 22, 783–796 CrossRef.
- D. T. Qui, S. Hamdoune, J. Soubeyroux and E. Prince, J. Solid State Chem., 1988, 72, 309–315 CrossRef.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. y. Adachi, J. Electrochem. Soc., 1990, 137, 1023–1027 CrossRef.
- K. Ado, Y. Saito, T. Asai, H. Kageyama and O. Nakamura, Solid State Ionics, 1992, 53, 723–727 CrossRef.
- A. Best, M. Forsyth and D. MacFarlane, Solid State Ionics, 2000, 136, 339–344 CrossRef.
- K. Arbi, M. Lazarraga, D. Ben Hassen Chehimi, M. Ayadi-Trabelsi, J. Rojo and J. Sanz, Chem. Mater., 2004, 16, 255–262 CrossRef.
- T. Šalkus, M. Barre, A. Kežionis, E. Kazakevičius, O. Bohnke, A. Selskienė and A. Orliukas, Solid State Ionics, 2012, 225, 615–619 CrossRef.
- K. Arbi, M. Hoelzel, A. Kuhn, F. García-Alvarado and J. Sanz, Inorg. Chem., 2013, 52, 9290–9296 CrossRef PubMed.
- M. Pérez-Estébanez, J. Isasi-Marín, D. Többens, A. Rivera-Calzada and C. León, Solid State Ionics, 2014, 266, 1–8 CrossRef.
- K. Arbi, R. Jimenez, T. Šalkus, A. Orliukas and J. Sanz, Solid State Ionics, 2015, 271, 28–33 CrossRef.
- C. Vinod Chandran, S. Pristat, E. Witt, F. Tietz and P. Heitjans, J. Phys. Chem. C, 2016, 120, 8436–8442 CrossRef.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G.-y. Adachi, Bull. Chem. Soc. Jpn., 1992, 65, 2200–2204 CrossRef.
- B. Lang, B. Ziebarth and C. Elsässer, Chem. Mater., 2015, 27, 5040–5048 CrossRef.
- R. Kahlaoui, K. Arbi, I. Sobrados, R. Jimenez, J. Sanz and R. Ternane, Inorg. Chem., 2017, 56, 1216–1224 CrossRef PubMed.
- H. Aono, E. Sugimoto, Y. Sadaaka, N. Imanaka and G. Adachi, J. Electrochem. Soc., 1989, 136, 590–591 CrossRef.
- Y. Kobayashi, M. Tabuchi and O. Nakamura, J. Power Sources, 1997, 68, 407–411 CrossRef.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G.-y. Adachi, Solid State Ionics, 1991, 47, 257–264 CrossRef.
- L. Xiong, Z. Ren, Y. Xu, S. Mao, P. Lei and M. Sun, Solid State Ionics, 2017, 309, 22–26 CrossRef.
- J. Fu, Solid State Ionics, 1997, 96, 195–200 CrossRef.
- J. Fu, Solid State Ionics, 1997, 104, 191–194 CrossRef.
- B. Chowdari, G. S. Rao and G. Lee, Solid State Ionics, 2000, 136, 1067–1075 CrossRef.
- J. S. Thokchom and B. Kumar, Solid State Ionics, 2006, 177, 727–732 CrossRef.
- J. S. Thokchom and B. Kumar, J. Am. Ceram. Soc., 2007, 90, 462–466 CrossRef.
- J. S. Thokchom and B. Kumar, J. Power Sources, 2008, 185, 480–485 CrossRef.
- J. S. Thokchom and B. Kumar, J. Power Sources, 2010, 195, 2870–2876 CrossRef.
- C. R. Mariappan, C. Yada, F. Rosciano and B. Roling, J. Power Sources, 2011, 196, 6456–6464 CrossRef.
- V. Thangadurai, H. Kaack and W. J. Weppner, J. Am. Ceram. Soc., 2003, 86, 437–440 CrossRef.
- V. Thangadurai and W. Weppner, J. Solid State Chem., 2006, 179, 974–984 CrossRef.
- S. Narayanan, F. Ramezanipour and V. Thangadurai, J. Phys. Chem. C, 2012, 116, 20154–20162 CrossRef.
- V. Thangadurai and W. Weppner, J. Am. Ceram. Soc., 2005, 88, 411–418 CrossRef.
- V. Thangadurai and W. Weppner, Adv. Funct. Mater., 2005, 15, 107–112 CrossRef.
- J. Percival, E. Kendrick and P. Slater, Mater. Res. Bull., 2008, 43, 765–770 CrossRef.
- J. Percival, E. Kendrick and P. Slater, Solid State Ionics, 2008, 179, 1666–1669 CrossRef.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef PubMed.
- J. Tan and A. Tiwari, Electrochem. Solid-State Lett., 2011, 15, A37–A39 CrossRef.
- J. Percival, E. Kendrick, R. Smith and P. Slater, Dalton Trans., 2009, 5177–5181 RSC.
- J. Awaka, N. Kijima, K. Kataoka, H. Hayakawa, K.-i. Ohshima and J. Akimoto, J. Solid State Chem., 2010, 183, 180–185 CrossRef.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430 CrossRef.
- J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, J. Solid State Chem., 2009, 182, 2046–2052 CrossRef.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg and A. Lotnyk, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392 RSC.
- C. A. Geiger, E. Alekseev, B. Lazic, M. Fisch, T. Armbruster, R. Langner, M. Fechtelkord, N. Kim, T. Pettke and W. Weppner, Inorg. Chem., 2010, 50, 1089–1097 CrossRef PubMed.
- Y. Li, J.-T. Han, C.-A. Wang, S. C. Vogel, H. Xie, M. Xu and J. B. Goodenough, J. Power Sources, 2012, 209, 278–281 CrossRef.
- A. A. Hubaud, D. J. Schroeder, B. Key, B. J. Ingram, F. Dogan and J. T. Vaughey, J. Mater. Chem. A, 2013, 1, 8813–8818 RSC.
- E. Rangasamy, J. Wolfenstine and J. Sakamoto, Solid State Ionics, 2012, 206, 28–32 CrossRef.
- D. Rettenwander, P. Blaha, R. Laskowski, K. Schwarz, P. Bottke, M. Wilkening, C. A. Geiger and G. Amthauer, Chem. Mater., 2014, 26, 2617–2623 CrossRef PubMed.
- N. Bernstein, M. Johannes and K. Hoang, Phys. Rev. Lett., 2012, 109, 205702 CrossRef PubMed.
- M. Kotobuki, K. Kanamura, Y. Sato and T. Yoshida, J. Power Sources, 2011, 196, 7750–7754 CrossRef.
- S. Kumazaki, Y. Iriyama, K.-H. Kim, R. Murugan, K. Tanabe, K. Yamamoto, T. Hirayama and Z. Ogumi, Electrochem. Commun., 2011, 13, 509–512 CrossRef.
- J. Wolfenstine, J. Ratchford, E. Rangasamy, J. Sakamoto and J. L. Allen, Mater. Chem. Phys., 2012, 134, 571–575 CrossRef.
- R. Jalem, M. Rushton, W. Manalastas Jr, M. Nakayama, T. Kasuga, J. A. Kilner and R. W. Grimes, Chem. Mater., 2015, 27, 2821–2831 CrossRef.
- C. Bernuy-Lopez, W. Manalastas Jr, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef.
- H. El Shinawi and J. Janek, J. Power Sources, 2013, 225, 13–19 CrossRef.
- M. Howard, O. Clemens, E. Kendrick, K. Knight, D. Apperley, P. Anderson and P. Slater, Dalton Trans., 2012, 41, 12048–12053 RSC.
- D. Rettenwander, C. A. Geiger, M. Tribus, P. Tropper and G. Amthauer, Inorg. Chem., 2014, 53, 6264–6269 CrossRef PubMed.
- S. Ramakumar, L. Satyanarayana, S. V. Manorama and R. Murugan, Phys. Chem. Chem. Phys., 2013, 15, 11327–11338 RSC.
- S. Ohta, T. Kobayashi and T. Asaoka, J. Power Sources, 2011, 196, 3342–3345 CrossRef.
- Y. Li, J.-T. Han, C.-A. Wang, H. Xie and J. B. Goodenough, J. Mater. Chem., 2012, 22, 15357–15361 RSC.
- C. Deviannapoorani, L. Dhivya, S. Ramakumar and R. Murugan, J. Power Sources, 2013, 240, 18–25 CrossRef.
- D. Wang, G. Zhong, W. K. Pang, Z. Guo, Y. Li, M. J. McDonald, R. Fu, J.-X. Mi and Y. Yang, Chem. Mater., 2015, 27, 6650–6659 CrossRef.
- D. Wang, G. Zhong, O. Dolotko, Y. Li, M. J. McDonald, J. Mi, R. Fu and Y. Yang, J. Mater. Chem. A, 2014, 2, 20271–20279 RSC.
- L. Dhivya and R. Murugan, ACS Appl. Mater. Interfaces, 2014, 6, 17606–17615 CrossRef PubMed.
- X. Tong, V. Thangadurai and E. D. Wachsman, Inorg. Chem., 2015, 54, 3600–3607 CrossRef PubMed.
- A. Raskovalov, E. Il'ina and B. Antonov, J. Power Sources, 2013, 238, 48–52 CrossRef.
- R. Murugan, S. Ramakumar and N. Janani, Electrochem. Commun., 2011, 13, 1373–1375 CrossRef.
- Y. Wang and W. Lai, Electrochem. Solid-State Lett., 2012, 15, A68–A71 CrossRef.
- M. P. O'Callaghan, D. R. Lynham, E. J. Cussen and G. Z. Chen, Chem. Mater., 2006, 18, 4681–4689 CrossRef.
- R.-J. Chen, M. Huang, W.-Z. Huang, Y. Shen, Y.-H. Lin and C.-W. Nan, Solid State Ionics, 2014, 265, 7–12 CrossRef.
- T. Thompson, J. Wolfenstine, J. L. Allen, M. Johannes, A. Huq, I. N. David and J. Sakamoto, J. Mater. Chem. A, 2014, 2, 13431–13436 RSC.
- R. Inada, K. Kusakabe, T. Tanaka, S. Kudo and Y. Sakurai, Solid State Ionics, 2014, 262, 568–572 CrossRef.
- D. Mazza, Mater. Lett., 1988, 7, 205–207 CrossRef.
- H. Hyooma and K. Hayashi, Mater. Res. Bull., 1988, 23, 1399–1407 CrossRef.
- V. Thangadurai, S. Adams and W. Weppner, Chem. Mater., 2004, 16, 2998–3006 CrossRef.
- E. J. Cussen, Chem. Commun., 2006, 412–413 RSC.
- L. van Wüllen, T. Echelmeyer, H.-W. Meyer and D. Wilmer, Phys. Chem. Chem. Phys., 2007, 9, 3298–3303 RSC.
- M. P. O'Callaghan and E. J. Cussen, Chem. Commun., 2007, 2048–2050 RSC.
- M. Xu, M. S. Park, J. M. Lee, T. Y. Kim, Y. S. Park and E. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 052301 CrossRef.
- J. Han, J. Zhu, Y. Li, X. Yu, S. Wang, G. Wu, H. Xie, S. C. Vogel, F. Izumi and K. Momma, Chem. Commun., 2012, 48, 9840–9842 RSC.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856 CrossRef PubMed.
- A. Hayashi, A. Sakuda and M. Tatsumisago, Front. Energy Res., 2016, 4, 25 Search PubMed.
- M. Murayama, R. Kanno, M. Irie, S. Ito, T. Hata, N. Sonoyama and Y. Kawamoto, J. Solid State Chem., 2002, 168, 140–148 CrossRef.
- Z. Liu, W. Fu, E. A. Payzant, X. Yu, Z. Wu, N. J. Dudney, J. Kiggans, K. Hong, A. J. Rondinone and C. Liang, J. Am. Chem. Soc., 2013, 135, 975–978 CrossRef PubMed.
- Z. Liu, F. Huang, J. Yang, B. Wang and J. Sun, Solid State Ionics, 2008, 179, 1714–1716 CrossRef.
- M. Tachez, J.-P. Malugani, R. Mercier and G. Robert, Solid State Ionics, 1984, 14, 181–185 CrossRef.
- B. T. Ahn and R. A. Huggins, Mater. Res. Bull., 1989, 24, 889–897 CrossRef.
- H. Yamane, M. Shibata, Y. Shimane, T. Junke, Y. Seino, S. Adams, K. Minami, A. Hayashi and M. Tatsumisago, Solid State Ionics, 2007, 178, 1163–1167 CrossRef.
- T. Kaib, S. Haddadpour, M. Kapitein, P. Bron, C. Schröder, H. Eckert, B. Roling and S. Dehnen, Chem. Mater., 2012, 24, 2211–2219 CrossRef.
- C. Dietrich, M. Sadowski, S. Sicolo, D. A. Weber, S. J. Sedlmaier, K. S. Weldert, S. Indris, K. Albe, J. Janek and W. G. Zeier, Chem. Mater., 2016, 28, 8764–8773 CrossRef.
- J. M. Whiteley, J. H. Woo, E. Hu, K.-W. Nam and S.-H. Lee, J. Electrochem. Soc., 2014, 161, A1812–A1817 CrossRef.
- Y. Kato, R. Saito, M. Sakano, A. Mitsui, M. Hirayama and R. Kanno, J. Power Sources, 2014, 271, 60–64 CrossRef.
- M. R. Busche, D. A. Weber, Y. Schneider, C. Dietrich, S. Wenzel, T. Leichtweiss, D. Schröder, W. Zhang, H. Weigand and D. Walter, Chem. Mater., 2016, 28, 6152–6165 Search PubMed.
- C. Dietrich, D. A. Weber, S. J. Sedlmaier, S. Indris, S. P. Culver, D. Walter, J. Janek and W. G. Zeier, J. Mater. Chem. A, 2017, 5, 18111–18119 RSC.
- Y. Kato, K. Kawamoto, R. Kanno and M. Hirayama, Electrochemistry, 2012, 80, 749–751 CrossRef.
- S. Wenzel, S. Randau, T. Leichtweiß, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, Chem. Mater., 2016, 28, 2400–2407 CrossRef.
- S. P. Ong, Y. Mo, W. D. Richards, L. Miara, H. S. Lee and G. Ceder, Energy Environ. Sci., 2013, 6, 148–156 RSC.
- A. Kuhn, O. Gerbig, C. Zhu, F. Falkenberg, J. Maier and B. V. Lotsch, Phys. Chem. Chem. Phys., 2014, 16, 14669–14674 RSC.
- Y. Sun, K. Suzuki, S. Hori, M. Hirayama and R. Kanno, Chem. Mater., 2017, 29, 5858–5864 CrossRef.
- T. Krauskopf, S. P. Culver and W. G. Zeier, Chem. Mater., 2018, 30, 1791–1798 CrossRef.
- S. Adams and R. P. Rao, J. Mater. Chem., 2012, 22, 7687–7691 RSC.
- A. Kuhn, J. Köhler and B. V. Lotsch, Phys. Chem. Chem. Phys., 2013, 15, 11620–11622 RSC.
- D. A. Weber, A. Senyshyn, K. S. Weldert, S. Wenzel, W. Zhang, R. Kaiser, S. Berendts, J. Janek and W. G. Zeier, Chem. Mater., 2016, 28, 5905–5915 CrossRef.
- H. J. Deiseroth, J. Maier, K. Weichert, V. Nickel, S. T. Kong and C. Reiner, Z. Anorg. Allg. Chem., 2011, 637, 1287–1294 CrossRef.
- N. J. de Klerk, I. Rosłoń and M. Wagemaker, Chem. Mater., 2016, 28, 7955–7963 Search PubMed.
- H. M. Chen, C. Maohua and S. Adams, Phys. Chem. Chem. Phys., 2015, 17, 16494–16506 RSC.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef PubMed.
- N. Minafra, S. P. Culver, T. Krauskopf, A. Senyshyn and W. G. Zeier, J. Mater. Chem. A, 2018, 6, 645–651 RSC.
- S. J. Sedlmaier, S. Indris, C. Dietrich, M. Yavuz, C. Dräger, F. von Seggern, H. Sommer and J. Janek, Chem. Mater., 2017, 29, 1830–1835 CrossRef.
- S. Sicolo, C. Kalcher, S. J. Sedlmaier, J. Janek and K. Albe, Solid State Ionics, 2018, 319, 83–91 CrossRef.
- W. D. Richards, Y. Wang, L. J. Miara, J. C. Kim and G. Ceder, Energy Environ. Sci., 2016, 9, 3272–3278 RSC.
- K. Kaup, F. Lalere, A. Huq, A. Shyamsunder, T. Adermann, P. Hartmann and L. F. Nazar, Chem. Mater., 2018, 30, 592–596 CrossRef.
- A. Kuhn, T. Holzmann, J. Nuss and B. V. Lotsch, J. Mater. Chem. A, 2014, 2, 6100–6106 RSC.
- J. A. Brant, D. M. Massi, N. Holzwarth, J. H. MacNeil, A. P. Douvalis, T. Bakas, S. W. Martin, M. D. Gross and J. A. Aitken, Chem. Mater., 2014, 27, 189–196 CrossRef.
- T. Holzmann, L. Schoop, M. Ali, I. Moudrakovski, G. Gregori, J. Maier, R. Cava and B. Lotsch, Energy Environ. Sci., 2016, 9, 2578–2585 RSC.
- H. Pan, Y.-S. Hu and L. Chen, Energy Environ. Sci., 2013, 6, 2338–2360 RSC.
- L. Mu, S. Xu, Y. Li, Y. S. Hu, H. Li, L. Chen and X. Huang, Adv. Mater., 2015, 27, 6928–6933 CrossRef PubMed.
- Y. Li, Y.-S. Hu, X. Qi, X. Rong, H. Li, X. Huang and L. Chen, Energy Storage Materials, 2016, 5, 191–197 CrossRef.
- K. B. Hueso, M. Armand and T. Rojo, Energy Environ. Sci., 2013, 6, 734–749 RSC.
- J. B. Goodenough, H.-P. Hong and J. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef.
- N. Anantharamulu, K. K. Rao, G. Rambabu, B. V. Kumar, V. Radha and M. Vithal, J. Mater. Sci., 2011, 46, 2821–2837 CrossRef.
- K.-D. Kreuer, H. Kohler and J. Maier, High Conductivity Solid Ionic Conductors: Recent Trends and Applications, World Scientific, 1989, pp. 242–279 Search PubMed.
- E. Vogel, R. Cava and E. Rietman, Solid State Ionics, 1984, 14, 1–6 CrossRef.
- T. Takahashi, K. Kuwabara and M. Shibata, Solid State Ionics, 1980, 1, 163–175 CrossRef.
- F. Krok, D. Kony, J. Dygas, W. Jakubowski and W. Bogusz, Solid State Ionics, 1989, 36, 251–254 CrossRef.
- Z. Khakpour, Electrochim. Acta, 2016, 196, 337–347 CrossRef.
- A. Kuriakose, T. Wheat, A. Ahmad and J. Dirocco, J. Am. Ceram. Soc., 1984, 67, 179–183 CrossRef.
- B. McEntire, R. Bartlett, G. Miller and R. Gordon, J. Am. Ceram. Soc., 1983, 66, 738–742 CrossRef.
- J. S. Lee, C. M. Chang, Y. I. Lee, J. H. Lee and S. H. Hong, J. Am. Ceram. Soc., 2004, 87, 305–307 CrossRef.
- R. Fuentes, F. Figueiredo, F. Marques and J. Franco, Ionics, 2002, 8, 383–390 CrossRef.
- S.-M. Lee, S.-T. Lee, D.-H. Lee, S.-H. Lee, S.-S. Han and S.-K. Lim, J. Ceram. Process. Res., 2015, 16, 49–53 Search PubMed.
- Q. Ma, M. Guin, S. Naqash, C.-L. Tsai, F. Tietz and O. Guillon, Chem. Mater., 2016, 28, 4821–4828 CrossRef.
- M. Guin and F. Tietz, J. Power Sources, 2015, 273, 1056–1064 CrossRef.
- A. G. Jolley, D. D. Taylor, N. J. Schreiber and E. D. Wachsman, J. Am. Ceram. Soc., 2015, 98, 2902–2907 CrossRef.
- Z. Zhang, Q. Zhang, J. Shi, Y. S. Chu, X. Yu, K. Xu, M. Ge, H. Yan, W. Li and L. Gu, Adv. Energy Mater., 2017, 7, 1101196 Search PubMed.
- U. Warhus, J. Maier and A. Rabenau, J. Solid State Chem., 1988, 72, 113–125 CrossRef.
- K. Kreuer and U. Warhus, Mater. Res. Bull., 1986, 21, 357–363 CrossRef.
- M. Tatsumisago, M. Nagao and A. Hayashi, J. Asian Ceram. Soc., 2013, 1, 17–25 CrossRef.
- M. Jansen and U. Henseler, J. Solid State Chem., 1992, 99, 110–119 CrossRef.
- T. Krauskopf, S. P. Culver and W. G. Zeier, Inorg. Chem., 2018, 57, 4739–4744 CrossRef PubMed.
- Z. Zhu, I.-H. Chu, Z. Deng and S. P. Ong, Chem. Mater., 2015, 27, 8318–8325 CrossRef.
- S.-H. Bo, Y. Wang and G. Ceder, J. Mater. Chem. A, 2016, 4, 9044–9053 RSC.
- I.-H. Chu, C. S. Kompella, H. Nguyen, Z. Zhu, S. Hy, Z. Deng, Y. S. Meng and S. P. Ong, Sci. Rep., 2016, 6, 33733 CrossRef PubMed.
- L. Zhang, K. Yang, J. Mi, L. Lu, L. Zhao, L. Wang, Y. Li and H. Zeng, Adv. Energy Mater., 2015, 5, 1501294 CrossRef.
- A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S. T. Hong and Y. S. Jung, Angew. Chem., Int. Ed., 2016, 128, 9786–9790 CrossRef.
- H. Wang, Y. Chen, Z. D. Hood, G. Sahu, A. S. Pandian, J. K. Keum, K. An and C. Liang, Angew. Chem., Int. Ed., 2016, 55, 8551–8555 CrossRef PubMed.
- L. Zhang, D. Zhang, K. Yang, X. Yan, L. Wang, J. Mi, B. Xu and Y. Li, Adv. Sci., 2016, 3, 1600089 CrossRef PubMed.
- N. Wang, K. Yang, L. Zhang, X. Yan, L. Wang and B. Xu, J. Mater. Sci., 2018, 53, 1987–1994 CrossRef.
- N. Tanibata, K. Noi, A. Hayashi and M. Tatsumisago, RSC Adv., 2014, 4, 17120–17123 RSC.
- Z. Zhang, E. Ramos, F. Lalère, A. Assoud, K. Kaup, P. Hartman and L. F. Nazar, Energy Environ. Sci., 2018, 11, 87–93 RSC.
- J. W. Fergus, Solid State Ionics, 2012, 227, 102–112 CrossRef.
- M. Ribes, B. Barrau and J. Souquet, J. Non-Cryst. Solids, 1980, 38, 271–276 CrossRef.
- S. Susman, L. Boehm, K. Volin and C. Delbecq, Solid State Ionics, 1981, 5, 667–669 CrossRef.
- V. S. Kandagal, M. D. Bharadwaj and U. V. Waghmare, J. Mater. Chem. A, 2015, 3, 12992–12999 RSC.
- W. D. Richards, T. Tsujimura, L. J. Miara, Y. Wang, J. C. Kim, S. P. Ong, I. Uechi, N. Suzuki and G. Ceder, Nat. Commun., 2016, 7, 11009 CrossRef PubMed.
- M. Duchardt, U. Ruschewitz, S. Adams, S. Dehnen and B. Roling, Angew. Chem., Int. Ed., 2018, 130, 1365–1369 CrossRef.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 15893 CrossRef PubMed.
- S. Shi, P. Lu, Z. Liu, Y. Qi, L. G. Hector Jr, H. Li and S. J. Harris, J. Am. Chem. Soc., 2012, 134, 15476–15487 CrossRef PubMed.
- Y. Yang, Q. Wu, Y. Cui, Y. Chen, S. Shi, R.-Z. Wang and H. Yan, ACS Appl. Mater. Interfaces, 2016, 8, 25229–25242 CrossRef PubMed.
- Y. Deng, C. Eames, J.-N. l. Chotard, F. Lalère, V. Seznec, S. Emge, O. Pecher, C. P. Grey, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2015, 137, 9136–9145 CrossRef PubMed.
- J. B. Boyce and B. A. Huberman, Phys. Rep., 1979, 51, 189–265 CrossRef.
- S. P. Culver, R. Koerver, T. Krauskopf and W. G. Zeier, Chem. Mater., 2018 DOI:10.1021/acs.chemmater.8b01293.
- T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869 CrossRef.
- R. Merkle and J. Maier, Z. Anorg. Allg. Chem., 2005, 631, 1163–1166 CrossRef.
- N. Hainovsky and J. Maier, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 15789 CrossRef.
- L. Strock, Z. Phys. Chem., Abt. B, 1934, 25, 441–459 Search PubMed.
- C. Liang, J. Electrochem. Soc., 1973, 120, 1289–1292 CrossRef.
- J. Maier, Prog. Solid State Chem., 1995, 23, 171–263 CrossRef.
- K. Hariharan and J. Maier, Solid State Ionics, 1996, 86, 503–509 Search PubMed.
- A. Schirmeisen, A. Taskiran, H. Fuchs, H. Bracht, S. Murugavel and B. Roling, Phys. Rev. Lett., 2007, 98, 225901 CrossRef PubMed.
- C. Pfaffenhuber, M. Göbel, J. Popovic and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 18318–18335 RSC.
- A. J. Bhattacharyya and J. Maier, Adv. Mater., 2004, 16, 811–814 CrossRef.
- R. Bouchet, S. Maria, R. Meziane, A. Aboulaich, L. Lienafa, J.-P. Bonnet, T. N. Phan, D. Bertin, D. Gigmes and D. Devaux, Nat. Mater., 2013, 12, 452–457 CrossRef PubMed.
- K. D. Kreuer, A. Wohlfarth, C. C. de Araujo, A. Fuchs and J. Maier, ChemPhysChem, 2011, 12, 2558–2560 CrossRef PubMed.
- X. Zhang, T. Liu, S. Zhang, X. Huang, B. Xu, Y. Lin, B. Xu, L. Li, C.-W. Nan and Y. Shen, J. Am. Chem. Soc., 2017, 139, 13779–13785 CrossRef PubMed.
- J. Zhang, N. Zhao, M. Zhang, Y. Li, P. K. Chu, X. Guo, Z. Di, X. Wang and H. Li, Nano Energy, 2016, 28, 447–454 CrossRef.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103 CrossRef.
- S. Ohta, T. Kobayashi, J. Seki and T. Asaoka, J. Power Sources, 2012, 202, 332–335 CrossRef.
- Y. J. Nam, S.-J. Cho, D. Y. Oh, J.-M. Lim, S. Y. Kim, J. H. Song, Y.-G. Lee, S.-Y. Lee and Y. S. Jung, Nano Lett., 2015, 15, 3317–3323 CrossRef PubMed.
- K. Takada, Acta Mater., 2013, 61, 759–770 CrossRef.
- K. H. Kim, Y. Iriyama, K. Yamamoto, S. Kumazaki, T. Asaka, K. Tanabe, C. A. Fisher, T. Hirayama, R. Murugan and Z. Ogumi, J. Power Sources, 2011, 196, 764–767 CrossRef.
- S. Wenzel, T. Leichtweiss, D. Krüger, J. Sann and J. Janek, Solid State Ionics, 2015, 278, 98–105 CrossRef.
- P. Hartmann, T. Leichtweiss, M. R. Busche, M. Schneider, M. Reich, J. Sann, P. Adelhelm and J. Janek, J. Phys. Chem. C, 2013, 117, 21064–21074 CrossRef.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef PubMed.
- F. Han, T. Gao, Y. Zhu, K. J. Gaskell and C. Wang, Adv. Mater., 2015, 27, 3473–3483 CrossRef PubMed.
- F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Adv. Energy Mater., 2016, 6, 1501590 CrossRef.
- A. Schwöbel, R. Hausbrand and W. Jaegermann, Solid State Ionics, 2015, 273, 51–54 CrossRef.
- J. Feng, L. Lu and M. Lai, J. Alloys Compd., 2010, 501, 255–258 CrossRef.
- U. Alpen, M. Bell, W. Wichelhaus, K. Cheung and G. Dudley, Electrochim. Acta, 1978, 23, 1395–1397 CrossRef.
- S. Wenzel, T. Leichtweiß, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2016, 8, 28216–28224 CrossRef PubMed.
- Y. Zhu, X. He and Y. Mo, J. Mater. Chem. A, 2016, 4, 3253–3266 RSC.
- A. Sakuda, A. Hayashi and M. Tatsumisago, Chem. Mater., 2009, 22, 949–956 CrossRef.
- W. Zhang, T. Leichtweiß, S. P. Culver, R. Koerver, D. Das, D. A. Weber, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2017, 9, 35888–35896 CrossRef PubMed.
- R. Koerver, F. Walther, I. Aygün, J. Sann, C. Dietrich, W. G. Zeier and J. Janek, J. Mater. Chem. A, 2017, 5, 22750–22760 RSC.
- N. Ohta, K. Takada, L. Zhang, R. Ma, M. Osada and T. Sasaki, Adv. Mater., 2006, 18, 2226–2229 CrossRef.
- H. Kitaura, A. Hayashi, K. Tadanaga and M. Tatsumisago, Solid State Ionics, 2011, 192, 304–307 CrossRef.
- K. Takada, N. Ohta, L. Zhang, K. Fukuda, I. Sakaguchi, R. Ma, M. Osada and T. Sasaki, Solid State Ionics, 2008, 179, 1333–1337 CrossRef.
- N. Ohta, K. Takada, I. Sakaguchi, L. Zhang, R. Ma, K. Fukuda, M. Osada and T. Sasaki, Electrochem. Commun., 2007, 9, 1486–1490 CrossRef.
- T. Kato, T. Hamanaka, K. Yamamoto, T. Hirayama, F. Sagane, M. Motoyama and Y. Iriyama, J. Power Sources, 2014, 260, 292–298 CrossRef.
- A. Sakuda, H. Kitaura, A. Hayashi, K. Tadanaga and M. Tatsumisago, Electrochem. Solid-State Lett., 2008, 11, A1–A3 CrossRef.
- Y. Jin, N. Li, C. Chen and S. Wei, Electrochem. Solid-State Lett., 2006, 9, A273–A276 CrossRef.
- Y.-S. Hu, Nat. Energy, 2016, 1, 16042 CrossRef.
- J. Schnell, T. Günther, T. Knoche, C. Vieider, L. Köhler, A. Just, M. Keller, S. Passerini and G. Reinhart, J. Power Sources, 2018, 382, 160–175 CrossRef.
- R.-J. Chen, Y.-B. Zhang, T. Liu, B.-Q. Xu, Y.-H. Lin, C.-W. Nan and Y. Shen, ACS Appl. Mater. Interfaces, 2017, 9, 9654–9661 CrossRef PubMed.
- T. Liu, Y. Zhang, X. Zhang, L. Wang, S.-X. Zhao, Y.-H. Lin, Y. Shen, J. Luo, L. Li and C.-W. Nan, J. Mater. Chem. A, 2018 10.1039/C7TA06833F.
- L. Chen, Y. Li, S.-P. Li, L.-Z. Fan, C.-W. Nan and J. B. Goodenough, Nano Energy, 2017, 46, 176–184 CrossRef.
- P. Hovington, M. Lagacé, A. Guerfi, P. Bouchard, A. Mauger, C. Julien, M. Armand and K. Zaghib, Nano Lett., 2015, 15, 2671–2678 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |







