Open Access Article
Open Access ArticleDesign principles for high transition metal capacity in disordered rocksalt Li-ion cathodes†
Daniil A.
Kitchaev‡
 *a,
Zhengyan
Lun‡
*a,
Zhengyan
Lun‡
 bc,
William D.
Richards
a,
Huiwen
Ji
bc,
Raphaële J.
Clément
bc,
William D.
Richards
a,
Huiwen
Ji
bc,
Raphaële J.
Clément
 c,
Mahalingam
Balasubramanian
c,
Mahalingam
Balasubramanian
 d,
Deok-Hwang
Kwon
b,
Kehua
Dai
e,
Joseph K.
Papp
f,
Teng
Lei
g,
Bryan D.
McCloskey
fh,
Wanli
Yang
d,
Deok-Hwang
Kwon
b,
Kehua
Dai
e,
Joseph K.
Papp
f,
Teng
Lei
g,
Bryan D.
McCloskey
fh,
Wanli
Yang
 e,
Jinhyuk
Lee
c and
Gerbrand
Ceder
*abc
e,
Jinhyuk
Lee
c and
Gerbrand
Ceder
*abc
aDepartment of Materials Science and Engineering, MIT, Cambridge, MA 02139, USA. E-mail: dkitch@alum.mit.edu
bMaterials Science Division, LBNL, Berkeley, CA 94720, USA
cDepartment of Materials Science and Engineering, UC Berkeley, Berkeley, CA 94720, USA. E-mail: gceder@berkeley.edu
dX-ray Science Division, Advanced Photon Source, Argonne National Laboratory, Argonne, Illinois 60439, USA
eAdvanced Light Source, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
fDepartment of Chemical and Biomolecular Engineering, UC Berkeley, Berkeley, CA 94720, USA
gDepartment of Chemistry, UC Berkeley, Berkeley, CA 94720, USA
hEnergy Storage and Distributed Resources Division, LBNL, Berkeley, CA 94720, USA
First published on 24th May 2018
Abstract
The discovery of facile Li transport in disordered, Li-excess rocksalt materials has opened a vast new chemical space for the development of high energy density, low cost Li-ion cathodes. We develop a strategy for obtaining optimized compositions within this class of materials, exhibiting high capacity and energy density as well as good reversibility, by using a combination of low-valence transition metal redox and a high-valence redox active charge compensator, as well as fluorine substitution for oxygen. Furthermore, we identify a new constraint on high-performance compositions by demonstrating the necessity of excess Li capacity as a means of counteracting high-voltage tetrahedral Li formation, Li-binding by fluorine and the associated irreversibility. Specifically, we demonstrate that 10–12% of Li capacity is lost due to tetrahedral Li formation, and 0.4–0.8 Li per F dopant is made inaccessible at moderate voltages due to Li–F binding. We demonstrate the success of this strategy by realizing a series of high-performance disordered oxyfluoride cathode materials based on Mn2+/4+ and V4+/5+ redox.
Broader contextElectrochemical energy storage is a key component of modern energy systems, providing portable power to devices ranging from personal electronics to electric vehicles, and enabling grid-scale mitigation of the fluctuating availability of renewable energy sources. The central role of energy storage systems motivates the search for, and optimization of, low-cost, environmentally-benign materials which can reversibly provide high energy density. Cathode materials, which are presently the performance-limiting components in state-of-the-art Li-ion batteries, have been traditionally limited to Ni and Co-based layered oxides. The recent discovery of Li-percolation in disordered rocksalts has expanded the structural space of materials which may serve as a Li-ion electrode, while the demonstration of Mn2+/4+ cathode electrochemistry and disordered rocksalt fluorination has opened to door to the use of cheap, environmentally-friendly chemistries. Here, we build on these demonstrations to derive optimization rules for designing disordered rocksalt oxyfluoride cathodes and provide an example of an optimized series of cathode materials. |
Introduction
The development of high-energy density cathode materials remains a bottleneck in the design of advanced Li-ion batteries. While the traditional space of layered oxides has been dominated by oxides of Ni, Mn, and Co,1 the discovery of facile Li transport in Li-excess disordered rocksalt materials2,3 has vastly expanded the chemical space for cathode design. Some of the advantages of Li-excess disordered rocksalts are now clear; by removing the demand that the cathode material remains layered, a much wider range of transition metals can be used as a redox reservoir, especially when d0 species are present to accommodate local strain and allow for facile disorder.4 Furthermore, recent theoretical5 and experimental6 work indicates that, unlike in layered materials, fluorine can be partially substituted for oxygen in disordered rocksalts. Fluorine substitution lowers the average anion valence, allowing Li-excess compositions to be combined with lower valence metals and reducing oxygen loss during cycling.A large number of high-performance cathodes have already been reported among Li-excess disordered rocksalts. To ensure that the composition is charge balanced, these materials have either relied on high-valence transition metals as the redox-active center, such as in Li3V23.5+O5,7 or used a combination of a trivalent redox-active transition metal oxide (LiM3+O2) mixed with a high-valence charge compensator, such as Li4MoO5,2,8,9 Li3NbO4,10–14 Li3SbO4,15 or Li2TiO3,8,16,17 where the metal is electrochemically inactive. Fluorination as a supplementary source of charge compensation has been used in Li2V3+O2F,18 Li2Cr3+O2F,19 and Li2Mo3+O2F20 compounds. Through a combination of these strategies, cathodes have also been reported based on high-voltage divalent transition metal centers, such as Li1.15Ni0.452+Ti0.3Mo0.1O1.85F0.15,6 Li2Mn2/32+Nb1/3O2F, and Li2Mn1/22+Ti1/2O2F.21 Despite the numerous reported compounds however, the question of which composition is optimal for high reversible capacity and energy density remains open.
The design of a disordered rocksalt cathode material essentially consists of choosing one or more active redox centers, the Li-excess content and F/O ratio on the anion site, while ensuring that the desired combination of oxidation states is stable and that the compound is synthetically accessible. High-valence multi-electron couples spanning the average oxidation states of V3+/5+, Mo3+/6+ and Cr3+/5+ have been successfully realized but suffer from a low average voltage.2,7,14,18–20 Higher voltage trivalent couples such as Mn3+/4+, Fe3+/4+ and Co3+/4+ in turn offer too little capacity on their own, and typically require additional anion redox for high energy density, which is accompanied by irreversibility due to oxygen loss and surface densification.9,11,16,22,23 Finally, while the high-voltage Ni2+/4+ couple promises high theoretical energy density, its practical realization has been to date hampered by overlap with oxygen redox at moderate levels of charge.6,8,11 The recently realized Mn2+/4+ couple avoids this limitation while providing high capacity at a high average voltage.21 However, as the low-valence of the discharged Mn2+ requires a source of charge compensation, previous reports have mixed the active Mn with redox-inactive elements, as well as fluorine. It is thus possible to obtain higher transition-metal capacity by using a redox-active charge compensator instead. Two examples of such high-valence compensators are V4+, providing relatively high-voltage V4+/5+ capacity, or Mo5+, providing Mo5+/6+ capacity. The combination of high-voltage Mn2+/4+ and a redox active high-valence charge compensator presents an opportunity to achieve high capacity based only on relatively high-voltage transition metal couples, minimizing anion redox and the associated oxygen loss and degradation processes.
Here, we investigate a series of novel cathode materials based on the proposed combination of Mn2+/4+ and V4+/5+ couples. We present a computational approach for evaluating synthetic accessibility in this space, which allows for the identification of optimal synthesizable compositions. We proceed to evaluate the mixed Mn/V redox mechanism through a combination of first-principles calculations and spectroscopy. Based on these results, as well as our computational models, we trace the sub-theoretical performance of our initial compositions to the presence of high-voltage Li sites associated with fluorine doping and the formation of tetrahedrally-coordinated Li. By considering the chemical and structural features, we derive an accurate model for the practical capacity of a disordered rocksalt. Based on these novel design criteria, we report a series of disordered rocksalt oxyfluoride cathodes which rely predominantly on transition metal redox and provide high capacity and energy density with good reversibility.
Methodology
Computational methods
In order to evaluate the Li+–Mn2+–V4+–O2−–F− phase diagram and obtain representative structures of fully lithiated Li+–Mn2+–V4+–O2−–F− materials, we constructed a cluster-expansion Hamiltonian of the LiF–MnO–Li2/3V1/3O system on a dense-rocksalt lattice following the same methodology we described in a previous report.5 To summarize, we computed approximately 600 orderings on the rocksalt lattice, iteratively chosen as low-energy states from Monte Carlo simulations across the LiF–MnO–Li2/3V1/3O space. We then fitted a cluster expansion consisting of pair interactions up to 7.1 Å, triplet interactions up to 4.0 Å, and quadruplet interactions up to 4.0 Å based on a primitive rocksalt unit cell with a = 3 Å, where the interactions were taken as an offset from a baseline of formal charge electrostatics with a fitted dielectric constant.24 The effective cluster interactions and dielectric constant were obtained from a L1-regularized least-squares regression, with the regularization parameter chosen to minimize cross-validation error.25 The root-mean-squared error obtained by this procedure was below 5 meV per atom. Finally, we evaluated the internal energy of the system as a function of composition and temperature using canonical Monte Carlo simulations, and obtained the Gibbs free energy from heat capacity integration.5To parameterize the LiF–MnO–Li2/3V1/3O cluster expansion, we relied on energies obtained from density functional theory (DFT) using the Vienna ab-initio simulation package (VASP)26 and the projector-augmented wave (PAW) method.27 These calculations were performed using a reciprocal space discretization of 25 Å−1, and converged to 10−6 eV for total energy and 0.02 eV Å−1 for interatomic forces. We relied on the PBE exchange–correlation functional28 with the rotationally-averaged Hubbard U correction, where the U value was chosen based on a previously reported calibration to oxide formation energies (3.1 eV for V and 3.9 eV for Mn),29 which has been shown to be broadly reliable for determining the formation enthalpies of similar compounds.30
To simulate the delithition behavior of disordered-rocksalt Li–Mn–V–O–F, we first obtained a set of representative structures of the lithiated compound from a Monte Carlo simulation at the binodal temperature of the composition of interest. We then obtained low-energy Li-vacancy orderings within these structures by first enumerating all possible Li-vacancy orderings in a sample of small unit cells, and then parametrizing a Li-vacancy cluster expansion to obtain Li orderings in larger cells. To obtain the relative energies of possible Li-vacancy orderings at a fixed composition, we relied on the SCAN meta-GGA exchange–correlation functional31 as it yields reliable structure selection and lattice geometries.32,33 For computational efficiency, these initial calculations were performed using fixed unit cells obtained from the lithiated structure. The restriction that the unit cell shape remains constant is consistent with our experimental observation that delithiation preserves the rocksalt lattice. However, by fixing the unit cell volume during this initial enumeration we assume that the favored arrangement of Li and vacancies is not significantly affected by lattice contraction during delithiation. All other computational parameters were the same as those used for parametrizing the dense rocksalt cluster expansion. As the Li-vacancy cluster expansion was once again taken as an offset from a baseline of formal charge electrostatics, the various oxidation states of Mn, V and O were taken as distinct species, and identified in DFT calculations based on their magnetic moments. The final root-mean-square error of this cluster expansion was below 5 meV per atom.
Finally, to obtain reliable oxidation potentials for each sampled Li–Mn–V–O–F cell, we fully relaxed the most stable Li-vacancy ordering at each delithiation step using the hybrid HSE functional34 with an exact-exchange fraction of 0.30. We set the exact-exchange fraction to reproduce the band gaps of MnO, α-Mn3O4, and δ-MnO2 obtained from experiment or single-shot G0W0 calculations, following the method proposed by Seo et al.35 To keep computational expense within reasonable bounds, we reduced the reciprocal space discretization in these simulations to 10 Å−1. We then constructed the total Li voltage curve for a given composition of the Li–Mn–V–O–F disordered rocksalt by taking a grand-canonical ensemble of Li potentials within each of the sampled unit cells. This voltage curve also yields a large set of representative structures for all stages of delithiation. All structure analysis and post-processing were done using the pymatgen software package.36
Synthesis
All Li–Mn–V–O/Li–Mn–V–O–F compounds were synthesized by mechanochemical ball-milling. For Li1.143Mn0.286V0.572O2 (ST-LMVO) and Li1.2Mn0.2V0.6O2 (LR-LMVO), Li2O (Alfa Aesar, ACS, 99% min), MnO (Sigma-Aldrich, 99.99%), and VO2 (Sigma-Aldrich, 99.9%) were used as precursors and mixed in a stoichiometric ratio, with the exception of Li2O, which was added in 10% excess, in order to compensate for potential Li2O loss during synthesis as suggested by previous work on similar materials.18,21 Precursors were mixed with a Retsch PM 200 planetary ball mill at a rate of 300 rpm for 12 hours. The mixed precursors were ball-milled for 40 hours in argon-filled stainless steel ball-mill jars, using a Retsch PM 200 planetary ball mill at 500 rpm. For Li1.171Mn0.343V0.486O1.8F0.2 (ST-LMVF20), Li1.133Mn0.400V0.467O1.8F0.2 (MR-LMVF20) and Li1.23Mn0.255V0.515O1.8F0.2 (LR-LMVF20), Li2O (Alfa Aesar, ACS, 99% min), MnO (Sigma-Aldrich, 99.99%), VO2 (Sigma-Aldrich, 99.9%) and LiF (Alfa Aesar, 99.99%) precursors were stoichiometrically mixed, adding 10% excess Li2O, for 12 hours at 300 rpm and then ball-milled for 50 hours at 500 rpm, using a Retsch PM 200 planetary ball mill. The total amount of precursors was 1 g. The ball-milling process rested for 5 minutes after every hour. All syntheses used five 10 mm (diameter) stainless balls and ten 5 mm (diameter) balls as the grinding media.Electrochemistry
The cathode films were composed of active materials, carbon black (Timcal, SUPER C65), and polytetrafluoroethylene (PTFE, DuPont, Teflon 8A) with a weight ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The components were manually mixed for 40 minutes using a mortar and pestle and then rolled into a thin film inside an argon-filled glovebox. 1 M LiPF6 in ethylene carbonate (EC) and dimethyl carbonate (DMC) solution (volume ratio 1
1. The components were manually mixed for 40 minutes using a mortar and pestle and then rolled into a thin film inside an argon-filled glovebox. 1 M LiPF6 in ethylene carbonate (EC) and dimethyl carbonate (DMC) solution (volume ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was used as electrolyte. Glass microfiber filters (Whatman) were used as the separator and Li metal foil (FMC) was used as the anode material. Coin cells were assembled inside an argon-filled glovebox and tested on a Maccor 2200 or Arbin battery test work station at room temperature in the galvanostatic mode unless otherwise specified. The loading density of the film was ∼5 mg cm−2 based on active materials. The specific capacity was calculated based on the weight of active materials (70%) in the cathode films.
1) was used as electrolyte. Glass microfiber filters (Whatman) were used as the separator and Li metal foil (FMC) was used as the anode material. Coin cells were assembled inside an argon-filled glovebox and tested on a Maccor 2200 or Arbin battery test work station at room temperature in the galvanostatic mode unless otherwise specified. The loading density of the film was ∼5 mg cm−2 based on active materials. The specific capacity was calculated based on the weight of active materials (70%) in the cathode films.
Characterization
X-ray diffraction (XRD) patterns for the as-synthesized compounds were collected using a Rigaku MiniFlex diffractometer (Cu source) in a 2θ range of 5°–85°. Rietveld refinement was done using PANalytical X'pert HighScore Plus software. Elemental analysis was performed by Luvak Inc. with direct current plasma emission spectroscopy (ASTM E 1079-12) for lithium, manganese, vanadium and with an ion selective electrode (ASTM D 1179-10) for fluorine. Scanning electron microscopy (SEM) images were collected using a JEOL JSM-6340F field emission scanning electron microscope. Scanning transmission electron microscopy (STEM)/energy dispersive spectroscopy (EDS) measurements were acquired from a part of the particles using a JEM-2010F with an X-max EDS detector in the Molecular Foundry at LBNL.Solid-state nuclear magnetic resonance (NMR) spectroscopy
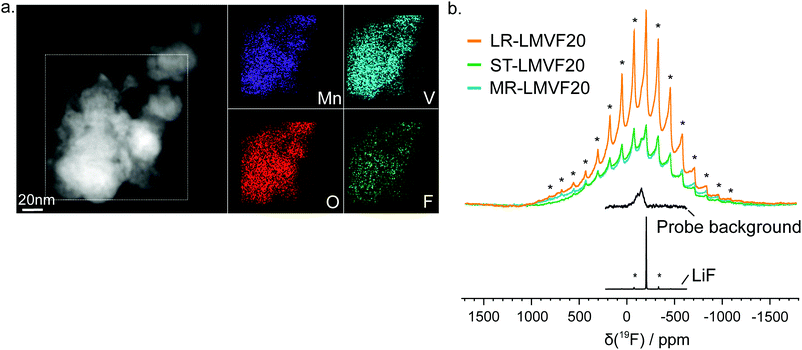
19F NMR data were acquired for the as-synthesized ST-, MR- and LR-LMVF20 powder samples at room temperature using a Bruker Avance500 WB spectrometer (11.7 T), at a Larmor frequency of −470.7 MHz. The data were obtained under 60 kHz magic angle spinning (MAS) using a 1.3 mm double-resonance probe, and chemical shifts were referenced against lithium fluoride powder (LiF, δiso(19F) = −204 ppm).Because the resonant frequency range of the 19F nuclei in the as-synthesized cathodes is larger than the excitation bandwidth of the radio frequency (RF) pulse used in the NMR experiment, seven spin echo spectra were collected for each sample, with the irradiation frequency varied in steps equal to the excitation bandwidth of the RF pulse (330 ppm or 155 kHz) from −1230 to 750 ppm. The individual sub-spectra were processed using a zero order phase correction so that the on-resonance signal was in the absorption mode. The seven sub-spectra were then added to give an overall sum spectrum with no further phase correction required. This method, termed ‘spin echo mapping’,37 ‘frequency stepping’38,39 or ‘VOCS’ (Variable Offset Cumulative Spectrum),40 is required to provide a large excitation bandwidth and uniformly excite the broad F signals. Individual 19F spin echo spectra were collected using a 90° RF excitation pulse of 1.6 μs and a 180° RF pulse of 3.2 μs at 76.3 W (or 156 kHz), with a recycle delay of 0.05 s. For comparison, a spin echo spectrum was collected for LiF using similar RF pulses but a longer recycle delay of 60 s. A 19F probe background spin echo spectrum, acquired under the same conditions as the individual LMVF20 spin echo spectra but with an empty rotor, revealed the presence of a low intensity background signal.
Ex situ hard X-ray absorption spectroscopy
Ex situ hard XAS measurements were performed in transmission mode using beamline 20BM at the Advanced Photon Source. The incident energy was selected using a Si(111) monochromator. The energy calibration was performed by simultaneously measuring the spectra of the appropriate metal foil. Harmonic rejection was accomplished using a Rh-coated mirror. All ex situ samples were electrode films, composed of active materials, carbon black and PTFE with a weight ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and a loading density of ∼5 mg cm−2 based on active materials. Ex situ charged samples were assembled as coin cells, charged to designated capacities at a rate of 10 mA g−1, then disassembled and washed with DMC for 5 minutes in an argon-filled glovebox. Kapton film was used to cover both sides of the samples. The pristine sample was not washed, but directly covered with Kapton film after being rolled into a thin film. Spectra of reference standards were also acquired to facilitate interpretation. Raw data was normalized and calibrated using Athena software.41
1 and a loading density of ∼5 mg cm−2 based on active materials. Ex situ charged samples were assembled as coin cells, charged to designated capacities at a rate of 10 mA g−1, then disassembled and washed with DMC for 5 minutes in an argon-filled glovebox. Kapton film was used to cover both sides of the samples. The pristine sample was not washed, but directly covered with Kapton film after being rolled into a thin film. Spectra of reference standards were also acquired to facilitate interpretation. Raw data was normalized and calibrated using Athena software.41
Ex situ soft X-ray absorption spectroscopy
O K-edge spectra were acquired from soft XAS measurements, performed in the iRIXS endstation at beamline 8.0.1 of the Advanced Light Source (ALS) at Lawrence Berkeley National Lab (LBNL).42 The experimental energy resolution is better than 0.15 eV without considering core–hole lifetime broadening. Experiments were performed at room temperature and with the linear polarization of the incident beam at 45° from the electrode surfaces. All spectra were normalized to the beam flux measured by the upstream gold mesh and calibrated based on a TiO2 (anatase) standard. All ex situ samples were electrode films, composed of active materials, carbon black and PTFE with a weight ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and a loading density of ∼4 mg cm−2 based on active materials. The pristine sample did not go through other treatments (e.g. washing) after being rolled into a thin film. The ex situ charged samples were marked front side and back side, assembled into coin cells with the front side facing the separator, charged to designated capacities at 10 mA g−1, and finally disassembled and washed with DMC in an argon-filled glovebox for 5 minutes, in order to wash away surface species deposited during charge and increase the signal quality. All samples were loaded into an in-house manufactured sample transfer kit in a glovebox, which was then directly mounted onto the ultra-high vacuum XAS characterization chamber to avoid any air exposure.43 XAS spectra were collected simultaneously through both TEY mode and TFY mode with the excitation X-ray beam hitting the same spot on the front side of the films.
1, and a loading density of ∼4 mg cm−2 based on active materials. The pristine sample did not go through other treatments (e.g. washing) after being rolled into a thin film. The ex situ charged samples were marked front side and back side, assembled into coin cells with the front side facing the separator, charged to designated capacities at 10 mA g−1, and finally disassembled and washed with DMC in an argon-filled glovebox for 5 minutes, in order to wash away surface species deposited during charge and increase the signal quality. All samples were loaded into an in-house manufactured sample transfer kit in a glovebox, which was then directly mounted onto the ultra-high vacuum XAS characterization chamber to avoid any air exposure.43 XAS spectra were collected simultaneously through both TEY mode and TFY mode with the excitation X-ray beam hitting the same spot on the front side of the films.
Differential electrochemical mass spectrometery (DEMS)
The custom-built DEMS and the cell geometry used here are described in previous publications.44–46 The electrochemical cells used with the DEMS device were prepared in an argon-filled glove box using a modified Swagelok design. The cathode film was composed of active materials, carbon black and PTFE with a weight ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and a loading density of ∼6 mg cm−2 based on active materials. A static head of positive argon pressure (∼1.2 bar) was applied to the assembled cells during charging at 20 mA g−1, and argon gas pulses periodically swept the accumulated gases to a mass spectrometer. The mass spectrometer absolute sensitivity was calibrated for the determination of the partial pressures of CO2 and O2. The amount of CO2 and O2 evolved was quantified using the partial pressures and the known volume of gas swept to the mass spectrometer per pulse.
1 and a loading density of ∼6 mg cm−2 based on active materials. A static head of positive argon pressure (∼1.2 bar) was applied to the assembled cells during charging at 20 mA g−1, and argon gas pulses periodically swept the accumulated gases to a mass spectrometer. The mass spectrometer absolute sensitivity was calibrated for the determination of the partial pressures of CO2 and O2. The amount of CO2 and O2 evolved was quantified using the partial pressures and the known volume of gas swept to the mass spectrometer per pulse.
Results and discussion
Synthetic accessibility
In order to identify synthetically accessible compositions of disordered rocksalt consisting of a mixture of Li+, Mn2+, V4+, O2− and F−, we compute a phase diagram of the MnO/Li2VO3/LiF system. As the mixing of the transition metals and incorporation of fluorine into the structure depend on a delicate balance of entropy and enthalpy arising from the coupling between the cation and anion sublattices, a finite-temperature analysis is necessary to identify compositions exhibiting sufficiently low enthalpy and high entropy at experimentally-relevant temperatures to be synthesizable. For this analysis, we evaluate the thermodynamics of this system using configurational Monte Carlo simulations, based on a cluster expansion Hamiltonian parametrized on the basis of first-principles density functional theory (DFT) calculations.5,24,25The phase diagram of the disordered rocksalt system, shown in Fig. 1a, gives the extent of the binodal region starting from the MnO and Li2/3V1/3O (Li2VO3) endpoints as a function of temperature, illustrating the range of mixed compositions which are thermodynamically stable at the given temperature. For example, the contour labeled 1250 °C indicates that at 1250 °C, the Li2/3V1/3O phase can accommodate up to 18% MnO or 30% LiF, while the MnO phase can accommodate 25% Li2/3V1/3O and 3% LiF. Similarly, the 1500 °C contour indicates that at this temperature, Li2/3V1/3O and MnO are fully miscible, but still have a limited solubility for LiF that increases with the Li2/3V1/3O fraction. As our goal is evaluating the relative stability of competing rocksalt-type phases, we neglect high-temperature gas evolution and melting, which limits the general applicability of this phase diagram. An important further assumption in the construction of this phase diagram is the metastability of the Li2V4+O3 (Li2/3V1/3O) endpoint phase, which has been previously reported to form as a disordered-rocksalt upon electrochemical cycling.47 While we find this phase to be globally metastable against phase separation into LiV3+O2 and Li3V5+O4, the formation of Li3V5+O4 requires the formation of a wurtzite-type lattice. We assume this transformation to be suppressed by ball-milling induced disorder in the otherwise rocksalt-type lattice, by analogy to the stabilization of V4+ in the disordered-rocksalt Li3V23+,4+O5 compound.7
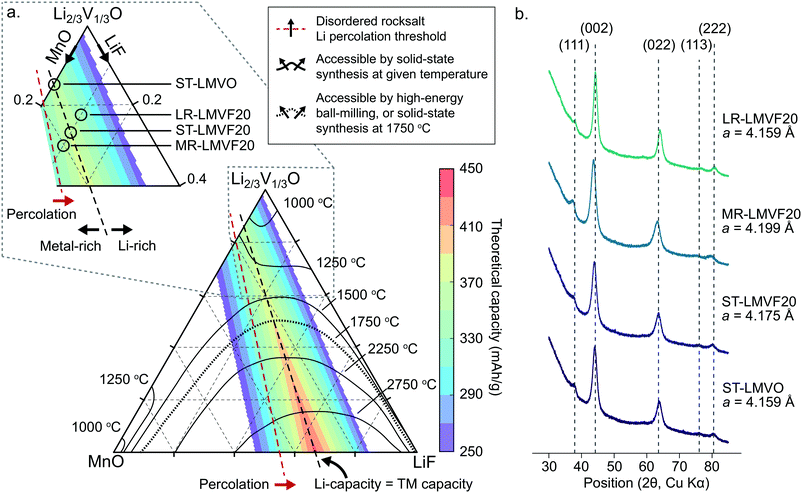 | ||
| Fig. 1 Thermodynamic stability and synthesis of mixed Mn2+/V4+ disordered rocksalt oxyfluorides. (a) Computed phase diagram of the MnO/Li2VO3/LiF alloy space. The temperature-marked contours denote the extent of the binodal, starting from the MnO and Li2VO3 endpoints, at the given temperature. The color-coded overlay plots the theoretical gravimetric capacity of compositions across the phase diagram based on Li and transition metal redox content. The percolation threshold marks compositions exceeding the 10% Li-excess requirement.2 The inset illustrates the region of the phase diagram we focus on to synthesize the stoichiometric, transition metal-rich, and Li-rich compositions. (b) XRD profiles and refined lattice parameters of the synthesized disordered rocksalt compounds. | ||
The finite temperature stability given by the phase diagram in Fig. 1a is informative for identifying compositions accessible by both high-temperature solid-state synthesis, and by high-energy ball-milling. In the case of high-temperature annealing, the synthesis proceeds at near-thermodynamic conditions, suggesting that any composition stable at the annealing temperature could be formed and then quenched to obtain a disordered metastable product.48 For example, firing at 1250 °C could yield Li2/3V1/3O doped with up to 18% MnO and 10% LiF, yielding a Li1.16Mn0.36V0.48O1.8F0.2 disordered rocksalt. In the case of high-energy ball-milling, the relationship between the phase diagram and synthetic accessibility is less clear. While some arguments have been made that mechanochemical synthesis proceeds due to local heating or shear-induced reactions,49,50 no definitive mechanism is known for predicting such synthesis outcomes from thermodynamic quantities. In the absence of a rigorous mechanism to evaluate, we determined the 1750 °C binodal as a heuristic boundary for synthetic accessibility by high-energy ball-milling, where the 1750 °C temperature is based on calibration to reported synthesis successes in similar Mn2+-containing disordered rocksalt oxyfluorides,21 as shown in ESI,† Fig. S1.
Electrochemical design and performance
To evaluate the approximate electrochemical performance of this system, we plot the theoretical capacity of possible compositions in this chemical space, given as a color-coded overlay in Fig. 1a. The given theoretical capacity assumes that the Mn2+/4+ and V4+/5+ redox couples are fully accessible, unless limited by the Li content in the structure. We do not include possible oxygen redox due to the reported difficulties in achieving reversible cathode performance when oxygen oxidation is activated.8,22,23 Within these assumptions, compositions that perfectly balance transition metal and Li capacity are optimal, with higher fluorination levels providing the greatest specific capacity, as can be observed in Fig. 1. Among the synthetically-accessible oxyfluorides, and even in the mixed-metal oxide without F, the theoretical capacity is above 360 mA h g−1 due to the high content of light, redox-active transition metals, motivating an in-depth study of these compounds and their realizable electrochemical performance.To investigate whether the high capacity of these materials can be experimentally realized, we synthesize Li1.143Mn0.286V0.572O2 (ST-LMVO) and Li1.171Mn0.343V0.486O1.8F0.2 (ST-LMVF20) as representative compounds stoichiometrically balancing Li and transition metal capacity, as well as Li1.133Mn0.400V0.467O1.8F0.2 (MR-LMVF20) and Li1.23Mn0.255V0.515O1.8F0.2 (LR-LMVF20) metal-rich and Li-rich variants, respectively. We choose to focus on these relatively low-fluorine content compositions as they are predicted to be more likely synthesizable than their highly-fluorinated counterparts, while providing only slightly lower theoretical capacities as is clear from Fig. 1a. We successfully synthesize all four compounds by high-energy ball-milling in an argon atmosphere. We confirm their disordered rocksalt structure by X-ray diffraction (XRD) as shown in Fig. 1b, and their composition by inductively coupled plasma optical emission spectrometry (ICP-OES) (see ESI,† Table S1). The secondary particle size of the as-synthesized compounds is 100–200 nm and the primary particle size is 20–50 nm as indicated by scanning electron microscopy (SEM) and transmission electron microscopy (TEM), respectively. Detailed XRD refinement, as well as SEM and TEM characterization data are available in ESI,† Fig. S2 and S3.
A important question in the characterization of the as-synthesized compounds is the degree to which fluorine is incorporated into the bulk of the material. XRD patterns for all LMVF20 materials, shown in Fig. 1b and ESI,† Fig. S2, indicate the absence of a crystalline LiF impurity phase, and TEM-EDS mapping, shown in Fig. 2a, suggests that fluorine is homogeneously distributed in the sample. However, previous studies have demonstrated that, at least in stoichiometric layered oxide cathodes, LiF may form electrochemically inactive coatings.51,52 We rely on 19F solid-state nuclear magnetic resonance spectroscopy (ssNMR) to confirm that, in our case, the fluorine is not segregated. The 19F NMR spectra collected for ST-LMVF20, MR-LMVF20 and LR-LMVF20, shown in Fig. 2b, differ significantly from the spectrum of the LiF reference, revealing a number of broad, overlapping signals shifted away from the resonance frequency of LiF at −204 ppm. As discussed in our recent 19F NMR study on the paramagnetic Li1.15Ni0.45Ti0.3Mo0.1O1.85F0.15 cathode, these broad signals result from short-range (<5 Å) paramagnetic (or hyperfine) interactions between unpaired d electrons on Mn or V and the F nucleus, consistent with the bulk incorporation of F into the disordered rocksalt phase.6 In addition, some of our ongoing work on related paramagnetic cation-disordered oxyfluorides indicates that observable paramagnetic 19F NMR signals can be assigned to F nuclei surrounded by 6 Li in their first coordination shell, with paramagnetic species (here Mn and V) in their second and/or third metal coordination shells (see ESI,† Fig. S2a in Lee et al.6 for a schematic diagram of coordination shells). When F is directly bonded to Mn or V, the paramagnetic interactions are so strong that the resulting signals are too broad to be observed and are lost in the background noise. Hence, the relatively weak 19F signal obtained for all three LMVF20 compounds suggests that a significant fraction of the F is bonded to at least one transition metal, consistent with the predicted fluorination behavior of disordered rocksalt materials.5 These invisible paramagnetic F sites prevent us from quantifying the fraction of F in LiF-like domains or particles in the pristine cathode samples, evidenced by the LiF-like signals (centered at −204 ppm) present in all the spectra. Nevertheless, the present data indicate that the as-synthesized materials have the great majority of their fluorine incorporated into the bulk of their particles.
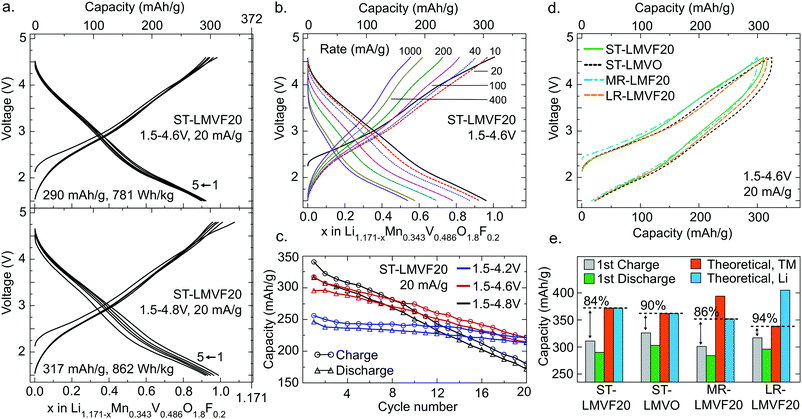
The electrochemical performance of the four compounds in a galvanostatic regime is shown in Fig. 3 for a range of voltage windows and cycling rates. Fig. 3a shows that ST-LMVF20 achieves 290 mA h g−1 (781 W h kg−1) on the first discharge within a voltage window of 1.5–4.6 V, and 317 mA h g−1 (862 W h kg−1) within 1.5–4.8 V, with good rate performance as evidenced in Fig. 3b. The capacity retention shown in Fig. 3c for ST-LMVF20 cycled between 1.5 V and 4.2 V, 4.6 V, or 4.8 V reveals generally reversible performance, especially when the charge is limited to 4.2 V. Analogous to the performance of previously-reported Mn2+/4+-based compounds,21 the second charge voltage curve is similar to subsequent charges, with minimal changes to the voltage profile after the first discharge, indicating highly reversible performance. The three remaining compounds perform similarly, with the first-cycle discharge from 4.6 V yielding 303 mA h g−1 (799 W h kg−1) for ST-LMVO, 284 mA h g−1 (746 W h kg−1) for MR-LMVF20, and 296 mA h g−1 (786 W h kg−1) for LR-LMVF20. The four compounds also have similar voltage profiles, as shown in Fig. 3d, despite variations in the composition and theoretical capacity (see ESI,† Fig. S4 for complete electrochemical data). Nonetheless, while all four compounds yield high reversible capacity and energy density, their capacities are somewhat below theoretical.
The difference between the observed and theoretical capacities of the four compounds, tabulated in Fig. 3e, lends insight to some of the mechanisms limiting performance. In this analysis, the Li theoretical capacity is based on the Li content of each composition, while the transition metal (TM) theoretical capacity is based on the total capacity of the Mn2+/4+ and V4+/5+ couples. While the first-charge Coulombic efficiency is similar in all four cases, the fraction of theoretical capacity achieved on the first-charge depends strongly on the Li content and the fluorination level. Fluorination increases both Li and transition metal theoretical capacity from ST-LMVO to ST-LMVF20, but a smaller fraction of this capacity can be obtained on the first-charge. Increasing the transition metal content in ST-LMVF20 to obtain MR-LMVF20 lowers the theoretical capacity and leaves the fraction of theoretical capacity obtained unchanged, suggesting that the capacity is not limited by the accessibility of transition metal redox couples. High-temperature galvanostatic cycling of ST-LMVF20 within the same 1.5–4.6 V voltage window, shown in ESI,† Fig. S5, does not yield an increase in long-term reversible capacity or a decrease in polarization, suggesting that the performance is not limited by Li transport kinetics. However, moving to the LR-LMVF20 Li-rich composition brings the observed capacity much closer to the theoretical value. Put together, these trends indicate that the limit on the performance of these compounds is not related to the accessibility of transition metal redox or kinetic features, leaving the distribution of Li site energies in the disordered compounds as the most probable explanation for the observed sub-theoretical capacity.
Redox mechanism
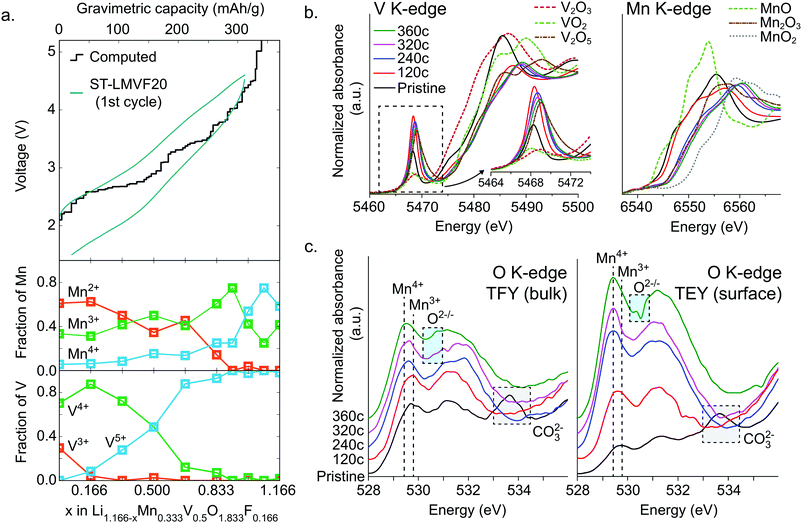
To resolve the oxidation mechanism of ST-LMVF20, we rely on a combination of density functional theory (DFT) and ex situ hard and soft X-ray absorption spectroscopy (XAS). The evolution of transition metal oxidation states, as computed from DFT, can be seen in Fig. 4a for Li1.166−xMn0.333V0.500O1.833F0.166, a composition representative of the ST-LMVF20 compound. The calculations suggest an initial mixed population of Mn2+, Mn3+, V3+ and V4+ due to partial charge transfer from Mn2+ to V4+, achieving a similar electronic configuration of V as seen in the classic disordered rocksalt Li3V2O5 compound.7 As Li is extracted from the structure from x = 0 to x = 0.166, the population of V3+ decreases rapidly while that of V4+ increases, indicating V3+/4+ oxidation. Between x = 0.166 and x = 0.666 the population of V5+ begins to increase at the expense of V4+, with minor changes in the Mn oxidation states, indicating that in this region V oxidation to V5+ provides the majority of electronic capacity, with minor contributions from Mn2+/3+ oxidation. Between x = 0.666 and x = 0.916, the population of Mn3+ rapidly increases at the expense of Mn2+, indicating the onset of dominant Mn2+/3+ oxidation, while from x = 0.916 to x = 1.08, Mn3+ begins to oxidize to Mn4+. However, the oxidation of Mn to Mn4+ does not go to completion. For 1.08 < x < 1.166 (V > 4.5 V), oxygen begins to be oxidized preferentially to Mn3+, indicating oxygen redox. The very top of the charge involves the extraction of Li from environments in which F is coordinated only by Li, resulting in a highly unstable charge configuration and a voltage above 6 V.The delithiation behavior of ST-LMVF20 as measured by ex situ hard and soft X-ray absorption spectroscopy (XAS) supports the oxidation mechanism obtained from DFT. We investigate the oxidation behavior during the first cycle, by studying samples obtained upon reaching 120 mA h g−1 (“120c”), 240 mA h g−1 (“240c”), 320 mA h g−1 (“320c”), and 360 mA h g−1 (“360c”) charge capacity at a rate of 10 mA h g−1, as well the as-synthesized material (“pristine”) as shown in ESI,† Fig. S6. Based on the X-ray absorption near edge structure (XANES) at the Mn K-edge and V K-edge shown in Fig. 4b, we confirm that both Mn and V in this compound are redox active with significant overlap between the redox couples, as indicated by their K-edge position in relation to binary standards.53,54 As the pristine material is charged to 120c, the V edge shifts from a position close to that of V4+, to one between V4+ and V5+, while the Mn edge moves slightly away from that of Mn2+, indicating dominant V oxidation with a small amount of Mn activity. Charging from 120c to 320c, corresponding to ∼4.6 V, the Mn K-edge moves beyond the position characteristic for Mn3+ to an intermediate oxidation state between Mn3+ and Mn4+, indicating that while Mn redox is activated at high voltage, Mn does not reach Mn4+ even at 4.6 V. In this segment of the charge, based on the V pre-edge in the 5467–5471 eV region, V continues to oxidize closer to V5+, consistent with dominant Mn oxidation with minor contribution from V. Upon further charging to 360c, both Mn and V are further oxidized towards Mn4+ and V5+ respectively, although we cannot quantitatively determine whether or not either transition metal reaches its maximal oxidation state in this generally irreversible region of the charge.
While hard X-ray spectra characterize the transition-metal redox mechanism, we rely on soft X-ray O-K XAS to directly study the corresponding oxygen state evolution. We acquire the O K-edge in the bulk-sensitive total fluorescence yield (TFY) and surface-sensitive total electron yield (TEY) modes at the same states of charge as in the hard X-ray characterization. We focus on the O pre-edge features below 535 eV, shown in Fig. 4c. In general, these features represent Mn/V-3d and O 2p orbital hybridization.55,56 The pristine material exhibits relatively low intensity in the Mn3+–O hybridization region near 530 eV, because Mn2+ does not contribute to the hybridization feature here.57 The broad peak near 534 eV indicates the presence of surface carbonate species,58 which are likely to form when the active materials are mixed with carbon black.21 We cannot see the evolution of the 534 eV feature in the ex situ charged samples because during the sample preparation, the surface carbonate species have been washed away.59 Upon charging, we observe an increasing intensity around 530 eV up to 320c, corresponding to continuous Mn3+ formation during the charging process. Additionally, between 120c and 320c, the weight of this hybridization feature shifts towards lower energy, 529.4 eV. Such a shift of O-K onset is one of the fingerprints of a finite amount of Mn4+ formation.57 This process largely stops in the 320c to 360c region, suggesting that Mn does not fully oxidize to Mn4+. Instead, this region sees the appearance of an intensity contribution between 530.5 and 531.0 eV, which sits in the valley of the expected hybridization features, and has been previously linked to oxygen oxidation.12,58 We note that the oxygen oxidation here is different from that recently discussed in the context of potentially reversible bulk oxygen redox in battery electrodes. Here, the oxygen oxidation peak is particularly pronounced in the surface-sensitive TEY probe of the 360c sample, suggesting that irreversible oxygen oxidation and potentially oxygen loss may be partially responsible for the irreversible capacity seen at high voltages and high states of charge. This conclusion is further supported by differential electrochemical mass spectroscopy (DEMS) for ST-LMVF20, shown in ESI,† Fig. S7, in which we observe a small amount of O2 gas evolution on charging over 4.6 V or 300 mA h g−1. Our DEMS results also reveal some CO2 evolution on the first charge originating from irreversible oxidation of surface carbonates, but as we discuss in the ESI,† the contribution of carbonates to the overall capacity is small.
The oxidation behavior of the Li–Mn–V–O–F compounds can generally be summarized by low-voltage V4+/5+ oxidation, with some potential contribution of V3+/4+ at the very beginning of the charge, followed by Mn2+/4+. There is however significant overlap between the Mn and V couples throughout the charge, and overlap between Mn redox and oxygen redox above 4.5 V. This redox mechanism confirms that both the V and Mn are redox-active, and fully account for the capacity obtained within the 1.5–4.6V voltage window shown in Fig. 3a. Thus, to explain the sub-theoretical capacity as a function of Li-content and fluorination, we must turn to the distribution of Li site energies.
Accessibility of Li on charging
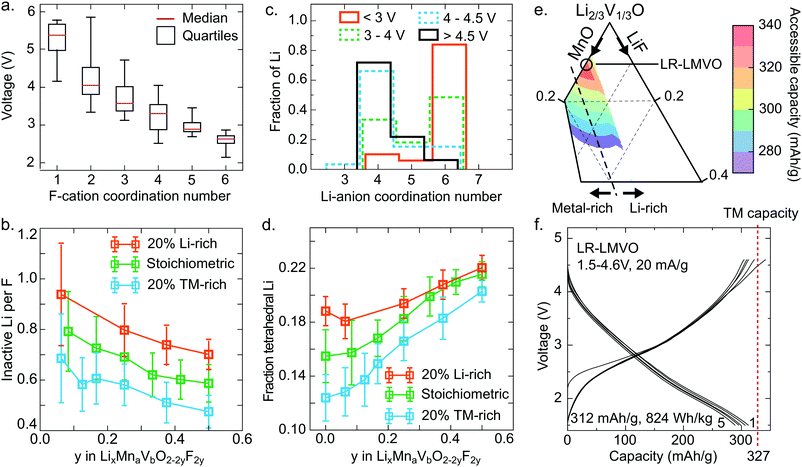
The Li site energy is determined by the local Li bonding environment. Any Li found in an environment with particularly low site energy, due to strong local bonding or instability upon delithiation, will require a high potential to be extracted. Thus the distribution of Li site energies describes the impact of structure on voltage, with a wide spread of local configurations and energies corresponding to an increase in voltage slope characteristic of disordered rocksalts.60 Here, we identify two mechanisms influencing this distribution in the high-voltage region – the presence of strong Li–F bonds, and the formation of high-voltage tetrahedral Li sites upon delithiation.As can be seen in Fig. 3e, comparing the pure oxide ST-LMVO to its fluorine doped counterpart ST-LMVF20, fluorine doping increases the fraction of Li made inaccessible on charging to 4.6 V, which we pick as a representative cutoff voltage for fairly reversible behavior on the basis of capacity fade data, shown in Fig. 3c. Fluorine doping introduces strong F–Li bonds, which are expected to lower the site energies of Li directly bonded to F. The impact of this effect on voltage can be seen in Fig. 5a, which plots the voltage range over which various F environments, characterized by their F-cation coordination number, appear within our computed, partially delithiated structures derived from ST-LMVF20. Environments containing F with 1 nearest neighbor nearly always occur above 4.6 V, indicating that for 75% of fluorine sites, the delithiation of a fluorine environment down to 1 remaining nearest neighbor cation (1 Li or transition metal, and 5 vacancies) will require more than 4.6 V. F is incorporated into disordered rocksalts at locally Li-rich sites, minimizing the number of high-energy metal–F bonds, while maintaining a sufficiently high entropy to stabilize the dopant in the structure.5 This short-range order implies that upon delithiation, certain fluorine atoms will become highly undercoordinated and strongly bind the remaining Li around them. Indeed, we compute that in ST-LMVF20, MR-LMVF20, and LR-LMVF20, a majority of fluorines have 5 Li nearest neighbors, with a minority of F with four or six Li nearest neighbors. As no F environments with zero Li or metal nearest neighbors can be created at a reasonable charge voltage, the distribution shown in Fig. 5a indicates that any F environment initially 6-fold coordinated by Li on average retains 1.75 Li, and any F environment with 5 Li nearest neighbors on average retains 0.75 Li, making these Li inaccessible at 4.6 V.
These findings on Li-binding by fluorine indicate a significant Li-gettering effect introduced by F doping across all Li–Mn–V–O–F oxyfluoride compositions. To more quantitatively analyze the impact of this effect on achievable capacity, we simulate fully discharged structures at their binodal temperatures, corresponding to the lowest temperature where these compositions are stable against phase separation. Based on the distribution of Li and F in these compounds, and the F–Li binding rules derived above, we obtain the quantity of Li made electrochemically inaccessible at 4.6 V by each F dopant. These results are shown in Fig. 5b as a function of fluorination level and the ratio of Li capacity to transition metal capacity. In all cases, fluorine doping Li-rich compounds leads to the largest fraction of Li-binding by F, with more than 0.8 Li made inaccessible by each F. At lower Li capacities, a smaller fraction of Li is rendered inactive, but at least 0.4 Li per F are bound in all cases. This trend is consistent with the relatively stronger 19F-NMR signal obtained for the Li-rich compound, indicating a greater fraction of F with 6 nearest-neighbor Li in LR-LMVF20, as compared to ST- and MR-LMVF20. The increase in Li-gettering by F at higher Li-excess levels indicates that fluorine doping may not increase Li capacity within a given voltage window even in the case where fluorine incorporates into the bulk lattice, even though fluorination is beneficial for other properties such as stability on cycling and obtainable metal-redox capacity.5,6,21 Thus, in broad terms, in a disordered rocksalt oxyfluoride material, one may expect a reduction in accessible Li capacity equal to 0.4–0.8 Li per F in the discharged cathode material.
While the effect of F in limiting delithiation explains the trend in accessible capacity between ST-LMVO and ST-LMVF20, it cannot explain the sub-theoretical capacity of ST-LMVO, where no F is present, or LR-LMVF20, where there is sufficient Li-excess even accounting for F–Li binding. One additional description of the Li site energy distribution is the Li-anion coordination number, shown in Fig. 5c as a function of voltage for computed structures obtained from the delithiation of ST-LMVF20. The distribution of Li-anion coordination numbers reveals a significant population of tetrahedral Li environments forming above 4 V, with nearly all Li remaining in the structure above 4.5 V existing in a tetrahedral environment. The formation of tetrahedral Li is a structural relaxation which necessarily lowers the Li site energy. Indeed, tetrahedral Li has been previously correlated to a significant increase in extraction voltage.61,62 Directly assessing the voltage of tetrahedral Li from the data shown in Fig. 5c is not straightforward, as it is the extraction potential of tetrahedral Li that is of interest, rather than the voltage at which it initially forms. Nonetheless, the consistent increase in tetrahedral Li as a fraction of total Li remaining in the material up to 4.5 V indicates that tetrahedral Li is the least likely to be extracted, meaning it has the lowest Li site energy and highest extraction potential.
We compute the population of tetrahedral Li expected to form during charge for a range of Li–Mn–V–O–F compositions, shown in Fig. 5d. In this analysis, we assume that tetrahedral Li forms from an adjacent octahedral Li during delithiation when the tetrahedral site is surrounded by 3 cation vacancies. Thus, any Li-conductive “0-TM” channel may create a single tetrahedral Li upon charge.60 Based on the distribution shown in Fig. 5d, 16% of the Li in ST-LMVO could be expected to move to a tetrahedral site. As shown in Fig. 3e, 10% of Li in ST-LMVO is inaccessible up to 4.6 V, suggesting that approximately 60% of tetrahedral Li lies at a potential exceeding 4.6 V. Furthermore, as fluorine content increases, the total fraction of Li expected to move to a tetrahedral site increases, exacerbating the capacity loss due to tetrahedral Li. The origin of this trend is two-fold. First, fluorine-induced segregation of Li into Li-rich environments increases the population of “0-TM” channels susceptible to the tetrahedral transformation. Second, in the compositions mapped in Fig. 5b, higher fluorine content necessarily corresponds to a higher overall fraction of Li on the cation sublattice, further increasing the population of “0-TM” environments. Thus, as both Li-excess and LiF incorporation increase the fraction of tetrahedral Li, the limit on accessible Li capacity due to the formation of tetrahedral Li presents an important constraint for composition optimization. In broad terms, one may expect that the formation of tetrahedral Li will result in a 10–12% reduction in accessible Li capacity with respect to the total Li content of the discharged cathode.
The combined effects of F–Li-gettering and tetrahedral Li formation yield a new map of accessible charge capacities in the Li–Mn–V–O–F space, shown in Fig. 5e by analogy to Fig. 1a. The computed first-charge capacities for ST-LMVO, ST-LMVF20, MR-LMVF20, and LR-LMVF20 match closely to those observed experimentally. The phase diagram shown in Fig. 5e suggests that a new composition, Li1.2Mn0.2V0.6O2 (LR-LMVO), may exhibit high first-cycle capacity and fully realize its theoretical transition metal capacity. Synthesizing and electrochemically characterizing this compound, we confirm that LR-LMVO achieves 312 mA h g−1 (824 W h kg−1) within a 1.5–4.6 V voltage window with good reversibility similar to that of the other compounds described here, as can be seen in Fig. 5f in comparison to its theoretical transition metal capacity (327 mA h g−1). Detailed characterization and electrochemical data for this compound are available in the ESI.†
The mechanisms governing accessible Li capacity in the Li–Mn–V–O–F space derived here suggest general rules for the optimization of oxyfluoride disordered rocksalt cathodes. Fluorination is an efficient route for introducing Li-excess, which is necessary for both Li percolation in disordered rocksalts, and high Li capacity. Fluorine doping has also been reported to reduce oxygen loss, improve capacity retention,6 and increase transition metal oxidation potential through the inductive effect.21 As shown here, fluorine also increases the extraction voltage of Li by strongly binding some of the Li directly bonded to F. This trend rationalizes the behavior of previously reported oxyfluorides, with between 0.2 and 0.4 Li reported to be inaccessible at moderate voltages in Li2VO2F, even when starting from an as-synthesized VO2F endpoint.18,63 The formation of tetrahedral Li upon delithiation further affects the voltage profile of a disordered rocksalt by increasing the extraction potential of Li at high states of charge. The impact of fluorine and tetrahedral Li on the voltage profile are linked but can still be controlled independently, yielding several handles which can be used to engineer the energy density of a disordered rocksalt cathode.
Conclusion
In this work, we have introduced a set of design principles for high-capacity disordered rocksalt cathodes relying on only reversible transition-metal redox. By combining the active Mn2+/4+ and V4+/5+ couples, as well as fluorination, we have removed all redox-inactive metal species, maximizing the specific energy density granted by transition metal redox. We demonstrated the selection of optimized, synthetically-accessible compositions based on a computed, finite-temperature phase diagram of the oxyfluoride alloy system. Next, we solved the oxidation mechanism of the mixed Mn2+/V4+ system, confirming the compatibility and accessibility of these redox couples. Finally, we identified fundamental mechanisms determining the observable Li capacity within a given voltage window based on a gettering effect of fluorine dopants, and the formation of high-voltage tetrahedral Li from the delithiation of “0-TM” environments. From these mechanisms, we conclude that in a disordered rocksalt cathode material, 10–12% of the total Li present is inaccessible at moderate voltages due to the formation of tetrahedral Li, and in oxyfluorides, 0.4–0.8 Li per F is inaccessible due to strong Li–F binding. The design rules identified here for maximizing electronic and Li capacity provide novel constraints on high-performing disordered rocksalt compositions and enable a more targeted design and optimization of these types of cathodes.Author contributions
D. A. K., W. D. R. and G. C. planned the project. D. A. K. designed the proposed compounds and performed computational analysis with help from W. D. R., Z. L. synthesized, characterized (XRD), and electrochemically tested the proposed compounds with help from H. J. and J. L. R. J. C. acquired and analyzed NMR data. M. B. acquired and analyzed hard XAS data. D.-H. K. acquired and analyzed TEM data. K. D. and W. Y. performed soft-XAS measurements and analyzed data with D. A. K. and Z. L., J. K. P. and B. D. M. acquired and analyzed DEMS data. T. L. acquired SEM data. G. C. supervised all aspects of the research. The manuscript was written by D. A. K. and revised by Z. L., R. J. C. and G. C. with the help of all other authors. All authors contributed to the discussion.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the NSF Software Infrastructure for Sustained Innovation (SI2-SSI) Collaborative Research program of the National Science Foundation under Award No. OCI-1147503, the Robert Bosch Corporation and Umicore Specialty Oxides and Chemicals, and the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of Vehicle Technologies of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, Subcontract No. 7056411, under the Advanced Battery Materials Research (BMR) Program. The computational analysis was performed using computational resources sponsored by the Department of Energy's Office of Energy Efficiency and Renewable Energy and located at the National Renewable Energy Laboratory, as well computational resources provided by Extreme Science and Engineering Discovery Environment (XSEDE), which was supported by National Science Foundation grant number ACI-1053575. The authors would like to acknowledge Dr Jerry Hu and the California NanoSystems Institute (CNSI) at the University of California Santa Barbara (UCSB) for experimental time on the 500 MHz NMR spectrometer. The NMR experimental work reported here made use of the shared facilities of the UCSB MRSEC (NSF DMR 1720256), a member of the Material Research Facilities Network. This research used resources of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, and was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357. This research also used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.References
- S. M. Whittingham, Chem. Rev., 2004, 104, 4271–4302 CrossRef PubMed.
- J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Science, 2014, 343, 519–522 CrossRef PubMed.
- A. Urban, J. Lee and G. Ceder, Adv. Energy Mater., 2014, 4, 1400478 CrossRef.
- A. Urban, A. Abdellahi, S. Dacek, N. Artrith and G. Ceder, Phys. Rev. Lett., 2017, 119, 176402 CrossRef PubMed.
- W. D. Richards, S. T. Dacek, D. A. Kitchaev and G. Ceder, Adv. Energy Mater., 2018, 8, 1701533 CrossRef.
- J. Lee, J. K. Papp, R. J. Clément, S. Sallis, D.-H. Kwon, T. Shi, W. Yang, B. D. McCloskey and G. Ceder, Nat. Commun., 2017, 8, 981 CrossRef PubMed.
- C. Delmas, S. Brethes and M. Menetrier, J. Power Sources, 1991, 34, 113–118 CrossRef.
- J. Lee, D.-H. Seo, M. Balasubramanian, N. Twu, X. Li and G. Ceder, Energy Environ. Sci., 2015, 8, 3255–3265 Search PubMed.
- T. Matsuhara, Y. Tsuchiya, K. Yamanaka, K. Mitsuhara, T. Ohta and N. Yabuuchi, Electrochemistry, 2016, 84, 797–801 CrossRef.
- R. Wang, X. Li, L. Liu, J. Lee, D.-H. Seo, S.-H. Bo, A. Urban and G. Ceder, Electrochem. Commun., 2015, 60, 70–73 CrossRef.
- N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki, T. Inamasu, K. Sato and S. Komaba, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650–7655 CrossRef PubMed.
- N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 13814 CrossRef PubMed.
- S. Hoshino, A. M. Glushenkov, S. Ichikawa, T. Ozaki, T. Inamasu and N. Yabuuchi, ACS Energy Lett., 2017, 2, 733–738 CrossRef.
- M. Nakajima and N. Yabuuchi, Chem. Mater., 2017, 29, 6927–6935 CrossRef.
- N. Twu, X. Li, A. Urban, M. Balasubramanian, J. Lee, L. Liu and G. Ceder, Nano Lett., 2014, 15, 596–602 CrossRef PubMed.
- S. L. Glazier, J. Li, J. Zhou, T. Bond and J. R. Dahn, Chem. Mater., 2015, 27, 7751–7756 CrossRef.
- A. Kitajou, K. Tanaka, H. Miki, H. Koga, T. Okajima and S. Okada, Electrochemistry, 2016, 84, 597–600 CrossRef.
- R. Chen, S. Ren, M. Knapp, D. Wang, R. Witter, M. Fichtner and H. Hahn, Adv. Energy Mater., 2015, 5, 1401814 CrossRef.
- R. Chen, S. Ren, X. Mu, E. Maawad, S. Zander, R. Hempelmann and H. Hahn, ChemElectroChem, 2016, 3, 892–895 CrossRef.
- N. Takeda, S. Hoshino, L. Xie, S. Chen, I. Ikeuchi, R. Natsui, K. Nakura and N. Yabuuchi, J. Power Sources, 2017, 367, 122–129 CrossRef.
- J. Lee, D. A. Kitchaev, D.-H. Kwon, C.-W. Lee, J. K. Papp, Y.-S. Liu, Z. Lun, R. J. Clément, T. Shi, B. D. McCloskey, J. Guo, M. Balasubramanian and G. Ceder, Nature, 2018, 556, 185 CrossRef PubMed.
- A. R. Armstrong, M. Holzapfel, P. Novák, C. S. Johnson, S.-H. Kang, M. M. Thackeray and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 8694–8698 CrossRef PubMed.
- S. Hy, H. Liu, M. Zhang, D. Qian, B.-J. Hwang and Y. S. Meng, Energy Environ. Sci., 2016, 9, 1931–1954 Search PubMed.
- W. D. Richards, Y. Wang, L. J. Miara, J. C. Kim and G. Ceder, Energy Environ. Sci., 2016, 9, 3272–3278 Search PubMed.
- L. J. Nelson, G. L. W. Hart, F. Zhou and V. Ozolinš, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035125 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115 CrossRef.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- D. A. Kitchaev, H. Peng, Y. Liu, J. Sun, J. P. Perdew and G. Ceder, Phys. Rev. B, 2016, 93, 045132 CrossRef.
- Y. Zhang, D. A. Kitchaev, J. Yang, T. Chen, S. T. Dacek, R. A. Sarmiento-Pérez, M. A. Marques, H. Peng, G. Ceder, J. P. Perdew and J. Sun, npj Comput. Mater., 2018, 4, 9 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef.
- D.-H. Seo, A. Urban and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115118 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef.
- M. T. Sananes, A. Tuel, J. C. Volta and G. J. Hutchings, J. Catal., 1994, 148, 395–398 CrossRef.
- L. A. O'Dell, A. J. Rossini and R. W. Schurko, Chem. Phys. Lett., 2009, 468, 330–335 CrossRef.
- A. J. Pell, R. J. Clément, C. P. Grey, L. Emsley and G. Pintacuda, J. Chem. Phys., 2013, 138, 114201 CrossRef PubMed.
- D. Massiot, I. Farnan, N. Gautier, D. Trumeau, A. Trokiner and J. P. Coutures, Solid State Nucl. Magn. Reson., 1995, 4, 241–248 CrossRef PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef PubMed.
- R. Qiao, et al. , Rev. Sci. Instrum., 2017, 88, 033106 CrossRef PubMed.
- W. Yang, X. Liu, R. Qiao, P. Olalde-Velasco, J. D. Spear, L. Roseguo, J. X. Pepper, J. D. Denlinger and Z. Hussain, J. Electron Spectrosc. Relat. Phenom., 2013, 190, 64–74 CrossRef.
- B. D. McCloskey, D. S. Bethune, R. M. Shelby, G. Girishkumar and A. C. Luntz, J. Phys. Chem. Lett., 2011, 2, 1161–1166 CrossRef PubMed.
- B. D. McCloskey, R. Scheffler, A. Speidel, D. S. Bethune, R. M. Shelby and A. C. Luntz, J. Am. Chem. Soc., 2011, 133, 18038–18041 CrossRef PubMed.
- B. D. McCloskey, A. Speidel, R. Scheffler, D. C. Miller, V. Viswanathan, J. S. Hummelshøj, J. K. Nørskov and A. C. Luntz, J. Phys. Chem. Lett., 2012, 3, 997–1001 CrossRef PubMed.
- V. Pralong, V. Gopal, V. Caignaert, V. Duffort and B. Raveau, Chem. Mater., 2011, 24, 12–14 CrossRef.
- D. A. Kitchaev and G. Ceder, Nat. Commun., 2016, 7, 13799 CrossRef PubMed.
- H. J. Fecht, E. Hellstern, Z. Fu and W. L. Johnson, Metall. Mater. Trans. A, 1990, 21, 2333–2337 CrossRef.
- J.-J. Kim, Y. Choi, S. Suresh and A. Argon, Science, 2002, 295, 654–657 Search PubMed.
- M. Ménétrier, J. Bains, L. Croguennec, A. Flambard, E. Bekaert, C. Jordy, P. Biensan and C. Delmas, J. Solid State Chem., 2008, 181, 3303–3307 CrossRef.
- L. Croguennec, J. Bains, M. Ménétrier, A. Flambard, E. Bekaert, C. Jordy, P. Biensan and C. Delmas, J. Electrochem. Soc., 2009, 156, A349–A355 CrossRef.
- J. Wong, F. W. Lytle, R. P. Messmer and D. H. Maylotte, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 5596 CrossRef.
- A. Manceau, M. A. Marcus and S. Grangeon, Am. Mineral., 2012, 97, 816–827 CrossRef.
- F. M. F. De Groot, M. Grioni, J. C. Fuggle, J. Ghijsen, G. A. Sawatzky and H. Petersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 5715 CrossRef.
- H. Kurata, E. Lefevre, C. Colliex and R. Brydson, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13763 CrossRef.
- R. Qiao, T. Chin, S. J. Harris, S. Yan and W. Yang, Curr. Appl. Phys., 2013, 13, 544–548 CrossRef.
- R. Qiao, Y.-D. Chuang, S. Yan and W. Yang, PLoS One, 2012, 7, e49182 Search PubMed.
- S. E. Renfrew and B. D. McCloskey, J. Am. Chem. Soc., 2017, 139, 17853–17860 CrossRef PubMed.
- A. Abdellahi, A. Urban, S. Dacek and G. Ceder, Chem. Mater., 2016, 28, 5373–5383 CrossRef.
- J. Bréger, Y. S. Meng, Y. Hinuma, S. Kumar, K. Kang, Y. Shao-Horn, G. Ceder and C. P. Grey, Chem. Mater., 2006, 18, 4768–4781 CrossRef.
- L. Croguennec and M. R. Palacin, J. Am. Chem. Soc., 2015, 137, 3140–3156 CrossRef PubMed.
- R. Chen, E. Maawad, M. Knapp, S. Ren, P. Beran, R. Witter and R. Hempelmann, RSC Adv., 2016, 6, 65112–65118 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee00816g |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2018 |