Design and understanding of encapsulated perovskite solar cells to withstand temperature cycling†
Rongrong
Cheacharoen
 a,
Nicholas
Rolston
a,
Nicholas
Rolston
 b,
Duncan
Harwood
c,
Kevin A.
Bush
a,
Reinhold H.
Dauskardt
b,
Duncan
Harwood
c,
Kevin A.
Bush
a,
Reinhold H.
Dauskardt
 a and
Michael D.
McGehee
a and
Michael D.
McGehee
 *a
*a
aDepartment of Materials Science and Engineering, Stanford University, Stanford, California 94305, USA. E-mail: mmcgehee@stanford.edu
bDepartment of Applied Physics, Stanford University, Stanford, California 94305, USA
cD2 Solar, San Jose, California 95131, USA
First published on 20th October 2017
Abstract
The performance of perovskite solar cells has rapidly increased above 22%, and their environmental stability is also progressing. However, the mismatch in thermal expansion coefficients and low fracture energy of layers in perovskite solar cells raise a concern as to whether devices can withstand mechanical stresses from temperature fluctuations. We measured the fracture energy of a perovskite film stack, which was shown to produce 23.6% efficiency when incorporated in a monolithic perovskite-silicon tandem. We found that the fracture energy increased by a factor of two after 250 standardized temperature cycles between −40 °C and 85 °C and a factor of four after laminating an encapsulant on top of the stack. In order to observe how the increased mechanical stability translated from film stacks to device performance and reliability, we carried out a comparative study of perovskite solar cells packaged between glass and two commonly used encapsulants with different elastic moduli. We demonstrated that solar cells encapsulated with a stiffer ionomer, Surlyn, severely decreased in performance with temperature cycling and delaminated. However, the solar cells encapsulated in softer ethylene vinyl acetate withstood temperature cycling and retained over 90% of their initial performance after 200 temperature cycles. This work demonstrates a need for an encapsulant with a low elastic modulus to enable mechanical stability and progress toward 25 year operating lifetime.
Broader contextHybrid organic–inorganic metal halide perovskite solar cells have rapidly increased in power conversion efficiency up to 22%. However, device stability must be improved to enable commercialization. Also, studies have raised concerns over the potential for delamination in service due to mismatches in thermal expansion coefficients and low fracture energies compared to other solar cell technologies. Despite these concerns, we previously demonstrated that perovskite solar cells exhibit remarkable environmental stability in damp heat and under full sunlight in operation. This work compares the fracture energy of perovskite solar cells before and after temperature cycling and with laminated encapsulants. Furthermore, we subjected encapsulated perovskite solar cells to the IEC 61646 standard test of 200 temperature cycles between −40 °C and 85 °C and observed no visible delamination and less than a 10% change in performance. Moreover, by performing fracture tests and comparing solar cells with two encapsulants varying in elastic modulus by a factor of 40, we developed a design principle to enable mechanical stability of perovskite solar cells. |
1. Introduction
Over the past five years, significant research has improved the power conversion efficiency (PCE) of single junction organic–inorganic metal halide perovskite solar cells from 12% to 22.1%.1 In addition, incorporating perovskite as a wide bandgap absorber on top of a silicon solar cell in a two-terminal tandem has increased the PCE to 23.6%.2 When perovskites were mechanically stacked in a four-terminal tandem on top of a silicon solar cell, the efficiency surpassed 26%.3 Perovskite solar cells can also be made on flexible substrates with 17.3% PCE4 and scaled up to 100 cm2 active area, showing potential for module-scale production, with 11.2% PCE.5 Moreover, environmental stability of perovskite solar cells has been demonstrated with proper packaging. With glass–glass encapsulation, the solar cells fully retained their performance after 1000 hours in 85 °C–85% RH, damp heat, environment.2 Also, with an ultraviolet light filter, the solar cells lasted a year in full sunlight under operating conditions.5 With a combination of high performance and promising preliminary results on stability,6 perovskite solar cells have become more commercially viable.Under outdoor operating conditions, solar modules experience a wide range of temperature fluctuations.7 The International Electrotechnical Commission (IEC) provides standard guidelines of accelerated tests to uncover any potential problems reducing operational lifetime and preventing modules from lasting 25 years in the field. One of the IEC 61646 thin film module reliability standards addressing temperature fluctuation in an accelerated version is the temperature cycling (TC) test. TC probes any delamination due to mismatch in thermal expansion coefficients as the module experiences 200 temperature cycles between −40 °C and 85 °C. Solar modules must not visually delaminate and performance must drop less than 10% to pass the test.8 TC tests have revealed a variety of failure modes in solar modules: micro crack formation in Si module,9 delamination,10 solder joint breakage,11 and junction box detachment.12 However, the guiding design principles to make perovskite solar cells mechanically stable remain to be explained.
A perovskite solar cell stack has multiple interfaces that could lead to mechanical failure during temperature cycling. Fig. S1 (ESI†) shows thermal expansion coefficients (TEC) according to literature13–19 of the perovskite solar cell stack that was used to make a 23.6% PCE tandem solar cell and passed the damp heat test. Large mismatches in TEC between adjacent materials could build up stress and lead to delamination during temperature cycling, which presents a direct path for moisture ingress to the solar cells. Fracture energy quantifies mechanical strength of a thin film stack to see which layer is the weakest and most prone to delamination.20 Fracture energy can be extracted from a double cantilever beam (DCB) measurement, which is a mechanical test that measures resistance to fracture when pulling apart a multilayer film bonded between two elastic substrates.21 Perovskites are more fragile than other solar cell materials regardless of device geometry,22 which means that it takes less energy to delaminate the perovskite when being strained by other layers due to mismatch in TEC.
For the water-sensitive perovskite6 to withstand condensation during temperature cycling and extreme environmental conditions in the field,23 it likely needs to be sealed hermetically with glass–glass encapsulation to minimize ingress of moisture and oxygen.24,25 Encapsulants need to be chosen carefully to be optically transparent, flexible enough to absorb any fluctuation in strain energy during temperature cycling, electrically insulating to mitigate potential induced degradation,26 to have a reasonably low water vapor transmission rate, and to not release by-products that would be harmful to the electrical contacts and solar cell absorber. Ethylene vinyl acetate (EVA) is the most commonly used encapsulant in the solar industry. However, it produces acetic acid,27 which releases sodium from soda lime glass in the presence of moisture and heat,28 and causes potential induced degradation.29 Ionomer-based Surlyn encapsulants have better electrical insulation and lower water vapor transmission (Table S1, ESI†). Fracture energies of EVA and Surlyn are at least three orders of magnitude higher than the perovskite.30 Integrating a deformable encapsulant on a perovskite device could enhance mechanical stability of the solar cells.
In this work, we studied perovskite solar cells with commonly used adjacent oxide transport layers, fullerene, and metal electrodes. Our device stack is identical to the one that produced 23.6% PCE when incorporated in tandem with a silicon solar cell. We used the double cantilever beam (DCB) method21 to compare fracture energies of perovskite film stacks before and after they went through temperature cycling and lamination. Furthermore, we compared performances of solar cells laminated with commonly used encapsulants, EVA and Surlyn, which have very different mechanical properties, as EVA has an elastic modulus of 10 MPa and Surlyn 394 MPa (Table S1, ESI†). We identified low elastic modulus of the encapsulant as a key parameter to enable mechanical stability of packaged perovskite solar cells.
2. Results and discussion
2.1 Fracture energy of perovskite solar cells before and after temperature cycling
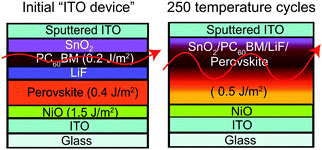
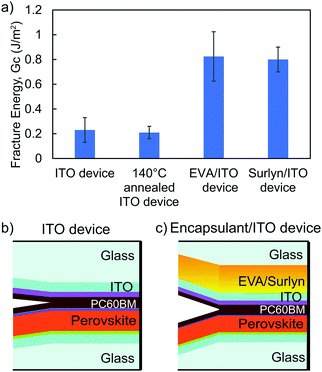
To quantitatively identify weak layers in the perovskite film stack, fracture energies were determined by the DCB method. Perovskite films and adjacent charge transport layers were deposited on glass microscope slides with an area of ∼10 cm2 for mechanical testing. By fracturing the unencapsulated perovskite film stacks, referred to as “ITO device”, with DCB and then measuring the fractured surfaces with XPS (Fig. S2, ESI†), we found PC60BM to be the weakest layer before thermal cycling, requiring only 0.2 J m−2 to delaminate (Fig. 1). After unencapsulated perovskite film stacks went through 250 temperature cycles, a change in color from brown to yellow (Fig. S3, ESI†) was observed, indicating degradation of perovskite into PbI2. The fracture energy increased to 0.5 J m−2. PC60BM likely diffused and strengthened the interface, as reported previously for organic solar cells.31 The root mean square (Rq) roughness of the fracture interface was investigated by atomic force microscopy (AFM) and found to increase from 26 nm to 75 nm after 250 temperature cycles in Fig. S4 (ESI†). XPS of the fracture surfaces after 250 temperature cycles in Fig. S5 (ESI†) shows a combination of SnO2, PC60BM, LiF, and perovskite at the interfacial front, indicating that the crack path propagated through more than just the PC60BM layer, which is shown by an arrow in Fig. 1.2.2 Improving mechanical integrity of perovskite solar cells using encapsulants
Encapsulation is a critical component of all solar modules for environmental and mechanical stability. Encapsulants were laminated on top of a perovskite film by pressing 650 mbar pressure on a sample that had been vacuumed and held at 140 °C for 20 minutes. The effect of encapsulation on perovskite mechanical integrity was studied by measuring the fracture energy of an identical perovskite film stack with laminated EVA or Surlyn on top. Despite the nature of the fragile unencapsulated perovskite device with a fracture energy of 0.2 J m−2 (Fig. 1), having either one of the encapsulants on top of perovskite film increased the fracture energy by a factor of four (Fig. 2a). In order to verify that the encapsulants directly contributed to this enhancement, the fracture energy of unencapsulated perovskite film stacks that underwent the same heat treatment as lamination was also measured. Previous work on organic solar cells showed fracture energy increase with annealing after device fabrication due to improved interfacial adhesion;32 however, the perovskite devices remained unchanged after the 140 °C heat treatment with a fracture energy of 0.21 J m−2 in Fig. 2a. Thus, the improvement in fracture energy for the perovskite device resulted from the encapsulant and not the heat treatment.Even with encapsulation, PC60BM was still the weakest layer. Fig. S6 (ESI†) shows that the representative fractured surfaces of all four conditions were consistent and uniform, which was verified by XPS in Fig. S7 (ESI†) to be PC60BM. Previous reports have shown that PC60BM is fragile and susceptible to fracture under applied loads.33 The encapsulants did not inherently strengthen the PC60BM, but their lower elastic moduli allows plastic deformation, where the material is irreversibly lengthened. The energy dissipated upon deformation of the encapsulants during mechanical testing could explain the increased fracture energy for the encapsulated perovskite film stack in Fig. 2. Fractured surfaces of film stacks with EVA and Surlyn encapsulants were slightly rougher with Rq of 68 nm and 51 nm in Fig. S8 (ESI†) compared to the unencapsulated film stack with Rq of 26 nm in Fig. S4a (ESI†). As previously described, the increased roughness after fracture indicates that the crack propagated across a larger thickness. In this case, the fracture path is still within the PC60BM layer, and the rougher fracture surface could result from encapsulant deformation during mechanical testing.
2.3 Temperature cycling of encapsulated perovskite solar cells
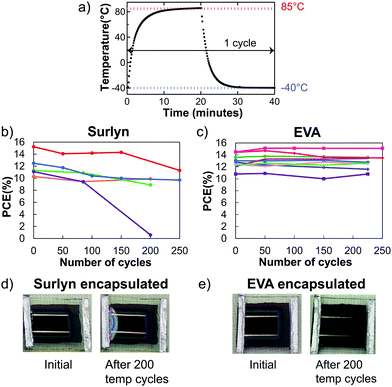
Perovskite solar cells laminated between glass with EVA or Surlyn and edge sealed with butyl rubber were subjected to at least 200 temperature cycles following the temperature profile in Fig. 3a. To investigate how the stiffness of an encapsulant affects device performance with temperature cycling, solar cells encapsulated in EVA and Surlyn were periodically compared. Packaged solar cells were loaded onto a tray that moved between two environmental chambers held at −40 and 85 °C, and they were periodically removed and measured with maximum power point tracking to obtain stabilized PCE values, as described in the Experimental section. Device performance was plotted as a function of temperature cycles in Fig. 3b and c. Unfortunately, only one out of five solar cells encapsulated in Surlyn retained 90% of their efficiency after 200 thermal cycles (Fig. 3b). Referring to the figures of merit for the Surlyn encapsulated solar cells in Fig. S9 (ESI†), most of the degradation was in the fill factor (FF). Fig. 3d shows delamination after the Surlyn encapsulated solar cell went through 200 temperature cycles, which likely was the cause for the drop in FF. Laser beam induced current mapping on these temperature cycled cells in Fig. S10 (ESI†) further showed no current in the delaminated area, which indicates a loss of Ohmic contact and suggests that delamination occurred within the perovskite solar cell stack. The stiff Surlyn, which adheres well to ITO and glass,34,35 likely pulls up the sputtered ITO through the PC60BM layer.In contrast, EVA packaged devices were mechanically stable during temperature cycling, showing no signs of cracking, blistering, or delamination (Fig. 3e). Pictures of the whole set of EVA encapsulated solar cells after the 200 temperature cycling test can be found in Fig. S11 (ESI†). Moreover, all nine solar cells retained more than 90% of their initial performance after 225 temperature cycles (Fig. 3c) and passed the TC test. All figures of merit of EVA encapsulated solar cells stayed approximately constant throughout the TC test in Fig. S12 (ESI†), which means there is no competing change in performance that makes the solar cells stable or any noticeable degradation modes in the device. We have thus demonstrated a key concept that using a low modulus encapsulant such as EVA enabled encapsulated perovskite solar cells to pass the standardized 200 temperature cycling test.
3. Conclusion
Perovskite solar cells have layers with thermal expansion coefficient mismatches and low fracture energies that seemingly limit their potential to be successfully commercialized. This work furthers our understanding on the mechanical properties of encapsulation required for perovskite solar cells to pass the IEC 61646 temperature cycling test. We observed that the high elastic modulus of Surlyn leads to delamination and a drop in performance when laminated on perovskite solar cells, whereas the lower modulus of EVA dissipates strain and enables encapsulated solar cells to retain 90% of the performance. This work shows promise for the operational stability of perovskite solar cells.4. Methods
4.1 Sample preparation
4.2 Glass–glass encapsulation of solar cells
Indium solar ribbon (part# WCD102-7747-6022) was soldered on to the evaporated metal electrode of the solar cells prior to assembly. Solar cell substrates were packaged between top and bottom sheets of encapsulant, either ethylene vinyl acetate or ionomer Surlyn 5400 and two sheets of 3 mm thick glass. The butyl rubber edge seal with added desiccant (Quanex, SET LP03) was placed as a frame around outer edge of the glass during assembly. The edge seal was used as a sandwich on both sides of the solar ribbon to minimize moisture ingress. The package was laminated in two steps: pull vacuum for 5 minutes then press with 650 mbar pressure at 140 °C for 20 minutes for the edge seal to soften and the encapsulant to cure. Total bond width of the edge seal is 1 cm, which can prevent moisture from diffusing in at 85 °C–85%RH condition for at least 1000 hours.36 Optimization steps for the encapsulation are included in the ESI,† section.4.3 Temperature cycling test
Packaged solar cells were placed on a tray inside a chamber (ESPEC TSE-11A) composed of two different compartments, the top one at 85 °C and the bottom one at −40 °C. The packaged was first equilibrated at 25 °C then was brought up to the top 85 °C chamber within a minute and held there for 20 minutes. Afterwards, the package was moved to the lower −40 °C chamber within a minute and also held there for 20 minutes. A cycle was completed when package went through both top and bottom compartments.4.4 Measuring solar cell performance
Current–voltage of a solar cells were performed using Keithley 2400 digital source meter. A 300 W Xenon arc lamp was used to irradiate solar cells from the bottom glass side. A reference KG5 Si photodiode was used to calibrate the solar simulator to match the integrated current measured from external quantum efficiency. The current–voltage was measured from forward to reverse bias between 1.2 V to −0.2 V. Afterwards, the solar cells were stabilized under light at maximum power point bias until reaching stabilized efficiency for 200 seconds. The solar cell current–voltage was then re-measured from forward to reverse, and reverse to forward to check for any hysteresis. The final power conversion efficiency after the solar cells were stabilized were used to monitor the performance of the solar cells as they went through different periods of temperature cycles.4.5 Double cantilever beam measurement for fracture energy
Double cantilever beam (DCB) specimens were fabricated by affixing a glass substrate to the solar cell with a brittle epoxy (E-20NS, Hysol), cured overnight at room temperature in a N2 glovebox. Before testing, excess epoxy was removed from the edges of the specimen with a razor blade.DCB specimens were loaded under displacement control in a thin-film cohesion testing system (Delaminator DTS, Menlo Park, CA) from which a load, P, versus displacement, Δ, curve was recorded. The cohesion energy or fracture energy, Gc (J m−2), was measured in terms of the critical value of the applied strain energy release rate, G. Gc can be expressed in terms of the critical load, Pc, at which crack growth occurs, the crack length, a, the plane-strain elastic modulus, E′, of the substrates and the specimen dimensions: width, B and half-thickness, h. Gc was calculated from eqn (1):21
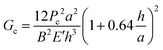 | (1) |
An estimate of the crack length was experimentally determined from a measurement of the elastic compliance, dΔ/dP, using the compliance relationship in eqn (2):
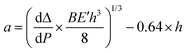 | (2) |
All Gc testing was performed in laboratory air environment at ∼25 °C and ∼45% R.H. The specimen was loaded in tension with a displacement rate of 1 μm s−1 until reaching Pc before unloading slightly to calculate dΔ/dP. The specimens were then loaded again to Pc and the process repeated until the crack length reached the end of the specimen. A representative loading curve and extracted fracture energy as a function of crack length were plotted in Fig. S13 (ESI†). The fracture energies reported in Fig. 1 and 2 are averaged values extracted from the repeating load–unload measurement as the crack propagated through the weakest layer in the device. There are at least seven measurements per sample, with total of three samples. Therefore, our fracture energy values are statistically significant.
4.6 Atomic force microscopy measurement
Atomic force microscopy (AFM) (XE-70, Park Systems) in non-contact mode was used to characterize the surface morphology and roughness of the fractured solar cells.4.7 X-ray photoelectron spectroscopy
X-ray photoelectron spectroscopy (XPS) measurements were taken on a PHI Versaprobe III Scanning XPS Microprobe (Physical Electronics Inc.) with a monochromatic Al Kα X-ray source (1486 eV) with survey scans from 0 to 1100 eV.4.8 Laser beam induced current measurement
Packaged solar cells were mounted onto a 2-axis motorized translation stage (Standa 8MT173-20). One of the solar cells was connected to a transimpedance amplifier (Oriel), where the signal was converted to a voltage and then sent to a lock-in amplifier (Stanford Research System SR830 DSP Lock-in Amplifier) for detection. A 488 nm laser light was focused down to approximately 10 μm diameter and was optically chopped (Stanford Research System SR540 Optical Chopper) as the sample moved in two dimensions. A LabVIEW interface was used to control the range of motion and record a current at each spot measured in two dimensional map.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by Bay Area Photovoltaics Consortium and Office of Naval Research. We would like to thank Jane Kapur from Dupont for her help and insightful discussion about PV5400 Surlyn. We would also like to thank Axel Palmstrom for his help with pulsed-CVD of SnO2 and Sunpreme Inc. for their ITO sputtering tool. We also really appreciated fruitful discussion about encapsulation with Jared Tracy. RC would like to thank Ministry of Science and Technology of Thailand fellowship for the support. NR would like to acknowledge NSF Graduate Research Fellowship no. DGE-1656518. Part of this work was performed at the Stanford Nano Shared Facilities (SNSF), supported by the National Science Foundation under award ECCS-1542152.References
- M. Saliba, T. Matsui, K. Domanski, J.-Y. Seo, A. Ummadisingu, S. M. Zakeeruddin, J.-P. Correa-Baena, W. R. Tress, A. Abate, A. Hagfeldt and M. Gratzel, Science, 2016, 354, 206–209 CrossRef CAS PubMed.
- K. A. Bush, A. F. Palmstrom, Z. J. Yu, M. Boccard, R. Cheacharoen, J. P. Mailoa, D. P. McMeekin, R. L. Z. Hoye, C. D. Bailie, T. Leijtens, I. M. Peters, M. C. Minichetti, N. Rolston, R. Prasanna, S. Sofia, D. Harwood, W. Ma, F. Moghadam, H. J. Snaith, T. Buonassisi, Z. C. Holman, S. F. Bent and M. D. McGehee, Nat. Energy, 2017, 2, 17009 CrossRef CAS.
- T. Duong, Y. Wu, H. Shen, J. Peng, X. Fu, D. Jacobs, E.-C. Wang, T. C. Kho, K. C. Fong, M. Stocks, E. Franklin, A. Blakers, N. Zin, K. McIntosh, W. Li, Y.-B. Cheng, T. P. White, K. Weber and K. Catchpole, Adv. Energy Mater., 2017, 1700228 CrossRef.
- J. Yoon, H. Sung, G. Lee, W. Cho, N. Ahn, H. S. Jung, M. Choi, J. W. Jung, B.-H. Sohn, M. J. Ko, H. J. Son, W. Chen, B. Özyilmaz, J.-H. Ahn, B. H. Hong and S. Iijima, Energy Environ. Sci., 2017, 10, 337–345 CAS.
- G. Grancini, C. Roldán-Carmona, I. Zimmermann, E. Mosconi, X. Lee, D. Martineau, S. Narbey, F. Oswald, F. De Angelis, M. Graetzel and M. K. Nazeeruddin, Nat. Commun., 2017, 8, 15684 CrossRef CAS PubMed.
- T. Leijtens, K. Bush, R. Cheacharoen, R. Beal, A. Bowring, M. D. McGehee, W. Tress, K. Schenk, J. Teuscher, J.-E. Moser, H. Rensmo, A. Hagfeldt, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, J. Mater. Chem. A, 2017, 5, 11483–11500 CAS.
- M. Koehl, M. Heck, S. Wiesmeier and J. Wirth, Sol. Energy Mater. Sol. Cells, 2011, 95, 1638–1646 CrossRef CAS.
- IEC 61646:2008|IEC Webstore|rural electrification, solar power, 2008.
- P. Hacke, K. Terwilliger, S. Glick, D. Trudell, N. Bosco, S. Johnston and S. Kurtz, 2010 35th IEEE Photovoltaic Specialists Conference, IEEE, 2010, pp. 000244–000250.
- D. Wu, J. Zhu, T. R. Betts and R. Gottschalg, Prog. Photovoltaics, 2014, 22, 796–809 CAS.
- T. J. McMahon, Prog. Photovoltaics, 2004, 12, 235–248 CAS.
- J. H. Wohlgemuth and S. Kurtz, 2011 37th IEEE Photovoltaic Specialists Conference, IEEE, 2011, p. 003601.
- D. Bhattacharyya and M. J. Carter, Thin Solid Films, 1996, 288, 176–181 CrossRef CAS.
- S. P. Srivastava, R. C. Srivastava, I. D. Singh, S. D. Pandey and P. L. Gupta, J. Phys. Soc. Jpn., 1977, 43, 885–890 CrossRef CAS.
- P. S. Peercy and B. Morosin, Phys. Rev. B: Condens. Matter Mater. Phys., 1973, 7, 2779–2786 CrossRef CAS.
- D. R. Hummer, P. J. Heaney and J. E. Post, Powder Diffr., 2007, 22, 352–357 CrossRef CAS.
- G. Paternò, A. J. Warren, J. Spencer, G. Evans, V. G. Sakai, J. Blumberger, F. Cacialli, B. Fraboni, C. Femoni, I. Mencarelli, L. Setti, R. Di Pietro, A. Cavallini, A. Fraleoni-Morgera, A. Fraleoni-Morgera, L. Benevoli, B. Fraboni, V. Podzorov, A. L. Briseno, S. C. Mannsfeld, M. M. Ling, S. Liu, R. J. Tseng, C. Reese, M. E. Roberts, Y. Yang, F. Wudl, Z. Bao, A. A. Virkar, S. Mannsfeld, Z. Bao, N. Stingelin, J. L. Brédas, J. Cornil, A. J. Heeger, A. L. Ayzner, C. J. Tassone, S. H. Tolbert, B. J. Schwartz, G. Yu, A. J. Heeger, J. J. M. Halls, C. A. Walsh, N. C. Greenham, E. A. Marseglia, R. H. Friend, S. C. Moratti, A. B. Holmes, W. Yin, M. Dadmun, X. N. Yang, J. K. J. van Duren, M. T. Rispens, J. C. Hummelen, R. A. J. Janssen, M. A. J. Michels, J. Loos, H. Hoppe, A. Drees, W. Schwinger, F. Schaffler, N. S. Sariciftci, X. N. Yang, J. K. J. van Duren, R. A. J. Janssen, M. A. J. Michels, J. Loos, H. Hoppe, T. Glatzel, M. Niggemann, A. Hinsch, M. Lux-Steiner, N. S. Sariciftci, F. Piersimoni, S. Chambon, K. Vandewal, R. Mens, T. Boonen, A. Gadisa, M. Izquierdo, S. Filippone, B. Ruttens, J. D’Haen, N. Martin, L. Lutsen, D. Vanderzande, P. Adriaensens, J. V. Manca, A. Swinnen, I. Haeldermans, M. vandeVen, J. D’Haen, G. Vanhoyland, S. Aresu, M. D’Olieslaeger, J. Manca, M. Reyes-Reyes, R. Lopez-Sandoval, J. Arenas-Alatorre, R. Garibay-Alonso, D. L. Carroll, A. Lastras-Martinez, L. Li, G. Lu, S. Li, H. Tang, X. Yang, M. Dante, J. Peet, T. Q. Nguyen, M. Casalegno, S. Zanardi, F. Frigerio, R. Po, C. Carbonera, G. Marra, T. Nicolini, G. Raos, S. Meille, M. T. Rispens, A. Meetsma, R. Rittberger, C. J. Brabec, N. S. Sariciftci, J. C. Hummelen, R. Dabirian, X. Feng, L. Ortolani, A. Liscio, V. Morandi, K. Müllen, P. Samorì, V. Palermo, L. Zheng, Y. Han, F. Gajdos, H. Oberhofer, M. Dupuis, J. Blumberger, D. L. Cheung, A. Troisi, H. Oberhofer, J. Blumberger, R. C. I. MacKenzie, J. M. Frost, J. Nelson, G. M. Sheldrick, W. L. Jorgensen, D. S. Maxwell, J. Tirado-Rives, P. A. Heiney, J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale, K. Schulten, F. Frigerio, M. Casalegno, C. Carbonera, T. Nicolini, S. V. Meille and G. Raos, J. Mater. Chem. C, 2013, 1, 5619 RSC.
- Y. Kawamura, H. Mashiyama and K. Hasebe, J. Phys. Soc. Jpn., 2002, 71, 1694–1697 CrossRef CAS.
- I. Chung, J.-H. Song, J. Im, J. Androulakis, C. D. Malliakas, H. Li, A. J. Freeman, J. T. Kenney and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 8579–8587 CrossRef CAS PubMed.
- R. H. Dauskardt, M. Lane, Q. Ma and N. Krishna, Eng. Fract. Mech., 1998, 61, 141–162 CrossRef.
- M. F. Kanninen, Int. J. Fract., 1973, 9, 83–92 Search PubMed.
- N. Rolston, B. L. Watson, C. D. Bailie, M. D. McGehee, J. P. Bastos, R. Gehlhaar, J.-E. Kim, D. Vak, A. T. Mallajosyula, G. Gupta, A. D. Mohite and R. H. Dauskardt, Extrem. Mech. Lett., 2016, 9, 353–358 CrossRef.
- A. Rougier, C. Guy, M. Koehl, M. Heck and S. Wiesmeier, Sol. Energy Mater. Sol. Cells, 2012, 99, 282–291 CrossRef.
- P. E. Burrows, V. Bulovic, S. R. Forrest, L. S. Sapochak, D. M. McCarty and M. E. Thompson, Appl. Phys. Lett., 1994, 65, 2922–2924 CrossRef CAS.
- D. Yu, Y.-Q. Yang, Z. Chen, Y. Tao and Y.-F. Liu, Opt. Commun., 2016, 362, 43–49 CrossRef CAS.
- J. Berghold, S. Koch, B. Frohmann, P. Hacke and P. Grunow, 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), IEEE, 2014, pp. 1987–1992.
- M. D. Kempe, G. J. Jorgensen, K. M. Terwilliger, T. J. McMahon, C. E. Kennedy and T. T. Borek, Sol. Energy Mater. Sol. Cells, 2007, 91, 315–329 CrossRef CAS.
- P. Hacke, K. Terwilliger, R. Smith, S. Glick, J. Pankow, M. Kempe, S. K. I. Bennett and M. Kloos, 2011 37th IEEE Photovoltaic Specialists Conference, IEEE, 2011, p. 000814.
- M. Schutze, M. Junghanel, M. B. Koentopp, S. Cwikla, S. Friedrich, J. W. Muller and P. Wawer, 2011 37th IEEE Photovoltaic Specialists Conference, IEEE, 2011, p. 000821.
- J. Tracy, N. Bosco, F. Novoa and R. Dauskardt, Prog. Photovoltaics, 2017, 25, 87–96 CAS.
- V. Balcaen, N. Rolston, S. R. Dupont, E. Voroshazi and R. H. Dauskardt, Sol. Energy Mater. Sol. Cells, 2015, 143, 418–423 CrossRef CAS.
- S. R. Dupont, E. Voroshazi, D. Nordlund, K. Vandewal and R. H. Dauskardt, Adv. Mater. Interfaces, 2014, 1, 1400135 CrossRef.
- B. L. Watson, N. Rolston, K. A. Bush, T. Leijtens, M. D. McGehee and R. H. Dauskardt, ACS Appl. Mater. Interfaces, 2016, 8, 25896–25904 CAS.
- U. Eitner, S. Kajari-Schröder, M. Köntges and H. Altenbach, Shell-like Structures, Advanced Structured Materials, Springer, Berlin, Heidelberg, 2011, pp. 453–468 Search PubMed.
- E. Ugel, G. Giuliano and M. Modesti, Soft Nanosci. Lett., 2011, 1, 105–119 CrossRef CAS.
- M. D. Kempe, A. A. Dameron and M. O. Reese, Prog. Photovoltaics, 2014, 22, 1159–1171 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee02564e |
| This journal is © The Royal Society of Chemistry 2018 |