Exceptionally slow magnetic relaxation in cobalt(II) benzoate trihydrate

Abstract

Cobalt(II) benzoate trihydrate prepared by the reaction of CoCO₃ with benzoic acid (HBz) in boiling water followed by crystallization has been structurally characterized as a chain-like system with the formula unit [Co(Bz)(H₂O)₂]Bz·H₂O where the Co(II) atoms are triply linked by one bridging syn–syn benzoato (Bz) and two aqua ligands; additional benzoate counter ions and solvate water molecules are present in the crystal structure. DC magnetic measurements reveal a sizable exchange coupling of a ferromagnetic nature between the Co(II) atoms. At T_N = 5.5 K the paramagnetic phase switches to the antiferromagnetic phase. Though the remnant magnetization is zero, the magnetization curve shows two lobes of a hysteresis loop and the DC relaxation experiments confirm a long relaxation time at T = 2.0 K. AC susceptibility data confirm a slow relaxation of magnetization even in the antiferromagnetic phase. In the absence of the magnetic field, two relaxation channels exist. The relaxation time for the low frequency channel is as slow as τ_LF > 1.6 s and data fitting yields τ_LF (2.1 K) = 14 s. The high-frequency relaxation time obeys the Orbach process at a higher temperature whereas the Raman process dominates the low-temperature region. Three slow relaxation channels are evidenced at the applied magnetic field B_DC = 0.1 T.

---

Introduction

Research into the magnetism of Co(II) complexes has yielded a number of unexpected results in recent times. Generally speaking, these systems possess a very high magnetic anisotropy that grows in the series of tetra-, penta- and hexa-coordinate complexes.^1–3 In terms of spin Hamiltonian theory, the axial zero-field splitting (ZFS) parameter can be as high as D/hc > 100 cm⁻¹ as can be confirmed not only by the magnetic data analysis (magnetic susceptibility transformed into the effective magnetic moment and/or product function χT, and the field dependence of the magnetization) but also in some cases by far-IR spectroscopy (electronic transitions among the crystal-field multiplets).^4,5

Most interesting is the identification of slow magnetic relaxation using AC susceptometry in the zero or applied magnetic field. The out-of-phase component gives information about the relaxation channels: two channels are common (low-frequency (LF) around f ∼ 1 Hz and high-frequency (HF) between f = 10²–10³ Hz) though three channels have also been identified.⁶ At a higher temperature the relaxation rates for the HF channel follow the Orbach process overcoming the energy barrier to spin reversal U = |D|(S² − 1/4). The Raman process of relaxation via the virtual states of the solid applies at low temperature. With D ≫ 0 the Kramers doublet |S = 3/2, M_S = ±3/2〉 might be increased beyond thermal activation and the ground multiplet refers to an effective spin |S* = 1/2, M_S = ±1/2〉. In such a case the Orbach process is unfavourable so that the Raman process would dominate.⁷ Also, the hyperfine interaction can assist in these processes due to the nuclear spin I(⁶³Co) = 7/2.

In search of new systems within the broad class of single molecule magnets (single ion magnets, single chain magnets) we have prepared cobalt(II) benzoate trihydrate, [Co(Bz)(H₂O)₂]Bz·H₂O (1), in single crystal form and elucidated its chain-like crystal structure. Several reports on the syntheses, properties and structures of cobalt(II) benzoate in the anhydrous form,^8–10 as the dihydrate¹¹ or as the tetrahydrate,^11,12 have been published, but to our knowledge no report on the trihydrate has been published so far. The magnetic properties of the two forms of anhydrous cobalt(II) benzoate were also studied.^10c Recently, the isostructural nickel(II) benzoate trihydrate was reported.¹³ [Cu(Bz)(H₂O)₂]Bz·H₂O has an analogous chain-like arrangement of Cu(II) atoms bridged by benzoato and aqua ligands with marked differences in Cu–O bond distances due to the Jahn–Teller effect.¹⁴

Even small changes in the chemical composition, such as the presence or absence of solvent molecules in the crystal lattice, can induce significant differences in the dynamics of the slow magnetic relaxation. This motivated us to study the SMM or SIM behaviour of 1.

Experimental

Materials and methods

Benzoic acid (C₆H₅COOH) and cobalt(II) carbonate (CoCO₃) were obtained from commercial sources and were used as received. Elemental analysis was performed using a PerkinElmer 2400 Series II CHNS/O analyzer. The infrared spectrum was recorded on a PerkinElmer Spectrum 100 CsI DTGS FTIR spectrometer with a UATR 1 bounce-KRS-5 in the range of 4000–300 cm⁻¹ using the ATR technique. X-ray powder diffraction patterns of 1 were obtained on a RIGAKU D-Max/2500 diffractometer; the theoretical powder diffraction pattern was calculated using the program PowderCell.^15a A comparison of the powder diffraction pattern of 1 with the calculated one can be found in the ESI (see Fig. S1†).

Single-crystal X-ray data of the sample were collected on an Oxford Diffraction Xcalibur diffractometer equipped with a Sapphire3 CCD detector and a graphite monochromator utilizing MoKα radiation (λ = 0.71073 Å). The details of the data collection,^15b structure solution^15c and refinement^15d are described in the ESI.† The crystal and experimental data are given in Table 1. Crystallographic data of compound 1 (CCDC 1536321†) have been deposited with the Cambridge Crystallographic Data Centre. The structural figures were drawn using Diamond software.^15e

Table 1 Crystal data and the results of refinement for 1

Empirical formula	CoC14H16O7
Formula weight Mr	355.20
Temperature [K]	173(1)
Wavelength [Å]	MoKα, 0.71073
Crystal system, space group	Monoclinic, I2/a
Unit cell parameters a [Å]	6.2318(4)
b [Å]	34.130(3)
c [Å]	6.9115(4)
β [°]	95.703(7)
Volume [Å^3]	1462.72(17)
Z	4
Density (calc.) [Mg m^−3]	1.613
Abs. coef., μ [mm^−1]	1.207
Crystal colour/shape	Pale pink, irregular
Crystal size [mm^3]	0.043 × 0.084 × 0.134
θ range for data collection [°]	3.022–27.498
Index range for data collection [°]	h = −8 → 8
	k = −43 → 42
	l = −8 → 8
Reflections collected	4782
Independent reflections (Rint)	1636 (0.0593)
Observed reflections [I > 2σI]	1323
Goodness-of-fit on F^2	1.044
Final R indices [I > 2σI] R1 wR2	0.0426
	0.0976
Final R indices (all) R1 wR2	0.0558
	0.1056
Diff. peak and hole [e Å^−3]	0.871; −0.519

---

The temperature dependence of the DC magnetization was measured with a SQUID magnetometer (MPMS-XL7, Quantum Design) using the RSO mode of detection. For magnetic susceptibility the applied field was B_DC = 0.1 T; raw data were corrected for the underlying diamagnetism and converted into the effective magnetic moment. The AC susceptibility measurements were conducted with the amplitude B_AC = 0.38 mT and ten scans were averaged.

Synthesis

0.0975 g of solid CoCO₃ (0.82 mmol) and 0.1 g of solid benzoic acid (0.82 mmol) were placed in a beaker with 75 cm³ of water. The reaction system was stirred and heated to boiling. After 3.5 hours of boiling the solution turned pink. The hot solution was filtered and left for crystallization at room temperature. Brown-green crystals of 1 suitable for a single crystal X-ray study appeared after three weeks. Yield: 0.0933 g (64%). Analysis calc. (found) for 1 (C₁₄H₁₆CoO₇, M = 355.20 g mol⁻¹): C, 47.34% (47.05%); H, 4.54% (4.07%). FT-IR (in cm⁻¹): 3054(vw); 2977(s, b); 1591(m); 1539(s); 1495(s); 1420(s); 1383(s); 1301(m); 1070(m); 1020(m); 905(m); 710(s); 683(s); 669(s); 606(s); 501(s); 429(m).

Results and discussion

Synthesis and characterisation

The trihydrate of cobalt(II) benzoate (1) in single crystal form was prepared by the direct reaction of cobalt(II) carbonate with benzoic acid in boiling water followed by crystallization. A similar procedure but followed by evaporation to dryness and using cobalt(II) basic carbonate led to the isolation of the anhydrous compound in the form of a microcrystalline powder.⁸ Alternatively, the anhydrous cobalt(II) benzoate (its monoclinic form) was prepared by the reaction of cobalt(III) acetylacetonate with benzoic acid in the melt (150 °C),⁹ or by the reaction of cobalt(II) nitrate with benzaldehyde in air yielding, depending on the temperature, the monoclinic or orthorhombic form of anhydrous cobalt benzoate.¹⁰ The resulting single crystals of 1 were characterized chemically and spectroscopically. The phase identity of the bulk sample with that obtained from the single crystal study was corroborated using powder X-ray diffraction (see Fig. S1†). The IR spectrum of the title complex contains several absorption bands among which some could be easily identified using the literature data.¹⁶ The presence of water molecules (in the form of solvate molecules and aqua ligands) manifests itself by a typical medium broad absorption band centred around 2977 cm⁻¹; the rather important shift of this band toward a lower energy can be explained by the participation of the water molecules in rather strong hydrogen bonds (Fig. S2, Table S1†). A typical, although very weak, absorption band at 3054 cm⁻¹ may arise from C_ar–H stretching vibrations. The most characteristic absorption bands are those originating from asymmetric and symmetric ν(COO) vibrations; these were found at 1539 and 1495 cm⁻¹ (asymmetric ones), and at 1420 and 1383 cm⁻¹ for the symmetric ones. In the spectrum of the isostructural Ni(II) complex the corresponding bands were observed at 1547, 1484 and 1424, 1384 cm⁻¹, respectively,¹³ while for anhydrous cobalt benzoate somewhat different values were reported: 1541 (ν_as(COO)) and 1433 cm⁻¹ (ν_s(COO))⁸ or 1522 cm⁻¹ (ν_as(COO)), and 1411 and 1380 cm⁻¹ (ν_s(COO)).⁹

Structure determination

The crystal structure of 1 (for details see the ESI†) is ionic and composed of positively charged [Co(Bz)(H₂O)₂]_nⁿ⁺ chains, benzoate anions and stoichiometrically one solvate water molecule (Fig. 1 left). The same type of crystal structure was reported for the isostructural Ni(II) analogue¹³ and for the similar Cu(II) complex which, however, crystallizes in a different space group.¹⁴ We note that the chain-like arrangements of Co(II) atoms were reported in both polymorphs of anhydrous Co(II) benzoate, where the chains are neutral, unlike the present case; in the monoclinic polymorph the zig-zag chains are formed by alternating octahedra and bicapped tetrahedra (the additional two Co–O bonds have a common length of 2.540(2) Å (2x)) linked by common edges,⁹ while in the orthorhombic form the double zig-zag chains consist of alternating octahedra and tetrahedra linked via common vertices.^10a

Fig. 1 Left: One segment of the structure of 1 displaying the coordination mode of two triply bridged Co(II) atoms and benzoate anions along with the atom numbering scheme. Displacement ellipsoids are drawn at the 50% probability level. Symmetry codes: i: 0.5 − x, y, −z; ii: 0.5 + x, 1 − y, z; iii: 1 − x, 1 − y, −z; iv: 1.5 − x, y, −z; v: 1 + x, y, z; vi: 0.5 − x, y, 1 − z. Right: View of the positively charged [CoBz(H₂O)₂]_nⁿ⁺ chain running along the a axis with delineated polyhedra {CoO₆}. For a more detailed description of the structure, see the main text.

The chains in 1 are formed by Co(II) atoms triply bridged by two μ₂-aqua ligands and one syn–syn benzoato bridge. Due to the triple bridging, neighbouring Co(II) atoms are relatively close to each other, with a Co⋯Co distance of 3.1159(2) Å; this value is longer than the corresponding Ni⋯Ni separation of 3.0671(1) Å in the isostructural nickel complex.¹³ Somewhat longer Co⋯Co distances were found in the monoclinic (3.145(1) Å) and orthorhombic (3.1657(4) and 3.1957(4) Å) forms of anhydrous cobalt(II) benzoate.^9,10a

Alternatively, the chains in 1 can be viewed as formed of {CoO₆} octahedra with common edges; neighbouring octahedra are canted (Fig. 1 right) with an angle of 26.27° between the O_ax–Co–O_ax vectors in the adjacent octahedra. In the hydrate complex 1 the central Co(II) atom occupies a special position (centre of inversion) and is hexacoordinated [O₂(benzoate)O₄(aqua) donor set]. Comparison of the axial Co–O bond of 1.9775(16) Å (twice) with the mean equatorial Co–O bond of 2.158(19) Å (Table 2) shows that the coordination polyhedron can be viewed as a tetragonally compressed octahedron, with the observed compression of the octahedron expressed by the ratio κ = (Co–O)_ax/〈(Co–O)_eq〉 = 0.92. The compression in the hydrate 1 is more pronounced than that in the anhydrous monoclinic complex [1.936(2) vs. 2.004(2) Å, κ = 0.97];⁹ on the other hand, in the orthorhombic form three pairs of Co–O distances with mean values of 2.02, 2.15 and 2.23 Å are present within the trigonally distorted octahedron. The neighbouring chains in 1 are interconnected, with the participation of solvate water molecules (O4 atoms) and benzoate anions, by rather strong hydrogen bonds of the O–H⋯O type with a mean O⋯O distance of 2.66(3) Å (Fig. S2, Table S1†), forming supramolecular layers.

Table 2 Selected geometric parameters [Å, °] for 1

Symmetry codes: (i) 1/2 − x, y, −z; (ii) 1/2 + x, 1 − y, z; (iii) 1 − x, 1 − y, −z; (iv) 3/2 − x, y, −z; (vi) 1/2 − x, y, 1 − z.
Co1–O1	1.9775(16)	O2–Co1–O2^i	83.83(7)
Co1–O2	2.1418(18)	O2^i–Co1–O2^iii	96.17(7)
Co1–O2^i	2.1745(18)	O1–Co1–O1^iii	180
Co1–Co1^iv	3.1159(2)	Co1–O2^ii–Co1^iv	92.42(7)
C1–O1	1.271(2)	O1–C1–O1^i	124.5(3)
C6–O3	1.265(2)	O3–C6–O3^vi	124.2(3)

---

Magnetic data

DC magnetic data. Based on the DC measurements, the effective magnetic moment increases from its room-temperature value of μ_eff = 5.6μ_B to its maximum μ_eff = 15.9μ_B at T = 6.5 K; then it drops rapidly to a value of μ_eff = 8.0μ_B at T = 1.9 K (Fig. 2). The molar magnetic susceptibility reaches a maximum on cooling and below 3.4 K it stays constant. These data indicate a transition of the paramagnetic phase with exchange interactions of a ferromagnetic nature to the antiferromagnetic phase at the Néel temperature T_N = 5.5 K. The position of this critical temperature slightly depends on the applied DC magnetic field (B_DC = 0.01 or 0.1 T). The higher-temperature tail above the Néel temperature is unaffected by the magnetic field (Fig. 2c and d).

Fig. 2 DC magnetic data for 1. a: Effective magnetic moment (inset: low temperature susceptibility data); b: magnetization data (inset: low-field window); c, d: effective magnetic moment and susceptibility data taken at different fields; e: inverse susceptibility; f, g: susceptibility transform of DC and AC data taken under different conditions. Full lines in a, b, e and g – fitted.

AC magnetic data. The AC susceptibility data, χ_av = (χ′² + χ′′²)^1/2, also confirm the existence of the Néel temperature; however, a bit shifted to T_N = 4.7 K. Data above T_N are independent of the frequency of the alternating magnetic field; below T_N, they are frequency dependent (Fig. 2f).

The function χT/C ∼ exp(Δ_ξ/k_BT) allows the determination of the energy of the domain wall.¹⁷ For this purpose the high-temperature data in Fig. 2f can be fitted by a straight line, which results in ln(χT) = (Δ_ξ/k_B)T⁻¹ + ln C; to this end, (Δ_ξ/k_B) = 17.6 K.

The magnetization per formula unit adopts a value of M_mol/N_Aμ_B = 2.98 at B = 7.0 T for both, T = 2.0 and 4.6 K. The magnetization grows with the magnetic field rapidly. There is no indication of remnant magnetization as the field decreases through zero.

In analyzing the DC magnetic data at a temperature above 7 K, the zero-field splitting model applicable to a compressed tetragonal bipyramidal geometry was used; the axial zero-field splitting parameters D > 0 and g_e = g_z < g_x are assumed from the spin-Hamiltonian analysis.⁴ This model is enriched by the exchange interaction in the finite ring approximation

with the Zeeman term for a = z, xy directions. Its eigenvalues enter the partition function and consequently the formulae of statistical thermodynamics for magnetic susceptibility and magnetization. The susceptibility data (above 7 K) and the magnetization data (at T = 2.0 K) were fitted simultaneously by using a joint functional F = wE(χ) + (1 − w)E(M) where the relative errors of susceptibility E(χ) and magnetization E(M) are equally weighted. The fitting procedure gave the following set of magnetic parameters: (J/hc) = 4.83 cm⁻¹, (D/hc) = 15.8 cm⁻¹, g_xy = 3.08, temperature-independent magnetism χ_TIM = −2.5 10⁻⁶ m³ mol⁻¹ and molecular-field correction (zj)/hc = 0.041 cm⁻¹; discrepancy factors of the fit R(χ) = 0.20 and R(M) = 0.14. Though the above fit for N = 4 centres in the ring is not perfect, it yields an estimate of the magnetic parameters J, D, and g_xy. Note the relationship D/J > 4/3.

The zero-field-cooled and field-cooled magnetization data merge to the same path (Fig. 3). Though there is no remnant magnetization at zero field, two lobes of the hysteresis loop are observed at T = 2.0 K. The hysteresis escapes at T = 5.0 K.

Fig. 3 (a) ZFCM/FCM records (red – ZFCM, blue – FCM); (b, c) search for the hysteresis (settle mode); and (d) relaxation of the DC magnetization for 1 in zero field (four cycles).

The relaxation experiments were conducted at T = 2.0 K. The initial field B_DC = 0.1 T has been switched off and then the magnetization was measured in intervals of 120 s (Fig. 3d). Note that there is some remnant magnetic field of about −1.7 mT in the SQUID apparatus. This could cause a drop in the magnetization below zero.

The AC susceptibility data were acquired as a function of the applied field B_DC = 0–0.5 T at T = 2.0 K for four representative frequencies of the oscillating field B_AC = 0.38 mT. This dependence is rather complex (Fig. 4a). The out-of-phase signal is non-zero even in the absence of an external field but it disappears at B_DC = 0.05 T. At B_DC = 0.1 T it passes through a sharp maximum and then it is attenuated with the increasing field. Subsequent measurements were thus done at B_DC = 0 and 0.1 T for 22 frequencies ranging between f = 0.1 and 1500 Hz for each temperature.

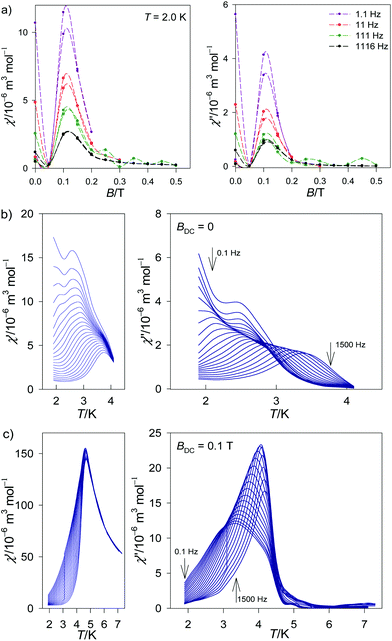Fig. 4 Field and temperature dependence of the AC susceptibility components for 1. Top – field dependence, two independent measurements. Lines serve as a guide to the eye.

The frequency dependence of the AC susceptibility components is presented in Fig. 5. The data show two maxima in the χ′′ vs. f curve, indicating two relaxation channels. The onset of the low-frequency (LF) mode is well visible in the range T = 1.9–3.3 K. Above 3.9 K the out-of-phase susceptibility is suppressed, in accordance with the data in Fig. 4b, and then the sample becomes a paramagnet. The high-frequency (HF) branch possesses its maximum between 1 and 1000 Hz and it continues above 1500 Hz. Both components of the AC susceptibility have been fitted simultaneously by minimizing an error functional F = wE( χ′) + (1 − w)E( χ′′) that consists of the weighted sum of relative errors of the individual components. A two-set Debye model was applied in reconstructing the AC susceptibility data; the corresponding set of parameters (isothermal susceptibilities, distribution factors, and relaxation times) are listed in the ESI.† These parameters were used for reconstructing interpolation/extrapolation lines that are drawn in Fig. 5. The LF branch at χ′′ starts growing below 1 Hz and its maximum lies outside the limits of the measurements −0.1 Hz. Therefore the relaxation time is τ(LF) > 1.6 s for a set of low temperatures irrespective of the data fitting (this indicates that τ_LF(2.1 K) = 14 s).

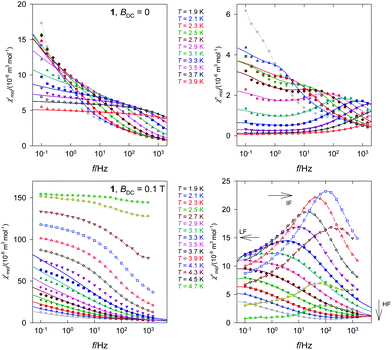Fig. 5 Frequency dependence of the AC susceptibility components for 1. Full lines – calculated interpolation/extrapolation and dashed – visual guide.

The out-of-phase susceptibility component for B_DC = 0.1 T rises to its maximum at T = 4.1 K and then it attenuates rapidly on further heating (in accordance with Fig. 4c). At T_N > 4.7 K it is almost zero because of the paramagnetic phase.

A plot of the out-of-phase component versus the in-phase member (Fig. 6) is an Argand diagram consisting of two overlapping arcs. The relaxation times derived from the data fitting are used for constructing the Arrhenius-like plot. As far as the HF branch is concerned, two relaxation regimes operate. The high-temperature one was analyzed in terms of the Arrhenius equation τ = τ₀ exp(U/k_BT) where the barrier to spin reversal U and the extrapolated relaxation time τ₀ appear. The linear fit using three higher-temperature points gave U/k_B = 81.3 K and τ₀ = 6.6 × 10⁻¹⁵ s. Though τ₀ is rather short (close to the spin glass behaviour), these values are consistent with the literature data on Co(II) based single chain magnets.¹⁸ For instance, the ferromagnetically coupled chain complex [Co(2,2-bithiazoline)(N₃)₂]_∞ possesses J/hc = +12.4 cm⁻¹, Δ_τ/k_B = 94 K, and τ₀ = 3.4 × 10⁻¹² s.¹⁹ Three complexes [Co₂(N₃)₄(DMF)₃], [Co₄(N₃)₈(DEF)₅], and [Co₂(N₃)₄(DIPF)₂] (DMF = N,N-dimethylformamide, DEF = N,N-diethylformamide, and DIPF = N,N-diisopropylformamide) displayed Δ_τ/k_B = 201.9, 60.2, 71.5 K and τ₀ = 1.7 × 10⁻¹⁸, 1.9 × 10⁻⁹, 7.1 × 10⁻¹² s.²⁰

Fig. 6 Argand diagram – left, and the Arrhenius-like plot – right for 1 at B_DC = 0. Dashed straight lines – fit for a limited data set. Non-linear curve – a fit to the full data set.

The low-temperature regime is dominated by the Raman process for which the relaxation time follows a power-law equation τ⁻¹ = CTⁿ or ln τ = −ln C − n ln T. The linear regression gave C = 1.5 × 10⁻³ s⁻¹ K⁻ⁿ and n = 12.1. The full data set was fitted with a joint relaxation equation τ⁻¹ = τ₀⁻¹ exp(−U/k_BT) + CTⁿ which gave U/k_B = 88.7 K, τ₀ = 1.2 × 10⁻¹⁵ s, and C = 1.4 × 10⁻³ s⁻¹ K⁻¹² for n = 12. These data were used for reconstructing the interpolation and extrapolation line in the curved Arrhenius-like plot.

DC magnetic studies were reported also on the two forms of anhydrous cobalt(II) benzoate exhibiting an analogous chain-like arrangement of Co(II) atoms (for a more detailed structural description see above).^10c In both forms likewise in 1 strongly anisotropic ferromagnetic chains of the Co(II) atoms were detected due to ferromagnetic interactions and the anisotropic nature of the Co(II) atoms (the reported values of g-parameters are g_T = 2.31 for both polymorphs and g_O = 2.72 and 2.75 for the monoclinic and orthorhombic forms, respectively;^10c the refined value for 1 is g_xy = 3.08). While in the orthorhombic form the spins are ordered three-dimensionally at T_C = 3.7 K, such ordering was not observed for the monoclinic form; this difference was ascribed to somewhat stronger interchain interactions in the orthorhombic phase. Further AC magnetic study of the monoclinic cobalt(II) benzoate down to 0.33 K revealed that this complex below 0.6 K behaves as a single chain magnet; from the experimental data the traditional SCM parameters were extracted: τ₀ = (1.1 ± 2.5)×10⁻¹¹ s and U/k_B = 5.5 K.^10c In the case of 1 we have detected two relaxation times with a considerably slower relaxation of τ_LF > 1.6 s for the low frequency channel and a much higher relaxation barrier of U/k_B = 81.3 K.

Conclusions

In conclusion, cobalt(II) benzoate trihydrate, [Co(Bz)(H₂O)₂]Bz·H₂O, possesses a positively charged chain in which the Co(II) atoms coordinated in the form of slightly compressed tetragonal bipyramids are triply linked by bridging benzoato and aqua ligands. DC magnetic measurements reveal a strong exchange coupling of a ferromagnetic nature. Below T_N = 5.5 K the paramagnetic phase switches to the antiferromagnetic phase. Though the remnant magnetization is zero, the magnetization curve shows two lobes of the hysteresis loop at T = 2.0 K. DC relaxation experiments confirm a long relaxation time. AC susceptibility data reveal slow magnetic relaxation in the absence of the magnetic field even for the antiferromagnetic phase where two relaxation channels exist. The relaxation time for the low frequency channel is as slow as τ_LF > 1.6 s and the data fitting indicates τ_LF (2.1 K) = 14 s. The high-frequency relaxation follows the Orbach process at a higher temperature whereas the Raman process dominates the low-temperature region. Three slow relaxation channels are evidenced for an applied magnetic field of B_DC = 0.1 T.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from Slovak grant agencies (APVV-14-0078, VEGA 1/0534/16 and VEGA 1/0063/17) is gratefully acknowledged, as is support from the Ministerio de Ciencia e Innovación (Spain, Grant MAT2015-68200-C2-1-P), the European Union Regional Development Fund (FEDER) and the Diputación General de Aragón, Project M4, E16. AV thanks the National Scholarship Programme of Slovak Republic and grant VVGS-PF-2018-777. This project was supported by P. J. Šafárik University in Košice, Faculty of Sciences.

References

1. G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135 and references therein.
2. S. Gomez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379 and references therein.
3. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470 and references therein.
4. (a) R. Boča, Struct. Bonding, 2006, 117, 1; (b) F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432.
5. (a) B. Papánková, R. Boča, Ľ. Dlháň, I. Nemec, J. Titiš, I. Svoboda and H. Fuess, Inorg. Chim. Acta, 2010, 363, 147; (b) M. Šebová, R. Boča, Ľ. Dlháň, I. Nemec, B. Papánková, J. Pavlik and H. Fuess, Inorg. Chim. Acta, 2012, 383, 143; (c) M. Idešicová and R. Boča, Inorg. Chim. Acta, 2013, 408, 162.
6. (a) R. Boča, J. Miklovič and J. Titiš, Inorg. Chem., 2014, 53, 2367; (b) C. Rajnák, J. Titiš, R. Boča, O. Fuhr and M. Ruben, Inorg. Chem., 2014, 53, 8200; (c) L. Smolko, J. Černák, M. Dušek, J. Miklovič, J. Titiš and R. Boča, Dalton Trans., 2015, 44, 17565; (d) C. Rajnák, J. Titiš, J. Moncoľ, F. Renz and R. Boča, Eur. J. Inorg. Chem., 2017, 1520; (e) C. Rajnák, F. Varga, J. Titiš, J. Moncoľ and R. Boča, Eur. J. Inorg. Chem., 2017, 1915.
7. S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300.
8. A. B. Sisqueira, E. Y. Ionashiro, C. T. de Carvalho, G. Bannach, E. C. Rodrigues and M. Ionashiro, Quim. Nova, 2007, 30, 318.
9. M. Spohn and J. Strahle, Z. Naturforsch., B: Chem. Sci., 1988, 43, 540.
10. (a) K. S. Gavrilenko, S. V. Punin, O. Cador, S. Golhen, L. Ouhab and V. V. Pavlishchuk, J. Am. Chem. Soc., 2005, 127, 12246; (b) M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379; (c) K. S. Gavrilenko, O. Cador, K. Bernot, P. Rosa, R. Sessoli, S. Golhen, V. V. Pavlishchuk and L. Ouhab, Chem. – Eur. J., 2008, 14, 2034–2043.
11. F. Ephraim and A. Pfister, Helv. Chim. Acta, 1925, 8, 369.
12. C. Balarew, D. Stoilova and R. Krasteva, Thermochim. Acta, 1985, 92, 719.
13. A. Vráblová, L. R. Falvello, J. Campo, J. Miklovič, R. Boča, J. Černák and M. Tomás, Eur. J. Inorg. Chem., 2016, 928.
14. H. Koizumi, K. Osaki and T. Watanabe, J. Phys. Soc. Jpn., 1963, 18, 117.
15. (a) W. Kraus and G. Nolze, J. Appl. Crystallogr., 1996, 29, 301; (b) Oxford Diffraction 2006 CrysAlisPro CCD and CrysAlisPro RED; (c) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3; (d) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2008, 64, 112; (e) K. Brandenburg and H. Putz, Crystal Impact GbR, Bonn, Germany, 1999.
16. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Wiley, New York, 1997.
17. C. Coulon, R. Clérac, W. Wernsforfer, T. Colin and H. Miyasaka, Phys. Rev. Lett., 2009, 102, 167204.
18. C. Coulon, H. Miyasaka and R. Clérac, Struct. Bonding, 2006, 122, 163.
19. T. Liu, D. Fu, S. Gao, Y. Zhang, H. Sun, G. Su and Y. Liu, J. Am. Chem. Soc., 2003, 125, 13976.
20. Z. Xin-Hua, D. Lin-Dan, Z. Yan, S. Dong, W. Dong-Qing, W. Xiao-Qin and W. Xin-Yi, Inorg. Chem., 2017, 56, 8058.

---

Footnote

† Electronic supplementary information (ESI) available: X-ray structure analysis. CCDC 1536321. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8dt03610a

---