Computational insights into the inhibition of β-haematin crystallization by antimalarial drugs

Abstract

During the red blood cell phase of their life cycle, malaria parasites digest their host's haemoglobin, with concomitant release of potentially toxic iron(III) protoporphyrin IX (FePPIX). The parasites’ strategy for detoxification of FePPIX involves its crystallization to haemozoin, such that the build-up of free haem in solution is avoided. Antimalarial drugs of both historical importance and current clinical use are known to be capable of disrupting the growth of crystals of β-haematin, which is the synthetic equivalent of haemozoin. Hence, the disruption of haemozoin crystal growth is implicated as a possible mode of action of such drugs. However, the details of β-haematin crystal poisoning at the molecular level have yet to be fully elucidated. In this study, we have used a combination of density functional theory (DFT) and molecular modelling to examine the possible modes of action of ten different antimalarial drugs, including quinine-type aliphatic alcohols, amodiaquine-type phenols, and chloroquine-type aliphatic diamines. The DFT calculations indicate that each of the drugs can form at least one molecular complex with FePPIX. These complexes have 1 : 1 or 2 : 1 FePPIX : drug stoichiometries and all of them incorporate Fe–O bonds, formed either by direct coordination of a zwitterionic form of the drug, or by deprotonation of water. Most of the drugs can form more than one such complex. We have used the DFT model structures to explore the possible formation of a monolayer of each drug–haem complex on four of the β-haematin crystal faces. In all cases, the drug complexes can form a monolayer on the fast-growing {001} and {011} faces, but not on the slower growing {010} and {100} faces. Additional modelling of the chloroquine and quinidine complexes shows that individual molecules of these species can also obstruct the growth of new layers on other crystal faces. The implications of these observations for antimalarial drug development are discussed.

---

Introduction

Malaria is a mosquito-borne disease resulting from infection with various species of Plasmodium genus parasites, of which P. falciparum and P. vivax pose the greatest risk to public health. Although the World Health Organization has been able to document significant inroads against this disease in previous years, their latest report notes a troubling slowdown in progress.¹ Moreover the eradication of malaria remains a distant goal, such that over 3 billion people are at risk worldwide, with 445 000 deaths in 2016 alone.¹ The global fight against malaria pursues a broad strategy, of which antimalarial drugs remain a key component. However, several previously highly efficacious and cost-effective antimalarials have been rendered less effective by the emergence of resistant Plasmodium strains, and it is surely only a matter of time before current front-line drugs go the same way. Therefore, the development of novel antimalarials remains an important objective in medicinal chemistry.

Although the precise modes of action of many antimalarial drugs are currently unknown, it is clear that one of the primary targets is not a protein or DNA, but rather the haem that is released by the Plasmodium parasite as it digests haemoglobin within the host's red blood cells.^2–4 This free haem is in the form of iron(III) protoporphyrin IX (FePPIX,§Scheme 1). In untreated patients, the parasite is able to detoxify this molecule by a type of biomineralization, such that at least 95% of the FePPIX is locked away in its iron(III) form as poorly soluble haemozoin crystals.⁵ A number of antimalarial drugs are thought to act by disrupting the process of haemozoin crystallization. This can be accomplished by poisoning the growing crystal surfaces, perhaps by formation of a surface monolayer that is no longer recognized by incoming FePPIX molecules.^2,3 It has recently been shown that crystals of β-haematin, which is accepted as the synthetic analogue of haemozoin, can adsorb chloroquine from solution, and that the abilities of several inhibitors to retard the growth of β-haematin in vitro are correlated with the strength of their adsorption on the crystal surfaces.⁶ The overall picture has been further refined by time-resolved atomic force microscopy (AFM) studies, which were used to characterize the in vitro growth of β-haematin crystals in both the absence and presence of antimalarial drugs.^6–8 These experiments indicated that the crystallization of FePPIX proceeds by a classical mechanism in which new 2D crystal layers are nucleated on existing crystal surfaces. In this scenario, relatively low concentrations of the drugs can poison crystal growth by a variety of molecular scale interactions at critical points of the developing 2D surface layers. Further studies revealed that chloroquine (CQ) binds preferentially to the {001} crystal surfaces, whereas amodiaquine (AQ) binds non-preferentially to both the {001} and {010} surfaces.⁹ Both CQ and AQ are able to form 2 : 1 FePPIX : drug complexes,⁸ but the formation of such complexes is not necessarily correlated with the ability to inhibit β-haematin crystal growth. More generally, published experimental studies have not yet been able to resolve the question of whether free drug molecules or molecular drug–haem complexes are responsible for crystal poisoning.

Scheme 1 Forms of iron(III) protoporphyrin IX featured in this study. Dimer (1) is found in crystalline β-haematin, whilst (2) is the π–π dimer encountered in solution.

The powder X-ray crystal structure of β-haematin has been reported by Pagola et al.² The structure is assembled from (FePPIXH)₂ dimers, in which the five-coordinate iron(III) centres are reciprocally bonded to propionate oxygens from their partners, with an Fe–O bond length of 1.886(2) Å. The second propionate group of each monomer is in its neutral, protonated form, and participates in a cyclic hydrogen bond with the neighbouring dimer (Scheme 1, 1). Given the enantiofacial symmetry of the FePPIX monomer, arising from the different positions of its two vinyl groups, the (FePPIXH)₂ dimer can in principle exist as four different stereoisomers; further examination of the β-haematin crystal structure led Straasø et al. to conclude that 86% of their sample was composed of the cd1̄₁ isomer as described by Pagola et al., whilst the remainder consisted of the cd1̄₂ isomer; both phases were also thought to be occluded with the two chiral cd2(+) and cd2(−) enantiomers.¹⁰ Density functional theory (DFT) calculations by Marom et al.¹¹ on the isolated dimers indicated that the cd1̄₁ dimer has the lowest energy in vacuo, but that the cd1̄₂ and cd(2) dimers are only marginally higher in energy, by ca. 2 kcal mol⁻¹; whilst in the crystalline phase, the preference for the cd1̄₁ dimer is enhanced by ca. 9–16 kcal mol⁻¹_. These results are also consistent with a model in which the major and minor crystal phases are composed of the cd1̄₁ and cd1̄₂ dimers respectively, plus occluded cd(2) dimers. In terms of crystal growth, it is generally the case that the size of a given crystal face is inversely proportional to its rate of propagation. On this basis, a theoretical study¹² identified the {100} and {010} faces as being the most developed, with smaller {011} and {001} faces; the latter two faces, as the fastest growing, would be the primary target for drugs that inhibit crystal growth by a face coating mechanism. Scanning electron microscopy showed changes in morphology of bulk β-haematin crystals grown in the presence of various antimalarials, consistent with inhibition of the (001), (01̄1̄) and possibly the {010} faces.⁸

Drugs that are thought to poison β-haematin crystal growth by surface adsorption, as shown in Scheme 2, can be classified according to their functional groups. All these drugs contain a secondary or tertiary amine, plus a planar aromatic system of 10 or 14 π-electrons. In addition, some drugs incorporate a secondary aliphatic alcohol; this group includes quinine (QN), quinidine (QD), mefloquine (MQ), halofantrine (HN) and lumefantrine (LM). A second group consists of phenols, and includes AQ and tebuquine (TQ). Finally, some drugs lack any –OH functionality; these include CQ, mepacrine (MP), and piperaquine (PQ). All ten of these drugs have been shown to inhibit the growth of β-haematin crystals in vitro.^13–15 Furthermore, representatives of all three groups, namely QN, MQ, LM, AQ and CQ, have been shown to cause a decrease in haemozoin and increase in free haem in P. falciparum parasites in vivo.⁴ The naturally occurring Cinchona alkaloids QN and QD are both specific stereoisomers, whilst the synthetic drugs MQ, HN, LM, CQ and MP, which all have at least one stereocentre, are used clinically as racemic mixtures.

Scheme 2 Antimalarial drugs featured in this study.

Important circumstantial evidence for the possible mode of action of the alcohol-containing drugs has been provided in the form of the X-ray crystal structures of 1 : 1 FePPIXH : drug complexes with QN and QD,¹⁶ HN¹⁷ and, most recently, MQ.¹⁸ These structures all show several common features. In each case the iron(III) centre is five-coordinate, being bound to the deprotonated alcohol group of the drug by an alkoxide bond. The amine nitrogen of the drug is protonated and forms a hydrogen bond with the deprotonated propionate group of FePPIXH. The exact details of the amine-propionate hydrogen bonds vary; for QN, QD and MQ they are intramolecular, whilst for HN they are intermolecular. In each case, the aromatic moiety of the drug shows a π–π stacking interaction with the porphyrin ring. Finally, the second propionic acid group of FePPIXH retains its proton, such that the iron(III) complex is neutral overall. In contrast to this wealth of structural data, and despite much effort, no X-ray crystal structure of a molecular complex of CQ with FePPIX has yet been published. Spectroscopic techniques show that drugs such as CQ do interact with FePPIX in solution,¹⁹ although the exact nature of the interaction has remained elusive. Recently, Kuter et al. have characterized the complex formed between FePPIX and CQ in aqueous solution by means of a combined approach involving EXAFS spectroscopy and molecular dynamics simulations.²⁰ A 2 : 1 ratio of Fe(III) : CQ in aqueous solution was established, leading to a model of stoichiometry [(FePPIXH)₂(μ-O)(CQH₂)], as shown in Scheme 3, generic complex C. This complex was characterized by EXAFS in terms of an Fe–O bond length of 1.87 Å, which is unusually long for an Fe(III)–O–Fe(III) dimer, and an asymmetric ν(Fe–O–Fe) stretch at 744 cm⁻¹ in the infrared. These indications of relatively weak Fe–O bonding were attributed to a hydrogen bond between the μ-oxo atom and the protonated quinoline nitrogen of the CQH₂²⁺ moiety. The protonated quinoline ring is intercalated between the two haem rings, such that π–π stacking interactions are another important feature of this complex.

Scheme 3 Generic complexes of FePPIX with antimalarial drugs. All structures are shown as neutral overall; formal atomic charges are omitted for simplicity. In the Venn diagram, the letters A, B and C pertain to the generic complexes in the main scheme.

Studies of the speciation of FePPIX in aqueous solution have been complicated by its tendency to adsorb onto glass and plastic surfaces. Using carefully prepared apparatus, de Villiers et al. were able to minimize this problem,²¹ allowing them to identify an equilibrium between the monomer and a π–π stacked (FePPIX)₂ dimer (Scheme 1, 2) as the dominant species in aqueous solution. In the π–π dimer, the iron(III) atoms are five-coordinate, the axial ligand being either H₂O or OH⁻. We have previously found from DFT calculations that whereas hydroxide is one of the most strongly bound ligands for Fe(III)PPIX, water is among the weakest, such that neutral water ligands should undergo rapid exchange.²² The addition of 10% pyridine (Py) to an alkaline solution of FePPIX is sufficient to induce formation of a μ-oxo [(FePPIX)₂(μ-O)(PyH)] dimer,²¹ analogous to the CQ complex discussed above. However, crystallization of β-haematin requires assembly of the propionate-bridged (FePPIXH)₂ dimer 1, and this process does not occur spontaneously from aqueous solutions of FePPIX under normal physiological conditions. Therefore, the malaria parasite facilitates the growth of haemozoin in its digestive vacuole (DV) by a combination of low pH (ca. 4.8) and the presence of lipids; in particular, a water–lipid interface appears to be required for crystal growth.^7,23 X-ray tomography experiments led Kapishnikov et al. to conclude that haemozoin nucleation occurs at the inner membrane of the DV, with subsequent crystal growth in the aqueous phase.²⁴ A somewhat different view was taken by Kuter et al., who showed that glycerolipids are the key players in haemozoin nucleation.²⁵ Using computational methods, they extended their studies to develop a molecular scale model of crystal growth in which the lipid interior is the site of conversion of the π–π (FePPIX)₂ dimer 2 into the propionate-bridged dimer 1, such that crystal growth is propagated at the lipid–water interface. Regardless of the exact mechanisms of haemozoin nucleation and growth, the acidic, lipid-rich conditions of the DV are conducive to attainment of the required FePPIXH protonation state, in which only one of the haem propionates is protonated (we have previously calculated pK_a values of 4.3 and 5.5 for the two propionates,²² compared to the pH of ca. 4.8 for the DV). Moreover, these conditions encourage protonation of strongly bound OH⁻ ligands to give weakly bound H₂O ligands; they also enhance the competitiveness of propionate over water for axial binding to the Fe(III) centre;^22,25 and attenuate the strength of π–π stacking interactions.²⁶ This is also consistent with in vitro crystal growth experiments under biomimetic conditions,²⁷ which showed that large β-haematin crystals can be obtained by nucleation at an octanol-citric buffer interface, followed by seeding into FePPIX-saturated octanol in contact with citric buffer for further growth. Attempts to grow crystals in either purely aqueous solutions or in anhydrous octanol gave much poorer results.

It is conceivable that the antimalarials in Scheme 2 poison the growth of β-haematin crystals by direct and possibly non-specific interactions with the crystal surfaces. However, the experimental evidence discussed above, showing that several drugs form molecular complexes with FePPIX, raises the question of whether such complexes, rather than the free drug molecules, might be responsible for inhibition of β-haematin growth. With respect to CQ, we have previously used DFT calculations to postulate a theoretical 1 : 1 complex between CQ and FePPIX, in which the drug stabilizes the coordination of a hydroxide ligand, generated from water, at the iron(III) centre (Scheme 3, generic complex B).²⁸ The recruitment of water to form a hydroxide ligand with transfer of the proton to the tertiary amine of CQ would then be analogous to the action of the alcohol-containing drugs, which act as alkoxide ligands to FePPIX with internal proton transfer to the amine. Meanwhile, as discussed above, experimental studies have confirmed that CQ can indeed recruit a water molecule to support an Fe–O bonded complex with FePPIX, however the observed FePPIX : drug stoichiometry is 2 : 1 rather than 1 : 1 (Scheme 3, complex C).²⁰

With these observations in mind, we set out to investigate by theoretical methods whether known and/or putative FePPIX–drug complexes could indeed be responsible for the disruption of β-haematin crystallization. We were particularly interested in exploration of the hypothesis that complexes of FePPIX with antimalarial drugs might poison the growth of β-haematin by forming a monolayer on the fastest growing crystal surfaces. To this end, we have carried out DFT calculations to obtain structures and formation energies for molecular complexes of the ten different β-haematin inhibiting drugs shown in Scheme 2 with FePPIX. We have also used rigid body modelling and molecular mechanics (MM) calculations to investigate the formation of monolayers of these complexes on the primary crystal surfaces of β-haematin. The results of our studies are presented in this paper.

Results and discussion

Methodology and overview

In our previous work,²² we used the experimental binding energies²⁶ of a series of N-donor ligands with FePPIX to evaluate the accuracy of three different DFT procedures employing the B3LYP and OPBE functionals in combination with the LanL2DZ and 6-311+G(d,p) basis sets. These ligands are all characterized as coordinating to the iron(III) centre of FePPIX, rather than interacting by π–π stacking. The best results were obtained by geometry optimization and zero-point energy (ZPE) calculations at the B3LYP/LanL2DZ level, followed by single point calculations with B3LYP/6-311+G(d,p) plus SMD implicit solvent corrections for n-octanol or water as required (method 3). This gave a correlation coefficient R² of 0.865 between the calculated ΔE values and experimental ΔG values. At the outset of the present work, two additional functionals were tested, namely B97D and wB97XD; these were developed to incorporate dispersion and are reported to give good performance in geometry optimizations of transition metal complexes.²⁹ First, the geometries previously obtained at the B3LYP/LanL2DZ level of theory were used for single point calculations in water, using the SMD implicit solvent model and either B97D/6-311+G(d,p) (method 4) or wB97XD/6-311+G(d,p) (method 5). Next, the geometries were recalculated at the B97D/LanL2DZ level and used for single point calculations in water using SMD plus wB97XD/6-311+G(d,p) (method 6). ZPE corrections were included in all cases. The results are summarized in Table 1, along with those previously obtained using method 3. In terms of the correlation with experimental data, methods 4–6 were all found to be somewhat inferior to method 3. Also, as found previously, the values of ΔE obtained with method 3 were closest to the experimental ΔG values. This agreement should not, of course, be taken at face value, since entropy has not been taken into account; although the gas phase entropies of the individual molecules are available from our calculations, we are unable to estimate the contributions from solvent. Nevertheless, based on these results, we have employed method 3 throughout this study also. DFT calculations on the very large [(FePPIXH)₂(μ-O)(drugH₂)] complexes investigated in this study presented some additional complications. The final single point calculations with the 6-311+G(d,p) basis set proved to be intractable for all the drugs except CQ. Exploratory calculations showed that the largest all-electron basis set that could be used successfully on these complexes was 6-31G, but evaluation of this method by the above procedure gave an R² value of 0.741. We therefore reverted to our previously described method 1,²² which uses B3LYP/LanL2DZ for geometry optimization, ZPE calculation, and SMD solvent steps, and gave an R² value for ΔE versus ΔG of 0.840. Meanwhile, using a fragment-based approach to set up the two Fe centres in the dinuclear complexes as antiferromagnetically coupled (overall S = 0) generally gave incorrect, low spins on each metal. To achieve the correct atomic spins, it was necessary to run a sequence of spin-perturbed calculations (S = 1/2, 3/2, 1/2, 0, using guess = read and varying the overall molecular charge as required), until the magnitude of the spin on each iron matched those seen in the corresponding mononuclear complexes. Final spin values are given in the ESI.†

Table 1 Comparison of experimentally obtained free energies (ΔG) and calculated bond energies (ΔE) for coordination of N-donor ligands in water

Species	ΔG^a/kcal mol^−1	Method 3^b	Method 4	Method 5	Method 6
		ΔE/kcal mol^−1	ΔE/kcal mol^−1	ΔE/kcal mol^−1	ΔE/kcal mol^−1
a Values calculated from the data given in ref. 26. b Values taken from ref. 22.
Pyridine	−1.05	−3.48	−16.6	−15.5	−15.0
4-Methyl pyridine	−1.83	−4.21	−17.4	−16.3	−15.8
Imidazole	−3.03	−5.75	−16.9	−16.6	−16.2
Morpholine	−4.88	−5.70	−22.4	−20.2	−20.3
4-Dimethyl aminopyridine	−5.44	−6.70	−20.3	−18.9	−18.3
n-Butylamine	−6.15	−8.56	−21.0	−19.2	−19.0
Correlation coefficient, R^2		0.865	0.745	0.842	0.790

---

Although method 3 does not incorporate dispersion and hence π–π stacking interactions, the strengths of such associations are quite well known from experimental studies. For example, measurements on the interactions of simple aromatic molecules with substituted porphyrins in aqueous solution showed an excellent linear correlation between the number of π-electrons in the aromatic ring system and the dispersion contribution to the free energy, ΔG_disp, equivalent to ca. 1.7, 3.8 and 4.4 kcal mol⁻¹ for aromatic systems of 6, 10 and 14 electrons of respectively.³⁰ The incorporation of heteroatoms made very little difference and the value for quinoline, of particular relevance to this study, was 3.9 kcal mol⁻¹. These dispersion interactions will be somewhat attenuated in solvents of higher polarizability than water,³¹ as found in the malaria parasite's lipid-rich DV.

In attempting to calculate the interaction energies of antimalarial drugs with FePPIX, proper account must be taken of the conformational flexibilities of these molecules, particularly the free drugs. Therefore, at least 30 different input geometries of each free drug molecule were used for the DFT calculations, in order to locate the global minimum with reasonable certainty. Input geometries were generated by torsional searching and/or molecular dynamics (further details are given under Computational methods). It should be noted that the minimum energy conformations found using implicit solvent n-octanol and water models were not always the same. X-ray crystal structures are available for several of the free drugs; these were also used as inputs for DFT calculations, and are compared with the calculated global minima in the following sections. For the FePPIX–drug complexes, fewer conformations were examined, due both to the reduced conformational flexibility of these molecules and the much greater expense of the calculations. Hence, any bias in our data is likely to be in favour of the free drug molecules, leading to underestimation of their FePPIX interaction energies. In the crystal structure of β-haematin, individual dimers are uncharged such that the crystal is a non-ionic lattice. Therefore, we have focussed our attention on neutral FePPIX–drug complexes, since the accretion of a layer of like-charged ions on a non-ionic crystal surface seems less likely on electrostatic grounds.

As an aid to analysis of the various FePPIX–drug complexes modelled in this study, Scheme 3 sets out the various possibilities that have been considered in this work. Generic complex A has a 1 : 1 FePPIXH : drug stoichiometry, and incorporates an alkoxide Fe–O bond, with the drug in its zwitterionic form. This possibility has been demonstrated experimentally by the X-ray crystal structures of FePPIX complexes with QN, QD, MQ, and HN.^16–18 Complex B is an analogous 1 : 1 complex, in which the Fe–O bond is supplied by hydroxide; we have previously postulated such a complex for CQ,²⁸ although there is no experimental evidence for this possibility at present. Finally, complex C has a 2 : 1 FePPIX : drug stoichiometry and includes a bridging oxo ligand; this type of structure has been demonstrated in solution for CQ.²⁰ For all ten drugs in this study, DFT calculations on each of the relevant possibilities, A, B, and C, have been carried out.

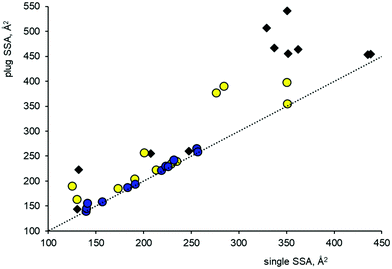
The ability of each FePPIX–drug complex to coat the {001}, {010}, {100} and {011} crystal faces of β-haematin was initially investigated by rigid body modelling; Fig. S1 in the ESI† illustrates the steps involved in these calculations. First, the required FePPIX–drug complex was placed within the β-haematin crystal unit cell as reported by Pagola et al.,² by overlaying selected haem atoms of the complex with the equivalent atoms in one half of the native (FePPIXH)₂ dimer. The original (FePPIXH)₂ dimer was then deleted to leave the FePPIX–drug complex within the β-haematin unit cell. For all ten drugs, some common features emerged at this point. Thus, it proved possible to stack each of the FePPIX–drug unit cells along their a and b axes, but stacking along the c axis invariably led to severe steric clashes. Consequently, we found that each of the complexes can form a monolayer on the {001} and {011} β-haematin crystal faces, but not the {100} or {010} faces. We note that the {010} and {100} faces are thought to grow more slowly than the {001} and {011} faces;¹² hence, all the drug complexes considered in this work are predicted to be selective in poisoning growth of the fastest growing crystal faces. This does not exclude the possibility that single molecules of the drug complexes could also interact with islands or steps on the growing {100} or {010} faces; this has been investigated for QD and CQ (see below). For the {001} and {011} crystal faces, unit cells containing the FePPIX–drug complex were assembled into a monolayer of (5 × 5 × 1) cells, which was then docked onto a (5 × 5 × 2) unit cell model of the appropriate β-haematin crystal face. The {100}, {001} and {011} faces of β-haematin all include one half of the propionate hydrogen bonded dimer which provides the only hydrogen bonding interaction between unit cell layers. Hence, in docking the FePPIX–drug layers onto the native structure, care was taken to orientate the two models such that the propionate groups matched up to form a new layer of hydrogen bonds. Completed (5 × 5 × 3) models were then subjected to geometry optimization as detailed below under Computational methods. This required extension of the CHARMm force field to include parameters for the haem group; although we employed ad hoc values that were not rigorously developed, they proved sufficient for our purposes, since the only major effect of geometry optimization was to resolve close contacts within the initial models. Also, geometry optimizations of a native β-haematin crystallite and the individual FePPIX–drug complexes using our parameters gave good results when compared to the X-ray crystal structure and the DFT geometries, respectively. The optimized (5 × 5 × 3) models were analysed in terms of overlapping surface area, which gives an indication of the extent to which a monolayer of the drug complex covers the surface of the crystal. This has been done in two ways; first, by measuring the shared surface area (SSA) of the central drug complex molecule in each model, subsequently referred to as the plug SSA; and second, by measuring the shared surface area of a single drug complex molecule placed on the centre of a (5 × 5 × 2) haematin model (obtained by editing the (5 × 5 × 3) model, and referred to as the single SSA; see Fig. S1 in the ESI†). Further details are given in the Computational methods section.

Mefloquine, halofantrine and lumefantrine

We commence our analysis of individual drugs with the simplest case, which is provided by MQ, HN and LM. These synthetic antimalarials are all employed as mixtures of the two possible stereoisomers at the alcohol function. HN and LM lack any quinoline-type nitrogen, hence they cannot stabilize a dinuclear [(FePPIXH)₂(μ-O)] core complex (see below). Although MQ includes a quinoline ring, it is easy to show by molecular modelling that its two –CF₃ substituents provide sufficient steric hindrance to prevent the protonated quinoline group from hydrogen bonding with the central oxygen of [(FePPIXH)₂(μ-O)]. Several X-ray crystal structures of free MQ are available;³² these all show intermolecular OH⋯N hydrogen bonds, together with intramolecular NH⋯O hydrogen bonds. Our DFT calculations indicated slightly different global minima in n-octanol and water; the former showed an intramolecular OH⋯N hydrogen bond, whilst the latter showed an NH⋯O hydrogen bond as observed in the crystal structures. The differences in energy between the two geometries were <0.4 kcal mol⁻¹ in both solvents (see the ESI†). Using similar DFT methodology, Fielding et al. also identified the NH⋯O hydrogen bonded structure as the lowest energy conformation in water,³³ whilst Dassonville-Klimpt et al. concluded that the choice of OH⋯N or NH⋯O intramolecular hydrogen bonding depends on the enantiomer.³²

The X-ray crystal structures of mononuclear alkoxide complexes of FePPIXH with HN¹⁷ and MQ¹⁸ have been reported. We have previously modelled the FePPIX–HN complex by DFT, and found that the intermolecular hydrogen bond to propionate observed in the crystal structure can be replaced by an intramolecular equivalent in the isolated complex.²⁸ In the present work, we have extended our studies to the analogous complexes of MQ and LM. The structures of all three DFT model complexes are shown in Fig. 1. The crystal structure of the FePPIXH–MQ complex shows a cyclic intramolecular hydrogen bonding network involving both H atoms of the protonated piperidinium nitrogen, plus both the propionate and propionic acid groups of FePPIXH;¹⁸ in our model, we have simplified this such that the propionic acid group is not involved in hydrogen bonding, and is therefore available for docking to the haematin crystal surface. In other respects, our model is in good agreement with the crystal structure.

Fig. 1 DFT-optimized structures of mononuclear FePPIXH–drug complexes. Atom colours are as follows; FePPIXH carbon, light grey; drug carbon, dark grey; hydrogen, white; chlorine, light green; fluorine, cyan; iron, dark green; nitrogen, blue; oxygen, red. Hydrogen atoms attached to carbon are omitted for clarity.

The calculated energies of complex formation, using method 3, are given in Table 2. We have previously²⁸ examined the energy profiles for the formation of such complexes in terms of two hypothetical reaction steps, namely the formation of the drug zwitterion (Scheme 3, step A1) followed by the reaction of the latter with FePPIX (step A2). The results of these calculations are also given in Table 2. The cost of zwitterion formation is always more than offset by the benefit of complexation, such that MQ, HN and LM are all predicted to form stable complexes with FePPIX, in both n-octanol and water. As discussed above, these complexes will be further stabilized by π–π stacking between their aromatic rings and the haem, which is not included in our calculations.

Table 2 Calculated method 3 energies for formation of 1 : 1 complexes of zwitterionic antimalarial drugs with FePPIXH in n-octanol (values for water are given in parentheses), together with Fe–O(drug) bond lengths^a

	ΔE (step A1)/kcal mol^−1	ΔE (step A2)/kcal mol^−1	ΔE (A1 + A2)/kcal mol^−1	Fe–O bond length/Å
a Experimental bond lengths are given in parentheses (see main text for references). b All 30 DFT calculations on zwitterionic conformers of DAQ reverted to the neutral form upon geometry optimization.
1. Secondary alcohols
MQ	+20.3 (+14.0)	−34.3 (−20.8)	−14.0 (−6.8)	1.873 (1.892, 1.899)
HN	+26.3 (+19.2)	−32.2 (−19.8)	−5.8 (−0.5)	1.865 (1.840)
LM	+22.4 (+16.4)	−28.8 (−17.9)	−6.4 (−1.4)	1.876
QN(1)	+18.6 (+13.8)	−31.5 (−18.9)	−12.9 (−5.1)	1.866 (1.866)
QN(2)	+18.6 (+13.8)	−29.6 (−16.9)	−11.0 (−3.1)	1.866
QD(1)	+18.5 (+13.4)	−31.8 (−19.5)	−13.3 (−6.1)	1.874 (1.862)
QD(2)	+18.5 (+13.4)	−29.1 (−16.9)	−10.7 (−3.5)	1.869
2. Phenols
AQ	+11.0 (+7.5)	−17.3 (−8.0)	−6.3 (−0.4)	1.885
DAQ	N/A^b	N/A	−10.3 (−3.7)	1.883
TQ	+14.0 (+10.8)	−17.9 (−10.1)	−3.9 (+0.7)	1.927

---

For all three of these zwitterionic complex models, the neutral propionic acid group is not involved in intramolecular hydrogen bonding, and is consequently available to form the intermolecular propionic acid hydrogen bond seen in the crystal structure of β-haematin. We have therefore investigated the ability of these FePPIX–drug complexes to form monolayers on the most important crystal surfaces of β-haematin, as described in the Methodology section. The SSA's for the single and plug models are shown graphically in Fig. 2. This plot shows that all the mononuclear drug complexes give broadly similar SSA's. Although the single SSA values for single drug complex molecules placed on the β-haematin faces are generally similar to those for the native (FePPIXH)₂ dimer placed on the {100} and {010} faces of the native crystal (horizontal axis), the plug SSA's (vertical axis) are appreciably smaller. In particular, the deep corrugations in the {001} faces remain largely unoccupied by these mononuclear FePPIXH–drug complexes. The surface coverage models for the HN complex, as representative of this class of drug, on the (001) and (011) crystal faces are illustrated in Fig. 3 (drug-surface combinations not shown in Fig. 3 are given in the ESI†). Apart from considerations of van der Waals surface contact areas, the drug complex monolayers on both the {001} and {011} faces can participate in cyclic propionate hydrogen bonding to dock with the β-haematin surface, as seen for the native (FePPIXH)₂ dimer. Hence, the results of this theoretical study lend support to the hypothesis that the crystallographically observed HN and MQ complexes of FePPIXH, and the analogous complex of LM, are all able to poison the growth of β-haematin by forming monolayers on the fast-growing {001} and {011} crystal faces. It should be noted that since the opposite crystal faces of β-haematin are mirror images, the complexes modelled here will only complement one of each pair of crystal faces. However, since these drugs are all used as racemic mixtures, each of the resulting pairs of complexes will complement one or other of the crystal face pairs.

Fig. 2 Calculated single and plug shared surface areas (SSA's) for FePPIXH–drug complexes. Black diamonds are values for the native (FePPIXH)₂ dimer; the dotted line linking these points is included as a visual aid. Circles and squares are points for the {001} and {011} faces respectively. Points inside and outside of the dashed circle are for the mononuclear complexes of zwitterionic drugs and the dinuclear μ-oxo complexes respectively. The data points for [(FePPIXH)₂(μ-O)(PQH₂)] are labelled ‘PQ’. Other points are coloured as follows; QN, cyan; QD, dark blue; MQ, red; HN, orange; LM, grey; AQ, light green; DAQ, dark green; TQ, pink; CQ, yellow; MP, black.

Fig. 3 MM-optimized models of the {001} and {011} β-haematin crystal faces coated by a monolayer of the FePPIXH–drug complex. The base β-haematin crystal is coloured blue. The central drug complex molecule is rendered in atomic colours (see Fig. 1 caption), and the surrounding drug complexes are coloured yellow.

Recently, Fielding et al. have concluded from DFT calculations that MQ could stabilize a hydroxy complex of FePPIX, formulated as [FePPIXH₂(OH)(MQH)]⁺, perhaps as an intermediate on the path to the experimentally characterized alkoxide complex.³³ Apart from the overall positive charge, this complex is analogous to the neutral 1 : 1 complex of CQ that we postulated previously,²⁸ and the hydroxy complexes of several other drugs as discussed below.

Quinine and quinidine

The alkaloids QN and QD are diastereomers; X-ray crystal structures of both the free drugs^34,35 and their 1 : 1 complexes with FePPIX¹⁶ are available. Our calculations on free QN indicated slightly different minimum energy structures in n-octanol and water, associated with rotations about the two C–C bonds adjacent to the hydroxy group; the difference in energy between the two conformers is ca. 0.5 kcal mol⁻¹ in both solvents (section 17 of the ESI† gives values of these torsion angles for the experimental and calculated structures of QN and QD). The calculated minimum in n-octanol is in excellent agreement with the X-ray crystal structure of QN.³⁴ For QD, a single conformer was identified as the global minimum in both solvents. This differs from the X-ray crystal structure of QD,³⁵ both in the torsion angles of the C–C bonds adjacent to the hydroxy group, and in the disposition of the MeO⁻ group, which is flipped by 180° between the experimental and calculated structures. In terms of these three torsion angles, the calculated minimum for QD is very similar to that obtained for QN in water. DFT calculations on the X-ray geometry of QD (including geometry optimization) indicated that it is 1.2 and 1.6 kcal mol⁻¹ higher in energy than our minimum, in n-octanol and water respectively. It is worth noting that since the crystal structures of both drugs show intermolecular hydrogen bonds, the crystal packing energies are probably greater than the small energy differences found in our calculations.

The crystal structures of the complexes of QN and QD with FePPIX show that in both cases, the drug has again adopted a zwitterionic form to provide a strong Fe–O(alkoxide) bond, plus an intramolecular hydrogen bond between the drug's NH⁺ moiety and the –CO₂⁻ group of FePPIXH. In principle, these drugs could form the intramolecular hydrogen bond with either of the propionate groups of FePPIXH, depending on the conformations of the complexes. We designate the conformations observed in the crystal structures as QN(1) and QD(1). Alternative conformations, allowing the drugs to switch to the other propionate, have also been modelled by DFT calculations and are designated as QN(2) and QD(2) respectively; pictures of all four structures are given in Fig. 1. These conformers proved to be slightly higher in energy, by 1.9 and 2.6 kcal mol⁻¹ respectively in n-octanol, compared to the crystal structure conformers. This is expected, since these conformations were not observed by crystallography; nevertheless, they are predicted to be energetically accessible in both n-octanol and water (see Table 2). Their significance is that one of each pair of complex structures is suitable for binding to the opposing {001} and {011} faces of the β-haematin crystal, as discussed below. The crystal structures of both the QN and QD complexes showed disorder of the vinyl and methyl groups of the FePPIX moieties; a calculation on the alternative arrangement for the QD(1) complex gave virtually identical energies, of +0.3 and +0.1 kcal mol⁻¹ in n-octanol and water respectively; this is within the error margin of our calculations. Hence, this type of isomerism has not been investigated further for any drugs.

Next, we spliced each of these four models within the β-haematin unit cell, to investigate their ability to coat the crystal faces. The usual trend was observed, such that steric hindrance prevented stacking along the c-axis only, but both the {001} and {011} faces could be coated by a monolayer of the complementary drug complex. Specifically, conformers QN(2) and QD(1) can form cyclic propionic acid hydrogen bonds with the (001) face, whilst QN(1) and QD(2) are suitable for the (001̄) face. The coverage of opposing {001} faces by the two QN complexes is illustrated in Fig. 3. The SSA analysis, Fig. 2, showed that these mononuclear complexes of QN and QD are typical in terms of their crystal surface coverage.

Recent AFM experiments have shown that CQ (or an FePPIX–CQ complex) absorbs on {100} terraces of growing β-haematin crystals, poisoning the growth of new layers on these crystal faces.^7,8 We decided to investigate this possibility for our FePPIXH–QD complex, as representative of the 1 : 1 complexes described in this work. In terms of crystal modelling, this presents a more complicated problem than the construction of monolayers on crystal surfaces, since a growing island presents many different environments for the attachment of inhibitors, rather than just one. Our approach was to construct an 8 × 10 unit cell model of the β-haematin (100) face, with an irregular island of 14 (FePPIXH)₂ dimers on its surface. It proved possible to surround this island with 12 FePPIXH–QD complexes, each of which is in a unique environment (Fig. 4). In all cases, the drug complexes were able to form the propionate hydrogen bond with the base layer of the crystal; in order to do this, the QD(1) isomer was required for nine of the positions, and the QD(2) isomer for the remaining three (see Fig. 4 caption). The resulting poisoned island model was analysed for SSA values in a similar way to the surface monolayer models; plug SSA's were measured by deleting each individual QD complex in turn from the complete model, and single SSA's were measured for each individual QD complex attached to the β-haematin surface plus island model. For comparison, a further model was constructed in which the QD complex molecules were replaced by (FePPIXH)₂ dimers, representing the normal growth of the island in the absence of the drug. The results of these SSA calculations are shown in Fig. 5. The dotted line represents the situation where the plug and surface SSA values are identical, which will be the case when there is no synergy between a bound molecule and its neighbours in the growing layer; all data points must lie on or above this line. We find that the overall range of single SSA's for the QD complexes lies within that of the (FePPIXH)₂ dimers, suggesting that FePPIXH–drug molecules can compete with native (FePPIXH)₂ dimers for individual island growth sites. Since all of the data points for the drug complexes lie very close to the limit where the surface and plug SSA's are equal, there is very little synergy between adjacent complex molecules; this is also evident from Fig. 4, where each drug complex is essentially independent of its neighbours. Overall, our results suggest that as well as coating the {001} and {011} faces, these 1 : 1 FePPIX–drug complexes can also hinder the growth of steps and/or islands on other crystal surfaces such as the {100} faces. Given the considerable variations in SSA's shown in Fig. 5, poisoning of these growth sites is likely to be anisotropic, with some binding sites preferred over others.

Fig. 4 Stereo views of island blocking by the mononuclear QD complex and the dinuclear CQ complex on the (100) face of β-haematin. The base β-haematin crystal is coloured blue. The surface island, composed of 14 (FePPIXH)₂ dimers, is shown in orange. The drug complexes are rendered in atomic colours (see Fig. 1 caption). In both cases, the three drug complex molecules on the bottom right diagonal are of the alternate conformation, in order to match the propionate hydrogen bonding pattern of the base layer.

Fig. 5 Single and plug SSA values for molecules surrounding an island of 14 (FePPIXH)₂ dimers on the (100) face of β-haematin. Black diamonds are for native (FePPIXH)₂ dimers, blue circles for mononuclear [FePPIXH(QD)] complexes, and yellow circles for dinuclear [(FePPIXH)₂(μ-O)(CQH₂)] complexes. The dotted line represents the case where plug SSA = single SSA.

To the best of our knowledge, there is no experimental evidence for a 2 : 1 FePPIX–drug complex of either QN or QD. However, since these drugs incorporate a quinoline moiety, we decided to investigate whether they can stabilise their corresponding oxo-bridged dinuclear complexes, analogous to the known complex of CQ (see Introduction). To our surprise, our DFT calculations yielded viable geometries for both [(FePPIXH)₂(μ-O)(QNH₂)] and [(FePPIXH)₂(μ-O)(QDH₂)], as shown in Fig. 6. In common with the equivalent CQ complex, the drug molecules are protonated at both the quinoline and amino nitrogen atoms, allowing hydrogen bonds with both the central oxo ligand and the FePPIX propionate group; these complexes should also benefit from very similar π–π stacking interactions. In addition, both the QNH₂²⁺ and QDH₂²⁺ moieties use their alcohol groups to form an additional hydrogen bond to a second FePPIX propionate group, which has no parallel for the CQ complex.

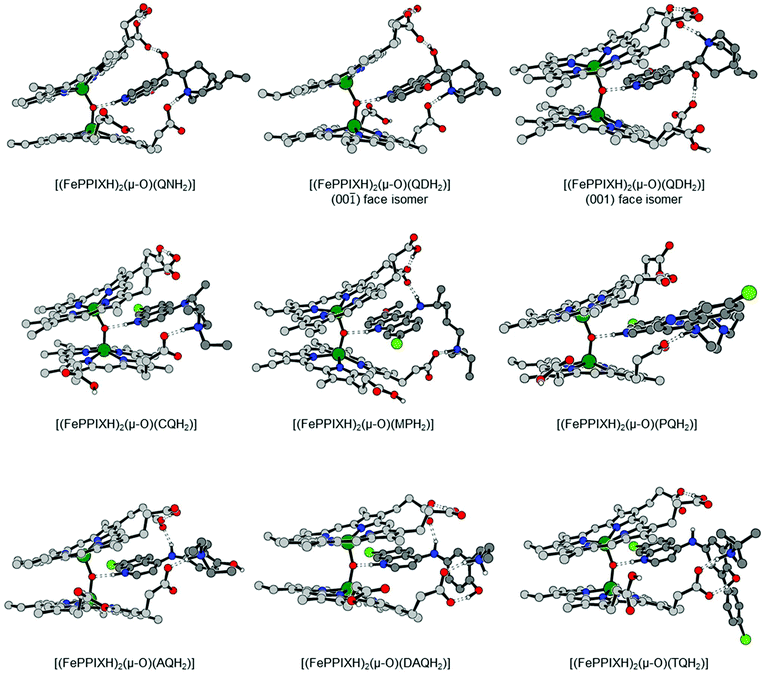Fig. 6 DFT-optimized structures of the dinuclear, μ-oxo bridged FePPIXH–drug complexes. Atom colours as in Fig. 1. Hydrogen atoms attached to carbon are omitted for clarity.

For purposes of comparison, we can define equations for the formation of these 2 : 1 complexes in two different ways, C1 and C2 (Scheme 3). The calculated energies for these reactions are given in Table 3, along with the calculated Fe–O bond lengths and asymmetric ν(Fe–O–Fe) frequencies. Except for CQ, all the 2 : 1 complexes considered in this work were too large to obtain method 3 energies; therefore, these values were calculated with method 1. The formation energies for the 2 : 1 complexes of QN and QD are very similar to those for the experimentally observed CQ analogue (see below). Hence, our DFT calculations imply that QN and QD can form either 1 : 1 or 2 : 1 complexes with FePPPIX, depending on the relative concentrations of the reactants, together with the availability of water for provision of the bridging oxo ligand in the latter. As with the 1 : 1 complexes, the 2 : 1 complexes of QN and QD will match only one of each pair of crystal faces; therefore, for QD, we have also modelled a second conformation in which the alternative propionate is available for docking with the crystal surface (the matching surfaces are given in the footnotes to Table 3). This alternative conformation is only 0.8 kcal mol⁻¹ higher in energy (in n-octanol). Our surface analyses indicate that these 2 : 1 complexes give better surface coverage of both the {001} and {011} faces than the corresponding 1 : 1 complexes, particularly with respect to the plug SSA values (Fig. 2). This can be ascribed to both to the larger sizes of the dinuclear complexes, and to partial occupation of the crystal surface corrugations by the quinuclidine vinyl group for the latter.

Table 3 Calculated method 1 energies for formation of 2 : 1 complexes of antimalarial drugs with Fe(PPIXH) in n-octanol (see Scheme 3; values for water are given in parentheses), together with Fe–O bond lengths and ν(Fe–O–Fe) frequencies^a

	ΔE (reaction C1)/kcal mol^−1	ΔE (reaction C2/C3)/kcal mol^−1	Fe–O /Å	ν(Fe–O–Fe)/cm^−1
a IR frequencies are uncorrected. b Experimental values taken from ref. 20. c Values for [(FePPIXH)2(μ-O)(CQH2)] shown in italics were obtained by method 3; the other complexes were too large for this method. d Isomer suitable for binding to the (001) crystal face of β-haematin. e Isomer suitable for binding to the (001̄) crystal face.
1. Drugs lacking –OH groups
[(FePPIXH)2(μ-O)(CQH2)]	−32.6 (−23.4)	−11.4 (−10.3)	1.849, 1.865 (1.87)^b	678 (744)^b
	−8.5 (0.0)^c	−1.0 (0.0)
[(FePPIXH)2(μ-O)(MPH2)]	−26.1 (−15.2)	−4.0 (−1.6)	1.851, 1.865	672
[(FePPIXH)2(μ-O)(PQH2)]	−10.2 (−0.2)	+12.2 (+11.9)	1.846, 1.862	685
2. Secondary alcohols
[(FePPIXH)2(μ-O)(QNH2)]^d	−32.8 (−21.2)	−10.8 (−7.3)	1.856, 1.873	661
[(FePPIXH)2(μ-O)(QDH2)]^e	−32.1 (−20.7)	−9.5 (−5.7)	1.857, 1.873	659
[(FePPIXH)2(μ-O)(QDH2)]^d	−31.4 (−19.6)	−8.7 (−4.6)	1.863, 1.864	661
3. Phenols
[(FePPIXH)2(μ-O)(AQH2)]	−17.4 (−7.1)	−6.0 (−3.6)	1.849, 1.861	683
[(FePPIXH)2(μ-O)(DAQH2)]	−25.0 (−12.7)	−11.7 (−7.4)	1.846, 1.860	684
[(FePPIXH)2(μ-O)(TQH2)]	−23.5 (−12.3)	−11.5 (−7.7)	1.848, 1.861	682

---

To summarize this section; we predict that both QN and QD can form either 1 : 1 or 2 : 1 complexes with FePPIX, depending on relative concentrations and the availability of water. The former have been observed by X-ray crystallography, whilst the latter are currently unobserved to the best of our knowledge, but are predicted to be the more stable form by our calculations (cf.Table 3 energies for step C2 in Scheme 3), and also give better crystal surface coverage.

Chloroquine, mepacrine and piperaquine

X-ray crystal structures of free CQ³⁶ and PQ³⁷ are available. Our calculated minima for CQ in n-octanol and water were slightly different, due to rotation of the –N(Et)₂ group, with very small associated energy differences (<0.2 kcal mol⁻¹). The X-ray structure of CQ differed from both, in that the CCCN torsion for the –N(Et)₂ group was −73.9° rather than values of ∼180° for the two model structures; since the all-trans arrangement should be preferred for an isolated molecule, this discrepancy can be attributed to compacting of the molecule in the crystal structure. Similarly, the single global minimum for PQ in both solvents had an all-trans conformation for the central –N(CH₂)₃N– moiety, compared to a gauche/trans arrangement in the X-ray structure. For both CQ and PQ, geometry optimizations of the X-ray crystal structures indicated that they were ca. 0.7 kcal mol⁻¹ higher in energy than the calculated global minima, in n-octanol as solvent.

Since CQ, MP and PQ lack any hydroxy functional groups, they cannot form an alkoxide complex. Furthermore, DFT calculations indicate that the three nitrogen atoms of CQ should all bind rather weakly to the iron(III) centre of FePPIX.²² We have previously postulated a 1 : 1 complex of CQ, formulated as [FePPIXH(OH)(CQH)], in which the drug stabilizes a hydroxyl ligand on the Fe(III) centre (Fig. 1).²⁸ Formation of this 1 : 1 complex is predicted to be energetically neutral in water, but favourable in n-octanol (see Table 4; as usual, these values do not include the π–π stacking contribution, which is expected to be ∼3.9 kcal mol⁻¹ for the quinoline group in water,³⁰ and rather less in n-octanol³¹). This 1 : 1 complex is currently unknown from experiment; however a related 2 : 1, oxo bridged complex has recently been experimentally characterized in solution.²⁰ Our DFT model of the 2 : 1 complex [(FePPIXH)₂(μ-O)(CQH₂)] is shown in Fig. 6; its direct formation is represented by reaction C1 in Scheme 3. Based on our method 3 DFT calculations, the energetics of this reaction are remarkably similar to those of the 1 : 1 complex, being neutral in water but favourable in n-octanol (Tables 3 and 4). Hence, π–π stacking is probably decisive in stabilizing the 2 : 1 complex over the 1 : 1 complex, since this interaction should be greater for the former compared to the latter. The calculated Fe–O bond lengths for [(FePPIXH)₂(μ-O)(CQH₂)] are in good agreement with experiment (Table 3); the calculated asymmetric ν(Fe–O–Fe) stretching frequency of 678 cm⁻¹ is rather lower than the experimental value of 744 cm⁻¹, but this is perhaps unsurprising given the complexity of this vibrational mode. For comparison, the experimental IR spectrum of the drug-free oxo complex shows the ν(Fe–O–Fe) stretch at 880 cm⁻¹, whilst DFT calculations on the [(FePPIX)₂(μ-O)]⁴⁻ ion using the OPBE functional and LanL2DZ basis set underestimated this frequency also, placing it at 724 cm⁻¹.³⁸ Meanwhile, a trial calculation on the drug-free hydroxyl complex [(FePPIXH)(FePPIXH₂)(μ-OH)] gave a much lower ν(Fe–O–Fe) frequency of 506 cm⁻¹ (note that for all of the 2 : 1 complexes in Table 3, the calculated geometries indicate a central oxo ligand supported by a hydrogen bond from the drug's protonated aromatic N, rather than proton transfer from the drug to give a bridging μ-OH ligand, such that the N–H and NH⋯O distances are 1.04–1.06 and 1.71–1.93 Å respectively).

Table 4 Calculated method 3 energies for formation of 1 : 1 hydroxide complexes of antimalarial drugs with Fe(PPIXH) in n-octanol (see step B1 in Scheme 3; values for water are given in parentheses), together with Fe–O bond lengths

	ΔE (step B1)/kcal mol^−1	Fe–O bond length/Å	π–π stacking^a
a Visual assessment of whether the geometry of the complex is suitable for π–π stacking between the drug's aromatic rings and the porphyrin.
1. Drugs lacking –OH groups
CQ	−7.5 (0.0)	1.836	Yes
MP	−8.4 (−0.5)	1.824	Marginal
PQ	−4.4 (+5.4)	1.788	Marginal
2. Phenols
AQ	−1.0 (+6.2)	1.908	Yes
DAQ	−4.3 (+2.7)	1.894	No
TQ	−4.1 (+2.6)	1.893	No

---

Overall, our calculations are consistent with the 2 : 1 complex of CQ being the preferred product, especially in view of the higher concentration of FePPIX compared to CQ under biological conditions; however, we cannot rule out a kinetic role for the 1 : 1 complex, either in the dynamic process of crystal growth poisoning, or as an intermediate in assembly of the 2 : 1 complex (reaction C3 in Scheme 3). Indeed, we found that shifting a proton from the free propionic acid group of the 1 : 1 complex to the quinoline nitrogen gave a tautomer, formulated as [FePPIX(OH)(CQH₂)], that was not much higher in energy (+3.9 and +3.5 kcal mol⁻¹ in n-octanol and water respectively), as shown in Fig. 1. This structure can be described as intermediate between the 1 : 1 and 1 : 2 complexes. It finds experimental precedent in the X-ray crystal structure of a 2 : 2 gallium(III) protoporphyrin IX complex of CQ, formulated by Dodd and Bohle as [GaPPIX(OMe)(CQ)]₂, in which the protonated quinoline of the CQH₂²⁺ moiety is hydrogen bonded to the methoxide O atom, whilst the protonated amine group is hydrogen bonded to propionate.³⁹

Turning to mepacrine, we were able to model a 1 : 1 hydroxyl complex of formula [(FePPIXH)(OH)(MPH)], whose energy of formation is similar to that of the analogous CQ complex (Table 4). Similarly, the 2 : 1 complex [(FePPIXH)₂(μ-O)(MPH₂)] was also modelled (Fig. 6). The energy of formation of the latter, using method 1 (Table 3), though somewhat less favourable than for the CQ analogue, suggests that this species would be accessible in solution. Overall, we infer that like CQ, either or both of the 1 : 1 and 2 : 1 complexes of MP could be present under the conditions within the parasite's DV. Similar results were obtained for piperaquine, although the 1 : 1 and the 2 : 1 complexes are both predicted to be less stable than their CQ and MP analogues (Tables 3 and 4). The large size of PQ limited the number of complex geometries that could be investigated, possibly biasing our results; the structures of the 1 : 1 and 2 : 1 complexes are given in the ESI† and Fig. 6 respectively. Although our method 1 calculations suggest that the 1 : 1 complex is more stable than the 2 : 1 complex in this case, we note that the geometry of the 1 : 1 complex is poorly suited for π–π interactions between the quinoline and haem rings, whereas the 2 : 1 complex should benefit from such interactions, since the quinoline ring is intercalated between the two haem rings. Hence, the two complexes should be more similar in energy than predicted by our DFT calculations.

In terms of their ability to poison the growth of β-haematin, the SSA's of the 1 : 1 complexes of CQ, MP and PQ on the {001} and {011} crystal faces were all in the typical ranges (see ESI, section 14†). However, all three 2 : 1 complexes gave significantly better surface coverage (Fig. 2). In particular, the piperaquine 2 : 1 complex gave the best surface coverage of all the drugs considered in this work. This can be attributed to the extra quinoline group of PQ, which fits very well within the corrugations of these crystal faces. It should be noted that CQ and MP are both used as mixtures of the two possible stereoisomers, whilst PQ lacks any stereocentres; hence the question of stereochemical matching between the drug complexes and opposing crystal surfaces does not require detailed analysis for these drugs.

In view of recent AFM observations of poisoning of the {100} terraces of β-haematin by CQ,^7,8 we investigated the ability of the 2 : 1 FePPIX–CQ complex to surround our model of an island on the (100) crystal face, as described above for the 1 : 1 QD complex (Fig. 4). Similar results were obtained; thus, 12 molecules of [(FePPIXH)₂(μ-O)(CQH₂)] were used to surround the island; as before, three of these required the alternative conformation in which the other propionate group is available for hydrogen bonding to the crystal surface (since CQ is used as a mixture of stereoisomers, this was generated by simply reflecting the original model). As shown in Fig. 5, the surface SSA's for the 2 : 1 CQ complex again fitted within the range of values for the native (FePPIXH)₂ dimer, and tended to be superior to the values for the smaller 1 : 1 QD complex. Furthermore, some of the plug SSA values suggest a degree of synergy for adjacent binding of 2 : 1 complex molecules. Since these results are in qualitative agreement with the crystal surface coverage properties shown in Fig. 2, we conclude that in general, the 2 : 1 complexes give better surface coverage than the 1 : 1 complexes, both in providing a monolayer on the {001} and {011} faces, and in blocking terrace or island growth on other faces.

Amodiaquine and tebuquine

The X-ray crystal structure of AQ propanol solvate is available.⁴⁰ Our calculated minimum, which was the same in both n-octanol and water, differed only in alternative arrangements of the ethyl groups of the –NEt₂ moiety; optimization of the crystal structure showed it to be <0.3 kcal mol⁻¹ higher in energy in both solvents, hence this difference can be attributed to crystal packing effects. Both the calculated and experimental structures show an intramolecular hydrogen bond between the phenol –OH and the tertiary amine; a feature that is also present in our calculated structure of TQ. AQ and TQ are representatives of a family of drugs that incorporate phenolic groups, in addition to quinoline and amine functionalities. Hence, these drugs might act in a similar way to CQ, recruiting water to form either a 1 : 1 or a 2 : 1 complex with FePPIX; or alternatively they might form a direct Fe–O bond via phenolate. Since AQ is rapidly hydrolysed to desethyl amodiaquine (DAQ) in vivo,⁴¹ we have also included the latter in our calculations. The calculated energies for formation of the three different complexes of each drug are given in Tables 2–4, and the structures of the zwitterionic and dinuclear complexes are shown in Fig. 1 and 6 respectively. The higher acidities of phenols should make zwitterion formation easier than for the alcohols, and this is confirmed by the lower step A1 energies for these drugs (Table 2); however, the Fe–O bonds (step A2) are proportionately weaker, such that the overall formation energies for the phenoxide complexes are very similar to those of the alkoxides.

DAQ always gives superior complexation energies than AQ, hence the rapid metabolism of AQ to DAQ should enhance the biological effect of this drug. For all three drugs, the two alternative 1 : 1 complexes involving phenoxide or hydroxide Fe–O bonds have favourable energies of formation in n-octanol (Tables 2 and 4 respectively); however these 1 : 1 complexes tend to have geometries that are poorly suited to π–π stacking of the quinoline with the porphyrin (Fig. 1 and Table 4). Also, the extra chlorophenyl group of TQ introduces steric bulk which destabilizes the phenoxide complex, reflected in a longer Fe–O bond length and weaker energy of formation compared to the AQ and DAQ complexes (Table 2). Comparison of the method 1 energies for formation of the 2 : 1 complexes with that for CQ (Table 3) suggests that these species should also be accessible, and will benefit from similar π–π stacking interactions (see Fig. 6). The chlorophenyl substituent of TQ does not perturb the structure of the 2 : 1 complex. Similar to the dinuclear complexes of QN and QD, the hydroxy groups of DAQ and TQ are involved in hydrogen bonding to the propionate groups of FePPIXH.

In terms of β-haematin surface coverage, these drugs give typical results (Fig. 2); both forms of the 1 : 1 complexes give single and plug SSA values in the usual ranges for the {001} and {011} crystal faces, whilst the 2 : 1 complexes give superior SSA values. Overall, our results suggest that the 2 : 1 complexes of DAQ and TQ are most likely to be the active forms of AQ and TQ respectively, in which case the main function of the phenol group is to provide an additional hydrogen bond to propionate within these complexes.

Conclusion

The ten antimalarial drugs considered in this work are all known to interfere with the growth of β-haematin crystals, but the precise molecular basis of this interaction is currently unknown from experiment. In particular, the question of whether the drugs adhere directly to the crystal surface, or whether they act by forming molecular complexes with FePPIX, remains unresolved. We do know from experiment that QN, QD, HN, and MQ all form 1 : 1 complexes with FePPIX, whilst CQ forms a 2 : 1 complex. In this work, we have shown that all ten drugs can form at least one type of complex with FePPIX, with geometries and energies that are comparable to the experimentally established cases. Our results are summarized in the Venn diagram in Scheme 3. Only three of the drugs, namely HN, MQ, and LM, are limited to 1 : 1 complexes with FePPIX, being unsuitable for the formation of a 2 : 1 μ-oxo complex (C). Since the 1 : 1 zwitterionic complexes (A) of HN and MQ have been experimentally characterized, we have not considered the alternative 1 : 1 hydroxide complexes (B) in this work; we note, however, that recently published DFT calculations on such a complex for MQ³³ suggest that this may be another possibility. On the other hand, CQ, MP, and PQ all lack hydroxy groups and so require water to form either 1 : 1 hydroxide (B) or 2 : 1 μ-oxo (C) complexes, whilst QN and QD can either recruit water to form a 2 : 1 μ-oxo complex, or react directly with FePPIX in their zwitterionic forms. TQ, AQ and DAQ are the most versatile of all; each can form three distinct complexes with FePPIX, at least in silico. The five drugs for which we have modelled 1 : 1 hydroxide complexes can also give 2 : 1 μ-oxo complexes, and furthermore the 2 : 1 complexes give better crystal surface coverage. Together with the lack of any experimental evidence for their existence, we suspect that the 1 : 1 hydroxide complexes are probably the least important in terms of crystal poisoning, although they may serve as intermediates in formation of the 2 : 1 μ-oxo complexes. The ability to complex with FePPIX in more than one way might be a useful property for these drugs, since it could help to keep the drug associated with FePPIX under conditions of different concentrations of the drug, FePPIX and water, as well as pH and solvent polarity. From an experimental point of view, our results reaffirm the caveat that observation of any particular complex under a given set of in silico or even in vitro conditions should not be over-interpreted to exclude other possibilities which could be more relevant in vivo. Indeed, although both MQ and LM have been shown to inhibit the growth of β-haematin in vitro, recent experiments suggest that they have little or no effect on the development of haemozoin crystals in living parasites.⁴²

Crystal growth poisoning is facilitated if a drug or its complex can recognise a variety of different crystal surfaces, including faces, steps and islands. This is probably the strongest indicator that their complexes with FePPIX are the functionally relevant forms of these drugs. Nothing resembles the native (FePPIXH)₂ dimer more closely than an FePPIX–drug complex. Each of these drug complexes has a free propionic acid group, which can form the hydrogen bonding dimer that is the only polar interaction on the crystal surfaces. Recurring structural motifs among these drugs (quinoline groups, amines, alcohols, and their geometric relationships) can all be rationalized in terms of the structures of their corresponding complexes with FePPIXH. According to our surface coverage models, a common shortcoming of most drugs is that they do not occupy the deep corrugations on the {001} crystal faces. For example, lumefantrine has the highest surface area among the free drugs, but the {001} face corrugations remain unoccupied by the [(FePPIXH)(LM)] complex, with the aromatic group projecting away from the surface (see sections 13 and 16 of the ESI†). The exception is the 2 : 1 complex of PQ, in which one of the two chloroquinoline groups is located within the corrugation, although this complex is predicted to be less stable than the other 2 : 1 complexes. This suggests a promising avenue for future drug design; to search for drugs that form stable 1 : 1 and/or 2 : 1 complexes with FePPIX, and also possess substituents that can occupy the β-haematin surface corrugations. Our own efforts in this regard have focussed on 1 : 1 complexes in which the zwitterionic form of the drug is more accessible than for known drugs; the results of these studies will be published in due course.

Finally, it should be remembered that poisoning haemozoin crystal growth is not, of itself, the final goal of such drugs. Rather, it is to increase the concentration of reactive FePPIX species in solution to levels that are toxic to the parasite. A five-coordinate alkoxide or μ-oxo FePPIX–drug complex, whilst desirable for crystal poisoning, is probably less toxic than free FePPIX to the parasite, since the iron centre(s) should be more inert than those of the free haem. Hence, these drugs must poison haemozoin formation in a concentration regime that is well below that of FePPIX in the digestive vacuole, as is indeed the case.⁷

Computational methods

DFT and MM calculations were performed with Gaussian09 ⁴³ ¶ and Accelrys Discovery Studio⁴⁴ respectively. Input geometries for both DFT and MM calculations were created using Hyperchem 8.0.10.⁴⁵ Gaussian input and output files were processed with MolDraw 2.0 ⁴⁶ and GaussView 5.0. Figures of molecular structures were prepared using Ortep-3 for Windows.⁴⁷ Conformations of the free drugs as inputs for DFT calculations were generated with Hyperchem, using the conformational searching facility on all rotatable bonds to locate sets of distinct, low energy conformations. Additional conformations were located with short (10–100 ps), high temperature (300–800 K) molecular dynamics runs, followed by MM geometry optimization.

The standard procedure for DFT calculations on the iron complexes using method 3 was as follows. An initial gas phase calculation and wavefunction stability check at the B3LYP/LanL2DZ level of theory was followed by geometry optimization and frequency calculations, also at the B3LYP/LanL2DZ level, and finally single point implicit solvent calculations at the optimized geometry using B3LYP/6-311+G(d,p) with SMD solvent corrections and additional wavefunction stability checks (the corresponding method 1 results, using B3LYP/LanL2DZ for the solvent calculations also, are given in the ESI†). Quadratic convergence (QC) was used sparingly, to assist convergence for particularly troublesome structures. Often, it proved more efficient to avoid QC and instead run a series of final single point calculations in which the basis set was successively incremented from 6-31G to 6-311+G(d,p). The ground spin state for the 1:1, 5-coordinate Fe–O haem complexes was taken as S = 5/2, as determined in our previous DFT studies²² and also observed experimentally for the 1 : 1 complex of QN.⁴⁸ Initial calculations on [(FePPIXH)₂(μ-O)(CQH₂)] showed that the antiferromagnetically coupled, S = (±5/2 = 0) species is more stable than the ferromagnetically coupled S = 10/2 state by ca. 5 kcal mol⁻¹ in both n-octanol and water, in agreement with NMR measurements that showed this species to be antiferromagnetically coupled.⁴⁸ All subsequent calculations on the 2 : 1 complexes were carried out with antiferromagnetic coupling (see Methodology section). All reported reaction energies have been corrected for zero-point energies (ZPE's), which were scaled by a factor of 0.981.²²

Models of the crystal surfaces with drug complex monolayers were assembled by rigid body modelling in Hyperchem, using the native β-haematin unit cell as a template (see Methods section). These were then converted into mdl format files, suitable for Discovery Studio, with OpenBabel.⁴⁹ Models of the (100) face islands surrounded by drug complex molecules were created within Discovery Studio, by substituting (FePPIX)₂ dimers in a pure β-haematin model with the required complex, using the heavy atoms of the hydrogen-bonded propionic acid group as a template. Subsequent geometry optimizations of both types of poisoned crystal models were carried out within Discovery Studio, using the CHARMm force field and adopted basis Newton–Raphson algorithm to an RMS gradient of 0.1 kcal mol⁻¹ Å⁻¹; other parameters were left at their default values. Surface areas for SSA calculations were measured using a 1.4 Å solvent probe; first, the surface area of the complete model was measured; then, the areas of two sub-components (one complex molecule plus the rest of the model); the difference between the complete model and the sum of its two components was divided by two to obtain the SSA.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Northumbria University and the EPSRC UK National Service for Computational Chemistry Software are acknowledged for the provision of computing facilities.

References

1. World Health Organization, World malaria report 2017, http://www.who.int/malaria/publications/world-malaria-report-2017/en/.
2. S. Pagola, P. W. Stephens, D. S. Bohle, A. D. Kosar and S. K. Madsen, Nature, 2000, 404, 307–310.
3. I. Weissbuch and L. Leiserowitz, Chem. Rev., 2008, 108, 4899–4914.
4. J. M. Combrinck, T. E. Mabotha, K. N. Ncokazi, M. A. Ambele, D. Taylor, P. J. Smith, H. C. Hoppe and T. J. Egan, ACS Chem. Biol., 2013, 8, 133–137.
5. T. J. Egan, J. M. Combrinck, J. Egan, G. R. Hearne, H. M. Marques, S. Ntenteni, B. T. Sewell, P. J. Smith, D. Taylor, D. A. van Schalkwyk and J. C. Walden, Biochem. J., 2002, 365, 343–347.
6. S.-M. Fitzroy, J. Gildenhuys, T. Olivier, N. O. Tshililo, D. Kuter and K. A. de Villiers, Langmuir, 2017, 33, 7529–7537.
7. K. N. Olafson, M. A. Ketchum, J. D. Rimer and P. G. Vekilov, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4946–4951.
8. K. N. Olafson, T. Q. Nguyen, J. D. Rimer and P. G. Vekilov, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7531–7536.
9. K. N. Olafson, T. Q. Nguyen, P. G. Vekilov and J. D. Rimer, Chem. – Eur. J., 2017, 23, 13638–13647.
10. T. Straasø, S. Kapishnikov, K. Kato, M. Takata, J. Als-Nielsen and L. Leiserowitz, Cryst. Growth Des., 2011, 11, 3342–3350.
11. N. Marom, A. Tkatchenko, S. Kapishnikov, L. Kronik and L. Leiserowitz, Cryst. Growth Des., 2011, 11, 3332–3341.
12. R. Buller, M. L. Peterson, Ö. Almarsson and L. Leiserowitz, Cryst. Growth Des., 2002, 2, 553–562.
13. A. Dorn, S. R. Vippagunta, H. Matile, C. Jaquet, J. L. Vennerstrom and R. G. Ridley, Biochem. Pharmacol., 1998, 55, 727–736.
14. D. C. Warhurst, J. C. Craig, I. S. Adagu, R. K. Guy, P. B. Madrid and Q. L. Fivelman, Biochem. Pharmacol., 2007, 73, 1910–1926.
15. J. Xue, B. Jiang, C.-S. Liu, J. Sun and S.-H. Xiao, Zhongguo Ji Sheng Chong Xue Yu Ji Sheng Chong Bing Za Zhi, 2013, 31, 161–169 (in Chinese).
16. K. A. de Villiers, J. Gildenhuys and T. le Roex, ACS Chem. Biol., 2012, 7, 666–671.
17. K. A. de Villiers, H. M. Marques and T. J. Egan, J. Inorg. Biochem., 2008, 102, 1660–1667.
18. J. Gildenhuys, C. J. Sammy, R. Müller, V. A. Streltsov, T. le Roex, D. Kuter and K. A. de Villiers, Dalton Trans., 2015, 44, 16767–16777.
19. D. S. Bohle, E. L. Dodd, A. J. Kosar, L. Sharma, P. W. Stephens, L. Suárez and D. Tazoo, Angew. Chem., Int. Ed., 2011, 50, 6151–6154; M. S. Walczak, K. Lawniczak-Jablonska, A. Wolska, A. Sienkiewicz, L. Suárez, A. J. Kosar and D. S. Bohle, J. Phys. Chem. B, 2011, 115, 1145–1150; M. S. Walczak, K. Lawniczak-Jablonska, A. Wolska, M. Sikora, A. Sienkiewicz, L. Suárez, A. J. Kosar, M.-J. Bellemare and D. S. Bohle, J. Phys. Chem. B, 2011, 115, 4419–4426; G. Macetti, S. Rizzato, F. Beghi, L. Silvestrini and L. Lo Presti, Phys. Scr., 2016, 91, 023001.
20. D. Kuter, V. Streltsov, N. Davydova, G. A. Venter, K. J. Naidoo and T. J. Egan, J. Inorg. Biochem., 2016, 154, 114–125; D. Kuter, S. J. Benjamin and T. J. Egan, J. Inorg. Biochem., 2014, 133, 40–49.
21. K. A. de Villiers, C. H. Kaschula, T. J. Egan and H. M. Marques, J. Biol. Inorg. Chem., 2007, 12, 101–117 , and references therein.
22. M. C. Durrant, Dalton Trans., 2014, 43, 9754–9765.
23. T. J. Egan, J. Inorg. Biochem., 2008, 102, 1288–1299; D. Fitch, Life Sci., 2004, 74, 1957–1972.
24. S. Kapishnikov, A. Weiner, E. Shimoni, P. Guttmann, G. Schneider, N. Dahan-Pasternak, R. Dzikowski, L. Leiserowitz and M. Elbaum, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11188–11193.
25. D. Kuter, R. Mohunlal, S.-M. Fitzroy, C. Asher, P. J. Smith, T. J. Egan and K. A. de Villiers, CrystEngComm., 2016, 18, 5177–5187.
26. D. Kuter, K. Chibale and T. J. Egan, J. Inorg. Biochem., 2011, 105, 684–692.
27. K. N. Olafson, J. D. Rimer and P. G. Vekilov, Cryst. Growth Des., 2014, 14, 2123–2127.
28. A. M. D. S. Delpe Acharige and M. C. Durrant, Transition Met. Chem., 2014, 39, 721–726.
29. Y. Minenkov, Å. Singstad, G. Occhipinti and V. R. Jensen, Dalton Trans., 2012, 41, 5526–5541.
30. H. J. Schneider, L. Tianjun, M. Sirish and V. Malinovski, Tetrahedron, 2002, 58, 779–786.
31. H.-J. Schneider, Acc. Chem. Res., 2015, 48, 1815–1822.
32. A. Skórska, J. Śliwiński and B. J. Oleksyn, Bioorg. Med. Chem. Lett., 2006, 16, 850–853; A. Dassonville-Klimpt, C. Cézard, C. Mullié, P. Agnamey, A. Jonet, S. Da Nascimento, M. Marchivie, J. Guillon and P. Sonnet, ChemPlusChem, 2013, 78, 642–646.
33. A. J. Fielding, V. Lukinović, P. G. Evans, S. Alizadeh-Shekalgourabi, R. H. Bisby, M. G. B. Drew, V. Male, A. Del Casino, J. F. Dunn, L. E. Randle, N. M. Dempster, L. Nahar, S. D. Sarker, F. G. Cantú Reinhard, S. P. de Visser, M. J. Dascombe and F. M. D. Ismail, Chem. – Eur. J., 2017, 23, 6811–6828.
34. S. Kashino and M. Haisa, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 310–312.
35. I. Hisaki, E. Hiraishi, T. Sasaki, H. Orita, S. Tsuzuki, N. Tohnai and M. Miyata, Chem. – Asian J., 2012, 7, 2607–2614.
36. C. Courseille, B. Busetta and M. Hospital, Cryst. Struct. Commun., 1973, 2, 283.
37. Q. Wang, Y. M. Huang, X. L. Ma, S. S. Li and H. Li, Powder Diffr., 2015, 30, 289–292.
38. D. Kuter, G. A. Venter, K. J. Naidoo and T. J. Egan, Inorg. Chem., 2012, 51, 10233–10250.
39. E. L. Dodd and D. S. Bohle, Chem. Commun., 2014, 13765–13768.
40. A. Semeniuk, A. Niedospial, J. Kalinowska-Tluscik, W. Nitek and B. J. Oleksyn, J. Mol. Struct., 2008, 875, 32–41.
41. F. C. Churchill, L. C. Patchen, C. C. Campbell, I. K. Schwartz, P. Nguyen-Dinh and C. M. Dickinson, Life Sci., 1985, 36, 53–62.
42. M. Vanaerschot, L. Lucantoni, T. Li, J. M. Combrinck, A. Ruecker, T. R. S. Kumar, K. Rubiano, P. E. Ferreira, G. Siciliano, S. Gulati, P. P. Henrich, C. L. Ng, J. M. Murithi, V. C. Corey, S. Duffy, O. J. Lieberman, M. I. Veiga, R. E. Sinden, P. Alano, M. J. Delves, K. L. Sim, E. A. Winzeler, T. J. Egan, S. L. Hoffman, V. M. Avery and D. A. Fidock, Nat. Microbiol., 2017, 2, 1403–1414.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (various revisions), Gaussian, Inc., Wallingford, CT, 2010.
44. Accelrys Discovery Studio, Version 1.7, Accelrys Software Inc., 2005–2006.
45. Hyperchem release 8.0.10 for Windows, Hypercube Inc., 2011.
46. MolDraw release 2.0, P. Ugliengo, D. Viterbo and G. Chiari, Z. Kristallogr., 1993, 207, 9–23.
47. Ortep-3 for Windows, version 2.02, L. J. Farrugia, J. Appl. Crystallogr., 1997, 30, 565.
48. L. B. Casabianca, D. An, J. K. Natarajan, J. N. Alumasa, P. D. Roepe, C. Wolf and A. C. de Dios, Inorg. Chem., 2008, 47, 6077–6081.
49. OpenBabel version 2.4.1, N. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Chemoinform., 2011, 3, 33.

---

Footnotes

† Electronic supplementary information (ESI) available: Atomic coordinates, energies and electronic spins at Fe for all DFT models; pictures of complexes not given in Fig. 1 and 6; pictures of all surface coverage models; shared surface area data used to construct Fig. 2 and 5; comparison of free drug surface areas versus β-haematin {001} face surface coverage. See DOI: 10.1039/c8dt03369b

‡ Retired.

§ Throughout this paper, FePPIX is used to indicate the generic form of iron(III) protoporphyrin IX. Specific forms of FePPIX in which one or both propionate groups are in their neutral, protonated form are designated as FePPIXH and FePPIXH₂ respectively.

¶ Although Gaussian16 became available in the later stages of this project, preliminary G16 calculations on free drug conformers returned differences of ∼0.5 kcal mol⁻¹ compared to G09. Therefore, Gaussian09 was used throughout for consistency.

---