The effect of conformational isomerism on the optical properties of bis(8-oxyquinolato) diboron complexes with a 2,2′-biphenyl backbone†
Abstract
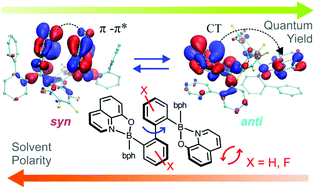
A fluorescent bis(8-oxyquinolato) diborinic complex with a central 2,2′-biphenyl backbone 1 and its octafluoro analogue 2 were synthesized to study the optical–structural relationship of sterically encumbered molecules featuring close intramolecular π-stacking interactions involving chromophore units. The crystal structure of 1 revealed a unique π-stacked arrangement of two pendant phenyl groups and two 8-oxyquinolato ligands (Q) located in the inner part of the complex. Unlike 1, the closely related complex 2 features conformational isomerism, and two major forms, namely 2-syn and 2-anti, are observed in solution to a varying extent depending on the solvent polarity. Form 2-syn, a geometrical analogue of 1, is preferable in polar solutions, whereas its rotational isomer 2-anti featuring π-stacking interactions between the terminal phenyl group and Q ligand dominates in benzene and chloromethane solutions. The observed conformational equilibria strongly affect the optical properties of the system, specifically leading to a significant increase of the quantum yield of emission (from 22% in MeCN to 38% in benzene) accompanied by a bathochromic shift (Δλ = 10 nm) of absorption and hypsochromic shifts (Δλ = −8 nm) of emission spectra with decreasing solvent polarity. This effect was ascribed to the variation in frontier orbital distributions.


 Please wait while we load your content...
Please wait while we load your content...