Open Access Article
Open Access ArticleDesign of oxophilic metalloporphyrins: an experimental and DFT study of methanol binding†
Sandra
Olsson
 ,
Christian
Dahlstrand
,
Christian
Dahlstrand
 and
Adolf
Gogoll
and
Adolf
Gogoll
 *
*
Department of Chemistry-BMC, Uppsala University, Box 576, Uppsala, S-75123, Sweden. E-mail: adolf.gogoll@kemi.uu.se
First published on 1st August 2018
Abstract
By systematic measurements we have evaluated a series of tetraphenyl metalloporphyrins and halogenated tetraphenyl metalloporphyrin derivatives for binding to ligands with oxygen containing functional groups, using methanol, acetic acid and acetone as examples. Experimental binding constants identified three metalloporphyrins with good binding to all three ligands: MgTPFPP, MgTPPBr8 and ZnTPPBr8 as well as a range of porphyrins binding to select ligands. Based on these results the optimal porphyrins can be selected for the desired binding interactions. We also show how to use DFT calculations to evaluate the potential binding between a metalloporphyrin and a ligand, which is deduced from free energies of binding ΔG, charge transfer ΔQ, and change of metal spin state. Computations on unsubstituted porphyrins in lieu of tetraphenyl porphyrin systems yield reliable predictions of binding interactions with good correlation to the corresponding experimental data. The calculations have also yielded interesting insights into the effect of halogenation in the β-position on the binding to ligands with oxygen containing functional groups.
Introduction
Metalloporphyrins are well known for their capability to bind ligands at the axial positions of the metal center.1 This results in a plethora of functionality, based on varying electronic properties of the metalloporphyrin, increased reactivity of the axial ligands, and the possible formation of supramolecular entities.2–8 Compounds with several metalloporphyrin units have attracted particular interest, since they allow for a stronger host–guest interaction due to cooperativity or preorganization. Amongst these, bisporphyrin molecular tweezers and clips with two metalloporphyrin units connected by a linker are particularly well known for their capacity of ditopic binding to guest molecules.9,10 This is the foundation of Exciton-Coupled Circular Dichroism (ECCD), aimed at the determination of the absolute stereochemistry of guest molecules.11 Recently, our group has extended the scope of such bisporphyrin tweezers to determine the relative stereochemistry of small flexible molecules using NMR spectroscopy via conformational restriction of the bound guest.12–14 In these studies, as in most ECCD investigations, zinc is the metal of choice. While zinc binds favorably to guests with nitrogen-containing functional groups, its affinity to oxygen-containing functional groups is much lower.15 Most molecules of interest for these analytical methods do not possess two nitrogen-containing functional groups, the presence of at least two oxygen-containing functional groups is more likely.16 Low affinity between host and guest may be compensated for in ECCD by a huge excess of the guest, since the signal originating from the bisporphyrin, and not the guest is detected. In our NMR-based method, instead we observe the signal originating from the guest molecule. Thus, a huge excess of guest is not tolerable, since it would result in NMR signals that are dominated by the contribution of unbound guest molecules.Our aim therefore is to identify metalloporphyrins with increased affinity to oxygen-containing functional groups. On one hand it has been shown that this affinity may be increased by a derivatization of the porphyrin that reduces the electron density at the metal center.15 On the other hand, choice of suitable “oxophilic” metals may result in stronger binding.11 Also, it should be possible to combine both parameters. Although both approaches have been reported, we found that a systematic approach is lacking. A more complete knowledge of possible binding interactions between metalloporphyrins and common oxygen-containing functional groups also should make it possible to choose a metal based on the desired binding behavior. For example, differences in affinity might be exploited to design bismetalloporphyrins that selectively bind components of a mixture. To facilitate both ECCD and NMR studies our aim is to find porphyrins binding strongly enough so that interactions between host and guests are easily detectible without requiring guest excess.
To achieve this, we investigate here a series of metallated porphyrins, including, based on previous results with electron poor metal centers a number of halogenated metalloporphyrins.15,17 To facilitate NMR studies most of the investigated metals are diamagnetic. We have also performed DFT calculations in order to devise a method for accurate prediction of whether a metalloporphyrin will bind strongly enough to oxygen containing functional groups to be detectible even at low guest concentrations. For practical reasons, some of the calculations have been carried out for simplified systems, while others used the full molecular structures used in the experimental study.
Results and discussion
Metalloporphyrins
The porphyrins used in this study are meso-tetraphenylporphyrins (TPP) and derivatives thereof. This porphyrin is widely used in host guest chemistry, molecular electronics and molecular materials due to the relatively good solubility in organic solvents.2–8,18 The TPP derivatives chosen are the tetra(pentafluorophenyl)porphyrin (TPFPP) and the octabromo tetraphenylporphyrin (TPPBr8). Metals were chosen based on their prospective oxophilicity. For example, on the oxophilicity scale calculated by Kepp Mg2+ is more oxophilic than Zn2+.19 The insertion of metals into the porphyrins followed standard methods.20,21 All metallopophyrins are shown in Scheme 1.Ligands
The target of this study is to achieve reasonably strong binding of the common oxygen containing functional groups –OH, –COOH and –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O to metalloporphyrins. To keep the studied systems as simple as possible the ligands chosen were methanol, acetic acid and acetone. The nitrogen containing ligand pyridine that is very well studied as a ligand to porphyrins was included as a reference.22–24
O to metalloporphyrins. To keep the studied systems as simple as possible the ligands chosen were methanol, acetic acid and acetone. The nitrogen containing ligand pyridine that is very well studied as a ligand to porphyrins was included as a reference.22–24
Determination of binding constants
While the standard way to measure binding constants involving porphyrins is UV-vis spectroscopy due to simplicity and high sensitivity, we opted for NMR spectroscopy instead. This allows for direct observation of ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
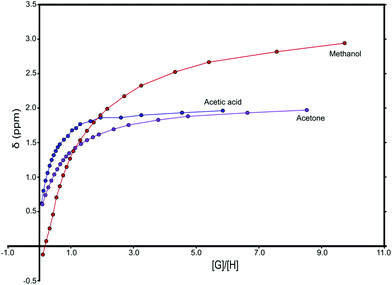
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metalloporphyrin stoichiometry. Furthermore, possible interference of water, the presence of which is difficult to avoid completely, may be indicated in the spectra. Binding of water during titration of porphyrins may result in ligand exchange rather than binding. In UV-vis titrations, this situation would result in a possibly very small and difficult to detect red-shift. For the NMR titrations, it needs to be considered that the chemical shifts of ligand protons are affected by two counteracting effects. Binding to the Lewis-acidic metal is expected to result in an increase of chemical shift (Δδ > 0), whereas the anisotropy effect of the porphyrin ring system results in decreased chemical shift (Δδ < 0). In practice, normally the anisotropy effect dominates. The gradual change in chemical shift is recorded and the binding constants are then obtained by non-linear fitting (Fig. 1). To probe if the binding constant was directly related to the magnitude of the chemical shift change Δδ, this parameter also was recorded at the same [G]/[H] = 1 ratio for various metalloporphyrin complexes with G = ligand and H = metalloporphyrin (Table 2).
metalloporphyrin stoichiometry. Furthermore, possible interference of water, the presence of which is difficult to avoid completely, may be indicated in the spectra. Binding of water during titration of porphyrins may result in ligand exchange rather than binding. In UV-vis titrations, this situation would result in a possibly very small and difficult to detect red-shift. For the NMR titrations, it needs to be considered that the chemical shifts of ligand protons are affected by two counteracting effects. Binding to the Lewis-acidic metal is expected to result in an increase of chemical shift (Δδ > 0), whereas the anisotropy effect of the porphyrin ring system results in decreased chemical shift (Δδ < 0). In practice, normally the anisotropy effect dominates. The gradual change in chemical shift is recorded and the binding constants are then obtained by non-linear fitting (Fig. 1). To probe if the binding constant was directly related to the magnitude of the chemical shift change Δδ, this parameter also was recorded at the same [G]/[H] = 1 ratio for various metalloporphyrin complexes with G = ligand and H = metalloporphyrin (Table 2).
The stoichiometry of the formed complexes are mostly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [eqn (1)], but the zinc porphyrins form 1
1 [eqn (1)], but the zinc porphyrins form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes with pyridine [eqn (2)]. As mentioned above, the stoichiometry can be directly observed in NMR as the integrals of the peaks correlates to the number of protons with that chemical shift.
2 complexes with pyridine [eqn (2)]. As mentioned above, the stoichiometry can be directly observed in NMR as the integrals of the peaks correlates to the number of protons with that chemical shift.
 | (1) |
 | (2) |
The binding constants can then be calculated from the measured NMR data utilizing an iterative fitting program, using eqn (3), for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry and eqn (4) for 1
1 stoichiometry and eqn (4) for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry.25
2 stoichiometry.25
 | (3) |
| [G]3(A) + [G2](B) + [G](C) − [G]0 = 0 | (4) |
The measured binding constants are presented in Table 1. In Fig. 2 the binding constants to different metallotetraphenylporphyrin-(MTPP) complexes are visualized.
 | ||
| Fig. 2 Binding constants Ka for metallotetraphenylporphyrins (MTPP).*Ka too high to measure. **Not measured. ***Demetallation. Data from Table 1. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, CDCl3 solutions). Standard errors are given in brackets
1 stoichiometry, CDCl3 solutions). Standard errors are given in brackets
| Porphyrin | K a (M−1), with standard error in brackets | |||||||
|---|---|---|---|---|---|---|---|---|
| Methanol | Acetic acid | Acetone | Pyridine | |||||
nb = no binding; nm = not measured; cc = cannot calculate, binding too strong; D = demetallation.a Very broad signals.b Stoichiometry 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. 2. |
||||||||
| Al(TPP)Cl | 3.8 × 10−3 | (2.2 × 10−2)a | 2.8 × 101 | (2.6 × 10−4) | nb | — | nb | — |
| Co(TPP)Cl | 3.2 × 10−3 | (1.5 × 10−4) | 1.7 × 102 | (4.9 × 10−3) | nb | — | cc | — |
| Co(TPFPP)Cl | 5.4 × 101 | (8.9 × 10−3) | 1.8 × 104 | (3.6 × 10−4) | nb | — | cc | — |
| Fe(TPP) | nb | — | nb | — | nb | — | nb | — |
| Mg(TPP) | 5.7 × 101 | (3.0 × 10−2) | D | — | 7.4 | (1.4 × 10−3) | 1.7 × 101 | (0.2) |
| Mg(TPFPP) | 1.5 × 102 | (8.6 × 10−2) | 2.3 × 103 | (8.0 × 10−2) | 3.1 × 102 | (2.9 × 10−2) | 1.3 × 104 | (1.9 × 10−2) |
| Mg(TPP)Br8 | 1.6 × 102 | (4.6 × 10−2) | 8.2 × 102 | (1.0 × 10−1) | 3.8 × 102 | (2.2 × 10−2) | 1.3 | (9.3 × 10−2) |
| Mn(TPP)Cl | nb | — | nb | — | nb | — | nb | — |
| Ni(TPP) | nb | — | nb | — | nb | — | nb | — |
| Sn(TPP)OH2 | nb | — | nm | — | nm | — | 1.3 × 104 | (6.6 × 10−3) |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ti(TPP) Ti(TPP) |
nb | — | 4.8 × 102 | (8.1 × 10−4) | nb | — | nb | — |
| Zn(TPP) | 2.4 × 10−3 | (3.8 × 10−3)a | 3.6 × 102 | (1.0 × 10−3) | nb | — | 6.8 × 103 | (0.2)b |
| Zn(TPFPP) | 1.5 × 101 | (1.0 × 10−2) | 1.2 × 103 | (1.1 × 10−3) | 1.1 × 10−2 | (1.4 × 10−3) | 2.7 × 104 | (0.5)b |
| Zn(TPP)Br8 | 2.0 × 101 | (1.1 × 10−2) | 2.5 × 102 | (3.1 × 10−3) | 6.0 × 10−3 | (1.4 × 10−3) | 3.2 × 102 | (6.0 × 10−2)b |
As can be clearly seen the metals binding to MeOH are Al(III), Co(III), Mg(II) and Zn(II). All these also bind to AcOH, with the exception of Mg(II) due to demetallation following porphyrin protonation.21 For Mg(II) we also observe binding to acetone. There is only one case where we observe binding to an oxygen containing functional group but not to methanol. This is in the case of Ti(IV) which binds readily to AcOH but to no other ligand. For Co(III)TPPCl the binding constant to pyridine is too high to be determined by this method. Here, pyridine binds to the metal without any exchange with free pyridine in the solution. This results in one set of signals for the bound pyridine and another set of signals for free pyridine at [G]/[H] > 1.
Somewhat surprisingly, Fe(II)TPP, Mn(III)TPPCl and Ni(II)TPP show no binding, as well as the Sn(OH)2TPP complex with two anionic hydroxide ligands on the metal which apparently bind more strongly than uncharged methanol ligands.22,26,27
Introduction of halogen substituents, either in the β-positions (i.e. TPPBr8) or as tetrakis(pentafluorophenyl) substituents (i.e. TPFPP) results in enhanced binding to the oxygen containing ligands (Fig. 3–5).
 | ||
| Fig. 3 Binding constants Ka for various ligands binding to MgTPP, MgTPFPP and MgTPPBr8. Data from Table 1. | ||
 | ||
| Fig. 4 Binding constants Ka for various ligands binding to ZnTPP, ZnTPFPP and ZnTPPBr8. Data from Table 1. | ||
 | ||
| Fig. 5 Binding constants Ka for various ligands binding to cobalt-metalloporphyrins CoTPPCl and CoTPFPPCl. Data from Table 1. | ||
When comparing MgTPFPP and MgTPPBr8 to MgTPP the binding to MeOH is slightly increased (factor 2.6 and 2.8, respectively), but the binding to acetone more substantially so (factor 42 and 51, respectively). It is also interesting to note that the well-known demetallation of MgTPP under acidic conditions is not observed for MgTPFPP and MgTPPBr8 allowing binding to all three oxygen containing functional groups.21 Another interesting feature is the low binding affinity of MgTPPBr8 to pyridine.
For the zinc porphyrins the binding to methanol increases for the halogenated MTPFPP and MTPPBr8 (factors 625 and 8333, respectively) but the binding to acetic acid shows only slight changes (factors 3.3 and 0.7, respectively). The most interesting point is that ZnTPPBr8 binds to acetone, unlike the ZnTPP and ZnTPFPP. This makes ZnTPPBr8 one of the most versatile metalloporphyrins investigated in this study as it binds to all four ligands with similar strength.
In the cobalt series the CoTPPBr8 was excluded as the reported synthetic procedures were unsuccessful in our hands. For the CoTPFPPCl porphyrin the binding to both methanol and acetic acid was increased as compared to CoTPPCl. None of the cobalt porphyrins binds to acetone.
The 1H chemical shift changes for the target ligands’ methyl groups are shown in Table 2. The largest changes for each ligand are indicated in bold face. The most apparent result is that all Mg(II)-metalloporphyrins produce a comparably large chemical shift change. The MgTPFPP has one of the highest values for all tested ligands. However, we cannot see a clear correlation to the binding constant, indicating that Δδ is influenced by additional parameters, e.g. the distance between the methyl protons and the porphyring ring. ZnTPPBr8 has good binding constants to all the target ligands, but the change in chemical shift is less impressive. The same can be said for the cobalt porphyrins. With the exception of the CoTPFPPCl binding to methanol, the chemical shift changes are small whereas the binding constants are good (Table 1). Thus, Δδ seems more dependent on the metal of the metalloporphyrin than the binding strength. This might be a result of the two counteracting effects, i.e. an electronic effect from the metal and an anisotropy effect from the porphyrin ring (and possibly the phenyl rings).
| Porphyrin |
1H chemical shift change Δδ (ppm) for ligand protons at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host 1 host![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) guest ratios guest ratios |
|||||
|---|---|---|---|---|---|---|
| Methanol | Acetic acid | Acetone | ||||
| δCH3 | Δδ | δCH3 | Δδ | δCH3 | Δδ | |
| a This metalloporphyrin could not be obtained free from water, thus the binding to oxygen containing functional groups here includes competition with water. nb = no binding. | ||||||
| Al(TPP)Cl | 3.01 | −0.48 | 2.09 | −0.01 | nb | — |
| Co(TPP)Cl | 3.47a | −0.02 | 2.07a | −0.03 | nb | — |
| Co(TPFPP)Cl | 1.15 | −2.34 | 2.09 | −0.01 | nb | — |
| Mg(TPP) | 2.25 | −1.24 | D | — | 2.02 | −0.15 |
| Mg(TPFPP) | 1.38 | −2.11 | 1.68 | −0.42 | 1.35 | −0.82 |
| Mg(TPP)Br8 | 1.76 | −1.73 | 1.64 | −0.46 | 1.56 | −0.61 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ti(TPP) Ti(TPP) |
nb | — | 2.09 | −0.01 | nb | — |
| Zn(TPP) | 3.33 | −0.16 | 2.09 | −0.01 | nb | — |
| Zn(TPFPP) | 2.79 | −0.70 | 2.04 | −0.06 | 2.13 | −0.04 |
| Zn(TPP)Br8 | 3.12 | −0.37 | 1.99 | −0.11 | 2.12 | −0.05 |
Computational studies
To rationalize the experimental results a DFT study was carried out. As almost all porphyrins binding to R–OH also bind to R–COOH the smaller hydroxyl group was chosen as functional group. Most of the calculations were carried out on simplified metalloporphyrin systems (MP) to reduce computational costs (vide infra). Calculations were also performed on β-halogenated porphyrins to investigate the effect of halogenation on the binding constant as well as the change in charge distribution. To investigate if calculations on the rudimentary metalloporphyrins (MP) gave results indicative of the full systems (i.e., MTPP), we performed a limited number of calculations on MTPP as well as halogenated MTPP derivatives (MTPFPP and MTPPBr8). All investigated systems are shown in Scheme 2.Calculations on the metalloporphyrins were performed on the DFT level using the B3LYP-D3 method as described by Grimme.28–32 This method has previously been shown to predict the geometry, vibrations and electronic structure of porphyrin systems with reasonable accuracy.33,34 No solvent model was used in these calculations since their primary purpose was a comparative binding study of various metalloporphyrins independent of choice of solvent. Choice of solvent has a substantial impact on complexations and therefore without a solvent model the calculated binding constants will be considerably higher than the experimentally measured values, but should show the same trends. As it is well known that metals can adopt several different spin states the three lowest spin states were investigated for each metalloporphyrin and its corresponding metalloporphyrin-methanol complex.35 For metals with an even number of electrons the states with total spin S = 0, 1, 2 and multiplicity M = 1, 3, 5 were calculated and for metals with an odd number of electrons the states with a total spin S = 1/2, 3/2, 5/2 and multiplicity M = 2, 4, 6 were calculated. The lowest states were used in the calculations of binding energies and theoretical binding constants. The energies of the chosen metalloporphyrins were calculated both with and without methanol as ligand. To investigate the change in charge distribution a natural population analysis (NPA) was carried out on the free methanol ligand and on its complexes.36–38
Geometries and symmetries
The simple MPs have planar structures whereas the substituted TPP, TPFPP and TPPBr8 porphyrins have more complex geometries. The phenyl rings are a source of steric repulsion and depending on their position will affect the symmetry and the energy of the system.39 Different rotamers with respect to the phenyl rings were used as starting geometries in order to find the most stable geometry. Our calculations show that for the free TPP metalloporphyrins (CoTPPCl, MgTPP, ZnTPP) the most stable positioning of the phenyl groups is with rings in opposing meso-positions in parallel orientation (\\, angle between ring planes ≈0°), but when binding to methanol both MgTPP and ZnTPP have the opposite rings in an angular orientation (✕, angle between ring planes ≈40°) (Fig. 6).For the TPFPP metalloporphyrins the (✕) configuration is favoured in both the free porphyrins and the complexes. The only exceptions are MgTPFPP where the (\\)-configuration is favoured for the free porphyrin, and ZnTPFPP where the (\\)-configuration is favoured in the methanol complex.
In the MTPPBr8 the meso-phenyl rings are restricted into adopting one position due to repulsion from the bromo substituents in the β-positions. These bromo substituents are also the cause of substantial distortions of the porphyrin ring planarity, resulting in a saddle shaped structure (Fig. 7).40
We have also observed a distortion of the porphyrin ring in the methanol complexes of Co(III)TPPCl, Co(III)TPFPPCl and to a lesser extent in the complexes of Zn(II)TPP and MgTPFPP, Fig. 8. This kind of distortion was previously observed for Co(II)TPP by de Melo et al.41
 | ||
| Fig. 8 Distortions of the porphyrin ring planarity in the methanol complexes of CoTPPCl, CoTPFPPCl, ZnTPP and MgTPFPP. | ||
Free energies of binding
The lowest calculated energies of the free porphyrins and their methanol complexes were used to determine the free energies of binding ΔG. From these energies the theoretical binding constants were calculated using (eqn (5)). | (5) |
| Complex formation (spin state of metal indicated) | Change in spin | ΔG (kJ mol−1) | K a,theo |
|---|---|---|---|
| a The singlet state is only 2.62 kJ mol−1 higher in energy. b The quintet state is only 0.58 kJ mol−1 higher in energy. c The triplet state is only 1.99 kJ mol−1 higher in energy. | |||
| 1Al(III)PCl + MeOH → [1Al(III)PCl-MeOH] | 1 → 1 | −20.4 | 3.70 × 103 |
| 5Co(III)PCla + MeOH → [1Co(III)PCl-MeOH] | 5 → 1 | −28.4 | 9.37 × 104 |
| 2Co(II)P + MeOH → [2Co(II)P-MeOH] | 2 → 2 | −22.0 | 7.06 × 103 |
| 6Fe(III)PCl + MeOH → [4Fe(III)PCl-MeOH] | 6 → 4 | 7.0 | — |
| 3Fe(II)Pb + MeOH → [5Fe(II)P-MeOH]c | 3 → 5 | −18.9 | 2.06 × 103 |
| 1Mg(II)P + MeOH → [1Mg(II)P-MeOH] | 1 → 1 | −48.1 | 2.65 × 108 |
| 5Mn(III)PCl + MeOH → [5Mn(III)PCl-MeOH] | 5 → 5 | −10.6 | 7.18 × 101 |
| 1Ni(II)P + MeOH → [3Ni(II)P-MeOH] | 1 → 3 | −21.8 | 6.72 × 103 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 1Ti(IV)P + MeOH → [O 1Ti(IV)P + MeOH → [O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 3Ti(IV)P-MeOH] 3Ti(IV)P-MeOH] |
1 → 3 | 235.5 | — |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 2V(IV)P + MeOH → [O 2V(IV)P + MeOH → [O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 2V(IV)P-MeOH] 2V(IV)P-MeOH] |
2 → 2 | −11.1 | 8.70 × 101 |
| 1Zn(II)P + MeOH → [1Zn(II)P-MeOH] | 1 → 1 | −21.3 | 5.41 × 103 |
The results are presented graphically in Fig. 9. As can be seen, MgP shows the strongest binding interaction followed by Co(III)P. For the other metalloporphyrins ΔG are at the same level or weaker than for Zn(II)P. As it is known from the literature that Zn(II)P binds weakly to alcohols the porphyrins of most interest are the ones that show stronger interactions, i.e. (Mg(II)P and Co(III)P).15
 | ||
| Fig. 9 The theoretical free energies of binding ΔG for the formation of a complex between the studied metalloporphyrins and methanol. The horizontal line is positioned at the value for Zn(II)P. | ||
The calculations on the β-halogenated porphyrins showed a stronger binding to methanol, Table 4 and Fig. 10. This effect seems independent of which halogen is used. As it has been observed that halogenation on the phenyl rings of TPP increases the binding constant this was an expected result.15,17 Worth noting is that for Co(III) and Mg(II) there is a clear trend with increased ΔG in the series F < Cl < Br, whereas for Zn(II) the brominated porphyrin shows the weakest increase in free energy of binding.
| Complex formation halogen | ΔG (kJ mol−1) | K a,theo |
|---|---|---|
| Co(III)PF8Cl + MeOH → [Co(III)PF8Cl-MeOH] | −32.6 | 5.18 × 105 |
| Co(III)PCl8Cl + MeOH → [Co(III)PCl8Cl-MeOH] | −33.1 | 6.34 × 105 |
| Co(III)PBr8Cl + MeOH → [Co(III)PBr8Cl-MeOH] | −32.3 | 4.65 × 105 |
| MgPF8 + MeOH → [MgPF8-MeOH] | −55.3 | 4.96 × 109 |
| MgPCl8 + MeOH → [MgPCl8-MeOH] | −59.3 | 2.43 × 1010 |
| MgPBr8 + MeOH → [MgPBr8-MeOH] | −62.7 | 9.72 × 1010 |
| Zn(II)PF8 + MeOH → [Zn(II)PF8-MeOH] | −26.3 | 4.07 × 104 |
| Zn(II)PCl8 + MeOH → [Zn(II)PCl8-MeOH] | −30.7 | 2.43 × 105 |
| Zn(II)PBr8 + MeOH → [Zn(II)PBr8-MeOH] | −24.0 | 1.60 × 104 |
The free energies of binding for the complexation between the MTPP and methanol are shown in Table 5. It can be seen that for Co(III)TPPCl and Zn(II)TPP the binding constants are similar to those for their MP congeners. For Mg(II)TPP the difference is almost one order of magnitude when compared to Mg(II)P. This supports the use of the simpler porphyrin derivatives (i.e. without meso-phenyl substituents) in most of the calculations.
| Complex formation | ΔG (kJ mol−1) | K a,theo |
|---|---|---|
| Co(III)PCl + MeOH → [Co(III)PCl-MeOH] | −28.4 | 9.37 × 104 |
| Co(III)TPPCl + MeOH → [Co(III)TPPCl-MeOH] | −26.7 | 4.74 × 104 |
| Mg(II)P + MeOH → [Mg(II)P-MeOH] | −48.1 | 2.65 × 108 |
| Mg(II)TPP + MeOH → [Mg(II)P-MeOH] | −52.2 | 1.44 × 109 |
| Zn(II)P + MeOH → [Zn(II)P-MeOH] | −21.3 | 5.41 × 103 |
| Zn(II)TPP + MeOH → [Zn(II)TPP-MeOH] | −23.3 | 1.24 × 104 |
The halogenated MTPP derivatives TPFPP and TPPBr8 show about as high or higher free energies of binding ΔG than the MTPP congener but, depending on the metal, different porphyrins present the best result (Table 6). With the distorted geometries of especially the MTPPBr8 in mind, a direct comparison is difficult. The structures of both the free porphyrin and the complex might be significantly stabilized by solvent. Further computational studies on those systems with different solvent models and ligands would be required to estimate this effect.
| Complex formation | ΔG (kJ mol−1) | K a,theo |
|---|---|---|
| Co(III)TPPCl + MeOH → [Co(III)TPPCl-MeOH] | −26.7 | 4.74 × 104 |
| Co(III)TPFPPCl + MeOH → [Co(III)TPFPPCl-MeOH] | −43.8 | 4.80 × 107 |
| Co(III)TPPBr8Cl + MeOH → [Co(III)TPPBr8Cl-MeOH] | −26.2 | 3.89 × 104 |
| Mg(II)TPP + MeOH → [Mg(II)P-MeOH] | −52.2 | 1.44 × 109 |
| Mg(II)TPFPP + MeOH → [Mg(II)TPFPP-MeOH] | −44.8 | 7.07 × 107 |
| Mg(II)TPPBr8 + MeOH → [Mg(II)TPPBr8-MeOH] | −71.7 | 3.70 × 1012 |
| Zn(II)TPP + MeOH → [Zn(II)TPP-MeOH] | −23.3 | 1.24 × 104 |
| Zn(II)TPFPP + MeOH → [Zn(II)TPFPP-MeOH] | −31.8 | 3.71 × 105 |
| Zn(II)TPPBr8 + MeOH → [Zn(II)TPPBr8-MeOH] | −40.5 | 1.25 × 107 |
The spin state of the metal
The investigated MPs have different spin states as their most stable state. In Table 3 the change in spin state when forming the MP-MeOH complex is shown. As it is known that DFT has limitations regarding the calculation of spin states we also indicate when another spin state is very close in energy.35,42 Considering the free energy of binding ΔG it is indicated that the Fe(III) and Ti(IV) porphyrins do not form stable complexes, as their ΔG are positive. For the Al(III), Co(II), Mg(II), Mn(III) and Zn(II) porphyrins there is no change in spin state during complex formation. Co(III) porphyrin goes from a quintet to a singlet when forming the complex and also shows the second highest energy of binding. Both Fe(II) and Ni(II) porphyrin complexes change to a higher spin state. In comparison with the experimental results (Table 1) we might expect detectible binding for any metalloporphyrins that have similar or higher free energy of binding than Zn(II)P. However, of these Fe(II) and Ni(II) porphyrins did not show any binding in the experiments. Experimental binding is observed for those metalloporphyrins (Al(III), Co(III), Mg(II) and Zn(II)) that preserve or lower their spin state when forming the complex. The non-binding Fe(II) and Ni(II) porphyrins both would increase their spin state to form a stable complex according to the computations. Apparently, here an increase of spin state indicates non-binding although a negative ΔG indicates binding. It would be interesting to extend this study to probe whether this is a general trend in metalloporphyrins.Bond length
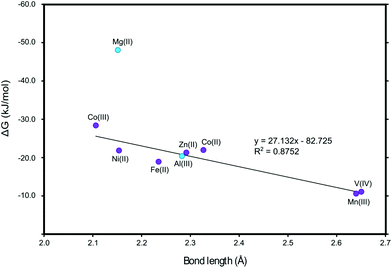
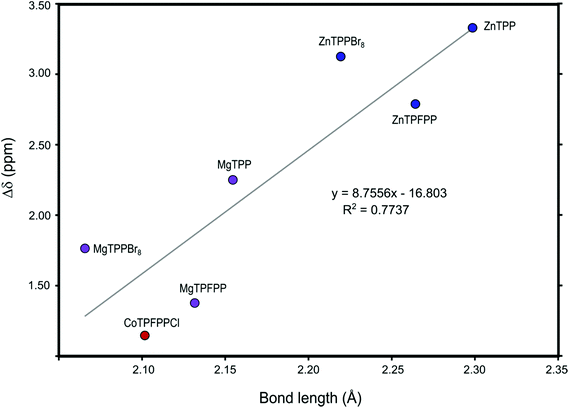
We also investigated the ligand–metal bond length, Fig. 11. We can see a clear correlation between the binding energies and the metal–ligand bond length. A stronger binding corresponds to a shorter bond. For the linear fitting the period 3 metals (Mg and Al) where omitted as they are smaller and differ in orbital composition as compared to the period 4 transition and post-transition metals.The calculated O–M bond lengths for the complexes of the full MTPP and halogenated MTPP derivative systems can be related to the change in chemical shifts observed on methanol during the experimental determination of the binding constants (Fig. 12). This effect is caused mainly by the anisotropy effect from the porphyrin ring current and is therefore directly related to the distance between the measured methyl group protons and the porphyrin ring.
Charge distribution
A natural population analysis (NPA) was performed on the optimized structures of the free metalloporphyrins and the methanol-metalloporphyrin complexes. To probe how the halogenation in β-position affected the charge distribution the change in natural charge for the metal and nitrogen atoms were investigated (Table 7). Interestingly the metals of Mg(II)PX8 and of Zn(II)PX8 become more electron depleted, as expected when introducing electron withdrawing groups, whereas the metal of Co(III)PX8Cl gets more electron rich. The nitrogens of Co(III)PX8Cl show mixed behaviour which suggest that looking on only the metal and nitrogens might be an oversimplification in the case of the Co(III)PX8Cl porphyrins. Further study of this, including comparison of orbital overlap and more metals would be interesting. For all the studied porphyrins we also observe an increased free energy of binding upon β-halogenation (Fig. 10).| Porphyrin | Charge of metal | Average charge of N1–N4 | ΔQmetal | ΔQN |
|---|---|---|---|---|
| a The LanL2DZ basis set was used on all metals. | ||||
| Co(III)P | 1.790 | −0.160 | — | — |
| Co(III)PF8Cl | 1.782 | −0.162 | −0.008 | −0.002 |
| Co(III)PCl8Cl | 1.781 | −0.155 | −0.009 | 0.004 |
| Co(III)PBr8Cl | 1.780 | −0.154 | −0.010 | 0.005 |
| Mg(II)P | 1.429 | −0.682 | — | — |
| Mg(II)PF8 | 1.436 | −0.680 | 0.007 | 0.001 |
| Mg(II)PCl8 | 1.446 | −0.669 | 0.018 | 0.012 |
Mg(II)PBr8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
1.451 | −0.663 | 0.022 | 0.019 |
| Zn(II)P | 1.236 | −0.649 | — | — |
| Zn(II)PF8 | 1.244 | −0.648 | 0.009 | 0.001 |
| Zn(II)PCl8 | 1.254 | −0.637 | 0.018 | 0.013 |
| Zn(II)PBr8 | 1.258 | −0.634 | 0.023 | 0.015 |
Investigating the change in charge distribution ΔQ in the MTPP and halogenated MTPP derivatives we can see a similar trend in the Mg(II) and Zn(II) metalloporphyrins (Table 8). For the Co(III) metalloporphyrins there is an increased charge on the nitrogen atoms in Co(III)TPFPPCl, but very little change on the metal. In Co(III)TPPBr8Cl however there is a large increase in negative charge on the metal and a decrease in negative charge on the nitrogen atoms.
| Porphyrin | Charge of metal | Average charge of N1–N4 | ΔQmetal | ΔQN |
|---|---|---|---|---|
| a The LanL2DZ basis set was used on all metals. | ||||
| Co(III)TPPCl | 1.788 | −0.158 | — | — |
| Co(III)TPFPPCl | 1.789 | −0.162 | 0.001 | −0.004 |
| Co(III)TPPBr8Cl | 1.742 | −0.151 | −0.046 | 0.007 |
| Mg(II)TPP | 1.427 | −0.677 | — | — |
| Mg(II)TPFPP | 1.439 | −0.674 | 0.012 | 0.003 |
Mg(II)TPPBr8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
1.453 | −0.663 | 0.026 | 0.015 |
| Zn(II)TPP | 0.616 | −0.322 | — | — |
| Zn(II)TPFPP | 0.623 | −0.321 | 0.006 | 0.002 |
| Zn(II)TPPBr8 | 0.628 | −0.317 | 0.012 | 0.005 |
The natural charges for free and complexed methanol were extracted (Table 9). A charge transfer can be observed in the porphyrin as well, but with the charge spread out over the system the change is more perspicuous for the methanol ligand. All of Al(III)PCl, Co(III)PCl, Mg(II)P and Zn(II)P show a negative change in charge when forming a complex with methanol. Those porphyrins also have calculated free energies of binding on the same level as Zn(II)P or higher. Co(II)P as well as the non-binding Fe(II)P and Ni(II)P also have calculated free energies of binding on the same level as Zn(II)P but show a positive change in charge.
| Porphyrin | Natural charges for methanol in porphyrin complexes. Difference to free methanol in brackets. | ||||
|---|---|---|---|---|---|
| H (ΔQ) | O (ΔQ) | C (ΔQ) | CH3 (ΔQ) | Total change | |
| None | 0.24 | −0.37 | −0.16 | 0.10 | |
| Al(III)P | 0.51 (0.28) | −0.75 (−0.38) | −0.31 (−0.16) | 0.22 (0.12) | −0.14 |
| Co(III)P | 0.52 (0.28) | −0.66 (−0.29) | −0.31 (−0.15) | 0.22 (0.12) | −0.04 |
| Co(II)P | 0.26 (0.02) | −0.35 (0.03) | −0.16 (0.001) | 0.11 (0.01) | 0.06 |
| Fe(II)P | 0.24 (0.01) | −0.35 (0.03) | −0.15 (0.003) | 0.11 (0.01) | 0.05 |
| Mg(II)P | 0.52 (0.28) | −0.78 (−0.41) | −0.31 (−0.16) | 0.22 (0.12) | −0.16 |
| Mn(III)P | 0.25 (0.01) | −0.34 (0.03) | −0.15 (0.01) | 0.10 (0.01) | 0.05 |
| Ni(II)P | 0.26 (0.02) | −0.34 (0.03) | −0.16 (0.001) | 0.11 (0.01) | 0.07 |
| V(IV)P | 0.25 (0.01) | −0.36 (0.03) | −0.15 (0.002) | 0.10 (0.01) | 0.04 |
| Zn(II)P | 0.51 (0.27) | −0.75 (−0.38) | −0.31 (−0.15) | 0.21 (0.11) | −0.14 |
The charge transfer when methanol forms complexes with the MTPP, MTPFPP and MTPPBr8 shows exactly the same pattern as observed for the simplified systems (MP) (Table 10).
| Porphyrin | Natural charges for methanol in porphyrin complexes. Difference to free methanol in brackets | ||||
|---|---|---|---|---|---|
| H (ΔQ) | O (ΔQ) | C (ΔQ) | CH3 (ΔQ) | Total change | |
| a The LanL2DZ basis set was used on all metals. | |||||
| None | 0.24 | −0.37 | −0.16 | 0.10 | |
| Co(III)P | 0.52 (0.28) | −0.66 (−0.29) | −0.31 (−0.15) | 0.22 (0.12) | −0.04 |
| Co(III)TPPCl | 0.52 (0.28) | −0.66 (−0.29) | −0.31 (−0.15) | 0.22 (0.12) | −0.04 |
| Co(III)TPFPPCl | 0.52 (0.28) | −0.66 (−0.30) | −0.31 (−0.15) | 0.22 (0.12) | −0.04 |
| Co(III)TPPBr8Cl | 0.52 (0.28) | −0.67 (−0.29) | −0.31 (−0.15) | 0.22 (0.12) | −0.04 |
| Mg(II)P | 0.52 (0.28) | −0.78 (−0.41) | −0.31 (−0.15) | 0.22 (0.12) | −0.16 |
| Mg(II)TPP | 0.52 (0.28) | −0.78 (−0.41) | −0.31 (−0.15) | 0.22 (0.12) | −0.16 |
| Mg(II)TPFPP | 0.52 (0.28) | −0.79 (−0.42) | −0.31 (−0.15) | 0.22 (0.12) | −0.16 |
Mg(II)TPPBr8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0.52 (0.28) | −0.80 (−0.43) | −0.31 (−0.15) | 0.22 (0.12) | −0.16 |
| Zn(II)P | 0.51 (0.27) | −0.75 (−0.38) | −0.31 (−0.15) | 0.21 (0.11) | −0.14 |
| Zn(II)TPP | 0.51 (0.27) | −0.75 (−0.38) | −0.31 (−0.15) | 0.21 (0.11) | −0.15 |
| Zn(II)TPFPP | 0.51 (0.27) | −0.76 (−0.39) | −0.31 (−0.15) | 0.22 (0.12) | −0.15 |
| Zn(II)TPPBr8 | 0.52 (0.28) | −0.77 (−0.40) | −0.31 (−0.15) | 0.22 (0.12) | −0.14 |
In Table 11 the data calculated for the simplified MP systems are compared to the experimental results for the corresponding MTPPs. The calculations of free energies of binding ΔG result in a number of false positives, i.e. for (Fe(II), Mn(III) and Ni(II)), for which experimentally no binding to methanol was found. In contrast, the change of charge on the ligand correlates well to the experimental results, with negative values indicating binding and positive values indicating non-binding. From this we conclude that the change in charge on the ligand gives a good indication of whether binding can be expected. As these are relatively easy calculations we suggest this to be a useful tool for evaluation of different ligand–metal complexes before synthesising the compounds.
| Metala | DFT calculations (MP) | Experimental (MTPP) | ||
|---|---|---|---|---|
| ΔG (kJ mol−1) | ΔQ on MeOH | Change in spin state | Binding constant Ka (M−1) | |
| a Only including metals binding in DFT study and also present in experimental study. nb = no binding. | ||||
| Al(III) | −20.4 | −0.14 | 1 → 1 | 3.8 × 10−3 |
| Co(III) | −28.4 | −0.04 | 5 → 1 | 3.2 × 10−3 |
| Fe(II) | −18.9 | 0.05 | 3 → 5 | nb |
| Mg(II) | −48.1 | −0.16 | 1 → 1 | 5.7 × 101 |
| Mn(III) | −10.6 | 0.05 | 5 → 5 | nb |
| Ni(II) | −21.8 | 0.07 | 1 → 3 | nb |
| Zn(II) | −21.3 | −0.14 | 1 → 1 | 2.4 × 10−3 |
In Table 12 the calculated binding energies and charge transfer for the full systems (TPP, TPFPP and TPPBr8) are compared to the experimentally determined binding constant Ka. They show similar results to those obtained for the simplified systems. The change in charge on the methanol ligand seems related to the metal centre rather than the porphyrin as all the Co(III), Mg(II) and Zn(II) porphyrins show almost identical results. When comparing the calculated free energies of binding to the experimentally determined binding constants we obtain a good linear correlation with a R2 = 0.9 (Fig. 13).
| Pophyrin | DFT calculations | Experimental | |
|---|---|---|---|
| ΔG (kJ mol−1) | ΔQ on MeOH | Binding constant Ka (M−1) | |
| Co(III)TPPCl | −26.7 | −0.04 | 3.20 × 10−3 |
| Co(III)TPFPPCl | −43.8 | −0.04 | 5.36 × 101 |
| Mg(II)TPP | −52.2 | −0.16 | 5.65 × 101 |
| Mg(II)TPFPP | −44.8 | −0.16 | 1.54 × 102 |
| Mg(II)TPPBr8 | −71.7 | −0.16 | 1.63 × 102 |
| Zn(II)TPP | −23.3 | −0.15 | 2.40 × 10−3 |
| Zn(II)TPFPP | −31.8 | −0.15 | 1.53 × 101 |
| Zn(II)TPPBr8 | −40.5 | −0.14 | 6.61 × 101 |
When performing calculations on the full systems instead of MP we also gain some additional insights into the relative strengths of the binding constants and the bond lengths (see ESI†), which can be related to chemical shift changes observed in the 1H NMR spectra. For the purpose of predicting if a certain metalloporphyrin will bind to methanol calculations on a simplified MP system are sufficient.
Conclusion
For the purpose of binding to oxygen containing ligands Mg(II)-porphyrins and to a lesser extent Co(III)- and Zn(II)-porphyrins are the prime choice. In particular, the porphyrin derivatives TPFPP and TPPBr8 support binding to various ligands, i.e. MeOH, AcOH, and acetone. The MgTPFPP is the most versatile porphyrin derivative in this study. A weaker binding is observed for ZnTPPBr8. Both the CoTPPCl and the ZnTPFPP bind to all ligands except acetone with reasonable strength. Also worth noting is that unlike most of the other porphyrins the MgTPPBr8 binds stronger to the oxygen containing ligands than to pyridine. This could potentially be very useful for ligand recognition and separation of mixtures. Another interesting porphyrin is the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) TiTPP that only binds to the carboxylic acid but binds with a high binding constant. This could also be used to discriminate between ligands or functional groups on the same ligand.
TiTPP that only binds to the carboxylic acid but binds with a high binding constant. This could also be used to discriminate between ligands or functional groups on the same ligand.
We also investigated the change in chemical shift of bound ligands caused by the porphyrin ring current anisotropy effect. With respect to maximization of this effect the TPFPP porphyrin stands out. The TPPBr8 also gives better results than the TPP. The best choice to get both binding to all tested ligands and a large change in chemical shift is the MgTPFPP metalloporphyrin.
The DFT calculations using B3LYP-D3 show that the metalloporphyrins with both a high free energy of binding and a negative change in charge on the methanol ligand are those that experimentally have been found to bind methanol. Thus we propose to use such calculations as a relatively fast and easy method to predict binding between metalloporphyrins and prospective ligands. The calculations on the full MTPP systems showed correlations to the experimental binding constants and the observed changes in chemical shifts, indicating that they are a good representation of the studied systems. Furthermore, the calculations also indicated that formation of a stable complex cannot be expected if a change to a higher spin state of the metal is required. It would be interesting to confirm this preliminary observation by more extended computations involving further metalloporphyrins.
Experimental
Commercially available compounds were used without purification. meso-Tetraphenylporphyrin (TPP) was purchased from Porphyrin Systems GbR, Germany. Octabromo meso-tetraphenylporphyrin (TPPBr8) was purchased from Frontier Scientific. meso-(Tetrapentafluorophenyl)porphyrin (TPFPP) was purchased from PorphyChem. The free porphyrins were metallated using known methods.21,43–50 Mn(III) meso-tetraphenylporphyrin chloride (Mn(TPP)Cl), Zn(II) meso-(tetrapentafluorophenyl)porphyrin (ZnTPFPP) and Sn(IV) meso-tetraphenylporphyrin dichloride (Sn(TPP)Cl2) were purchased from Porphyrin Systems GbR, Germany. Ni(II) meso-tetraphenylporphyrin (Ni(TPP)) was purchased from Frontier Scientific. Analytical TLC was performed using Merck precoated silica gel 60 F254 plates and for column chromatography Matrex silica gel (60 Å, 35–70 μm) or Merck basic aluminum oxide (60–200 mm) was used.Computational details
The calculations were performed with the B3LYP functional as implemented in the Gaussian 09 program package.28,30 Geometries were optimized using the 6-31G(d,p) basis set for the H-, C-, O-, F-, Cl-atoms and SDD basis set and pseudo potential for all metals.30,31 Frequency calculations were performed at the same level to confirm that a minimum had been reached and to extract free energy corrections which were evaluated at 298.15 K. The energies were also corrected for dispersion effects according to the B3LYP-D3 method by Grimme.32 When optimizing the geometries of the MTPP and MTPFPP structures different rotations of the phenyl rings where used as starting points in order to find the most stable geometry.As metals can adopt several different spin states the three lowest spin states were investigated for each species.35 For species with an even number of electrons the states with total spin S = 0, 1, 2 (M = 1, 3, 5) were calculated and species with an odd number of electrons the states with total spin S = 1/2, 3/2, 5/2 (M = 2, 4, 6) were calculated. A stability analysis was performed to ensure that a stable wave-function was attained for all species. As the goal of the computational study was to compare the most stable free metalloporphyrin and methanol-metalloporphyrin complex, the states which did not converge after repeated tries were deemed unstable and not relevant to this study.
Natural charges were calculated with Natural Population Analysis (NPA) using Natural Bond Orbital analysis (NBO) version 3 with the B3LYP functional and the 6-31G(d,p) basis set for the H-, C-, O-, F-, Cl-atoms and SDD basis set and pseudo potential for all metals.36 For the MgPBr8 and MgTPPBr8 the LanL2DZ basis set was used for all metals.37,38
UV-Vis spectra were recorded on a Varian Cary 3 Bio spectrophotometer using 5 mm quartz cuvettes.
1H and 13C NMR spectra were recorded on Varian Mercury Plus (1H at 300.03 MHz, 13C at 75.45 MHz), Agilent 400-MR DD2 (1H at 399.98 MHz, 13C at 100.58 MHz), or Varian Unity Inova (1H at 499.94 MHz, 13C at 125.7 MHz) spectrometers at 25 °C unless noted otherwise. Chemical shifts are reported referenced to tetramethylsilane via the residual solvent signal (CDCl3, 1H at 7.26 and 13C at 77 ppm).
Mass spectra were recorded on a Voyager-DE PRO MALDI-TOF spectrometer in positive or negative ion-mode without matrix.
For NMR titrations, aliquots of freshly prepared ligand solutions (CDCl3, AlOx-filtered, dried over 3 Å molecular sieves) were added to a solution of the porphyrin in an NMR tube. All NMR spectra were recorded on a 500 MHz spectrometer with d1 = 5 s and nt = 32. The precise host/ligand ratios were calculated from the integrals at the estimated 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Most ligands were titrated to [G]/[H] = 9 unless the titration curve had already levelled out or the ligand showed no binding at all (Fig. 1).
1 ratio. Most ligands were titrated to [G]/[H] = 9 unless the titration curve had already levelled out or the ligand showed no binding at all (Fig. 1).
The binding constants (Ka) for the complexes were determined by NMR titration utilizing the iterative fitting program published by P. Thordarsson25 in Matlab R2012b. Both 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexation models were tested. Ka is calculated by (eqn (3) and (4)). The standard error (SEy) is estimated by (eqn (6)).
2 complexation models were tested. Ka is calculated by (eqn (3) and (4)). The standard error (SEy) is estimated by (eqn (6)).
 | (6) |
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Professor Helena Grennberg for valuable insights into porphyrin synthesis and purification. Financial support by the Swedish Research Council (grant nr. 621-2012-3379) and by the Carl Tryggers Foundation (CTS 16:156) is gratefully acknowledged. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at National Supercomputer Centre (NSC), Linköping University.References
- R. J. P. Williams, The properties of metalloporphyrins, Chem. Rev., 1956, 56, 299–328 CrossRef.
- C. H. Devillers, A. K. D. Dimé, H. Cattey and D. Lucas, Crystallographic, spectroscopic and electrochemical characterization of pyridine adducts of magnesium(II) and zinc(II) porphine complexes, C. R. Chim., 2013, 16, 540–549 CrossRef.
- X. Huang and J. T. Groves, Oxygen Activation and Radical Transformations in Heme Proteins and Metalloporphyrins, Chem. Rev., 2018, 118, 2491–2553 CrossRef PubMed.
- I. Beletskaya, V. S. Tyurin, A. Y. Tsivadze, R. Guilard and C. Stern, Supramolecular Chemistry of Metalloporphyrins, Chem. Rev., 2009, 109, 1659–1713 CrossRef PubMed.
- X. Huang and J. T. Groves, Oxygen Activation and Radical Transformations in Heme Proteins and Metalloporphyrins, Chem. Rev., 2018, 118, 2491–2553 CrossRef PubMed.
- M. Jurow, A. E. Schuckman, J. D. Batteas and C. M. Drain, Porphyrins as molecular electronic components of functional devices, Coord. Chem. Rev., 2010, 254, 2297–2310 CrossRef PubMed.
- L. P. Cook, G. Brewer and W. Wong-Ng, Structural Aspects of Porphyrins for Functional Materials Applications, Crystals, 2017, 7, 223 CrossRef.
- H. Huang, W. Song, J. Rieffeland; and J. F. Lovell, Emerging applications of porphyrins in photomedicine, Front. Phys., 2015, 3, 23 Search PubMed.
- A. G. Petrovic, G. Vantomme, Y. Negrón-Abril, E. Lubian, G. Saielli, I. Menegazzo, R. Cordero, G. Proni, K. Nakanishi, T. Carofiglio and N. Berova, Bulky Melamine-Based Zn-Porphyrin Tweezer as a CD Probe of Molecular Chirality, Chirality, 2011, 23, 808–819 CrossRef PubMed.
- X. Huang, N. Fujioka, G. Pescitelli, F. E. Koehn, R. T. Williamson, K. Nakanishi and N. Berova, Absolute Configurational Assignments of Secondary Amines by CD-Sensitive Dimeric Zinc Porphyrin Host, J. Am. Chem. Soc., 2002, 124, 10320–10335 CrossRef PubMed.
- (a) A. Dhamija, B. Saha and S. P. Rath, Metal-Center-Driven Supramolecular Chirogenesis in Tweezer Amino Alcohol Complexes: Structural, Spectroscopic, and Theoretical Investigations, Inorg. Chem., 2017, 56, 15203–15215 CrossRef PubMed; (b) S. Brahma, S. A. Ikbal and S. P. Rath, Synthesis, Structure, and Properties of a Series of Chiral Tweezer-Diamine Complexes Consisting of an Achiral Zinc(II) Bisporphyrin Host and Chiral Diamine Guest: Induction and Rationalization of Supramolecular Chirality, Inorg. Chem., 2014, 53, 49–62 CrossRef PubMed; (c) S. Brahma, S. A. Ikbal, A. Dhamija and S. P. Rath, Highly Enhanced Bisignate Circular Dichroism of Ferrocene-Bridged Zn(II) Bisporphyrin Tweezer with Extended Chiral Substrates due to Well-Matched Host-Guest System, Inorg. Chem., 2014, 53, 2381–2395 CrossRef PubMed.
- S. Norrehed, P. Polavarapu, W. Yang, A. Gogoll and H. Grennberg, Conformational Restriction of Flexible Molecules in Solution by a Semirigid Bis-Porphyrin Molecular Tweezer, Tetrahedron, 2013, 69, 7131–7138 CrossRef.
- M. Blom, S. Norrehed, C.-H. Andersson, H. Huang, M. E. Light, J. Bergquist, H. Grennberg and A. Gogoll, Synthesis and Properties of Bis-Porphyrin Molecular Tweezers: Effects of Spacer Flexibility on Binding and Supramolecular Chirogenesis, Molecules, 2016, 21, 16, DOI:10.3390/molecules21010016.
- S. Norrehed, H. Johansson, H. Grennberg and A. Gogoll, Improved Stereochemical Analysis of Conformationally Flexible Diamines by Binding to a Bisporphyrin Molecular Clip, Chem. – Eur. J., 2013, 19, 14631–14638 CrossRef PubMed.
- (a) D. Dolphin, T. G. Traylor and L. Y. Xie, Polyhaloporphyrins: Unusual Ligands for Metals and Metal-Catalyzed Oxidations, Acc. Chem. Res., 1997, 30, 251–259 CrossRef; (b) E. K. Woller and S. G. DiMagno, 2,3,7,8,12,13,17,18-Octafluoro-5,10,15,20-tetraarylporphyrins and Their Zinc Complexes: First Spectroscopic, Electrochemical, and Structural Characterization of a Perfluorinated Tetraarylmetalloporphyrin, J. Org. Chem., 1997, 62, 1588–1593 CrossRef; (c) X. Li, M. Tanasova, C. Vasileiou and B. Borhan, Fluorinated Porphyrin Tweezer: A Powerful Reporter of Absolute Configuration for erythro and threo Diols, Amino Alcohols, and Diamines, J. Am. Chem. Soc., 2008, 130, 1885–1893 CrossRef PubMed.
- K. Ermanis, K. E. B. Parkes, T. Agback and J. M. Goodman, Doubling the Power of DP4 for Computational Structure Elucidation, Org. Biomol. Chem., 2017, 15, 8998–9007 RSC.
- X. Li, C. E. Burrell, R. J. Staples and B. Borhan, Absolute Configuration for 1,n-Glycols: A Nonempirical Approach to Long-Range Stereochemical Determination, J. Am. Chem. Soc., 2012, 134, 9026–9029 CrossRef PubMed.
- G. P. Dechaine, Y. Maham, X. Tan and M. R. Gray, Regular solution theories are not appropriate for model compounds for petroleum asphaltenes, Energy Fuels, 2011, 25, 737–746 CrossRef.
- K. P. Kepp, A Quantitative Scale of Oxophilicity and Thiophilicity, Inorg. Chem., 2016, 55, 9461–9470 CrossRef PubMed.
- O. I. Koifman and T. A. Ageeva, Metalloporphyrins in macromolecular chemistry, Russ. Chem. Bull., Int. Ed., 2015, 64, 2001–2011 CrossRef.
- J. S. Lindsey and J. N. Woodford, A Simple Method for Preparing Magnesium Porphyrins, Inorg. Chem., 1995, 34, 1063–1069 CrossRef.
- K. M. Kadish and L. A. Bottomley, Substituent effects on the formation constants of iron(III) and iron(II) tetraphenylporphyrin-pyridine complexes, J. Am. Chem. Soc., 1977, 99, 2380–2382 CrossRef PubMed.
- E. V. Goldammer, Interactions of some nitrogenous bases with low-spin ferriporphyrins, J. Mol. Struct., 1980, 60, 127–130 CrossRef.
- V. P. Andreev, P. S. Sobolev and V. A. Tafeenko, Coordination of Zinc Tetraphenylporphyrin with Pyridine Derivatives in Chloroform Solution and in the Solid Phase, Russ. J. Gen. Chem., 2017, 87, 1070–3632 Search PubMed.
- P. Thordarsson, Determining association constants from titration experiments in supramolecular chemistry, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- M. Sankaralingam, Y.-M. Lee, S. Hyun Jeon, M. Sook Seo, K.-B. Cho and W. Nam, A mononuclear manganese(III)–hydroperoxo complex: synthesis by activating dioxygen and reactivity in electrophilic and nucleophilic reactions, Chem. Commun., 2018, 54, 1209–1212 RSC.
- T. K. Chandrashekar and V. Krishnan, Coordinative Interaction of Morpholine With Divalent Metallo Tetraphenyl Porphyrins, J. Inorg. Nucl. Chem., 1981, 43, 328–3290 CrossRef.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- P. C. Hariharan and J. A. Pople, The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Energy-Adjusted ab Initio Pseudopotentials for the Second and Third Row Transition Elements, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef PubMed.
- W. Wei, F.-Q. Bai, B.-H. Xia, J. Wang and H.-X. Zhang, A density functional theory investigation of the stability, aromaticity, and photophysical behavior for the highly conjugated macrocycles containing 4 pyrroles, J. Phys. Org. Chem., 2017, 30, e3617 CrossRef.
- Z. Cao, Q. Chen, Y. Lu, H. Liu and Y. Hu, Density functional theory study on the interaction between metalloporphyrins and NH3, Int. J. Quantum Chem., 2013, 113, 1137–1146 CrossRef.
- A. Ghosh, Transition metal spin state energetics and noninnocent systems: Challenges for DFT in the bioinorganic arena, J. Biol. Inorg. Chem., 2006, 11, 712–724 CrossRef PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, Natural-population analysis, J. Chem. Phys., 1985, 83, 735–746 CrossRef.
- T. H. Dunning Jr. and P. J. Hay, in Modern Theoretical Chemistry, ed. H. F. Schaefer III, Plenum, New York, 1977, vol. 3, pp. 1–28 Search PubMed.
- P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations – potentials for the transition-metal atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef.
- S. Cho, Y. Lee, H. S. Han, H. K. Lee and S. Jeon, Characteristic electronic perturbation by asymmetric arrangements of p -aminophenyl substituents in free-base porphyrins, J. Phys. Chem. A, 2014, 118, 4995–5001 CrossRef PubMed.
- G. A. Spyroulias, A. Despotopoulos, C. P. Raptopoulou, A. Terzis and A. G. Coutsolelos, First X-ray crystal structure of a lanthanide(III) monoporphyrinic complex using non-planar porphyrin rings, Chem. Commun., 1997, 783–784 RSC.
- C. C. de Melo, W. da, C. Moreira, T. J. Martins, M. R. Cordeiro, J. Ellena, F. F. Guimarães and F. T. Martins, Saddle-shaped macrocycle distortion and symmetry decrease in cobalt(II) meso-tetraphenylporphyrin: Structure of a dichloromethane solvate and DFT calculations, J. Mol. Struct., 2014, 1076, 468–474 CrossRef.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Insights into current limitations of density functional theory, Science, 2008, 321(5890), 792–794 CrossRef PubMed.
- P. Chen, M. H. Chisholm, J. C. Gallucci, X. Zhang and Z. Zhou, Binding of Propylene Oxide to Porphyrin- and Salen-M(III) Cations, Where M=Al, Ga, Cr, and Co, Inorg. Chem., 2005, 44, 2588–2595 CrossRef PubMed.
- C. E. Anderson, S. I. Vagin, W. Xia, H. Jin and B. Rieger, Cobaltoporphyrin-Catalyzed CO2/Epoxide Copolymerization: Selectivity Control by Molecular Design, Macromolecules, 2012, 45, 6840–6849 CrossRef.
- Y. Qin, X. Wang, S. Zhang, X. Zhao and F. Wang, Fixation of Carbon Dioxide into Aliphatic Polycarbonate, Cobalt Porphyrin Catalyzed Regio-Specific Poly(propylene carbonate) with High Molecular Weight, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 5959–5967 CrossRef.
- D. F. O'Shea, M. A. Miller, H. Matsueda and J. S. Lindsey, Investigation of the Scope of Heterogeneous and Homogeneous Procedures for Preparing Magnesium Chelates of Porphyrins, Hydroporphyrins, and Phthalocyanines, Inorg. Chem., 1996, 35, 7325–7338 CrossRef.
- V. F. Slagt, P. W. N. M. van Leeuwen and J. N. H. Reek, Supramolecular bidentate phosphorus ligands based on bis-zinc(II) and bis-tin(IV) porphyrin building blocks, Dalton Trans., 2007, 2302–2310 RSC.
- A. M. Stolzenberg and G. S. Haymond, Activation Barriers to meso-Aryl Group Rotation in Titanyl Tetraaryltetrapyrroles. An Investigation of the Out-of-Plane Flexibility of Hydroporphyrins, Inorg. Chem., 2002, 41, 300–308 CrossRef PubMed.
- S. A. Vail, D. I. Schuster, D. M. Guldi, M. Isosomppi, N. Tkachenko, H. Lemmetyinen, A. Palkar, L. Echegoyen, X. Chen and J. Z. H. Zhang, Energy and Electron Transfer in β-Alkynyl-Linked Porphyrin-[60]Fullerene Dyads, J. Phys. Chem. B, 2006, 110, 14155–14166 CrossRef PubMed.
- R. Wang, Z. Hailin, B. Gao, R. Wang, Á. H. Zhu and Á. B. Gao, The catalytic activity of poly(N-vinylimidazole)/SiO 2 -supported metalloporphyrins in ethyl benzene oxidation, React. Kinet., Mech. Catal., 2011, 103, 431–441 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8dt02432d |
| This journal is © The Royal Society of Chemistry 2018 |